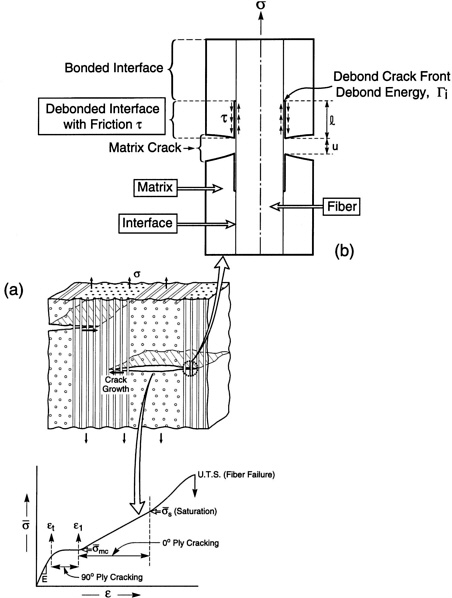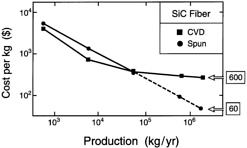
FIGURE 6 The effect of production volume on the manufacturing cost for two types of SiC fiber. The dashed region for the polymer-derived fiber assumes a reduction in the price of the organic precursors, below present prices, as the production volume becomes large.
throughput. Moreover, most manufacturing operations involve multiple steps. Those steps that dominate the cost need to be identified and addressed through process understanding and by the use of process models. While such models are incompletely developed and not broadly available, some general conclusions can still be reached.
Small-volume production is an overriding nontechnical factor that can be rectified only by either diversifying the range of products or by writing off the development costs. Technical factors arise from the important contributions to the costs originating with long cycle times for the high-temperature steps in the production, expensive chemicals and powders, and high capital costs. These can be systematically addressed through combinations of modeling, process optimization, lower-cost ingredients, and the matching of capital costs to product volumes.
For composites the costs of the fibers and the fiber coatings often dominate [35] (Figure 6). One clear implication is that fiber reinforcement should be used judiciously and selectively. That is, composite regions should be embedded in monolithic material through a complete redesign, wherein the benefits provided by the fibers are introduced only in critical regions. This strategy has been used with TMCs for struts, fan blades, and so forth, with the TMC emplaced selectively within an otherwise cast Ti alloy product [36]. Here the TMC is used to enhance the overall bending stiffness. This extra stiffness enables a weight reduction. Then the performance advantages of the TMC/Ti system are in balance with the manufacturing costs.
Comparable strategies are less tractable with CMCs and PMCs, because of design problems with the surrounding monolithic material. Hence, for these materials, manufacturing strategies focus on low-cost methods for introducing the fiber coatings and the matrix in order to minimize the overall cost (beyond that for the woven fiber preform) [37]. Transfer molding and its derivatives are preferred, because of the diminished number of processing steps, with a consequent reduction in overall cycle time and labor costs. Processes with inherently long cycle times (such as CMC production by chemical vapor infiltration) are disadvantaged.
PROPERTY PROFILES
Ultimate Tensile Strength
Key issues associated with the UTS are its scale dependence and its statistical variability. All materials subject to stress-controlled fracture are susceptible to such effects. They arise from weakestlink considerations. Such scale dependence is frequently associated with an extreme value distribution
[27,28]. These factors present important design challenges. Monolithic brittle materials subject to small-scale toughening are particularly challenging, because it is imperative that the scaling behavior be well calibrated, as well as manufacturing invariant [15]. The associated costs are often prohibitive. By introducing inelastic mechanisms that stabilize damage, through plasticity, internal friction, and so forth, progressive reduction in the scale sensitivity can be achieved. Eventually, as the inelastic mechanisms are made more effective and the number density of active inelastic strain sites is increased, macroscopic inelastic strain can be induced prior to the UTS [8,38,39]. Such deformations profoundly change the design philosophy. With sufficient inelastic deformation, the scale dependence is virtually eliminated, the UTS distribution is essentially Gaussian, and design strategies used for metals can be applied.
When size scaling of the UTS obtains, it is vividly manifest upon testing specimens that have vastly different stressed volumes, for example, tension relative to bending [27]. The goal of the testing is to characterize the population of defects that control the strength, S (Figure 7a). This population can be represented by a frequency distribution, designated g(S) dS [28], the fraction of defects per unit volume (or per unit surface area for surface flaws) that cause failure when the stresses are between S and S + dS. Then, the survival probability of a small-volume element, ∆V, subject to uniaxial stress σ is [28]
where δϕ is the failure probability. This relates to the overall failure probability Ф through [27,28],
where N is the number of volume elements in the component and Π refers to the product over all elements. G(S) for each flaw population can be fit by a power law,
where m is the shape parameter, So the scale parameter, and Su the offset parameter. However, the strength is affected by more than one defect population, and G(S) is not normally single-valued. That is, different m, So, and Su are needed to represent the defect populations over the full stress range relevant to specimen testing and design. This presents stringent testing requirements for the acquisition of accurate design data.
When inelastic deformation mechanisms operate around the defects, G(S) can be dramatically modified. These mechanisms include plastic yielding and internal friction. The most comprehensive illustration is for fiber-reinforced composites that exhibit large-scale debonding and friction, such as CMCs and TMCs. These mechanisms “blunt” and stabilize the damage emanating from failed fibers, by redistributing stresses in the surrounding material, thereby reducing the stress concentrations in the nearest fibers [40-42]. The consequence is that multiple fiber failures can occur before the UTS is reached [43], often allowing other inelastic mechanisms to be activated in the matrix. The stabilization
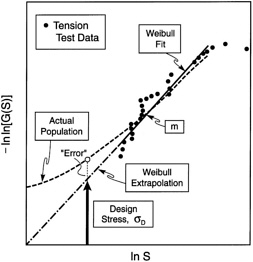
FIGURE 7a The cumulative flaw strength distribution estimated by using tension test data. The data and the region of extrapolation are indicated. The Weibull fit does not represent the actual flaw population in this case, resulting in an overestimate of the strength in that part of the population relevant to the design. SOURCE: Reprinted (modified) from Evans (1997) [26], copyright 1997, with permission from Elsevier Science.
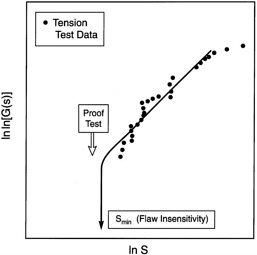
FIGURE 7b Truncation of the strength at a minimum achieved either by proof testing or by developing inelastic mechanisms in the material that provide stress redistribution with an attendant insensitivity to large manufacturing flaws.
efficiency increases as the interface debond and friction stresses decrease [42-45]. A practical measure of the efficacy of these mechanisms is the width of the unload/reload hysteresis loops measured upon tensile testing [46-48]: wide loops correspond with small friction and debond stresses (Figure 8). As these mechanisms come into operation, there is a markedly diminished scale dependence of the UTS.
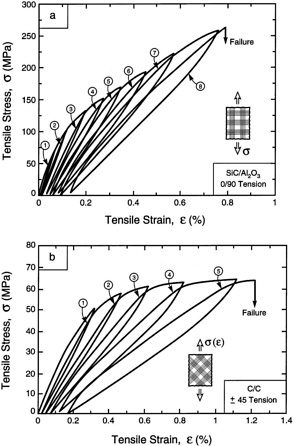
FIGURE 8 Hysteresis loops measured on the tensile testing of CMCs: (a) 0/90, (b) ±45. SOURCE: Reprinted from Evans (1997) [26], copyright 1997, with permission from Elsevier Science.
Friction at the interfaces dictates the dimension over which stress concentrations around failed fibers are eliminated. This dimension becomes an internal scale parameter, which allows fiber failures to occur in a spatially uncorrelated manner. When this happens, global load sharing (GLS) ensues with an associated UTS given by
where
and
with Lo being a reference gauge length (normally 25 mm), τ the friction stress, R the fiber radius, f the fiber volume fraction, and Sg the tensile strength at length Lo. The first term is that contributed by the fibers. The second is provided by the matrix. For TMCs, σo is the matrix yield strength. For CMCs, σo ≈ 0, because of multiple matrix cracking. The main features described by this result are as follows: (i) The UTS is affected by friction. (ii) There is a weak dependence on the shape parameter, m, characterizing the individual fiber strengths. (iii) There is a strong effect of the mean reinforcement strength, Sg.
Usually, low friction is not sufficient to realize GLS conditions. Concentrated stresses persist upon fiber failure, resulting in local load sharing (LLS) [49,50]. The ensuing UTS decreases below that given by (6) and becomes scale-dependent. But the effects are not especially deleterious. In practice, the UTS scales in accordance with (3) to (5), subject to a large effective shape parameter, m* [49]. More importantly, the behavior is insensitive to the occurrence of large manufacturing flaws, because of the existence of a robust strength minimum, Smin (see Figure 7b). This attribute is understood upon examining the stress concentrations induced by large flaws. Two effects are involved: (i) One is associated with large-scale fiber bridging (LSB), governed by the index [50]
where a is the size of the flaw, E is Young's modulus, A is an anisotropy coefficient of order unity, with the subscripts f and m referring to the fibers and matrix, respectively. Based on this index, the strength contributed by the fibers through LSB is [50,51]
Note that when τ is small, η→ 0 and the flaws have no effect on the strength. (ii) The second effect is related to the notch performance enabled by large-scale inelastic strains [4,6,8,9]. These dominate at larger τ. Such strains diminish the stress concentrations around the manufacturing flaws, leading to tensile behavior independent of the flaw size, analogous to the notch insensitivity.
Inelastic Strain and Ductility
When the number density and the potency of the inelastic deformation sites increase, macroscopic inelasticity initiates at stresses below the UTS. This typically causes a marked increase in the failure strain, or ductility. The inelastic strain now allows stress redistribution. An illustration for a mechanical attachment to a CMC is presented in Figure 9 , along with an experimental validation, obtained using Moire interferometry [5,9]. The key feature is that the stress concentration factor around the hole diminishes upon increasing the load, as an inelastic zone develops. This diminished stress concentration combines with an elevation in the local UTS arising from volume scaling [50,52]. The overall effect is a component performance unaffected by the presence of the hole. These characteristics originate with the inelastic strain mechanisms, manifest in the stress-strain curves.
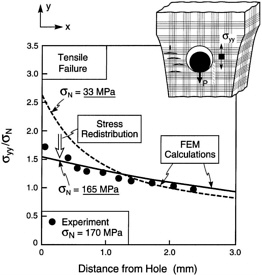
FIGURE 9 Stress redistribution effects around a pin-loaded hole. The experimental results have been obtained by Moire interferometry. The constitutive law used for the FEM calculations is based on (12). Note that the stress concentration factor decreases as the net section stress, σN, increases. SOURCE: Reprinted from Evans (1997) [26], copyright 1997, with permission from Elsevier Science.
Brittle Matrix Composites
For CMCs, multiple matrix cracking with interface debonding and friction enable appreciable inelastic strain in tension and shear [8] (see Figure 8). Two cell models represent most of the important physical relationships between the inelastic strains and the mechanisms of matrix cracking, friction, and debonding. One model applies to cracks that first form on the 90° plies (Figure 10) [53,54]. The other represents cracks that penetrate the 0° plies (see Figure 10) [40]. Cracks in the 90° plies tunnel with an associated inelastic strain (see Figure 10a). Upon subsequent loading, as the cracks penetrate the 0° plies, they interact with the fibers and the coatings. When debonding and slip occur within the coating, two stresses characterize the inelastic strain: a friction stress τ and a debond stress σi (see Figure 10b). The latter is related to the debond toughness for the coating and the residual stress [40]. The consequent inelastic tensile strain ε depends on the stress σ acting on the 0° plies. It has linear and parabolic terms, given by
where ∑i is the non-dimensional debond stress, (∑i = σi/σ), E* is the diminished elastic modulus caused by matrix cracking, σT is the residual stress (∑T = σT/σ), and L is an interface friction index, given by
with d being the crack spacing. The parameters, E*, L, and ∑i, evaluated from hysteresis loops (see Figure 8), provide understanding about the separate influences of debonding, friction, and matrix cracking on the inelastic strain [55]. They also provide the insight needed to develop a constitutive law compatible with finite element codes [9,56]. Simulations, as well as hysteresis measurements, have established the influence of friction and debonding on the stress-strain behavior of CMCs [55-57]. The principal effects associated with (10) are as follows. The inelastic strain and the hysteresis loop width increase as the friction stress τ decreases (or L increases). Small τ accounts for the wide hysteresis loops in SiC/CAS [55]. A large debond stress σi limits the role of friction and diminishes both the inelastic strain and hysteresis. Large σi accounts for the narrow hysteresis loops in SiC/SiC and SiC/ MAS [55]. These insights have led to the formulation of a constitutive law [9,56]. The plane stress relation for the stresses and strains in directions (1,2) obtained by expressing the inelasticity through the stress drops that occur upon matrix cracking is
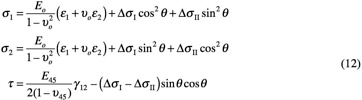
where τ is now the macroscopic shear stress, ε1,2 the normal strains, and γ12 the shear strain. ∆σI,II are the stress drops upon matrix cracking at fixed strain, parallel and normal to the fiber directions, and θ is the angle between (1) and the fiber direction. This constitutive law has been used to calculate the results presented in Figure 9 , which vividly illustrate the role of ductility in design.
Ductile Matrix Composites
The stress-strain response of unidirectional TMCs is quite different (see Figure 4). These materials are anisotropic [17]. They are almost linear in longitudinal tension but exhibit some ductility in transverse tension and shear, controlled by matrix yielding and plastic hole coalescence. This anisotropy causes problems in longitudinal performance, in addition to the issues that arise upon transverse loading, elaborated below.
Implementation of a constitutive law to calculate stress concentrations at holes and slots [17] (Figure 11) indicates that the stresses in axially loaded configurations are unaffected by the plastic deformation [58-60]. That is, elastic stress concentrations are retained and even exacerbated by anisotropy, despite the extensive plastic zone in the matrix. This behavior is typical of that found for anisotropic materials that respond linearly in one direction, as previously elaborated for layered materials and coatings [42,59,60]. This effect accounts for the relative notch sensitivity found for TMCs, differing dramatically from that for metals in which isotropic plastic deformation greatly diminishes stress concentrations.
But the extreme notch sensitivity that might be expected from the stress concentrations is ameliorated in TMCs by inelasticity arising after localization by fiber bundle failure. The effect is depicted in Figure 11 . When the fiber bundle at the notch front attains the UTS, it fails but transfers the load to the intact matrix. This causes the matrix to yield in a band contiguous with the notch. This plastic band acts
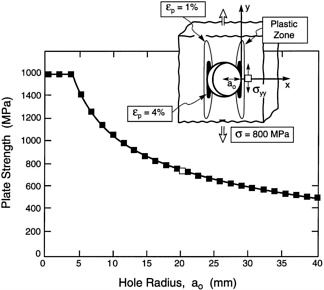
FIGURE 11 Stress concentrations around holes in unidirectional TMCs calculated using the constitutive law obtained from Figure 4 . Also shown are the post-localization effects that enable bridging by the intact matrix that leads to the notch insensitivity found at larger notch sizes.
as a bridging zone subject to tractions that provide the extra toughness needed to prevent unstable fracture. Composite failure occurs only when the matrix in the plastic band stretches to its rapture strain. This constitutes a large-scale bridging (LSB) phenomenon, which can be analyzed using standard LSB mechanics [19-21]. The results for TMCs are indicated in Figure 5 [23]. That is, notch degradation is ameliorated at larger notch sizes. But there is still a strong sensitivity of TMC performance to small notches. This problem can be obviated in design, but re-emerges as an issue in fatigue, through its effect on the fatigue threshold.
Transverse Properties
Low transverse strengths constrain designs and limit application. An understanding of the transverse responses is essential to effective implementation. These properties are dominated by the matrix and the interfaces. They have monolith counterparts. Cracking and delamination occur in CMCs [8,31]. Yielding and plastic straining obtain in TMCs [17]. But in both cases the fibers and the interfaces require that new factors be addressed.
For TMCs there are two principal factors. (i) The interface has minimal tensile strength, such that debonding occurs when the transverse stress exceeds the residual compression induced by thermal expansion mismatch [17,61,63]. At this “elastic limit,” σe, there is a reduction in the transverse modulus to about half its initial value [17,61]. (ii) At larger strains, matrix yielding occurs, but the hydrostatic tensions in the matrix induced by the fibers are an appreciable fraction of the matrix yield strength, despite interface debonding. This stress state accentuates plastic hole growth and leads to low transverse ductility (relative to monoliths having the same composition and microstructure) [17]. The elastic