Preserving Strength While Meeting Challenges: Summary Report of a Workshop on Actions for the Mathematical Sciences (1997)

Michael S. Waterman

Department of Mathematics, Department of Biological Sciences, and Department of Computer Science University of Southern California

The second half of the twentieth century has been a time of great scientific progress in biology, starting with the discovery of the double helix by Watson and Crick in 1953. Dramatic breakthroughs are reported in newspapers and popular magazines as well as in the scientific literature. Despite the heady times biology has been experiencing, these are early days: the next century is likely to be a golden age of biology, when scientists will build on the fundamental progress made recently. In this short paper I will sketch some of the areas in molecular biology where mathematics and theoretical computer science have had genuine application. (By genuine I mean that the application has actually mattered to scientific progress.) Fortunately, the Board on Mathematical Sciences recently sponsored a project that resulted in a book published by the National Academy Press, Calculating the Secrets of Life (NRC, 1995), that treats these topics, the subtitle being Applications of the Mathematical Sciences in Molecular Biology. Therefore anyone wishing more complete treatments can start with that book (which is not too expensive either!). In addition, I have written a textbook, Introduction to Computational Biology (Waterman, 1995), at the beginning graduate level, which allows a person to systematically learn about a subset of the topics in substantially more detail.

This paper is organized as follows. The Human Genome Project (HGP) is described. This project has attracted many new workers to biology. Then short descriptions are given of several areas where mathematical sciences have had application: genetic mapping, physical mapping, DNA sequencing, DNA and protein sequence comparisons, and evolutionary biology. Other very important topics are not covered due to time, space, and the limitations of the author; they include determination of protein structure, and the topology and geometry of DNA and protein structure.

The genome of an organism is all of the DNA in the chromosomes of the organism. The genome contains the DNA of the genes and much DNA that is not genes. The human genome of 3 × 10⁹ letters of DNA uses less than 1 percent of that DNA for its genes. The use—if any—of much of the remainder is unknown. As the DNA is a blueprint encoding an organism, knowing the genetic text is very valuable in the larger context of learning the biology of an organism. DNA is ''written" in an alphabet of four letters, A, T, G, and C, which are symbols for the nucleotides or bases in the linear chain that makes up one strand of the macromolecule. There is

another complementary strand, where A base-pairs with T, and G base-pairs with C. The strands have a chemically defined direction, so that the strands of the double helix are complementary and have opposite polarities. This is the key to molecular genetics; the double-stranded DNA separates into single strands, and each strand is then used to template a new double-stranded molecule. Protein molecules are themselves linear macromolecules that are written in the alphabet of 20 amino acids. Genes then encode proteins using the genetic code, a mapping from triplets of bases to the 20 amino acids (including three triplets that spell "stop").

In 1985 scientists began to discuss sequencing (reading the DNA) of the entire human genome. This was a huge leap from then-current technology. Only about 7 million letters were in the international databases; even if that was only half the then-sequenced DNA, it was a small fraction of the 3 billion letters of the human genome. And sequence length was daunting: a few sequences in the 50,000-letter range had been determined, but they were regarded as extraordinary feats. Reading a 15,000-letter sequence was more within the range of mortals. Even if chromosomes could be isolated, the 3 × 10⁹ length would be reduced by only one order of magnitude. The first discussions were about creating a mega-project, where biology would be done in a factory. By the time the project had its official start in 1990, there was a big-science flavor to the project but the work was very distributed, involving many laboratories. The U.S. agencies funding the HGP are the National Institutes of Health and the Department of Energy; the project was to take 15 years and cost $3 × 10⁹, a dollar per base. The HGP goals include the efficient and cost-effective development of genetic and physical maps of the human genome, the determination of the complete nucleotide sequence of the human genome, and the development of technology to achieve these goals. In addition, genetic and physical map and sequence information is to be collected for several model organisms such as mouse and yeast.

It was not evident to many that these goals were possible in the proposed time frame. Fortunately, progress in genome research has exceeded the initial guidelines, and a complete human genome sequence is hoped for by 2003. (See the recent review by Guyer and Collins (1995).) Some of the mathematical aspects of this project and of molecular biology are discussed in succeeding sections. GenBank is the U.S. public DNA database. Figure 1 shows GenBank growth since 1984; it is an indication of the explosion of knowledge in the biological sciences.

Human genomes are 99.9% identical; only 1 letter in 1,000 is different. Although any two human genomes are thus very closely related, one genome might encode Albert Einstein while another encodes John Lennon. Genetic variations can also cause cancer in one person and let another live to the age of 120. The differences matter! Genetic mapping uses variations in genomes to approximately locate a gene on a chromosome without knowing its precise identity.

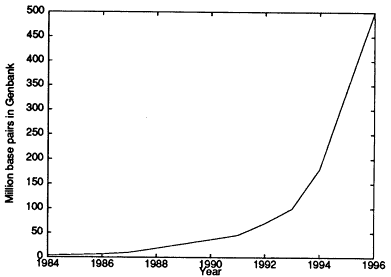
Figure 1.

Growth from 1984 to 1996 of the number of human genome base pairs (in millions) in the GenBank DNA database. Source: National Center for Biotechnology Information, available online at <www.ncbi.nlm.nih.gov> through the release notes at <ncbi.nlm.nih.gov/genbank/gbrel.txt>.

Our model is Mendelian genetics, where each individual has chromosomes in pairs. An offspring gets its chromosomes from its parents, and each parent transmits one of its chromosomes at random. Look at Figure 2, where at two locations (loci) there are genes A and B that have distinct versions on each of the chromosomes, designated by different shades. If this was all that happened, we as a population of organisms would not be so interesting and varied. But according to a random process, the pair of chromosomes cross over, giving novel associations of the regions A and B (see Figure 3). This greatly enriches the variety in the population.

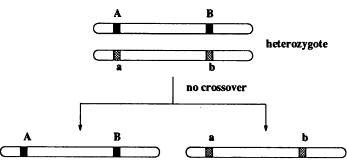
Figure 2.

Inheritance of genes when there is no crossover (mixing) between chromosomes from the two parents.

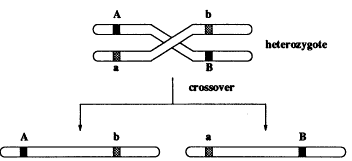
Figure 3.

Inheritance of genes when there is crossover (mixing) between chromosomes from the two parents.

Genetic mapping is founded on the idea that the fraction of times that the dark A and B alleles are together in the offspring can be used to estimate how close the genes A and B are on the chromosome. The first genetic map showed the relative locations of six genes in the fruit fly and was constructed in 1911 by Sturtevant when he was a sophomore at Columbia University. The map was built without knowing that chromosomes and genes were DNA. From one point of view, genetic mapping is a statistical problem.

In 1980 David Botstein started the modern era of genetic mapping with the recognition that naturally occurring variation in DNA can be used for mapping. Until then only genes with changes that resulted in observable differences in offspring could be mapped. Using Botstein's idea, many sites along the genome can be mapped. When a disease gene, for example, is near a mapped DNA location, the geneticist can then learn the approximate location of the disease gene. This requires having a fairly dense set of so-called DNA markers. Genes ranging from those for cystic fibrosis to the so-called fat gene have been mapped, and mapping is part of the discovery process that is so often in the headlines of our newspapers. By 1994 there were 5,826 loci mapped in an international collaboration. This represents a marker for approximately every 700,000 nucleotides along the human genome.

The mathematical issues are statistical as the problem is one of estimation of marker order, and the location of a disease gene is of statistical significance. The ordering is done using a maximum likelihood statistic, and issues of algorithm efficiency are critical in these problems. Details of the affected families and of human genetics must be incorporated in order to have useful results. See the book Analysis of Human Genetic Linkage (Ott, 1991).

Genetic mapping gives locations between markers in units of genetic distance. Genetic distance is not measured in numbers of letters, and although it is obviously valuable to map a gene, what next? Biologists then make physical maps of large regions of DNA, even as large as chromosomes, by constructing overlapping sets of intervals of DNA called clones. DNA in the

clones can be manipulated easily (whereas chromosomes cannot), and they allow for more detailed characterization later such as sequencing.

Here is the most straightforward model. We wish to map the DNA in a genome [0,G]. We can draw N random samples of shorter intervals, of length L. For each length L interval, we can characterize the interval by performing experiments obtaining data that is called a fingerprint. The most detailed fingerprint is the DNA sequence, but usually the fingerprint is much less detailed. Then the fingerprints are examined for commonalities, and when overlapping clones can be identified (Figure 4), those overlaps are information that can be used for map construction. Ideally we can establish all the islands of overlapping clones from the genome.

Figure 4.

Graphical depiction of overlapping clones from a genome [0,G].

With perfect data, this is just an interval graph problem, but with realistic data sets, the problem is NP-hard. Consequently, algorithms for map assembly are an interesting area for the computational biologist.

Another mathematical issue arises here, that of predicting the progress of a mapping experiment. How many clones must be examined before a given fraction of the genome is paved with clones? Here probability and statistics have been applied to study the coverage problem. The statistical results obtained are basic to the design of physical mapping experiments. See Chapter 6 of Waterman (1995).

In 1980 a Nobel prize was given to Gilbert and Sanger for their 1976 inventions of two methods of reading DNA sequences. Today refinements of these methods are routinely used to read a contiguous interval or string of DNA up to 450 base pairs in length. The process of using this ability to read short substrings to determine strings that are 100 to 1,000 times longer is quite involved. First I discuss the so-called shotgun sequencing method. Shotgun sequencing has been employed since the invention of rapid sequencing in 1976 and, although there are many methods that modify this essentially random approach, it is still widely used. For our purposes shotgun sequencing is physical mapping with a one sequence as a fingerprint.

Real DNA sequence assembly has several difficulties that idealized problems do not. There is an issue about whether a clone sequence or its reverse complement has been read. More problematic is the fact that real sequence data comes with errors, in the form of mismatches, and insertions or deletions (indels). Several strategies have been developed for sequence assembly, but all have the following outline: (1) Compute fragment overlap statistics, (2) then make an approximate alignment, and (3) finally make a multiple alignment from the approximate

alignment. This is clearly another problem involving algorithms and statistics. See Chapter 7 of Waterman (1995).

Recently, a new approach to sequencing DNA was proposed, sequencing by hybridization (SBH). This method might also be called sequencing by k-word composition. The idea is to build a two-dimensional grid or matrix of all 4k k-words. At each (i,j) is attached a distinct k-word or probe. This matrix of probes is referred to as a sequencing chip. Then a sample of the single-stranded DNA to be sequenced is presented to the matrix. This DNA is labeled with a radioactive or fluorescent material. Each k-word present in the sample is hybridized with its reverse complement in the matrix. Then, when unhybridized DNA is removed from the matrix, the hybridized k-words can be determined using a device to detect the labeled DNA.

The mathematical problem of determining sequences by SBH goes as follows: given the k-word content of a sequence, what is the sequence? The scientist's first approach was to represent the k-words as vertices of a graph with edges between vertices that shared (k - 1)-word prefixes and suffixes. The problem is to search for tours that visit all vertices. This is an instance of the Hamiltonian path problem, and it is another NP-complete problem. Pavel Pevzner pointed out the connection between SBH chip technology and the Koenigsberg bridge problem, reducing the problem of reading sequences to a very computable Eulerian path problem. Now the (k-1)-words are vertices and the k-words are edges. The length of sequences read by SBH is quite short because values of k that are practical are not much beyond 12 today. In addition the data are not precise 0-1, no-yes values. See Chapter 7 of Waterman (1995). Scientists are at work to overcome these problems.

Molecular biology depends on databases that contain the known sequences. Almost all sequences are entered before or within a month of publication. Rapid entry is important so that biologists can learn the relationship of new sequences with other sequences that have been determined. The Human Genome Project has increased the rate and volume of DNA sequencing. One reason for organizing biological sequences into databases is to learn new biology. Evolution can conserve useful sequence patterns over evolutionary time. When a new sequence has significant similarity with a known sequence, there is a good chance that the biological functions might also be similar. Thus, new and useful biological hypotheses are created by the results of sequence comparison.

For some notation, let a = a₁a₂...a_n and b = b₁b₂...b_m be two sequences of length n and m. An alignment is produced when null elements,—, are inserted into the sequences. The new sequences should both be of the same length L. Now write the two sequences one over the other. With the insertion of —, a = a₁a₂...a_n becomes a* = a₁* a₂*...a_L*, and b = b₁b₂...b_m becomes b* = b₁*b₂*...b_L*. The subsequence of a* or b* of those elements that are not equal to — is the original sequence. The sequence alignment is now

Now take s(a,b) to be a real-valued function for pairs of letters from the alphabet.

The similarity S(a,b) of a and b is defined by

where the maximum is over all alignments.

The computation of the minimum over the exponential number of alignments can be found using dynamic programming in time and space O(nm). This is an appropriate function to compute when two sequences have a common evolutionary ancestor, from which all letters in each sequence have been derived. In modern molecular biology, it is common to find a stretch of sequence that matches well between two otherwise unrelated sequences. This is a more complex algorithm question. First define the objective function, H(a,b).

Define H_i,j to be the maximum similarity of two segments ending at a_i and b_j:

A dynamic programming recursion can be given for H_i,j.

Theorem 1 For the above assumptions, also let s(-,b)= s(a,-) = -δ for all letters a, b. Set H_i,0 = H_0,j = 0 for and . Then

The point of all this is that when H(a,b) is greater than or equal to 0, then the maximum value of H_ij for and is equal to H(a,b).

The last algorithm for H and a number of even more rapid heuristic algorithms are widely used for comparing sequences with databases. Almost any disease-gene discovery has involved running sequence comparison programs to locate the critical relationships from among millions of potential ones. See Chapter 9 of Waterman (1995).

This leads directly to another mathematical question. Since we are making millions of sequence comparisons, how do we locate the statistically significant ones from those that are just the result of the extremes of comparisons of sequences related only randomly? The answer involves some pretty probability and statistics, including use of Poisson approximation via the Chen-Stein method. Statistical methods are critical to the biological discoveries as well as algorithms. See Chapter 11 of Waterman (1995).

It might not be evident to a non-biologist that evolution has already been discussed in this short manuscript. Genetic mapping today is founded on knowledge of Mendelian genetics and on DNA sequence structure. Sequence comparisons find valuable biological information and create useful hypotheses by locating sequence regions that might have common evolutionary history and therefore might have common structure or function. But there are fascinating questions that arise from a close look at sequences and evolution.

DNA is copied by a very accurate process, and if no errors were ever made, there would be no molecular evolution. But of course errors do occur, at a very low rate. Errors that are saved in the population are called mutations. The descendants of the ancestral individual accumulate these mutations and they diverge from the individual over time. By examining DNA sequences from a specific gene or region of the chromosome from different species or different individuals from one species, the evolutionary biologist tries to reconstruct aspects of evolutionary history. Headlines have been made by studies of DNA sequences of human mitochondrial genomes. The mutations have been used to argue for African human origins as well as estimates of the time that humans left Africa. The analyses leading to mitochondrial Adam and Eve are based on a collection of statistical, algorithmic, and heuristic arguments.

A beautiful stochastic process, the coalescent, introduced by John Kingman (1980), arises as an approximation to many models of reproduction in genetic systems. See also Tavaré (1984). The genealogy of a sample of n DNA sequences (which we take to be aligned sequences) from a large population is described in terms of independent exponential random variables T_n, T_n-1, ..., T₂. The length of time to the first common ancestor (at which time there are now n-1 common ancestors) has an exponential distribution with parameter n (n - 1)/2. Two of the individuals are chosen to coalesce, and the process is run again independently with n-1 individuals to find the second coalescent time, until there is only one "individual" left, and we have found the most recent common ancestor. This time in units of N generations, where the effective population size is N, is 2(1-1/n). Many useful and pretty results come from this model and its generalizations, including the Ewen's sampling formula.

A wide collection of problems exist in connection with sorting molecular evolution out. These include more stochastic processes on trees where a mathematically solid model for inserted or deleted letters has not yet been formulated. In addition, trees that "best fit" a collection of molecular sequences are inferred by a variety of methods and theories based on the resulting trees, although usually only heuristic methods have been employed. See Chapter 14 of Waterman (1995).

Guyer, M.S., and F.S. Collins, 1995, "How is the Human Genome Project doing, and what have we learned so far?", Proc. Natl. Acad. Sci. USA 92:10841-10848.

Kingman, J., 1980, Mathematics of Genetic Diversity, Society for Industrial and Applied Mathematics, Philadelphia.

National Research Council (NRC), 1995, Calculating the Secrets of Life: Applications of the Mathematical Sciences in Molecular Biology , Eric S. Lander and Michael S. Waterman, editors, Board on Mathematical Sciences, National Academy Press, Washington D.C.

Ott, J., 1991, Analysis of Human Genetic Linkage, rev. ed., Johns Hopkins University Press, Baltimore.

Tavaré, S., 1984, "Lines of Descent and genealogical processes, and their application in population genetics models," Theor. Popul. Biol . 26:119-164.

Waterman, M.S., 1995, Introduction to Computational Biology, Chapman & Hall, New York.