D
Exploratory Analysis
Paul K. Davis, RAND and the RAND Graduate School
In Chapter 4 of this report, it is argued that most models used to describe phenomena relevant to military operations, training, or acquisition will contain substantial uncertainty. This uncertainty can arise, for example, from a lack of knowledge about the operational circumstances of future battles, the combat processes being described, simplifying assumptions that lead to stochastic components in the model, or human behavioral elements. While such uncertainty is generally intrinsic to such models, all too frequently attempts are made to remove uncertainty from the model, that is, to suppress the issue. For example, stochastic effects are replaced by a notion of their average value. Parameter estimates of highly uncertain variables (e.g., a future war's warning time) are treated as correct. Moreover, if uncertainty is recognized at all, it usually is through conducting sensitivity analyses on a few variables while pretending that other highly uncertain variables are known. While such an approach can often be seriously misleading, it is difficult indeed to treat uncertainty comprehensively. Techniques such as exploratory analysis are just now becoming increasingly available; the difficulties cannot be underestimated, and considerable research on this problem will be needed for years. This should include development of new analytical tools.
Exploratory analysis attempts to seriously confront uncertainty in a given model rather than ignoring or removing it. When uncertainty is involved, however, the parameter space in “soft problems” such as those that arise when considering operational-level planning becomes very large. One possible approach is to run the model over a huge domain of parameter values (input assumptions)—not merely in the manner of common sensitivity analysis, but in ways that examine
much of the outcome space. 1 Of course, there are temporal limitations to this approach—even more so if some of the parameters are stochastic, requiring repeated runs to establish a distribution of results. Even without stochastic effects, problem dimensionality can explode as one acknowledges additional uncertainty. As a result, it becomes necessary to adopt a highly structured approach. For example, the field of statistical design of experiments with tools such as fractional factorial or Latin hypercube designs can substantially reduce the number of trials needed to identify important variables, significant combinations of variables, and the optimal combination of variables. 2
These design techniques are widely used in industrial applications (albeit applications with fewer uncertain variables than often occur in military problems) where the purpose is to determine the best combination of variables to optimize an industrial process. Generally, a fractional factorial design identifies a relatively small number of experiments to be run of a highly structured sort. Once the results from these runs have been obtained, some variables are identified as being important, and a new set of runs is determined. This process continues as long as time and resources permit. At the end, one obtains reliable information on the most significant variables or combinations of variables and their influence on the outcome. As computing power increases, the size and complexity of problems that can be explored in the fashion will also increase. Thus, statistical design of experiments holds the promise of being an approach to cope with uncertainties in complex models. Much progress has been made (Bos, et al., 1978; Davis, 1994), but much more work needs to be done to tailor these methods to problems of military relevance. 3
This approach represents a sharp departure from the long-standing legacy of using allegedly representative “point scenarios” and altogether ignoring major uncertainties (e.g., regarding the fighting capability, for constant equipment, of different nations' forces, or the “true” equation describing the movement rate of a division as a function of various combat variables).
Unfortunately, current M&S has not been designed with uncertainty analysis
|
1 |
RAND has done considerable work on this approach over the last decade, beginning with development of the RAND Strategy Assessment System (RSAS), which evolved into the JICM operational-level model, sponsored by OSD's Director of Net Assessment (see Davis and Winnefeld, 1983, pp. 62-65 for early visions). The original technology, however, was not yet powerful enough for what is becoming feasible now. For a broad and thorough description of exploratory modeling and analysis from a computer science perspective, see Bankes (1993, 1996). For applications to defense planning and adaptive planning involving global warming, see Davis et al. (1996) and Lempert et al. (1996) (a reprint from the journal article in Climatic Change, 33(2), 1996). |
|
2 |
For practical discussion of such matters and citations to the literature on experimental design, see Committee on National Statistics (1995). |
|
3 |
Alternative approaches or formulations are possible as well. For example, control theorists have focused on consequences of unmodeled dynamics. Dynamical systems focus on chaos as the explanation for apparent random behaviors. These are discussed in Appendix B . |
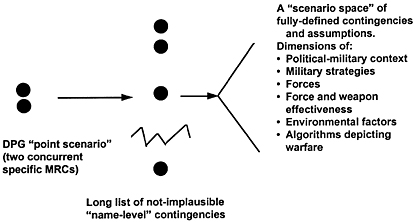
FIGURE D.1 Moving from point scenarios to a scenario-space exploration.
of this sort in mind. Yes, some M&S accommodates varying some types of data readily, but almost no M&S has yet been designed to facilitate meaningful exploratory analysis of the sort we have in mind here. Much less has it been designed with tools permitting workers to search for critical domains or draw synoptic conclusions. Much could be done, however, with future M &S, assuming appropriate designs and infrastructure. One key to such design is multi-resolution modeling, as discussed in Appendix E. Such an emphasis on uncertainty analysis would revolutionize the use of “soft” models such as those describing force-on-force battles and operational and theater-level conflict. It would also be essential for the engineering of complex physical systems that must operate in diverse circumstances of environment, tempo, and commander style.
Figure D.1 illustrates the concept in the context of rethinking higher-level defense planning. It depicts moving from point scenarios such as those used in the Defense Planning Guidance to an exploratory analysis framework. It shows expanding the set of “name-level” scenarios, and then recognizing that each such scenario (e.g., Iraq versus Kuwait) actually consists of an infinite number of variations. These can be explored by conceiving the “scenario space” formed by the axes shown: political-military context (e.g., who is allied with whom, what are the objectives, and what are the time lines); military strategies; forces; force and weapon effectiveness (remembering that planning factors are often wrong); environmental factors (e.g., weather); and, finally, the algorithms and algorithm parameters depicting warfare (despite pretenses to the contrary, these are highly uncertain as well).
Having conceived the scenario space, one can—in the context of a particular study—design an exploratory analysis covering the uncertainties of interest. One can then use modern computers and graphics to “fly through the outcome space”
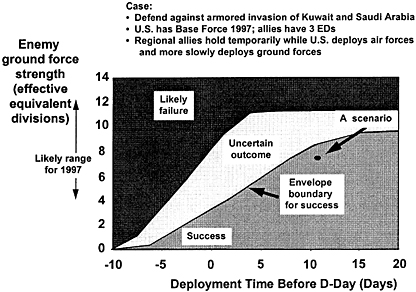
FIGURE D.2 Capabilities through a slice of scenario space.
to see when (under what assumptions) war outcomes would be favorable, unfavorable, and so on ( Figure D.2 ). The purpose, of course, is insight. With enough insight, one could do a great deal to hedge against ever being in one of the “bad” regions. Some of the hedges would be obvious (e.g., prepositioning to increase deployment rates), but others might be less so (e.g., having a variety of systems to avoid common-mode failures of critical precision-strike weapons)—until after the exploration makes them obvious. 4
|
4 |
See Davis, Gompert, and Kugler (1996) for a relatively short account of this work and some of the unclassified insights from initial exploratory analysis of future regional contingencies, the upshot of which was to focus attention on Achilles' heel problems and the potential for “asymmetric strategies” by the adversary, rather than different ways to add marginally to the already substantial U.S. capability for “canonical” major regional contingencies with, for example, good use of warning and effective allies. For more discussion of how this relates to adaptive planning for military operations, see “Planning for Adaptiveness” in Davis (1994), which summarizes work over the preceding half-dozen years. A number of the ideas and methods referred to in this work were applied in the 1997 Quadrennial Defense Review. For an independent discussion of similar ideas, see the work of Bonder and Cherry in Vector Research, Inc. (1992). |




