Large-Eddy Simulation of Decaying Free-Surface Turbulence with Dynamic Mixed Subgrid-Scale Models
M.Salvetti (Università di Pisa, Italy), Y.Zang, R.Street (Stanford University, USA), S.Banerjee (University of California at Santa Barbara, USA)
Abstract
This paper describes the large eddy simulation of the decaying turbulence in an open channel, using the dynamic two-parameter model of Salvetti and Banerjee [Phys. of Fluids, 7, 1995] and the finite volume Navier-Stokes equations solver of Zang, Street and Koseff [J. Comp. Phys., 114, 1994]. A direct numerical simulation of this flow conducted by Pan and Banerjee [Phys. of Fluids, 7, 1995] showed that near the free surface turbulence has a quasi-two-dimensional behavior. Moreover, the quasi-two-dimensional region increases in thickness with the decay time, although the structure remains three dimensional in the central regions of the flow. The objective of this work is to study the behavior of the subgrid-scale model in the neighborhood of the free surface, and, in particular, to demonstrate the ability of the two-parameter model to handle the anisotropic nature of the flow.
1
Introduction
Many environmental flows, e.g., interactions between the atmosphere and the ocean or the persistent signature of vessel wakes, are strongly influenced by free-surface turbulence. Due to difficulties in measurement and simulation, the amount of information presently available on the structure of turbulence near the interfaces is far from exhaustive. Direct numerical simulation (DNS) is restricted to low Reynolds number flows and simple geometries, because of the need to resolve all the spatial scales of turbulence. On the other hand, large eddy simulation (LES), in which only the large scale motion is computed and the subgrid scales are modeled, provides an effective tool for tackling this type of flow. The critical point in LES is to accurately capture the effects of the unresolved subgrid-scale (SGS) motion.
The dynamic model (DSM) proposed by Germano et al. (1) has been succesfully applied in several LES computations. In the DSM the base model is the Smagorinsky eddy-viscosity model, widely used in earlier LES, in which the coefficient is computed using the information from the smallest resolved scales. In spite of its many desirable features, the DSM has still some aspects to be improved, related to the use of the Smagorinsky model. The most serious problem in LES computations with the DSM is the presence of large fluctuations of the model coefficient, arising when it is computed locally, which often lead to numerical instability.
Zang et al. (2) proposed a dynamic mixed model (DMM) using an extension (the modified Leonard term) of the Bardina scale-similarity model, together with the dynamic model with a Smagorinsky kernel. Salvetti and Banerjee (3) improved upon that model and employed two dynamic coefficients in constructing their dynamic two-parameter model (DTM). They showed that dynamic coefficients could be computed for each element of the model, i.e., for the modified Leonard term and for the Smagorinsky term. The dynamic two-parameter model was evaluated through the use of a priori tests. The dynamic-mixed model was tested by using it in the LES of a recirculating, lid-driven flow in a cavity (2). The results showed that these models combine the essential features of energy dissipation and energy backscatter, needed for modeling SGS effects.
The main objective of this work is to investigate the behavior of these SGS models in the large eddy simulation of free-surface turbulent flows. To this end, we simulate the decaying free-surface turbulence in an open channel. Starting from the statistically steady state computed in the direct simulation of Pan and Banerjee (4), we simulate a case where the no-slip boundary condition on the bot
tom solid wall is changed to a free-slip condition. By this changing of boundary conditions, the mechanism of turbulence generation is eliminated and the flow begins to decay. This problem is of interest to understand how the free-surface turbulence evolves far from the region of turbulence generation, e.g., in the wake of a vessel. The direct simulation by Pan and Banerjee showed that, near the free surface, the structure of turbulence is quasi two-dimensional, with the quasi-two-dimensional-region increasing in thickness in the decaying process. Thus, this test case is particularly severe for SGS models, which have a three-dimensional structure. The point at issue in this work is whether large eddy simulation, using SGS dynamic mixed models and, in particular, the dynamic two-parameter model, may reproduce the nearly two-dimensional nature of the turbulence near the free surface.
2
Mathematical formulation and numerical method
We now briefly summarize the mathematical formulation of the dynamic-mixed models used in the present simulations. More details can be found in (2) and (3).
For the incompressible and constant density flow considered here, the basic governing equations are the grid-filtered Navier-Stokes and continuity equations (omitted here for sake of brevity), in which the effect of the unresolved subgrid scales is represented by the SGS stress tensor:
(1)
The overbar denotes a grid-filtered variable.
In the dynamic two-parameter model, the SGS stress tensor is modeled as follows (3):
(2)
where: ![]() is the resolved strain rate tensor,
is the resolved strain rate tensor, ![]() and
and ![]()
![]() is the “modified Leonard stress” (5). It represents the resolved part of the SGS stress. The grid filter width
is the “modified Leonard stress” (5). It represents the resolved part of the SGS stress. The grid filter width ![]() is defined as:
is defined as:
where ![]() is the grid spacing in i direction. The two unknown coefficients C and K in (2) are computed dynamically in the way described below.
is the grid spacing in i direction. The two unknown coefficients C and K in (2) are computed dynamically in the way described below.
Following the procedure of Germano et al. (1), a test-filter, denoted by a hat, is applied to the governing equations; the sub-test scale stress tensor is then obtained:
(3)
It is modeled in the same manner as the SGS stress tensor:
(4)
where: ![]() and
and ![]() is the modified Leonard term for the test-scale filter (2) (3). The width of the test filter
is the modified Leonard term for the test-scale filter (2) (3). The width of the test filter ![]() is assumed to be larger than that of the grid filter. The ratio between the width of the test and grid filters is denoted by α (=2 here as in most applications in the literature).
is assumed to be larger than that of the grid filter. The ratio between the width of the test and grid filters is denoted by α (=2 here as in most applications in the literature).
Using the Germano identity (1) and equations (2) and (4), we obtain:
(5)
where: ![]() and
and ![]() . Using a least square approach as suggested by Lilly (6), the unknown coefficients are evaluated by setting ∂Q/∂C=0 and ∂Q/∂K=0, where Q is the square of the error in (5).
. Using a least square approach as suggested by Lilly (6), the unknown coefficients are evaluated by setting ∂Q/∂C=0 and ∂Q/∂K=0, where Q is the square of the error in (5).
The expression of the SGS stress tensor in the DMM is given by Eq. (2) in which K is set equal to unity (2). Following the same dynamic procedure as previously, the model parameter C can be obtained by setting ∂Q/∂C=0, Q being the square of the error in (5) with K=1.
For reference, the dynamic subgrid-scale model (DSM) of Germano et al. (1), is obtained by setting K=0 above and the model parameter C can be computed by setting ∂Q/∂C=0, Q being the square of the error in (5) with K=0.
For our computations, the governing equations are trasformed into a general curvilinear coordinate system and discretized on a non-staggered grid using a Finite-Volume approach. A fractional step method is employed and the pressure Poisson equation is solved with a multigrid method. Time marching is semi-implicit with the formal accuracy being second order in both space and time. The details of the numerical method can be found in (7) and (8).
3
Results and discussion
The simulation starts from the statistically steady pressure-driven flow between a no-slip wall and a rigid free-slip surface computed in Ref. (4). The streamwise direction is denoted by x1, the spanwise direction by x2, and the normal direction by x3. The velocity components in these directions are given by u1, u2 and u3. All quantities are nondimensionalized with the channel half-depth h and the effective shear velocity ue, defined as (4):
(6)
where ![]() is the magnitude of the mean pressure gradient which drives the flow and ρ is the fluid density. Thus, the effective Reynolds number, equal to 60.4, is defined as:
is the magnitude of the mean pressure gradient which drives the flow and ρ is the fluid density. Thus, the effective Reynolds number, equal to 60.4, is defined as:
(7)
where v is the kinematic viscosity. A nondimensional time is also defined as: ![]() . In the following, for simplicity, t denotes the nondimensional time. Periodical conditions are applied in the streamwise and spanwise directions. The dimensions of the computational box are L1=4π, L2=2π and L3=2, in the streamwise, spanwise and normal directions, respectively.
. In the following, for simplicity, t denotes the nondimensional time. Periodical conditions are applied in the streamwise and spanwise directions. The dimensions of the computational box are L1=4π, L2=2π and L3=2, in the streamwise, spanwise and normal directions, respectively.
In the direct numerical simulation of Pan and Banerjee, 64 Fourier modes were used in the streamwise and spanwise directions and 65 Chebyshev modes in the wall-normal direction. The details of the direct simulation can be found in Ref. (4). For our computations, a grid of 32×32×32 points was used. The grid is non-uniform in the normal direction to cluster the points near the wall and the free-surface, but is uniform in the streamwise and spanwise directions.
At the beginning of the simulation the no-slip boundary condition on the bottom wall is changed to a free-slip boundary condition and at the same time the pressure gradient which drives the flow is turned off. This change of boundary conditions eliminates turbulence generation and the flow begins to decay.
Large-eddy simulations have been carried out with the DSM, DMM and DTM. The results showed that both the DMM and the DTM are able to reproduce the features of the decay process observed in the DNS and that they have similar mechanisms of interaction between subgrid and resolved scales. Nevertheless, the addition of the second model coefficient in the DTM improved the agreement with the direct simulation. Therefore, we will present the results of a comparison of the DTM and DMM in (9). Here, we present the results obtained with the DSM and compare these to the DTM results, in order to show the significant differences in the modelling of the interactions between subgrid and resolved scales and their effects on the decay process.
3.1
The decay process
The time evolution of the plane averaged streamwise velocity, obtained respectively with DSM and DTM, is shown in Figs.1a and 1b (here the wall is at x3=0 and the free surface at x3=2). Once the bottom boundary condition is changed to free slip ( t=0), the velocity profile decays and tends to become essentially uniform, as found also in Ref. (4). A slight delay is observed in the time evolution of the profiles obtained with the DTM compared to those shown in Fig.6a of Ref. (4), but the trend is the same, and, within 6 nondimensional time units, the velocity profile is nearly flat. The delay is more noticeable with the DSM.
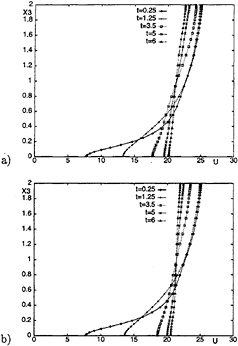
Figure 1: Time evolution of the plane-averaged streamwise velocity. a) DSM b) DTM
In Fig.2a the r.m.s. of the three velocity components at the initial statistically-steady state are plotted with respect to the depth of the channel. The fluctuating velocity component in the i direction is defined as: ![]() where <ui> is the average on the homogeneous horizontal planes. A high peak in the r.m.s of streamwise velocity is observed near the wall, and is related to the quasi-streamwise structures typical of this region (4).
where <ui> is the average on the homogeneous horizontal planes. A high peak in the r.m.s of streamwise velocity is observed near the wall, and is related to the quasi-streamwise structures typical of this region (4).
The r.m.s. values obtained with the DSM and the DTM are shown in Figs.2b and 2c, which correspond to t=3.5 and t=7. As expected, since the mechanisms of turbulence generation are turned off by the change in boundary conditions at the wall, the r.m.s. values of all the velocity components decrease during the decay process. Moreover, the r.m.s. distribution of the streamwise and spanwise components tends to become uniform along the channel depth.
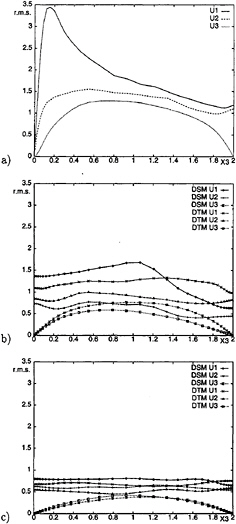
Figure 2: R.m.s. of the velocity components, a) t=0 b) t=3.5 c) t=7.
For the DSM a noticeable variation of the r.m.s of
u1 along the channel depth is still present at t=3.5, indicating a delay in the decay process, as already observed from Fig.1a. Also, at t=3.5 the r.m.s. of all the velocity components obtained with the DSM in the region near the free surface are noticeably lower than those obtained with the DTM. This is still true at t=7, but the differences are less important. Thus the DSM seems to be considerably more dissipative near the free surface than the DTM, especially in the first phase of the decay process.
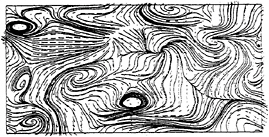
Figure 3: Streamlines at t=0.25. DTM
In Fig.3 the instantaneous streamlines of the fluctuating velocity field obtained with the DTM are shown at the beginning of the simulation (t=0.25). The typical structures of fully developed free surface turbulence, identified in Ref. (4), can be observed: upwellings, corresponding to the zones where streamlines fan out, attached vortices, mostly at the edges of upwellings, and downdrafts, corresponding to the stagnation lines (in the right lower part, for example). At this early stage of the simulation, the instantaneous streamlines obtained with the DSM are almost identical than those obtained with the DTM in Fig.3, because the differences in the SGS models have not yet had enough time to manifest themselves. As observed in Ref. (4), since turbulence generation is suppressed, the upwellings and downdrafts become less pronounced with increasing time, as shown for instance by the instantaneous streamlines obtained by DTM at t=7.17 in Fig.4. The signature of the large structures found in the DNS at the same nondimensional time (Figure 7d of Ref. (4)) are present in the flow obtained with the DTM. Some vortices and small scales are missing in Fig.4, but this is caused by the filtered velocity field of the large eddy simulation and it is consistent with the analysis of filtering effects in Fig.17 of Ref. (4). The instantaneous streamlines obtained at the same nondimensional time with the DSM (Fig.5) are completely different, indicating again that the SGS modelling noticeably affects the decay process.
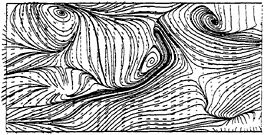
Figure 4: Streamlines at t=7.17. DTM
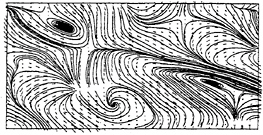
Figure 5: Streamlines at t=7.17. DSM
Figs.6a and 6b show the evolution during the decay process of the one-dimensional, streamwise and spanwise energy spectra for the surface-parallel
velocity components at the free surface obtained with the DTM. Good agreement is obtained with the DNS (Fig.10 of Ref. (4)) and, in particular, the reverse cascade of energy from high to low wave numbers observed at the free surface in the DNS seems to be properly taken into account in the large eddy simulation with the DTM. Indeed, as in Ref. (4), the spectra change primarily by steepening at large wave numbers from the initial slope of k–3.5 to k–9.5 and k–5.5 for spanwise and streamwise spectra, while low wave numbers decay much more slowly. As pointed out also by Pan and Banerjee, this behavior is typical of decaying two-dimensional turbulence.
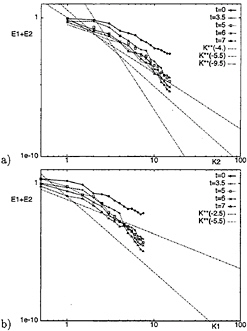
Figure 6: Time evolution of one-dimensional energy spectra E1+E2 of the surface-parallel velocity components obtained with the DTM: a) spanwise; b) streamwise.
Pan and Banerjee also found that at t=3.5 the high wave-number spectra at various depths from the free surface become identical and that at low wave numbers the k–5./3. region propagates downwards during the decay, i.e., the quasi-two-dimensional region thickens.
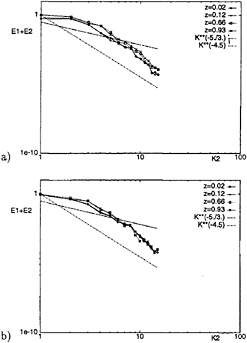
Figure 7: Spanwise one-dimensional energy spectra E1+E2 of the surface-parallel velocity components obtained with the DTM on different horizontal planes, with z measured down from the free surface: a) t=3.5; b) t=4.
In Figs.7a and 7b, the spanwise one-dimensional energy spectra of the surface-parallel velocity components obtained with the DTM on different horizontal planes are shown, at t=3.5 and t=4. The distance from the free surface is denoted by z. At t=3.5 differences can be observed in the high wave numbers portion of the spectra on the different planes , but they have disappeared at t=4. Moreover, at
t=4 a slope of k–5/3 is found in the low wave number part of the spectra, also on the planes near the center of the channel. As concerns direction-related aspects of the energy spectra, Fig.8 shows the spanwise one-dimensional energy spectra of the surface-normal velocity component, obtained with the DTM on different horizontal planes at t=4. As in the DNS, the spectra for the surface-normal velocity undergo little change in slope compared to the steady state (Fig.12a in Ref. (4)), except for decay. Thus, even with a slight delay, already pointed out in the analysis of Fig.1b, the large eddy simulation with the DTM reproduces the spectral features of the decay process observed in the DNS in Ref. (4).
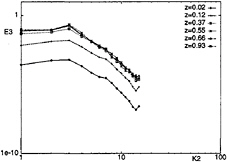
Figure 8: Spanwise one-dimensional energy spectra E3 of the surface-normal velocity at t=4.
In Figs.9a and 9b the time evolution of the one-dimensional energy spectra of the surface-parallel velocity components obtained with the DSM is shown. Some discrepancies from the DNS can be observed in the decay of the energy spectra. First, the high wave-numbers portion of the streamwise spectrum, with increasing time, takes a slope of k–9.5 instead of k–5.5. Moreover, for both spanwise and streamwise spectra, a rapid decrease of energy for all the wave-numbers is observed in the first phase of the decay process at t=3.5 and the slope of the high wave-numbers portion steepens to k–9.5 (see Fig.10a). Between t=3.5 and t=5 (Fig.10b) the energy contained in all the wave numbers increases again and the shape of the spectrum does not change. Finally, as time icreases, high wave numbers continue to decay faster than low wave numbers and the slope of the intermediate portion of spectrum changes. On the contrary, in the DNS and in the large eddy simulation with the DTM a progressive decay and change in slope of the energy spectra is observed.
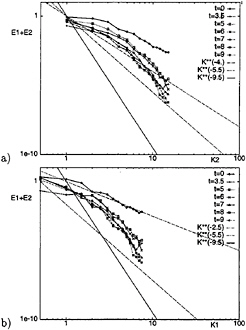
Figure 9: Time evolution f one-dimensional energy spectra of the surface-parallel velocity components obtained with the DSM: a) spanwise; b) streamwise.
Moreover, the spanwise energy spectra in Fig.11, obtained with the DSM at t=10 on different normal planes, show that even very late in the simulation the high wave-numbers portion is different on different planes and that, on planes close to the center of the channel, the low wave-numbers portion does not take the k–5./3. slope.
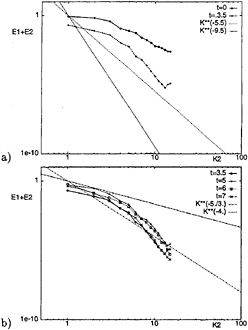
Figure 10: Time evolution of spanwise energy spectrum of the surface-parallel velocity components obtained with the DSM: a) t=0.–3.5; b) t=3.5–7.
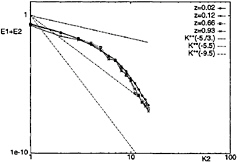
Figure 11: Spanwise one-dimensional energy spectra of the surface-parallel velocity components obtained with the DSM on different horizontal planes at t=10.
In order to investigate the effects of grid refinement on the decay process, the same large eddy simulation has been carried out on a finer grid of 64×64×64 points with the DTM. As in the previous case, the grid is non uniform in normal direction and the points are clustered near the wall and the free-surface. Incidentally, even if the number of computational points is equal to the number of modes used in the direct numerical simulation in Ref. (4), the resolution obtained with a second-order accurate Finite-Volume simulation is much lower than that of a Fourier-Chebyshev spectral method, especially in the normal direction near the wall and the free surface.
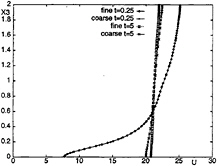
Figure 12: Effects of grid refinement on the time evolution of mean streamwise velocity. DTM.
At the beginning of the simulation (t=0.25) the profile of mean streamwise velocity is the same as that obtained previously on the coarser grid (Fig.12) and then a slight delay is observed with respect to the DNS. Afterwards, the time evolution of the mean velocity profile obtained with the finer grid is faster and closer to the DNS (see for example t=5 in Fig.12). An acceleration of the decay process is confirmed by the r.m.s. of the three velocity components on horizontal planes, plotted in Fig.13 for t=5: for all the components, the r.m.s. obtained with the finer grid is noticeably lower than that with the coarser grid. This acceleration is also confirmed by the comparison of the one-dimensional energy spectra of the surface-parallel velocity components obtained with the two different grids (Fig.14a and 14b) at t=5.
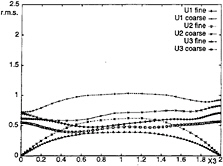
Fig 13: Effects of grid refinement on the r.m.s of the velocity components at t=5. DTM
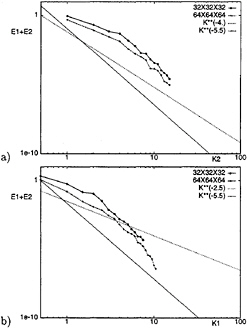
Fig 14: One-dimensional energy spectra of the surface-parallel velocity components obtained with the DTM on two different grids at t=5: a) spanwise; b) streamwise.
Indeed, the energy contained both at low and high wave numbers in the streamwise and spanwise spectra is less with the finer grid than with the coarser grid. Nevertheless, the shape of the spectra is practically the same and, hence, the basic mechanisms of the decay process are not affected by the grid resolution.
3.2
Subgrid scale energy transfer and model parameters
In the previous Section we pointed out that the SGS modelling strongly affects the basic features of the decay process at the free surface. In order to investigate more in detail the behavior of the subgrid model during the decay process, we examine now the energy transfer between resolved and subgrid scales, obtained in the simulations with the DSM and the DTM. The energy transfer between resolved and subgrid scales is represented by the ”subgrid-scale dissipation”, ![]() . If this quantity is negative, the subgrid scales remove energy from the resolved ones, which is called forward scatter; if it is positive, they release energy to the resolved scales, which is called backscatter. The backward and forward scatter components of εsgs, respectively denoted by ε+ and ε_, are defined as (10) (4):
. If this quantity is negative, the subgrid scales remove energy from the resolved ones, which is called forward scatter; if it is positive, they release energy to the resolved scales, which is called backscatter. The backward and forward scatter components of εsgs, respectively denoted by ε+ and ε_, are defined as (10) (4):
(8)
Both the SGS backward and forward scatter are normalized by the volume averaged absolute value of the viscous dissipation defined as:
(9)
In Fig.15a the distribution along the channel depth of plane-averaged SGS backward and forward scatter, obtained with the DTM, is shown. At the beginning of the computation, both the backward and forward scatter peak in the near ”wall” region, at approximately z=0.2, since this region is still characterized by strong Reynolds shear stress. This result is consistent with the analysis of subgrid-scale energy transfer carried out in Ref. (10) using the DNS data of a turbulent channel flow. However, even at the very beginning of the computation a noticeable amount of backscatter is present at the ”wall”, because of the new free-slip boundary conditions. As the time increases, the peak of forward scatter disappears and the distribution tends to become uniform
along the channel depth. In a first phase of the decay process (t=3.5) a larger amount of forward scatter is found everywhere, except in the former peak region; in a second phase, the forward scatter decreases everywhere, except near the free surface. During the whole decay process, a large amount of backscatter is present at the free surface and near the ”wall”: the ratio between backward and forward scatter is noticeably higher there than in the center of the channel. This result seems to confirm that the DTM properly takes into account the reverse cascade of energy from small to large scales at the free surface, as observed also previously from the energy spectra.
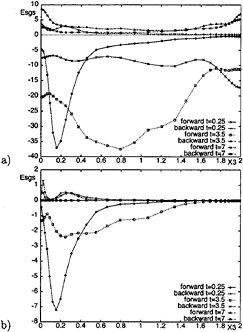
Figure 15: Time evolution of plane-averaged forward and back scatter, a) DTM b) DSM
In Fig.15b the distribution along the channel depth of plane-averaged SGS backward and forward scatter, obtained with the DSM, is plotted. At the beginning of the simulation the distribution is qualitatively similar to that obtained with the DTM, but the amount of both backward and forward scatter is significantly smaller: for instance, the peak of forward scatter is approximately five times lower than that obtained with the DTM. Later on, the peak in the wall region disappears, as for the DTM, but in this case both backward and forward scatter decrease noticeably everywhere during the whole decay process. At the free surface the SGS energy transfer is very low during all the simulation: in particular the reverse energy transfer, which is a basic feature of freely decaying two-dimensional turbulence, is negligible compared to the volume averaged viscous dissipation.
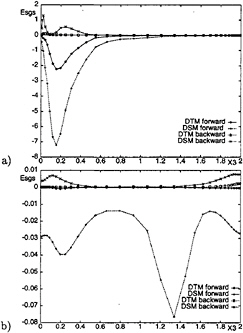
Figure 16: Plane-averaged forward and back scatter obtained with DSM and the Smagorinsky part of the DTM. a) t=0.25 b) t=7.
Significantly, the SGS backward and forward scatter obtained with the DTM are mainly due to the
model component which is proportional to the modified Leonard tensor. This is evident from Figs.16a and 16b, in which the backward and forward scatter due to the Smagorinsky part of the DTM are compared to those obtained with the DSM at t=0.25 and t=7. Both backward and forward scatter given by the Smagorinsky part of the DTM (except in a region near the wall at the beginning of the simulation) are negligible compared to those obtain with the DSM, which in turn are much lower than those given by all the terms in the DTM. This result is confirmed by the comparison of the Smagorinsky part coefficient in the DTM and the model parameter in the DSM during the decay process.
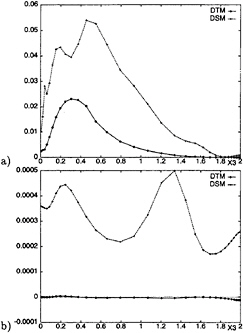
Figure 17: Plane-averaged vt/v obtained with DSM and DTM. a) t=0.25 b) t=7.
In Figs.17a and 17b the plane-averaged values of vt/v obtained with the DSM and the DTM are compared at the same previous nondimensional times; vt is the eddy viscosity, defined as:
(10)
The eddy viscosity given by the Smagorinsky part in the DTM is always much lower than that obtained with the DSM, and tends to vanish faster, with increasing time during the decay. This result is not surprising, since, as pointed out in Ref. (3), in the DTM less burden is put on the coefficient related to the Smagorinsky part, and it is consistent with the results of the a priori tests in Ref. (3).
The plane-averaged value of the second parameter in the DTM (Fig.18), at the beginning of the simulation, shows a peak at the ”wall”, probably related to the change in boundary conditions, then decreases to reach a value of approximately 1.2, almost uniform along the rest of the depth. During the decay, the value of K is almost constant along the whole channel depth and decreases slightly with increasing time.
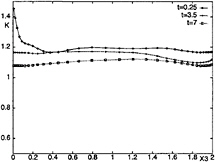
Figure 18: Time evolution of the plane-averaged K parameter in the DTM.
In order to analyse the behavior of the model parameters more locally at the free surface, the values of vt/v obtained with the DSM and the DTM at the free surface for t=0.25 are shown in Figs.19a and 19b, respectively. The eddy viscosity for the DSM shows large peaks, both positive and negative, about two order of magnitude larger than the plane-averaged value. Incidentally, the model coefficient C, computed by the dynamic procedure described in
Section 2, is averaged locally in space within the test-filtering volume with a stencil of three grid points in each direction. As expected on the basis of the results in Ref. (3), these peaks disappear in the DTM. This behavior is clearly a desirable feature in LES computations to avoid numerical instabilities. The second parameter in the DTM also varies on horizontal planes (Fig.20) but as a small percentage of its averaged value, vithout exhibiting large isolated peaks.
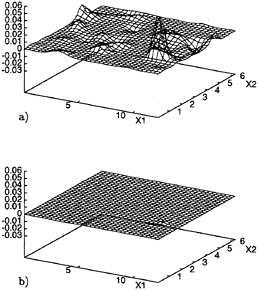
Figure 19: vt/v at the free surface obtained with DSM and DTM at t=0.25. a) DSM (Plane-averaged value: 8.6 10–4) b) DTM (Plane-averaged value: 1.3 10–5).
The isocontours of the SGS energy transfer (normalized by the volume-averaged absolute value of the viscous dissipation) given at the free surface by the Leonard part of the DTM are plotted in Fig.21 for t=0.25. As previously pointed out, the Smagorinsky part in the DTM gives a negligible contribution to the SGS energy transfer at the free surface: thus, the isocontours in Fig.21 practically represent the whole SGS energy transfer obtained with the DTM. The regions of high forward energy transfer correspond to the stagnation streamlines and to the outskirts of the vortices, where high shear stress is present (see Fig. 3). Strong backward energy transfer occurs mostly in the regions with upwelling. The same qualitative behavior of the SGS energy transfer was observed at the free-surface by Pan and Banerjee in Ref. (4), by filtering their DNS data with a cutoff filter in the wave-number space. Thus, the DTM, and, in particular the part related to the modified Leonard tensor, captures the basic mechanisms of SGS energy transfer at the free surface.
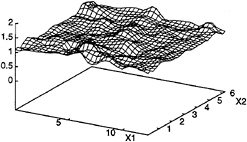
Figure 20: K parameter in the DTM at the free surface for t=0.25. Plane-averaged value: 1.17.
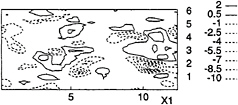
Figure 21: Iso-contours of the SGS energy transfer due to the Leonard part of the DTM at the free surface. t=0.25.
The same isocontours obtained with the DSM are shown in Fig.22. First, as previously noted for the analysis of plane-averaged values, noticeably less SGS energy transfer (both forward and backward) occurs with the DSM than with the DTM. Moreover, it is clear that the zones of non-negligible backward and forward scatter correspond to the peaks (negative and positive) of the model parameter, observed in Fig.19a. In particular, most of the forward transfer corresponds to the stagnation streamline in the right lower part (see Fig.3), where vt/v assumes the highest positive peak. Only a region of very low backscatter is observed in the right upper part of the domain, where an upwelling occurs. Thus, even if the dynamic procedure of determination of the model parameter seems to be effective in someway, since high peaks of C correspond to regions where physical phenomena (downdraft or upwelling) actually occur, the DSM seems to be generally inadequate to account for the energy transfer between unresolved and resolved scales at the free surface.
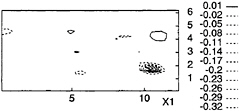
Figure 22: Iso-contours of the SGS energy transfer obtained at the free surface by the DSM. t=0.25.
4
Conclusions
The large eddy simulation of free-surface decaying turbulence with the dynamic two-parameter model compares very favorably with the direct numerical simulation. In particular, the reverse cascade of energy from small scales to large scales at the free surface, which is a feature of freely decaying two-dimensional turbulence, is properly taken into account by the DTM. Moreover, as in the DNS, the two-dimensional region thickens during the decay. A slight delay in the decay process is observed in the large eddy simulation, with respect to the DNS, but it is reduced by increasing the grid resolution near the free surfaces. Nevertheless, the basic mechanisms of the decay process are not affected by grid resolution.
Using the dynamic subgrid model (DSM), a large eddy simulation was carried out for the same flow geometry and boundary and initial conditions as for the DTM. Significant discrepancies were observed between the DSM and the DNS simulations during the decay process at the free surface.
The analysis of the SGS energy transfer shows that the DTM, and, in particular, the part related to the modified Leonard tensor, captures the basic mechanisms of interscale energy transfer, observed at the free surface by filtering the DNS data. Conversely, the DSM seems to be generally inadequate to account for the energy transfer between resolved and unresolved scales at the free surface: in particular, very low backscatter is observed there during the whole simulation.
As expected, the magnitude of the dynamically computed eddy viscosity in the DTM is significantly reduced compared with that in the DSM; the contribution of the Smagorinsky part to SGS energy transfer in the DTM becomes negligible with increasing decay time. Moreover, the large isolated peaks observed in local values of the eddy viscosity in the DSM almost disappear for the DTM.
References
1. Germano M., Piomelli U., Moin P., Cabot W.H., ”A dynamic subgrid-scale eddy-viscosity model”, Phys. Fluids A, Vol. 3, No. 7, 1991, pp. 1760–1765.
2. Zang Y., Street R.L., Koseff J.R., ”A dynamic mixed subgrid-scale model and its application to turbulent recirculating flows”, Phys. Fluids A, Vol. 5, No. 12, Dec. 1993, pp. 3186–3196.
3. Salvetti M.V., Banerjee S., “A Priori Tests of a New Dynamic Subgrid-Scale
Model for Finite-Difference Large-Eddy Simulations”, Phys. Fluids, Vol. 7, No. 11, Nov. 1995, pp. 2831–2847.
4. Pan Y., Banerjee S., ”A numerical study of free-surface turbulence in channel flow”, Phys. Fluids, vol. 7, No. 7, July 1995, pp. 1649– 1664.
5. Germano M., ”A proposal for a redefinition of the turbulent stresses in the filtered Navier-Stokes equations”, Phys. Fluids 29, 1986, pp. 2323.
6. Lilly D.K., ”A proposed modification of the Germano subgrid scale closure method ”, Phys. Fluids A, vol. 4, No. 3, March 1992, pp. 633– 635.
7. Zang Y., Street R.L., Koseff J.R., “A non-staggered grid, fractional step method for time-dependent incompressible Navier-Stokes equations in general curvilinear coordinate systems ”, J. Comput. Phys., vol. 114, n. 1, 1994, pp. 18–33.
8. Zang Y., Street R.L., “A composite multigrid method for calculating unsteady incompressible flows in geometrically complex domains”, Int. Journal for Num. Meth. in Fluids, vol. 20, 1995, pp. 341–361.
9. Salvetti M.V., Zang Y., Banejee S., Street R.L., ”A two-parameter, dynamic-mixed subgrid-scale model applied to a turbulent recirculating incompressible flow”, to be submitted to Phys. of Fluids.
10. Piomelli U., Cabot W.H., Moin P., Lee S., ”Subgrid-scale backscatter in turbulent and transitional flows”, Phys. Fluids A 3, Vol. 3, No. 7, July 1991, pp. 1766–1771.
DISCUSSION
M.Sreedhar and F.Stern
University of Iowa, USA
The authors should be congratulated for such an interesting paper. The dynamic two-parameter model (DTM) seems to have overcome many of the drawbacks of the original Smagorinsky (DSM) subgrid scale model. We have the following questions and comments.
-
Usually, in the quasi-two dimensional free surface turbulent field, the energy of the surface-parallel velocity components tends to increase while the surface normal velocity component decays. The one dimensional energy spectrum (Fig.7 in the paper) which shows the energy contents of the surface parallel velocity components obtained with the DTM model at different horizontal components planes does not seem to indicate this feature. Is it due to the decaying nature of the turbulent field? Any comments on this?
-
The figures and discussion on the time evolution of plane-averaged forward and back scatter are very interesting. The superiority of the DTM model is very clearly demonstrated. Inclusion of the results of forward and back scatter computed from the DNS data (after proper filtering) in a few of the figures would be very welcome.
AUTHORS' REPLY
-
This behavior is actually due to the decaying nature of the flow. Indeed, since the mechanisms generating turbulence are eliminated, the normal velocity component is generally lower than in the turbulent open channel and hence, the damping of this component at the free surface is less important. As a consequence, the increase in the surface normal components at the free surface becomes negligible; this can be seen, for example, from the r.m.s. of these components in Fig.2 that tend to become straight along the channel depth.
-
We agree with this excellent suggestion, and we have been developing more quantitative comparisons for this flow. In Salvetti and Banerjee (Phys. Fluids, vol. 7, n. 11, Nov 1995) quantitative comparisons were made between DNS, DMM, and DTM behaviors.
DISCUSSION
E.Novikov
University of California, San Diego, USA
In this paper the decaying turbulence is considered in an open horizontally periodic flow with free-slip top and bottom conditions. Large eddy simulation (LES) is described for dynamic models with Smagorinsky term and with a combination of Smagorinsky and Bardina terms. A quantitative comparison is made between results, obtained with these models. Some qualitative comparison of LES results with direct numerical simulation (DNS) is also mentioned. The value of this work will be greatly increased if the comparison between LES models and DNS will be made quantitative.
AUTHORS' REPLY
As we noted in response to the second point by Sreedhar and Stern, we are continuing work on this flow and will add more quantitative comparisons in future publications. The quality of the DMM and DTM SGS models has, however, been directly compared to DNS results via a priori tests in Salvetti and Banerjee (Phys. Fluids, vol. 7, n. 11, Nov. 1995) as we note above.















