Fully Nonlinear Hydrodynamic Calculations for Ship Design on Parallel Computing Platforms
G.Cowles, L.Martinelli (Princeton University, USA)
1
Introduction
The prediction of the total drag experienced by an advancing ship is a complicated problem which requires a thorough understanding of the hydrodynamic forces acting on the ship hull, the physical processes from which these forces arise and their mutual interaction. The advent of powerful computers —exhibiting both fast processing speed and large storage capabilities—has now made possible computational solutions of the full set of mathematical equations which describe the coupled wave structure and viscous boundary layer interaction. Notable previous computational approaches in this area include: the finite difference, velocity-pressure coupling approach of Hino [ 3]; the finite volume, velocity-pressure coupling approach of Miyata et. al. [4]; and the interactive approach of Tahara et. al. [5] which combines the finite analytic approach of Chen et. al. [6] and the “SPLASH” panel method of Rosen et. al. [7]. These methods all represent major advances in the computational solution of the coupled wave structure and viscous boundary layer interaction problem as it applies to ship hulls in general. However, they are all computationally intensive, requiring significant amounts of CPU time.
The motivation behind the present work follows directly from the shortcomings of the CFD techniques currently available for ship analysis and design. A method which is robust and accurate for realistic hull shapes will greatly enhance hull design capabilities—from the naval architect designing frigates and destroyers, to the sailing yacht designer optimizing the performance of an America's Cup hull. This task demands that techniques for incorporating the fully nonlinear free surface boundary condition be included in the CFD analysis.
The ability to model the fully nonlinear ship wave problem, in a robust and accurate fashion, is in and of itself still not sufficient for effective design practice. Thus, despite the advances that have been made, CFD is still not being exploited as effectively as one would like in the design process. This is partly due to the long set-up and high costs, both human and computational of complex flow simulations, and improvements are still needed. In particular, the fidelity of modelling of high Reynolds number viscous flows continues to be limited by computational costs. Consequently accurate and cost effective simulation of viscous flow at Reynolds numbers associated with full scale ships, remains a challenge. Several routes are available toward the reduction of computational costs, including the reduction of mesh requirements by the use of higher order schemes, improved convergence to a steady state by sophisticated acceleration methods, and the exploitation of massively parallel computers.
This paper presents recent advances in our work to accomplish these goals. The basic flow solver methodology follows directly from the cell-vertex formulation outlined in our previous work [8, 9]. This approach has proven to be accurate, through use of an efficient moving grid technique which permits application of the fully nonlinear free surface boundary condition, and which in turn permits simulation of the interaction between wavemaking and the viscous boundary layer. A cell-center formulation is also developed and used in the present work because it facilitates the implementation on parallel architectures using the method of domain decomposition.
The establishment of an efficient baseline steady state flow solver is extremely important because it provides the platform from which several powerful ship analysis tools can be launched. In particular, it enables the implementation of
automatic design techniques based on control theory [10] as well as the extension of a time accurate multigrid driven, implicit scheme [11] for the analysis of “seakeeping”, and maneuvering.
2
Mathematical Models
For a Viscous incompressible fluid moving under the influence of gravity, the differential form of the continuity equation and the Reynolds Averaged Navier-Stokes equations (RANS) in a Cartesian coordinate system can be cast, using tensor notation, in the form,
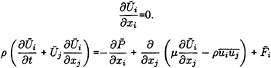
Here, Ūi is the mean velocity components in the xi direction, ![]() the mean pressure, and
the mean pressure, and ![]() the gravity force acting in the i-th direction, and
the gravity force acting in the i-th direction, and ![]() is the Reynolds stress which requires an additional model for closure. For implementation in a computer code, it is more convenient to use a dimensionless form of the equation which is obtained by dividing all lengths by the ship (body) length L and all velocity by the free stream velocity U∞. Moreover, one can define a new variable Ψ as the sum of the mean static pressure P minus the hydrostatic component –xkFr–2. Thus the dimensionless form of the RANS becomes:
is the Reynolds stress which requires an additional model for closure. For implementation in a computer code, it is more convenient to use a dimensionless form of the equation which is obtained by dividing all lengths by the ship (body) length L and all velocity by the free stream velocity U∞. Moreover, one can define a new variable Ψ as the sum of the mean static pressure P minus the hydrostatic component –xkFr–2. Thus the dimensionless form of the RANS becomes:
where ![]() is the Froude number and the Reynolds number Re is defined by
is the Froude number and the Reynolds number Re is defined by ![]() where v is the kinematic viscosity, and
where v is the kinematic viscosity, and ![]() is a dimensionless form of the Reynolds stress.
is a dimensionless form of the Reynolds stress.
Figure 1 shows the reference frame and ship location used in this work. A right-handed coordinate system Oxyz, with the origin fixed at the intersection of the bow and the mean free surface is established. The z direction is positive upwards, y is positive towards the starboard side and x is positive in the aft direction. The free stream velocity vector is parallel to the x axis and points in the same direction. The ship hull pierces the uniform flow and is held fixed in place, ie. the ship is not allowed to sink (translate in z direction) or trim (rotate in x–z plane).
It is well known that the closure of the Reynolds averaged system of equation requires a model for the Reynolds stress. There are several alternatives of increasing complexity. Generally speaking, when the flow remains attached to the body, a simple turbulence model based on the Boussinesq hypothesis and the mixing length concept yields predictions which are in good agreement with experimental evidence. For this
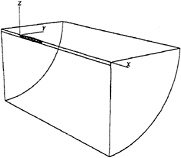
Figure 1: Reference Frame and Ship Location
reason a Baldwin and Lomax turbulence model has been initially implemented and tested [14]. On the other hand, more sophisticated models based on the solution of additional differential equations for the component of the Reynolds stress may be required. Notice that when the Reynolds stress vanishes, the form of the equation is identical to that of the Navier Stokes equations. Also, the inviscid form of the Euler equations is recovered in the limit of high Reynolds numbers. Thus, a hierarchy of mathematical model can be easily implemented on a single computer code, allowing study of the controlling mechanisms of the flow. For example, it has been shown in reference [18] that realistic prediction of the wave pattern about an advancing ship can be obtained by using the Euler equations as the mathematical model of the bulk flow, provided that a non-linear evolution of the free surface is accounted for. This is not surprising, since the typical Reynolds number of an advancing vessel is of the order of 108.
Free Surface Boundary Conditions
When the effects of surface tension and viscosity are neglected, the boundary condition on the free surface consists of two equations. The first, the dynamic condition, states that the pressure acting on the free surface is constant. The second, the kinematic condition, states that the free surface is a material surface: once a fluid particle is on the free surface, it forever remains on the surface. The dynamic and kinematic boundary conditions may be expressed as
(1)
where z=β(x,y,t) is the free surface location.
Hull and Farfield Boundary Conditions
The remaining boundaries consist of the ship hull, the meridian, or symmetry plane, and the far field of the computational
domain. In the viscous formulation, a no-slip condition is enforced on the ship hull. For the inviscid case, flow tangency is preserved. On the symmetry plane (that portion of the (x,z) plane excluding the ship hull) derivatives in the y direction as well as the v component of velocity are set to zero. The upstream plane has u=Uo, v=0, w=0 and ψ=0 (p=–zFr–2). Similar conditions hold on the outer boundary plane which is assumed far enough away from the hull such that no disturbances are felt. A radiation condition should be imposed on the outflow domain to allow the wave disturbance to pass out of the computational domain. Although fairly sophisticated formulations may be devised to represent the radiation condition, simple extrapolations proved to be sufficient in this work.
For calculations in the limit of zero Froude number (double-hull model) the (x,y) plane is also treated as a symmetry plane.
3
Numerical Solution
The formulation of the numerical solution procedure is based on a finite volume method (FVM) for the bulk flow variables (u,v,w and ψ), coupled to a finite difference method for the free surface evolution variables (β and ψ).
Bulk Flow Solution
The finite volume solution for the bulk flow follows the same procedures that are well documented in references [8, 9]. The governing set of differential flow equations are expressed in the standard form for artificial compressibility [15] as outlined by Rizzi and Eriksson [16]. In particular, letting w be the vector of dependent variables:
wt*+(f–fv)x+(g–gv)y+(h–hv)z=0 (2)
Here f,g,h and fv,gv,hv represent, respectively, the inviscid and viscous fluxes.
Following the general procedures used in the finite volume formulation, the governing differential equations are integrated over an arbitrary volume V. Application of the divergence theorem on the convective and viscous flux term integrals yields
(3)
where Sx, Sy and Sz are the projections of the area ∂V in the x, y and z directions, respectively. In the present approach the computational domain is divided into hexahedral cells. Two discretization schemes are considered in the present work. They differ primarily in that in the first, the flow variables are stored at the grid points (cell-vertex) while in the second they are stored in the interior of the cell (cell-center). While the details of the computation of the fluxes are different for the two approaches, both cell-center and cell-vertex schemes yield the following system of ordinary differential equations [13]
where Cijk and Vijk are the discretized evaluations of the convective and viscous flux surface integrals appearing in equation 3 and Vijk is the volume of the computational cell. In practice, the discretization scheme reduces to a second order accurate, nondissipative central difference approximation to the bulk flow equations on sufficiently smooth grids. A central difference scheme permits odd-even decoupling at adjacent nodes which may lead to oscillatory solutions. To prevent this “unphysical” phenomena from occurring, a dissipation term is added to the system of equations such that the system now becomes
(4)
For the present problem a fourth derivative background dissipation term is added. The dissipative term is constructed in such a manner that the conservation form of the system of equations is preserved. The dissipation term is third order in truncation terms so as not to detract from the second order accuracy of the flux discretization.
Discretization of the Viscous Terms
The discretization of the viscous terms of the Navier Stokes equations requires an approximation to the velocity derivatives ![]() in order to calculate the stress tensor. In order to evaluate the derivatives one may apply the Gauss formula to a control volume V with the boundary S.
in order to calculate the stress tensor. In order to evaluate the derivatives one may apply the Gauss formula to a control volume V with the boundary S.
where nj is the outward normal. For a hexahedral cell this gives
(5)
where ûi is an estimate of the average of ui over the face. Alternatively, assuming a local transformation to computational coordinates ξj, one may apply the chain rule
(6)
Here the transformation derivatives ![]() can be evaluated by the same finite difference formulas as the velocity derivatives
can be evaluated by the same finite difference formulas as the velocity derivatives ![]() In this case
In this case ![]() is exact if u is a linearly varying function.
is exact if u is a linearly varying function.
For a cell-centered discretization (figure 2a) ![]() is needed at each face. The simplest procedure is to evaluate
is needed at each face. The simplest procedure is to evaluate ![]() in each cell, and to average
in each cell, and to average ![]() between the two cells on either side of a face. The resulting discretization does not have a compact stencil, and supports undamped oscillatory modes. In a one dimensional calculation, for example,
between the two cells on either side of a face. The resulting discretization does not have a compact stencil, and supports undamped oscillatory modes. In a one dimensional calculation, for example, ![]() would be discretized as
would be discretized as ![]() [17]. In order to produce a compact stencil
[17]. In order to produce a compact stencil ![]() may be estimated from a control volume centered on each face, using formulas (5) or (6). This is computationally expensive because the number of faces is much larger than the number of cells. In a hexahedral mesh with a large number of vertices the number of faces approaches three times the number of cells.
may be estimated from a control volume centered on each face, using formulas (5) or (6). This is computationally expensive because the number of faces is much larger than the number of cells. In a hexahedral mesh with a large number of vertices the number of faces approaches three times the number of cells.
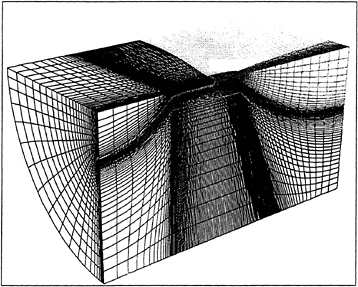
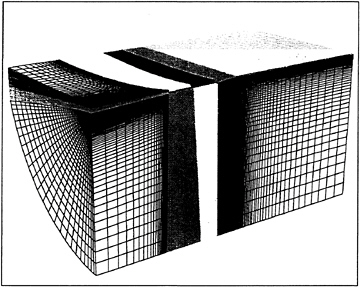
This motivates the introduction of dual meshes for the evaluation of the velocity derivatives and the flux balance as sketched in figure 2. The figure
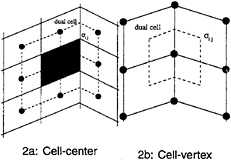
Figure 2: Viscous discretizations for cell-centered and cell-vertex algorithms.
shows both cell-centered and cell-vertex schemes. The dual mesh connects cell centers of the primary mesh. If there is a kink in the primary mesh, the dual cells should be formed by assembling contiguous fractions of the neighboring primary cells. On smooth meshes comparable results are obtained by either of these formulations [23, 24, 25]. If the mesh has a kink, the cell-vertex scheme has the advantage that the derivatives ![]() are calculated in the interior of a regular cell, with no loss of accuracy.
are calculated in the interior of a regular cell, with no loss of accuracy.
Multigrid time-stepping
Equation 4 is integrated in time to steady state using an explicit multistage scheme. For each bulk flow time step, the grid, and thus Vijk, is independent of time. Hence equation 4 can be written as
(7)
where the residual is defined as
Rijk (w)=Cijk (w)–Vijk (w)–Dijk (w)
and the cell volume Vijk is absorbed into the residual for clarity.
The full approximation multigrid scheme of this work uses a sequence of independently generated coarser meshes by eliminating alternate points in each coordinate direction. In order to give a precise description of the multigrid scheme, subscripts may be used to indicate the grid. Several transfer operations need to be defined. First the solution vector on grid k must be initialized as
where wk–1 is the current value on grid k–1, and Tk,k–1 is a transfer operator. Next it is necessary to transfer a residual forcing function such that the solution grid k is driven by the residuals calculated on grid k–1. This can be accomplished by setting
where Qk,k–1 is another transfer operator. Then Rk(wk) is replaced by Rk (wk)+Pk in the time- stepping scheme. Thus, the multistage scheme is reformulated as
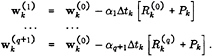
The result ![]() then provides the initial data for grid k+1. Finally, the accumulated correction on grid k has to be transferred back to grid k–1 with the aid of an interpolation operator Ik–1,k. Clearly the definition of Tk,k–1,Qk,k–1,Ik–1,k depends on whether a cell-vertex or a cell-center formulation is selected. A detailed account can be found in reference [22].
then provides the initial data for grid k+1. Finally, the accumulated correction on grid k has to be transferred back to grid k–1 with the aid of an interpolation operator Ik–1,k. Clearly the definition of Tk,k–1,Qk,k–1,Ik–1,k depends on whether a cell-vertex or a cell-center formulation is selected. A detailed account can be found in reference [22].
With properly optimized coefficients, multistage time-stepping schemes can be very efficient drivers of the multigrid process. In this work we use a five stage scheme with three evaluation of dissipation [ 17] to drive a W-cycle of the type illustrated in Figure 3.
In a three-dimensional case the number of cells is reduced by a factor of eight on each coarser grid. On examination of the figure, it can therefore be seen that the work measured in units corresponding to a step on the fine grid is of the order of
1+2/8+4/64+…<4/3,
and consequently the very large effective time step of the complete cycle costs only slightly more than a single time step in the fine grid.
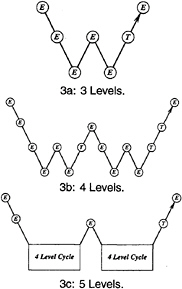
Figure 3: Multigrid W-cycle for managing the grid calculation. E, evaluate the change in the flow for one step; T, transfer the data without updating the solution.
Free Surface Solution
Both a kinematic and dynamic boundary condition must be imposed at the free surface which require the adaption of the grid to conform to the computed surface wave. Equation 1 can be cast in a form more amenable to numerical computations by introducing a curvilinear coordinate system that transforms the curved free surface β(x,y) into computational coordinates β(ξ,η). This results in the following transformed kinematic condition
βt*+ũβξ+![]() βη=w (8)
βη=w (8)
where ũ and ![]() are contravariant velocity components given by
are contravariant velocity components given by
ũ=uξx+vξy=(uyη–vxη) J–1
![]() =uηx+vηy=(vxξ–uyξ) J–1
=uηx+vηy=(vxξ–uyξ) J–1
and J=xξyη–xηyξ is the Jacobian.
Equation 8 is essentially a linear hyperbolic equation, which in our original method was discretized by central differences augmented by high order diffusion [8,9]. Such a scheme can be obtained by introducing anti-diffusive terms in a standard first order formula. In particular, it is well known that for a one-dimensional scalar equation model, central difference approximation of the derivative may be corrected by adding a third order dissipative flux:
(9)
where ![]() at the cell interface. This is equivalent to the scheme which we have used until now to discretize the free surface, and which has proven to be effective for simple hulls. However, on more complex configurations of interest, such as combatant vessels and yachts, the physical wave at the bow tends to break. This phenomenon cannot be fully accounted for in the present mathematical model. In order to avoid the overturning of the wave and continue the calculations lower order dissipation must be introduced locally and in a controlled manner. This can be accomplished by borrowing from the theory of non-oscillatory schemes constructed using the Local Extremum Diminishing (LED) principle [19, 20]. Since the breaking of a wave is generally characterized by a change in sign of the velocity across the crest, it appears that limiting the antidiffusion purely from the upstream side may be more suitable to stabilize the calculations and avoid the overturning of the waves [21]. By adding the anti-diffusive correction purely from the upstream side one may derive a family of UpStream Limited Positive (USLIP) schemes:
at the cell interface. This is equivalent to the scheme which we have used until now to discretize the free surface, and which has proven to be effective for simple hulls. However, on more complex configurations of interest, such as combatant vessels and yachts, the physical wave at the bow tends to break. This phenomenon cannot be fully accounted for in the present mathematical model. In order to avoid the overturning of the wave and continue the calculations lower order dissipation must be introduced locally and in a controlled manner. This can be accomplished by borrowing from the theory of non-oscillatory schemes constructed using the Local Extremum Diminishing (LED) principle [19, 20]. Since the breaking of a wave is generally characterized by a change in sign of the velocity across the crest, it appears that limiting the antidiffusion purely from the upstream side may be more suitable to stabilize the calculations and avoid the overturning of the waves [21]. By adding the anti-diffusive correction purely from the upstream side one may derive a family of UpStream Limited Positive (USLIP) schemes:
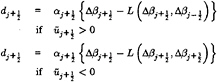
Where L(p,q) is a limited average of p and q with the following properties:
P1. L(p,q)=L(p,q)
P2. L(αp,αq)=αL(p,q)
P3. L(p,p)=p
P4. L(p,q)=0 if p and q have opposite signs.
A simple limiter (α-mean) which limits the arithmetic mean by some multiple of the smaller of |p| or |q|, has been used with success. It may be cast in the following form:
It is well known that schemes which strictly satisfy the LED principle fall back to first order accuracy at extrema even when they realize higher order accuracy elsewhere. This
|
Properties P1–P3 are natural properties of an average, whereas P4 is needed for the construction of an LED scheme. |
difficulty can be circumvented by relaxing the LED requirement. Therefore the concept of essentially local extremum diminishing (ELED) schemes is introduced as an alternative approach. These are schemes for which, in the limit as the mesh width Δx ![]() 0, maxima are non-increasing and minima are non-decreasing. In order to prevent the limiter from being active at smooth extrema it is convenient to set
0, maxima are non-increasing and minima are non-decreasing. In order to prevent the limiter from being active at smooth extrema it is convenient to set
where D(p,q) is a factor designed to reduce the arithmetic average, and become zero if u and v have opposite signs. Thus, for an ELED scheme we take
D(p,q)=1–R(p,q) (10)
where
(11)
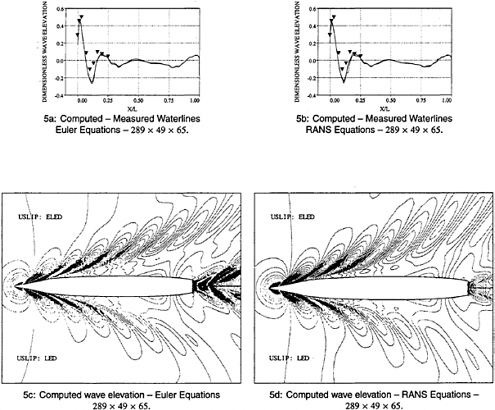
and ![]() >0, r is a positive power, and s is a positive integer. Then D(p,q)=0 if p and q have opposite signs. Also if s=1, L(p,q) reduces to minmod, while if s=2, L(p,q) is equivalent to Van Leer's limiter. By increasing s one can generate a sequence of limited averages which approach a limit defined by the arithmetic mean truncated to zero when p and q have opposite signs. These smooth limiters are known to have a benign effect on the convergence to a steady state of compressible flows. Figures 5a and 5b compare waterline profiles on a combatant vessel using ELED and LED methods in the free surface dissipation. One can see that, when compared with the experimental data, the ELED (solid line) profile is more accurate. Figures 5c and 5d show overhead free surface contours for the same geometry. The ELED scheme gives better resolution of the far field waves in solution of both the Euler and RANS equations.
>0, r is a positive power, and s is a positive integer. Then D(p,q)=0 if p and q have opposite signs. Also if s=1, L(p,q) reduces to minmod, while if s=2, L(p,q) is equivalent to Van Leer's limiter. By increasing s one can generate a sequence of limited averages which approach a limit defined by the arithmetic mean truncated to zero when p and q have opposite signs. These smooth limiters are known to have a benign effect on the convergence to a steady state of compressible flows. Figures 5a and 5b compare waterline profiles on a combatant vessel using ELED and LED methods in the free surface dissipation. One can see that, when compared with the experimental data, the ELED (solid line) profile is more accurate. Figures 5c and 5d show overhead free surface contours for the same geometry. The ELED scheme gives better resolution of the far field waves in solution of both the Euler and RANS equations.
Integration and Coupling with The Bulk Flow
The free surface kinematic equation may be expressed as
where Qij(β) consists of the collection of velocity and spatial gradient terms which result from the discretization of equation 8.
Once the free surface update is accomplished the pressure is adjusted on the free surface such that
ψ(n+1)=β(n+1)Fr–2.
The free surface and the bulk flow solutions are coupled by first computing the bulk flow at each time step, and then using the bulk flow velocities to calculate the movement of the free surface. After the free surface is updated, its new values are used as a boundary condition for the pressure on the bulk flow for the next time step. The entire iterative process, in which both the bulk flow and the free surface are updated at each time step, is repeated until some measure of convergence is attained: usually steady state wave profile and wave resistance coefficient.
Since the free surface is a material surface, the flow must be tangent to it in the final steady state. During the iterations, however, the flow is allowed to leak through the surface as the solution evolves towards the steady state. This leakage, in effect, drives the evolution equation. Suppose that at some stage, the vertical velocity component w is positive (cf. equation 1 or 8). Provided that the other terms are small, this will force βn+1 to be greater than βn. When the time step is complete, ψ is adjusted such that ψn+1> ψn. Since the free surface has moved farther away from the original undisturbed upstream elevation and the pressure correspondingly increased, the velocity component w (or better still q · n where ![]() and F=z–β(x,y)) will then be reduced. This results in a smaller Δβ for the next time step. The same is true for negative vertical velocity, in which case there is mass leakage into the system rather than out. Only when steady state has been reached is the mass flux through the surface zero and tangency enforced. In fact, the residual flux leakage could be used in addition to drag components and pressure residuals as a measure of convergence to the steady state.
and F=z–β(x,y)) will then be reduced. This results in a smaller Δβ for the next time step. The same is true for negative vertical velocity, in which case there is mass leakage into the system rather than out. Only when steady state has been reached is the mass flux through the surface zero and tangency enforced. In fact, the residual flux leakage could be used in addition to drag components and pressure residuals as a measure of convergence to the steady state.
This method of updating the free surface works well for the Euler equations since tangency along the hull can be easily enforced. However, for the Navier-Stokes equations the no-slip boundary condition is inconsistent with the free surface boundary condition at the hull/waterline intersection. To circumvent this difficulty the computed elevation for the second row of grid points away from the hull is extrapolated to the hull. Since the minimum spacing normal to the hull is small, the error due to this should be correspondingly small, comparable with other discretization errors. The treatment of this intersection for the Navier-Stokes calculations, should be the subject of future research to find the most accurate possible procedure.
4
Parallelization Strategy
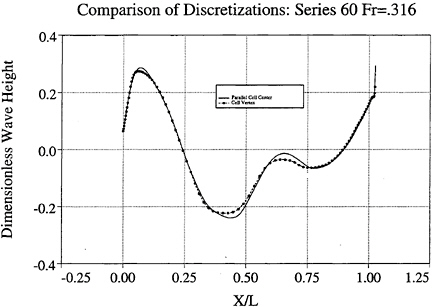
The objective of a fast flow solver for design and analysis motivates parallel implementation. The method of domain decomposition is utilized for this work. The grid is divided into sections which are sent to separate processors for solution. This method is very compatible with the cell-center flux discretization. In the cell-vertex scheme, processors corresponding to adjoining sections of the mesh must update coincidental locations on the common face. Thus both single processor and parallel versions of the code have been developed using the cell-center formulation. Figure 6 displays
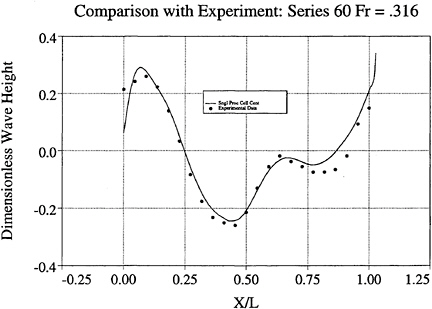
validation of the parallel, cell-center version by comparison with the previously developed, single processor, cell-vertex code. Figure 7 displays comparison between a single processor cell-center code and experimental data. Figures 8 and 9 show overhead wave profiles around the Model 5415 hull [26] for speeds of 15 and 20 knots respectively. These were computed using the cell-center discretization and the limited free surface dissipation described in section 3. Figure 14 displays pressure contours on the bulbous bow of the 5415 using this method. The parallelization strategy has been developed and extensively tested thus far using a single block implementation. Due to topological constraints, more complicated geometries cannot be treated with a single block structured mesh. As an example, the racing yacht pictured in figure 15 has multiple appendages which result in skewness and lowered efficiency of a single block grid. Transom sterns and inclusion of propellers cause similar difficulties. To circumvent these problems, a multiblock version of the code is currently being developed.
Single Block Parallel Implementation
The initial three-dimensional meshes for the hull calculations are generated using the GRIDGEN [27].
The computer code is parallelized using a domain decomposition model, a SPMD (Single Program Multiple Data) strategy, and the MPI (Message Passing Interface) Library for message passing. The choice of message passing library was determined by the requirement that the resulting code be portable to different parallel computing platforms as well as to homogeneous and heterogeneous networks of workstations [29].
Communication between subdomains is performed through halo cells surrounding each subdomain boundary. Since both the convective and the dissipative fluxes are calculated at the cell faces (boundaries of the control volumes), all six neighboring cells are necessary, thus requiring the existence of a single level halo for each processor in the parallel calculation. The dissipative fluxes are composed of third order differences of the flow quantities. Thus, at the boundary faces of each cell in the domain, the presence of the twelve neighboring cells (two adjacent to each face) is required. For each cell within a processor, Figure 4 shows which neighboring cells are required for the calculation of convective and dissipative fluxes. For each processor, some of these cells will lie directly next to an interprocessor boundary, in which case, the values of the flow variables residing in a different processor will be necessary to calculate the convective and dissipative fluxes.
In the finest mesh of the multigrid sequence, a two-level halo was sufficient to calculate the convective and dissipative fluxes for all cells contained in each processor. In the coarser levels of the multigrid sequence, a single level halo suffices since a simplified model of the artificial dissipation terms is used.
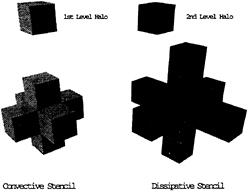
Figure 4: Convective and Dissipative Discretization Stencils.
Similar constructs are required for the free surface solution. A double halo of free surface locations is passed across interprocessor boundaries.
The communication routines used are all of the asynchronous (or non-blocking) type. In the current implementation of the program, each processor must send and receive messages to and from at most 6 neighboring processors (left and right neighbors in each of the three coordinate directions). The communication is scheduled such that at every instant in time pairs of processors are sending/receiving to/from one another in order to minimize contention in the communication schedule.
For a given number of subdomains in a calculation, there are several ways to partition the complete mesh according to the scheme explained above. Depending on the choice of partitions, the bounding surface area of each subdomain will vary, reaching a minimum when the sizes in each of the three coordinate directions are equal. Figure 10 shows an H-O grid around a combatant ship divided into 8 subdomains corresponding to 8 processors. Currently the partition of the global mesh is an input to the code, but work is in progress to determine, in a pre-processing step, the optimal block distribution in order to minimize the communication requirements. Efficiency of the parallelization is is a function of many factors, including numerical discretization, system of equations, choice of hardware/software, number of processors, and size of the mesh. The granularity, or ratio of bytes a processor passes to work it performs, helps quantify several of these aspects. The lower the granularity, the higher the efficiency. Switching to a more complex set of equations, for example, a RANS set, increases the amount of processor effort with only a small effect on the total message passes. Granularity decreases. Cutting a given mesh into more pieces(processors), or equivalently, using a coarser mesh, increases the ratio of
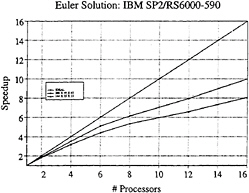
interprocessor faces to interior cells which is directly proportional to the granularity, and efficiency decays. Figure 11 displays parallel performance for the Euler equations, evaluated on an IBM SP2, a distributed memory machine, and confirms the good scalability of our algorithm. The effects of increasing the number of processors and increasing the size of the mesh are both apparent. Results of parallel RANS solvers under development in our laboratory for aeronautical applications confirm the theoretical efficiency increase that will be obtained when viscous fluxes are switched on.
Multiblock Parallel Implementation
The essential algorithm (convective and dissipative flux calculation, multigrid, viscous terms, etc.) is exactly the same as the one applied to the single block case. The only difference resides in the fact that an additional outer loop over all the blocks in the domain is added [28]. The parallelization strategy, however, is quite different. Similarly to the single block code, the multiblock is parallelized using a domain decomposition model, a SPMD strategy, and the MPI Library for message passing. Since the sizes of the blocks can be quite small, sometimes further partitioning severely limits the number of multigrid levels that can be used in the flows. For this reason, it was decided to allocate complete blocks to each processor.
The underlying assumption is that there always will be more blocks than processors available. If this is the case, every processor in the domain would be responsible for the computations inside one or more blocks. In the case in which there are more processors than blocks available, the blocks can be adequately partitioned during a pre-processing step in order to at least have as many blocks as processors. This approach has the advantage that the number of multigrid levels that can be used in the parallel implementation of the code is always the same as in the serial version. Moreover, the number of processors in the calculation can now be any integer number, since no restrictions are imposed by the partitioning in all coordinate directions used by the single block program.
The only drawback of this approach is the loss of the exact load balancing that one has in the single block implementation. All blocks in the calculation can have different sizes, and consequently, it is very likely that different processors will be assigned a different total number of cells in the calculation. This, in turn, will imply that some of the processors will be waiting until the processor with the largest number of cells has completed its work and parallel performance will suffer. The approach that we have followed to solve the load balancing problem is to assign to each processor, in a pre-processing step, a certain number of blocks such that the total number of cells is as close as possible to the exact share for perfect load balancing.
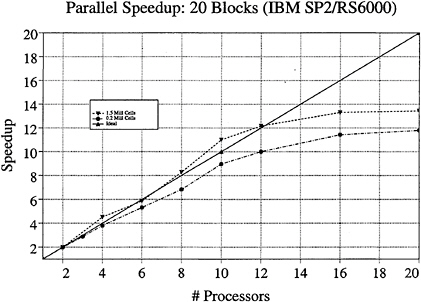
One must note that load balancing based on the total number of cells in each processor is only an approximation to the optimal solution of the problem. Other variables such as the number of blocks, the size of each block, and the size of the buffers to be communicated play an important role in proper load balancing, and are the subject of current study. The implementation is fully scalable. Figure 12 shows an H-O grid around the Model 5415 hull divided into 20 blocks. Figure 13 shows speedups obtained on the 5415 for the zero Froude number condition. The shapes in the curves results from an interplay of forces. Increased cache hits push the curve to a superlinear (better than ideal) region. The wiggles are a result of deviations in the load balance from unity, or equal work (number cells) in each processor. Since the blocks are not all equal in size, the constraint that blocks are not shared among processors causes the taper as the number of processors approaches the number of blocks in the grid.
Conclusion
By utilizing a cell-center formulation suitable for parallel computing, flow solutions about complex geometries on the order of a half hour for a grid size up to one million mesh points have been achieved on 16 processors of an IBM SP2. Such efficiency makes our methodology suitable for routine calculations in the early stages of ship design. Also, an extension to the computation of unsteady flows has been made feasible by the speedup. Underwater control surfaces and transom sterns warrant the necessity of multiblock meshes. Preliminary testing of a multiblock version displays the scalability and efficiency of the method.
Acknowledgment
Our work has benefited greatly from the support of the Office of Naval Research through Grant N00014–93-I-0079, under the supervision of Dr. E.P.Rood. The selection, and implementation of the parallelization strategy presented here is the fruit of extensive collaborations with other students of the Princeton University CFD Laboratory. In particular we wish to acknowledge the contribution of Juan J.Alonso, and Andrey Belov.
REFERENCES
[1] Toda, Y., Stern, F., and Longo, J., “Mean-Flow Measurements in the Boundary Layer and Wake and Wave Field of a Series 60 CB=0.6 Ship Model-Part 1: Froude Numbers 0.16 and 0.316,” Journal of Ship Research, v. 36, n. 4, pp. 360–377, 1992.
[2] Longo, J., Stern, F., and Toda, Y., “Mean-Flow Measurements in the Boundary Layer and Wake and Wave Field of a Series 60 CB=0.6 Ship Model-Part 2: Effects on Near-Field Wave Patterns and Comparisons with Inviscid Theory,” Journal of Ship Research, v. 37, n. 1, pp. 16–24, 1993.
[3] Hino, T., “Computation of Free Surface Flow Around an Advancing Ship by the Navier-Stokes Equations,” Proceedings,
Fifth International Conference on Numerical Ship Hydrodynamics, pp. 103–117, 1989.
[4] Miyata, H., Zhu, M., and Wantanabe, O., “Numerical Study on a Viscous Flow with Free-Surface Waves About a Ship in Steady Straight Course by a Finite-Volume Method,” Journal of Ship Research , v. 36, n. 4, pp. 332–345, 1992.
[5] Tahara, Y., Stern, F., and Rosen, B., “An Interactive Approach for Calculating Ship Boundary Layers and Wakes for Nonzero Froude Number,” Journal of Computational Physics, v. 98, pp. 33–53, 1992.
[6] Chen, H.C., Patel, V.C., and Ju, S., “Solution of Reynolds-Averaged Navier-Stokes Equations for Three-Dimensional Incompressible Flows,” Journal of Computational Physics, v. 88, pp. 305–336, 1990.
[7] Rosen, B.S., Laiosa, J.P., Davis, W.H., and Stavetski, D., “SPLASH Free-Surface Flow Code Methodology for Hydrodynamic Design and Analysis of IACC Yachts,”, The Eleventh Chesapeake Sailing Yacht Symposium, Annapolis, MD, 1993.
[8] Farmer, J.R., Martinelli, L., and Jameson, A., “A Fast Multigrid Method for Solving the Nonlinear Ship Wave Problem with a Free Surface,” Proceedings, Sixth International Conference on Numerical Ship Hydrodynamics, pp. 155–172, 1993.
[9] Farmer, J.R., Martinelli, L., and Jameson, A., “A Fast Multigrid Method for Solving Incompressible Hydrodynamic Problems with Free Surfaces,” AIAA Journal, v. 32, no. 6, pp. 1175– 1182, 1994.
[10] Jameson, A., “Optimum Aerodynamic Design Using CFD and Control Theory,” Proceedings, 12th Computational Fluid Dynamics Conference, San Diego, California, 1995
[11] Belov, A., Martinelli, L., Jameson, A., “A New Implicit Algorithm with Multigrid for Unsteady Incompressible Flow Calculations,” AIAA Paper 95–0049, June 1995
[12] Farmer, J.R., Martinelli, L., and Jameson, A., “Multigrid Solutions of the Euler and Navier-Stokes Equations for a Series 60 Cb=0.6 Ship Hull For Froude Numbers 0.160, 0.220 and 0.316,” Proceedings, CFD Workshop Tokyo 1994, Tokyo, Japan, March 1994.
[13] Jameson, A., “A Vertex Based Multigrid Algorithm For Three Dimensional Compressible Flow Calculations,” ASME Symposium on Numerical Methods for Compressible Flows, Annaheim, December 1986.
[14] Baldwin, B.S., and Lomax, H., “Thin Layer Approximation and Algebraic Model for Separated Turbulent Flows,” AIAA Paper 78–257, AIAA 16th Aerospace Sciences Meeting, Reno, NV , January 1978.
[15] Chorin, A., “A Numerical Method for Solving Incompressible Viscous Flow Problems, ” Journal of Computational Physics, v. 2, pp. 12–26, 1967.
[16] Rizzi, A., and Eriksson, L., “Computation of Inviscid Incompressible Flow with Rotation,” Journal of Fluid Mechanics, v. 153, pp. 275–312, 1985.
[17] Martinelli, L., “Calculations of Viscous Flows with a Multigrid Method,” Ph.D. Thesis, MAE 1754-T, Princeton University, 1987.
[18] Farmer, J., “A Finite Volume Multigrid Solution to the Three Dimensional Nonlinear Ship Wave Problem,” Ph.D. Thesis, MAE 1949-T, Princeton University, January 1993.
[19] A.Jameson, “Analysis and design of numerical schemes for gas dynamics 1, artificial diffusion, upwind biasing, limiters and their effect on multigrid convergence,” Int. J. of Comp. Fluid Dyn., To Appear.
[20] A.Jameson, “Analysis and design of numerical schemes for gas dynamics 2, artificial diffusion and discrete shock structure,” Int. J. of Comp. Fluid Dyn., To Appear.
[21] J.Farmer, L.Martinelli, A.Jameson, and G.Cowles, “Fully-nonlinear CFD techniques for ship performance analysis and design,” AIAA paper 95–1690, AIAA 12th Computational Fluid Dynamics Conference, San Diego, CA, June 1995.
[22] A.Jameson, “Multigrid algorithms for compressible flow calculations,” In Second European Conference on Multigrid Methods, Cologne, October 1985. Princeton University Report MAE 1743.
[23] L.Martinelli and A.Jameson, “Validation of a multigrid method for the Reynolds averaged equations, ” AIAA paper 88– 0414, 1988.
[24] L.Martinelli, A.Jameson, and E.Malfa, “Numerical simulation of three-dimensional vortex flows over delta wing configurations,” In M.Napolitano and F.Sabbetta, editors, Proc. 13th International Conference on Numerical Methods in Fluid Dynamics, pages 534–538, Rome, Italy, July 1992. Springer Verlag, 1993.
[25] F.Liu and A.Jameson, “Multigrid Navier-Stokes calculations for three-dimensional cascades, ” AIAA paper 92–0190, AIAA 30th Aerospace Sciences Meeting, Reno, Nevada, January 1992.
[26] T.Ratcliffe W.Lindenmuth, “Kelvin Wake Measurements Obtained on Five Surface Ship Models,” DTRC Report DTNSRDC 89/038
[27] J.Steinbrenner J.Chawner, “User's Manual for Gridgen,”
[28] J.Reuther, A.Jameson, J.Farmer, L.Martinelli, and D.Saunders, “Aerodynamic Shape Optimization of Complex Aircraft Configurations via an Adjoint Formulation,” AIAA Paper 96– 0094, AIAA 34th Aerospace Sciences Meeting, Reno, NV, January 1996.
[29] J.Alonso, and A.Jameson “Automatic Aerodynamic Optimization on Distributed Memory Architectures, ” AIAA paper 96–0409, AIAA 34th Aerospace Sciences Meeting, Reno, NV, January 1996.