Validation of Incompressible Flow Computation of Forces and Moments on Axisymmetric Bodies Undergoing Constant Radius Turning
C.-H.Sung, T.-C.Fu, M.Griffin, T.Huang (David Taylor Model Basin, USA)
ABSTRACT
A numerical approach based on multiblock, multigrid, local refinement and preconditioning methods has been developed to solve the incompressible Reynolds-averaged Navier-Stokes (RANS) equations. Three-dimensional flow computations for axisymmetric bodies at angles of attack and yaw with and without steady turn are presented. In solving engineering problems, a numerical solution is considered “converged” after 4 to 5 orders of magnitude drop in the root-mean-square residual of the pressure and is considered grid-independent if all of the computed flow variables change less than 1% after the grid space has been reduced by at least a 50% increase in the grid cells in all three directions. Computations on four grids: 24×8×12, 48×24×32, 96×48×64 and 144×48×72 were performed to study the behavior of convergence and grid sensitivity. It is concluded that the solution with the 144×48×72 grid for bodies at incidence is both converged and grid independent. The convergence rate is fast and is on the order of 1.5×10–5 cpu second per grid point per multigrid cycle based on a computation on a grid with 0.5 million grid cells on a single Cray C90 processor. The accuracy in the prediction of the forces and moments at various incidence angles is as good as the experimental accuracy (±5%). To achieve this level of accuracy, it is essential to use a k-ω turbulence model and to modify the standard Baldwin-Lomax turbulence model for the effects of the thick boundary layer near the stern and the cross-flow separation near the leeward side as the angle of attack increases. Both modifications are described. The converged solutions with the 96×64×48 grid for body undergoing steady turns at various angles of attack and yaw may still be grid dependent. However, the computed forces and moments are within ±20% of the measured results and the trends of the computed results are in agreement with the data. The unique features of separated flow fields associated with turning bodies at combined angles of attack and yaw are illustrated. The present work has made a significant advance towards the accurate prediction of the forces and moments acting on axisymmetric bodies at various angles of attack and yaw with and without steady turns, which is an essential step towards the accurate hydrodynamic prediction on realistic maneuvering vehicles for practical design purposes.
INTRODUCTION
Recent advances in Computational Fluid Dynamics (CFD) based on the numerical solutions of the Reynolds-Averaged Navier-Stokes (RANS) equations have demonstrated the capability to simulate complex turbulent flows of practical interest. Two major requirements for practical engineering applications are computational speed and accuracy. In particular, the computational accuracy must meet the accuracy required by the designers in order for a computer code to be really useful. One of the most challenging problems today in CFD is the prediction of the forces and moments acting on a realistic body at high Reynolds numbers on the order of 106 to 109 with computational accuracy within ±5% of the measured data. To meet the stringent requirements of speed and accuracy, sophisticated numerical techniques must be implemented. The purpose of this paper is to demonstrate that the speed and accuracy requirements can be met in the prediction of the forces and moments acting on the bodies of revolution at a Reynolds number on the order of 107 and at a wide range of incident angles. The accuracy of forces and moments predictions for a turning axisymmetric body at various angles attack and yaw achieved is about ±20%. This achievement is a key step towards the realization of using a computer code as a practical design tool for maneuvering marine vehicles.
The computer code used in this paper is called IFLOW and has been developed by the authors over
the past few years (References 1–5). IFLOW incorporates most of the recently developed numerical techniques, including multiblock, multigrid, local refinement, preconditioning, and adaptive artificial dissipation model. The code is designed for general-purpose applications. It can be used for arbitrary 2D and 3D complex geometries and it can also be used to solve both steady and unsteady problems. At present, only the k-ω and the modified Baldwin-Lomax turbulence model are actively being used. These two simple models are quite adequate for attached turbulent boundary layer flows. Modifications of Baldwin-Lomax model are necessary because of some unique flow characteristics often encountered in ship hydrodynamic applications. These include the so-called thick boundary layers near ship sterns and the cross-flow separations typically occurring on maneuvering vehicles. In this paper, the numerical schemes implemented will be described and the modifications necessary to overcome the difficulties mentioned above will be presented. Practical definitions of a converged solution, a grid-independent solution and two measures of errors are given. The computed results on the 4 grids are then analyzed based on the definitions given.
NUMERICAL METHOD
The three-dimensional, incompressible, Reynolds-averaged Navier-Stokes equation is solved using the artificial compressibility approach first proposed by Chorin6 and subsequently generalized and improved by Turkel.7–8 This approach has been successfully used by Chang and Kwak9 and many others. The origin of the body coordinate system is fixed at the center of gravity of the vehicle as shown in Fig.1. The xb-axis is along the longitudinal axis of the vehicle with the positive xb pointing forward, yb in lateral direction with the yb positive pointing to the starboard, and zb in normal direction with the positive zb pointing downward. Fig.2 shows the velocity and angle of inclination of an axisymmetric body undergoing steady right turn. The turning radius is denoted by R turn and the body with a total length L is rotating around a center point C with an angular velocity Ω in the positive z direction (pointing downward). The velocity components [u, v, w] and angular velocity components [p, q, r] relative to the body fixed axes [xb, yb, zb]. The coordinate system attached to the rotating center C is [x, y, z]. The angles of attack and drift α and β are related to the velocity components by sin β=–v/U and tan α= +w/u, where U2=u2+v2+w2. For a constant radius steady turn we have x=xb, z=zb y=yb-Rturn, when α=β=0. In hydrodynamics the orientation of a body in space is usually described in terms of angles of yaw (ψ), then of pitch (θ), and finally of roll (![]() ) and has the following relationship:
) and has the following relationship:
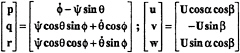
When the axisymmetric body executes a constant radius steady turn, the heading angular velocity is equal to the angular velocity of turn ![]() and the angles of pitch and roll (
and the angles of pitch and roll (![]() =0) are constant. Then:
=0) are constant. Then:
Let τc.f. be the local resultant cross flow angle positive clockwise (looking forward) with respect to the body coordinate yb (positive starboard). Then:
In this case α=θ and β=ψ. The nondimensional turning angular velocity ![]()
![]() for small angles of pitch and yaw, where Rturn is the turning radius and L is the body length.
for small angles of pitch and yaw, where Rturn is the turning radius and L is the body length.
The formulation of IFLOW developed at the David Taylor Model Basin is based on the following conservative formulation
(1)
where the subscripts indicate partial differentiations with respect to time t, and the three Cartesian coordinates x, y, and z. The preconditioned matrix Po in the conservative form and the column vectors of the dependent variable q and fluxes F, G, H and the source term S are defined as
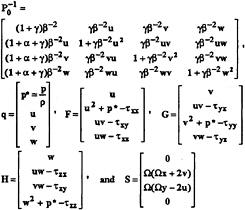
(2)
where p is the pressure, ρ is the constant density, u, v and w are the three Cartesian velocity components. The Reynolds stresses are defined as
(3)
where u=(u, v, w), x=(x, y, z), v is the sum of the kinematic and eddy viscosities, and RL is the Reynolds number based on the body length. The variables are nondimensionalized in the conventional manner.
The three parameters α, β–2, and γ are the preconditioning parameters to be determined for fast convergence. The spatial discretization is based on the cell-centered central difference finite-volume formulation in the semi-discrete form. An explicit one-step, five-stage Runge-Kutta time-stepping scheme is used. In this scheme the artificial dissipation term is evaluated only at the first, third and fifth stage with an appropriate weighting at each stage to increase the stability limit. Specifically, the parabolic stability limit along the real axis has been raised to 9 which has some advantage in stability when solving the Navier-Stokes equations. The techniques used to accelerate the rate of convergence are particularly emphasized. They include preconditioning, bulk viscous damping, local time-stepping, implicit residual smoothing, adaptive artificial dissipation and multigrid.1,2
Multiblock Multigrid Local Refinement Technique
The multigrid method developed by Jameson10 to accelerate the convergence of a system of hyperbolic equations has been adopted. By the cyclic use of a sequence of fine to coarse grids, the multigrid technique is very effective in damping the solution modes with long wave lengths which are primarily responsible for slow convergence. V-, W-, and F-cycle multigrid techniques have been implemented. Boundary conditions are updated at each Runge-Kutta stage at every grid level in the fine-to-coarse path, but they are not updated in the coarse-to-fine path. This practice is mainly to avoid introducing boundary condition interpolation errors to finer grids. For ease of coding the grid cell number in each coordinate direction for a coarse grid is half of that used in the next finer grid.
A new numerical technique based on multiblock, multigrid and local refinement methods has been implemented in IFLOW. In this approach, the computational grid is generated in the following manner: A very fine grid with a sufficiently large number of grid cells to achieve the desired resolution including the near wall region is first generated. In complex geometry, a multiblock structure may be used. The purpose of the multiblock structure is designed mainly to make the grid generation of complex geometries easier and smoother. The grid is then locally refined by patches of finer meshes in the regions where flow variation is relatively rapid. Thus, the final grid will have a hierarchical structure with different mesh levels, blocks and zones. The grid spacing of the fine grid is kept at one half of the next coarser grid spacing as in the standard multigrid. The solution procedure is the following: First, a global solution is obtained by a standard multigrid method on a global grid with the multiblock structure. The resolution of the global solution is then successively improved by a local refinement technique which is also based on the multigrid method for fast convergence. The coupling of multigrid and local refinement is the main difference between the present method and the conventional local refinement methods. Numerical instability and lack of flux conservation may occur in the coarse/fine grid interface. The possibility of these numerical difficulties is believed to be greatly minimized by using the present local refinement method for the following reason. In the present method, the finer mesh is embedded entirely in the next coarser mesh while in the conventional methods, the fine and coarse meshes are connected only by the coarse/fine grid interface. Clearly the communication between the fine and coarse mesh is much better in the present method. The communication is further enhanced by the use of the multigrid technique. Despite all the arguments, it has been found that although it is easy to maintain continuity of the mean flow variables such as the pressure and the mean velocity across the coarse/fine interface, the continuity across the interface is much harder to achieve with the shear stress near the wall. This is an area which requires further research.
Preconditioning Technique
Preconditioning is a method used to reduce the condition number of the iterative methods in linear algebra. This concept used to accelerate the rate of convergence was applied by Chorin6 to obtain the steady-state solution of the incompressible flow problems. Chorin introduced an artificial time derivative of the pressure to the continuity equation with a multiplicative variable β which has the physical meaning of the speed of sound. Since the speed of sound in incompressible flow is much faster than the fluid velocity, the system of the governing equations is very stiff with a large condition number. Consequently, the rate of convergence of the numerical solution will be very slow. However, if only the steady-state solution is of interest and the accuracy during the transient state is not of concern then the value of β can be kept on the
same order of magnitude as the fluid velocity during the transient state. In this manner, the condition number is small and the rate of convergence will be significantly improved. This is the so called artificial compressibility method and is a primitive form of preconditioning. Rewriting the system of equations in conservative form (1) in nonconservative form
P–1qt+Aqx+Bqy+Cqz=0 (4)
where q=(p,u,v,w)t. The preconditioning matrix P–1 in nonconservative form is different from Po–1 in conservative formulation and is given by
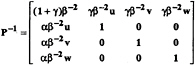
(5)
Appropriate choice of the three preconditioning parameters α, β, and γ can improve convergence and stability. It can also improve the accuracy in the sense that a smaller amount of artificial dissipation can be used. Therefore, a smaller numerical diffusion is introduced in the solution. The original Chorin preconditioning is obtained by setting α=0 and γ=0. The condition gives a symmetric precondition and ensures that the system of partial differential equations (4) is well-posed. Recent numerical experimentation indicates that an optimal choice of the preconditional parameters is
α=1, γ=0 and β–2=max(|u|2,εβ), εβ=0.7 (6)
This can be understood by an observation that the four eigenvalues of the characteristic matrix have the same magnitude (implying a condition number of 1).
To maintain numerical stability, a proper amount of artificial dissipation must be added to the right hand side of (4)
qt+PAqx+PBqy+PCqz =|PA|qxxxx+|PB|qyyyy+|PC|qxxxx (7)
Thus for conservation formulation:
(8)
The present formulation shown in (8) for the incompressible flow with preconditioning parameters given in (6) is equivalent to the highly accurate matrix dissipation technique demonstrated by Swanson and Turkel11 and Turkel and Vatsa12 for the compressible flow.
Boundary Conditions
The boundary conditions used on the solid wall of a rotating body are that the three velocity components and the normal pressure gradient are set equal to zero:
u=v=w=0, and
(9)
The far field inflow boundary conditions relative to the rotating system are based on the prescribed values for the three velocity components and pressure:
[u, v, w, p]=[Ωy, –Ωx, 0, po], (10)
The far field outflow boundary conditions are based on a zero-gradient for the three velocity perturbation components and a non-reflecting condition for the pressure:
[u, v, w]=[Ωy+u′, –Ωx+v′, w′],
![]() •
•![]() [u′, v′, w′]=0, p: nonreflecting (11)
[u′, v′, w′]=0, p: nonreflecting (11)
The non-reflecting boundary condition used here evolved from the technique developed in Hedstrom13, and Rudy and Strikewerda14 and is particularly important for computation when a relatively small computational domain is used as in the present computation. This condition is obtained by setting the time derivative of the characteristic variable corresponding to the wave coming into the computational domain as described by Sung.15
Turbulence Model
The standard k-ω turbulence model16 and Baldwin-Lomax turbulence model17 with modifications are used in this paper. The standard two-equation k-ω model developed by Wilcox16 is used in this paper,
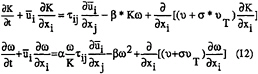
Where ![]()
Near the wall: ![]()
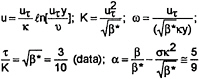
The model can be extended to treat flow transition and surface roughness (Wilcox16).
The Baldwin-Lomax formulation of the eddy viscosity without using the boundary layer displacement thickness is easier to implement than the equivalent model of Cebeci and Smith.18 Crucial to the model is the maximum value Fmax of the F-function defined as F(y)=ylωl[1–e–y+/A+] and ymax of the corresponding value of y where Fmax occurs. Modification of them and the correct way to locate them constitute the main changes to the standard Baldwin-Lomax turbulence model.
Two major modifications are made to overcome the difficulties arising from (1) the so-called thick boundary layer unique in ship hydrodynamic application occurring near the ship stern and (2) the cross-flow separation in a maneuvering vehicle. Both difficulties result in excessive eddy viscosity causing the mean velocity to be overpredicted and the flow separation to be delayed or suppressed.
Two corrections are needed to overcome the difficulty in the thick boundary layer. The experimental data of Huang, et al.19,20,21 indicate that the mixing length computed by a standard eddy viscosity model is approximately twice as large compared to the mixing length derived from the experimental data near the stern where the body cross sectional area is rapidly diminishing. A correction on the outer eddy viscosity near the stern has been proposed by Huang.19,20,21 The other correction is an attempt to account for the effect of the adverse pressure gradient which also occurs near the stern and has been discussed in Refs. 3 and 4. In the symmetric wake of a single axisymmetric body or a two-dimensional foil, the modified eddy viscosity of Renze, Buning, and Rajagopalan 22 is considered.
The second modification to account for the cross-flow separation is the most crucial to accurate prediction of the forces and moments. As the incidence angle increases, the cross-flow separation eventually results in vortex roll-up which then departs from the body. As a result, another local maximum of the F-function occurs near center of the departing concentrated vorticity in addition to the local maximum near the center of the attached wall shear layer. Since the distance to the wall of the departing vortex can be several orders of magnitude larger than that of the wall shear layer, the predicted eddy viscosity may be several orders of magnitude too large and flow separation is likely to be delayed or suppressed. The problem of multiple peaks just described has been reported by Degani and Schiff 23 and they have also proposed a method to locate the correct peak in the wall shear layer, or the so-called first peak. The modification of the Baldwin-Lomax model made by them has been implemented in IFLOW. The search for the first peak has been found to be notoriously difficult and unreliable. This difficulty has been overcome by using a method where a range is first defined and then a maximum is searched for just inside the range.
RESULTS AND DISCUSSION
Solution Convergence and Grid-Independent Solution
Validation of computed results with measured data must be performed with care. This is because both computation and experiment have their own errors and, in addition, there are many factors which can affect the computed result but can not be precisely defined. In general, code validation can be meaningful only if the numerical solution can be shown to have converged and is also grid independent. It is possible to drive the convergence to machine zero but it will not be necessary nor practical to make such a demand for real engineering problems. It is our experience after many comparisons between computations and experiments that a numerical solution can be considered as converged after 4 to 5 orders of magnitude drop in theroot-mean-square residual of the pressure. It is even harder to give a meaningful definition of grid independence for practical engineering problems. Nevertheless, a numerical solution will be called grid independent if the pressure, mean velocity components, the shear stress, and the force and moment do not change more than 1% after the grid space has been reduced by at least a 50% increase in grid cells in all three directions.
Solution Convergence
The optimal preconditioning described by (6) has been implemented in IFLOW. The overall quality of the optimal preconditioning technique is illustrated in Figs.3 through 5. The residual is defined as the RMS difference between the nondimensional pressures at the current and previous multigrid cycles. Fig.3 shows that the residuals drop to machine zero in about 2000 iterations for a 24×8×12 grid and in about 4000 iterations for a 48×24×32 grid of a SUBOFF axisymmetric body at angles of attack of 0 and 16 degrees. Fig.4 illustrates the rates of convergence for a 144×48×72 grid at various angles of attack. The reduction of residuals by 4 or 5 orders of magnitude can be
achieved very quickly for all angles of attack. The residual continues to drop for zero angle of attack but not for higher angles of attack. This probably implies that the grid quality must be refined for higher angles of attack in order to further improve the convergence rate. Fig.5 demonstrates the rates of convergence for the flow on DTMB body1 executing steady starboard turn. Both 0° and 8° yaw angles with a constant turning radius of Rturn=1.54L are included in Fig.5. A 48×32×24 grid and a 96×48×32 grid are used. The reduction of residuals by 4 orders of magnitude can also be achieved within 100 iterations for turning computations. During the course of computation it was noted that grid cells with large aspect ratios and rapid variation of two adjacent grid spacings tend to reduce the rate of convergence. In order to improve the rate of convergence the values of y1+, the aspect ratios of grid cells, and the variation of adjacent grid spacings must be carefully controlled and must also be adapted to the flow field characteristics. How adapted grid distributions to improve the rate of convergence is an area for further research. It is important to note that the present computational speed of 1.5 ×10–5 cpu second per grid cell per multigrid cycle in a single Cray C90 processor has been achieved for all angles of attack with the one-half million grid cells.
Grid-Independent Solution
To identify a grid independent solution, computations on 4 grids: ((axial)×(circumferential)× (normal))=24×8×12, 48×24×32, 96×48×64 and 144×48×72 were performed. The outflow boundary is located 2.5 body lengths downstream of the tail of the body and the outer boundary is about 0.68 body lengths. The grid distributions in the axial and circumferential directions were selected with finer grids concentrated in rapidly changing flow regions such as the nose, tail and near the leeward side where the flow separates. The distribution in the direction normal to the wall is made so that the boundary layer characteristics on the hull can be resolved. This requires that the maximum value of y1+ be limited to less than 7 and the average value of y1+ not to exceed 5. Comparison of the results from the 96×32×48 and 144×48×72 grids shows that the computed pressure, the mean velocity, force and moment differ by less than 1% and the shear stress differs by less than 2%. Thus the computed solutions based on a 96×32×48 grid and a 144×48×72 grid satisfy the definition of a grid-independent solution for an axisymmetric body at incidence. Because of limited experience in computing a turning axisymmetric body, we are not sure that a 96×48×32 grid presented in this paper had achieved the grid-independent solution. The present computed force and moment coefficients are within the ±20% of the unpublished measured data. The computed results have revealed many unique flow features associated with a turning axisymmetric body, especially at combined yaw and pitch.
Error Analysis
Two measures of error will be used. One is the root-mean-square (RMS) value of the difference between the reference and the solution to be compared denoted as vf and vc respectively. The second measure is the distance weighted average angle error. They are defined respectively as
RMS Error,
(12)
Distance Weighted Average Angle Error,
(13)
where ![]() and
and
where N is the total number of data values used in the comparison. These definitions can also be applied to experimental data. Applying these error measures to the computed results shown in Fig.6 gives the following error estimates.
Computed Force and Moment on Axisymmetric Bodies at Incidence
The comparison of the computed (144×48×72 and 96×32×48 grids) and the measured values of the axial force X, normal force Z, and the pitching moment M for the SUBOFF (L/D=8.6) body is shown in Fig.6 and for Body 1 (L/D=11.0), Albacore (L/D=7.3), and DTMB Model 4156 (L/D=6.0) in Fig. 7. These models cover the range of typical underwater vehicle geometry. The experiments were conducted in the Deep Water Basin of the David Taylor Model Basin by Roddy.24 The measurements of the Albacore body were made by Dempsey25 in the same model basin. The unpublished data for Body 1 and Model 4156 were also obtained by Dempsey using the same measuring apparatus in the same facility. The measurement uncertainties of the data are estimated to be 5% for the normal force and pitch moment and 15% for the axial force. It is important to note that both the RMS errors of the computed axial and normal forces and the pitching moment for all the axisymmetric bodies at incidence shown in Figs.6 and 7 are all within 5% from the faired
measured data when either the standard k-ω or the modified Baldwin-Lomax turbulence model is used with either the 96×32×48 or 144×48×72 grid. The standard Baldwin-Lomax turbulence model underpredicts the magnitudes of the normal force and overpredicts the magnitudes of the pitching moment. The present work has made a significant advance towards the accurate prediction of the forces and moments on the axisymmetric bodies at incidence. This achievement is an essential step towards the prediction of the forces and moments on maneuvering vehicles.
Computed Force, Moment, and Flow Field on Axisymmetric Bodies Undergoing Steady Turns
Using the nomenclature shown in Figs.1 and 2, the nondimensional forces [X', Y', Z'] and moments [K', M', N'] coefficients are the linear forces [X, Y, Z] along the body axes divided by ρU2L2/2 and moments [K, M, N] about the body axes by ρU2L3/2. The nondimensional turning radius is denoted by r'=L/Rturn=Ω/(U/L), where U=ΩRturn. The unpublished DTMB data of Bedel, et al., obtained in the DTMB Rotating Arm Facility with an uncertainty of ±20% are used to compare the computed force and moment coefficients. This type of comparison can only be used to guide the development computational capability for maneuvering applications and may not be used for rigorous code validation.
When the axisymmetric body executing a constant radius right turns at a zero angle of attack and yaw, the body is subjected to a negative side force (–Y) due to centrifugal force and a negative yawing moment (–N), and they are in the plane of motion. The computed and measured unbalance “in-plane” side force and yawing moment coefficients, Y' and N', are shown in Fig.8 for the DTMB body 1 at various turning radii. The amplitude of both –Y' and N increase with decreasing turning radius, Rturn, or increasing nondimensional yaw rate r'=L/Rturn. The computed values agree with the measured data to within ±20%.
The effect of yaw angle on the “in-plane” axial force (drag=–X), side force and yawing moment coefficients are shown in Fig.9 for the nondimensioal turning radius of r'=0.65 at zero angle of attack. As expected the drag coefficient increases with increasing yawing angle during a turn. The negative values of side force and yawing moment coefficients, –Y' and –N', decrease with increasing yawing angle. It is interesting to note that the zero yawing moment is at yaw angle equal to about 10 degrees. Again the computed values agree with the measured data to within ±20%.
Fig.10 shows the computed and measured vertical force and pitch moment coefficients, Z' and M', which is out of the plane of motion. It is important to note that the “out-of plane” pitching moment coefficient increases with increasing pitch angle for the body at zero yaw angle; this is a destabilizing condition. The “out-of-plane” pitch moment coefficient, however, decreases with increasing pitch angle for body at 12° yaw angle; this becomes a stabilizing condition. The combination of yaw and pitch angles during a turn can produce drastic different stability conditions for a body undergoing a steady turn.
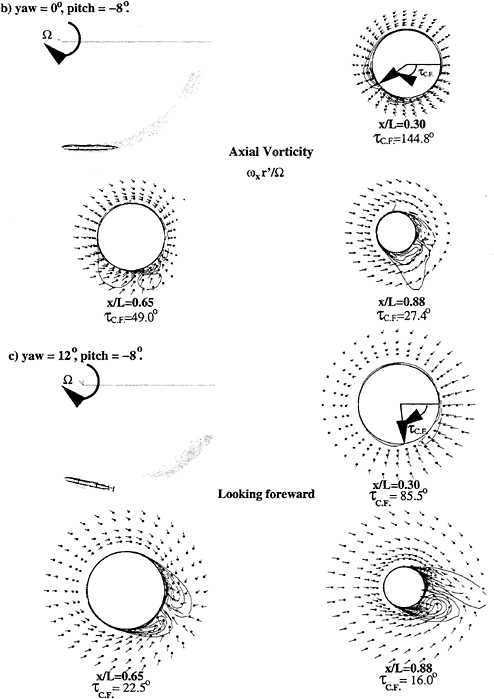
The separated flow fields associated a turning body at combined angles of attack and yaw are very complex. Fig.11 shows the computed vorticity field of a starboard turning body at pitch angle equal to –4°. positive clockwise (looking forward) with respect to Recall that τc.f. is the local resultant cross flow angle yb.
When θ=ψ=0, then τc.f. is zero. Upstream of the center of gravity (C.G.) xb is positive, the resultant cross flow points to port. The dotted cross flow vector shown in Fig.11 indicates the cross flow at the body nose (xb=![]() C.G.–
C.G.–![]() , and
, and ![]() =0 is at the body nose and points to the stern). The resultant cross flow points to starboard for negative xb (solid cross flow vector Shown in Fig.11). The resultant cross flow is in the plane of motion and changes direction at C.G.. The separated flow field is symmetrical with respect to the yb axis shown in Fig 11a. When the body with a pitch angle of –8° is executing a port turn as shown in Fig.11b, the resultant cross-flow angle is no longer in the plane of motion and changes direction along the body. The separated flow is no longer symmetrical with respect to the yb axis. The variation of cross-flow angle along the body axis shown in Fig.11b is caused by the combined negative pitch angle of –8° and the nondimensional turn rate of r'=0.65. Under these conditions the cross-flow angle for a left turning body is τc.f.=tan– 1[0.2162/(xb/L)]. The computed vorticity field of a starboard turning body at a combination of yaw and pitch angles equal to 12°, and –8° is shown in Fig11c. The variation of cross-flow caused by combination of yaw and pitch angles and turning rate of r'=0.65 are shown in Fig.11c. The solid and dotted vectors indicate the directions of the local cross flow and reference cross flow at the body nose. As indicated in Fig.10, the cross flow variation along the body axis has a profound influence on the “out-of-plane” forces and moments. It is the first time that this type of complex flow has satisfactorily been predicted by a Reynolds-Averaged Navier-Stokes (RANS) calculation and the computed forces and moments are within the measurement uncertainties.
=0 is at the body nose and points to the stern). The resultant cross flow points to starboard for negative xb (solid cross flow vector Shown in Fig.11). The resultant cross flow is in the plane of motion and changes direction at C.G.. The separated flow field is symmetrical with respect to the yb axis shown in Fig 11a. When the body with a pitch angle of –8° is executing a port turn as shown in Fig.11b, the resultant cross-flow angle is no longer in the plane of motion and changes direction along the body. The separated flow is no longer symmetrical with respect to the yb axis. The variation of cross-flow angle along the body axis shown in Fig.11b is caused by the combined negative pitch angle of –8° and the nondimensional turn rate of r'=0.65. Under these conditions the cross-flow angle for a left turning body is τc.f.=tan– 1[0.2162/(xb/L)]. The computed vorticity field of a starboard turning body at a combination of yaw and pitch angles equal to 12°, and –8° is shown in Fig11c. The variation of cross-flow caused by combination of yaw and pitch angles and turning rate of r'=0.65 are shown in Fig.11c. The solid and dotted vectors indicate the directions of the local cross flow and reference cross flow at the body nose. As indicated in Fig.10, the cross flow variation along the body axis has a profound influence on the “out-of-plane” forces and moments. It is the first time that this type of complex flow has satisfactorily been predicted by a Reynolds-Averaged Navier-Stokes (RANS) calculation and the computed forces and moments are within the measurement uncertainties.
CONCLUSIONS
An incompressible Reynolds-averaged Navier-Stokes computational procedure has been presented. Numerous computations were carried out on axisymmetric bodies at various angles of attack and yaw, with and without a steady turn to investigate the effects of grid sensitivity and turbulence model on the computed flows and the forces and moments acting on the body. We consider that a numerical solution is “converged” after 4 to 5 orders of magnitude drop in the root-mean-square residual of the pressure. We define that a solution is grid-independent when all the computed flow variables change less than 1% after the grid space has been reduced by at least a 50% increase in grid cells in all three directions.
The standard k-ω and modified Baldwin-Lomax turbulence models are used in this paper. Two simple modifications of the standard Baldwin-Lomax turbulence model were made: one for the ship stern flows where the boundary layer is thick and the other for the flows with cross-flow separations. The accuracy in the prediction of the forces and moments at various incidence angles using the two turbulence models with a 144×48×72 grid is as good as the experimental accuracy (within ±5% of the measured data).
The converged solutions with the 96×48×64 grid for a body undergoing steady turns at various angles of attack and yaw may still be grid dependent. However, the computed forces and moments for a body undergoing steady turns at various angles of attack and yaw agree with the measured results to within ±20% and the trends of the computed results are in agreement with the data. The unique features of separated flow fields associated with turning bodies at combined angles of attack and yaw were illustrated.
The present work has made a significant advance towards the accurate prediction of the forces and moments acting on axisymmetric bodies at various angles of attack and yaw with and without steady turns. This advance is an essential step towards the accurate prediction of the forces and moments on realistic maneuvering vehicles for practical design purposes.
It has been observed that when the average values of y1+ of the first grid cell center from the wall is smaller than 5, both the RMS and average angle error between all the measured forces and moments are within the measurement uncertainties. Present computations indicate that multiblock (for complex geometry), multigrid (for fast solution) and local refinement (for efficient use of grid cells) techniques implemented in the computer code called IFLOW is fast. A typical computation based on one half million grid cells requires 300 multigrid cycles using 37 cpu minutes of a single Cray C90 processor to reduce the pressure residual by 5 to 6 orders of magnitude. This implies a speed of approximately 1.5×10–5 cpu seconds per grid point per multigrid cycle in a single Cray C90 processor.
ACKNOWLEDGMENT
This work was supported by the Office of Naval Research under the Fluid Dynamics Programs, element 61153N. We are grateful for the technical support of the ONR scientific officers, Dr. L.P. Purtell and Mr. James A.Fein. The authors appreciate the contributions of our long time friends, Mr. W.E.Smith and Dr. M.Martin for their tutor and introduction to the prediction techniques and flow physics associated with vehicle maneuvers. The concept of asymmetric flow separation from an axisymmetic body caused by combined rotation, pitch, and yaw was first developed by Dr. M.Martin (1991) and then refined by Drs. M.Martin and M.S. Chang (1994). The authors thank our colleagues, Mr. R.M.Curphey and Dr. M.S.Chang, for their technical discussions during the course of this work.
REFERENCES
1. Sung, C.-H., and Griffin, M.J., “Improvement in Incompressible Turbulent Horseshoe Vortex Juncture Flow Calculations,” AIAA Paper 91–0022, AIAA 29th Aerospace Sciences Meeting, Reno, Nevada, January 7–10, 1991.
2. Sung, C.-H., Griffin, M.J., and Coleman, R.M., “Numerical Evaluation of Vortex Flow Control Devices,” AIAA paper 91–1825, AIAA 22nd Fluid Dynamics, Plasma Dynamics & Laser Conference, Honolulu, Hawaii, June 24–26, 1991.
3. Tsai, J.F., Sung, C.H., Griffin, M.J., and Huang, T.T., “Effects of Grid Resolution on Axisymmetric Stern Flows Computed by an Incompressible Viscous Flow Solver,” paper presented at the ASME Summer Fluids Engineering Conference, FED-Vol. 158, pp 99–108, June 20–24, 1993.
4. Sung, C.-H., Tsai, J.F., Huang, T.T., and Smith, W.E., “Effects Of Turbulence Models on Axisymmetric Stern Flows Computed by An Incompressible Viscous Flow Solver,” paper presented at the 6th International Conference on Numerical Ship Hydrodynamics , Iowa City, Iowa, August 2–5, 1993.
5. Sung, C.-H., Griffin, M.J., Huang, T.T., and Fu, T.C., “A Multiblock Multigrid Local Refinement Method for the Prediction of Double-Model Viscous Ship Flows,” paper presented at an
International Workshop for Improvement of Hull Form Designs, Tokyo, Japan, March 22–24, 1994.
6. Chorin, A.J., “A Numerical Method for Solving Incompressible Viscous Flow Problems, ” J. Comp. Phys., vol. 2, pp. 12–26, 1967.
7. Turkel, E., “Preconditioned Methods for Solving Incompressible and Low Speed Compressible Equations,” NASA ICASE Report 86–14, 1986.
8. Turkel, E.,” A Review of Preconditioning Methods for Fluid Dynamics,” Applied Numerical Mathematics, 12, pp. 257–284, 1993.
9. Chang, J.L.C., and Kwak, D., “On the Method of Pseudo Compressibility for Numerically Solving Incompressible Flows,” AIAA Paper-0252, 1984.
10. Jameson, A., “Multigrid Algorithms for Compressible Flow Calculation,” in Multigrid Methods II, Lecture Notes in Mathematics series, no. 1228 , Hackbusch, W., and Trottenberg, U. Eds., Spring-Verlag, New York, 1986.
11. Swanson, R.C. and Turkel, E., “Aspects of a High-Resolution Scheme for the Navier-Stokes Equations, ” AIAA-93–3372-CP, AIAA 11th Computational Fluid Dynamics Conference, Orlando, FL, July 6–9, 1993.
12. Turkel, E., and Varsa, V.N., “Effect of Artificial Viscosity on Three Dimensional Flow Solutions, ” AIAA 90–1444, AIAA 21st Fluid Dynamics, Plasma Dynamics and Lasers Conference , Seattle, WA, June 18–20, 1990.
13. Jameson, A., “Multigrid Algorithms for Compressible Flow Calculation,” in Multigrid Methods II”, Lecture Notes in Mathematics series, no. 1228, Hackbusch, W., and Trottenberg, U. Eds., Spring-Verlag, New York, 1986.
14. Hedstrom, G.W., “Nonreflecting Boundary Conditions for Nonlinear Hyperbolic System, ” J. Computational Physics, vol. 30, pp 222–237, 1979.
15. Rudy, D.H., and Strikewerda, J.C., “Boundary Conditions for Subsonic Compressible Navier-Stokes Equations, ” Computers and Fluids, vol. 9, pp 327–338, 1981.
16. Sung, C.-H., “An Explicit Method for 3D Incompressible Turbulent Flows,” Report DTNSRDC/SHD-1244–01, July, 1987.
17. Wilcox David C., Turbulence Modeling for CFD, DCW Industries, Inc., La Canada, CA 1993.
18. Baldwin, B.S., and Lomax, H., “Thin Layer Approximation and Algebraic Model for Separated Turbulent Flows,” AIAA 78–257, AIAA 16th Aerospace Sciences Meeting, Huntsville, Alabama, January 16–18, 1978.
19. Cebeci, T. and Smith, A.M.O., Analysis of Turbulent Boundary Layers, Academic, New York, 1974.
20. Huang, T.T., Santelli, N., Belt, G., “Stern Boundary-Layer Flow on Axisymmetric Bodies,” Paper presented at the 12th Symposium on Naval Hydrodynamics, Wash. D.C., June 5–9, 1978, National Academy of Sciences Wash. D.C., pp 127– 157, 1978.
21. Huang, T.T., Groves, N.C., and Belt, G. S., “Boundary Layer Flow on an Axisymmetric Body with an Inflected Stern, ” DTNSRDC Report 80/064, 1980.
22. Huang, T.T., Liu, H.-L., Groves, N.C., Forlini, T.J., Blanton, J.N., and Gowing, S., “Measurements of Flows Over an Axisymmetric Body with Various Appendages (DARPA SUBOFF Experiments)” Paper presented at the 19th Symposium on Naval Hydrodynamics, Seoul, Korea,
23. Renze, K.J., Buning, P.G., and Rajagopalan, R.G., “A Comparative Study of Turbulence Models for Overset Grids, paper 92–0437, AIAA 30th Aerospace Sciences Meeting, Reno, Nevada, Jan. 6–9, 1992.
24. Degani, D., and Schiff, L.B., “Computation of Turbulent Supersonic Flows around Pointed Bodies Having Crossflow Separation,” J. Comp. Phys., Vol. 66, pp 173–196, 1986.
25. Munk, Max M., “Aerodynamics of Airships,” Division Q, Volume VI, in Aerodynamics Theory, W.F.Durand, Editor-in-Chief, Dover Publications, Inc., New York, 1963.
26. Roddy, R.F., “Investigation of the Stability and Control Characteristics of Several Configurations of the DARPA SUBOFF Model (DTRC Model 5470) from Captive-Model Experiments,” David Taylor Research Center Report DTRC/SHD-1298–08, September, 1990.
27. Dempsey, E., “Static Stability Characteristics of a Systematic Series of Stern Control Surfaces on a Body of Revolution,” David Taylor Naval Ship Research and Development Center Report 77 –0085, Aug. 1977.
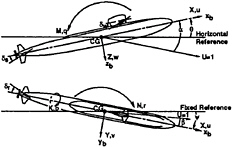
Fig. 1. Sketch showing positive directions of axes, angles, velocities, forces, and moments.
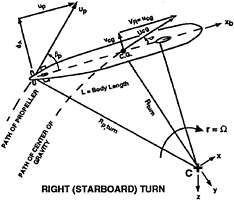
Fig. 2. Velocity and angle of inclination of a body undergoing a steady turn.
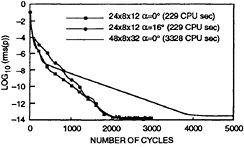
Fig. 3. Demonstration of pressure residual convergence to machine 0, SUBOFF bare hull RL=1.2×107.

Fig. 4. Demonstration of pressure residual convergence of 144×48×72 grid for various angles of attack. (2230 Cray C90 CPU seconds, RL=1.2×107).
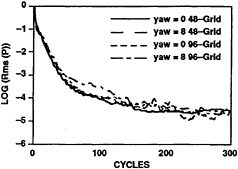
Fig. 5. Demonstration of pressure residual convergence of 96×64×48 and 48×48×32 grids for constant radius turning with yaw angles of 0° and 8°. (RL=1.4×107).

Fig. 6. Comparison of measured and computed non-dimensional axial force X′, normal force Z′, and pitching moment M′ on the SUBOFF axisymmetric body at incidence. (Grid size: 144×48×72 and 96×32×48, RL=1.2×107)
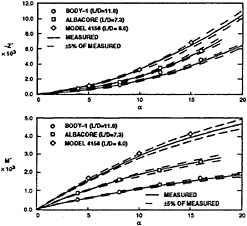
Fig. 7. Comparison of measured and computed non-dimensional normal force Z′, and pitching moment M′ on Body 1, Albacore and DTMB Model 4156 axisymmetric bodies at incidence. (Grid Size: 144×48×72, RL=1.2×107)
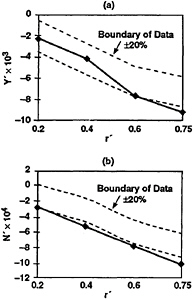
Fig. 8. Effect of nondimensional turning radius, r'=(L/Rturn) on the computed coefficients of (a) side force (Y') and (b) yawing moment (N') of DTMB Body 1, at zero yaw and pitch angle.
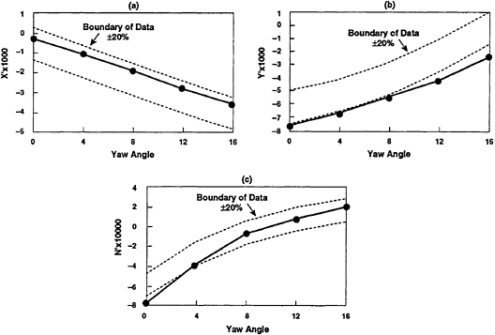
Fig. 9. Effect of yaw angle on the computed coefficient of (a) axial force (X'), (b) side force (Y'), and (c) yawing moment (N'), for DTMB Body 1 undergoing a constant radius turn of r'=(L/Rturn)=0.65.
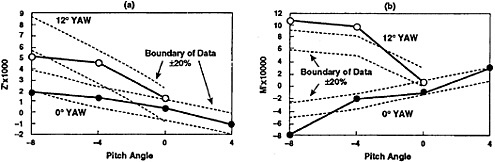
Fig. 10. Effect of pitch angle on the computed coefficient of (a) normal force (Z') and (b) pitching moment (M'), for DTMB Body 1 undergoing a constant radius turn of r'=(L/Rturn)=0.65.
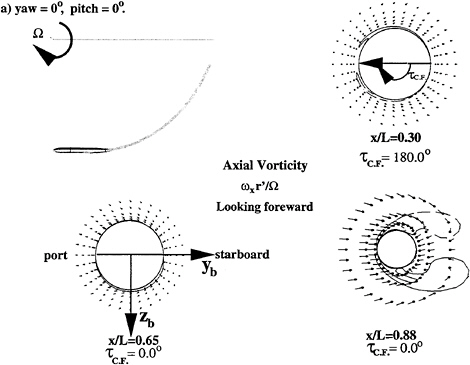
Figure 11: Computed cross flows and vorticities on a turning axisymmetric body at Re=1.4×107 and r'~0.65. Dashed contours denote negative vorticity. The magnitude of the outermost contours is 7 and the increment between contours is 15.