Fourier-Kochin Theory of Free-Surface Flows
F.Noblesse (David Taylor Model Basin, USA), X.-B.Chen (Bureau Veritas, France), C.Yang (George Mason University, USA)
ABSTRACT
A recently-developed theoretical formulation of wave diffraction-radiation by a ship advancing in regular waves is summarized and extended. The basic results underlying the formulation, called the Fourier-Kochin theory because it is based on a Fourier representation of free-surface effects and an extension of Kochin's approach, are summarized. Two applications and extensions of the theory, to the coupling between an inner viscous flow and an outer potential flow and the representation of time-harmonic ship waves generated by an arbitrary singularity distribution, are also presented.
INTRODUCTION
For most practical purposes, the flow due to a ship advancing in waves is effectively potential and linear beyond a small distance from the ship hull, although viscous and nonlinear effects can be significant near the hull. Linear free-surface potential flows therefore are of fundamental importance in ship hydrodynamics.
A recently-developed theoretical formulation of wave diffraction-radiation by ships or offshore structures, motivated by the practical and theoretical importance of free-surface potential flows and the considerable complexities of existing calculation methods based on free-surface Green functions, is considered here. This formulation is called the Fourier-Kochin theory because it is based upon a Fourier representation of free-surface effects and an extension of the approach used by Kochin [1,2].
The basic results underlying the FK theory [3,4,5] are summarized. Two applications and extensions of the theory, to the coupling between viscous and potential flows and the representation of time-harmonic ship waves generated by an arbitrary singularity distribution, are also given.
BACKGROUND
We consider the potential flow due to a ship advancing at constant speed along a straight path through a train of regular waves in water of effectively infinite depth and lateral extent. The flow due to the ship is expressed in the usual way as the sum of the steady flow about the ship advancing in calm water and the time-harmonic flow associated with the incoming and diffracted-radiated waves. Thus, a frequency-domain analysis is considered. In addition, the steady ship waves and the time-harmonic diffracted-radiated waves are analyzed within the classical potential-flow theory.
Nondimensional coordinates ![]() time t, velocity potential
time t, velocity potential ![]() and related flow variables are defined with respect to the ship length L, the acceleration of gravity g, and the density of water ρ as basic reference units. The flow is observed from a moving system of coordinates (x,y,z) in steady translation with the mean forward speed u of the ship, and ω is the encounter frequency of the ambient waves. The nondimensional frequency and the Froude number are defined as
and related flow variables are defined with respect to the ship length L, the acceleration of gravity g, and the density of water ρ as basic reference units. The flow is observed from a moving system of coordinates (x,y,z) in steady translation with the mean forward speed u of the ship, and ω is the encounter frequency of the ambient waves. The nondimensional frequency and the Froude number are defined as ![]() and
and ![]() The x axis is along the path of the ship and points toward the bow. The z axis is vertical and points upward, and the undisturbed free surface is taken as the plane z=0.
The x axis is along the path of the ship and points toward the bow. The z axis is vertical and points upward, and the undisturbed free surface is taken as the plane z=0.
The velocity potentials of the time-harmonic and steady (f=0) flow components are defined in terms of an exponential time-growth parameter ε as lim![]() and satisfy the linear free-surface boundary condition
and satisfy the linear free-surface boundary condition
[(f+iε–iF∂x)2–∂z]![]() =0. (1)
=0. (1)
The Green function G associated with the boundary condition (1) may be expressed as
G=GS+GF (2)
where GS represents a local flow disturbance defined in terms of simple (Rankine) singularities as
4πGS=–1/r+1/r′ (3)
with ![]()
and GF accounts for free-surface effects. The free-surface component GF is given by
(4)
with ![]()
Here, ![]() and
and ![]() respectively stand for the singularity and flow-observation points. Furthermore, Dε is the dispersion function
respectively stand for the singularity and flow-observation points. Furthermore, Dε is the dispersion function
Dε=(f+iε–Fα)2–k (5a)
where ![]() is the wavenumber. The function Dε is equal to the real dispersion function D
is the wavenumber. The function Dε is equal to the real dispersion function D
D=(f–Fα)2–k (5b)
in the limit ε=0.
The velocity potential ![]() at a point
at a point ![]() of the mean wetted surface of the ship (where the normal derivative ∂
of the mean wetted surface of the ship (where the normal derivative ∂![]() /∂n is presumed known) is defined by the solution of an integral equation of the form
/∂n is presumed known) is defined by the solution of an integral equation of the form
![]() /2+χ=ψ (6a)
/2+χ=ψ (6a)
where the potentials ψ and χ respectively correspond to a-priori given and unknown distributions of sources and normal dipoles, with densities determined by the values of ∂![]() /∂n and
/∂n and ![]() , at the mean wetted hull H and the mean waterline W of the ship. The potential
, at the mean wetted hull H and the mean waterline W of the ship. The potential ![]() at a point
at a point ![]() in the mean flow domain outside H is given by
in the mean flow domain outside H is given by
![]() =ψ–χ. (6b)
=ψ–χ. (6b)
The source and dipole potentials ψ and χ in the integral equation (6a) and the flow representation (6b) can be expressed as
(7)
where the potentials ψS and χS correspond to the simple-singularity component GS in expression (2) for the Green function, and the components ψF and ![]() correspond to the free-surface component GF. Thus, the components ψS and χS and the components ψF and
correspond to the free-surface component GF. Thus, the components ψS and χS and the components ψF and ![]() defined by (16) and (17–18) in [3], are expressed in terms of source and dipole distributions involving the simple singularity GS and the free-surface term GF, respectively.
defined by (16) and (17–18) in [3], are expressed in terms of source and dipole distributions involving the simple singularity GS and the free-surface term GF, respectively.
FOURIER-KOCHIN FORMULATION
The free-surface potentials ψF and ![]() in (7) are now considered. In the usual free-surface Green-function approach, based on the Green function (2) associated with the free-surface condition (1), the Green function is evaluated and subsequently integrated over the ship hull and waterline to determine the source and dipole potentials ψ and χ. The well-known difficulties (stemming from the complex singularity of the free-surface component GF for x=ξ,y=η,z+ζ=0) involved in this classical approach are partially circumvented in Kochin's formulation, in which the surface and line distributions of sources and dipoles over the ship hull and waterline defining the free-surface components ψF and
in (7) are now considered. In the usual free-surface Green-function approach, based on the Green function (2) associated with the free-surface condition (1), the Green function is evaluated and subsequently integrated over the ship hull and waterline to determine the source and dipole potentials ψ and χ. The well-known difficulties (stemming from the complex singularity of the free-surface component GF for x=ξ,y=η,z+ζ=0) involved in this classical approach are partially circumvented in Kochin's formulation, in which the surface and line distributions of sources and dipoles over the ship hull and waterline defining the free-surface components ψF and ![]() are considered directly.
are considered directly.
Within the Fourier-Kochin formulation, the potentials ![]() and
and ![]() are defined by (24) and (12) in [3] as
are defined by (24) and (12) in [3] as
(8)
where N and ![]() are spectrum functions defined by distributions of the elementary wave function ε over the mean ship hull H and waterline W. The spectrum function
are spectrum functions defined by distributions of the elementary wave function ε over the mean ship hull H and waterline W. The spectrum function ![]() associated with the potential χ in the integral equation (6a), is called the kernel spectrum function.
associated with the potential χ in the integral equation (6a), is called the kernel spectrum function.
Two alternative mathematical representations, called the potential representation and the velocity representation because they respectively involve the potential ![]() and the velocity ∇
and the velocity ∇![]() , of the kernel spectrum function
, of the kernel spectrum function ![]() are given in [3]. The potential representation follows from Kochin's formulation in a straightforward way. The velocity representation is obtained in [3] from the potential representation via an integration by parts based on Stokes' theorem. The velocity representation of the kernel spectrum function
are given in [3]. The potential representation follows from Kochin's formulation in a straightforward way. The velocity representation is obtained in [3] from the potential representation via an integration by parts based on Stokes' theorem. The velocity representation of the kernel spectrum function ![]() is shown in [3] to provide a substantially more solid mathematical basis than the potential representation for the purpose of numerically evaluating influence coefficients. The velocity representation is also preferable for coupling viscous and potential flows, as is shown further on. Thus, only the velocity representation is considered here.
is shown in [3] to provide a substantially more solid mathematical basis than the potential representation for the purpose of numerically evaluating influence coefficients. The velocity representation is also preferable for coupling viscous and potential flows, as is shown further on. Thus, only the velocity representation is considered here.
The velocity representation of the spectrum function ![]() is defined by (65), with Δ=0, in [3]. A useful extension of this representation is obtained
is defined by (65), with Δ=0, in [3]. A useful extension of this representation is obtained
if we use the identity ![]() so that the spectrum function
so that the spectrum function ![]() can be expressed as
can be expressed as ![]() Here, D is the dispersion function (5b), the function
Here, D is the dispersion function (5b), the function ![]() is defined as
is defined as
(9)
and the function M is defined by (13b)–(13d) below. By using the relation ![]() in (8) we can express the potential
in (8) we can express the potential ![]() as
as
(10)
The potential ![]() is defined by (8) as
is defined by (8) as
(11)
where the spectrum function ![]() is given by (9). Expression (11) does not involve the dispersion function D. The analysis given in [4] shows that the potential φS therefore corresponds to a nonoscillatory near-field disturbance. Indeed, the potential φS is expressed in terms of a distribution of simple singularities further on. By substituting (10) into (7) we obtain
is given by (9). Expression (11) does not involve the dispersion function D. The analysis given in [4] shows that the potential φS therefore corresponds to a nonoscillatory near-field disturbance. Indeed, the potential φS is expressed in terms of a distribution of simple singularities further on. By substituting (10) into (7) we obtain
(12)
The superscipts S and F identify simple-singularity and free-surface components, respectively. The representation χ=(χS–φS)+χF is a modification of the representation χ=χS+![]() given in [3]. Specifically, the simple-singularity component φS is extracted from the free-surface potential
given in [3]. Specifically, the simple-singularity component φS is extracted from the free-surface potential ![]()
The free-surface potentials ![]() and
and ![]() are given by the Fourier representation
are given by the Fourier representation
(13a)
where the spectrum functions N and M are defined by (66)–(68)1 in [3] as
(13b)
The functions NH and MH and the functions NW, ![]()
![]() and
and ![]() are given by
are given by
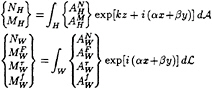
(13c)
where dA and dL are the differential elements of area and arc length of H and W. The amplitude functions ![]()
![]()
![]()
![]()
![]() and
and ![]() in (13c) are given by
in (13c) are given by
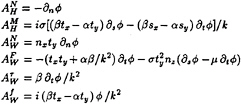
(13d)
where ![]() with
with ![]() Furthermore,
Furthermore, ![]() where the unit vector
where the unit vector ![]() is normal to H and points into the ship, and the unit vectors
is normal to H and points into the ship, and the unit vectors ![]() and
and ![]() are tangent to H . The vector
are tangent to H . The vector ![]() points downward, as is shown in Fig.1, and the vector
points downward, as is shown in Fig.1, and the vector ![]() is oriented so that
is oriented so that ![]() At the waterline, the unit vector
At the waterline, the unit vector ![]() is tangent to W, as is indicated in Fig.1.
is tangent to W, as is indicated in Fig.1.
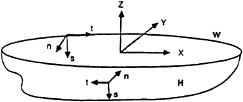
Fig.1 Definition sketch
The spectrum functions NH, NW, MH, ![]()
![]() and
and ![]() defined by (13c) and (13d) are independent of the parameters F and f, which appear as coefficients in (13b). The formulation (13) partially circumvents the difficulties associated with the free-surface component (4) in the Green function by avoiding the direct calculation of GF, which corresponds to a point source. Instead, the free-surface potentials (13a) due to surface and line distributions of sources and dipoles over the ship hull and waterline, or over hull patches and waterline arcs, are considered directly. A significant property of this approach is that the Fourier integrals (13a) are not singular because the spectrum functions N and M vanish in the large-wavenumber limit k → ∞ for a singularity distribution, whereas (4) is singular for ξ=x, η=y, ζ+z=0. Thus, the difficulties associated with the numerical integration of the free-surface component GF over a hull-panel or a waterline-segment in the vicinity of the singular point ξ=x, η=y, ζ+z=0 are
defined by (13c) and (13d) are independent of the parameters F and f, which appear as coefficients in (13b). The formulation (13) partially circumvents the difficulties associated with the free-surface component (4) in the Green function by avoiding the direct calculation of GF, which corresponds to a point source. Instead, the free-surface potentials (13a) due to surface and line distributions of sources and dipoles over the ship hull and waterline, or over hull patches and waterline arcs, are considered directly. A significant property of this approach is that the Fourier integrals (13a) are not singular because the spectrum functions N and M vanish in the large-wavenumber limit k → ∞ for a singularity distribution, whereas (4) is singular for ξ=x, η=y, ζ+z=0. Thus, the difficulties associated with the numerical integration of the free-surface component GF over a hull-panel or a waterline-segment in the vicinity of the singular point ξ=x, η=y, ζ+z=0 are
|
1 |
where Δ is set equal to 0 and an integration by parts is performed in expression (66) for the function |
avoided. In fact, the space integration over hull-panels and waterline-segments, which consists in integrating the exponential function ε in (4), is an elementary task within the FK formulation.
The simple-sigularity potentials ![]() and
and ![]() in (12) are defined by (16) in [3] as
in (12) are defined by (16) in [3] as
(14)
where ∇x=(∂x,∂y,∂z). By substituting (9) into (11) and exchanging the order in which the Fourier and space integrations are performed, we can express the potential ![]() as the waterline integral
as the waterline integral
(15a)
where ![]() is the unit vector along the z axis, Θ is the function
is the unit vector along the z axis, Θ is the function
(15b)
and ![]() is the unit vector tangent to the waterline W as was already noted.
is the unit vector tangent to the waterline W as was already noted.
COUPLING OF VISCOUS AND POTENTIAL FLOWS
In the past few years, viscous-flow calculation methods accounting for viscous and nonlinear effects, and potential-flow calculation methods (based on Rankine singularities) accounting for nonlinear free-surface effects have been developed to compute steady ship waves. These calculation methods can be used to compute the velocity field (u,v,w) at a control surface Σ chosen at a sufficiently large distance from a ship, so that the flow may be regarded as effectively potential and linear outside Σ. A linear potential-flow representation can then be used to define the potential flow outside Σ in terms of a given nonlinear and/or viscous flow inside Σ, i.e. to extend a near-field flow (predicted via any calculation method) into the far field. This approach, a weak (one-way) inner nonlinear viscous flow ⇒ outer linear potential flow coupling, can be useful to determine far-field waves and wave drag (which can be evaluated more accurately via Havelock's formula for the energy radiated in the trailing wave pattern than by integration of the hull pressure), and to analyze the far-field influence (notably upon the wave pattern and the drag) of near-field viscous and nonlinear features. Hybrid calculation methods based on a strong (two-way) inner nonlinear viscous flow ⇔ outer linear potential flow coupling have also been developed recently, e.g. [6,7], and will likely be used more widely.
This strong two-way coupling and the weak one-way coupling mentioned previously involve the basic task of determining the velocity field outside a control surface Σ enclosing a ship in terms of the velocity distribution ![]() at Σ. This task is considered here for wave diffraction-radiation by a ship. Specifically, the flow in the region outside the control surface Σ is regarded as effectively potential and linear, i.e. the classical free-surface boundary condition (1) is assumed to hold outside Σ. In the special case of a body submerged deeply enough, a closed control surface Σ may be defined. Otherwise, the surface Σ intersects the mean free-surface plane z=0 along a curve Γ.
at Σ. This task is considered here for wave diffraction-radiation by a ship. Specifically, the flow in the region outside the control surface Σ is regarded as effectively potential and linear, i.e. the classical free-surface boundary condition (1) is assumed to hold outside Σ. In the special case of a body submerged deeply enough, a closed control surface Σ may be defined. Otherwise, the surface Σ intersects the mean free-surface plane z=0 along a curve Γ.
The outer potential flow under consideration can be defined explicitly, using a well-known Green identity, if both the normal velocity ∂![]() /∂n and the potential
/∂n and the potential ![]() are known at the inner boundary surface Σ. However, this classical explicit representation of potential flows in terms of boundary values of
are known at the inner boundary surface Σ. However, this classical explicit representation of potential flows in terms of boundary values of ![]() and ∂
and ∂![]() /∂n cannot be used for a viscous inner flow, for which the potential
/∂n cannot be used for a viscous inner flow, for which the potential ![]() is not defined. The difficulty can be circumvented in a straightforward manner, employed in the matching procedure between a viscous inner flow and an outer potential flow developed in [6,7], since the potential
is not defined. The difficulty can be circumvented in a straightforward manner, employed in the matching procedure between a viscous inner flow and an outer potential flow developed in [6,7], since the potential ![]() at the surface Σ is defined in terms of the normal velocity ∂
at the surface Σ is defined in terms of the normal velocity ∂![]() /∂n at Σ via an integral equation.
/∂n at Σ via an integral equation.
A more direct and simpler alternative approach, which avoids the nontrivial task of solving an integral equation to determine the potential ![]() at Σ, to this matching procedure is expounded below. Specifically, the Fourier-Kochin formulation is used to obtain a mathematical representation of the velocity
at Σ, to this matching procedure is expounded below. Specifically, the Fourier-Kochin formulation is used to obtain a mathematical representation of the velocity ![]() in the outer potential flow region (outside Σ) that defines ∇
in the outer potential flow region (outside Σ) that defines ∇![]() explicitly in terms of a prescribed velocity distribution
explicitly in terms of a prescribed velocity distribution ![]() at Σ, i.e. that does not involve the potential
at Σ, i.e. that does not involve the potential ![]() at Σ (unlike the usual Green identity which defines
at Σ (unlike the usual Green identity which defines ![]() within a flow domain in terms of boundary values of
within a flow domain in terms of boundary values of ![]() and ∂
and ∂![]() /∂n). Furthermore, ∇
/∂n). Furthermore, ∇![]() is defined directly (not by numerical differentiation of
is defined directly (not by numerical differentiation of ![]() ).
).
By substituting (12) into (6b) we can express ![]() where ∇ξ=(∂ξ,∂η,∂ζ), in the form
where ∇ξ=(∂ξ,∂η,∂ζ), in the form
(16)
with ![]()
The component ![]() is defined by (13a) as
is defined by (13a) as
(17a)
with S=N–M. Expressions (13b)–(13d), where the ship hull H and waterline W become the control surface Σ and curve Γ, yield
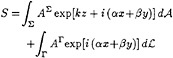
(17b)
where the functions AΣ and AΓ are given by
(17c)
(17d)
The identity ![]() at Σ was used in (17c) and (17d) and the control surface Σ is assumed to intersect the free-surface plane z=0 orthogonally. The free-surface condition (1) yields
at Σ was used in (17c) and (17d) and the control surface Σ is assumed to intersect the free-surface plane z=0 orthogonally. The free-surface condition (1) yields
f2![]() =w+2iFfu+F2∂xu. (17e)
=w+2iFfu+F2∂xu. (17e)
This relation can be used in (17d), so that expressions (17) define the free-surface component ∇ξ![]() F in terms of the velocity (u,v,w) at Σ.
F in terms of the velocity (u,v,w) at Σ.
The simple-singularity component ∇ξ(ψS–χS) is now considered. Expressions (14) readily yield
(18a)
(18b)
Expression (18a) defines the velocity field ∇ξψS in terms of the velocity distribution ∇x![]() at Σ. However, expression (18b) for the velocity field ∇ξχS involves the potential
at Σ. However, expression (18b) for the velocity field ∇ξχS involves the potential ![]() at Σ (which is not known directly if the flow inside Σ is viscous). Furthermore, (18b) involves the second derivative
at Σ (which is not known directly if the flow inside Σ is viscous). Furthermore, (18b) involves the second derivative ![]() of the simple-singularity component GS of the Green function. This second derivative is highly singular for points
of the simple-singularity component GS of the Green function. This second derivative is highly singular for points ![]() in the vicinity of Σ, so that (18b) is not well suited for numerical evaluation. A useful alternative expression for the velocity field ∇ξχS is
in the vicinity of Σ, so that (18b) is not well suited for numerical evaluation. A useful alternative expression for the velocity field ∇ξχS is
(18c)
This alternative expression defines the velocity field ∇ξχS in terms of the velocity distribution ∇x![]() at Σ and only involves the first derivative
at Σ and only involves the first derivative ![]() The simple-singularity component
The simple-singularity component ![]() in (16) is then defined by (18a) and (18c) as
in (16) is then defined by (18a) and (18c) as
(19a)
The simple-singularity component ![]() can be expressed in the form
can be expressed in the form
(19b)
with ![]() and Θ given in (15). Expressions (19) define the simple-singularity component ∇ξ(
and Θ given in (15). Expressions (19) define the simple-singularity component ∇ξ(![]() S+φS) in terms of the velocity
S+φS) in terms of the velocity ![]() at a control surface.
at a control surface.
FOURIER REPRESENTATION OF GENERIC DISPERSIVE WAVES
The most difficult aspect of the Fourier-Kochin formulation, indeed of any approach based on a Green function satisfying the free-surface condition (1), resides in the free-surface components ∇ξ![]() F, ψF and χF in the decompositions (16) and (12) into simple-singularity and free-surface components. These components are examined in [4,5], which are summarized and extended below. Expression (5a) yields Dε~ D+iεDf as ε → 0 where D is given by (5b) and Df=∂D/∂f=2(f–Fα). The dispersion function Dε in the Fourier representations (17a) and (13a) of the free-surface components ∇ξ
F, ψF and χF in the decompositions (16) and (12) into simple-singularity and free-surface components. These components are examined in [4,5], which are summarized and extended below. Expression (5a) yields Dε~ D+iεDf as ε → 0 where D is given by (5b) and Df=∂D/∂f=2(f–Fα). The dispersion function Dε in the Fourier representations (17a) and (13a) of the free-surface components ∇ξ![]() F, ψF and χF can then be replaced by D+iε sign(Df) with sign(Df)=sign(f–Fα). Thus, the Fourier representations (17a) and (13a) are of the form
F, ψF and χF can then be replaced by D+iε sign(Df) with sign(Df)=sign(f–Fα). Thus, the Fourier representations (17a) and (13a) are of the form
(20)
where φF/(4π) stands for ψF, χF, or ∇ξ![]() F, and S likewise stands for N, M, or
F, and S likewise stands for N, M, or ![]()
In a typical numerical solution procedure, spectrum functions corresponding to distributions of sources and/or dipoles over flat or curved panels are defined. These spectrum functions are of the form S=Apexp[kzp+i(αxp+βyp)] where (xp, yp, zp) define the centroids of the panels, and Ap is a slowly-varying function of α and β which vanishes as α2+β2→∞. The contribution of a panel ![]() to the free-surface potential φF is then given by
to the free-surface potential φF is then given by
with (X, Y, Z)=(ξ–xp, η–yp, ζ+zp). Expression (4) for the free-surface component GF in the Green function corresponds to the special case Ap=1/(4π) and (X, Y, Z)=(ξ–x, η–y, ζ+z).
The Fourier representation of free-surface effects defined by (20) is considered in [4,5] for a generic spectrum function S (assumed to be a slowly-varying function of α and β) and for a generic dispersion function D, so that the analysis and results given in [4,5], and below, are valid for an arbitrary distribution of singularities (sources and/or dipoles) and for a wide class of linear dispersive waves.
The Fourier integral (20) is expressed in [4] as
φF=φW+φN(21)
where φW and φN respectively correspond to a wave component and a near-field component. The near-field component φN in the decomposition (21) is significant in the near field but is negligible in comparison to the wave component φW in the far field. The wave component φW is given by a single Fourier integral along the dispersion curve(s) defined in the Fourier plane by the dispersion relation D=0. Specifically, (31a,b) in [4] yield
(22)
where ∑D=0 stands for summation over the dispersion curve(s), ds is the differential element of arc length of the dispersion curve(s), ![]() with (Dα, Dβ)=(∂αD, ∂βD), and Σ1 and Σ2 are the sign functions defined as
with (Dα, Dβ)=(∂αD, ∂βD), and Σ1 and Σ2 are the sign functions defined as
Σ1=sign(Df) (23)
and Σ2=sign(ξDα+ηDβ). These sign functions are associated with the single and double integrals ![]() 1 and
1 and ![]() 2 in (16) of [4]. The single integral
2 in (16) of [4]. The single integral ![]() 1 is obtained in the limit ε=+0 of (20). The sign function Σ2 stems from a far-field single-integral approximation of the double integral
1 is obtained in the limit ε=+0 of (20). The sign function Σ2 stems from a far-field single-integral approximation of the double integral ![]() 2. We have
2. We have
ξDα+ηDβ=h||∇D||cos(θ–γ)
where (ξ, η)=h(cosγ, sinγ) with ![]() and (Dα, Dβ)=||∇D)|| (cosθ, sinθ). The sign function Σ2, given by
and (Dα, Dβ)=||∇D)|| (cosθ, sinθ). The sign function Σ2, given by
Σ2=sign(ξDα+ηDβ)=sign[cos(θ–γ)], (24a)
is discontinuous at a point of a dispersion curve where θ=γ±π/2.
The far-field waves contained in the wave component (22) stem from the point(s) of the dispersion curve(s) where the phase ξα+ηβ is stationary, i.e. from the points defined by ξdα/ds+ηdβ/ds=0. The unit vectors (dα/ds,dβ/ds) and (Dα,Dβ)/||∇D|| are tangent and normal to a dispersion curve D=0, respectively, so that a stationary point is defined by ξDβ–ηDα=0. We have
ξDβ–ηDα=h||ΔD||sin(θ–γ),
so that the angle θ at a point of stationary phase is equal to γ or γ+π. The function Σ2 defined by (24a) is equal to
Σ2=sign(ξDα)=sign(ηDβ) (24b)
at a point of stationary phase. Expressions (24b) can be useful to represent far-field waves in regions centered around the axes η=0 and ξ=0, but are not convenient for far-field waves in the vicinity of the axes ξ=0 and η=0, respectively. The composite expression
(24c)
generalizes (24b). The differences between the four wave components associated with expressions (24) for the term Σ2 represent local flow disturbances since these expressions yield identical values of Σ2 at a stationary point. Thus, the representations of the wave component φW associated with (24) correspond to alternative decompositions into wave and near-field components. The decomposition (21) indeed is nonunique.
A more general representation of the wave component φW (and related decomposition into wave and local components) can in fact be defined. In particular, the sign function Σ2 may be taken as
Σ2=E2sign(ξDα+ηDβ) (24d)
where E2 is a real positive function that is equal to 1 at a stationary point. For instance, the function E2=exp[–tan2(θ–γ)], where we have
tan(θ–γ)=(ξDβ–ηDα)/(ξDα+ηDβ),
is equal to 1 at a stationary point ξDβ–ηDα=0 and vanishes at a point of discontinuity ξDα+ηDβ=0. The integrand of the wave integral (22) may also be multiplied by a function E that is equal to 1 at a stationary point. Two such functions are
E=exp{–C[(ξDβ–ηDα)/(ξDα+ηDβ)]2N} (25)
where C≥0 is a real constant and N≥1 is an integer, and
where ![]() is the radius of curvature of the dispersion curve at the stationary point. The latter function E is equal to 1 at a stationary point and decreases away from a stationary point at a rate independent of h and
is the radius of curvature of the dispersion curve at the stationary point. The latter function E is equal to 1 at a stationary point and decreases away from a stationary point at a rate independent of h and ![]() The radius of curvature is given by
The radius of curvature is given by
for a curve defined by the equation D(α, β)=0.
The method of stationary phase shows that the wave component (22) and the modified wave component
(26)
where any one of the four alternative expressions (24) may be used for Σ2, yield identical far-field waves. However, the near-field waves defined by (26) evidently depend on the functions E and Σ2.
The near-field component φN in the decomposition (21) is examined in [5]. The modified form of the Fourier representation (30) in [5] associated with the modified wave component (26) is
(27)
where Λr and Λi are defined by (30b,c) in [5]. It is shown in [5] that the integrand of (27) is continuous (in fact varies smoothly) across a dispersion curve, and that the Fourier representation (27) is well suited for numerical evaluation.
The Fourier representation of the generic free-surface potential (20) defined by (21), (26) and (27) is a generalization of the representation given by (5) and (30) in [5], which is obtained if E=1 and (24a) is used for Σ2. Although the sum φF of the wave component φW and the near-field component φN is independent of the functions E and Σ2, each of the two components φW and φN depends on the functions E and Σ2. In the near field, the function E may simply be chosen equal to 1. However, the function Σ2 can be chosen for the purpose of eliminating the discontinuity associated with (24a). Indeed, the term Σ2 stems from a far-field approximation of the double integral ![]() 2 in (16) of [4], as was already mentioned. This far-field approximation is not relevant in the near field, so that near-field modifications, e.g. of the form (24d), of the term Σ2 are permitted.
2 in (16) of [4], as was already mentioned. This far-field approximation is not relevant in the near field, so that near-field modifications, e.g. of the form (24d), of the term Σ2 are permitted.
The Fourier representation of (20) defined by (21), (26) and (27) is valid for generic dispersive waves and for arbitrary singularity distributions, including the special case of the Green function (i.e. a point source). Applications of this generic Fourier representation to wave diffraction-radiation by an offshore structure (without forward speed) and steady flows, and to the Green function of wave diffraction-radiation at small forward speed, are examined in [4,5]. Another application, to time-harmonic ship waves characterized by the dispersion function (5), is considered below. Only the wave component φW is considered here.
TIME-HARMONIC SHIP WAVES
The dispersion function (5b) is an even function of β, so that the dispersion curves are symmetric with respect to the axis β=0 and the integration in (26) can be restricted to the upper halves of the dispersion curves. In the upper half β≥0 of the Fourier plane, the dispersion curves are given by
(28a)
The dispersion function (5b) yields Dβ=–β/k and ![]() with
with
(28b)
so that we have
||∇D||2=1+4(τ–F2α) α/k+4(τ–F2α)2. (28c)
The term ||∇D|| is an even function of β. The element of arc length ![]() can be expressed as ds=dα ||∇D|| k/β. The sign function Σ1 defined by (23) becomes
can be expressed as ds=dα ||∇D|| k/β. The sign function Σ1 defined by (23) becomes
Σ1=sign(f–Fα) (29a)
and is an even function of β. Expression (24a) for the function Σ2 yields
(29b)
where ![]() with β≥0. The function E defined by (25) becomes
with β≥0. The function E defined by (25) becomes
(29c)
where E±=E(α,±β) and The ![]() wave component (26) then becomes
wave component (26) then becomes
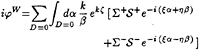
(30)
where ![]() S±=S(α,±β) and the integration is restricted to the upper halves of the dispersion curves (in the upper half plane β≥0).
S±=S(α,±β) and the integration is restricted to the upper halves of the dispersion curves (in the upper half plane β≥0).
Dispersion curves
Expression (28a) defines several distinct dispersion curves and related distinct wave components, which include systems of inner and outer V waves, complete or partial ring waves and fan waves. The dispersion curves defined by (28a) are now analyzed. Equation (28a) can be expressed as
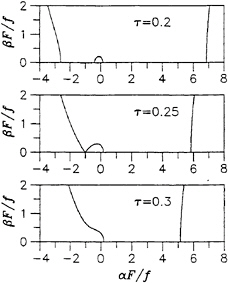
(31)
where τ=fF=uω/g is the Strouhal number. We have two or three distinct dispersion curves if τ is larger or smaller than 1/4, respectively.
If τ<1/4 the three dispersion curves intersect the axis β=0 at four values of α, denoted ![]() and
and ![]() which are given by
which are given by
(32a)
and satisfy the inequalities
(32b)
These dispersion curves are located in the regions
(32c)
if τ<1/4. We have ![]() if τ=1/4 and the dispersion curves in the regions
if τ=1/4 and the dispersion curves in the regions ![]() and
and ![]() are connected. The roots
are connected. The roots ![]() and
and ![]() are complex if τ>1/4. Thus, we have only two distinct dispersion curves located in the regions
are complex if τ>1/4. Thus, we have only two distinct dispersion curves located in the regions
(32d)
if τ>1/4. The dispersion curves defined by (31) are depicted in Fig.2 for τ=0.2, 0.25 and 0.3.
The inequalities (32b) show that the sign function Σ1 defined by (29a) is equal to
(33)
so that Σ1 in (30) is equal to 1 for all the dispersion curves except that in the region ![]()
Expressions (32a) yield ![]() and
and ![]() in the limit τ → 0, so that the values of the wavenumber k associated with the dispersion curve located in the inner region
in the limit τ → 0, so that the values of the wavenumber k associated with the dispersion curve located in the inner region ![]() are much smaller than those corresponding to the dispersion curves in the outer regions
are much smaller than those corresponding to the dispersion curves in the outer regions ![]() and
and ![]() Indeed, (32a) yield
Indeed, (32a) yield
(34)
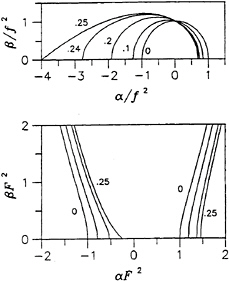
Thus, the outer dispersion curves correspond to values of the wavenumber k which are greater than 1/F2, whereas we have k ≈ f2 for the inner dispersion curve. The upper part of Fig.3 depicts the inner dispersion curve, in the frequency-scaled Fourier plane (α/f2, β/f2), for τ=0, 0.1, 0.2, 0.24, and 0.25; and the lower part of Fig.3 depicts the outer dispersion curves, in the Froude-scaled Fourier plane (F2α, F2β), for τ=0, 0.1, 0.2, and 0.25. The dispersion function (5b) shows that the outer dispersion curves are symmetric with respect to the axis α=0 in the limit τ=0; (5b) also shows that that the inner dispersion curve is given by (α/f2+2τ)2+(β/f2)2=1+O(τ2) as τ → 0, so that the inner dispersion curve is approximately a circle of radius f2 centered at (α, β)=(–2τf2, 0).
Component wave systems
For τ<1/4 the wave component φW defined by (30) can be expressed as
φW=φR+φV with φV=φoV+φiV (35a)
where the components φR, φoV and φiV respectively correspond to the dispersion curves in the inner region ![]() and the outer regions
and the outer regions ![]() and
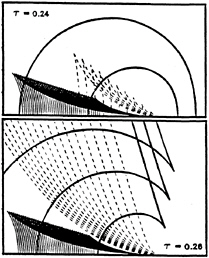
and ![]() The component φR represents a system of ring-like waves, identified hereafter as ring waves. The components φoV and φiV represent two systems of V waves contained within wedges and identified as outer V waves and inner V waves, respectively. Curves of constant phase corresponding to the ring waves (thick solid lines) and the outer (dashed lines) and inner (thin solid lines) V waves are depicted in Fig.4 for τ=0.24. In the limit τ=0, the components φR and φV represent the ring waves generated by an offshore structure without forward speed (F=0) and the Kelvin ship waves generated by a ship advancing in calm water (f=0), respectively.
The component φR represents a system of ring-like waves, identified hereafter as ring waves. The components φoV and φiV represent two systems of V waves contained within wedges and identified as outer V waves and inner V waves, respectively. Curves of constant phase corresponding to the ring waves (thick solid lines) and the outer (dashed lines) and inner (thin solid lines) V waves are depicted in Fig.4 for τ=0.24. In the limit τ=0, the components φR and φV represent the ring waves generated by an offshore structure without forward speed (F=0) and the Kelvin ship waves generated by a ship advancing in calm water (f=0), respectively.
For τ>1/4 the wave component φW given by (30) can be expressed in the form
φW=φRF+φiV (35b)
where the components φRF and φiV are respectively associated with the dispersion curves in the regions ![]() and
and ![]() The component φiV represents a system of inner V waves, qualitatively similar to the inner V waves φiV in (35a), contained within a wedge. The component φRF represents a system of incomplete ring waves and
The component φiV represents a system of inner V waves, qualitatively similar to the inner V waves φiV in (35a), contained within a wedge. The component φRF represents a system of incomplete ring waves and
fan waves, identified as ring-fan waves, that are also contained within a wedge. The system of ring-fan waves can be further divided into a system of inner fan waves and a system of partial ring and outer fan waves, which correspond to the portions –∞≤α≤–f/F and ![]() of the dispersion curve in the range
of the dispersion curve in the range ![]() Constant-phase curves corresponding to the partial ring and outer fan waves (thick solid lines), the inner fan waves (dashed lines), and the inner V waves (thin solid lines) are depicted in Fig.4 for τ=0.26.
Constant-phase curves corresponding to the partial ring and outer fan waves (thick solid lines), the inner fan waves (dashed lines), and the inner V waves (thin solid lines) are depicted in Fig.4 for τ=0.26.
General features of component waves
For τ<1/4, Fig.4 shows that curves of constant phase for the outer V waves and the inner V waves are contained within wedges and are cusped at the wedge boundaries. Let θo and θi represent the wedge angles (i.e. the angles between the ship track and the cusp lines) for the outer and inner V waves, respectively. In the limit τ=0 the outer and inner wedge angles θo and θi are identical and equal to the Kelvin angle 19°28′. The wedge angles θo and θi increase and decrease monotonically in the range 0≤τ≤1/4, respectively, and we have
19°28′≤θo≤54°44′, 19°28′≥θi≥15°48′
for 0≤τ≤1/4. The angle θo increases rapidly for values of τ in the vicinity of 1/4.
For τ>1/4, Fig.4 shows that the ring-fan waves also have a cusp, at an angle with respect to the ship track denoted θr, and that the outer/inner fan waves are located outside/inside a wedge, at an angle denoted θf. Thus, Fig.4 shows that ring waves, outer fan waves, and inner fan waves exist within the regions |θ|≤θr, θf≤|θ|≤θr, |θ|≤θf, respectively. The ring angle θr and the fan angle θf decrease monotonically for τ≥1/4, with
125°16′≥θr≥0, 90°≥θf≥0
for 1/4≤τ≤∞. The angles θr and θf decrease rapidly for values of τ in the vicinity of 1/4. The angle θr is equal to 90° for ![]() Thus, if
Thus, if ![]() a ship only generates trailing waves, whereas waves are radiated both ahead and behind a ship if
a ship only generates trailing waves, whereas waves are radiated both ahead and behind a ship if ![]() The upstream waves are ring waves if 0≤τ<1/4 or incomplete ring waves and outer fan waves if
The upstream waves are ring waves if 0≤τ<1/4 or incomplete ring waves and outer fan waves if ![]()
The systems of waves associated with the dispersion curves located in the regions defined by (32c) and (32d) involve waves of widely different length, as can be observed in Fig.4. The wavelengths of the transverse waves, i.e. the waves at the ship track η=0, in the various component wave systems depicted in Fig.4 can easily be compared. Specifically, (32b) shows that the wavenumber k of the waves at the ship track in Fig.4 is equal to ![]() for the inner V waves,
for the inner V waves, ![]() for the outer V waves (if τ<1/4),
for the outer V waves (if τ<1/4), ![]() for the upstream (forerunning) waves in the system of ring waves (if τ<1/4), and
for the upstream (forerunning) waves in the system of ring waves (if τ<1/4), and ![]() for the downstream (trailing) waves in the system of ring waves (if τ<1/4) or partial ring waves (if τ>1/4). Expressions (32a) then show that the corresponding values of the wavelength λ=2π/k are given by
for the downstream (trailing) waves in the system of ring waves (if τ<1/4) or partial ring waves (if τ>1/4). Expressions (32a) then show that the corresponding values of the wavelength λ=2π/k are given by
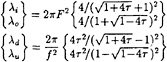
(36)
where λi and λo are the wavelengths of the transverse waves in the systems of inner and outer V waves, and λd and λu correspond to the downstream and upstream ship-track waves in the systems of (complete or partial) ring waves.
Expressions (36) yield
λd=λu=2π/f2, λi=λo=2πF2 (37a)
for τ=0, in accordance with (34), and show that
λd,u=O(2π/f2), λi,o=O(2πF2) (37b)
for 0≤τ≤1/4. Furthermore, (36) show that the downstream/upstream waves in the system of ring waves and the outer/inner V waves become longer/shorter with increasing values of τ, i.e. with increasing forward speed. The wavelength λo of the outer V waves increases rapidly in the vicinity of τ=1/4. The wavelengths λu and λo are defined only if τ<1/4, whereas λd and λi are defined for all values of τ.
The wavelengths λi and λd can be scaled with respect to F2 and 1/f2 as in (36), or with respect to F/f. Specifically, we have λif/F=τ λi/F2 and λdf/F=f2λd/τ. The functions λd/(2π/f2) and λi/(2πF2) are equal to 1 for τ=0 (as was already noted), whereas we have λdf/F~1/τ and λif/F ~ τ as τ → 0. Thus, for small values of τ the wavelengths λd and λi are more appropriately scaled with respect to 1/f2 and F2, in accordance with (37b), than with respect to F/f. However, λd and λi are most appropriately scaled with respect to F/f for values of τ>1. Indeed, expressions (36) yield λd,i ~ 2πF/f as τ → ∞ and
λd=O(2π/f2) and λi=O(2πF2) for τ≤1
λd,i=O(2πF/f) for τ≥1. (38)
For typical values of f and F in the ranges 1≤f≤5 and 0.1≤F≤0.5, we have 0.1≤τ≤2.5, and
the wavelengths of the component wave systems may reasonably be scaled in accordance with (37b), although scaling in accordance with (38) is more appropriate for τ>1.
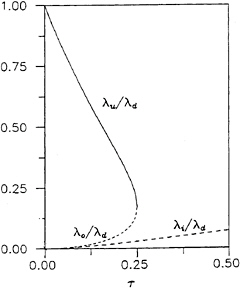
Figure 5 depicts the ratios λu/λd and λo/λd for τ≤1/4 and the ratio λi/λd for τ≤1/2. This figure and Fig.4 show that the (complete or partial) ring waves are much longer than the V waves except for a fairly narrow range of values of τ in the vicinity of τ=1/4 (for which λo and λu are comparable), and for very large values of τ (for which λi and λd are comparable).
The wave components φiV, φoV, φRF and φR in (35) are now successively considered.
Fourier representations of wave components
The inner V wave component φiV exists for all values of τ and corresponds to the dispersion curve in the region ![]() where
where ![]() is defined by (32a) as
is defined by (32a) as ![]() The Froude-scaled Fourier variables
The Froude-scaled Fourier variables
F2(α,β,k)=(A,B,K) (39)
are used to represent inner V waves. The dispersion curve associated with inner V waves is defined via a parametric representation. Specifically, we define the functions ![]() K(σ; τ), A(σ; τ), B(σ; t) and
K(σ; τ), A(σ; τ), B(σ; t) and ![]() where 0≤σ<∞, as
where 0≤σ<∞, as
We have ![]() and (33) yields Σ1=–1. It follows that (30) becomes
and (33) yields Σ1=–1. It follows that (30) becomes
where the functions ![]() and S± are defined as
and S± are defined as
(40)
S±=S(A/F2, ±B/F2). (41)
Furthermore, the functions ![]() and
and ![]() are defined by (29b) and (29c) with
are defined by (29b) and (29c) with ![]()
![]() We thus have
We thus have
(42)
(43)
We have ![]() as σ → ∞ and
as σ → ∞ and
![]() as σ → 0,
as σ → 0,
so that ![]() is continuous for σ≥0 and τ≥0.
is continuous for σ≥0 and τ≥0.
The outer V wave component φoV exists if τ<1/4 and corresponds to the dispersion curve in the region ![]() where
where ![]() is defined by (32a) as
is defined by (32a) as ![]() The Froude-scaled Fourier variables (39) are used to represent outer V waves. The dispersion curve associated with outer V waves is defined via a parametric representation. Specifically, we define the functions
The Froude-scaled Fourier variables (39) are used to represent outer V waves. The dispersion curve associated with outer V waves is defined via a parametric representation. Specifically, we define the functions ![]() K(σ; τ), A(σ; τ), B(σ; τ) and
K(σ; τ), A(σ; τ), B(σ; τ) and ![]() where 0≤σ<∞, as
where 0≤σ<∞, as
We have ![]() and (33) yields Σ1=1. Thus, (30) becomes
and (33) yields Σ1=1. Thus, (30) becomes
where the functions ![]() and S± are given by (40) and (41). Furthermore, the functions
and S± are given by (40) and (41). Furthermore, the functions ![]() and e± = E±, defined by (29b) and (29c) with
and e± = E±, defined by (29b) and (29c) with ![]() are given by (42) and (43). We have
are given by (42) and (43). We have ![]() as σ → ∞ and
as σ → ∞ and
![]() as σ → 0,
as σ → 0,
so that ![]() is continuous for σ≥0 and τ<1/4.
is continuous for σ≥0 and τ<1/4.
The wave component φV is defined by (35a) as the sum of the components φiV and φoV associated with inner and outer V waves. In the special case τ=0, corresponding to steady ship waves, now considered we have K0=1, ![]() B=σ,
B=σ, ![]() and
and ![]() for the inner/outer V waves. For steady flows the spectrum function S(α, β) satisfies the identity
for the inner/outer V waves. For steady flows the spectrum function S(α, β) satisfies the identity ![]() where
where ![]() is the complex conjugate of S. It can then be shown that the V wave component is given by
is the complex conjugate of S. It can then be shown that the V wave component is given by
where ![]() µ± and e± are given by (42) and (43), and A± are defined as
µ± and e± are given by (42) and (43), and A± are defined as
Thus, the sum of the components φiV and φoV, which contain real and imaginary parts, is real in the steady-flow limit τ=0.
The ring-fan wave component φRF exists if τ>1/4 and corresponds to the dispersion curve
in the region ![]() where
where ![]() is defined by (32a) as
is defined by (32a) as ![]() The frequency-scaled Fourier variables
The frequency-scaled Fourier variables
(α, β, k)/f2=(A, B, K) (44)
are used for the component φRF. The dispersion curve corresponding to ring-fan waves is defined via a parametric representation. Specifically, we define ![]() K(σ; τ), A(σ; τ), B(σ; τ) and
K(σ; τ), A(σ; τ), B(σ; τ) and ![]() with 0≤σ<∞, as
with 0≤σ<∞, as
We have ![]() and (33) yields Σ1=1. It follows that (30) becomes
and (33) yields Σ1=1. It follows that (30) becomes
where ![]() is given by (40), the functions S± are defined as
is given by (40), the functions S± are defined as
S±=S(f2A, ±f2B) (45)
and the functions ![]() and e±≡E±, defined by (29b) and (29c) with
and e±≡E±, defined by (29b) and (29c) with ![]()
![]() are given by (42) and (43). We have
are given by (42) and (43). We have ![]() as σ → ∞ and
as σ → ∞ and
![]() as σ → 0,
as σ → 0,
so that ![]() is continuous for σ≥0 and τ>1/4.
is continuous for σ≥0 and τ>1/4.
The ring wave component φR exists if τ<1/4 and corresponds to the dispersion curve in the inner region ![]() where
where ![]() are defined by (32a) as
are defined by (32a) as ![]() The frequency-scaled Fourier variables (44) are used for ring waves. The dispersion curve associated with ring waves is defined by a parametric representation in which A is expressed as A=A0+K0 cosθ with
The frequency-scaled Fourier variables (44) are used for ring waves. The dispersion curve associated with ring waves is defined by a parametric representation in which A is expressed as A=A0+K0 cosθ with ![]() and 0≤θ≤π, i.e.
and 0≤θ≤π, i.e.
Thus, we define the functions A(θ; τ), B(θ; τ), K(θ; τ), and ![]() as
as
A=A0+K0 cosθ, K=(1-τA)2
We have dα=–f2dθ K0 sinθ and (30) becomes
where ![]() is defined as
is defined as ![]() =(K/B) sinθ and S± is given by (45). Furthermore, the terms
=(K/B) sinθ and S± is given by (45). Furthermore, the terms ![]() and e±≡E±, defined by (29b) and (29c) with
and e±≡E±, defined by (29b) and (29c) with ![]() are given by (42) and (43). The function B vanishes for θ=0 and θ=π, but we have
are given by (42) and (43). The function B vanishes for θ=0 and θ=π, but we have
with ![]() Thus, the integrand of the Fourier integral defining the ring waves is continuous for 0≤θ≤π and 0≤τ<1/4.
Thus, the integrand of the Fourier integral defining the ring waves is continuous for 0≤θ≤π and 0≤τ<1/4.
In the limit τ=0, i.e. for wave diffraction-radiation without forward speed, we have A0=0, K0=1, (A, B, K)=(cosθ, sinθ, 1) and ![]() The functions µ± and e± are then given by (42) and (43) with
The functions µ± and e± are then given by (42) and (43) with ![]() and B=sinθ. The ring-wave component becomes
and B=sinθ. The ring-wave component becomes
where the functions A± are defined as
A±=S(f2cosθ,±f2sinθ) exp[–if2(ξ cosθ±η sinθ)].
Here, the relation ![]() which holds for time-harmonic flows without forward speed, was used.
which holds for time-harmonic flows without forward speed, was used.
Illustrative calculations
The foregoing Fourier representations of the wave components φiV, φoV, φRF and φR in (35) provide simple analytical representations of the wave components generated by an arbitrary (volume, surface, and/or line) distribution of singularities (e.g. sources and/or dipoles), characterized by the spectrum function S. For purposes of illustration, the wave potential φW in (21) is now considered for a simple example spectrum function.
Specifically, a uniform distribution of sources with density m/(4π) within a flat rectangular panel Hp of length 2hp and depth dp contained in a vertical plane making an angle γp with the x axis is considered. The source panel is centered at the point (xp, yp, zp≤0) and is defined by x=xp+u cosγp, y=yp+u sinγp, z=zp+v with –hp≤u≤hp and –dp≤v≤0. The free-surface potential ![]() generated by this source distribution is integrated over a flat rectangular panel Hq of length 2hq and depth dq contained in a vertical plane making an angle γq with the x axis. Thus, we consider the free-surface component
generated by this source distribution is integrated over a flat rectangular panel Hq of length 2hq and depth dq contained in a vertical plane making an angle γq with the x axis. Thus, we consider the free-surface component ![]() in the influence coefficient defined via a Galerkin integration (corresponding to domain collocation instead of point collocation)
in the influence coefficient defined via a Galerkin integration (corresponding to domain collocation instead of point collocation)

Fig. 6a Inner and Outer V waves for τ=0 and F=0.245 (–4.2≤ξ≤0.3, –1.8≤η≤0≤η≤1.8 and ζ=0)

Fig.6b Ring waves for τ=0 and f=2 (–8≤ξ≤4, –4.8≤η≤0≤η≤4.8 and ζ=0)

Fig. 6c Inner and Outer V waves for τ=0.2 and F=0.245 (–4.2≤ξ≤0.3, –1.8≤η≤0≤η≤1.8 and ζ=0)

Fig. 6d Ring waves for τ=0.2 and f=0.816 (–30≤ξ≤15, –18≤η≤0≤η≤18 and ζ=0)

Fig. 6e Inner and Outer V waves for τ=0.245 and F=0.245 (–4.2≤ξ≤0.3, –1.8≤η≤0≤η≤1.8 and ζ=0)

Fig. 6f Ring waves for τ=0.245 and f=1 (–15≤ξ≤7.5, –9≤η≤0≤η≤9 and ζ=0)

Fig. 6g Ring-Fan and Inner V waves for τ=0.255 and f=1 (–22.5≤ξ≤7.5, –12≤η≤0≤η≤12 and ζ=0)

Fig. 6h Ring-Fan and Inner V waves for τ=0.272 and f=1 (–22.5≤ξ≤7.5, –12≤η≤0≤η≤12 and ζ=0)

Fig. 6i Ring-Fan and Inner V waves for τ=0.5 and f=1 (–28≤ξ≤2, –12≤η≤0≤η≤12 and ζ=0)

Fig. 6j Ring-Fan and Inner V waves for τ=1 and f=1 (–28≤ξ≤2, –12≤η≤0≤η≤12 and ζ=0)
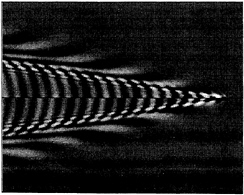
Fig. 6k Ring-Fan and Inner V waves for τ=2 and f=2 (–28≤ξ≤2, –12≤η≤0≤η≤12 and ζ=0)
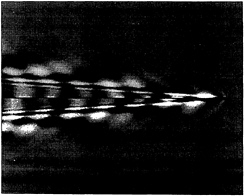
Fig. 6l Ring-Fan and Inner V waves for τ=4 and f=2 (–28≤ξ≤2, –12≤η≤0≤η≤12 and ζ=0)
of ![]() over the influenced panel Hq. This panel is centered at the point (ξq,ηq,ζq≤0) and is defined by ξ=ξq+u cosγq, η=ηq+u sinγq, ζ=ζq+v with –hq≤u≤hq and –dq≤v≤0. The influence coefficient
over the influenced panel Hq. This panel is centered at the point (ξq,ηq,ζq≤0) and is defined by ξ=ξq+u cosγq, η=ηq+u sinγq, ζ=ζq+v with –hq≤u≤hq and –dq≤v≤0. The influence coefficient ![]() can be expressed in the form
can be expressed in the form ![]()
![]() where M=m/(4π), ap=2hpdp and aq=2hqdq are the areas of the panels Hp and Hq, and cF is given by (20) with
where M=m/(4π), ap=2hpdp and aq=2hqdq are the areas of the panels Hp and Hq, and cF is given by (20) with
φF→cF, (ξ,η,ζ)→(ξq–xp, ηq–yp, ζq+zp), S→ApAq;
the functions Ap and Aq are defined as
with ![]()
The free-surface influence coefficient cF can then be expressed as the sum of a wave component cW and a near-field component cN, as in (21). The wave component cW is considered here for a source panel Hp and an influenced panel Hq of sizes hp= 0.025=hq and dp=0.015=dq. Furthermore, both the source panel and the influenced panel are at the free surface, so that we have ζ=ζq+zp=0 and the orientations of these panels with respect to the x axis are chosen as γp=π/4 and γq=–π/4.
Illustrative calculations of the real and imaginary parts of the V waves φiV+φoV, the ring waves φR, and the ring-fan and inner V waves φRF+φiV associated with the foregoing spectrum function are depicted in the upper and lower halves of Figs 6a-l for ζ=0 at several values of the Strouhal number. Specifically, the inner and outer V waves and the ring waves are depicted in Figs 6a,c,e and Figs 6b,d,f for τ=0,0.2,0.245; and the ring-fan and inner V waves are depicted in Figs 6g-l for τ=0.255,0.272,0.5,1,2,4.
CONCLUSION
Extensions of the Fourier-Kochin theory of wave diffraction-radiation by ships or offshore structures expounded in [3,4,5] have been presented. The main results given in the study are now briefly summarized.
The source and dipole potentials ψ and χ in the integral equation (6a) and the flow representation (6b) can be expressed in the form (12), i.e.
ψ=ψS+ψFχ=(χS–φS)+χF
where the superscipts S and F identify simple-singularity and free-surface components, respectively. The representation χ=(χS–φS)+χF is a modification of the representation ![]() given in [3]. Specifically, the simple-singularity component φS is extracted from the free-surface potential
given in [3]. Specifically, the simple-singularity component φS is extracted from the free-surface potential ![]() The free-surface potentials ψF and χF in (12) are given by the Fourier representation (13a) where
The free-surface potentials ψF and χF in (12) are given by the Fourier representation (13a) where ![]() is the dispersion function (5) associated with the linear free-surface boundary condition (1), and the spectrum functions N and M are defined in terms of distributions of elementary waves exp[kz+i(αx+βy)] over the mean wetted hull H and waterline W of the ship. These distributions, defined by (13c) and (13d), are independent of the Froude number F and the nondimensional frequency f, which appear as coefficients in (13b). Expressions (13b)–(13d) for the spectrum functions N and M are shown in [3] to be well suited for the purpose of numerically evaluating influence coefficients, and are shown here to be useful also for coupling viscous and potential flows. The simple-singularity potentials ψS, χS and φS in (12) are defined by (14) and (15) in terms of distributions of simple singularities over H and W, respectively.
is the dispersion function (5) associated with the linear free-surface boundary condition (1), and the spectrum functions N and M are defined in terms of distributions of elementary waves exp[kz+i(αx+βy)] over the mean wetted hull H and waterline W of the ship. These distributions, defined by (13c) and (13d), are independent of the Froude number F and the nondimensional frequency f, which appear as coefficients in (13b). Expressions (13b)–(13d) for the spectrum functions N and M are shown in [3] to be well suited for the purpose of numerically evaluating influence coefficients, and are shown here to be useful also for coupling viscous and potential flows. The simple-singularity potentials ψS, χS and φS in (12) are defined by (14) and (15) in terms of distributions of simple singularities over H and W, respectively.
The Fourier-Kochin flow representation (12), (13), (14) and (15) is used to obtain a mathematical representation of the velocity ∇![]() defined explicitly in terms of a prescribed velocity distribution
defined explicitly in terms of a prescribed velocity distribution ![]() at a control surface Σ, i.e. that does not involve the potential
at a control surface Σ, i.e. that does not involve the potential ![]() at Σ (unlike the usual Green identity which defines
at Σ (unlike the usual Green identity which defines ![]() within a flow domain in terms of boundary values of
within a flow domain in terms of boundary values of ![]() and ∂
and ∂![]() /∂n). Specifically, the velocity field
/∂n). Specifically, the velocity field ![]() where ∇ξ=(∂ξ,∂η,∂ζ), is defined by (16) as
where ∇ξ=(∂ξ,∂η,∂ζ), is defined by (16) as
The free-surface component ∇ξ![]() F is given by the Fourier representation (17) where the spectrum function S is defined in terms of distributions of elementary waves over the control surface Σ and its intersection Γ with the mean free-surface plane z=0. The simple-singularity components ∇ξ
F is given by the Fourier representation (17) where the spectrum function S is defined in terms of distributions of elementary waves over the control surface Σ and its intersection Γ with the mean free-surface plane z=0. The simple-singularity components ∇ξ![]() S and ∇ξφS in (16) are defined by (19) in terms of distributions of simple singularities over Σ and Γ. The flow representation (16), (17) and (19) defines ∇
S and ∇ξφS in (16) are defined by (19) in terms of distributions of simple singularities over Σ and Γ. The flow representation (16), (17) and (19) defines ∇![]() directly rather than by numerical differentiation of the potential
directly rather than by numerical differentiation of the potential ![]() . This potential flow representation can be used for coupling an inner viscous flow and an outer potential flow. Expressions (15), (18c) and (19b) for the simple-singularity components φS, ∇ξχS and ∇ξφS, given here without demonstration, will be established elsewhere.
. This potential flow representation can be used for coupling an inner viscous flow and an outer potential flow. Expressions (15), (18c) and (19b) for the simple-singularity components φS, ∇ξχS and ∇ξφS, given here without demonstration, will be established elsewhere.
The most difficult aspect of the Fourier-Kochin formulation, indeed of any approach based on a Green function satisfying the free-surface condition (1), resides in the free-surface components
∇ξ![]() F, ψF and χF in the decompositions (16) and (12) into simple-singularity and free-surface components. These components are examined in [4,5] and in this study. Specifically, the Fourier representation of free-surface effects defined by (20) is considered for a generic spectrum function S and a generic dispersion function D. The generic Fourier integral (20) is expressed in (21) as
F, ψF and χF in the decompositions (16) and (12) into simple-singularity and free-surface components. These components are examined in [4,5] and in this study. Specifically, the Fourier representation of free-surface effects defined by (20) is considered for a generic spectrum function S and a generic dispersion function D. The generic Fourier integral (20) is expressed in (21) as
φF=φW+φN
where φW and φN respectively correspond to a wave component and a near-field component. The wave component φW is given by (26), a single Fourier integral along the dispersion curve(s) defined in the Fourier plane by the dispersion relation D=0. The Fourier representation (26) is a generalization of the representation given in [4], which is obtained if E=1 and (24a) is used for Σ2. The near-field component φN in the decomposition (21) is significant in the near field but is negligible in comparison to the wave component φW in the far field. The component φN corresponding to the wave component (26) is defined by (27), which is a generalization of (30) in [5]. This expression for the near-field component φN is shown in [5] to be well suited for accurate numerical evaluation.
The Fourier representation of (20) defined by (21), (26) and (27) is valid for generic dispersive waves and for arbitrary singularity distributions, including the special case of the Green function (i.e. a point source). Applications of this generic Fourier representation to wave diffraction-radiation by an offshore structure (without forward speed) and steady flows, and to the Green function of wave diffraction-radiation at small forward speed, are presented in [4,5]. Another application, to time-harmonic ship waves characterized by the dispersion function (5), is examined here. Only the wave component φW is considered; a complementary detailed study of the near-field component φN will be reported elsewhere.
The wave component φW is defined by (35) as
where φiV, φoV, φR and φRF represent distinct wave components, associated with the dispersion curves located within the regions of the Fourier plane defined by (32), which correspond to inner V waves, outer V waves, ring waves and ring-fan waves. Fourier representations of these wave components are given in the study. The spectrum function S, typically associated with a continous or discrete distribution of sources and/or dipoles over the hull of a ship, is arbitrary in these Fourier representations, which therefore provide simple explicit analytical representations of the wave components radiated by an arbitrary (volume, surface, and/or line) distribution of singularities (e.g. sources and/or dipoles), including the special case of a point source, i.e. the free-surface Green function. The integrands of the Fourier integrals defining the wave components φiV,φoV, φR and φRF are continuous, so that these expressions are well suited for numerical evaluation. For purposes of illustration, the wave potential φW in (21) is considered for a simple example spectrum function.
ACKNOWLEDGMENTS
The first and second authors were supported by DTMB's Independent Research program and a DRET research grant, respectively.
REFERENCES
[1] Kochin, N.E. ( 1937) On the wavemaking resistance and lift of bodies submerged in water, translated in SNAME Tech. and Res. Bull. 1–8 (1951).
[2] Kochin, N.E. ( 1940) The theory of waves generated by oscillations of a body under the free surface of a heavy incompressible fluid, translated in SNAME Tech. and Res. Bull. 1–10 (1952).
[3] Noblesse, F. and Yang, C. ( 1995) Fourier-Kochin formulation of wave-diffraction-radiation by ships or offshore structures, Ship Technology Research, 42/3, 115–139.
[4] Noblesse, F. and Chen, X.B. ( 1995) Decomposition of free-surface effects into wave and near-field components , Ship Technology Research, 42/4, 167–185.
[5] Noblesse, F. and Yang, C. ( 1996) Fourier representation of near-field free-surface flows, Ship Technology Research, 43/1, 19–37.
[6] Campana, E.; Di Mascio, A.; Esposito, P.G.; Lalli, F. ( 1993) Domain decomposition in free surface viscous flows, 6th Intl Conf. Numerical Ship Hydro.
[7] Chen, H.C.; Lin, W.M.; Weems, K.M. ( 1993) Interactive zonal approach for ship flow including viscous nonlinear and wave effects, 6th Intl Conf. Numerical Ship Hydro.