Radar Backscatter of a V-like Ship Wake from a Sea Surface Covered by Surfactants
G.Zilman, T.Miloh (Tel-Aviv University, Israel)
ABSTRACT
In calm water synthetic aperture radar (SAR) ship wake images frequently form of a bright V with a narrow half angle of 2–3 deg. These images persist for many kilometers behind the ship and can be explained as a result of the Bragg scattering from ship-generated divergent waves (Milgram 1988). The present work is concerned with the generation of short divergent gravity waves and their radiation from the hull of a displacement ship moving on a free-surface covered by surfactants. Here it is shown that a contaminated free-surface significantly reduce the radar back scatter cross-section and drastically influence the V-wake detectability. Explicit formulas for the radar back scatter cross-section are obtained and numerical examples for their use are presented. The theoretical results are sown to be in a good qualitative and quantitative agreement with the experimental results of Shemdin (1990).
1
Introduction
Background. A moving ship generates a distinctive Kelvin free-surface waves system. It consists of two types of waves, transverse and divergent, which are located between two lines with a half angle of 19.5°. However, airborne synthetic aperture radar (SAR) images of the sea surface frequently display quite a different noticeable wave pattern in a form of a narrow V-like angle of 2°–3° degrees (Munk, Scully-Power & Zachariasen 1986, Lyden et al. 1988, Shemdin 1990). Such wakes exhibits a central “dark area” and two ”bright white arms” existing as far as 6–8 km behind surface ships.

Figure 1: The wave pattern behind a displacement ship can be separated on:
-
Dark V-wake visible only in SAR images;
-
Two confining bright arms;
-
Optically visible Kelvin waves which are usually invisible in SAR images.
There is a believe that the bright arms of the V-wake stem from the radar back-scattering of short surface waves which are generated by the ship hull or its turbulent wake. Such a hypothesis is based on the Bragg scattering mechanism, which implies that a radar, roughly speaking, picks up a single wave number. The typical wavelength selected by L-band radars varies somewhat between 25–30 cm. Thus, it is plausible that such waves are presented in the ship wake.
To explain the V-wake phenomenon so far three alternative and somewhat mutually incompatible mechanisms have been invoked. They relate to:
-
Short divergent waves generated by a ship moving with a constant speed (Milgram 1988); in this approach the wave wake is a
-
result of wave interference between coherent sources replacing the hull of the vessel.
-
Short surface waves induced by the free-surface strain which is affected by ship-generated internal waves; the internal waves result from the interference of coherent sources replacing the hull (Keller & Munk 1970, Tulin & Miloh 1990, Miloh, Tulin & Zilman 1993).
-
Generation of short waves by incoherent point sources behind the ship (Munk et al. 1988); in the approach of Gu & Phillips (1995) incoherent sources simulate the oscillations of the edges of the turbulent wake.
In the present paper we investigate the attenuation of the short waves due to the presence of surfactant films compacted in the vicinity of the V-wake. Surfactants tend to concentrate at the free-surface and to alter the surface properties. In particular, this may result in a strong damping of ripples and short gravity waves (Levich 1962). It is common to interpret such a phenomenon as a Marangoni effect which is due to the gradient of the surface tension varying from point to point of the free-surface. The level of wave damping depends on many physical parameters of the water and the surfactants. The simplest mathematical model of the Marangoni phenomenon is based on the concept of a viscoelastic surface film and incorporates only three essential parameters: the water kinematic viscosity, v, the surface tension coefficient, σ, and the elasticity of the surface film, ![]() , (Levich 1962). There exist strong experimental evidence that the elasticity of the surfactant film depends on the concentration of surfactants (Pelinovsky and Talipova 1990) and can be as high as 30 dyne/cm for natural surfactants of Black Sea.
, (Levich 1962). There exist strong experimental evidence that the elasticity of the surfactant film depends on the concentration of surfactants (Pelinovsky and Talipova 1990) and can be as high as 30 dyne/cm for natural surfactants of Black Sea.
The characteristics features of the radar return such as the brightness of the V-arms and their extent can be expressed in terms of the radar back scatter cross-section. As was indicated by Peltzer et al. (1991) these characteristics may depend on the density of the surfactant films covering the sea surface.
The basic mechanism of radar backscattering. Herein we follow the work of Milgram (1988), where the radar back-scattering stems from the deformation of the initially flat free-su rface by a system of ship generated divergent waves with the wave length about 20– 30cm. This range is consistent with the L-band radar wave length and provides the Bragg resonance. However, as it was indicated in the work of Munk, Scully-Power & Zachariansen (1986) the radar picks up not only the particular magnitude of a wave number, but also the direction of wave propagation, i.e., the direction for which the wave crests are normal to the look of sight of the radar. Thus, the brightness and the extent of the two bright arms can be different. If the direction of the radar look of sight a provides the maximal available signal for the, say, right V-arm, the left V-arm may be practically invisible on SAR images. For instance, the experimental database of Brown (1985) includes 49 SAR images of different ships; 24% percents of them have wakes with two arms, 41% show one arm, while 35% of the images do not exhibit any bright envelopes. 1 In all SAR images obtained by Shemdin (1990) the bright V-arms are visible only for those ships which travel in the same direction as the aircraft (α=0). Close scrutiny of SAR images presented in Shemdin (1990) shows that the extent, as well as the brightness of the arms are not the same. Moreover, in one of the reported images only one bright arm is visible.
The radar back scatter cross-section Θ depends on the wave elevation ![]() in the illuminated area, on the radar wave number kr, the angle of incidence ψ, the length and width of the resolution cell 2lc and 2bc respectively and the complex bask scatter coefficient, C, depending on the particular type of radar. For radars with a horizontal polarization the back scatter coefficient can be expressed approximately as |C|
in the illuminated area, on the radar wave number kr, the angle of incidence ψ, the length and width of the resolution cell 2lc and 2bc respectively and the complex bask scatter coefficient, C, depending on the particular type of radar. For radars with a horizontal polarization the back scatter coefficient can be expressed approximately as |C| ![]() cos2ψ.
cos2ψ.
According to the Bragg model the radar backscatter cross-section of a wavy surface per unit area is given by the following formula of Wright (1966, 1968):
(1)
Here the coordinates (ξ,η) pertain to a local coordinate system of a rectangular resolution cell co-planar with the radar line of sight. Thus, if the wave elevation ![]() (ξ,η) is known, the radar return also can be also computed.
(ξ,η) is known, the radar return also can be also computed.
Peculiarities of the ship wave-wake simulations. Simulation of the clean wave-wake of a ship is a classical problems of naval hydrodynamics and was considered by Kelvin (1891), Peters (1949), Ursell(1960, 1988), Wehausen & Laitone (1960), Sharma (1969), Newman (1970, 1971, 1987), Tuck, Collins & Wells (1971), Barnell
|
1 |
The authors are gratefull to Dr. P.Wang for this information. |
& Noblesse (1986), Barr & Price (1988), Noblesse, Hendrix & Barnell (1989), Nobless & Hendrix (1991), Ponizy et al. (1994), Nakos & Sclavounos (1994). The effect of viscosity on ship waves has been investigated, for example, by Wu & Messick (1958), Cumberbatch (1965) and Kinoshita (1981). The effect of the surface tension on ship waves was investigated by Crapper (1964) and Sharma (1969). The unsteady Kelvin wake was investigated by Mei & Naciri (1991), Eggers & Schultz (1992) and Cao, Schultz and Beck (1992).
The striking feature of the numerical simulations implemented by Noblesse and Hendrix (1991) is that they ..”predict short divergent waves too steep to exist in reality within a significant sector in the vicinity of the ship track ”. This difficulty was attributed by Milgram (1988) to a collapse of the divergent waves. In the framework of the present formulation such a pure theoretical obstacle can be lifted in a natural way since all short and non-realistic steep waves are completely damped out by a surfactant film.
The V-wake persist for many kilometers. Obviously, such a distance is much larger then the typical ship length. Thus, one can employ an asymptotic far field estimate for the wave elevations which greatly alleviate the consequent analysis. However, even a simplified expression for the wave elevation ![]() still makes the integration in the formula (1) not easy to perform. The relevant computations usually are time consuming and quite demanding of computer resources. The reason being that the expressions for the wave elevation
still makes the integration in the formula (1) not easy to perform. The relevant computations usually are time consuming and quite demanding of computer resources. The reason being that the expressions for the wave elevation ![]() are represented by integrals which hardy can be evaluated in an explicit form, and the numerical computation of (1) may involve millions of grid points.
are represented by integrals which hardy can be evaluated in an explicit form, and the numerical computation of (1) may involve millions of grid points.
It was noted by Milgram (1988), that in the far field the waves generated by a ship behaves almost as they came from a single location. In other words, far behind a ship the fine details of its shape may be inessential. It allows us to use a simplified description of the ship hull which takes into account only such gross geometrical parameters as ship length/beam ratio and the fullness coefficient of the waterline αW. Such an approach provides an opportunity to select from the variety of ship forms only those which allows us to obtain an analytic representation of the wave elevation in the far field. Once such an analytic expression is known, one can try to find an asymptotic expression for the radar back scatter cross-section Θ.
The plan of the present work. Section 2 of this paper provides the mathematical outline for evaluating the wave elevations. It is based on linear water wave theory. In Section 3 we present the derivation of the Green function for a source moving below the free-surface covered by insoluble surfactant and an asymptotic expression for wave elevations. In this section we also discuss the damping effect of the surfactant film. An analytic expression for the radar back scatter cross-section is derived in Section 4. Starting from Section 5 the theoretical results are compared against the experimental data of Shemdin (1988). The particular numerical example involves a tanker Bay Ridge with the following characteristics:
Table 1. The particulars of the tanker Bay Ridge.
|
Length, m |
334.9 |
|
Bean, m |
43.7 |
|
Draft, m |
21.4 |
|
Speed, m/s |
7.5 |
The characteristics of the radar with received horizontal polarization which was used in the experiment of Shemdin are represented in Table 2:
Table 2. Aircraft L-Band SAR parameters.
|
Wavelength, m |
0.246 |
|
Nominal resolution, m×m |
11×11 |
|
Ground range resolution (at incident angle 30°),m |
16×16 |
|
Ground range resolution (at incident angle 50°),m |
10×10 |
2
Wave elevations induced by a moving ship.
Let us select the rectangular axes of the coordinate system attached to a moving ship in such a manner that the x and y-axes are situated on the undisturbed free-surface, and the z-axis is directed upward. We define the surface S of the hull by the function y=±f(x,z). Our goal is to determine the free-surface profile ![]() =
=![]() (x,y) generated by a ship moving with constant velocity U in the direction of the positive x-axis. In the frameworks of the linear analysis we represent the resulting wave elevation
(x,y) generated by a ship moving with constant velocity U in the direction of the positive x-axis. In the frameworks of the linear analysis we represent the resulting wave elevation ![]() (x,y) induced by the ship as a sum of wave elevations due to sources of intensity qh(x,y,z) distributed over the surface S and wave elevations which stem from the sources qw(x,y) distributed over the contour of the waterline lw (Brard 1972):
(x,y) induced by the ship as a sum of wave elevations due to sources of intensity qh(x,y,z) distributed over the surface S and wave elevations which stem from the sources qw(x,y) distributed over the contour of the waterline lw (Brard 1972):
(2)
where
(3)
and
(4)
Here N(x0,y0,z0) is a point on the surface S and M(x,y,z) is a field point · ζh=G(M,N) and ζw=ζw(M,N) are two related Green functions. In general, for irrotational fluid motion the source density qh(x,y,z) can be found as the numerical solution of a corresponding boundary integral equation. The relation between the strength of the surface and the line source distribution is:
where nx=cos(n,x) is the projection of the normal to the ship surface on the x-axis, and g is the acceleration of gravity.
In the present work we consider a viscous fluid, but assume that the source density still can be calculated by invoking the potential theory. The combined effect of the fluid viscosity and the surfactant film elasticity will be included in the Green function. Such a heuristics approach has a real physical background. For the potential flow the source density distribution displays the form of the ship whereas the Green function manifests the physical properties of the fluid and the specific kinematic and dynamic boundary conditions to be applied on the free-surface. This approach can be partially improved by accounting for the thickness of ship boundary layer. Based on the work of Lavretntiev (1951) Kinoshita (1980) has been demonstrated that the Michell source distribution with the effect of the boundary layer displacement thickness is almost identical to the source distribution without a viscous effect, except a particular range near the stern. Havelock (1935) demonstrated many decades ago that the influence of the viscosity on the near stern flow can be accounted for by introducing a proper small “deformation” of the stern. It has been mentioned above that far behind a ship the fine details of its surface may be inessential. Thus, we assume that for estimating the far field wave wake the source density can be calculated on the basis of potential theory according to the formula:
(6)
where γ(x,y,z) is a function which lamps the specific features of the shape of a ship. For a thin Michell type ship γ(x,y,z)=2, and the integration in the formulas (3) and (4) can be performed at the ship the centerplane. For a ship of finite width γ varies from point to point of the ship surface, but it is bounded, i.e., 1<γ <1.5 (Kostyukov 1968). In order to simplify the analysis and to obtain analytical results we employ the relation (6) with a constant coefficient γ ![]() 1, but perform the integration on both sides of the surface S. Such an approach has been previously justified by Milgram [20] who noted that ”comparative calculations of divergent waves and their scattering cross-section using thin ship source distribution (distributed on the actual ship shape-not the centerplane), and the source distribution obtained from its linear theory integral equation, show differences in details, but not in general form”.
1, but perform the integration on both sides of the surface S. Such an approach has been previously justified by Milgram [20] who noted that ”comparative calculations of divergent waves and their scattering cross-section using thin ship source distribution (distributed on the actual ship shape-not the centerplane), and the source distribution obtained from its linear theory integral equation, show differences in details, but not in general form”.
3
The Green function of a moving surface disturbance.
3.1
Governing equations.
We consider a disturbance (a normal stress Pn) concentrated over a infinitesimally small area in the vicinity of the origin O of the coordinate system Oxyz. The disturbance moves rectilin-early with constant velocity U on the free-surface ζp=ζp(x,y) of an incompressible viscous water covered by a surfactant film. A strong similarity between the wave elevation induced by a moving source and the wave elevation induced by a moving impulse of a normal stress applied to the free-surface is well known. For an inviscid fluid and irrotational fluid motion the wave elevation induced by a pressure impulse Pn moving over the free-surface is:
Once the function ζp is defined, the functions Gh,w can be reconstructed by using a formal substitution:
Pn=2iU sin θ. (7)
The linearized (Oseen) equation of fluid motion is expressed in the moving coordinate system as:
(8)
divV=0, (9)
where V is the vector of fluid velocity, p is the pressure in the fluid, ρ is the water density and v is the kinematic viscosity. This equation can be splited into potential and rotational parts
V=grad ![]() +VR(u,v,w),
+VR(u,v,w),
such that
∇2![]() =0, (10)
=0, (10)
and
(11)
divVR=0. (12)
3.2
Boundary conditions.
The linearized kinematic condition on the free-surface is:
(13)
In the presence of surface tension the linearized normal stress dynamics boundary condition on the free-surface can be written as:
(14)
where µ is the water dynamic viscosity and σ is the surface tension coefficient. In general σ depends on the surfactant concentration Γ which, in turn, is a function of the coordinates (x,y) and thus, σ=σ[Γ(x,y)]. We assume that the concentration Γ of a surface-active agent is Γ=Γ0+Γ′, where Γ0 is the constant concentration on the undeformed surface and Γ′≪Γ0. For slightly viscous fluid, low fluid velocity and small-amplitude waves it is common to assume that in equation (14) the surface tension coefficient is constant, σ=σ(Γ0). However, the gradient of the surface tension affects the tangential force
and the tangential shear stress conditions on the free-surface become:
(15)
(16)
where ptx and pty are the x and y-components of the shearing stress. Here the shearing stress vector can be expressed through the surfactant film concentration Γ(x,y) and the concentration Γ0 as (Levich 1962):
where ![]() is the elasticity of the surfactant film
is the elasticity of the surfactant film
and ![]()
We assume that the insoluble surface-active agent is fully swept along with the liquid and that the influence of diffusion on the concentration distribution of the surface active agent may be disregarded. For low fluid velocity and small-amplitude waves the equation for the conservation of matter in the case of mass flow on an almost planar free-surface yields:
(17)
3.3
Fourier transformation of the boundary-value problem
Let us denote the Fourier transform (FT) with respect to x and y as:
(18)
The Fourier transform of (10) gives:
(19)
with a solution
(20)
where ![]() The FT of (11) yields:
The FT of (11) yields:
with a solution
where
(21)
and Re(l)>0. Applying FT to (12) and (14) we have:
(22)
where T=σ/ρ. From (15) and (15) it follows:
(23)
(24)
Finally, equations (12) and (17) yield:
(25)
(26)
The next step is to find the Fourier transform ![]() and its inverse ζp. This can be done by solving a system of linear algebraic equations with respect to unknown parameters A, C1, C2, C3. After some simple, but somewhat tedious calculations we obtain the following expression for
and its inverse ζp. This can be done by solving a system of linear algebraic equations with respect to unknown parameters A, C1, C2, C3. After some simple, but somewhat tedious calculations we obtain the following expression for ![]()
where
D=–k(ω2–βmk2)(s–2viωl)+ ω(2vkm+iω)[2vωk2+i(βlk2–ω2)]
β=![]() /ρ, m=l–k, ω=Ukx and s=g+Tk2. Performing the integration in the polar system of coordinates, taking into account (7), neglecting in the numerator a small term incorporating β ≪1 and small terms of order v2 in the denominator, we obtain the following expression for the regular part of the Green function:
/ρ, m=l–k, ω=Ukx and s=g+Tk2. Performing the integration in the polar system of coordinates, taking into account (7), neglecting in the numerator a small term incorporating β ≪1 and small terms of order v2 in the denominator, we obtain the following expression for the regular part of the Green function:
where
(27)
Ω±=(x sin θ±y cos θ)
E(k,θ)=(kτ2–s)(τ2–βl)+2ivkτ2,
τ=U sin θ,
and
(28)
Here and in the sequel it is understood that in all complex expressions for the wave elevation similar to (27) have to be considered only the real part.
3.4
Poles of the integrand.
In the far field the asymptotic behavior of the Green function is determined through the poles of the integrand, or, in fact, by the roots of the equation:
E(k,θ)=0. (29)
The effect of the inclusion of viscosity is to move the poles off the real axis, and viscous damping is thereby obtained. In the case of an inviscid fluid the two corresponding roots are real and can be found explicitly as:
(30)
They corresponds to the capillary, capillary-gravity and gravity waves regions. The upper sign in this expression pertains to short capillary waves which are not important for our analysis for two reasons. First of all, they decay very fast with increasing distance from the disturbance and, secondly, they do not resonant with the radar wave length λr ~ 20–30cm. Thus, in the sequel we will
be concerned with short gravity-capillary waves which are defined by the lower sign of this relation. It is important to note that far downstream from the disturbance the integration in formula (27) is essential only for such values of θ which satisfies the inequality:
(31)
For a viscous fluid with contaminated free-surface the roots of (30) become complex and the yielding poles can not be solved exactly. Only an approximate location of the poles can be obtained. To a good approximation the real part of the roots obeys the relation (30) while the imaginary part may depend on the elasticity of the surfactant film significantly. Thus, the complex roots may be written as follows:
kc=k0(θ)–iδ(θ), (32)
where δ>0 incorporates the damping effects of the water viscosity and the surfactant elasticity. If the initial value of the real root k0(θ) is known, then the perturbation analysis of the of the dispersion relation (29) with respect to the small parameter δ/k0≪1 yields an algebraic expression for the function δ=δ[k0(θ),θ,v,![]() ]. The additional complication for such an analysis arises from the branch points of the function E which are imposed by the relation (28). In order to avoid this mathematical difficulty we assume that
]. The additional complication for such an analysis arises from the branch points of the function E which are imposed by the relation (28). In order to avoid this mathematical difficulty we assume that
Actually, since our interest resides in the range of wave numbers k ~ 25 m–1, ship velocity U ~ 10 m/s, water kinematic viscosity v=10–6 m2/s and θ satisfying the inequality (31), it follows that |k2|≪|ikU sin θ/v|. In the limiting case of a viscous non-contaminated water the damping coefficient can be written as:
δ0=–4g2v/U5 sin5θ. (33)
The ratio γ=δ/δ0 characterizes the damping amplification factor which stems from the presence of surfactant film. It is plotted in Fig.2.
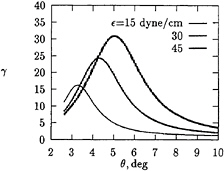
Figure 2: Relative viscous damping coefficient for different values of the surfactant film elasticity.
It can be seen clearly that the surfactant film greatly intensify the wave damping for small θ angles.
3.5
The Kochin function.
According to (3) and (4) the wave elevation induced by sources distribution over the hull surface S and the waterline contour lw can be written as follows:
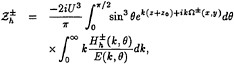
(34)
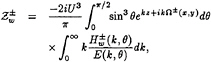
(35)
where
and
(36)
represent the Kochin functions. For short divergent waves with the wave length λw ~ 20–30cm the hull integral ![]() is significant only over a small depth of order λw. In this case Hh(x,y,z)
is significant only over a small depth of order λw. In this case Hh(x,y,z) ![]() Hh(x,y,0) and qh(x0,y0,z0)
Hh(x,y,0) and qh(x0,y0,z0)![]() qh(x0,y0,–0). In
qh(x0,y0,–0). In
the vicinity of the waterline a ship has almost a vertical board and thus:
(37)
where
It can be demonstrated that for short divergent waves the ![]() which implies that the contribution of the line integral is dominant in the final expression for the wave elevation.
which implies that the contribution of the line integral is dominant in the final expression for the wave elevation.
3.6
Simplified waterline
As it was earlier mentioned, the fine details of hull shape are not really essential as far as the far wave field is concerned. Thus, we choose a particular polygonal contour of ship waterline as:
where L is ship length, (L0/L) ~ 0.6–0.7 and
Straightforward calculations give the following expression for the wave elevations:
(38)
where
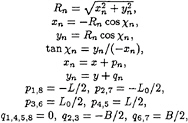
and
3.7
Asymptotic expression for the wave elevation.
In order to determine the asymptotic behavior of (38) well downstream let us consider some n-component of the integrand tacitly omitting the subscript n:
(39)
Following Whitham (1974) let us represent the integral with respect to θ as a sum of two integrals:
In the first of them the function sin(θ–χ) is positive whereas in second one it is negative. We deform the contour of integration with respect to the complex variable k and represent the corresponding integral as a sum of three integrals: an integral along the real half-axis, an integral along the positive (negative) imaginary half-axis and a semi-circle of an infinitely large radius connecting the ends of the real and imaginary axes. The roots of the equation E(k,θ)=0 with respect to k are located in the lower half-plane. Thus, if sin(θ–χ)>0 the contour of integration is directed along the negative imaginary half-axis and the poles of the integrand give a contribution; if sin(θ–χ)<0 the contour of integration is directed along the positive imaginary half-axis and the poles of the integrand do not give a contribution. This also insures that the contour integral along the semi-circle vanishes. For the purpose of estimating the order of magnitude of the integrals along the imaginary axes their limiting values as R → ∞ may be taken in the first approximation for a clean inviscid water without surface tension. It has been shown by Ursell (1960) that for R≫1 they are of the order of R–3 and thus can be neglected. We may conclude therefore that for large values of R formula (39) can be written as:
(40)
where
Δ(θ)=exp[δR sin(θ–χ)],
and
Φ(θ)=k0(θ)sin(θ–χ).
Similar analysis can be performed for the integrand of (38) incorporating the terms sin(θ+χ). However, as it will be shown below, within the intended accuracy such integrals do not contribute to the final result.
Further calculations are based on the stationary phase method. For large values of R the integral (40) can be estimated as follows:
where θs denotes the root of the equation
Φ′(θ)=0.
We intend to find an analytic expression for the wave elevation in the vicinity of a small angle χ which is comparable to the magnitude of the V-wake angle χV. Thus, it can be assumed that sin(θ±χ) ≃ θ±χ. Furthermore, since χV≫ 4gT/U4, the root of (30) can be estimated as follows:
which yields
It is possible now to obtain a simple expressions for the only point of the stationary phase θs
θs=2χ,
which define the function Φ(θs) and its second derivative Φ″(θs):
(41)
Hence the final expression for the wave elevation can be written as:
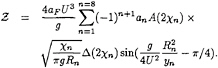
(42)
4
Asymptotic expression for the radar back scatter cross-section.
Consider an orthogonal local coordinate system O1ξη with an origin located at the center of the resolution cell. The coordinates (ξ,η) are rotated by an angle α in the counter clockwise direction from (x,y) coordinates:
x=–X+ξ cos α+η sin α,
y=Y+η cos α–ξ sin α.
Here (–X<0,Y>0) are the coordinates of the center of the resolution cell in the coordinate system Oxyz. Substituting (42) into (1) we have:
(43)
where
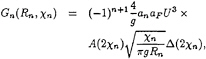
(44)
and ke=2kr sin ψ. The function ![]() n(Rn,η) for Rn≫1 has a distinctive extremum in some points
n(Rn,η) for Rn≫1 has a distinctive extremum in some points ![]() It allows us to employ the idea of the stationary phase method, but with some modification since the phase function by itself depends on a large parameter. We expand next the function
It allows us to employ the idea of the stationary phase method, but with some modification since the phase function by itself depends on a large parameter. We expand next the function ![]() n in Taylor series
n in Taylor series
(45)
in the vicinity of some point |η0|≤bc such that ![]() In order to simplify the final results we assume that X≫1, cos α=1 and sin α= α. After some tedious calculations the following expressions can be obtained:
In order to simplify the final results we assume that X≫1, cos α=1 and sin α= α. After some tedious calculations the following expressions can be obtained:
(46)
(47)
where
For U ~ 10m/s, kr ≈ 25m–1, sin ψ ~ 1/2 and X ~ 1,000m the numerical estimates of the derivatives show that ![]() and
and ![]() . Thus, the higher derivatives in the expansion (45) can be disregarded but the second derivative should be kept.
. Thus, the higher derivatives in the expansion (45) can be disregarded but the second derivative should be kept.
In the expression (46) the coordinates of the resolution cell are the geometrical parameters of the problem which can be chosen in order to provide the maximal back scatter cross-section. Let us further assume that
where j is some particular integers (i=1,…,8 ). In this case the coordinates of the center of the resolution cell are situated on the line
(48)
where ![]() Thus, we can define the V-wake angle as:
Thus, we can define the V-wake angle as:
(49)
Consequently, the point of stationary phase is:
The substitution of (48) into (47) gives the following expression of the phase function:
Finally, the dependence of the function (44) on the coordinates of the local system is rather weak, and thus it can be estimated as:
Gn(Rn,χn)~Gn(R0,χv),
where ![]()
Now the integration in the formula (43) can be performed analytically which yields the following expression for the radar back scatter cross-section:
Θ=A1A2A3A4A5, (50)
where
(51)
(52)
(53)
(54)
and
A5=Δ2(2χv). (55)
Here
and
(56)
Each factor in the product (50) allows a clear physical interpretation: A1 reflects the characteristics of the radar, A2 the parameters of the ship, A3 the direction of propagation of the divergent waves and the radar look of sight, A4 the interference between waves and their radiation decay and
A5 the radar back scatter cross-section attenuation affected by the fluid viscosity and surfactant film elasticity. It is interesting to note that for a ship with a length, say, L ~ 200m and width of a resolution cell about 2bc ~10m, at least one point of the stationary phase ![]() (n=1,…,8) is equal to zero whereas the rest of them are situated outside the resolution cell. Thus, the contribution from the rest of these points in the formula (54) is negligible. That leads to an additional simplification of (54):
(n=1,…,8) is equal to zero whereas the rest of them are situated outside the resolution cell. Thus, the contribution from the rest of these points in the formula (54) is negligible. That leads to an additional simplification of (54):
(57)
where C(ρ0) and S(ρ0) are the Fresnel integrals and
(58)
It is seen now that for ρ0≫1 the asymptotic estimates of Fresnel integral gives: C(ρ0)=S(ρ0) ~ 1/2 which means that the brightness of the signal does not decay along the bright arms. In practice the value of ρ0 is finite, but still can be large enough to provide a strong bask-scattering signal. In fact, if ρ0<1.5 the function A4 behaves as 1/X whereas for larger values of ρ0 it is an oscillatory function with a slowly decaying envelope.
5
Numerical simulation.
It is common to represent the radar cross-section in terms of its nondimensional rise above the background radar back scatter cross-section Θ0 which depends on the sea state. The value Θ0 can be estimated by a simple formula of Wright (1968). However, herein for the sake of consistency we prefer to invoke the experimental data of Shemdin (1990) which are represented in Table 3.
Table 3. Radar cross-section Θ0for different wind speed (ψ=30°).
|
Sea state |
Wind speed, m/s |
Θ0(dB) |
|
1 |
1–2 |
–30 |
|
2 |
2–4 |
–22 |
|
3 |
4–6 |
–17 |
|
4 |
6–8 |
–13 |
The dependence of the nondimensional rise of the radar back scatter cross-section above the background ![]() =Θ/Θ0 for Sea State 1 is shown in Fig.3.
=Θ/Θ0 for Sea State 1 is shown in Fig.3.
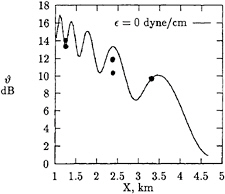
Figure 3: Rise of the radar cross-section above background versus distance aft of ship Bay Ridge. (Sea State 1) • –experimental data of Shemdin [35].
According to the experimental data of Shemdin the radar cross section decay along bright arms exhibits distinctive extrema, which, apparently, can not be explained by the noise of measurements. Moreover, the last significant maximum of the decaying curve occurs at the distance X about 3–4 km aft of the ship. According to the presented theory the various extrema result from the wave interference reflected by the relation (54). Noticeable, that according to the experimental data the length of the V-like bright arms varies between 5–6 km. It is reasonable to define the length of the bright arms LV as a coordinate XV where |Θ0|<1.0 dB. Under such a definition the theoretical prediction gives the value of LV ~ 4.5–6.0 km which is a good agreement with the experiment.
The bright V-wake arms appear in the SAR images only under the conditions of light wind and small wave height. The theoretical results presented in Fig.4 are in a good agreement with these experimental observations.
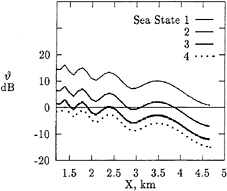
Figure 4: Rise of radar cross-section above background versus distance aft of ship Bay Ridge for different sea states.
It is seen that for Sea State 2 the visibility of the bright arms is actually much less then for the Sea State 1 but still noticeable. For Sea State 3 the visibility of the bright arms is doubtful. For Sea State 4 the magnitude of the radar cross-section is below the radar cross-section of the background level and thus can not be observed.
In Fig.5 it is demonstrated the dependence of the radar cross-section on the elasticity of surfactant film.
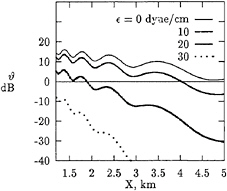
Figure 5: Radar cross-section versus distance aft of ship Bay Ridge for different surfactant film elasticity.
It is seen that even a relatively small surfactant elasticity (about 10 dyne/cm) significantly reduce the radar cross-section and the length of the V-wake. For relatively large but plausible values of surfactant elasticity about 25 dyne/cm the V-wake can not be anymore detected.
6
Summary.
An important progress has been achieved toward improving our general understanding of intriguing phenomenon of ship generated narrow V-wakes. The proposed analytic solution of the problem incorporates the important effect of sea surface contamination. It has been shown that the radar cross-section is a decaying oscillatory function along the bright V-arms. The asymptotic behavior of radar cross-section for a large distance X aft of a ship is governed by the asymptotic behavior of the Fresnel integrals C(ρ0), S(ρ0) where ρ0 is defined by (58) and (49).
The theory predicts a slow decay of the radar cross-section with increasing distance X until the value of the parameter ρ0 exceeds some threshold value ρthresh![]() 1.5. When ρ0 is below this critical value, the radar cross-section decays along the bright V-arms as 1/X.
1.5. When ρ0 is below this critical value, the radar cross-section decays along the bright V-arms as 1/X.
It has been demonstrated also that even a relatively small contamination of sea surface can change the radar back scatter cross-section drastically. According to the results of the present study the distance behind the ship for the surfactant film with elasticity ![]() ~ 20 dyne/cm to diminish the radar back scatter cross-section by a factor e–1 can be only few hundreds meters.
~ 20 dyne/cm to diminish the radar back scatter cross-section by a factor e–1 can be only few hundreds meters.
In this context of the present research it has to be mentioned that the visibility of the dark turbulent wake in Sea States 1–4 presumably can be explained by the attenuation of wind-generated waves due to the contamination of sea surface within the V-wake (Peltzer et al. 1991). The physical mechanism of compacting surfactant films in the immediate vicinity of the V-wake is an important follow-up to this investigation.
7
Acknowledgment
The authors would like to express their gratitude to Dr. L.Shemer for many valuable advises. Dr. E.Kit made interesting comments influencing the research. Dr. E.Pelinovsky during his visit to Tel-Aviv University read the draft of the manuscript and his critical comments are appreciated by the authors.
The research was partially supported by the Israeli Ministry of Science.
References
[1] Baar, J.J and Price, W.G. 1988 Evaluation of the wave-like disturbance in the Kelvin wave source potential. J. Ship Research, 32, 1, pp. 44–53.
[2] Barnell, A. and F.Noblesse. 1986 Far-field features of the Kelvin wake. Proc. 16th Symposium on Naval Hydrodynamics, University of California, Berkeley, pp. 18–36.
[3] Brard, R. The representation of a given ship form by singularity distributions when the boundary condition on the free surface is linearized. J. Ship Research, 6, pp. 79–92.
[4] Brown, E.D. 1985 Integrated Report on Mechanisms Responsible for Narrow Angle V-Wakes in the Georgia Strait Experiment, Final Report, Science Applications International Corporation, La Jolla, CA.
[5] Brown, E.D., Buchsbaum, S.B, Hall, R.E., Penhum, J.P., Schmitt, K.F., Watson, K.M. and Wyatt, D.C. 1989 Observation of a nonlinear solitary wave packet in the Kelvin wake of a ship. J. Fluid Mechanics, 204, pp. 263–293.
[6] Cao,Y., W.W.Schultz and R.F.Beck. 1992 Inner-angle wavepackets in unsteady wake. Proc. 19th Symposium on Naval Hydrodynamics, Seoul, Korea.
[7] Crapper, G.D. 1964 Surface waves generated by a travelling pressure point. Proc. Royal Society, ser.A, 282, pp. 547.
[8] Cummerbatch, E. 1965 Effect of viscosity on ship waves. J. Fluid Mechanics, 23, pp. 471– 479.
[9] Eggers, K. and Schultz, W.W. 1992 Investigation on time-harmonic disturbances for inner-Kelvin-angle wave packets. Seven International Workshop on Water Waves and Floating Bodies, pp. 87–91.
[10] Gu, D. and Phillips, O.M. On narrow V-like ship wakes J. Fluid Mechanics, 275, pp. 301– 321
[11] Havelock, T.H. 1935 Ship Waves: The relative Efficiency of Bow and Stern. Proc. Royal Society London, A, 149, pp. 417–426.
[12] Keller, J.B. and Munk, W.H. 1970 Internal wave wakes of a body in a stratified fluid. Physics of Fluid, 13, pp. 1425–1431
[13] Kelvin 1987 On the waves produced by a single impulse in water of any depth or in a dispersive medium. Proc. Royal Society London, A, 42, pp. 80–85.
[14] Kinoshita, T. 1980 Viscous effect on waves of thin ship. Proc. Thirteen Symp. on Naval Hydrodynamics, Tokyo, pp. 793–703.
[15] Kostyukov, A.A. 1968 The theory of ship waves and wave resistance. Effective Communication Inc., Iowa City, 1968.
[16] Lavrentiev, V.M. 1951 The influence of the boundary layer on the wave resistance of a ship . Doklady Akad. Nayuk USSR, 80.
[17] Levich, V.G. 1962 Physycochemical Hydrodynamics, Pretice-Hall, Elmsford Park, N.J.
[18] Lyden, J.D., Hammond, R.R., Lyzenga, D.R. and Shuchman, R. 1988 Synthetic aperture radar imaging of surface ship wakes. J. of Geophysical Research, 93, C10, pp. 12293– 12303.
[19] Mei, C.C and Naciri, M. 1991 Note on ship oscillations and wake solitons. Proc. Royal Society London, A, 432, pp. 535–546,
[20] Milgram, J.H. 1988 Theory of radar backscatter from short waves generated by ships, with application to radar (SAR) imagery. J. Ship Research, 32, pp. 54–69.
[21] Miloh, T., Tulin, M. and Zilman, G. 1993 Dead water effects of a ship moving in stratified seas. J. of Offshore Mechanics and Arctic Engineering, 115, pp. 105–110.
[22] Munk, W.H., Scully-Power, P. and Zachariasen, F. 1987 Ship from Space. Proc. Royal Society London, A 412, pp. 231–254.
[23] Nakos, D.E. and Sclavounos, P.D. 1994 Kelvin wakes and wave resistance of cruiser and transom-stern ships . J. Ship Research, 38, pp. 9–29.
[24] Newman, J.N. 1970 Recent Research on Ship Wakes, Proc. 8th Symposium on Naval Hydrodynamics: Hydrodynamics in the Ocean Environment, Arlingthon, Virginia, Office of Naval Research, Department of Navy, pp. 519–545.
[25] Newman, J.N. 1971 Third order interaction in the Kelvin ship wave system. J. Ship Research, 15, pp. 1–10.
[26] Newman, J.N. 1987a Evaluation of the wave resistance Green function: part 1-the double integral. J. Ship Research, 31, 2, pp. 79–90.
[27] Newman, J.N. 1987b Evaluation of the wave-resistance Green function: part 2-single integral on the center-plane. J. Ship Research, 31, 3, pp. 145–150.
[28] Noblesse, F., Hendrix, D. and Barnell, A. 1989 The slender-ship approximation: comparison between experimental data and numerical prediction. Journees de l'Hydrodynamique, ENSM, Nantes. France, pp. 175–187.
[29] Noblesse, F., and Hendrix, D. 1991 Near Field Nonlinearities and Short-Field ship Waves. Proc. 18th Symposium on Naval Hydrodynamics, Ann Arbor, Micihigan, pp. 465–476.
[30] Pelinovsky, E.H. and Talipova, T.G. 1990 Films of surface active materials on the sea surface (Russian). Preprint No. 219, Institute of Physics of Heat, Academy of Science USSR (Siberia Department) .
[31] Peltzer, R., J.H.Milgram, R.Skop, J.Kaiser, O.Griffin, W.Barger. 1991 Hydrodynamics of ship wake surfactant films. Proc. 18th Symposium on Naval Hydrodynamics, National Academy Press, Ann Arbor, Michigan, USA, pp. 533–552.
[32] Peters, A.S. 1949 A new treatment of the ship wave problem . Committe on Pure and Applied Mathematics, 2, pp.123–148.
[33] Ponizy, C.J., Noblesse, F., Ba, M., Guilband, M. 1994 Numerical evaluation of the free surface Green function. J. Ship Research, 38, pp. 193–203.
[34] Sharma, S.D. 1969 Some results concerning the wavemaking of a thin ship. J. Ship Research, 13, 3, pp. 72–81.
[35] Shemdin, O.H. 1990 Synthetic aperture radar imaging of ship wakes in the Gulf of Alaska . J. of Geophysical Research, 95, C9, pp. 16319–16338.
[36] Tuck, E.O., J.I.Collins and W.H.Wells. 1971 On ship wave patterns and their spectra. J. Ship Research, 15, pp. 11–21.
[37] Tulin, M.P. and Miloh, T. 1990 Ship internal waves in shallow thermocline: the supersonic case. Proc. of the 18th Symposium on Naval Hydrodynamics, Ann Arbor, Michigan, USA, pp. 567–584.
[38] Ursell, F. 1960 On Kelvin's ship-wake pattern. J. Fluid Mechanics, 8, pp. 418–431.
[39] Ursell, F. 1988 On the theory of the Kelvin ship-wave source: asymptotic expansion of an integral. Proc. Royal Society London, A 418, pp. 81–93
[40] Whitham, G.B. 1974 Linear and nonlinear waves. Jonn Wiley & Sons, N.Y.
[41] Wehausen, J.V and Laitone, E.V. Surface waves in Encyclopedia of Physics, 9, Springer-Verlag.
[42] Wright, J.W. 1966 Backscattering from capillary waves with application to sea clutter . IEEE Trans. Antennas and Propagation, 14, pp. 749–754.
[43] Wright, J.W. 1968 A new model for sea clutter. IEEE Trans. Antennas and Propagation, 16, pp. 217–223.
[44] Wu, T,Y. and Messick, R.E. 1958 Viscous effect on surface waves generated by steady disturbances. Caltech. Rep. No. 85–8.














