Time-Marching CFD Simulation for Moving Boundary Problems
H.Miyata (University of Tokyo, Japan)
Abstract
The state of the art of the CFD application to the ship hydrodynamics and ocean engineering is overviewd. The solution procedure for the unsteady fluid flow phenomena is briefly explained and the substantial techniques to treat moving boundaries are reviewed as well as the appropriate choice of the grid system. Simulation results are summarized from the research works of the author's laboratory for the problems of free-surface shock wave, wave resistance, ship maneuvering, sailing mechanism, ocean wave and bubble flow.
1
INTRODUCTION
How can we make progress in ship hydrodynamics? How the technology for hydrodynamical design of ships has been advanced? We may have three important factors of substantial importance for the progress of technology, they are science, analysis and synthesis. Scientific finding provides sound understanding of the nature of the fluid motion and this can directly contribute to the improvement of hull form in an intuitive manner or through reasoning based on theoretical analysis. The theoretical and computational analyses give us clear understanding of the structure and mechanism of fluid flow and these lead to the ideas of controlling the fluid flow aiming at the optimization of the ship. Synthetic works are substantially important for the conceptual development of the new hull-form, new devices or new system of transportation.
It is often the case that the research works are focused on analysis although we well realize that the innovation of technology is mostly achieved either by scientific findings or by synthetic ideas. However, in our field of naval architecture, the scientific finding and synthesis have not greatly contributed to the progress in comparison with other field of engineering. Analysis is usually very useful for the improvement of industrial products and it reinforces the design procedure. Design is performed with good help of analysis. It may be safe to say that the most important part of the progress of ship technology in the past half century is made by the development of production technique and analysis technique. The enlargement of ship size, the improvement of hydrodynamical performance and many others are attributable to these techniques.
Computational fluid dynamics (CFD), to which research efforts have been focused in the past 15 years in our field, is one of the most effective techniques of analysis. The flow-field and resultant forces and moments are estimated by computer simulations. Since the Navier-Stokes equation is solved, they can cope with a variety of nonlinear flow, such as turbulent flow, shock wave and breaking wave. Considerable part of tank test can be taken place by the CFD simulation on the computers. Almost all fluid motions are unsteady. Almost steady flow also contains unsteady aspects, especially when the Reynolds number is high and turbulence occurs. Therefore the time-marching CFD technique is essentially suitable to fluid dynamics.
Recently the advance of CFD technique enables us to simulate moving body or body in deformation by some special technique. On the other hand the technique of treating the moving free-surface is established long ago in the 1960's. Therefore we can simulate moving or deformed body in the fluid domain with moving free-surface. This means that we can simulate a sailing ship in arbitrary motions. Considering that tank experiments are usually performed by restricting the freedom of model ship, the CFD simulation is now going to surpass tank test in some respects. The purpose of the present review paper is to summarize the state of art of such CFD technology used for the design of ships and related researches. A large number of examples are collected from the simulation results at the author's laboratory.
2
TIME-MARCHING SOLUTION METHOD AND GRID SYSTEM
2.1
Solution algorithm
The development of CFD code was started at the author's laboratory in 1979 when the author noticed the existence of the nonlinear ship wave called free-surface shock wave [1]. The typical codes developed in the past 17 years are listed in Table 1. The series of TUMMAC code is based on the finite-difference method in the rectangular grids and those of WISDAM code is based on the finite-volume method in the curvilinear, boundary-fitted grids [ 2], but they all follow the same solution algorithm of the MAC-type [3]. The MAC-type solution algorithm is based on the LU decomposition and explicit time-differencing and it is most suitable to the time-marching solution.
The velocity and pressure field are separately solved in the time-marching process. The velocity field is updated by the following Navier-Stokes equation modified by the explicit time-differencing.
(1)
Here, two-dimensional equation is used and the terms ξ and ζ contain previous velocity, convection terms and diffusion terms. Pressure devided by the density of fluid is denoted ϕ. The pressure field is determined by the following Poisson equation of which implementation means conservation of mass.
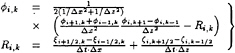
(2)
With these two equations the flow-field is sequentially updated in the time-marching procedure under the boundary conditions on the body-surface, free-surface and open boundary.
The block-diagram is shown in Fig.1 for the case of two-layer flow solution making use of the density-function for the implementation of the free-surface conditions. From the velocity field and their boundary conditions the source term for the Poisson equation of the pressure is given. Then the pressure fields of the two layers are solved with the source term under appropriate boundary conditions. The updated pressure gives new velocity field through the relation of the Navier-Stokes equation. This is repeated with the time-dependent boundary configuration and conditions imposed on it. In the open flow problems the disturbance of the flow takes place by the interaction between fluid and body and the disturbance may be artificially given by the generation of the waves at the inflow boundary or by the movement of the body.
2.2
Grid System
In the past 30 years the technique of solving the Navier-Stokes equation has made remarkable progress and the gradient of improvement has recently been decreased. The CFD technology is now putting more stress on customizing, for which the grid generation technique plays an important role. Since we have reliable solution method for the Navier-Stokes equation, the success of the CFD simulation rely on the grid generation to a larger extent than before. Actually a large part of the efforts is devoted to the grid generation when a three-dimensional body of complex geometry is deal with. Although the gridless technique is continuously investigated, it still has some substantial difficulties, such as poor implementation of the conservation laws. Presently we must work within the framework of the method with grid system.
Since the unstructured grids like those for the finite element method (FEM) still have difficulties in developing into three-dimensional (3D) cases, we can choose either the rectangular grids of the boundary-fitted, curvilinear grids (structured grids). When we employ the rectangular grids both the body-boundary and the free-surface cannot be fitted to the grid lines, while the body-boundary-fitted grids can be either fitted to the free-surface or not. In general the structured grids find difficulties in the representation of the boundary of extreme complexity, such as the automobile shape or free-surface shape of breaking wave. In this context the choice and design of the grid system is of significant importance for the appropriateness, convergence, robustness and accuracy of the CFD simulation.
The cross-sectional grids of the TUMMAC-IV[4][5] and WISDAM-V [9][10] methods are shown in Fig.2. Apparently the degree of accuracy for the implementation of the body-boundary condition is deteriorated in the TUMMAC-IV method. However the purpose of the TUMMAC-IV method is to simulate free-surface waves and the advantage of the shorter CPU time due to the larger spacing and of the needless efforts of grid generation made this code very popular. The boundary-fitted grids are
designed so that the delicate fluid motions both on the body surface and free-surface are well resolved and the degree of accuracy is raised as far as possible within the limited number of grid points. However the small spacing and the singularity give rise to the problem of convergence and robustness. A grid system for a tanker is shown in Fig.3 in which it is well noted that the grid spacing abruptly varies in all directions.
3
MOVING BOUNDARY TREATMENT
3.1
Moving body-boundary conditions
In case the rectangular grids are used for a body of arbitrary configuration, the body-boundary condition is very approximately implemented. In the typical 2D case of Fig.4 either no-slip or free-slip condition can be satisfied even if the divergence free condition is fulfilled in the cell together with the no penetrating condition on the boundary. However, it is almost impossible to realize the velocity profile of turbulent boundary layer with such grid system.
In case the boundary-fitted grids are used we can put one or two grid points within the thickness of viscous sublayer. However, we still find it difficult to realize the turbulent boundary layer with sufficient degree of accuracy. In the 3D case the number of grid points increases 8 times when the spacing is reduced to half length, which means the number of grid points are always insufficient in spite of the rapid advance of the semiconductor technology. The cell on the body surface is usually disproportionate, i.e. the length and width is more than 100 times larger than the thickness. Therefore the present turbulence models do not work well, and we often impose an empirical formula of wall function as shown in Fig.5.
For the numerical simulation of moving boundary problems the grid system must be accordingly deformed as shown in Fig.6 for the case of a fish in propulsive motion at a low Reynolds number. Since the variables and all related quantities are defined by the underlying grid coordinates, their movement is supposed to cause serious difficulties in the solution procedure. Actually when we tried to solve both viscous flow on the body surface and waves on the free-surface simultaneously in a structured grid system[9], the formulation resulted in a very complicated form, almost all terms containing the velocity of grid movement in the framework of the finite-difference method. However the finite-volume method appeared to have sufficient degree of robustness and the ALE method improved to implement the conservation laws in the boundary cells as shown in Fig.8 [12][13].
In the case of Fig.6 the grid points on the body surface remains at the fixed position and the surrounding grids are regenerated. However, such treatment is not suitable to the rolling motion of a boat in Fig.7, because the intersection of the body on the free-surface moves in time and the wetted surface, on which grid points are located, significantly changes. For such motions with large amplitude the grid regeneration is performed in two steps as shown in Fig.7. The velocity of rotation is separated and this is not used for the deformation of the grids, but it is assumed to be the given fluid velocity on the body surface. This technique enables us to solve the problem of a boat moving with arbitrary degrees of freedom [ 14].
3.2
Free-surface conditions
There are a number of technique of implementing the free-surface conditions; i.e., the Eulerian method, the Lagrangian method, the ALE method, the VOF method and the marker-density method. The free-surface conditions are composed of the dynamic and kinematic conditions each comes from the conservation laws of momentum and mass, respectively. When the fluid motion above the free-surface can be ignored and the viscous stress as well as the surface tension on the free-surface can be neglected, the dynamic condition is simplified to be a condition of giving the atmospheric pressure on the free-surface. When the small-scale free-surface motions can be assumed out of the scope of the research, the free-surface conditions can be well implemented both in the boundary-fitted grids and in the rectangular grids.
In most of the methods using free-surface-fitted grids the Eulerian method is employed and the Lagrangian method, following the original MAC method, is often used in the framework of the rectangular grids, see Fig.10. The difference of the two methods is not so substantial, since the boundary-fitted grids is transformed into the rectangular grids as shown in Fig.9. The difference consists in the way of determining the free-surface location by satisfying the kinematic condition. It is usually difficult to exactly fulfill the conservation law of mass, but by use of the ALE method the degree of accuracy in the implementation of the mass conservation law is remarkably raised.
The VOF (volume of fluid) and the density-function method [11] implement the mass-conservation law by the transport of the fluid volume or fluid flux instead of the tangential movement of the fluid on the free-surface. This treatment of the mass conservation law enables us to model the free-surface configuration of complexity such as that of overturning wave as shown in Fig.11.
4
SHIP FLOW SIMULATION
4.1
Bow wave simulation
After the author clearly noticed the inadequacy of the wave resistance theories during the practical work of hull form design at a shipbuilding company, the experimental work to investigate into the nonlinearity of bow wave was started in 1977. When some of the important features of the nonlinear bow waves called free-surface shock wave (FSSW) were elucidated, we started CFD works for nonlinear bow waves in 1979 when the author first discussed FSSW with Prof. Wehausen and when the workshop on wave resistance computation was organized by Dr. Bai at DTNSRDC. The MAC method developed at Los Alamos scientific laboratory seemed us most suitable to nonlinear ship waves, since it was already demonstrated that this numerical technique can deal with nonlinear waves including breaking wave.
The development of the TUMMAC method had been continued with the multi-purpose mainframe computer of the University of Tokyo and the TUMMAC-IV method for ship waves was completed in 1983 [4][5][16] when the first supercomputer from HITACHI was introduced and the second workshop on wave resistance computation was organized by Dr. Noblesse at DTNSRDC. In the subsequent 10 years the TUMMAC-IV method has been widely employed as a reliable tool to optimize the fore-part of the hull-form in Japan and later in Korea. The TUMMAC-IV method cannot estimate the wave resistance value of the whole ship but it can simulate the wave system and resultant pressure distribution on the hull with sufficient degree of accuracy. Its reliability mostly consists in the property of accuracy in discriminating the better hull-form from others.
For the TUMMAC-IV method the rectangular grid system shown in Fig.12 is employed and the marker is used to implement the kinematic free-surface condition. The dynamic condition for the pressure is satisfied on the exact location of the free-surface. A large part of the difficulties consists in the technique of implementing the free-slip body-boundary conditions in the irregularly distributed boundary cells denoted B in Fig.12. The treatment at the singular points such as the bow-end or the intersection of the free-surface with the body surface necessitates special techniques.
Simulation results for bow waves of bulk carriers are shown in Figs. 13 and 14 comparing with the measured wave contours. The hull form M55FO has a conventional bow-bulb and M55F1 has a thin, long-protrudent bulb which is designed from the knowledge of the characteristics of FSSW. The hull-form design of a bulk carrier ”USUKI PIONEER” based on the lines of M55F1 and the verification of the computation was performed in 1983 and since then both the TUMMAC-IV method and the thin-long protrudent bulb have been widely employed for low-speed and middle-speed marchant ships. Although the difference of the waves between two hull-forms seems to be gentle, the value of wave resistance has meaningful difference. Since the nonlinearity of the bow wave is mostly governed by the Froude number based on draft, waves show nonlinearity more strongly on the ballast condition, in which the agreement is deteriorated due to the occurrence of wave breaking. However the accuracy in relative magnitude is usually correct probably because the steep waves before breaking are well simulated.
4.2
Diffraction waves at a bow
Since the TUMMAC-IV method is a finite-difference time-accurate simulation, it can be applied to a wave diffraction problem [6]. The experimental results are shown in Fig.15 for the most simple case of a fixed wedge model advancing steadily against incoming regular periodic waves with their crests normal to the direction of model advancement. It is clearly noted that shock-like waves are generated and they show different formation, normal, oblique and mixed type depending on the phase of the incident waves.
The simulation for this problem gives rise to the difficulty of the location of the wave-maker. In a towing tank where the experiments shown in Fig.15 are performed the wave-maker is set at a fixed location and the wedge model is towed reducing the distance to the wave-maker. However in the numerical simulation the coordinates are fixed to the wedge model and the computational domain is limited within the area surrounding the model. The incident waves need to be generated at the inflow boundary of the computational domain. Therefore
the distance between the numerical wave-maker and the wedge-model is invariant, and the numerical wave generation is performed by considering the encounter frequency. However the generated waves are slightly different from the physical experiments.
The comparison is made in Figs.16 and 17 between computed and measured wave contours at five phase angles. Due to the above-mentioned condition as well as the fact that the breaking phenomenon is not interpreted in this code the agreement is beyond satisfaction. However the typical features of varying wave formation are well simulated.
4.3
Free-surface shock wave
The 3D wave breaking can be simulated by the TUMMAC-VIII method which makes use of the density-function technique. The physical stages of FSSW is (1) steep wave generation, (2) breaking and (3) dissipation. The TUMMAC-IV method can simulate (1) and the TUMMAC-VIII (2), but the wave dissipation into momentum loss cannot be well simulated caused by the numerical dissipation of comparable magnitude by the coarse grid spacing.
As shown in Fig.18 the typical wave breaking features are simulated for a wedge model at three Froude numbers [15]. Detailed analysis of the computed results shows that the shock condition of the horizontal velocity vector is almost completely fulfilled on the layer near the free-surface and that the shock phenomenon is limited within the thin-layer of which depth is grossly 20% of the ship draft.
4.4
Stern wave of fast ship
The wave from the transom stern of high-speed vessels is one of the difficult problem for theoretical fluid dynamics, since the cornered end is a singular point for the fluid flow. Some special treatment is introduced here in the previous attempts. However, by use of the density-function technique for the kinematic free-surface condition the flow and waves about the transom corner can be simulated without any additional assumptions as shown in Figs.19 and 20, which are results of the WISDAM-VI method in the framework of curvilinear coordinates fitted to the body surface but not to the free-surface.
4.5
Maneuvering motion
Because of the facts that the tank test to predict the maneuvering properties requires a lot of time and efforts and that some of the maneuvering motions cannot be well realized in the experimental facilities, the realization of the maneuvering simulation in the computer is of significant importance.
In case the motion is steady such as oblique towing or steady circling motion, the movement of the ship is represented by the body-force term added to the Navier-Stokes equation, and in case the motion is unsteady the moving grid technique becomes useful. In the past 5 years the maneuvering simulation has been studied within the framework of the WISDAM-V method for which boundary-fitted grid system is employed. We still find some difficulties in realizing the Z-test motion mostly due to the wide variation of the heading angle. However, the oblique tow test, steady circling test and PMM test have been achieved [ 19]. An example of steady circling test is shown in Figs.21 and 22. It is demonstrated that the advantage of CFD simulation is that instantaneous pressure distribution and flow features can be clearly explained. The degree of accuracy in the magnitude of forces and moments is almost of the satisfactory level for low speed ships. For instance, the effect of the difference of the framelines of the after-part is explained as a difference of longitudinal distribution of lateral force in the circling motion.
5
SAILING BOAT SIMULATION
5.1
Steady motion
In comparison with large-scale marchant ships the dynamics of sailing boat is much more complicated. They have absolutely larger freedom of motion in 6 degrees. When a sailing boat moves in the upwind direction the VMG speed is more important than the boat speed, which means that not only the resistance but also the balance of forces and moments are important to achieve high performance. This situation is similar to airplanes or hydrofoil crafts. A sailing boat obtains propulsion force from wind through the work of sails. This implied that the actual sailing condition is very difficult to realize in the model tests. Sailing boat simulation by the combination of the CFD simulation with the solution of the equations of motion seems to be substantially useful for its design when sufficient degree of accuracy is attained.
The development of the WISDAM-VII code for sailing boat was started in the middle of 1993 when the author was assigned to be a general coordinator for the technical team supporting the Nippon
Challenge for the America's Cup 1995. It was evident that this development cannot contribute to the challenger's series started in the beginning of 1995 and actually other codes TUMMAC-IV and WISDAM-V were used for the development of new hulls.
Considering the six degrees of freedom of motion for sailing boats, the 0–0 type grids shown in Fig.23 are employed. Since the Froude number based on the boat length exceeds 0.3, free-surface waves must be taken into account. Therfore, the grids are clustered to the free-surface and body-surface. The finite-volume method is employed and the moving grid technique is fully utilized including the hull-surface slipping technique for the rolling motion.
Exerting forces are illustrated in Fig.24 for the vertical section of a boat on the upwind sailing condition. Sails and appendages would better be simulated in the same way with the hull. But at present they are treated as simple lifting surfaces and generated forces are incorporated into the equation of motion.
This simulation method for sailing boat composed of the WISDAM-VII method and the solution of the equations of motion is also connected to the CAD system. Thus, the difference of performance by the modification of hull-form can be studied in a straightforward manner in the computer simulation. The results of the study of beam-length series are shown in Figs.25 to 27. The forces and moments by the sails and appendages are set at constant and the sailing boats are set to be free to trim, heave and heel. Then the fluid-dynamical properties are compared as shown in Figs. 26 and 27. When the advance speed is set at constant the forces and values determining the sailing performance are all provided and compared.
5.2
Unsteady motion
By changing the freedom of the boat and introducing the control of rudder and other moving surfaces into the equation of motion arbitrary sailing behavior can be simulated. The case of course changing by 4 degrees during upwind sailing is shown in Fig.28 with two variation of gains of the automatic control system for the rudder. The results of the simulation of this maneuver are shown in Figs.29 and 30. It is understood that the time-variation of rudder angle and the components of lateral forces depends on the helmsman's technique although steering is automatically made in this simulation. Unfortunately such simulation requires almost 1000 times longer time in an engineering workstation than the actual maneuvering time of a sailing boat. Therefore this technique cannot be used as a real-time sailing simulator for the purposes of the training of helmsman and the development of boats of better performance. However, it may be safe to say that it is a most advanced design tool for sailing boats of high performance.
6
OCEAN WAVE SIMULATION
6.1
2D breaking wave
More than 10 years ago 2D breaking simulation was first completed by use of the movement of free-surface segment within the framework of rectangular grid system [7] [16]. A typical result of a 2D bow wave in front of an advancing floating body is shown in Fig.31. Due to the robustness of the method with equal spacing and staggered arrangement of variables the overturning motion together with the impingement of the breaking wave front is well simulated. As seen in Fig.31, the successive overturning motion of the type of plunging breaker is realistically solved.
However this technique cannot be extended to the 3D problem since the complicated free-surface configuration may not be represented by the succession of segments or something similar. The free-surface may intersects the rectangular cells in a variety of manner. The free-surface-fitted curvilinear grids may resolve the fluid motion on the breaking free-surface with sufficient degree of accuracy. However such grids find serious difficulties in making the configuration of overturning wave front. Furthermore the 3D impinging motion cannot be imagined to be deal with by such a technique.
6.2
3D breaking wave
For the numerical representation of the extremely complicated configuration of the 3D breaking free-surface the density-function method is developed. The density is a scalar value to determine the fluid fraction in a rectangular cell, i.e., porosity of fluid in a cell. The free-surface location is approximately represented by this value and the slope of the free-surface by the combination of these values in the neighboring cells.
The first idea was to solve both gas and liquid regions continuously. However it turned out to be unsuccessful firstly because the density was 1000 times different between water and air and small difference of water pressure gave rise to very large difference
of air velocity and secondly because the equation of density-function showed excessive diffusive effect. Therefore it is used only for the determination of the interface location and the fluid flow is separately solved as shown in the block diagram in Fig.1 [8].
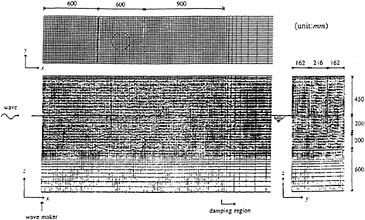
A grid system for the simulation of a wave flow about a part of semisubmergible is shown in Fig.32. In order to compensate the low degree of accuracy inherent to the density-function method the variable grid system is employed in the vertical direction.
The results of time-marching simulation of wave diffraction with semisubmergible are shown in Fig.33. Since steep regular waves of large wavelength interact with a lowerhull and a number of vertical pillars, which is realized by the symmetric condition on the side boundaries, a peculiar wave is formed behind the pillar [20].
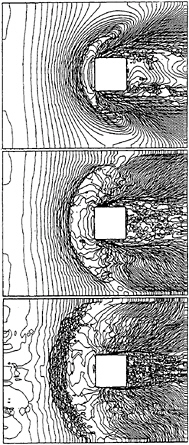
The case of extremely nonlinear waves about a vertical pillar in a uniform stream of air and water is shown in Fig.34 to 36. Since the Froude number based on the horizontal length is 1.25 the bow wave shows breaking phenomenon and almost vertical free-surface configuration appears on the sides and behind the cylinder. Spray and air-entrainment are also observed in the vicinity of the cylinder, although their reality is not well guaranteed.
This simulation technique is easily applied to another two-layer flow, i.e., water flow above liquefied sand layer by simply changing the density value of the fluid. One feature of scoring sand layer by the water flow interaction with the pillar is shown in Fig.37. First the sand in front of the pillar is suppressed by the stagnation pressure and secondly the horseshoe vortex here accelerates the scoring and thirdly the scoring intensifies the horseshoe vortex until the scored region reaches a certain upstream point. This process is simulated by the time-marching simulation started from the rest condition. Although the degree of accuracy is not high, the TUMMAC-VIII method with the density-function technique can be applied to a variety of two-layer flow with strongly interacting interface.
7
MULTI-PHASE FLOW SIMULATION
7.1
Bubble flow simulation
The technique of treating the free-surface can be applied to other fluid phenomenon with interface. The density-function method has good versatile properties for the resolution of the interface. A lot of fluid phenomena associated with environmental engineering or production process engineering seem to be simulated by the CFD techniques slightly modified from those described in this article and the simulation results will contribute to the improvement of technology. The single experience of the author is the simulation of continuous casting for steel plate production for which modified TUMMAC-IV method is useful.
Quite recently two CFD research works for bubble flow are executed at the author's laboratory. One is the method using an overlapping grid system fitted both to the wall boundary and bubble surface, and the other is that of TUMMAC-VIII, i.e., the combination of rectangular grid system with the density-function technique for the bubble surface. The surface tension is incorporated into the bubble surface conditions.
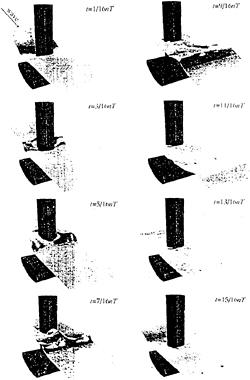
The results of a bubble freely rizing in a still water region are presented in Figs.38 and 39. The Weber number is 4.8 and the Reynolds number is 1440 [21]. The bubble makes a spiral trajectory after the vortex shedding downward reaches the periodically steady state. It is interesting to note that the successive shedding of horseshoe vortices shown in Fig.39 is common to many other vortex shedding from blunt bodies such as a sphere and an automobile.
8
CONCLUSION
It is described in this article that the time-marching CFD technique for moving or deforming problems provides us wide possibility to improve the understanding of unsteady fluid phenomenon and the design of moving objects. In the field of naval architecture one symbolic goal is to complete simulation technique for a ship in slamming motion at rough sea. However it must be also noted that such technique can contribute to a lot of problems in the fields of process engineering, environmental engineering and so on.
One of the serious problem is that a great deal of efforts by able CFD researchers must be devoted for the customizing the software. Since the progress of computer technology remarkably reduced the problem of hardware investment, almost all the computations have been executed by workstations at the author's laboratory in the past seven years. Therefore all the results in this article, except those of Figs.13, 14 and 16, are provided by workstations.
References
[1] Miyata, H. and Inui, T.,” Nonlinear ship waves,” Advances in Applied Mechanics, Vol. 24, 1984, pp. 215–288.
[2] Miyata, H.,” Free-surface flow simulations by finite-difference techniques,” Computational Fluid Dynamics '94, Sept. 1994, pp. 61– 71. ECOMAS Computational Fluid Dynamics Conference, Stuttgart.
[3] Welch, J.E., Harlow, F.H., Shannon, J.P. and Daly, B.J.,” The MAC method,” Los Alamos Scientific Lab. Report, LA-3425, Univ. California, 1966, Los Alamos, New Mexico.
[4] Miyata, H. and Nishimura, S., ”Finite-difference simulation of nonlinear ship waves,” Journal of Fluid Mechanics, Vol. 157, Aug. 1985, pp. 327–357.
[5] Miyata, H., Nishimura, S. and Masuko, A.,” Finite difference simulation of nonlinear waves generated by ships of arbitrary three-dimensional configuration,” Journal of Computational Physics, Vol. 60, No. 3, 1985, pp. 391–436.
[6] Miyata, H., Kanai, M., Yoshiyasu, N. and Furuno, Y.,” Diffraction waves about an advancing wedge model in deep water,” Journal of Ship Research, 34–2, June 1990, pp. 105–122.
[7] Miyata, H.,” Finite-difference simulation of breaking waves,” Journal of Computational Physics, Vol. 65, No. 1, 1986, pp. 179–214.
[8] Miyata, H., Katsumata, M., Lee, Y.G. and Kajitani, H.,” A finite-difference simulation method for strongly interacting two-layer flow,” Journal of the Society of Naval Architects of Japan, Vol. 163, 1988, pp. 1–16.
[9] Miyata, H., Sato, T. and Baba, N.,” Diffrence solution of a viscous flow with free-surface wave about an advancing ship,” Journal of Computational Physics, 72–2, Oct, 1987, pp. 393–421.
[10] Miyata, H., Zhu, M. and Watanabe, O., ”Numerical study on a viscous flow with free-surface waves about a ship in steady straight course by a finite-volume method,” Journal of Ship Research, Vol. 36, No. 4, 1992, pp. 332– 345.
[11] Park, J.C., Zhu, M. and Miyata, H.,” On the accuracy of numerical wave making techniques,” Journal of the Society of Naval Architects of Japan, Vol. 173, 1993, pp. 35–44.
[12] Roseneld, M. and Kwak, D.,” Time-dependent solution of viscous incompressible flows in moving coordinates,” Intern. Journal for Numerical Methods in Fluids, Vol. 13, 1991, pp. 1311– 1328.
[13] Akimoto, H. and Miyata. H.,” Finite-volume smulation of a flow about a moving body with deformation ,” Proceedings of the 5th Intern. Smposium on Computational Fluid Dynamics , Vol. 1, Aug. 1993, pp. 13–18. Sendai.
[14] Akimoto, H.,” Development and application of CFD simulation technique for a hull in 3D motions,” Ph. D thesis, University of Tokyo, 1996.
[15] Kanai, A. and Miyata, H.,” Elucidation of the structure of free surface shock waves about a wedge model by finite-difference method,” Journal of the Society of Naval Architects of Japan, Vol. 177, 1995, pp. 147–159(in Japanese).
[16] Miyata, H., Nishimura, S. and Kajitani, H., ”Finite difference simulation of non-breaking 3-D bow waves and breaking 2-D bow waves,” Proceedings of the Intern. Conference on Numerical Ship Hydrodynamics, Sept. 1985, pp. 259–292. Washington. D.C.
[17] Kawamura, T. and Miyata, H.,” Simulation of nonlinear ship flows by density-function method,” Journal of the Society of Naval Architects of Japan, Vol. 176, 1994, pp. 1–10.
[18] Kawamura, T. and Miyata, H.,” Simulation of nonlinear ship flows by density-function method. (Second report),” Journal of the Society of Naval Architects of Japan, Vol. 178, December. 1995, pp. 1–7.
[19] Omori, T., Miyata, H., Fujino, M., Usami, S. and Eguti, S.,” A study of flow field around full ship forms in maneuvering motion (second report: Hydrodynamic forces and pressure distribution on ship's hull in steady turning condition),” Journal of the Society of Naval Architects of Japan, Vol. 177, May. 1995, pp. 13–28.
[20] Park, J.C. and Miyata, H.,” Numerical simulation of 3D breaking wave motions about an offshore structure under a severe sea condition,”
Table 1: Characteristics of finite-difference and finite-volume methods developed at the University of Tokyo.
|
Body boundary fitted grid |
Free surface fitted grid |
Wave breaking consideration |
Moving coordinate |
Code name |
Application |
|
x |
x |
x |
x |
TUMMAC-IV |
Ship wave |
|
◯ |
x |
TUMMAC-VIII |
breaking ocean wave beach wave, bubble flow |
||
|
◯ |
x |
◯ |
x |
WISDAM-VI |
breaking ship wave |
|
◯ |
◯ |
x |
◯2D |
WISDAM-V |
ship viscous flow ship maneuvering |
|
◯3D |
WISDAM-VII |
sailing boat simulation |
|||
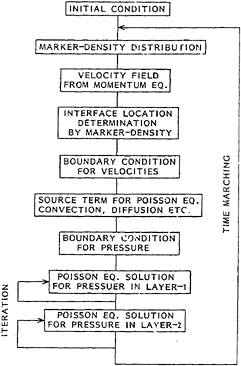
Figure 1: Block diagram of the MAC-type solution procedure for two-layer flow.
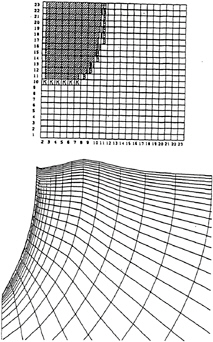
Figure 2: Rectangular and curvilinear grid system.
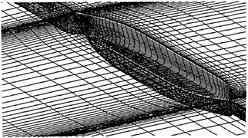
Figure 3: Boundary-fitted coordinate system for a tanker hull.
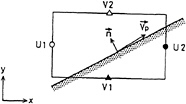
Figure 4: Schematic sketch for the body boundary condition in the rectangular grid system.
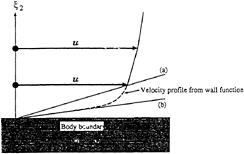
Figure 5: Schematic sketch for the body boundary condition in the boundary-fitted grid system.
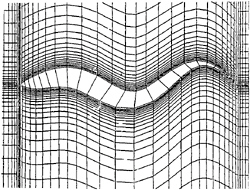
Figure 6: Moving grid system for a 2D case.
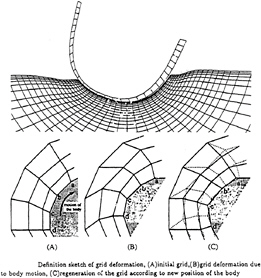
Figure 7: Moving grid system for a rolling ship.
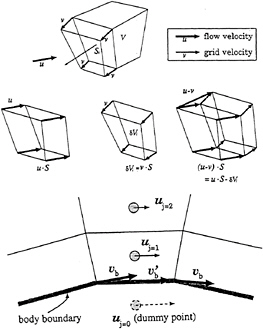
Figure 8: Schematic sketch for the treatment of the moving velocities on the body boundary.
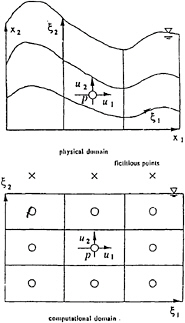
Figure 9: Velocity and pressure points of the grid system fitted to the free-surface.
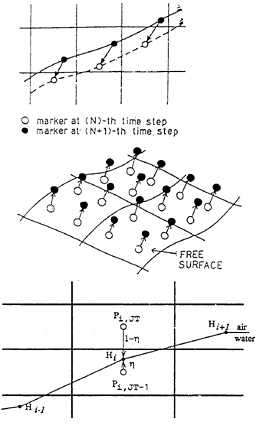
Figure 10: Schematic sketch for the fulfillment of the kinematic and dynamic conditions on the free-surface in the rectangular grid system.
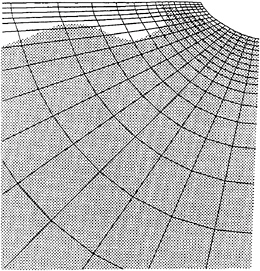
Figure 11: Schematic sketch for the determination of the free-surface location by the density-function method used in the body-boundary-fitted grid system.
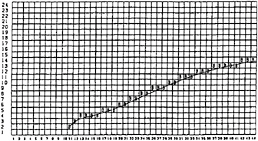
Figure 12: The horizontal grid arrangement and body-boundary cells of the TUMMAC-IV code for ship waves.
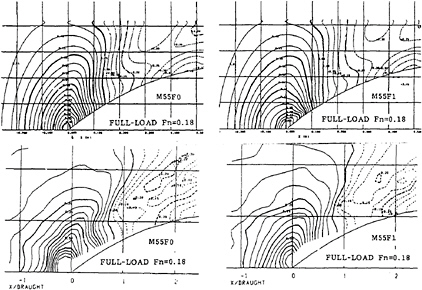
Figure 13: Comparison of computed and measured wave contours of two hull-forms of a 26000 DWT bulk carriers M55 F0 and M55 F1 at Fn=0.18.
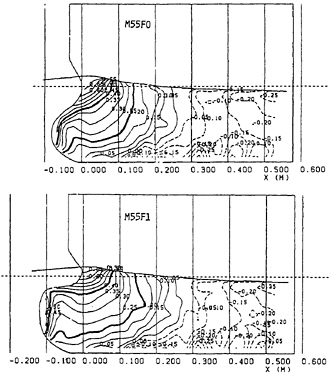
Figure 14: Comparison of pressure distribution on the hull of the two ships of Fig.13.

Figure 18: Perspective view of the computed bow waves about a 20° wedge model at three Froude numbers, Fd=0.8, 1.1 and 1.4 from above.
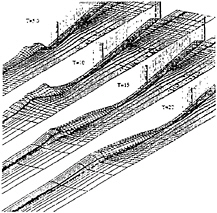
Figure 19: Perspective view of the computed stern wave emanating from a high-speed vessel.
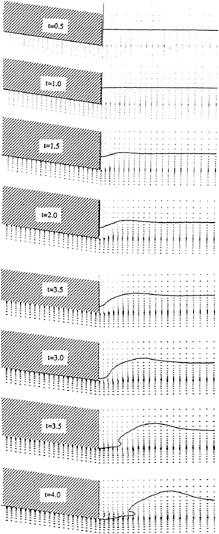
Figure 20: Time-sequence of the evolution of the stern wave at a high Froude number.
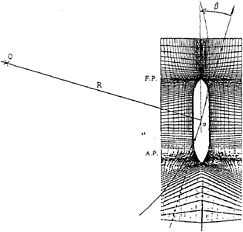
Figure 21: Grid system for a ship in steady turning motion.
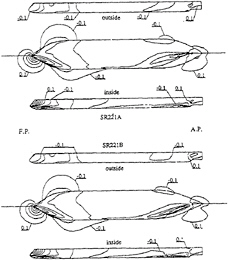
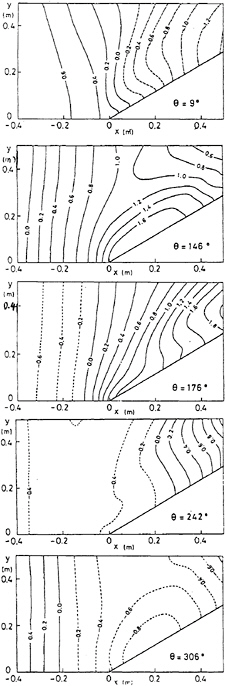
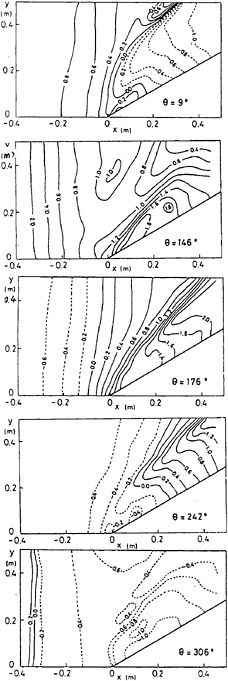
Figure 22: Distribution of pressure coefficient on the hull surface and water surface of two tanker hulls SR221A and SR221B in steady turning motion, r′=0.4, β=0°, contour interval is 0.1.
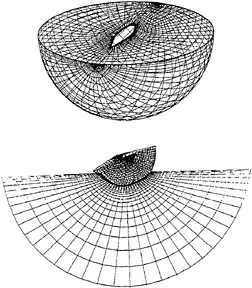
Figure 23: Grid system for the hull of a sailing boat.
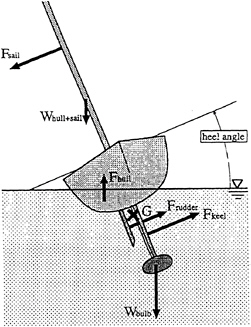
Figure 24: Forces exerted on a sailing boat in a upwind course.
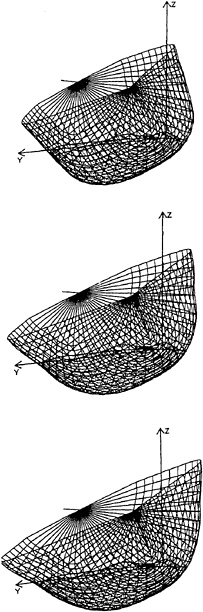
Figure 25: Body and free-surface configuration of sailing boats with different framelines on a upwind sailing condition.
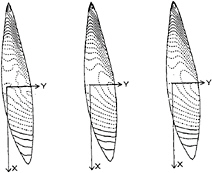
Figure 26: Comparison of pressure distribution of the three boats in Fig.25.
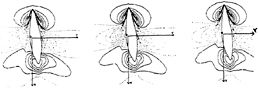
Figure 27: Wave contours of the three boats in Fig.25.
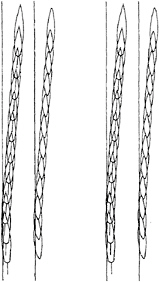
Figure 28: Time-sequential variation of the location, sheerline configuration and waterline configuration of a sailing boat in course changing maneuver during upwind sailing, case 1 (left) and case 2 (right).
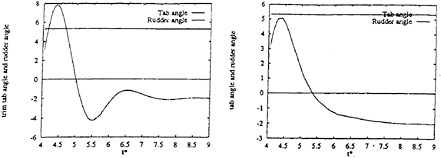
Figure 29: Time-sequence of rudder angle in the course of maneuvering in Fig.28, case 1 (left) and case 2 (right).
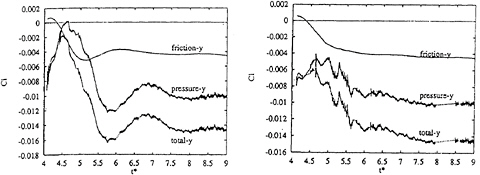
Figure 30: Time-history of the longitudinal and transverse forces in the course of maneuvering in Fig.28, case 1 (left) and case 2 (right).
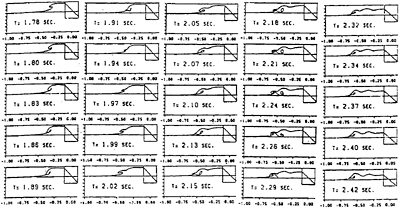
Figure 31: Evolution of breaking bow wave in a 2D case.
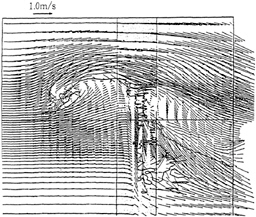
Figure 35: Wave profile and velocity vectors on a vertical plane including the side-surface of a vertical cylinder.
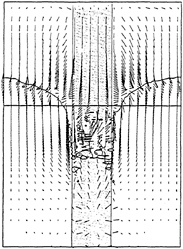
Figure 36: Same as Fig.35, on the vertical plane including the back-surface of a vertical cylinder.
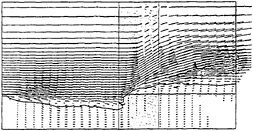
Figure 37: Interface configuration and velocity vectors of the simulation of sand-scoring by water current interacting with a vertical cylinder.

Figure 38: Time-evolution of longitudinal vortices behind a rising bubble, contours of vorticity about a vertical axis.

Figure 39: Iso-surface of the second-derivative of pressure in the flow-field about a rising bubble.