The Shoulder Wave and Separation Generated by a Surface-Piercing Strut
E.Pogozelski, J.Katz (Johns Hopkins University, USA) T.Huang (David Taylor Model Basin, USA)
ABSTRACT
The flow near a surface piercing, symmetric body with a long draft is examined, focusing in particular on the structure of the shoulder wave and the separated region behind it. The experiments are performed in a towing tank at FrL=0.25, and include velocity measurements using PIV as well as video and film photography above and below the free surface. At FrL≥0.15, formation of the shoulder wave is preceded by impingement of the flow on the model, a process associated with the bow wave, which generates a turbulent, bubbly wake. Consequently, the origin of the shoulder wave consists of several powerful counter-rotating vortices which entrain bubbles from the free surface. The wave crest becomes milder and eventually irrotational with increasing distance from the model. Behind the shoulder wave, at x/L=0.7, boundary layer separation begins, but only near the free surface. The separated zone contains several large scale streamwise vortices that detach from the model; the first one from the intersection with the free surface, and later ones from below the free surface. At FrL=0.25, there is no reverse flow within the separated region, but at FrL>0.30, flow reversal does occur. The entire process involves considerable energy dissipation.
INTRODUCTION
The flow around a surface piercing body is a very complex phenomenon, involving both viscous effects near the surface of the body, and free surface phenomena, including waves of various forms, formation of liquid sheets, bubble entrainment and three dimensional flow separation. For bodies with a long draft, where the model length is the only significant length scale, data is particularly scarce and includes mostly surface wave mapping. Most of the available data related to surface piercing bodies involves flows around ships, i.e., shallow bodies. Velocity measurements are scarce, even for ships.
A comprehensive review of flow structures and wave patterns around ships is provided by Miata and Inui (1), who observe strong dependence on Froude number and bow shape. Using Pitot tubes, they show that flow moving across the wave crest involves significant energy loss and an abrupt change in flow direction. The velocity component normal to the wave decreases significantly, but the parallel component remains largely unchanged. This observation naturally leads to an analogy between these bow waves and oblique shock waves. Miata and Inui (1) also discovered that the dominating length scale for ships is the draft, which for the present study is very large. Their studies do not include velocity measurements in the immediate vicinity of the wall. Some LDV measurements near a ship, performed by Fry and Kim (2), indicate that this three dimensional flow involves interaction of the boundary layer with the non-linear bow waves and the formation of large scale vortices. Combined mean velocity, pressure, and wave height measurements around a ship were performed also by Toda et al (3) and Longo et al.(4). These studies provide data on the distribution of mean axial velocity and energy loss around the model. PIV measurements within the bow wave and near the body were performed by Dong et al. (5), focusing on the vorticity distribution within the wave and the liquid sheet attached to the model.
Averaged measurements and computations performed by Stern et al. (6) around a surface piercing flat plate with a horizontal submerged foil, demonstrate that the presence of surface waves alter the pressure distribution around the body and cause massive flow separation. There was qualitative agreement in overall wave shape and trends between the measurements and computations, but the
quantitative results differ substantially. A recent paper dealing with the flow around a surface piercing blunt body by Zhang and Stern (7) contains mostly results of a numerical analysis, but also some surface elevation measurements at the intersection with the model. They predict that separation with reverse flow occurs at virtually all Froude numbers, and that the separation is limited to a region near the free surface for FrL≤0.55. Some of their trends will be compared later to the present results. To the best of our knowledge, there isn't any other source that provides data on the velocity distribution and vorticity structure around a surface piercing blunt body with a long draft. Due to the occurrence of flow separation and the formation of a bubbly wake at the trough of the bow wave (even in full scale models, such as catamarans and SWATH), they represent a unique problem. The present paper deals with such a flow.
EXPERIMENTAL PROCEDURES
The experiments were performed in the 140 ft towing tank located at the David Taylor Model Basin. The facility is 152 cm deep, 305 cm wide, and 4270 cm long. The experimental setup and model are shown in Figure 1. The model draft is 1.37 m. Experiments are performed at 0° incidence, at Froude numbers based on model length, FrL, ranging between 0.051 and 0.51. The corresponding range of Reynolds numbers is 1.39×105 to 1.39×106, respectively.
PIV measurements are conducted with three orientations of the laser sheet: a vertical plane inclined 115° to the streamwise direction (Figure 1c), a sheet inclined 59° to the streamwise direction and tilted 9° to the vertical (Figure 1b), accounting for the majority of presented data, as well as a sheet inclined 34° and tilted 9° to the vertical. The slight vertical tilt facilitates observations of the wave crest by avoiding any blockage caused by the wave trough. As shown in Figure 1, the primed coordinates (x', y', z') refer to the plane of a given image. Note that the axial position, x/L, varies across any given image. The reference to a specific x/L for an image indicates the position of the origin of the (x,y',z') frame on the center line of the model.
The 6 mm thick laser sheet is generated by a 15W, air cooled, copper vapor laser. The optical setup is sketched in Figure 1b. Data is recorded using a 35 mm film camera, equipped with a 90 mm lens, that has a maximum recording rate of 65 frames per second. The actual rate is approximately 10 frames per second, in order to allow adequate time delays between laser pulses while recording a single photograph. Each image consists of three exposures, with delays ranging from 3 to 15 ms. The images are recorded on Kodak TMAX ASA 3200 B&W film. The acrylic particle tracers are 40 to 60 µm diameter, neutrally buoyant (specific gravity ranging from 0.95 to 1.05), and fluorescing (they respond in the 550 to 560 nm range when subjected to green excitation), as described by Dong, et al. (9). The water is seeded with particles prior to each run. Fine aluminum powder is added to the free surface before some of the runs to improve the visualization of the free surface. Comparison of data with and without the aluminum powder confirms that the presence of the powder has an insignificant impact on the flow. A band-pass filter is inserted in front of the camera to reduce glare caused by the reflection of the light sheet from the model, free surface, and large entrained bubbles. It partially eliminates the green reflections without significantly affecting the fluorescence from the particles. A sample image is shown in Figure 2.
Photographic images are digitized using a Nikon LS3500 slide scanner, at magnifications ranging between 8–22 pixels/mm of fluid, as needed. The digitized images are enhanced and particularly bright objects, such as the model and the free surface, are removed. Velocities are computed using in-house auto-correlation software, as described by Dong et al. (8), and Roth et al.(9). The interrogation window size is 64×64 pixels, and the distance between adjacent windows is 32 pixels (i.e., 50% overlap). The typical uncertainty level is about 0.4 pixels, which for a typical 20 pixel displacement yields a characteristic uncertainty of 2%. The free surface contour for each vector map is measured directly from the digitized image. Video images, recorded with a submerged camera are also used for mapping the free surface elevation and for qualitative observations on the flow structure.
RESULTS
Sample photographs of the free surface at different Froude numbers are presented in Figure 3. They clearly show the increase in elevation of the bow wave with Froude number and the generation of bubbles (splashing) within the trough behind the bow wave. This splashing occurs at FrL≥0.15 and curiously, it begins near x/L=0.41, regardless of Froude number. At FrL=0.205 (Figure 3a) it is possible to identify several additional waves behind the bubbly trough. At FrL=0.255 the second shoulder wave crest is pushed further downstream, and at FrL=0.36 the flow becomes extremely unsteady, violent, and turbulent, without any additional steady crests. However, the front of the bubbly region involves an abrupt change in surface elevation, much like a hydraulic jump. For all FrL≥0.25, the shoulder
wave and the separated region behind it are extremely dissipative (data and discussions follow), and seem to overcome the system of Kelvin's waves. The majority of the data presented in this paper is at FrL=0.255. This condition is selected since there is already considerable bubble generation, significant changes in surface elevation, and the appearance of turbulence in the flow, as seen in Figure 3d. Additionally, unlike higher Froude numbers, at this condition the number of entrained bubbles is still small enough that we can still measure the velocity distribution accurately all the way to the free surface.
At FrL=0.255, the bow wave still contains several clear capillary waves near its crest (Figure 3d). However, the PIV data clearly indicates that there is already considerable vorticity entrainment, both at the toe, similar to the two dimensional waves demonstrated by Lin & Rockwell (10,11), and along the wave crest. This can be seen in Figure 4. Downstream of the bow wave crest, the free surface is bumpy, which as Dong et al. (5) and Sarpkaya (12) show, is indicative of subsurface vortices. At higher Froude numbers the organized capillary waves disappear and wave breaking as well as transition to turbulence at the toe of the bow wave become clearly evident. There is no bubble entrainment in the bow wave at FrL≤0.255.
The shoulder wave, whose crest is located behind the splashing region (see Figure 3b), is obviously turbulent from its onset, as Figure 3d shows. The splashing is caused by energy dissipation in the bow wave. Further downstream, where the bow wave is milder, the resulting discrepancy in total head causes an inrush of fluid towards the body that impacts on the surface and causes the splashing, as discussed in Pogozelski et al. (13). This lateral flow can be seen also on a ship model (Dong, et al. (5), for example), but does not impact on the body due to the formation of the shoulder wave, which diverts the flow away from the model.
A contour map of the wave profile near the model, measured by video photography, is shown in the bottom side of Figure 4. The maximum wave height measured upstream of the model, z/L=0.33, is within 2% of the total head of the incoming flow, z=Uo2/2g, or z/L=0.324 for FrL=0.255. The difference is consistent with our estimated measurement error. The experimental data is compared to results of numerical predictions using a free surface potential flow paneling program developed by Hendrix and Noblesse (14). This program involves several simplifying assumptions, including a slender body and linearized free surface conditions. There is some agreement in general trends, especially in the forward side. The discrepancy is mostly evident when energy dissipation due to bow wave breaking, splashing, shoulder wave breaking and flow separation are significant.
For example, the peak elevation in the experimental bow wave is located upstream of the model and not on its side, due to bow wave breaking and the associated dissipation. Note that in ship flows, where the Froude number based on draft is super-critical, the origin and crest of the bow wave are located on the side of the model (Miata and Inui (1), for example). Another discrepancy is that the experimental trough is deeper and longer, and occurs at x/L=0.4 instead of the theoretical x/L=0.3. The Kelvin wave structure, which is evident in the potential flow solution, disappears close to the model due to the impingement, splashing and flow separation that occurs at x/L>0.6 (detailed data follows). However, remnants of the Kelvin wake structure are still evident in the experimental data away from the model, but with a phase shift that starts in the longer trough.
When the instantaneous velocity distribution is available in more than one light sheet orientation, one can determine all three velocity components along the intersection lines of the sheets. Uncertainties in the sheet angle and in the measured velocities result in an error of approximately 0.7 pixels in vx and vy, but only 0.4 pixels in vz. (v is the velocity and the subscript denotes the direction). The latter is more accurate since one of the sheets is vertical, so that vz is calculated from a single sheet. Using the measured free surface elevation and the three velocity components along the intersection line, it is possible to estimate the total head of the fluid. Sample results of such an analysis are presented in Figure 5, along with the local values of vx and vy. It can be seen that the total head decreases to about 0.9U02/2g across the bow wave, except very near the body where ~50% of the energy is lost. Even at a very mild slope of the bow wave, there is already considerable entrainment of vorticity, as seen in Figure 6. A second sudden decrease occurs across the shoulder wave, where the total head is reduced to values ranging between 0.64–0.77. Near the body the levels remain near 50%. Thus, the shoulder wave and the separated region behind it are dissipating one third to one half of the total energy along the free surface. The velocities behind the shoulder wave are also slower, ranging between 0.5–0.75U0. Away from the model, near the thickest part of the body, the near surface velocity is 1.4 U0.
Velocity and vorticity distributions demonstrating the development of the shoulder wave
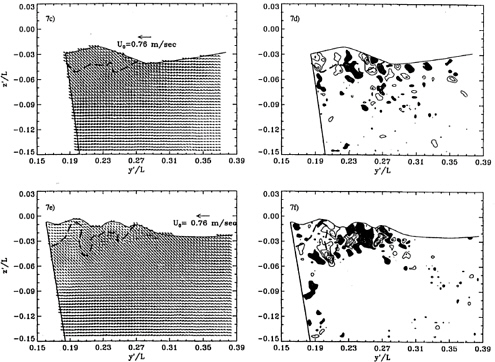
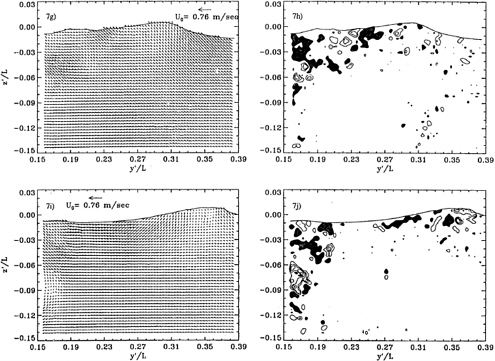
during a single experiment are shown in Figure 7. Due to the impingement that occurs just upstream of the wave, the flow at the origin of the shoulder wave (Figure 7a and b) is already unsteady, turbulent and bubbly. In this particular case, most of the vorticity is negative, much like the two dimensional spilling breaker of Lin and Rockwell (10,11), but there is positive vorticity at the crest. Further downstream, however (Figure 7d), the wave contains several distinct vorticity structures of both signs. To illustrate the unsteady nature of this flow, Figure 8 contains several velocity and vorticity maps at the same location, x/L=0.6, and flow conditions, recorded during different runs. There are common phenomena, but the flow is clearly unsteady and contains several large scale vorticity structures of alternating signs. Their existence contributes substantially to the entrainment of bubbles both by convecting them away from the surface and by trapping them. Video images (see a sample in Figure 10c) of this flow show some bubbles trapped in the vortex cores. However, the regions containing bubbles, which are marked on each map, also vary substantially in shape and correspond to the large eddies only in some of the cases. The common phenomena include negative vorticity entrainment at the toe of the wave, and in all but one case the vorticity near the wall is positive. Further downstream, at x/L=0.7 (Figure 7e & f), the surface elevation is higher, the free surface is more wavy, and the near surface flow still consists of several counter-rotating vortices, most of which are located away from the model. The dominant phenomenon seems to be an upward flow (upwelling) that splits near the surface at y'/L=0.21 to create a pair of counter rotating eddies. In this plane the presence of bubbles far from the surface is clearly associated with the large eddies. With increasing distance from the model (Figures 7g–j) the wave becomes milder in size, slope and extent of vorticity production. Residuals of vortices that are generated in upstream planes are still distributed along the free surface, but they eventually disappear. The large structures that appear near the model are associated with flow separation rather than the shoulder wave, and will be discussed shortly.
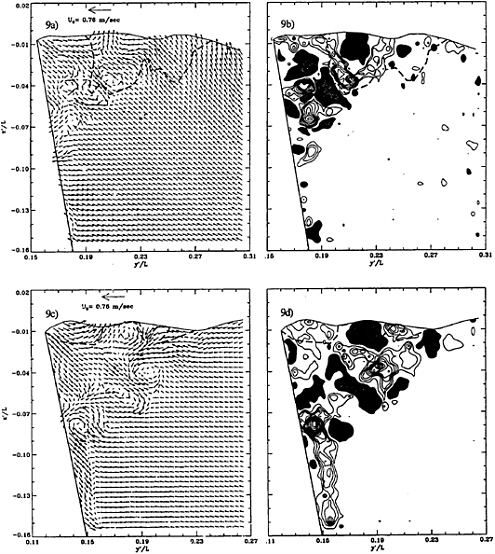
A series of velocity and vorticity distributions from a single run (Figure 9) focuses on the flow near the model between x/L=0.73 and x/L=0.91. Sample video images of the same flow, as seen using the optical setup of Figure 1c, is provided in Figure 10. It is clearly evident that boundary layer separation occurs near the free surface. The separated region increases in width and depth between x/L=0.73 and 0.82, and in depth only between 0.82 and 0.91. This region contains several large scale vortices with peak vorticities of about 80U0/L—4 to 10 times higher that the vorticity peaks within the breaking waves upstream. The magnitudes of the velocity in these planes reach levels of approximately 0.5U0. Although their exact shapes and sizes vary, the existence of these vortices is consistent and repeatable. Bubble entrainment and trapping in the vortex cores also occurs consistently. A sample video image of an entrained bubble is shown in Figure 10c. Using the quantitative data and the video images, we attempted to construct an overall sketch of the flow structure within the separated region, as shown in Figure 11a–d. Data from two inclined planes was used to determine all three components of the velocity along the intersection lines. The arrows shown in Figure 11d are actually quantitative data with a reference velocity provided on the same figure. There is no reverse flow in the entire separated region at this Froude number. This trend contradicts the conclusions of a computational study performed by Zhang and Stern (7). However, in agreement with their conclusions, reverse flow near the present body has been observed at Froude numbers exceeding 0.30, using video cameras above the surface.
Note that in the bottom parts of Figures 9c–e that there is a change in flow direction near the model. This effect is caused by the boundary layer on the model, as seen in the inclined light sheet. The projection of the model speed onto the plane of the laser sheet (Figure 1b) points to the right, and as a result, the fluid within the boundary layer has a velocity component in that direction. The outer flow is affected only by the narrowing of the body, moving to the left, which causes the observed effect. The characteristic thickness of this layer, .01L at x/L=0.82 and .025L at x/L=0.91, is consistent with the expected width of a laminar boundary layer.
Repeated examination of the video records has shown that the origin of the separated zone at Fr=0.255 is at the intersection of the model with the free surface, at the trough behind the shoulder wave. The vortex with positive vorticity, which appears at y'/L=0.21 and z'/L=–0.035 in Figure 9a and y'/L=0.195, z'/L=–0.04 in Figure 9c, originates in this corner. The negative vortex located near it (y'L=0.19 and z'/L=–0.045 in Figure 9a) is originated on the model, below the free surface a short distance downstream. Only the positive vortex remains at x/L=0.91 (Figure 9e). A second pair of counter-rotating vortices is generated on the model in the same sequence, well below the free surface and further downstream. The positive vortex is already visible near the model, at z'/L=–0.06 and –0.08 in Figures 9a
and c, respectively; however, its negative partner appears only at x/L=0.91 (Figure 9e). Figure 10 shows the second pair (but in a different run) moving away from the surface, shortly after the negative vortex is generated. These images are recorded with a video camera using the setup of Figure 1c. As noted before, one of the vortices in Figure 9e traps a bubble. Figure 11c attempts to illustrate the sequence of vortex generation on the model. The entire process has some resemblance to three dimensional, open separation in the lee side of inclined bodies of revolution. However, considerably more data analysis, which is still in progress, is required before we are able to construct the complete flow topology. In addition to the repeatable vortices that develop near on the model, the flow near the free surface contains numerous vortices with alternating signs. Their locations and spatial distributions are unsteady and they regularly entrap bubbles.
CONCLUSIONS
For the present surface piercing model with a long draft a bubbly wake is generated at the trough between the bow and the shoulder wave. This phenomenon occurs at x/L=0.41 and FrL≥0.153 due to impingement of the flow on the model, a process associated with energy dissipation in the bow wave. Consequently, the origin of the shoulder wave consists of several powerful counter-rotating vortices which entrain bubbles from the free surface. The wave crest becomes milder and eventually irrotational with increasing distance from the model. Behind the shoulder wave, at x/L=0.7, boundary layer separation begins, but only near the free surface. The flow within the separated region consists of two pairs of counter rotating vortices that detach from the boundary layer on the model. The first vortex is generated at the intersection of the body with the free surface, but the following ones are originated below the free surface. At FrL=0.255 there is no reverse flow within the separated region, but flow reversal seems to occur at FrL≥0.307. The flow structure is turbulent and involves considerable dissipation.
ACKNOWLEDGMENTS
This project is sponsored by the Office of Naval Research under grant number N00014–93–10–204, under the management of Dr, Edwin Rood. Thanks are also due to R.Dong for his assistance.
REFERENCES
1. Miata, H., Inui, T., “Nonlinear Ship Waves,” Advances in Applied Mechanics, Vol. 24, 1984, pp. 215–288.
2. Fry, D.J., and Kim, Y.H., “Bow Flow of Surface Ships,” Proc. of the 15th Symp. on Naval Hydrodynamics, Hamburg, Germany, pp. 319–346.
3. Toda, Y., Stern, F., and Longo, J., “Mean-Flow Measurements in the Boundary Layer and Wake and Wave Field of a series 60 CB=0.6 Ship Model—Part 1: Froude Numbers 0.16 and 0.316,” J. of Ship Res., Vol. 36, No. 4, 1992, pp. 360–377.
4. Longo, J., Stern, F., and Toda, Y., “Mean-Flow Measurements in the Boundary Layer and Wake and Wave Field of a series 60 CB=0.6 Ship Model—Part 2: Scale Effects on Near-Field Wave Patterns and Comparisons with Inviscid Theory,” J. of Ship Res., Vol. 37, No. 1, 1993, pp. 16–24.
5. Dong, R.R., Katz, J., and Huang, T.T., “PIV Measurements of the Flow Structure Around a Ship Model,” ASME/EALA Sixth International Symp. on Laser Anemometry, 1995, pp. 425–434.
6. Stern, F., Hwang, W.S., Jaw, S.Y., “Effects of Waves on the Boundary Layer of a Surface-Piercing Flat Plate: Experiments and Theory,” J. Ship Res., Vol. 33, No. 1, 1989, pp. 63–80.
7. Zhang, Z.J., and Stern, F., “Wave-Induced Separation,” Forum on Advances in Numerical Modeling of Free Surface and Interface Fluid Dynamics, 1995, ASME IMECE, San Francisco, CA.
8. Dong, R., Chu, S., and Katz, J., ( 1992), “Quantitative Visualization of The Flow Structure Within The Volute of a Centrifugal Pump, Part A: Technique,” J. Fluids Eng., Vol. 114, No. 3, 1992, pp. 390–395.
9. Roth, G., Hart, D., and Katz, J., “Feasibility of Using the L64720 Video Motion Estimation Processor (MEP) to Increase Efficiency of Velocity Map Generation for PIV, ” ASME/EALA 6th International Symp. on Laser Anemometry, August 1995, pp. 387–394.
10. Lin, J.C., and Rockwell, D., “Instantaneous Structure of a Breaking Wave,” Physics of Fluids, Vol. 6, No. 9, 1994, pp. 2877–2879.
11. Lin, J.C, and Rockwell, D., “Evolution of a Quasi-Steady Breaking Wave,” Journal of Fluid Mech., vol. 302, 1995, pp. 29–44.
12. Sarpkaya, T., “Vorticity, Free Surface, and Surfactants,” Ann. Rev. Fluid. Mech., Vol. 28, 1996, pp. 83–128.
13. Pogozelski, E., Katz, J., and Huang, T., “How Structure Around a Surface-Piercing Blunt Body,” Proc. 20th ONR Symposium on Naval Hydrodynamics, August 1994.
14. Hendrix, D., and Noblesse, F., “Recipes for Computing the Free-Surface How Due to a Source Distribution, ” Journal of Ship Research, vol. 36, No. 4, Dec. 1992, pp. 346–359.
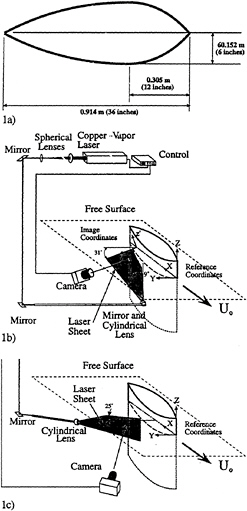
Figure 1: Schematic desciption of the model and the experimental setup; a) cross section of the model, b) primary orientation of the underwater camera and the light sheet, and c) orientation of the camera and light sheet during observations from upstream. In b), the origin of the x'-y'-z' coordinate system is on the centerline of the model at the intersection of the light sheet and the undisturbed free surface.
Figure 2 : Three-exposure image at x/L=0.27 and FrL=0.255, viewed with the setup shown in figure 1b. A 64×64 pixel correlation window is shown magnified. The model is on the left and the free surface is on top.
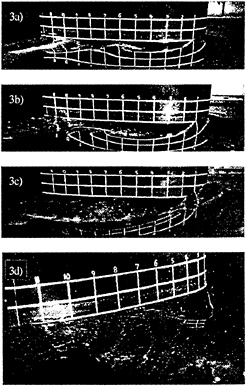
Figure 3: Starboard views at a) FrL=0.204, b) FrL=0.255, c) FrL=0.357; d) back-starboard view at FrL=0.255. The painted rectangles on the model are 3 inches long (L/12) and 2 inches high. The lowest line indicates the position of the undisturbed free surface.

Figure 4: Elevation contours of the free surface at FrL=0.255. The blank area near the center of the model is due to the presence of bubbles, which make it difficult to accurately establish the position of the free surface.
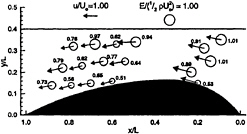
Figure 5: Total energy ![]() and velocity on the free surface at FrL=0.255. Data is provided at the intersection of light sheets.
and velocity on the free surface at FrL=0.255. Data is provided at the intersection of light sheets.
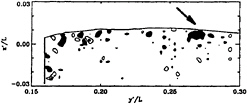
Figure 6: Vorticity (ωL/Uo) distribution within the bow wave at x/L=.22 and FrL=0.255, as seen from behind (at 34°). The contour interval is 8; shaded areas indicate negative vorticity. The vertical line on the left side of the figure is the model.
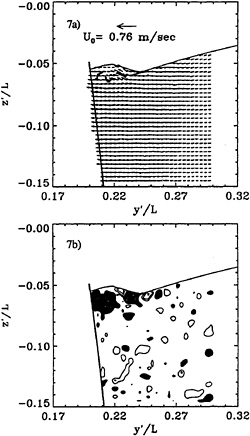
Figure 7 ( following pages): Velocity and vorticity (ωL/Uo) distributions of the shoulder wave at FrL=0.255, viewed as shown in figure 1b. a,b) x/L=0.49; c,d) x/L=0.58; e,f) x/L=0.69; g,h) x/L=0.78; i,j) x/L=0.88. The contour interval is 4; shaded areas indicate negative vorticity, and dashed lines indicate the boundaries of the bubbly region. In figures 6g–j, the model has moved out of the picture.
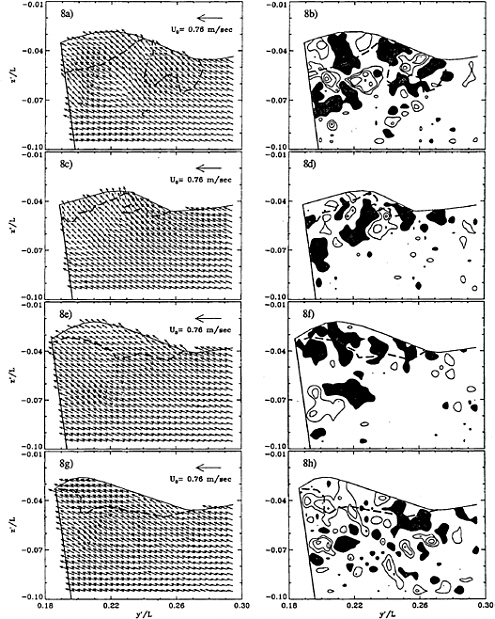
Figure 8: Velocities and vorticity contours (ωL/Uo) at FrL=0.255, viewed with the figure 1b setup. a,b) x/L=0.58; c,d) x/L=0.59; e,f,g,h) x/L=0.60. The vorticity contour interval is 4; shaded areas indicate negative vorticity, and dashed lines indicate the presence of bubbles.
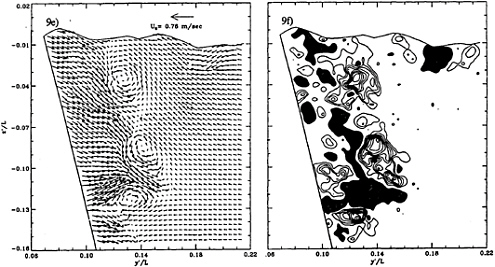

Figure 10: Video images from a single run at FrL=0.255, at a) x/L=0.83, b) x/L=0.88, and c) x/L=0.89, viewed as shown in Figure 1c. The arrow indicates an entrained bubble.
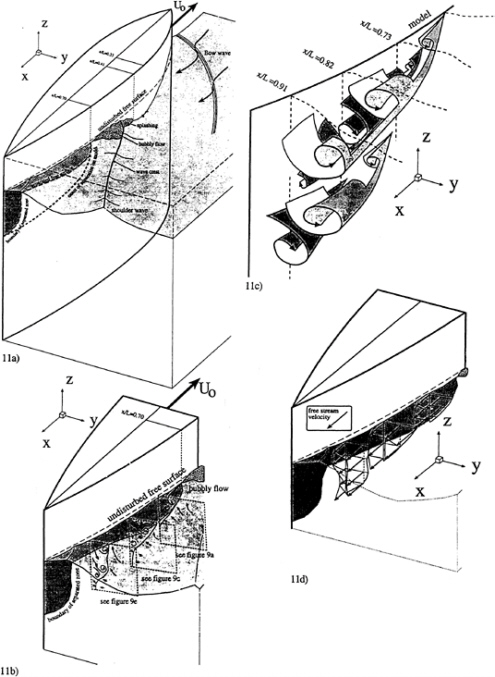
Figure 11: Sketches of the flow structure at FrL=0.255: a) overall view, b) view of the separated zone data included in Figure 9, c) schematic of vortex growth in the separated region, d) quantitative axial velocity components in the separated region, in the model's frame of reference.