Near- and Far-Field CFD for a Naval Combatant Including Thermal-Stratification and Two-Fluid Modeling
E.Paterson,1 M.Hyman,2 F.Stern1P.Carrica,3 F.Bonetto,3 D.Drew,3 R.Lahey, Jr.3
(1University of Iowa, 2Naval Surface Warfare Center [Panama City], 3Rensselaer Polytechnic Institute, USA)
ABSTRACT
A computational fluid dynamics approach for simulating the near and far field of a Naval combatant in a thermally-stratified two-phase flow is presented. The approach is based upon, for the near field, coupling a single-phase Reynolds-averaged Navier-Stokes method with both the energy equation, to account for transport of thermal energy and creation of buoyancy forces, and a two-fluid model, to account for the transport of monodisperse microbubbles and their interaction with the liquid phase. Far-field solution is based upon parabolic Reynolds-averaged Navier-Stokes equations with the initial data plane prescribed by the near-field solution. An extensive number of conditions are simulated: model-scale Re; medium and high speeds; with and without thermal stratification; with and without propeller; and two-fluid calculations over a range of bubble sizes. The two-fluid near-field results, however, are preliminary in that they are for zero Fr and are not coupled to the far-field. For the single-phase, unstratified, and unpropelled case, a detailed uncertainty analysis following ASME guidelines is performed. The results show that both global and detailed features of Naval combatant flows can be accurately predicted and, despite many uncertainties and lack of validation data, the prognosis with regard to predicting two-phase surface-ship wake signatures is optimistic.
1
INTRODUCTION
Knowledge of surface-ship flow fields is useful in many aspects of ship design and in the evaluation of their performance. Applications of such knowledge range from powering, structural loading, and noise production to far-field signature estimation. These phenomena are dependent on both Froude (Fr) and Reynolds (Re) number and so require testing or simulation at full scale to be adequately determined. The cost and uncertainty of full-scale measurements provides strong motivation to utilize scale model testing and scaling relationships to obtain full-scale estimates. In many cases, scaling relationships are not known or are based upon very limited data. This is particularly true in the design of new hulls. As a result, there is a pressing need to develop computational tools to either help with scaling model data or to enable the calculation of full-scale flows.
The flow in question is quite complex. It involves a deforming surface which undergoes breaking in certain regions, an extensive three dimensional boundary layer, air entrapment in the form of bubbles at the surface, and a strong momentum source at the propeller plane. There are additional influences including ambient density stratification due to thermal and salinity variations, sea state and other environmental effects, and particulates and surfactants suspended in the fluid which have a poorly understood effect, if any, on the flow. It is clear that bubbles, in particular, can become sufficiently numerous to locally interact with the flow, but that density stratification influences generally take place over a long time scale and so are important primarily in the wake.
While direct simulation of these flows is many years away, a considerable amount of very useful information can be extracted from ensemble-average modeling. Over the past several years, a number of ensemble-average models have reached a level of maturity that allows them to be applied to some of these problems. In this paper we will focus on modeling the near and far wakes for the purpose of signature estimation but the modeling capability is general and likely to be equally applicable to other problems of concern.
As noted, the near ship flow responds to a no-slip boundary, a strong local momentum source, and a free surface. Reynolds-averaged Navier-Stokes (RANS) solvers have evolved to the point where they can be applied to model-scale Reynolds number, full-scale Froude number ship flow simulation with propulsion effects and non-linear free surface boundary conditions. The algorithm discussed in (1,2) in particular has demonstrated the ability to accurately calculate the viscous-flow and wave fields, resistance,
and propeller-hull interaction. While most applications of the algorithm have been to generic hull forms such as the Wigley hull and to research forms such as the Series 60, accurate simulation of the flow around these hulls suggest that it is capable of general application and represents a good starting point for complex forms such as combatants with transom sterns and bulbous bows.
At full scale, this flow is not uniformly single phase. Air bubbles from boundary-layer entrainment, propeller ventilation and/or cavitation, and breaking waves serve to inject bubbles into the flow. In most regions the void fraction is small and does not influence the flow, but in others it can become large enough to play a significant role on flow dynamics. Even though the degree of complexity of the problem increases considerably when the bubbles are taken into account, two phase flow modeling of (3,4,5) can be used to determine the spatial distribution of moderately high concentration (i.e., alpha less than 10%), monodisperse air bubble populations and the associated fluid coupling in turbulent flows. While the mechanisms and degree of air entrainment at the free surface remain unresolved, considerable insight can be achieved by introducing air void at likely injection locations and calculating its evolution.
More or less simultaneously, considerable effort has been devoted toward developing computational models of surface ship wakes. The effort has been motivated by a desire to estimate micro-bubble populations in the far wake as well as predict the radar scattering characteristics of the free surface. The work in (6,7,8) detail application of far-wake modeling to micro-bubble evolution. In general, the strategy has been to model the hydrodynamic and relevant scalar fields via a parabolic subset of the RANS equations. Scalar fields such as temperature, micro-bubble populations, salinity and surface contaminants have been included because of their influence on the flow field and because they are of interest in their own right.
The ability to predict the near and far fields of naval surface ships requires that these models be extended to include realistic hull geometries and operating environments and coupled together. The work presented in this paper discusses some of the extensions necessary to use these tools to simulate the flow fields associated with naval combatants operating in commonly encountered conditions. They are illustrated via a set of simulations on a U.S. Navy FF-1052 (figure 1). This ship represents most of the geometric complexities found in modern combatant forms; a transom stern and bulbous bow. The near-and far-field flow is computed for both the unpropelled and propelled hull operating in a thermally-stratified environment. The transport of a monodisperse microbubble population introduced in the near-bow region is also computed for the unpropelled hull at zero Froude number.
This paper is arranged in the following manner. The problem formulation is described in section 2. In section 3 the computational methods are briefly discussed. The conditions and grids are presented in section 4 and the uncertainty analysis in section 5. Results for both the FF-1052 near and far field are presented in section 6. Finally, concluding remarks and discussion of future work are provided in section 7.
2
PROBLEM FORMULATION
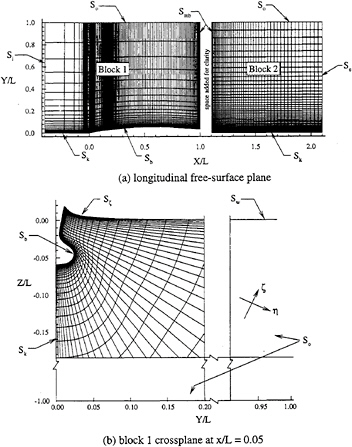
To predict surface-ship bubbly wakes, separate, but coupled, CFD methods are used for the near and far fields. Formulation of the problem is based upon coupling the RANS method (1), which has been extended for combatant geometries (9) [i.e., multi-block to handle transom stern and propeller-hull interaction using (2)] and thermal stratification, and an Eulerian two-fluid ensemble-averaged model (4) for the near field and a parabolic method (6) for the far field with its initial data plane (IDP) prescribed by the near-field solution. It should also be noted that (9) provides detailed documentation, user instructions, and discussion of and implementation recommendations for uncertainty analysis. Figure 2 provides a schematic of the relationship between near-and far-field domains.
2.1
Near Field
The unsteady three-dimensional continuity and RANS equations for a gas-liquid two-phase flow are written for each phase separately and derived assuming: negligible bubble inertia (i.e., ρg « ρℓ); small void fraction and void-fraction gradients; spherical bubbles; and constant liquid density. Using Cartesian tensor notation and in non-dimensional form, the liquid-phase equations are
(1)
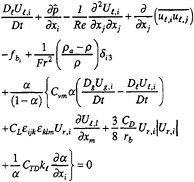
(2)
and the gas-phase equations are
(3)
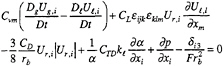
(4)
where the subscripts ℓ and g indicate liquid and gas, xi =(X,Y,Z) are the Cartesian coordinates, ![]() are the substantial derivatives with respect to each phase, Uℓ,i=(Uℓ,Vℓ,Wℓ) and Ug,i=(Ug,Vg,Wg) are the liquid and gas mean-velocity components, Ur,i is the relative velocity between phases (Uℓ,i–Ug,i),
are the substantial derivatives with respect to each phase, Uℓ,i=(Uℓ,Vℓ,Wℓ) and Ug,i=(Ug,Vg,Wg) are the liquid and gas mean-velocity components, Ur,i is the relative velocity between phases (Uℓ,i–Ug,i), ![]() are the Reynolds stresses,
are the Reynolds stresses, ![]() is the piezometric pressure (p+Z/Fr2), v is the kinematic viscosity,
is the piezometric pressure (p+Z/Fr2), v is the kinematic viscosity, ![]() are the body-force terms which represent the effects of the propeller, Re=UoL/v,
are the body-force terms which represent the effects of the propeller, Re=UoL/v, ![]() and α is the gas-phase volume fraction. Coupling between the liquid- and gas-phase momentum equations is accomplished through the continuity equation (1) and the last- and first-four terms of (2) and (4), respectively, which represent interfacial momentum transfer due to virtual mass (i.e., acceleration of the liquid caused by the bubbles), lift, drag, and turbulent dispersion effects. Derivations and model constants for each term are provided in (3,4). The sixth term of (2) represents buoyancy due to thermal stratification, where ρa represents the ambient density of sea water prescribed by an equation of state, and is used only for single-phase simulations. The equations are normalized by ship speed Uo and length L, and liquid density ρℓ. Note that for α=0, (2) reduces to the single-phase RANS equations.
and α is the gas-phase volume fraction. Coupling between the liquid- and gas-phase momentum equations is accomplished through the continuity equation (1) and the last- and first-four terms of (2) and (4), respectively, which represent interfacial momentum transfer due to virtual mass (i.e., acceleration of the liquid caused by the bubbles), lift, drag, and turbulent dispersion effects. Derivations and model constants for each term are provided in (3,4). The sixth term of (2) represents buoyancy due to thermal stratification, where ρa represents the ambient density of sea water prescribed by an equation of state, and is used only for single-phase simulations. The equations are normalized by ship speed Uo and length L, and liquid density ρℓ. Note that for α=0, (2) reduces to the single-phase RANS equations.
The temperature field is obtained from the energy equation which is written for an incompressible fluid as
(5)
where κ is the non-dimensional thermal diffusivity and T and t are the ensemble-averaged and fluctuating temperatures, respectively. The velocity and temperature fields interact through the previously mentioned buoyancy term in the Z-momentum equation, the energy equation (5), and the equation of state.
The Reynolds stresses and turbulent transport of thermal energy are modeled using a Boussinesq assumption, i.e., linear relationship with mean rate-of-strain and temperature gradient, respectively, and an isotropic eddy viscosity vt
(6)
(7)
Although higher-order models (i.e., both linear and non-linear k-ω-ε) have/will be used, the Baldwin-Lomax algebraic turbulence model is used here to determine vt because of its simplicity, efficiency, and stability. Bubble-induced turbulence, which is expected to be important in the near wall region, contributes to both the total effective viscosity and the turbulent kinetic energy
veff=v+vt+vb
k=kℓ+kb (8)
where kℓ is determined using vt and the mixing length, and vb and kb are determined from model equations (10).
Referring to figure 3, the specified boundaries of the solution domain are the body surface Sb (η=1), the inlet plane Si (ξ=1), the exit plane Se(ξ=imax), the symmetry plane Sk (ζ=1 and parts of η=1), the outer boundary So(η= jmax), the multi-block interfaces Smb, and the free-surface Sζ(ζ=kmax and, for full-domain simulation, ζ=1). Note that for zero Fr, Sζ becomes the waterplane Sw.
For the liquid phase and zero Fr the boundary conditions are as follows: on Sb
Uℓ=Vℓ=Wℓ=∂p/∂n=∂T/∂n=0 (9)
where n is normal tothe body; on Si, free-stream values are imposed
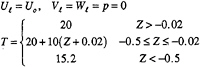
(10)
on Se, a zero gradient condition is used
∂(Uℓ,Vℓ,Wℓ,p,T)/∂X=0 (11)
on Sk
∂(Uℓ,Wℓ,p,T)/∂Y=Vℓ=0 (12)
on Sw
∂(Uℓ,Vℓ,p,T)/∂Z=Wℓ=0 (13)
on So
Uℓ=Uo, Vℓ=∂p/∂r=0 (14)
and Wℓ is extrapolated; and, on Smb, a parametrically-mapped bilinear-interpolation scheme (9) is used to interpolate all dependent variables between overlapping planes in each block.
For the liquid phase and nonzero Fr, the boundary conditions are similar, except: p is replaced by ![]() and on Sζ, exact nonlinear kinematic free-surface conditions
and on Sζ, exact nonlinear kinematic free-surface conditions
(15)
and approximate dynamic free-surface conditions
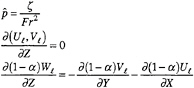
(16)
are applied on the actual free-surface, which is determined as part of the solution.
The determination of the boundary conditions for the complete two-fluid model is not a simple problem. Bubble sources and entrainment mechanisms are not well understood. Possible sources include: wave breaking; bow, contact-line, and stern flows; propulsor aeration and cavitation; and ambient sea state. Properly stated boundary conditions must provide the gas flux through the generating surfaces including the gas-volume fraction, bubble-size distribution, and net bubble velocity. Herein, bubbles are introduced on the free surface near the bow modeling breaking-wave sources.
Since a finite-volume method is used for the gas phase, the boundary conditions are formulated in terms of fluxes. The boundary conditions are as follows: on Sb, a zero-flux condition is used; on Si, the gas velocity equals the liquid velocity and the void fraction is zero; on Se, a free gas-flow condition is used in which the flux at the boundary is set to the value at the center of the control volume; on Sk, a zero-flux condition is used; on Sw, free gas-flow condition is used except at the inlet where the flux and void fraction are specified; on So, free gas-flow condition is used; and on Smb, the multi-block interpolation scheme in (9) is used.
2.2
Far Field
Simulation of the far-field consists of modeling the flow, temperature, and micro-bubble fields. The parabolized RANS (PRANS) equations, i.e., (1) and (2) with α=0 and ∂2Uℓ,i/∂X2=0, and k-ε turbulence-model, with modifications to account for production of turbulence due to buoyancy and interaction with the free surface, are solved for the velocity and turbulence fields. Temperature is determined by solving a parabolic version of (5). Given the temperature, ρ is determined from an equation of state. A transport equation for the evolution of the micro-bubble field is derived assuming that the bubbles are sufficiently numerous such that they can be treated as a continuum and that they neither coalesce nor divide.
The specified boundaries of the solution domain are the IDP SIDP, the top boundary ST, the bottom boundary SB, the right boundary SR, and the left boundary SL. The boundary conditions are as follows: on SIDP, all variables are provided by the near-field solution; on SRand SL, k,ε are fixed to free-stream values, zero-gradient conditions are used for U,W,p,T,S; and V is determined from continuity, on SB, U,k,ε,T,S are fixed to free-stream values and zero-gradient conditions are used for V,W,p; and on ST, zero-gradient conditions are used for U,V,k,ε,T,S, and W=p=0.
3
COMPUTATIONAL METHODS
3.1
Near Field
The liquid-phase continuity (1), momentum (2), and energy (5) equations are transformed into nonorthogonal curvilinear coordinates such that the computational domain forms a simple rectangular parallelepiped with equal grid spacing. The transformation is a partial one since it involves the coordinates only and not the velocity components Uℓ,i. The transformation is accomplished through use of the expression for the divergence and “chain-rule” definitions of the gradient and Laplacian operators which relate the Cartesian coordinates xi to the nonorthogonal coordinates (ξ, η, ζ). The equations are reduced to algebraic form through the use of the 12-point finite-analytic method. The pressure equation is derived using the generalized continuity equation in discrete form and a staggered-grid control volume. Herein, prescribed body forces are used in lieu of an interactive solution and are based upon
known thrust and torque coefficients ![]() speed of advance J, and an assumed circulation distribution (9). The overall solution algorithm is based on the pressure-implicit split-operator (PISO) algorithm where the velocity and pressure fields are coupled through a two-step iterative procedure. In the first step, the momentum equations are solved implicitly using a tridiagonal algorithm and the method of lines and the pressure from the previous time step for an intermediate velocity field. The second step consists of sub-iterations. First, the pressure equation is solved implicitly using a tridiagonal algorithm and the method of lines for an intermediate pressure. Second, the momentum equation is solved explicitly using the intermediate pressure for the momentum correction which is then used to update the pressure. For steady flow, convergence of the second step is not required; therefore, only several sub-iterations are used. For stratified flows, the energy equation is solved implicitly using a tridiagonal algorithm and the method of lines and the buoyancy term in the Z-momentum equation is updated each time step. Convergence is determined using the L2 norms (residuals) of U,V,W, p̂,T, when appropriate, and ζ between time steps (n) and (n-1) and should ideally display 3 or 4 orders of magnitude drop for a converged solution.
speed of advance J, and an assumed circulation distribution (9). The overall solution algorithm is based on the pressure-implicit split-operator (PISO) algorithm where the velocity and pressure fields are coupled through a two-step iterative procedure. In the first step, the momentum equations are solved implicitly using a tridiagonal algorithm and the method of lines and the pressure from the previous time step for an intermediate velocity field. The second step consists of sub-iterations. First, the pressure equation is solved implicitly using a tridiagonal algorithm and the method of lines for an intermediate pressure. Second, the momentum equation is solved explicitly using the intermediate pressure for the momentum correction which is then used to update the pressure. For steady flow, convergence of the second step is not required; therefore, only several sub-iterations are used. For stratified flows, the energy equation is solved implicitly using a tridiagonal algorithm and the method of lines and the buoyancy term in the Z-momentum equation is updated each time step. Convergence is determined using the L2 norms (residuals) of U,V,W, p̂,T, when appropriate, and ζ between time steps (n) and (n-1) and should ideally display 3 or 4 orders of magnitude drop for a converged solution.
The gas-phase continuity (3) and momentum (4) equations are solved on the same grid as the liquid-phase equations, and as such, are transformed into the computational domain using the relations outlined above. The equations are reduced to algebraic form using a second-order control-volume upwind approach for the spatial derivatives and a first-order finite difference for the temporal derivative. Due to the homogeneous nature of the continuity equation, the superbee TVD flux limiter, although computationally expensive to evaluate, is used to reduce non-physical oscillations through the prescription of an optimal artificial viscosity. In contrast, the momentum equations are dominated by the source terms due to the interfacial momentum transfer. This effectively eliminates the need for the flux limiter. To maintain diagonal dominance, the source term is partitioned into parts that can/cannot be included into the implicit operator acting on the variable being solved. Both equations are solved implicitly using a tridiagonal algorithm and the method of lines.
The overall solution procedure for a two-phase solution is as follows. First, several hundred iterations of the liquid equations with zero void fraction are performed to establish the liquid flow field. Next, the gas and liquid equations are solved iteratively to establish coupling between the phases. Finally, because the effect of the gas phase in the liquid phase is weak, as was assumed in the derivation of the two-fluid model, final convergence is achieved through several hundred iterations of the gas equations.
3.2
Far Field
Because the far-field grid is nonuniform in the cross planes and stretched in the axial direction, the PRANS equations are also transformed and solved in the computational domain. The momentum equations are discretized using second-order central differences for the cross-stream directions and Crank-Nicholson differencing with Newton linearization in the axial direction. The algebraic equations form a large sparse matrix which is iteratively solved with a modified conjugate-gradient minimization method. This procedure explicitly couples the pressure into the momentum equation and simultaneously satisfies mass conservation. The k-ε equations are discretized using second-order central differences and solved using an alternating direction implicit (ADI) scheme with under-relaxation and Newton linearization. The micro-bubble transport equation is discretized using second-order finite-volume approach and the QUICK algorithm and solved using an ADI scheme. Finally, the free-surface elevation is determined using a linearized implementation of (15).
4
CONDITIONS AND GRIDS
The computational conditions are for two Fr =(0.29, 0.39) corresponding to medium and high speeds. At full scale, L=415.3 ft and (U0, Re)=(20 knots, 1.3×109) and (27 knots, 1.7×109). At model scale, L=21.28 ft. (i.e., scale ratio=19.5) and (U0, Re) =(4.53 knots, 1.49×107) and (6.11 knots, 2.01×107). However, note that the two-phase simulations were performed at Fr=0 and liquid Re=4.3×106 and gas Re=1.7×109. Also, available experimental fluid dynamics (EFD) validation data (11,12,13) is for the free condition, i.e., the model was free to sink and trim where for Fr=0.29 σ=0.0264 and τ=–0.0450 and for Fr=0.39 σ=0.0405 and τ=–0.0120, and for nominal-wake data, includes appendages. The CFD, on the other hand, is for the bare hull in the fixed condition (i.e., σ=0 and τ=0). For the propelled calculations, the thrust and torque coefficients and speed of advance are based upon balancing the thrust with the model-scale values of resistance. Using the experimental CT, wake fraction, thrust deduction, and the open-water curves, ![]() KQ=0.031, and J=0.797.
KQ=0.031, and J=0.797.
4.1
Near-Field
The near-field grid has its inlet, exit, and outer boundaries located at X=(–.4, 2.0) and R=1. For the unpropelled cases, the flow is symmetric about the centerplane which allows a half-domain grid to be used. Four such grids were generated: 110×31×22 (very coarse=75,020); 207×60×40 (coarse=496,800);
252×60×45 (medium=680,400); and 302×60×50 (fine=906,000). The first grid is used for the Fr=0 two-phase simulations and the latter three for single-phase simulations. Since the FF1052 has a single propeller, the propelled cases are asymmetric about the centerplane and, as such, require a full-domain grid (i.e., the unpropelled grid is doubled in the ζ-direction). Propelled calculations were made only on the doubled coarse grid 207×60×79=981,180. For each grid, the first point off the body surface is located in the range Y+<2, and the number of points over the bow/dome, afterbody, and wake are (10, 74, 26), (30, 95, 50), (40, 110, 65), and (50, 120, 80), respectively. An overview of the RANS grids is shown in figure 3. The free-surface boundary conditions grid is 460×100 and fixed for all cases.
The time step is 0.1 and the under-relaxation factors for velocity and pressure are 0.2 and 0.02, respectively. On a CRAY C90, CPU-time and memory requirements were 25 hours and 32 megawords, respectively, for the single-phase simulations on the coarse grid.
The two-phase flow cases were run with a gas entrance near the bow simulating a breaking wave. The entrance region is rectangular and extended from Y/L=3.95×10–3 to 7.9×10–3 and from X/L=0 to 2.13×10–2. The gas and liquid velocity were assumed to have a vertical component of –2.7 m/s at the entrance and the gas volume fraction was set to 10%. The bubble radius at the gas entrance was varied in different runs from Rb=25 to 200 µm. The lift coefficient CL was set to 0.1, based on the experience in high-shear flows. The virtual mass coefficient Cvm was set to 0.5, its theoretical value for spheres. The turbulent dispersion coefficient is nominally set to CTD=0.1 which is taken from experiments in pipe flows with medium size particles. Since small bubbles are of interest here, sensitivity to CTD is investigated through a calculation for CTD=1.0 and a single bubble radius Rb=150mm.
4.2
Far-Field
The far-field grid has its inlet, exit, side, and bottom boundaries located at X=1.75 and 20.75, Y=±0.5, and Z=–0.5, respectively. The grid is 200×161×51 (1,642,200), stretched in the axial direction, and regular and rectangular in the cross-stream directions. Data on the upstream boundary is obtained by interpolating mean velocity, turbulent viscosity, temperature, and surface elevation from the RANS solution onto the PRANS grid. Turbulent kinetic energy and dissipation rate, which are required for the far-wake simulation, are computed from the viscosity by assuming a length scale of ℓt=0.01 and that the kinetic energy is given by:
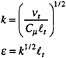
5
Uncertainty Analysis
Uncertainty analysis follows the ASME guidelines and implementation recommendations provided in (9). Grid design was based on user experience and the Series 60 CB=0.6 zero and non-zero Fr results of (1). Preliminary calculations aided in determining grid-clustering in the bow and sonar dome regions. Due to the flow features associated with the sonar dome, skeg and transom stern, grid number in both ξ (axial) and ζ (girthwise) directions were varied. Minimum Y+, η-direction variation, and leading- and trailing-edge clusterings are constant and their effect upon uncertainty was not studied.
Using the residuals, each solution displays iterative convergence by displaying 3 orders-of-magnitude drop and a magnitude less than 10–4. Grid convergence is evaluated for the single-phase unstratified solutions using both integral and pointwise quantities. Detailed grid studies have not yet been performed for the near-field solutions with propeller, stratification, or two-fluid modeling or for the far-field solutions. Integral grid convergence is shown in Table 1 for CT, CF, and CP. The relative change between grids, as indicated by the grid convergence parameter ε, decreases with increasing grid resolution and, in general, the changes in CT, CF, and CP are less than 2% between grids. Pointwise grid convergence, which is shown and discussed in (9), unfortunately is not as conclusive in that it shows that the wall-shear stress on the fine grid contains oscillations and is not fully converged.
Assessment of overall uncertainty is difficult with a limited analysis. Experience has shown that continued iteration beyond what has normally been considered converged (i.e., as described above) leads to a 2% iterative-convergence uncertainty in CT due to oscillations which are not damped with further iterations. Since calculations for the FF1052 were not extended past 6000 iterations, the Series 60 CB=0.6 value of 2%, which was determined from a 20,000 iteration run, will be assumed valid. Grid convergence, however, is good and shows a 2% uncertainty for a grid-refinement ratio of 1.25 between the medium and fine grids. Summing these components into an overall uncertainty for CT gives a total of 4%. Note, however, that basing overall uncertainty on integral parameters is very optimistic.
Finally, order-of-accuracy was not calculated and validation, which involves detailed comparisons with EFD validation data, is discussed where appropriate in the following and in detail in (9).
6
RESULTS
6.1
Near Field
In the following, near-field results are first discussed for the baseline flow, i.e., single phase, unstratified, and without propeller. For brevity, however, discussion focuses solely on Fr=0.39 results. Discussion of medium-speed single-phase solutions and effects of Fr are provided in (9). Then, modifications to this flow are discussed: stratification, with propeller, and two-phase flow, the latter of which is somewhat preliminary in that it is for Fr=0 and has not yet been coupled to the far-wake bubble-transport CFD.
6.1.1
Single phase, unstratified flow, without propeller
Table 1 shows the wetted surface area S, breakdown of resistance, and comparison of CT to data and CF to the ITTC friction line. In the table, the wetted surface area below both the DWL and the wave are shown. As discussed in detail in (9), the difference for the below-DWL (or static) area between the different grids and data indicates geometry uncertainty. This creates an imbalance of the axial hydrostatic force of magnitude 1% of CT. However, the accuracy of the data area is unknown. With the wave, S decreases in comparison to the static area indicating that the area between the wave troughs and DWL is larger than the area between the wave crests and DWL. In comparison to data, CT is within 10%. This is in contrast to the Series 60 CB=0.6 results which showed negligible geometry error and 2% difference with the data. The total resistance is 48% CF and 52% CP. In comparison to the ITTC friction line, CF ranges from 90% to 105% of CF0, and as such, indicates small and, in some cases, negative form-related frictional resistance. Current research on full-scale Re flows indicates that a new CFD-generated friction line is more appropriate and, if used, results in positive form factors for all cases. The force due to pressure is split into piezometric and hydrostatic components to show their relative magnitude. This shows that the hydrostatic force due to waves, which is created primarily at the bow due to the bow-wave height and axial-projected area, is significant, i.e., 27% of the piezometric component, and effectively reduces CP magnitude.
Ship wave systems are complex and comprised of divergent and transverse wave systems formed at the bow, shoulder, and stern. The global ship-wave pattern is due to interactions between these systems and can be characterized using parameters based upon the Kelvin-source solution: the angle αk of the Kelvin boundary (=19.5°); the angle θ of the wave crests at the Kelvin boundary (=55°); the transverse λt (=2πFr2) and divergent λd (=λtcos θ) wavelengths, wave amplitude A, and velocity of the transverse Ut(=U0) and divergent Ud (=U0cos θ) waves. Although useful for providing a gross far-field description, the Kelvin solution is obviously an over simplification for real ships, especially in the near field. Combatant geometries display many local complexities (e.g., spray, breaking and spilling waves, free-surface turbulence, transom flow and “rooster tail”) which interact to create a wave pattern which is markedly different from the Kelvin model. Further complicating prediction are the differences between full-and model-scale flows. Full-scale flows display, in comparison to model scale, increased breaking, air entrainment, spray formation, and free-surface turbulence. Also, there are additional full-scale complexities such as sea state, density stratification, and suspended particulates and surfactants.
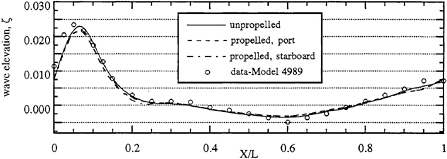
Figure 4 shows a comparison of the wave profile to data. As previously mentioned, the model was free to sink and trim whereas the simulation was performed in the fixed condition. The effects of sinkage and trim are significant, therefore, to compare to data, the solutions were corrected by translating and rotating the free surface by the amount of sinkage and trim in the experiments. After making the corrections, the level of agreement is similar to the Series 60 CB=0.6 and, in general, the solutions show both correct amplitude and phase1. Despite agreement with the data, some details are lacking: the location of the bow crest is slightly displaced aftward; the wave height is under predicted at the stern; and similar to the Series 60 CB=0.6, the wave height upstream of the bow-wave crest is under predicted.
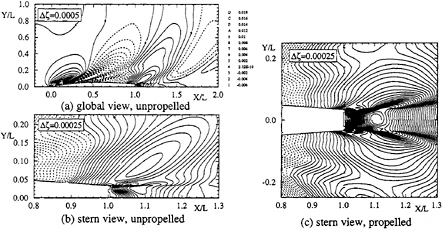
Figures 5(a) and (b) show wave-elevation contours which display patterns described earlier: divergent and transverse wave systems and a rapid rise from the transom to a “rooster tail”, which in this case happens to be double-humped at X/L=1.09. Using the axial wave slopes, (αk,θ) are graphically estimated to be 14° and 15°. These values are greater than and less than the Kelvin values, respectively, and indicate that the diverging waves travel nearly in the direction of the ship. With θ, the diverging wavelength may be estimated from λd=λtcos2θ. Given the small θ, λd is nearly the same as λt. Finally, data for combatant model 5415 confirms the results for the FF1052, particularly the transom flow, however, the FF1052 solution does not resolve the wave breaking and free-surface turbulence shown in the data.
Figure 6 shows details of the flow field through axial velocity (U) contours, cross-plane (V-W) vectors, piezometric pressure (![]() ) contours, and
) contours, and
|
1 |
Note that for the Series 60 CB=0.6, both EFD and CFD were conducted for zero sinkage and trim. |
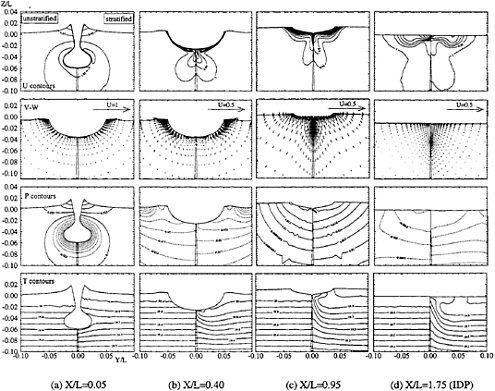
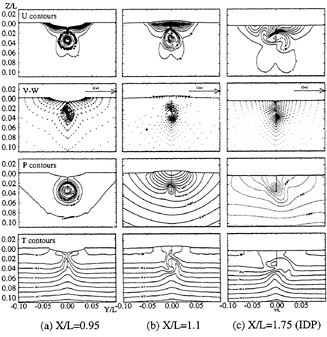
temperature (T) contours for both unstratified (left side) and stratified (right side) flow at X=0.05, 0.40, 0.95 (propeller plane), and 1.75 (IDP). For the unstratified flow, since the temperature and velocity fields are uncoupled, the T contours simply are an indication of the ambient stratification. At X=0.05, the U contours show a reduced magnitude near the hull/free-surface juncture due to the bow wave. The flow accelerates around the sonar dome indicating increased magnitude and is insensitive to wave effects. The boundary layer over the hull and sonar dome is thin. The vectors show the displacement effects of the hull and the upward flow near the free surface due to the bow wave. The ![]() contours correlate with the wave elevation and dome flow, i.e., high and low pressures, respectively. At X=0.4, the U contours show a thickening of the boundary layer which interacts with the large sonar-dome wake. The vectors clearly show a downward flow, an enlarged and outwardly displaced sonar-dome vortex, and reduced free-surface effects. The
contours correlate with the wave elevation and dome flow, i.e., high and low pressures, respectively. At X=0.4, the U contours show a thickening of the boundary layer which interacts with the large sonar-dome wake. The vectors clearly show a downward flow, an enlarged and outwardly displaced sonar-dome vortex, and reduced free-surface effects. The ![]() contours indicate small magnitudes with the largest variations near wave troughs between 0.05<Y<0.10 on the free surface. At X=0.95, which corresponds to the propeller plane, the U contours show a hull boundary layer with a minimum/maximum boundary layer thickness of δ≈0.015/0.022 where the former occurs near the free surface and the latter at mid-girth. For comparison, the thickness of a flat plate boundary layer at the corresponding Rex is δ≈0.013. The larger hull δ is consistent with Uτ at this location: it is smaller than the zero pressure-gradient flat-plate value. Also, U contours show a reduced sonar-dome wake with a deficit of approximately 0.1, and the appearance of the skeg wake along the centerplane. Since the sonar-dome wake is large and, therefore, will have significant influence upon the propeller inflow, the wake rate-of-recovery is qualitatively checked through comparison to an axisymmetric body. It is known that beyond 5 body lengths downstream for a 6:1 prolate spheroid that the wake achieves similarity and the wake-deficit recovery follows the well-known 2/3-power law relationship, wake deficit
contours indicate small magnitudes with the largest variations near wave troughs between 0.05<Y<0.10 on the free surface. At X=0.95, which corresponds to the propeller plane, the U contours show a hull boundary layer with a minimum/maximum boundary layer thickness of δ≈0.015/0.022 where the former occurs near the free surface and the latter at mid-girth. For comparison, the thickness of a flat plate boundary layer at the corresponding Rex is δ≈0.013. The larger hull δ is consistent with Uτ at this location: it is smaller than the zero pressure-gradient flat-plate value. Also, U contours show a reduced sonar-dome wake with a deficit of approximately 0.1, and the appearance of the skeg wake along the centerplane. Since the sonar-dome wake is large and, therefore, will have significant influence upon the propeller inflow, the wake rate-of-recovery is qualitatively checked through comparison to an axisymmetric body. It is known that beyond 5 body lengths downstream for a 6:1 prolate spheroid that the wake achieves similarity and the wake-deficit recovery follows the well-known 2/3-power law relationship, wake deficit ![]() . At 6.5L downstream, which corresponds to the distance between the dome trailing edge and the propeller plane, the spheroid wake deficit is 0.1, which is the same as the sonar-dome wake deficit. Although the 2/3-power law proportionality constants are a function of geometry (i.e., the dome length/diameter is closer to 4:1), this provides an estimate of the recovery. The vectors indicate a general upward flow as the body contracts and the pressure contours indicate very small waves and gradients in this region. Finally, at X=1.75, which corresponds to the far-wake IDP the axial-velocity contours show the overall wake recovery and the persistence of the dome wake. The vectors indicate small cross-plane flow towards the centerplane and the pressure contours show correspondingly small pressure-gradient and wave magnitudes.
. At 6.5L downstream, which corresponds to the distance between the dome trailing edge and the propeller plane, the spheroid wake deficit is 0.1, which is the same as the sonar-dome wake deficit. Although the 2/3-power law proportionality constants are a function of geometry (i.e., the dome length/diameter is closer to 4:1), this provides an estimate of the recovery. The vectors indicate a general upward flow as the body contracts and the pressure contours indicate very small waves and gradients in this region. Finally, at X=1.75, which corresponds to the far-wake IDP the axial-velocity contours show the overall wake recovery and the persistence of the dome wake. The vectors indicate small cross-plane flow towards the centerplane and the pressure contours show correspondingly small pressure-gradient and wave magnitudes.
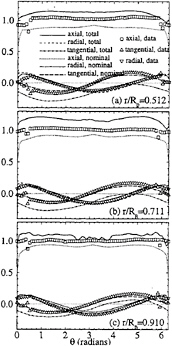
Comparisons are made to the nominal-wake data which was obtained for a hull including appendages, i.e., propeller shaft and struts, whereas, as previously mentioned, the CFD was for the bare hull. Figure 6(d), which was discussed above, showed the details of the flow at the propeller plane. Figure 8 shows the axial-, tangential-, and radial-velocity components in a local propeller coordinate system [i.e., the propeller is centered at (X0,Y0,Z0)= (0.9488, 0.0, –0.035516), has a radius Rp=0.01806, and is mounted on a shaft with an angle of 4.3° downward from the X-axis] at three different radii in the propeller disk including comparisons to data. For each radii, it can be seen that the axial component has small circumferential variation and, on average, is equal to 0.9 and 1.0 for the CFD and data, respectively. In addition, there are other differences in comparison to the data. The CFD shows a large skeg wake (i.e., at θ=0 and 2π,) which is not in the data, and, as expected, the data shows the strut wakes (i.e., at θ≈π/4 and 7π/8). In contrast to the axial component, the tangential and radial components show a nearly pure first-harmonic response and good agreement with the data for both amplitude and phase at all three radii.
6.1.2
Stratification
Calculations of the near field when thermal stratification is included were performed for the temperature profile (10) which consists of a layer of warm, uniform temperature fluid over an increasingly cold mass. The result is a stable thermal structure with the ambient gradient just under the ship keel. The right-hand side of the plots in Figure 6 show the near-field stratified solution and indicate that the velocity and pressure fields are relatively unaffected by the presence of stratification. This is not a surprising result since the time scale of the stratified field (t′=28, where t′=TUo/L and T is the Brunt-Vaisaila period) is considerably longer than the ship passage time scale (=1). This point is further strengthened by noting that the differences between the resistance, wave field, and nominal wake for the stratified vs. unstratified solutions are very small.
On the other hand, the thermal field is strongly altered by the passage of the ship and can be seen in the temperature contours shown in Figure 6. The influence takes the form of a strong upwelling in the near wake in which deep colder water is brought to the surface in a plume at the centerline. Because it is dependent on details of the cross flow in the wake, this feature will vary considerably with ship geometry and propulsor type and operating conditions. While not presented, far wake calculation show that the plume subsides, creating internal waves propagating
within the thermal gradient. In doing so, it creates a set of vortices on either side of the wake center which serve to amplify the lobed appearance.
6.1.3
With Propeller
The prescribed body forces used herein are axisymmetric distributions which are simple functions of ![]() KQ, and J. As discussed, the parameters are based upon matching
KQ, and J. As discussed, the parameters are based upon matching ![]() to the EFD CT and, as such, does not correspond to a self-propelled condition for the CFD. It should be noted that even the simplified approach used herein, as opposed to the more rigorous approach in (2), is amenable to interactive calculations. By setting thrust equal to the CFD resistance and calculating speed of advance from the Taylor-wake fraction, “updated” values of
to the EFD CT and, as such, does not correspond to a self-propelled condition for the CFD. It should be noted that even the simplified approach used herein, as opposed to the more rigorous approach in (2), is amenable to interactive calculations. By setting thrust equal to the CFD resistance and calculating speed of advance from the Taylor-wake fraction, “updated” values of ![]() KQ and J can then be determined from the open-water curves.
KQ and J can then be determined from the open-water curves.
Table 1 shows that the total resistance coefficient CT increases from 5.15×10–3 to 5.25×10–3. If thrust is assumed to be equal to CT, the thrust deduction factor is 0.02. This is significantly smaller than data values of 0.07 to 0.105. Using the nominal-wake analysis to determine speed of advance VA, the thrust coefficient when nondimensionalized in the same fashion as the resistance coefficients is 4.36×10–3. This is only 85% of the bare-hull resistance and indicates an under-propelled condition.
Figure 4 also shows the wave profiles on both sides of the hull for the propelled solution. The difference between starboard and port sides is very small. The difference between the unpropelled and propelled solutions is also very small up to about the propeller plane. Fore and aft of this point, the low and high pressure associated with the propeller slightly decreases and increases the wave-profile slope, respectively.
Figure 5(c) shows a detailed view of the wave-elevation contours in the stern region and shows that the propeller has a large effect aft of the propeller and in the transom wake, and in general, affects the overall stern wave pattern. The contours between X/L=0.95 and 1.0 indicate the increased wave-profile slope, and in the wake, the close contour spacing indicates a single-hump rooster tail with a dramatically increased wave steepness and peak magnitude.
Figure 7 shows details of the flow field. The effect of the propeller is limited to about one propeller diameter upstream. At the propeller plane X/L=0.95, the propeller slipstream and swirl is clearly shown in the U and P contours and cross-plane vectors. The temperature field at this point, however, is essentially unchanged from that shown in Figure 6(d). At X/L=1.1, which corresponds to the location of maximum wave elevation in the wake, it is most interesting to note the high-pressure region between the center of propeller swirl and the free surface and the corresponding increase, in comparison to the unpropelled case, in wave height. At X/L=1.75, the propeller wake is still clearly seen and, interestingly the perturbation of the thermal field is smaller than in the unpropelled case in which colder water reaches the surface and the thermal scar is broader. This is due to the propeller swirl which effectively mixes and transports the thermal energy away from the surface. Obviously, this result will depend on temperature profile, its relationship to the propeller location, and overall propulsor geometry.
Finally, Figure 8 shows the axial-, radial-, and tangential-components of the total wake in the propeller disk. The axial velocity shows the accelerated flow associated with the slipstream and the radial velocity remains essentially unchanged from the nominal wake distribution. Interestingly, the tangential distribution has exactly the same distribution as the nominal wake but is simply offset by an amount equal to the swirl induced by the propeller.
6.1.4
Two-Phase Flow
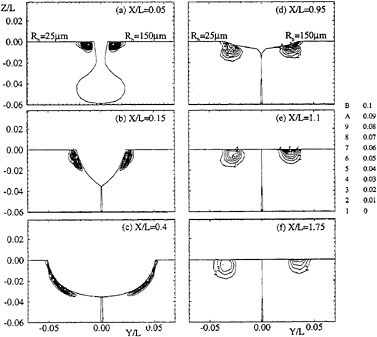
Bubble size plays a major role in the volume-fraction distribution. This is expected since the drag-related term of (4) is directly related to the inverse of the bubble radius and also to the bubble Re through the drag coefficient. Figure 9 shows the streamwise evolution of the bubble field. Void-fraction contours for bubble radius Rb=25µm (left) and 150µm (right) show that the larger the bubble radius the larger the peak in volume fraction at the hull of the ship. This is due to two effects which attract the bubbles towards the hull, gravity and lift, the latter of which acts towards the hull over the entire boundary layer. Also, from the shape of the contours, it is clear that in the wake, the larger bubbles get transported more easily to the surface.
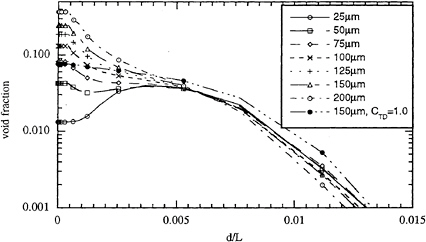
Figure 10 shows the void fraction at X/L=0.95 for a range of bubble radii along a line which cuts perpendicular to the hull and passes through the maximum value. The bubble accumulation below the hull is largest for large bubbles and decreases for small bubbles.
As previously mentioned, the validity of using the turbulent dispersion coefficient CTD=0.1, which was taken from pipe flows with medium-sized particles, is unknown given the application to small bubbles. Figure 10 shows that by increasing CTD to 1.0, the peak at the wall disappears and the gradient is reduced resulting in a more uniform distribution. Therefore, it appears that correct determination of CTD is important because the void-fraction distribution is sensitive to its magnitude and because it is the only term in (4) that avoids unphysical accumulation of gas and the situation of gas-phase streamlines ending at the hull surface. Also, the validity of neglecting
important forces in high void-fraction or void-fraction-gradient regions such as bubble-bubble collisions, induced shear stress, and non-uniform bubble distribution, appears to be dependent upon the value of CTD which is used.
6.2
Far Field
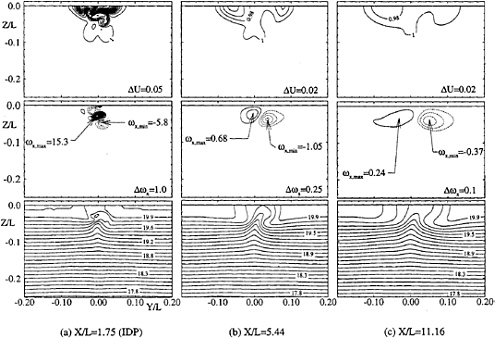
Far-field simulations were performed using both the unstratified and stratified propelled RANS solutions to prescribe the IDP. However, in the following, the discussion is only for the stratified results. Figure 11 shows axial-velocity (U), axial-vorticity (ωx), and temperature contours (T) at the X/L=1.75, 5.44 and 11.15 cross planes. These show the gradual decay of both velocity and vorticity with distance. However, both the sonar-dome wake and propeller swirl remain visible at 11.15 and, in fact, they do so all the way to the exit plane. A small secondary vortex forms on the other side of the centerline from the principal swirl structure which has migrated a small distance. One feature that is missing (as compared to qualitative observations of full scale data) is a strong near surface outward velocity component. One of the goals of applying RANS solvers to upstream condition estimation was to determine if this feature is due to bulk flow phenomena or to turbulence/free-surface interaction. It is likely to be due to the latter. The strong, though compact, propeller swirl causes the axial velocity and turbulent energy fields to form two maxima at the surface. This agrees qualitatively with aerial photographs of the far wake. The deep axial velocity contours seen in the figure are remnants of the decaying surface wave induced axial velocities. They are present, but not too small to be discernible in the cross flow velocity plots. One may note that the wake has net momentum defect. This is due, as previously mentioned, to using ![]() KQ, and J, which correspond to an under-propelled condition. Use of interactively-obtained propulsion parameters is expected to produce stronger axial and swirling velocities. The thermal field evolves such that a persistent cold water region near the centerline at the surface remains through 10 ship lengths and in fact considerably further. At 10 ship lengths, internal waves begin to form from the displaced cold water. Outer boundary conditions on temperature in the model are imperfect wave absorbers and so there is some solution contamination. The error however remains local to the boundaries for the time scales of our interest. Finally, comparison with the semi-empirical IDP generation method used previously shows that the RANS computed momentum defect wake is narrower and shallower and therefore the defect axial velocities are larger. The general ratios between wake width and depth however, are very similar between the two estimates. Since the semi-empirical method is based on satisfying global constraints, such as axial and circumferential momentum, the RANS propeller effects are weaker than expected for the reasons noted above. This also means that turbulent kinetic energy in the propeller jet is smaller than estimated by the semi-empirical method.
KQ, and J, which correspond to an under-propelled condition. Use of interactively-obtained propulsion parameters is expected to produce stronger axial and swirling velocities. The thermal field evolves such that a persistent cold water region near the centerline at the surface remains through 10 ship lengths and in fact considerably further. At 10 ship lengths, internal waves begin to form from the displaced cold water. Outer boundary conditions on temperature in the model are imperfect wave absorbers and so there is some solution contamination. The error however remains local to the boundaries for the time scales of our interest. Finally, comparison with the semi-empirical IDP generation method used previously shows that the RANS computed momentum defect wake is narrower and shallower and therefore the defect axial velocities are larger. The general ratios between wake width and depth however, are very similar between the two estimates. Since the semi-empirical method is based on satisfying global constraints, such as axial and circumferential momentum, the RANS propeller effects are weaker than expected for the reasons noted above. This also means that turbulent kinetic energy in the propeller jet is smaller than estimated by the semi-empirical method.
7
CONCLUDING REMARKS
A CFD approach for simulating the near and far field of a Naval combatant in a thermally-stratified two-phase flow has been presented. This approach is based upon, for the near field, coupling a single-phase RANS method with both the energy equation, to account for transport of thermal energy and creation of buoyancy forces, and a two-fluid model, to account for the transport of monodisperse microbubbles and their interaction with the liquid phase. Far-field solution is based upon PRANS equations with the IDP prescribed by the near-field solution.
An extensive number of conditions were simulated: model-scale Re; medium and high speeds; with and without thermal stratification; with and without propeller; and two-fluid calculations over a range of bubble sizes. The two-fluid near-field results, however, are more preliminary in that they are only for zero Fr and have not been coupled to the far-field through the IDP. For the single-phase, unstratified, and unpropelled case, a detailed uncertainty analysis following ASME guidelines was performed.
The single-phase results show that both global and detailed features of Naval combatant flows can be accurately predicted, particularly the total resistance, wave profiles, and nominal wake. With regard to interaction with the ambient temperature field, the ship flow field transports cold water to the surface creating a thermal scar, which is an excellent tracer. However, the thermal field has small influence on the flow. The effect of the propeller is qualitative shown by the slipstream, swirl, and increased wave height in the near wake. Also, it is shown that the propeller moderately affects the thermal field, such that the scar on the free surface is reduced in comparison to the unpropelled calculation. The two-phase results show that void-fraction introduced near the bow, as a model of breaking-wave entrained bubbles, accumulates in the boundary layer and creates large void-fraction gradients near the wall, where the velocity gradients are large and is strongly influenced by bubble size. In the wake, the bubbles are transported as two streaks, which in general, qualitatively agree with observations of wake white water. The far-field simulations successfully used the near-field results as the IDP and showed that the dome wake, propeller swirl, and cold-water region near the centerline persist 10 ship lengths downstream.
In conclusion, the prognosis of the approach is optimistic, however, there are many uncertainties
which must be addressed. By using systematic verification analysis, numerical uncertainties can be made relatively small. However, improvement in numerics is required, particularly, efficiency and accuracy. Modeling uncertainties are daunting and their estimation requires EFD validation data which, unfortunately, is very difficult to obtain. For single-phase flow, modeling uncertainty is due to geometry, turbulence, wave-breaking, and free-surface boundary conditions. In contrast, there are many areas of concern for two-phase flow. The accumulation of bubbles in the boundary layer suggests that other possible mechanisms of interfacial momentum and mass transfer may be important in this region, such as bubble-bubble collision and interfacial pressure, Einstein forces, dissolution, and breakup. Some of these models will require incorporation of an approach to handle polydisperse bubble populations: a formidable computational challenge.
To accurately predict bubbly-wake signatures, much future work remains. For the near-field RANS, farther improvements in both numerics and models will be made in conjunction with work on more complex single-phase flows, e.g., unsteady flow. Also, capability to resolve appendages, calculate sinkage and trim, and employ more sophisticated propeller-hull interaction methods must be incorporated. The lack of strong thermal-hydrodynamic interaction suggests that a variety of common and in-situ temperature profiles be studied. In certain environments, salinity fields may need to be included in the transport and density calculations. Finally, work on two-fluid modeling will focus on extending the method for nonzero Fr, development of a coupled multigroup scheme to calculate bubble-size distribution, including bubble breakup and dissolution, and inclusion of propulsor effects on the bubble size distribution.
ACKNOWLEDGMENTS
This research was sponsored by Office of Naval Research Grants N00014 –93–1–0052 (Iowa), N00014–96-AF00002 (NSWC CSS), and N00014–91-J-1271 (RPI) under the administration of Dr. E.P. Rood. The computations were performed on the Naval Oceanographic Office, NASA Numerical Aerodynamic Simulation Program, and San Diego Supercomputer Center supercomputers. The assistance of Dr. Rood and Ms. Margo Frommeyer is especially acknowledged.
REFERENCES
1. Tahara, Y. and Stern, F., “A Large-Domain Approach for Calculating Ship Boundary Layers and Wakes for Nonzero Froude Number”, Proc. of the CFD Workshop, Tokyo, March, 1994; also, to appear Journal of Computational Physics.
2. Stern, F., Kim, H., Zhang, Z., Toda, Y., Kerwin, J. and Jessup, S., “Computation of Viscous Flow around Propeller-Body Configurations: Series 60 CB=0.6 Ship Model, Journal of Ship Research, Vol. 38. No. 2, June, 1994
3. Bonetto, F., Drew, D., and Lahey, R.T., “A Numerical Simulation of a Turbulent Two-Phase Jet Using a Multidimensional Two-Fluid Model,” in review, International Journal of Numerical Methods in Fluids.
4. Carrica, P., Bonetto, F., Drew, D., and Lahey, R.T., “Gas-Liquid Two-Phase Flow Around a Ship,” in preparation, International Journal of Multiphase Flow.
5. Lahey, R.T., and Drew, D.A., “The Current State-of-the-Art in Modeling of Vapor/Liquid Two-Phase Flows,” ASME paper 90-WA/HT-13, 1990.
6. Smith, R.W., and Hyman, M., “Convective-Diffusive Bubble Transport in Ship Wakes,” NCSCTN 857–87, 1987.
7. Hyman, M., “Modeling Ship Microbubble Wakes,” CSS/TR-94/39, 1994.
8. Hyman, M., Influence of Temperature Stratification On The Development of Surface Ship Micro-Bubble Wakes,” NCSCTN 1017–90, 1990.
9. Stern, F., Paterson, E., and Tahara, Y., “CFDSHIP-IOWA: Computational Fluid Dynamics Method for Surface-Ship Boundary Layers, Wakes, and Wave Fields,” IIHR Report 666, Iowa City, Iowa, Februrary 1996.
10. Lopez de Bertodano, M., “Turbulent Bubbly Two-Phase Flow in a Triangular Duct,” Ph.D. Thesis, Rensselaer Polytechnic Insitute, Troy, NY, 1992.
11. West, E.E., “Reisitance Characteristics and Appendage Orientation Data for DE 1052 Represented by Model 4989,” DTNSRDC/SPD-C-011_H01, Unclassified 3/13/81, September 1964.
12. Day, W.G.Jr. and Hurwitz, R.B., “Propeller-Disk Wake Survey Data for Model 4989 Representing the FF 1052-Class Ship in a Turn and with a Bass Dynamometer Boat,” DTNSRDC/SPD-0011–21, December 1980.
13. Ratcliffe, T., and Lindenmuth, W.T., “Kelvin-Wake Measurements Obtained on Five Surface Ship Models,” DTRC-89/038, 1990.
Table 1. Resistance and grid convergence
|
Conditions |
Fr=0.29 Re=14,900,000 |
Fr=0.39 Re=20,100,000 |
Fr=0.39 w/prop |
|||
|
Grid |
207×60×40 |
302×60×50 |
207×60×40 |
252×60×45 |
302×60×50 |
207×60×40 |
|
Surface Area (S/L*L) |
||||||
|
calculation |
0.117909 |
0.117304 |
0.117313 |
0.117413 |
0.117540 |
0.116420 |
|
calc. (DWL) |
0.117609 |
0.117706 |
0.117609 |
0.117695 |
0.117706 |
0.117609 |
|
data (DWL) |
0.118166 |
0.118166 |
0.118166 |
0.118166 |
0.118166 |
0.118166 |
|
% diff |
–0.47% |
–0.39% |
–0.47% |
–0.40% |
–0.39% |
–0.47% |
|
Total Resistance (CT×1000) |
||||||
|
calculation |
4.57 |
4.59 |
5.15 |
5.10 |
5.07 |
5.25 |
|
ε |
–0.5% |
0.9% |
0.6% |
|||
|
data |
4.27 |
4.27 |
4.61 |
4.61 |
4.61 |
|
|
% diff |
7.0% |
7.5% |
11.6% |
10.6% |
10.0% |
|
|
Frictional Resistance (CF×1000) |
||||||
|
calculation |
2.95 |
2.83 |
2.55 |
2.46 |
2.41 |
2.7 |
|
ε |
4% |
4% |
2% |
|||
|
ITTC line |
2.80 |
2.80 |
2.67 |
2.67 |
2.67 |
2.67 |
|
% diff |
5% |
1% |
–4% |
–8% |
–10% |
1% |
|
Pressure Resistance (CP×1000) |
||||||
|
calculation |
1.62 |
1.76 |
2.60 |
2.64 |
2.66 |
2.56 |
|
piezometric (p hat) |
2.22 |
2.40 |
3.27 |
3.35 |
3.42 |
3.17 |
|
hydrostatic (z/Fr*Fr) |
–0.60 |
–0.64 |
–0.678 |
–0.71 |
–0.759 |
–0.617 |
|
ε |
–8% |
–2% |
–1% |
|||
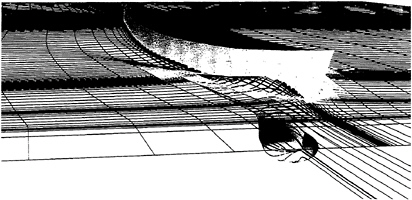
Figure 1. Naval combatant FF1052: free-surface conforming grid colored by wave elevation and surface streamlines
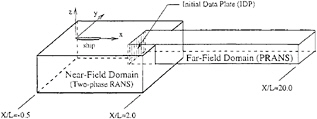
Figure 2. Relationship between near- and far-field domains.