A Practical Prediction of Wave-Induced Structural Responses in Ships with Large Amplitude Motion
M.-K.Wu, J.Aarsnes, O.Hermundstad (MARINTEK, Norway), T.Moan (Norwegian University of Science and Technology, Norway)
Abstract
A practical nonlinear time-domain simulation method for predicting structural responses in ships at head or following sea is presented. The total response is decomposed into linear and nonlinear parts. The linear part is evaluated by using appropriate linear potential flow theory. The nonlinear part comes from the convolution of the impulse response function of the ship-fluid system and the nonlinear modification in hydrodynamic forces. The method is applied to a high-speed catamaran model running in regular head waves. The calculated structural responses are compared with those from model tests. Although the comparison is rather limited, the satisfactory agreement between numerical and experimental results is quite encouraging.
1.
Introduction
In the traditional ship design the wave-induced ship motions, hydrodynamic forces and structural responses are evaluated directly or indirectly by applying the linear potential flow theory, especially the strip theory. With the growing interest in fast monohulls and catamarans, this design method has been challenged to a greater extent. The linearity assumption of small ship motions relative to the wave surface is violated at the fore quarter of most fast ships even in moderate sea states. This violation, together with the V-shaped cross section of the ship hull in that region, will introduce significant nonlinear effects in the hydrodynamic forces, though the heave and pitch may be predicted quite well by linear theory. An increase of sagging moment in both magnitude and frequency is one of the consequences. It might cause severe structural damage such as the buckling of the main deck, and it will also reduce the fatique life of bottom structures. Therefore, the prediction of nonlinear hydrodynamic forces and structural responses is extremely important to the safety of ship structures.
For the past two decades, significant research efforts have been devoted to the nonlinear hydrodynamic analysis. The most recent developments can be found in Maskew(1991), Pawlowski and Bass(1991), and Lin et al(1994) among others. Three-dimensional time-domain potential flow theory is used. Both incident waves and ship motions are assumed to be large. The free surface condition is satisfied on the exact wave surface or the incident wave surface. The body boundary condition is satisfied on the exact wetted surface or the wetted surface below the incident wave profile. However, it does not enjoy the universal success as linear strip theory did in ship hydrodynamics. It is partly because of the difficulties involved in the theory and implementation such as the treatment of transom stern effects and the numerical stability and accuracy in the computational methods. Mainly it is due to the requirement of tremendous computer power. Therefore, it may only serve as validation
tools of less sophisticated methods at present and in the near future.
On the other hand, driven by the need of ship design some simplified approaches emerged at the expense of accuracy, see e.g. Meyerhoff and Schlachter(1980), Yamamoto et al(1978–1979), Jensen and Pedersen(1979,1981), Schlachter(1989) and Xia et al(1995). Almost all of them use the combination of the conventional strip theory and nonlinear modifications of some kind. As a new effort in this direction, Wu and Moan(1996) presented a nonlinear hydroelastic simulation method for the prediction of wave-induced structural responses in ships with large amplitude motion in head or following sea. The total response is decomposed into linear and nonlinear parts. The linear part is evaluated by using appropriate linear potential flow theory. The nonlinear part comes from the convolution of the impulse response function of the ship-fluid system and the nonlinear hydrodynamic force caused by slamming and nonlinear modifications of added mass, damping, restoring and wave forces. Unlike the previous ones, it can be used with high-speed strip theory or three-dimensional flow theory and the frequency dependence of added mass and damping has been taken care of, to some extent. However, it has not yet been verified by experiments.
In this paper, we will apply the method to a high-speed catamaran model in regular head waves. We will compare the calculated structural responses with those from model tests which were conducted at MARINTEK. The main purpose of the model tests is to verify the linear hydroelastic formulation of high-speed strip theory (Wu et al 1993, Hermundstad et al 1995, Hermundstad 1995). However, strong nonlinear effects are observed at some frequencies of regular waves. It offers an opportunity for verifying the proposed formulation which is outlined in the next section. Although the comparison is rather limited, the satisfactory agreement between numerical and experimental results is quite encouraging.
2.
Theoretical Background
Consider a flexible ship moving in the long-crested head waves on deep water. Let (x,y,z) be a right-handed coordinate system with the positive z-direction vertically upwards. The ship has a forward speed U in the negative x-direction. Only the global structural responses are investigated here and the hydrodynamic forces are understood in this sense. We assume that
-
the nonlinearity comes from the large ship motions in heave and pitch while the structural deformation remains small,
-
the incident waves can be described sufficiently by linear wave theory,
-
the influence of ship motions on the incident wave elevation is not significant,
-
the hydrodynamic interaction among the multiple hulls of high speed vessels(Froude number Fn>0.4) is negligible.
In addition, the radiation and diffraction velocity potentials are assumed to be zero on the free surface which means there is no free surface memory effect. The memory effect of free surface will be introduced later and therefore this assumption is actually removed, to a great extent. The dynamic vertical force per unit length exerted by the fluid on each hull of the ship at position x may be expressed as(e.g. Faltinsen 1990)
(1)
where m(x,t) is the high-frequency added mass of the submerged cross section. f(x,t) consists of the Froude-Krylov force and hydrostatic restoring force per unit length on the instantaneous wetted surface. D/Dt represents the total derivative with respect to time t,
(2)
ξ(x,t) is the vertical displacement of the ship hull relative to the wave surface,
ξ(x,t)=w(x,t)–ζ(x,t). (3)
The vertical displacement of the ship hull w(x,t) is approximated by the s lowest symmetric dry eigenmodes, wk(x), including heave and pitch which are the dominant part,
(4)
Here p(t)=[p1(t),p2(t),…,ps(t)]T is the vector of generalized coordinates. Multiplying Eq.(1) by wk(x) and integrating over the length of hulls, we get the kth generalized, or modal hydrodynamic force
(5)
where N is the number of hulls.
The governing equation of the nonlinear ship-fluid system can be written as
(6)
in which M, C and K are the generalized structural mass, damping and stiffness matrices. A0, B0 and R0 represent the generalized linear fluid added mass, damping and restoring coefficient matrices. F0(t) is the generalized linear wave force vector. They come from the hydrodynamic pressure over the mean wetted surface. All the nonlinear effects have been put into the generalized force vector F(t). The elements of F(t) are
Fk(t)=F1k(t)+F2k(t)+F3k(t)+F4k(t),
k=1,2,…,s (7)
where
(8)
is the slamming force.
(9)
and
(10)
are the hydrodynamic forces due to the nonlinear modifications of the two-dimensional added mass and its derivative with respect to x. They reflect, to some extent, the nonlinear effects in the fluid added mass, damping, hydrodynamic restoring force and diffraction force. F4k(t) is the nonlinear modification of the Froude-Krylov force and hydrostatic restoring force,
(11)
m0(x) represents the high-frequency added mass of the mean submerged cross section. Q(x,t) and Q0(x) are the areas of instantaneous and mean submerged cross section, respectively. b0(x) denotes the beam at mean draft.
If we decompose the total generalized response p(t) into its linear and nonlinear parts,
p(t)=pl(t)+pn(t), (12)
then (6) can be rearranged as
(13)
(14)
In order to take into account the memory effect of the free surface, we respectively replace A0, B0, R0 and F0 with frequency dependent added mass A, damping B, restoring coefficient matrix R, and Froude-Krylov and diffraction force Ff+Fd derived in linear theory, see e.g. the high-speed strip theory(Wu et al 1993,1996), the three-dimensional flow theory(Wu 1984, Bishop et al 1986) or the conventional strip theory(Bishop and Price 1979). Eq.(13) and Eq.(14) now have the form
(15)
(16)
The linear and nonlinear responses are found by applying convolution integrations,
(17)
(18)
where
(19)
is the impulse response function matrix. In the time
domain simulation, the linear response pl(t) may be obtained by superposing the frequency-domain solutions instead of using Eq.(17).
The way we deal with the nonlinear hydrodynamic force implies that although large amplitude relative motion is introduced, the memory effect of the free surface is still treated in a linear manner. The slamming force in Eq.(8) always acts upwards regardless of the direction of relative motion. This feature implies that the momentum of the fluid will be transferred back to the ship hull during a fast reduction of the submerged cross section. However, it is not supported by experiments (Greenhow 1988). There is a general agreement that the slamming force should be neglected during water-exit and this is done in the present analysis. More discussion on the formulation can be found in Wu and Moan(1996).
3.
Numerical Procedures
In the calculation of nonlinear responses, each hull is divided into r segments along the longitudinal direction. The number of segments is normally in the range of 20–40. The vertical displacements of those segments relative to the wave surface as well as their first and second total derivatives can be written in vector form,
Ξ(t)=[ξ(x1,t), ξ(x2,t),…, ξ(xr,t)]T
=W(pl+pn)–Z
(20)
(21)
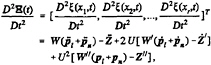
(22)
where xi, i=1,2,…,r, is the x-coordinate of the ith segment. Z denotes the wave elevation vector,
Z(t)=[ζ(x1,t),ζ(x2,t),…,ζ(xr,t)]T. (23)
W is the eigenvector matrix,
W=[w1,w2,…ws],
wk=[wk(x1),wk(x2),…,wk(xr)]T,
k=1,2,…,s. (24)
Overdot and prime represent the differentiation with respect to time t and x-coordinate, respectively. In the same manner, the nonlinear generalized force vector is written as
F(t)=F1(t)+F2(t)+F3(t)+F4(t), (25)
(26)
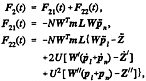
(27a,b,c)
(28)
F4=NρgWTL{Q–Q0 +b0[W(pl+pn)–Z]}, (29)
in which
Q=[Q(x1,t),Q(x2,T),…,Q(xr,t)]T, (30)
Q0=[Q0(x1),Q0(x2),…,Q0(xr)]T. (31)
The matrices m, mt, mx, L and b0 are diagonal. The kth diagonal elements of m, mt and mx are m(xk,t)– m0(xk), ∂m(xk,t)/∂t and ∂[m(xk,t)m0(xk)]/∂x, respectively. The kth diagonal elements of L and b0 are the length and beam at mean draft of the kth hull segment.
The problem is solved numerically in the time-domain. The nonlinear generalized displacement, velocity and acceleration are evaluated through discrete convolutions,
(32)
(33)
(34)
Here T is the time step. ![]()
![]() and
and ![]() are the discrete impulse response function matrices of displacement, velocity and acceleration, respectively. The continuous versions of
are the discrete impulse response function matrices of displacement, velocity and acceleration, respectively. The continuous versions of ![]() and
and ![]() take the form
take the form
(19)
(19)
Unlike pn(t) and ![]() depends partly on F(t). Therefore,
depends partly on F(t). Therefore, ![]() and F(t) should be solved simultaneously. Substituting Eq.(34) and Eq.(27) into Eq.(25) and rearranging it, we get
and F(t) should be solved simultaneously. Substituting Eq.(34) and Eq.(27) into Eq.(25) and rearranging it, we get
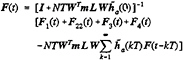
(37)
with I being an identity matrix. In this way, the present nonlinear forces and responses are determined by the past nonlinear forces and the present linear responses. No iteration is needed because the present linear responses can be calculated separately using linear theory.
In order to save computer time, m, mt, mx and Q are evaluated beforehand for a given number of drafts from bottom to deck and stored for interpolation during the simulation. Furthermore, we can truncate the impulse response functions without significant loss of accuracy since ![]() and
and ![]() decay rapidly as k increases due to the damping.
decay rapidly as k increases due to the damping.
4.
Application to a High-Speed Catamaran Model
4.1
Description of Model Tests
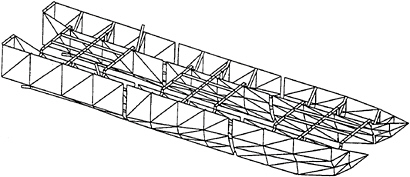
As mentioned in the introduction, the main purpose of the model tests is to verify the linear hydroelastic formulation of high-speed strip theory and therefore a very flexible catamaran model is adopted. The main particulars and the body plan of the model are given in Tab. 1 and Fig.1, respectively. Each hull consists of three separate rigid segments. They are made of Divinycell foam/GRP in which stiff aluminum beams are mounted in order to make them rigid. Two longitudinal elastic hinges made of slender steel beams are used to connect the hull segments. Rubber bands are introduced to cover the gap between the segments and make it watertight. Another three transverse elastic hinges are also used as connecters of the two hulls, see Fig.2. Since wetdeck slamming is a part of the experiment, the model is equipped with three wetdeck plates. Each plate is connected to the hull segments at four points via two stiff aluminum beams. A pinned joint is adopted to transfer only vertical forces due to wetdeck slamming without taking up the bending moments or shear forces between the two hulls. In this way, the influence of the wetdeck plates on the global stiffness of the catamaran model is minimized.
The model is first tested in air to determine the dry natural frequencies, vibration shapes and structural damping. It is suspended from six springs, one at the midpoint of each segment. The natural frequencies of the springs are much lower than those of the model and hence their influence is negligible. Different modes can be vibrated by giving the model an impulse excitation at different places. The model is also tested statically in order to make sure that the wetdeck plates contribute as little as possible to the global stiffness.
The wave tests are performed in the Ocean Basin at MARINTEK. A free running model is used. It is self propelled and can be directed arbitrarily to the incident waves. The model direction is kept stable by an auto-pilot system which controls the rudder angle. The Ocean Basin is equipped with a high speed carriage system. It has the capacity of following free running models at speeds from zero to 6 m/s. The tests include regular, irregular and impulse waves. Wave heading 0°(head
Table 1 Main particulars of the catamaran model. Values refer to zero speed condition
|
Description |
Unit |
Value |
|
Length over all |
m |
4.1 |
|
length between perpendiculars |
m |
3.78 |
|
Total beam at waterline amidships |
m |
1.02 |
|
Beam of each hull at waterline amidships |
m |
0.267 |
|
Distance between center of hulls |
m |
0.753 |
|
Draft at aft perpendicular |
m |
0.197 |
|
Draft at fore perpendicular |
m |
0.207 |
|
Total mass |
kg |
203 |
|
Block coefficient |
m |
0.54 |
|
Vertical center of gravity (above keel) |
m |
0.352 |
|
Longitudinal center of gravity (from AP) |
m |
1.65 |
|
Roll radius of gyration |
m |
0.38 |
|
Pitch radius of gyration |
m |
1.03 |
|
Yaw radius og gyration |
m |
1.09 |
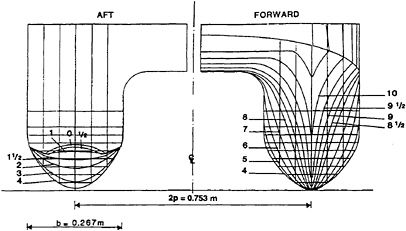
Fig. 1 Body plan of the catamaran model
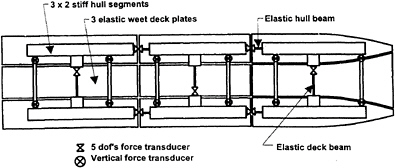
Fig. 2 Top view of the catamaran model
sea), 30° (bow sea) and 90° (beam sea) are covered. Two different speeds, 3m/s and 4m/s, are used. Based on the length overall, they correspond to Froude number 0.47 and 0.63, respectively.
During the tests a comprehensive measuring program is carried out. Among other things, the vertical and horizontal bending moments and shear forces as well as the torsional moment in each elastic hinge are measured by using a 5 d.o.f. strain gauge transducer which is located at one end of the hinge, see Fig.2. The time histories of those moments and forces are recorded digitally at a sampling rate of 100 Hz. To avoid noise and Nyquist phenomena, all the signals are lowpass filtered before digitalization. The cut-off frequency is 40 Hz.
4.2
Numerical and Experimental Results
In order to evaluate the dry eigenmodes of the catamaran, a finite element model of 2112 degrees of freedom has been made, see Fig.3. Hull surfaces are represented by triangular shell elements. Two-node beam elements are used for the backbone frame, the elastic hinges (slender steel beams), the force transducers and other beam-like structural parts. Wetdeck plates are also modelled by two-node beam elements with equivalent mass distribution. Lumped masses are employed for the motors and other objects. The modelling details are given in Hermundstad(1995). Table 2 shows the measured natural frequencies and modal damping in air together with the calculated dry natural frequencies of the first four symmetric flexible modes using a finite element program PUSFEA (Wu 1994). Fig.4 depicts the calculated vibration shapes. 1.7% is adopted as the structural damping for the first mode and 2.6% will be used for the remaining flexible modes throughout the calculation.
Based on the theory and numerical process described in the previous sections, a computer program has been developed. The linear part of response pl(t) and the frequency dependent added mass A, damping B and restoring coefficient matrix R are evaluated by applying high-speed strip theory (Faltinsen and Zhao, 1991a,b). The detailed linear hydroelastic formulation of this theory can be found in Wu et al(1993,1996). The ship hull is divided into 80 segments on account of the relatively small wave lengths in the high frequency range which is needed for the evaluation of impulse response function matrices. The calculation is carried out at 200 equally spaced wave frequencies. The solution is obtained by solving a two-dimensional Laplace equation in each cross-sectional plane. But as opposed to the conventional strip theory, a three-dimensional free surface condition is used so that the divergent wave system generated by high-speed vessels is properly incorporated.
Table 2 Calculated and measured dry natural frequencies(Hz) together with measured modal damping
|
mode no. |
calculated freq. |
measured freq. |
measured damp. |
|
1 |
4.24 |
4.2 |
1.7% |
|
2 |
4.98 |
5.1 |
2.6% |
|
3 |
10.64 |
10.5 |
|
|
4 |
12.94 |
- |
The discrete impulse response function matrices ![]() and
and ![]() play an important role in the calculation of nonlinear responses. In order to verify those matrices, we use the generalized linear wave force caused by irregular waves as the external force vector and calculate the generalized linear displacement pl(t), velocity
play an important role in the calculation of nonlinear responses. In order to verify those matrices, we use the generalized linear wave force caused by irregular waves as the external force vector and calculate the generalized linear displacement pl(t), velocity ![]() and acceleration
and acceleration ![]() in time-domain by discrete convolution and in frequency-domain by superposition, respectively. The results of the two approaches are shown in Fig.5 for the first flexible mode. The general agreement between the two approaches is excellent.
in time-domain by discrete convolution and in frequency-domain by superposition, respectively. The results of the two approaches are shown in Fig.5 for the first flexible mode. The general agreement between the two approaches is excellent.
By investigating the measured bending moments and shear forces in the seven slender steel beams of the catamaran at two different forward speeds and three different regular wave headings, we find that most of them display a linear behaviour for most wave periods. However, severe nonlinear effects are found in the vertical shear force of the fore longitudinal elastic hinges when the ship model is running at forward speed 4 m/sec. in regular head waves of period 2.2 sec., 2.0 sec. and 1.8 sec., respectively. Further observation shows that wetdeck slamming occurs at wave period 1.8 sec. The numerical prediction of structural responses due to wetdeck slamming is beyond the scope of the present paper.
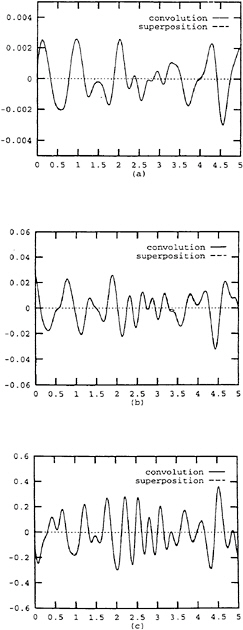
Fig. 5 Time history of the first flexible modal response. abscissa: sec. (a) displacement. (b) velocity. ordinate: 1/sec. (c) acceleration. ordinate: 1/sec.2.
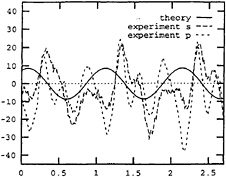
Fig. 6 Calculated linear vertical shear force and the measurements in the fore longitudinal elastic hinges, s and p stand for starboard and port hull, respectively. abscissa: sec. ordinate: N. Ship forward speed=4 m/sec. Wave period=2.2 sec. Wave height=0.087 m.
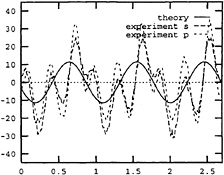
Fig. 7 Calculated linear vertical shear force and the measurements in the fore longitudinal elastic hinges. s and p stand for starboard and port hull, respectively. abscissa: sec. ordinate: N. Ship forward speed=4 m/sec. Wave period=2.0 sec. Wave height=0.052 m.
The calculated linear vertical shear forces in the fore longitudinal elastic hinges as well as the measured time histories at wave periods 2.2 sec., 2.0 sec. and 1.4 sec. are depicted in Fig.6 through Fig.8. Large discrepancies between the linear prediction and the measurement can be clearly observed in Fig.6 and 7. If we introduce the nonlinear force components described in Eqs.(8 –11), the discrepancies are reduced remarkably, see Fig.
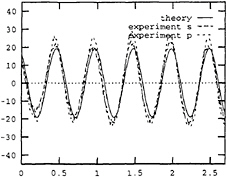
Fig. 8 Calculated linear vertical shear force and the measurements in the fore longitudinal elastic hinges. s and p stand for starboard and port hull, respectively. abscissa: sec. ordinate: N. Ship forward speed=4 m/sec. Wave period=1.4 sec. Wave height=0.042 m.
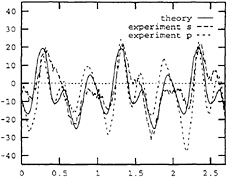
Fig. 9 Calculated total vertical shear force and the measurements in the fore longitudinal elastic hinges. s and p stand for starboard and port hull, respectively. abscissa: sec. ordinate: N. Ship forward speed=4 m/sec. Wave period=2.2 sec. Wave height=0.087 m.
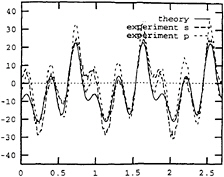
Fig. 10 Calculated total vertical shear force and the measurements in the fore longitudinal elastic hinges. s and p stand for starboard and port hull, respectively. abscissa: sec. ordinate: N. Ship forward speed=4 m/sec. Wave period=2.0 sec. Wave height=0.052 m.
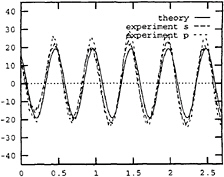
Fig. 11 Calculated total vertical shear force and the measurements in the fore longitudinal elastic hinges. s and p stand for starboard and port hull, respectively. abscissa: sec. ordinate: N. Ship forward speed=4 m/sec. Wave period=1.4 sec. Wave height=0.042 m.
9 and 10. However, as shown in Fig.8 and 11 the nonlinear effect at wave period 1.4 sec. is insignificant because the ship motion is relatively small, see Fig.12. Further, the responses obtained by only including the nonlinear modification of Froude-Krylov and hydrostatic restoring force Eq.(11), the slamming force Eq.(8) or the combination of Eq.(11) and Eq.(8) are also depicted in Fig.13 through Fig.18 for comparison. In the integral-differential method presented by Xia(1994) and Xia et al(1995), only the nonlinear modification of Froude-Krylov and hydrostatic restoring force, and the slamming force are taken into consideration. Therefore, their method is a special case of our more general approach, Fig 17 and 18.
In the above nonlinear analysis, time step T=0.002 sec., segment number r=30 and the first six
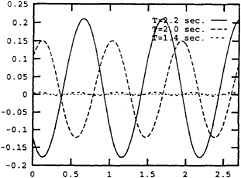
Fig. 12 Calculated ship bow displacements at three different wave periods 2.2 sec., 2.0 sec and 1.4 sec. The corresponding wave heights are 0.087 m, 0.052 m and 0.042 m, respectively. Ship forward speed= 4 m/sec. abscissa: sec. ordinate: m.
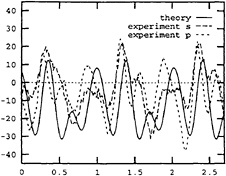
Fig. 13 Calculated vertical shear force. Only part of the nonlinear forces, namely Eq.(11), is included. abscissa: sec. ordinate: N. Ship forward speed=4 m/sec. Wave period=2.2 sec. Wave height=0.087 m.
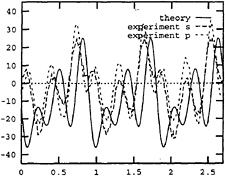
Fig. 14 Calculated vertical shear force. Only part of the nonlinear forces, namely Eq.(11), is included. abscissa: sec. ordinate: N. Ship forward speed=4 m/sec. Wave period=2.0 sec. Wave height=0.052 m.
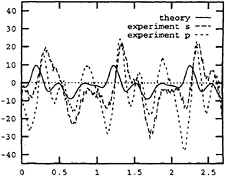
Fig. 15 Calculated vertical shear force. Only part of the nonlinear forces, namely Eq.(8), is included. abscissa: sec. ordinate: N. Ship forward speed=4 m/sec. Wave period=2.2 sec. Wave height=0.087 m.
flexible modes are used. The influence of more global modes and segments, and smaller time step to the total responses is not significant. The steady sinkage and trim caused by high forward speed have been taken care of in the calculation. But other effects of the steady wave are neglected both in linear and nonlinear analysis. For the high speed vessels the steady wave elevation may not be very small and therefore it seems reasonable to use the wetted surface under the steady wave profile instead of that under the calm water as the mean wetted surface if it is available.
From Fig.9 we can see some discrepancy in the measurements around time 1.0 and 2.0 between port hull and starboard hull. The same phenomenon is also found in Fig.10. It is probably due to the fact that the configuration of the transverse elastic hinges and transducers is not symmetric about the
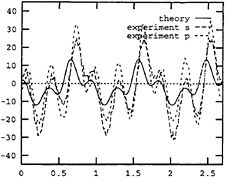
Fig. 16 Calculated vertical shear force. Only part of the nonlinear forces, namely Eq.(8), is included. abscissa: sec. Ordinate: N. Ship forward speed=4 m/sec. Wave period=2.0 sec. Wave height=0.052 m.
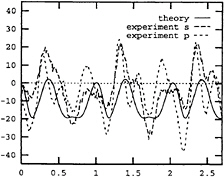
Fig. 17 Calculated vertical shear force. Only part of the nonlinear forces, namely Eq.(8) and Eq.(11), is included. abscissa: sec. ordinate: N. Ship forward speed=4 m/sec. Wave period=2.2 sec. Wave height=0.087 m.
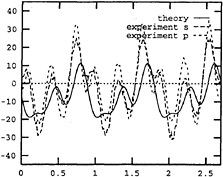
Fig. 18 Calculated vertical shear force. Only part of the nonlinear forces, namely Eq.(8) and Eq.(11), is included. abscissa: sec. ordinate: N. Ship forward speed=4 m/sec. Wave period=2.0 sec. Wave height=0.052 m.
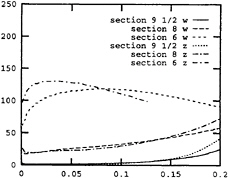
Fig. 19 Comparison of 2-dimensional slamming force. w denotes the results by using the present method. z denotes the results from a more sophisticated approach(Zhao et al 1996). Dropping speed=1.0 m/s. abscissa: sec. ordinate: N/m.
catamaran's centerplane, see Fig.2. This results from practical considerations during the fabrication process. However, it has been made symmetric in the FEM model so that the added mass A, damping B, Froude-Krylov and diffraction force Ff+Fd can be evaluated more quickly and efficiently. Small deviations in the catamaran's heading will also trigger the excitation of antisymmetric modes, like the one-node torsion mode.
At the beginning of section 2 we assume that the influence of ship motion on the wave elevation is negligible and then use (8) to calculate the slamming force. This is a von Karman type of solution where the pile-up water around the intersection between the free surface and the ship hull is not accounted for. In order to investigate the influence of the pile-up water upon the 2-dimensional slamming force, we have compared our
calculations with those from a more sophisticated method(Zhao et al 1996), which is a generalization of Wagner's solution to the water entry problem. In that method the jet flow occurring in the vicinity of the intersection when the ship hull impacts the water is handled properly and the slamming force is obtained by integrating the pressure distribution at each time step.
The results of the comparison are shown in Fig.19 for cross section no. 6, 8 and 9 1/2 at a constant dropping speed of 1 m/s. The aggreement is quite good for the early part of the impact at cross section no. 8 and 9 1/2 and for the later part at cross section no. 6. They correspond to regions where the local deadrise angle(angle between hull section and water surface) is large, see Fig.1, and therefore little pile-up water exists. When the local deadrise angle gets smaller due to the increased flare or near the bottom of full cross sections, the present method will underpredict the slamming force. However, the three-dimensional effect could cancel, to some extent, the extra slamming force caused by the pile-up water. Therefore, our simplified evaluation of slamming force is acceptable from a practical point of view. Further, slamming is only one source of nonlinear forces. The overall influence of any underprediction of slamming force on the structural responses is believed to be less significant than it is shown in Fig.19.
5.
Concluding Remarks
A simplified method for the prediction of wave-induced structural responses in ships with large amplitude motion at head or following sea is presented. The total response is decomposed into linear and nonlinear parts. The linear part is calculated by using appropriate linear potential flow theory, such as high speed strip theory or conventional strip theory. The nonlinear part comes from the convolution of the impulse response function of ship-fluid system and the nonlinear modification in hydrodynamic forces. The method is then applied to a high-speed catamaran model running in regular head waves. The calculated structural responses are compared with those from model tests. The satisfactory agreement between numerical and experimental results shows that the present method is able to capture the nonlinear effects with reasonable accuracy in this specific case. However, more verification work should be carried out through both experiment and more sophisticated numerical methods before any general conclusions can be reached.
Acknowledgements
This work has been partly financed by the Hydroelasticity Project of NTNU and the Dynamic Analysis Support System Project of MARINTEK AS. Both of them are sincerely acknowledged.
References
Bishop, R.E.D. and Price, W.G. ( 1979), Hydroelasticity of Ships, Cambridge University Press , Cambridge.
Bishop, R.E.D., Price, W.G. and Wu, Y. ( 1986), A General Linear Hydroelasticity Theory of Floating Structures Moving in Seaway, Phil. Trans. Soc. Lond., A 316, pp. 375–426.
Faltinsen, O. ( 1990), Sea Loads on Ships and Offshore Structures, Cambrige University Press.
Faltinsen, O. and R.Zhao ( 1991a), Numerical Prediction of Ship Motions at High Forward Speed, Phil. Trans. R. Soc. Lond., A 334, pp. 241–252.
Faltinsen, O. and R.Zhao ( 1991b), Flow Predictions Around High-speed Ships in Waves, Mathematical Approaches in Hydrodynamics, SIAM, pp. 265–288.
Greenhow, M. ( 1988), Water-Entry and -Exit of a Horizontal Circular Cylinder, Applied Ocean Research, Vol. 10, No. 4.
Hermundstad, O.A., Aarsnes, J.V. and Moan, T. ( 1995), Hydroelastic Analysis of a Flexible Catamaran and Comparison with Experiments, Proc. Third Int. Conf. on Fast Sea Transportation FAST'95, Germany, pp. 487–500.
Hermundstad, O.A. ( 1995), Theoretical and Experimental Hydroelastic Analysis of High Speed Vessels, Ph.D. Thesis, Dept. of Marine Structures, The Norwegian Institute of Technology .
Jensen, J.J. and Pedersen, P.T. ( 1979), Wave-induced Bending Moments in Ships—A Quadratic Theory, Trans. RINA, Vol. 121, pp. 151–165.
Jensen, J.J. and Pedersen, P.T. ( 1981), Bending Moments and Shear Forces in Ships Sailing in
Irregular Waves, Journal of Ship Research, Vol. 24, No. 4, pp. 243–251.
Lin, W.M., Meinhold, M.J., Salvesen, N. and Yue, D.K.P. ( 1994), Large-Amplitude Motions and Wave Loads for Ship Design, Twentieth Symposium on Naval Hydrodynamics, August, University of California, Santa Barbara, California, USA.
Maskew, B. ( 1991), A Nonlinear Numerical Method for Transient Wave/Hull Problems on Arbitrary Vessels, Tran. SNAME, Vol. 99, pp. 299–318.
Meyerhoff, M.K. and Schlachter, G. ( 1980), An Approach for the Determination of Hull-Girder Loads in a Seaway Including Hydrodynamic Impacts, Ocean Engng., Vol. 7, pp. 305–326.
Pawlowski, J.S. and Bass D.W. ( 1991), A Theoretical and Numerical Model of Ship Motions in Heavy Seas, Trans. SNAME, Vol. 99, pp. 319–352.
Schlachter, G. ( 1989), Hull Girder Loads in a Seaway Including Nonlinear Effects, Schiffstechnik, 36, pp. 169–189.
Wu, M.K., Hermundstad, O.A. and Moan, T. ( 1993), Hydroelastic Analysis of Ship Hulls at High Forward Speed, Proc. Sec. Int. Conf. on Fast Sea Transportation FAST'93, Yokohama, Japan, pp. 699–710.
Wu, M.K. ( 1994), How to Use PUSFEA—A Complete Manual, Dept. of Marine Structures, Norwegian Institute of Technology, Trondheim.
Wu, M.K. and Moan, T. ( 1996), Linear and Nonlinear Hydroelastic Analysis of High Speed Vessels, to appear in Journal of Ship Research.
Wu, Y. ( 1984), Hydroelasticity of Floating Bodies, Ph.D. Thesis, Dept. Mech. Engng., Brunel University, U.K.
Xia, J. ( 1994), Hydroelasticity Theories of Slender Floating Structures, Ph.D. Thesis(in Chinese), China Ship Scientific Research Center, Wuxi, China, 204 pp.
Xia, J., Wang, Z., Gu, X., Shen, J. and Wu, Y. ( 1995), Numerical Simulation of the Wave-induced Non-linear Bending Moment of Ships, OMAE'95.
Yamamoto, Y., Fujino, M. and Fukasawa, T. ( 1978– 1979), Motion and Longitudinal Strength of a Ship in Head Sea and Effects of Nonlinearities, Journal Soc. Nav. Arch. of Japan, Vol. 143–145.
Zhao, R., Faltinsen, O. and Aarsnes, J.V. ( 1996), Water Entry of Arbitrary Two-dimensional Sections with and without Flow Separation, 21st Symposium on Naval Hydrodynamics, June, Trondheim, Norway.
DISCUSSION
G.Schlachter
MTG, Germany
The authors should be thanked for their effective contribution to more reliable design loads on ships in a seaway. Different from the approach of Meyerhoff/Schlachter (1980), the present method contains a clear separation of linear and nonlinear loads neglecting the frequency influence only with impact, i.e., slamming effects. The approach of Schlachter (1989) is different because it is based on frequency-independent hydrodynamic coefficients. All three methods calculate the elastic response of the hull girder by superposition of eigenmodes. However, the present approach is based on “dry” modes, whereas the other two mentioned use “wet” modes assuming that orthogonality is still given.
In order to make the present method even more attractive for practical use, the future development of it should aim at the solution of the following problems:
-
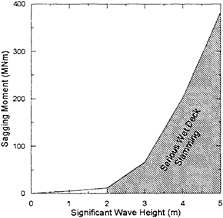
Wet-deck slamming: The figure below shows how wet-deck slamming dominates the hull girder loads of a 700 t SES in higher sea states (from calculations verified by tank tests).
-
Deformation of incoming waves by the ship: It can have a considerable impact on local pressures on the shell.
Furthermore, a statistical evaluation should be part of the computer program which enables the user to extrapolate extreme, i.e., design loads.
AUTHORS' REPLY
Thank you for your kind comments. The purpose of the current paper was to verify our nonlinear simulation method which did not take into account the wet-deck slamming. We agree that the whipping response due to wet-deck slamming might be significant as you suggested in your figure and therefore deserves a thorough investigation on its own. We have been working on this problem for some time. Parts of the results will be published in the near future.
Also, statistical analysis of extreme responses is beyond the scope of the current paper. This issue was, however, touched upon in an accompanying paper (Wu and Moan, 1996). But the activity in this area will be emphasized in order to establish results for probability-based design of advanced vessels.
We totally agree with you that the pile-up water should be taken into consideration as far as local pressure and local structure are concerned.