On the Modeling of the Flow Past a Free-Surface-Piercing Flat Plate
A.Di Mascio, M.Landrini, E.Campana (Istituto Nazionale per Studi ed Esperienze di Architettura Navale, Italy)
Abstract
Some numerical simulations and experiments for the analysis of the free surface flow past a flat plate in drift motion have been carried out. Two mathematical models were used in the simulation: the first one is a linear inviscid model with a vortex layer shed from the trailing edge and from the tip of the plate; the second one is described by the Navier-Stokes equations with the algebraic Baldwin-Lomax turbulence model. The computed forces acting on the plate are compared with the data measured in the towing tank at INSEAN and with those found in the literature. Though the accuracy of both models is satisfactory in the low Froude number range (below Fr=0.5 for the aspect ratios considered), the inviscid model overestimates the forces acting on the plate when increasing the velocity and/or the angle of incidence. This deviation seems to be related to the absence of nonlinear effects in the inviscid model, that cannot be neglected when a “jump” in the free surface height appears at the trailing edge.
1
Introduction
The prediction of the maneuverability performances of a ship can be gained by simple models based on the knowledge of possibly few coefficients that summarize the dynamical behaviour of the vessel. Actually, these parameters are obtained by means of extensive experimental tests in towing tanks. Such predictive tools accurately depict the maneuvering capability in most cases. Nevertheless, experimental observations [6] reveal that slight geometrical differences sometimes have a great influence on the maneuvering performances. With this regard, the availability of a numerical tool for the prediction of the ship behaviour can be helpful to reduce the design costs.
If the main features of the flow are retained, a reasonable description of the flow can be obtained with relatively simple models. The rotational inviscid model, in which a vortex sheet mimics the formation and evolution of the wake in the real flow, gives satisfactory information about the hydrodynamic coefficients in most cases.
The complete description of the flow field requires, however, additional information regarding the separation lines from which the wake is shed, and the mechanism for its evolution. These information can be gained by both experiments and Navier-Stokes numerical simulations.
In order to grasp a deeper insight of the phenomenon we have decided to study a model problem that allows to guess the configuration of the separation lines in advance, the study of their correct location being postponed to the future research. The flow past a flat plate in a steady drifting motion is the simplest prototype, in that the separation lines can be assumed to coincide with the tip and the trailing edge.
In spite of its geometrical simplicity, this flow embodies very interesting features. Indeed, previous experimental observations [10] detect the existance of two distinct sub- and supercritical flow regimes, the latter being characterized by the appearance of a free-surface jump, localized at the intersection between the free surface and the trailing edge.
It will be shown in the following that, when the jump at the trailing edge appears, the inviscid flow model overestimates the side force, whereas the Navier-Stokes model with nonlinear boundary conditions on the free-surface, used in the present work, succeeds in dealing with the flow in both subcritical and supercritical regime.
At present, the reasons of the inaccurate prediction obtained by the inviscid flow model are not clear. In fact, it seems not to be related to the geometrical nonlinearity of the boundary condition at the free-surface, because a Navier-Stokes computation with a “frozen” free surface yields almost the same answer
as the fully nonlinear simulation. Moreover, the discrepancy has probably nothing to do with the separation bubble at the leading edge. This can be inferred from the zero-Froude number results, for which the inviscid model gives an excellent prediction of the hydrodynamic coefficients, in spite of the recirculation.
The present paper is organized as follows: the mathematical models used in the simulation are briefly described in Sec.1, while in Sec.2 the experimental apparatus is illustrated. Then, numerical results with both the inviscid model and the Navier-Stokes model will be reported in Sec.3, and they will be discussed in comparison with the experiments.
2
Mathematical Models
In this section, the mathematical models used in the simulation of the flow past a flat plate are described. The first one is the inviscid flow model with a vortex sheet. The second one is the more complex Navier-Stokes model, with an algebraic turbulence model.
2.1
Inviscid Model
In this model viscous effects are supposed to be confined close to the rigid boundary, where the fluid viscosity determines the generation of vorticity. The vorticity evolution and shedding are described by means of the inviscid fluid mechanics, that is viscous effects are completely neglected and rotational zones are modelled as vorticity layers, emerging from known separation lines (the lower tip and the trailing edge).
The fluid is supposed to fill a domain Ω of infinite depth, bounded by the free surface ![]() by the plate surface and by a zero thickness wake W emanating from the tip and the trailing edge.
by the plate surface and by a zero thickness wake W emanating from the tip and the trailing edge.
The total fluid velocity U=(U,V,W)T, with respect to a reference frame fixed with the plate, is written in the form U=U∞+u, U∞ being the undisturbed flow velocity. The flowfield is supposed to be solenoidal, i.e.
![]() ·u=0 in Ω (1)
·u=0 in Ω (1)
and irrotational, that is
![]() ×u=0 in Ω (2)
×u=0 in Ω (2)
The perturbation velocity u satisfies the impermeability constraint on the body surface ![]()
(3)
A kinematic condition in terms of the wave height h is enforced on the free surface ![]()
(4)
together with a dynamic boundary condition, that fix the pressure p, computed from the Bernoulli theorem, to the atmospheric pressure (set to zero)
(5)
Continuity of pressure and normal velocity are required through the wake W
p+=p–u·n+=u·n– at W (6)
Finally, the Kutta condition is enforced along the separation lines and the radiation condition is required far from the body.
In the general case, the free surface and the wake shapes are unknown and therefore are to be determined as a part of the solution.
It may be shown that, under quite general assumptions [2], the field u(Q) may be expressed by the integral form of the Helmholtz decomposition (Poincaré Formula [5]), that specializes, when dealing with zero-thickness bodies, in
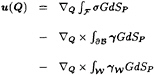
(7)
where the source distribution σ accounts for the free surface effects, ![]() is the bound vorticity and
is the bound vorticity and ![]() represents the vorticity confined in the wake. It is relevant to recall that, by virtue of the Helmholtz theorem applied to a vortex layer, both the bound vorticity and the trailing vorticity satisfy the continuity relation
represents the vorticity confined in the wake. It is relevant to recall that, by virtue of the Helmholtz theorem applied to a vortex layer, both the bound vorticity and the trailing vorticity satisfy the continuity relation ![]()
The unknown source and vortex distributions are computed by enforcing the boundary conditions. The problem is strongly nonlinear and, consequently, very CPU time consuming. In order to make the computation as cheap as possible, the problem is simplified on both the free surface and the wake: free surface boundary conditions are linearized by using the double model flow as basis flow, while the dynamics of the wake is simplified by constrainig the wake “particles” to move only in the horizontal plane, thus preventing the wake roll-up (see [8, 9] for details). In the numerical solution, the source and the vorticity distribution are supposed to be piecewise constant. The enforcement of the boundary condition at control points yields a set of algebraic equations to be used in the computation of the unknown discrete values of σ, ![]() and
and ![]() .
.
Some examples of numerical simulation are reported in figures 1 and 2, where the wave pattern is depicted for two values of the Froude number and
incidence α=9°. In fig.3 the computed forces are compared with experiments. Whilst the prediction is excellent when the Froude number is low, an increasing deviation is noticed when the forward speed grows. This effect is more pronounced for the larger aspect ratio (Ar=draught/chord length)
2.2
Viscous Model
Also a more complex Navier-Stokes model was used in the computations reported in the following. The fluid is again supposed to fill all the space below the free surface around the flat plate. In this case, the velocity u=(u1,u2,u3)T=(u,v,w)T and the pressure p are the solution of the system of partial differential equations
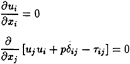
(8)
where the first equation is the mass conservation equation, while the second one represent the momentum equation parallel to the xi-axis, i=1,2,3 and
τij=(vT+v) (ui,j+uj,i) (9)
v being the kinematic viscosity, vT the eddy viscosity computed with the algebraic Baldwin-Lomax model
[1]. δij is the Kronecker symbol.
The no-slip condition is enforced on the body surface
(10)
On the free surface, if the action of the wind and the surface tension are neglected, the dynamic boundary conditions to be satisfied are
(11)
while the kinematic boundary condition reads
(12)
In the numerical solution, these equations are discretized by means of a standard finite volume technique on a curvilinear grid, that moves to fit the actual free surface shape. All the derivative are expressed by centered differentiation, and the variables at cell interfaces are evaluated by simple averaging from the neighbouring points. A fourth order artificial dissipation term is added to stabilize the calculation.
With regard to the boundary conditions, there is no particular problem to enforce the no-slip condition on the wall of the plate and the kinematic boundary condition at the free surface. On the contrary,
the dynamic boundary condition (11) is simplified to p=0. Moreover, the velocity vector at the free surface is extrapolated from the first inner point. This simplified boundary condition are a common practice when computing free surface viscous flows, because in general the grid near the water-air interface is too coarse to resolve the boundary layer.
The nonlinear algebraic equation system, that stems from the discretization process, is solved by a Collective S.O.R. algorithm, whose speed of convergence is increased by a Full Approximation Storage-Full Multigrid (FAS-FMG) algorithm (see [4] for details).
Two kind of grids were used in the computation: a two-block grid with H-H topology (fig.4), each block being a cartesian grid 80×32×32, and a two-block grid with O-O topology shown in fig..5, with 40×24× 16 cells each. In both cases, the cells were clustered near the wall, in order to have the proper resolution of the boundary layer.
3
Experimental set-up
The numerical study of the flow past a flat plate was integrated by some experiments carried out in the towing tank at INSEAN. The aluminuim flat plate used in the tests has chord length 50 cm, height 100 cm and thickness 0.6cm. Both the trailing edge and the leading edge were rounded. The plate was fixed to carriage by means of a mechanism able to position it with any draught and angle of incidence.
The experiments were carried out in the smaller tank at INSEAN. The tank is 220 meters long, 9 meters wide and 3.6 meters deep.
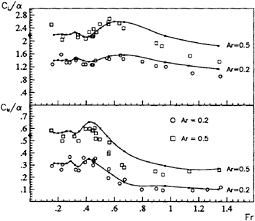
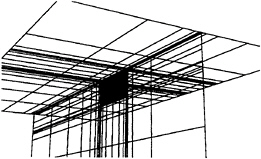
Figure 4: Sample grid. H-H topology
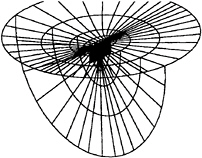
Figure 5: Sample grid. O-O topology
The forces acting on the plate were measured by a six-component balance Kempf & Remmers. Analogic force-tension transducer were used in the measures. A/D conversion was done with sampling frequency equal to 240 Hz. The equipment was calibrated in the measured force range with assigned weights, resulting in a deviation of 1.4 per cent at most.
The wave elevation on the wetted surface was evaluated by photographic observations on the two sides of the plate. A regular grid with 1 cm spacing was drawn on the body surface to facilitate observations.
A picture of the plate during the test is shown in fig.6
4
Discussion of Results
First of all, the inviscid model with vortex layer and the Navier-Stokes model were tested in the zero-Froude number case. Fig.7 reports the computations for a flat plate with unit aspect ratio and Reynolds number (for the RANSE calculation) Re= 1×105. The grid for the inviscid calculation was 32×32 on the plate, while a two-block 80×32×32

Figure 6: Experimental set-up
grid was used in the RANSE calculation, with 32×16 cell faces on each side of the flat plate.
It can be seen that the prediction of lift CL, drag CD and moment CN coefficients is very accurate for both models when compared with experiments, in spite of the fact that the inviscid model does not take into account the separation bubble predicted by the Navier-Stokes computation. This flow separation is caused by the sharp leading edge, and it grows when the angle of incidence increases. Nevertheless, the prediction of the hydrodynamic coefficients is very good also at 20 degrees of angle of attack.
On the contrary, the numerical prediction of the lateral force coefficient CY, gained by the inviscid model, departs from both the Navier-Stokes calculations
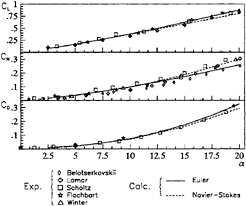
Figure 7: Hydrodynamic coefficients for a flat plate, AR=1, for a zero-Froude number flow. Comparison of the inviscid calculation, viscous calculation and experiments
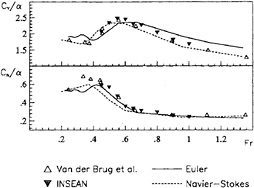
Figure 8: Ratio of the force normal to the plate (top) or the yaw moment (bottom) to the incidence as function of the Froude number. Comparison of the inviscid calculation, the Navier-Stokes simulation and experimantal data measured at INSEAN and by van den Brug et al. [12]. Incidence 4.5 degrees.
and experimental data when computing free-surface flows beyond certain values of the Froude number and angle of attack. Fig. 8 and 9 show the hydrodynamic coefficients as functions of the Froude number, with 4.5 and 9 degrees of incidence and aspect ratio equal to 0.5. In the same figures, the data measured in the experiments carried out at INSEAN and those obtained by van den Brug et al. [12] are also reported.
The dependence of the Navier-Stokes solution on the grid was checked by repeating the computation with the O-O grid shown in fig.5. It can be inferred from figure 10, that, in spite of the different size and topology of the grids, the two predictions are reasonably similar to each other.
The first thing to be noticed is that both our measures and Navier-Stokes predictions mirror exactly the data reported in [12], and this seems to confirm the reliability of the viscous model predictions and the experimental equipments. Moreover, altough the numerical predictions with the inviscid model are good up to Fn=0.60, they depart from experimental data when the velocity increases, for both values of incidence.
It is interesting to stress that the prediction with the inviscid model begin to depart from the experiments and from the Navier-Stokes computation when, in addition to the separation bubble at the leading edge, another interesting phenomenon appears at the trailing edge. In fig.11 and 12 the wave elevation along the plate are reported for 4.5 and 9
degrees of angle of attack, as computed by means of the Navier-Stokes model. It can be seen that, as the Froude number increases, a “jump ” in the wave heigth is clearly observed.
The occurence of this phenomenon is not new. Maniar et al. [10] observed a similar behaviour in their experiments in a water tunnel, and reported the measured wave height. To the purpose of comparison, we repeated the experiments in the INSEAN towing tank and the numerical simulation with the two models for the same conditions (6 degrees of incidence and unit aspect ratio). A perspective view of the free surface is shown in fig.13 for Fr=0.63 and Fr=0.74, whereas Fig.14 reports the numerical calculation together with the experimental wave profiles on both sides of the plate. In particular, it can be seen that the Euler prediction (dashed lines) oscillates around the experimental data (symbols), while the Navier-Stokes computation (solid lines) correctly mirrors the measurements of the INSEAN experiment. It can be also seen that, for the higher Froude number flow, our data significantly differ from those by Maniar et al. The reason of this discrepancy is currently under analysis.
The increasing inaccuracy of the inviscid model in the high Froude number range is not well understood. In fact, it seems not to be caused by the separation at the leading edge: the same happens in the double model flow and, nevertheless, the prediction is still very good. Moreover, it seems not to be related to the geometrical nonlinearities of the free
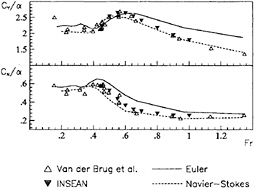
Figure 9: Ratio of the force normal to the plate (top) or the yaw moment (bottom) to the incidence as function of the Froude number. Comparison of the inviscid calculation, the Navier-Stokes simulation and experimantal data measured at INSEAN and by van den Brug et al. [12]. Incidence 9.0 degrees.
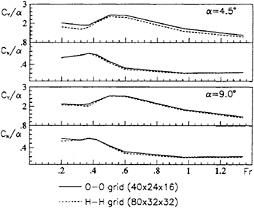
Figure 10: Ratio of the force normal to the plate and the yaw moment to the incidence as function of the Froude number. Comparison of two the Navier-Stokes simulations. Incidence 4.5 degrees (top) and 9.0 degrees(bottom).
surface. The role of the actual wave displacement was in fact analysed with the Navier-Stokes model, retaining the usual form of the free surface boundary conditions, but preventing the motion of the boundary, and therefore enforcing them on the undisturbed water plane z=0. As shown in fig.15, the effect on the hydrodynamic coefficients is very small, also in the supercritical regime.
5
Conclusion and Perspectives
This work is the first stage on a more general program concerning the prediction of the hydrodynamic coefficients of maneuvering ships. In particular, the capabilities of simple inviscid rotational models was considered for free surface flows. The very simple case of a flat plate in drift motion was analysed and the results were compared with a Navier-Stokes computation and with experimental data. The geometry of the problem was choosen so simple because we wanted to postpone the location of vortex sheet separation lines to further research, and to concentrate on global force prediction.
In spite of the simple shape, some interesting features were detected. In fact, the prediction of the hydrodynamic coefficients is rather inaccurate when the velocity and/or the angle of incidence is increased beyond certain values. This happens in conjunction with the appearence of a jump in the free surface elevation at the trailing edge, which is likely to be somehow in connection with the poor prediction.
The reason of the discrepancy of the prediction by
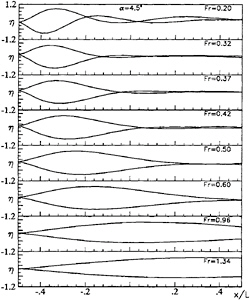
Figure 11: Wave profile along the plate for incresing Froude number (top to bottom). Normalized wave height η=h/(αFr), α=4.5°. Navier-Stokes simulation: two-block O-O grid 40×24×16.
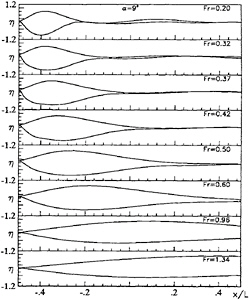
Figure 12: Wave profile along the plate for incresing Froude number (top to bottom). Normalized wave height η=h/(αFr), α=9.0°. Navier-Stokes simulation: two-block O-O grid 40×24×16.
means of the inviscid model with respect to the experiments and to the Navier-Stokes calculation is not clear at the present stage. In more details, the gap between the two predictions seems not to be due to the separation bubble at the leading edge, otherwise the same problem would be observed when computing double model flows. Moreover, it is unlikely to be caused by geometrical linearization of the free surface, because the same condition has very little effects on the forces when applied to the Navier-Stokes calculation.
Therefore, a possible reason of such a behaviour must be sought in the nonlinear terms in the free surface boundary conditions, neglected in our inviscid computations. Another possible cause could be related to the Kutta condition imposed at the trailing edge. In fact, this condition implies continuity of the total pressure, and therefore it does not allow a free surface jump across the vortex layer. Future investigations will try to clarify the question.
References
[1] Baldwin, B.S., Lomax, H. “Thin Layer Approximation and Algebraic Model for Separated Turbulent Flows”, AIAA Paper 78–257, 1978.
[2] Bassanini P., Casciola C., Lancia M.R., Piva R., “A Boundary Integral Formulation for the Kinetic Field in Aerodynamics ”, Eur. J. Mech., B/Fluids, vol 10, 605–627, 1991; vol 11, 69–92, 1992.
[3] Belotserkovskii, S.M. ( 1969). “Calculation of the flow around wings of arbitrary planforms in a wide range of angles of attack”. NASA TT F-12.
[4] Brandt A., “Multigrid Techniques: 1984 Guide with Application to Fluid Dynamics ”, The Weizmann Institute of Science, Rehovot (Israel), 1984.
[5] Brard R., “A Vortex theories for bodies moving in water”, 9th Symp. on Naval Hydrodynamics, R.Brard and A.Castera Eds, Washington, U. S.Gov. Printing Office, 1187–1284.
[6] Burcher R.K., “The prediction of the manoeuvring characteristics of vessels” Phil. Trans. R. Soc. Lond., A, 334, 265–279, 1991.
[7] Lamar, J.E. ( 1974). “Extension of leading-edge suction analogy to wings with separated flow around the side edges at subsonic speeds”. NASA TR R-428.
[8] Landrini M., Campana E., “Wave and Forces about a Turning Flat Plate”, 10th Inter. Workshop on Water Waves and Floating Bodies, Oxford, UK, April 1995.
[9] Landrini M., Campana E., “Steady Waves and Forces about a Yawing Flat Plate”, INSEAN Tech. Report, Progr. Ricerca 1991–1993, area 3, July 1995. Also submitted to J. Ship Res.
[10] Maniar H., Newman J.N., Xű H., “Free surface effects on a yawed surface-piercing plate”, 18th Symp. on Naval Hydro., Ann Arbor, Michigan, 1990.
[11] Scholz, N. ( 1949) “Kraft un Druckverteilungmessungen an Tragflächen Kleiner Steckung”. Forsch. Ingenieurwes, Vol. 16, 3.
[12] van den Brug J.B., Beukelman W., Prins G.J., “Hydrodynamic forces on a surface piercing flat plate”, Rep. 325, Shipbuilding laboratory, Delft Univ. of Tech., 1971.
[13] Winter, H. “Flow phenomena on plates and airfoils of short span”. NACA Tech. Mem. No 798 ( 1936).

Figure 13: Numerical viscous simulation in subcritical (top, Fr=0.63) and supercritical (bottom, Fr=0.74) flow regime. Ar=1.0, α=6.°
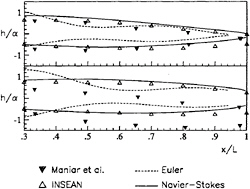
Figure 14: Wave profile along the plate at Fr=0.63 (top) and Fr=0.74 (bottom) for Ar=1.0 and α=6.0. Wave height is normalized by the incidence α.
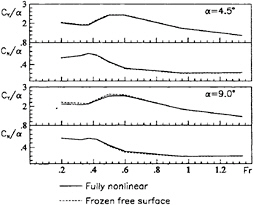
Figure 15: Ratio of the force normal to the plate and the yaw moment to the incidence as function of the Froude number. Comparison of two the Navier-Stokes simulations, one with standard free surface condition and with “frozen” free surface. Incidence 4.5 degrees (top) and 9.0 degrees(bottom).








