Generation Mechanisms and Sources of Vorticity Within a Spilling Breaking Wave
D.Dabiri, M.Gharib (California Institute of Technology, USA)
ABSTRACT
Sources of vorticity are examined for a spilling breaking wave. Through the use of a honeycomb/screen section, spilling breaking waves are generated and examined. Two cases were studied. For the first case, based on the breaker height, the Reynolds and Froude numbers were 7370 and 2.04, respectively. The breaker is preceded by 1 mm wavelength capillary waves, with the largest amplitude to wavelength ratio equal to 0.18. For this case, it is found that the dominant source of vorticity flux is a viscous process, and is due to the deceleration of a thin layer of the surface fluid. Furthermore, a thin free surface fluid layer is found to precede wave breaking that moves at a faster speed with respect to the fluid directly beneath it and to the fluid bulk. For the second case, also based on the wave height, the Reynolds and Froude numbers were 1500 and 1.35, respectively. No breaking is observed for this case; rather a capillary-gravity wave is observed with 4 mm wavelength capillaries preceding the gravity wave. The largest amplitude to wavelength ratio of these capillary is 0.28. This case shows that capillary waves do not contribute to the vorticity flux, rather the only dominant source of the vorticity flux into the flow is the free surface fluid deceleration. Lastly, similar to case 1, a thin free-surface fluid layer, which moves faster than the fluid beneath it and to the fluid bulk is found preceding the capillary-gravity wave.
1.
INTRODUCTION
Breaking waves are a phenomena quite common in nature. Historically, breakers have been categorized as either spilling breakers, where the water spills down the front face of the wave, and plunging breakers, where a jet emanating through the water crest falls into the base of the wave. The most commonly occurring breakers are spilling breaking waves which occur mostly in deep ocean waters. These spilling breakers, known as white caps, are responsible for the most of the air/sea interactions, and consequently the air entrainment which is important for the life under the sea (1). Likewise, one can easily observe the wave breaking phenomena in shallow water hydraulic jumps or bow and stern waves of boats. One important aspect of wave breaking is the subsequent spray formation and air entrainment in the form of bubbles which can be important in terms of ship wake signatures.
It is not clear whether the breaking process or bubble entrainment has any connection to the near surface turbulence or vorticity field. However, it is known that the onset of spilling is connected to the near surface vorticity field as well as the dynamic characteristics of the near surface shear layers (2, 3). In this respect, studies of near surface shear layers or vorticity fields and their sources is important to the understanding of the breaking process.
Several investigators have contributed to our basic understanding of spilling breaking waves. Elementary models showed breaking as laminar flow suddenly erupting into a breaker, where the breaker was initially modeled as a roller residing over the front face of a wave. However, Banner and Phillips (2), being the first to experimentally study the spilling breaking wave, showed that there exists a turbulent wake beneath the spilling breaker which extended downstream beyond the breaker, even though the flow remains highly laminar and steady prior to breaking. Peregrine and Svendson (4), after a series of experiments, suggested that it may be best to model the whole region beneath the spilling breaking wave as a turbulent region, rather than a roller residing over a wave. Battjes and Sakai (5) used a hydrofoil to induce spilling breakers, and obtained velocity profiles at various stations downstream of the hydrofoil. They determined that the turbulent wake downstream of the separation at the surface is self-preserving, indicating the possible existence of a shear layer. Tulin and Cointe (3, 6), present a detailed and comprehensive theory of steady wave breaking. Their model also presents the breaker as a stagnant eddy held in place over the front face of the wave. These and further results were then compared with experimental work performed by Duncan (7, 8) and found to agree quite well. In their most recent work, Duncan and Philomin (9) show some of the features associated with the development of spilling breaking waves. Finally, using the Particle Image Velocimetry (PIV) technique, Lin and Rockwell (10) were able to map the flow field directly beneath the spilling breaker, and were therefore able to show the existence of a shear layer beneath the breaking wave. Through further study, they were also able to characterize the evolution of wave breaking (11).
Thus, once organized vorticity was observed within the breaker, the question arose, where does this vorticity come from? Banner and Phillips suggest that “incipient breaking in a steady wave train is characterized by the occurrence of stagnation points at wave crests, but not necessarily by discontinuities in slope”. Longuet-Higgins (12) predicts that parasitic capillaries seen on the forward slope of gravity waves contribute significantly to
the vorticity seen in the crest roller. After a series of analyses, he shows that due to surface curvature, there exists a Stokes layer δ=(2v/γ)2, where v is the kinematic viscosity, and γ is the radian frequency of the wave, within which vorticity is generated, and beyond which vorticity escapes and is ω≈2(aκ)2γ, where a is the wave amplitude, κ is the wave number, and aκ describes the wave steepness. After detailed observations, Lin and Rockwell (10, 11) conclude that the sharp surface curvature serves as a source of vorticity, thereby giving rise to a separated mixing layer. They also observe that the region between the free surface and the mixing layer contains vorticity levels which are small compared with the mixing layer itself. Lastly, Hornung, et. al. (13) suggest that the substantial vorticity seen downstream of a hydraulic jump is due to the entrainment of bubbles during breaking. This was further explained by suggesting that the circulation around a loop, drawn directly beneath the free surface on oneside and stretching into the fluid bulk on all other sides such that the loop incorporates a bubble, is non-zero. Furthermore, they also suggest that the entrainment of vorticity is also connected to how the circulation loop is drawn.
It is therefore the purpose of this paper to shed some light on the origins of the source of vorticity seen within a spilling breaking wave. Specifically, the questions that will be answered are a) What is the source of the vorticity seen beneath and downstream of the breaker? b) Do capillary waves contribute to the vorticity? c) Do we need large breaking and therefore air entrainment in order to generate vorticity?
2.
EXPERIMENTAL SET-UP
2.1
The test facility
In order to answer these questions, a series of spilling wave breaking experiments were performed in a closed-loop water tunnel facility at CALTECH. The water tunnel has a contraction ratio of 4:1, with a 15.2× 15.2×61 cm3 test section. Previous approaches for generating spilling breaking waves have been to situate a hydrofoil located at some distance below the water level in a water tunnel. This caused the fluid above the
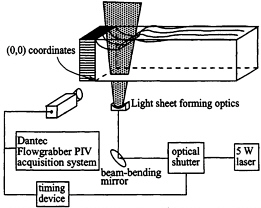
Figure 2. Image acquisition set-up.
hydrofoil to accelerate, and therefore generate spilling breaking waves. For the present experiments, an original technique was devised to generate spilling breaking waves. A 15.2×15.2×2.54 cm3 honeycomb section with a screen is placed at the beginning of the test section, where the honeycomb straws are 2.3 mm in diameter, and the wire screen is 50 mesh/inch stainless steel (see figure 1). Due to the pressure drop across the honeycomb/screen section, the fluid is accelerated to a maximum velocity, while dropping in height, and thereby generating spilling breaking waves.
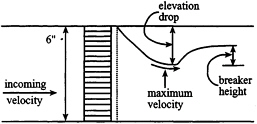
Figure 1. Wave breaking experimental set-up (not to scale).
2.2
The DPIV set-up and acquisition system
Figure 2 shows a schematic for the experimental setup for data acquisition. The flow is seeded with 14 +/– 5 micrometer silver-coated hollow glass spheres with a specific gravity of 1.4 g/cm3. Through a series of optics and mirrors, a laser light sheet with a maximum thickness of 1 millimeter is generated. This light sheet is then set parallel to the flow direction allowing the wave to be viewed before, during, and after breaking. The Dantec Flowgrabber DPIV system is used to record images onto a laser disk, which are subsequently digitized onto the hard disk. The Dantec Flowgrabber DPIV system is based on the cross-correlation technique. Therefore, images are exposed only once and are recorded at 30 frames per second. For analysis, a small

Figure 2. Image acquisition set-up.
interrogation window uniformly steps through the same locations within sequential pairs of images, performing a cross-correlation analysis at each location. Finally, a guassian curve-fit is used to obtain sub-pixel accuracy of the cross-correlation peak. Once this is done at all locations within the image pairs, a displacement field in pixel values is obtained. By calibrating the pixels to spatial values, and knowing the time difference between exposures, the velocity field can be obtained. A more detailed description of the cross-correlation technique used here can be found in Willert and Gharib (14). Unfortunately, previous cross-correlating hardware limited the technique to slow flows, since each image
could only be exposed at the same location within the frame, as shown in the second timing diagram of figure 3. Therefore, the pulse separation, Δt, was always limited to 1/30 second, limiting this approach to maximum velocities of ~10 cm/s for typical applications. However, the present modified system used for the present experiments is capable of exposing full-frame pulsed images at any point within the frame.
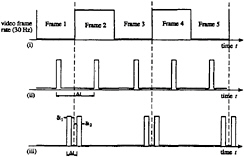
Figure 3. High speed cross-correlation DPIV timing diagram in relation to conventional cross-correlation DPIV timing diagram, (i) shows the frame rate of the video camera, (ii) shows the pulsed exposure of CCD camera for typical cameras, (iii) shows the pulsed exposure capability of the Dantec Flowgrabber camera.
Therefore, it is possible to expose the first image of the cross-correlating pairs towards its very end, while exposing the second image of the cross-correlating pairs towards its very beginning, as shown in (iii) of figure 3. Consequently, this allows for very short pulse separations between two image pairs, denoted by Δt in (iii) of figure 3, thereby making cross-correlation DPIV measurements possible at high-speeds. For the present experiment, δt1=δt2=150 microseconds, and Δt=200 microseconds. The typical field of view is 2.5×1.8 cm2. This area is digitized at 768×480 pixels2, and processed with an interrogating window size of 32×32 pixels2 with a step size of 16×16 pixels2 (50% window overlap). Particles images are 28.8 +/– .5 micrometers. The uncertainties are 1.4% in the velocities and 3.9% in the vorticities.
2.3
Free surface treatment of the DPIV images
The acquired images have reflections over the free surface that may affect the DPIV processing and result in erroneous velocity results. It is therefore imperative to treat the image area above the free surface. First, the image area above and including the free surface is replaced with a constant value equal to the image background of the fluid beneath the free surface. Then DPIV is performed on these images. Since the area above the free surface has no particles, the cross-correlation produces a zero shift. Interrogation windows which incorporate part of the image above the free surface and part below the free surface will therefore produce cross-correlation peaks that are due only to particles below the free surface. For these windows, results are only considered valid when the windows' center is either at or below the free surface. If the vorticity were to be calculated from these vector fields, an artificial shear layer would be generated at the free surface. Therefore, in order to minimize this effect, the no-shear boundary condition is applied at the free surface. All vectors above the last valid vector within a column are replaced by that vector for each column within the velocity field. Then vorticity is calculated. Since there are only velocity gradients in the x-direction above the free surface, only artificial vertical contours will be generated above the free surface in the vorticity plots, while accurate vorticity contours will be generated below the surface. Details concerning this approach will be published in a separate paper.
3.
RESULTS & DISCUSSION
Two sets of experiments were done in order to answer the questions posed in the Introduction. The first set was done at higher Reynolds and Froude numbers.
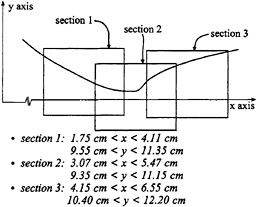
Figure 4. Imaged areas within higher Froude number spilling wave (not to scale).
Though very informative, this set of results produced capillary waves which were too, and therefore, were unable to ascertain the role of capillary waves in the flux of vorticity. Therefore a second set of experiments were done at lower Reynolds and Froude numbers to produce larger capillary waves, in order to determine their role in the vorticity flux.
3.1
Case 1: Higher Froude & Reynolds numbers
For this case, the incoming velocity into the grid is 24.6 cm/s. Due to the pressure drop across the honeycomb/screen section, the fluid accelerates to a
maximum velocity of 67 cm/s, while dropping in height by 4.2 cm ( figure 1). Breaking occurs at the point when the fluid elevation sharply rises. The breaker rises to a maximum height of 1.1 cm (figure 1). Based on the velocity at the point immediately prior to breaking and the breaker height, the Reynolds and Froude numbers are 7370 and 2.04, respectively. For this case, three regions shown in figure 4 are interrogated. Section 1 interrogates the wave region such that breaking occurs at the far right of the imaged area. Section 2 interrogates the wave such that breaking occurs at the middle of the imaged area. Lastly, section 3 interrogates the wave such that breaking occurs at the left of the imaged area.
3.1.1
Velocity and vorticity fields
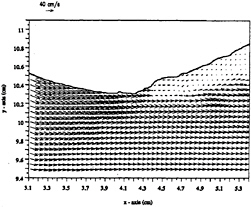
The velocity and vorticity fields for case 1 are plotted in figures 5, 6, and 8 through 13. The vectors within the velocity fields show the magnitude and direction of the velocity vectors throughout each of the three sections. For the vorticity plots, positive vorticity are shown by solid lines while negative vorticity are shown by dashed lines. The capillaries preceding spilling wave breaking are ≤1 mm in wavelength, and were too small to produce results that clearly determine the role of the capillaries in vorticity production. Yet, the raw images do show that the amplitude (crest-to-trough height) to wavelength ratio is ~.18. These capillaries correspond to a calculated phase speed of 68.7 cm/s. It therefore becomes obvious that the phase speed has matched the velocity just prior to wave breaking, thus exciting these capillaries (15, 16).
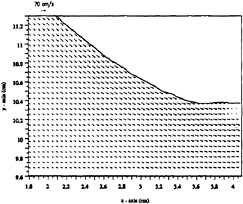
Figure 5. Vector field of section 1 of case 1.
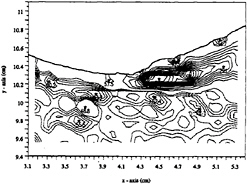
Figures 5, 6 show the velocity and vorticity field at section 1. The velocity field shows high velocities, except for a small region just beneath the free surface at 3.9 cm downstream from the grid, where the velocities are almost negligible. The vorticity field shows that the fluid mostly contains negative vorticity except for a small region just below the surface between 3.7 and 4.0 cm downstream from the grid which contains positive vorticity. Note that upstream from this positive
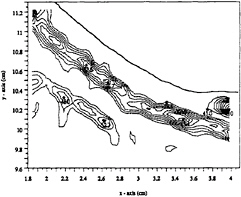
Figure 6. Vorticity field of section 1 of case 1. The negative contours (dashed lines) are in increments of 10 1/s while the positive contours (solid lines) are in increments of 40 1/s.
vorticity, the fluid directly beneath the free surface for a depth of 0.2 cm is almost vorticity-free. Furthermore, the vorticity field also shows the existence of a negative vorticity layer located 0.3 cm below the free surface, which exists directly below the vorticity-free layer, and has a thickness of ~0.3 cm. The negative vorticity layer starts upstream, extends downstream up to the positive vorticity region located at 3.68 cm, and continues further downstream, but below the positive vorticity layer.

Figure 7. Shadowgraph for case 1. Flow is from left to right. “a” shows the capillaries, while “b” shows the boundary at which wave breaking initiates
The shadowgraph for section 2 is shown in figure 7, where the flow is from left to right. The capillary waves preceding wave breaking are clearly seen and are shown by “a”. The beginning of breaking is
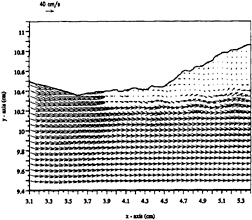
Figure 8. Vector field of section 2 of case 1.
shown by the line labeled “b”, and finally spilling breaking is seen to the right of “b”. The shadowgraph shows that the breaker free surface is deformed
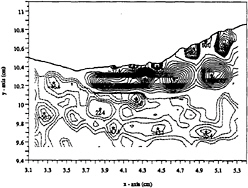
Figure 9. Vorticity field of section 2 of case 1. The negative contours (dashed lines) are in increments of 10 1/s while the positive contours (solid lines) are in increments of 40 1/s.
non-uniformly. This is due to the turbulent zone directly beneath the breaker, the existence of which will be shown below. Figures 8 through 11 show the velocity and vorticity fields at section 2 for two different times, with a time difference of .267 seconds. The vector plots show that directly beneath the breaker the velocities are quite small with respect to the rest of the flow. This is due to the spilling on its front surface, thus, creating the spilling breaker, and thus a turbulent region beneath the breaker. Furthermore, note that for both these cases, the higher-velocity free surface layers directly beneath the free
surface and upstream of the positive vorticity layer are also evident. Also, the negative vorticity layer which was shown to exist beneath the free surface higher-velocity layer in section 1 still continues further downstream beneath the positive vorticity layer. Also,
the fully developed positive vorticity layer which was initially seen in section 1 is captured in figures 9 and 11, and seen to convect downstream. This positive vorticity layer, however, does not separate into a shear layer until the free surface sharply curves upwards. Note that there are also areas of negative vorticity at the free surface that are not as strong in magnitude as those in the mixing
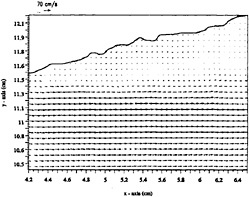
Figure 12. Vector field of section 3 of case 1.
layer. Upon comparison of the flow of figures 9 and 11, it is seen that the positive vorticity shear layer origin has been displaced by 0.5 cm in the x-direction. In fact, after examining several minutes of the flow in detail, it became evident that this “breathing” effect is quite persistent yet erratic in amplitude, with an oscillation
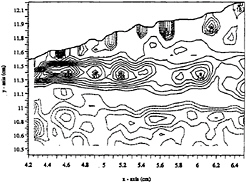
Figure 13. Vorticity field of section 3 of case 1. The negative contours (dashed lines) are in increments of 10 1/s while the positive contours (solid lines) are in increments of 40 1/s.
frequency of ~3.75 Hz. It was initially believed that this frequency might be the shedding frequency. Figure 9 shows the necessary parameters to determine this frequency. The convective velocity of the rollers in the shear layer is about the average of the velocity across the shear layer, or ~33.5 cm/s. The average spacing between the rollers is .35 cm, resulting in a shedding frequency of (33.5 (cm/s)/.35 cm) ~96 Hz. Finally, figures 12, 13 show the velocity and vorticity field associated with section 3. The vorticity field shows the persistence of the shear layer beneath the breaker. It is also interesting to note that even though the flow between the shear layer and the free surface is turbulent, its vorticity field is quite weak with respect to the vorticity within the shear layer. This is in fact consistent with the observations of Lin and Rockwell.
3.1.2
Sources of Vorticity
As has been seen by the previously mentioned investigators and shown in the present velocity and vorticity fields, almost irrotational flow, immediately after breaking, becomes highly rotational.
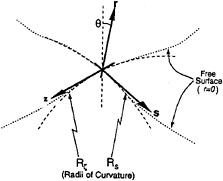
Figure 14. The natural curvilinear orthogonal coordinates. r is the unit vector perpendicular to the free surface, s is the unit vector parallel to the free surface, and perpendicular to r, and z is the unit vector parallel to the free surface and perpendicular to s and r.
In order to understand the origin of this vorticity, one must first look at the terms which contribute to sources of vorticity. The vorticity flux of surface-parallel vorticity through the surface given in natural curvilinear orthogonal coordinates is (17, 18, 19):
(1)
where v is the kinematic viscosity, ωz is the surface-parallel vorticity, us is the velocity parallel to the free surface, ur is the velocity normal to the free surface, ρ is the fluid density, P is the pressure, and θ is the angle of the surface with respect to the gravity vector.
Figure 9 shows the system of coordinates used for the equation shown above. For the steady breaker,
(2)
through time. Therefore
(3)
Likewise, the pressure along the free surface is constant. Therefore,
(4)
Furthermore,
|gcosθ|≤|g|=981 cm/s2 (5)
Therefore, the dominant terms contributing to the vorticity flux are the gravity term and the deceleration term. Equation (1) thus reduces to:
(6)
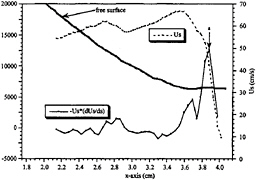
Figure 15. The free surface velocity and deceleration for section 1 of the higher Froude number case. The vorticity flux is shown on the left axis, while the velocity scale is shown on the right axis. Marker “a” at 3.84 cm shows the position of the maximum deceleration, and therefore flux of vorticity into the flow.
3.1.3
Experimental observations of the sources of vorticity
As shown in the previous section, in order to understand the behavior of the vorticity flux, one must first examine the behavior of the deceleration and the gravity term. Figure 15 shows the deceleration and the surface velocity for section 1. The deceleration shows a strong peak at 3.84 cm from origin. This coincides with the strong generation of positive vorticity seen in figure 6. The velocity curve shows that the velocity rapidly decreases after 3.5 cm from the origin. However, the fluid does not approach the stagnation point until at least 0.15 cm farther downstream from the peak. Figure 16 shows the deceleration and the surface velocity for section 2. The deceleration reaches a peak at 3.75 cm from the origin, shown by marker “a”. This coincides with the strong generation of positive vorticity seen in figure 9. The free-surface velocity curve shows that the fluid reaches a stagnation point at 4.58 cm shown by marker “b”, 0.83 cm downstream from the vorticity flux peak. Consequently, it is important to realize that the generation of vorticity does not coincide with the stagnation point. Furthermore, the initiation of wave breaking does not contribute to the positive vorticity generation.
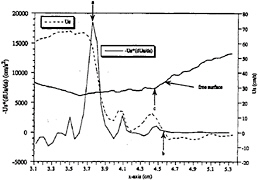
Figure 16. The free surface velocity and deceleration for section 2 of the higher Froude number case. The vorticity flux is shown on the left axis, while the velocity scale is shown on the right axis. Marker “a” at 3.75 cm shows the position of the maximum deceleration, and therefore flux of vorticity into the flow. Marker “b” at 4.58 cm shows the stagnation point of the free surface fluid, and marker “c” at 4.47 cm shows initiation of wave breaking observed visually.
This can be seen by observing that the vorticity is generated 3.75 cm from the honeycomb/screen section, while visually observed breaking occurs at 4.47 cm, shown by marker “c”. Figure 17 shows the deceleration and the surface velocity for section 2 at 0.267 seconds
later with respect to figure 16. The deceleration reaches its peak at 4.25 cm from the origin, shown by marker “a”, while the fluid stagnates at 4.4 cm, shown by marker “b”. Therefore, as in the previous figure, the strong generation of vorticity represented by the deceleration of the free-surface fluid coincides with the appearance of strong positive vorticity. Curiously, figure 17 seems to indicate that the source of vorticity might be the sharp curvature of the free surface due to breaking, shown by marker “ c” at 4.35, since vorticity generation and the sharp free surface curvature coincide. However, this coincidence is due solely to the “breathing ” effect mentioned earlier where the positive vorticity layer oscillates at a lower frequency to and from the sharp free surface curvature. Once again, it should be emphasized that figure 16 clearly shows that the source of vorticity is not due to the free surface's sharp curvature, but due to the deceleration term shown in equation 6. It should be pointed out, however, that perhaps the best indication of breaking is the occurrence of the stagnation points shown by markers “b” in figures 13 and 17.
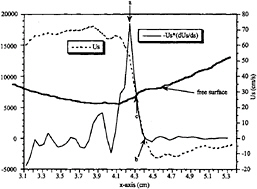
Figure 17. The free surface velocity and deceleration for section 2 at 0.267 seconds after that shown in figure 16. The vorticity flux is shown on the left axis, while the velocity scale is shown on the right axis. Marker “a” at 4.25 cm shows the position of the maximum deceleration, and therefore flux of vorticity into the flow. Marker “b” at 4.4 cm shows the stagnation point of the free surface fluid, and marker “c” at 4.35 cm shows initiation of wave breaking observed visually.
For both these cases, even though the vorticity flux peaks fluctuate back and forth with respect to breaking, the stagnation points are consistently within 0.1 cm of breaking, thus verifying the observations of Banner and Phillips. Finally, figure 18 shows the deceleration and the velocity profiles shown for section 3. This plot does not show any strong peaks as in the previous figures, since vorticity is not generated, rather convected downstream. Thus, the important point to realize in figures 15 through 17 is that given equation 6, the dominant contributing term to the vorticity flux is the deceleration term, which is of the order of 20,000 cm/s2, while the gravity term, which can be no greater than 981 cm/s2, is negligible with respect to the deceleration term.
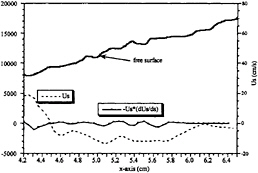
Figure 18. The free surface velocity and deceleration for section 3 for the higher Froude number case. The vorticity flux is shown on the left axis, while the velocity scale is shown on the right axis. Note that in this case, there are no outstanding peaks, since there are no fluxes of vorticity at this section.
Up to present, it has been shown that the flux of vorticity into the flow is due primarily to viscous effects. However, it can be argued that perhaps the vorticity flux is due to the velocity difference across the shear layer, thus making the vorticity flux an inviscid effect. Further reflection, however, can resolve this issue. The reduced vorticity flux equation derived earlier is shown below for convenience:
(7)
This equation, evaluated at the free surface, specifically shows that the source of vorticity is from the free surface, and that its flux from the free surface to the fluid, although equal to the free surface fluid deceleration, is entirely a viscous process. However, the free surface fluid not only decelerates with respect to the free surface fluid upstream of itself, but also with respect to fluid directly beneath it, thus creating a sharp velocity gradient, or “slip velocity”.
Figure 19 shows several velocity profiles which are perpendicular to the free surface at section 2 of case 1, corresponding figures 8, and 9. These velocity profiles are from various x-locations about x=3.7 cm, illustrating the large velocity gradient, or “slip velocity” directly
beneath the free surface. It is this “slip velocity” which is the origin of the shear layer evident in figures 9, 11, and
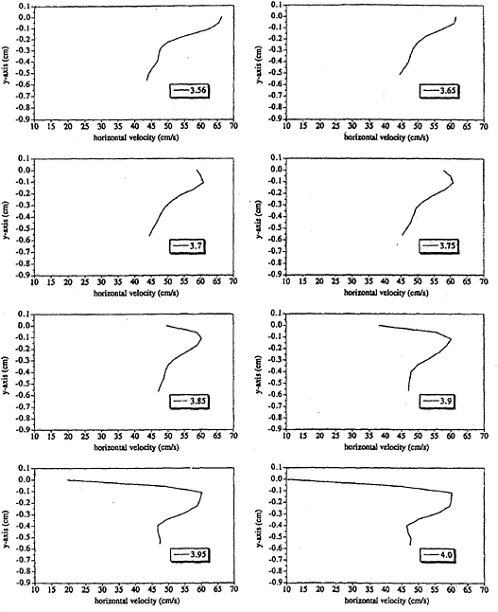
Figure 19. Velocity profiles taken from section 1 for case 1 at different x-locations. The profiles are perpendicular to the free surface, and the stated x-locations are x-locations of the free surface. The origin on the y-axis indicates the free surface.
13. It can therefore be concluded that the free surface deceleration not only
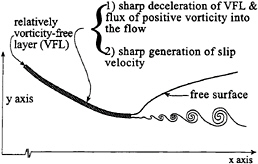
Figure 20. Diagram demonstrating the process of flux of vorticity into the flow.. The vorticity free layer decelerates sharply, introducing a high flux of vorticity into the flow, and simultaneously producing a sharp slip velocity which then grows into the shear layer seen beneath spilling breaker waves. (Drawing not to scale)
produces a vorticity flux into the flow through a diffusive process, but in doing so, simultaneously generates a sharp slip velocity which grows into a shear layer, convecting the vorticity downstream which has been fluxed into the fluid from the free surface (see figure 20).
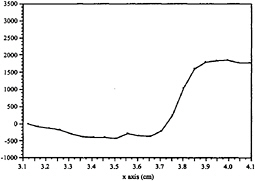
Figure 21. The running integral of the viscous vorticity flux of section 2.
This can also be seen by realizing that the free surface fluid decelerates to a stagnation point. Therefore, the vorticity must be fluxed deeper into the fluid, beyond the stagnation region, so that it can be convected downstream through the shear layer. A good check of the above analysis is to first calculate the net vorticity flux from the free surface into the fluid bulk by integrating the fluid deceleration at the free surface; second, calculate the convected vorticity flux by integrating the vorticity flux in the y-direction for each x-location; and finally show that the vorticity fluxed into the flow is equal to the vorticity being convected through the flow.
Figure 21 shows the integrated viscous vorticity for section 2, corresponding to figures 8, 9 and figure 16. Note that there is a sharp jump at 3.65 cm indicating a large injection of vorticity into the flow. The total jump is ~2250 cm2/s2. Beyond this injection, the level of integrated vorticity flux remains constant, indicating that there is no more vorticity flux from the free surface into the fluid, rather convection of the existing vorticity downstream.
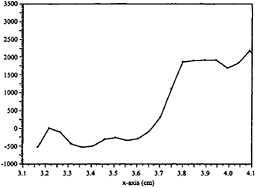
Figure 22. The integrated connective vorticity flux for section 2.
Figure 22 shows the integrated convected vorticity flux for section 2 corresponding to figures 8, 9 and figure 16. Also seen is a sharp jump of vorticity flux at 3.6 cm indicating a large injection of vorticity into the flow. The total jump is also ~2250 cm2/s2. Thus, the integral convective flux value is almost identical to the jump value found for the viscous flux integration. This clearly confirms that the vorticity is fluxed into the flow from the free surface, and is convected downstream by the shear layer, without the need to break, or entrain air into the fluid.
3.2
Case 2: Lower Froude & Reynolds numbers
For the second case, the incoming velocity into the grid is 17 cm/s. Due to the pressure drop across the honeycomb/screen section, the fluid accelerates to a maximum velocity of 30 cm/s. For this case, instead of the occurrence of breaking, a capillary-gravity wave is seen. The shadowgraph for this case is shown in figure 23, where the flow is from left to right. The capillary waves preceding wave breaking are shown by “a”, and the gravity wave begins and continues after “b”. The
shadowgraph clearly shows the last capillary wave, as in case 1, thus indicating that breaking has not occurred.

Figure 23. Shadowgraph for case 2. The flow is left to right “a” shows the capillaries, while “b” shows the boundary at which the gravity wave initiates.
This will be further discussed below. Based on the velocity at the point immediately after the last capillary wave and the final fluid elevation after the last capillary wave, the Reynolds and Froude number are 1500 and 1.35, respectively. For this case, two regions are interrogated (figure 24). Section 1 interrogates the wave region such that capillaries are seen within the imaged area, while section 2 interrogates the wave such that the portion of the wave after the capillaries is seen in the imaged area. The physical dimensions of these sections are given in figure 24. The origin of these coordinates is the bottom right corner of the honeycomb/screen section.
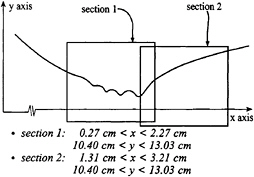
Figure 24. Imaged areas within higher Froude number spilling wave (not to scale).
3.2.1
Velocity and vorticity fields
The velocity and vorticity fields for this case are plotted in figures 25 through 28. The vectors within the velocity fields show the magnitude and direction of the velocity vectors throughout each of the three sections. For the vorticity plots, positive vorticity are shown by solid lines while negative vorticity are shown by dashed lines. The capillaries preceding the gravity wave are 4 mm in wavelength, and therefore large enough to extract related velocity, vorticity, and flux information. The raw images further show that the amplitude (crest-to-trough height) to wavelength ratio is ~.28. These capillaries correspond to a phase speed of 35 cm/s since the maximum speed of the flow prior to the gravity wave is 30 cm/s. It is therefore evident that the phase speed has matched the velocity just prior to wave breaking, thus exciting the capillaries. Figures 25, 26 show the velocity and positive vorticity fields at section 1. The velocity field through the capillaries is fully attached despite the high curvature, thus resembling flow through a series of converging and diverging sections.
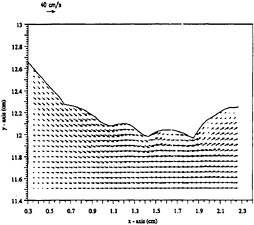
Figure 25. Vector field of section 1 of case 2.
Therefore, the turning of the flow through the capillaries generates a series of quasi-stationary negative and positive regions of vorticity that exists solely due to the curvature of the free surface (20). The velocity fields show that there are no separation of the flow from the free surface, or recirculation zones. Likewise, the vorticity plots show no separation of a shear layer as seen in the higher Froude number case, rather a positive shear layer is seen that bends upwards, following the contour of the gravity wave. This thus confirms that breaking has not occurred, as was shown in the shadowgraph for this case (figure 23). This positive vorticity layer is seen to be connected to the last positive vorticity situated under the last capillary trough just prior to the gravity wave. Lastly, a small region of negative vorticity is seen on the gravity wave, below the surface, and above the positive shear layer at x=1.95 cm,
indicating the existence of a stagnation point at that location.
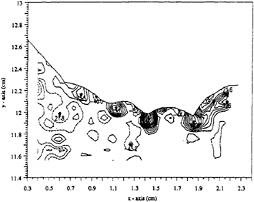
Figure 26. Vorticity field of section 1 of case 2. The negative contours (dashed lines) are in increments of 20 1/s while the positive contours (solid lines) are in increments of 20 1/s.
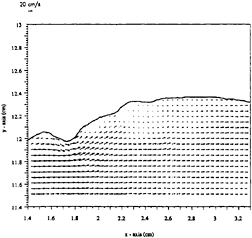
Figure 27. Vector field of section 2 of case 2.
Figures 27, and 28 show the velocity and positive vorticity field at section 2. The vorticity field from this section confirms that the positive shear layer seen within the gravity wave does not separate from the free surface, but follows its contour. Also, it is seen that this vorticity seems to be connected to the positive vorticity located beneath the trough of
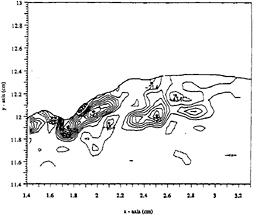
Figure 28. Vorticity field of section 2 of case 2. The negative contours (dashed lines) are in increments of 20 1/s while the positive contours (solid lines) are in increments of 20 1/s.
that last capillary prior to wave breaking. Lastly, the small region of negative vorticity, though very small is also present, and is located beneath the free surface and above the positive shear layer at x=1.85 cm.
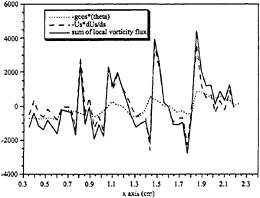
Figure 29. Contributing terms to the vorticity flux. The kinematic deceleration is shown by the dashed line, the gravity term by the dotted line, and their sum is shown by the solid line.
3.2.2
Experimental observations of the sources of vorticity
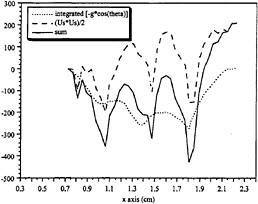
Since the flow is slower in this case, the capillaries are larger, and can therefore be resolved, thus determining the importance of the gravity term in equation 7. Figure 29 shows the deceleration, the gravity term, and their sum for section 1, and how these terms vary as the fluid flows through the capillaries. It is seen that the contribution to the vorticity flux is due mostly to the deceleration term and not the gravity term.
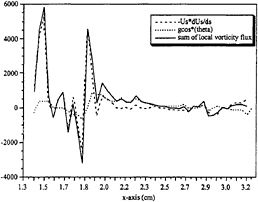
Figure 30. Contributing terms to the vorticity flux. The kinematic deceleration is shown by the dashed line, the gravity term by the dotted line and their sum is shown by the solid line.
Figure 30 shows the deceleration, the gravity term, and their sum for section 2. Likewise, the variations of these terms are seen with the passing of the fluid through the capillaries. Similarly, the contribution to the local vorticity flux is due mostly to the deceleration term and not the gravity term. Furthermore, note that the vorticity flux goes to zero after the last capillary, indicating that there is no flux of vorticity from the free surface beyond the capillaries. Also, the integrated vorticity flux due to the free surface acceleration, the gravity term, and their sum for section 1, corresponding to figure 25, is plotted starting from the first capillary and is shown in figure 30. The integrated viscous vorticity flux shows that after the last trough, the final value achieved is ~200 cm2/s2 at x=2.2 cm, while that achieved by the integrated vorticity flux due to the gravity term at that point is ~0 cm2/s2. Thus, the capillaries do not contribute to the generation of positive vorticity. The sum of these vorticity fluxes show that the total flux of positive vorticity is ~200 cm2/s2. Clearly, capillary waves are not major sources of positive vorticity generation, rather the dominant source of positive vorticity flux is the deceleration of the free surface.
Aside from the visual observations that breaking does not occur for this case, the mild injection of positive vorticity, of ~200 cm2/s2, into the flow is further indication that breaking has not occurred, and that the phenomena seen is a capillary-gravity wave.
4.
CONCLUSION
The sources of vorticity flux are examined for the spilling wave. For the steady spilling breaker, the vorticity flux equation shows contributions from two terms: the fluid deceleration term, and the gravity term. Furthermore, the present results reveal the underlying structure within a spilling breaker responsible for the vorticity flux into the flow. A thin higher-velocity free surface fluid layer decelerates, thus injecting a large amount of vorticity into the fluid bulk, entirely through a viscous process. Moreover, the vorticity injection due to the free surface deceleration is seen to dominate over the gravity-generated vorticity flux. As suggested by Banner and Phillips (2), the higher Froude number data presented indicates that the breaking of the steady spilling wave is characterized by the occurrence of the stagnation point rather than by the discontinuities of the slope due to the breaker. However, further study shows that the source of the viscous vorticity flux for a steady spilling wave is due to the deceleration of the surface fluid, rather than the free surface stagnation point or its sharp curvature, as Lin and Rockwell (10, 11) have suggested. Their setup shows that the transformation to a breaker is particularly abrupt, and the severe changes in the velocity field suggest that the region of deceleration, onset of wave breaking, and stagnation point location are extremely close together. This lead them to the conclusion that the process of flow separation, which is due to the sharp free surface curvature, is the apparent source of vorticity. Our setup, which allows for the clear
distinction between these regions, shows that the surface discontinuous point does not serve as a source of vorticity, but rather as point from which the vorticity separates into a shear layer.
Case 2, the lower Reynolds and Froude number case, shows that the capillary curvature provides a negligible contribution of the gravity term to the vorticity flux, and that the contribution is dominated by the deceleration term as the flow passes through the capillaries. The net flux of vorticity into the flow is shown to be one order of magnitude smaller than that seen in case 1, which would also serve as an indication of the separating shear layer in case 2. Also, the vorticity seen beneath the capillaries is due to the free surface curvature, and while remaining at the free surface, does not flux into the flow from the free surface. The vorticity is thus confined to a region within a thickness of the order of the capillary amplitude.
ACKNOWLEDGMENTS
This work is supported by URI research grant number N00014–92-J-1618 by the office of Naval Research. We gratefully acknowledge the insightful discussions with Dr. Longuet-Higgins, Dr. Doug Dommermuth, and Dr. Edwin Rood that lead to our insight into this topic.
REFERENCES
1. Banner, M.L. & Peregrine, D.H., “Wave Breaking in Deep Water,” Annu. Rev. fluid Mech., Vol. 25, 1993, pp. 373–397
2. Banner, M.L. & Phillips, O.M., “On the Incipient Breaking of Small Scale Waves,” J. Fluid Mech., Vol. 65, 1974, pp. 647–656.
3. Tulin, M.P. & Cointe, R., “A Theory of Spilling Breakers,” Proc. 16th Symp. Naval Hydrodynamics, Berkeley, pp. 93–105. National Academy Press, Washington D.C., 1986
4. Peregrine, D.H. & Svendson, I.A., “Spilling breakers, bores and hydraulic jumps,” Proc. 16th Coastal Engng. Conf: ASCE, Hamburg, Germany, 1978, pp. 540–550.
5. Battjes, J.A., & Sakai, T., “Velocity Field in a Steady Breaker,” J. Fluid Mech., Vol. 111, 1981, pp. 421–437.
6. Cointe, R. & Tulin, M., “A Theory of Steady Breakers,” J. Fluid Mech., Vol. 276, 1994, pp. 1–20.
7. Duncan, J.H. “An Experimental Investigation of Breaking Waves Produced by a Towed Hydrofoil,” Proc. R. Soc. Lond. A, Vol. 377, 1981, pp. 331–348.
8. Duncan, J.H., “The Breaking and Non-breaking Wave Resistance of Two-Dimensional Hydrofoil,” J. Fluid Mech., Vol. 126, 1983, pp. 507–520.
9. Duncan, J.H. & Philomin, V., “The Formation of Spilling Breaking Water Waves,” Phys. Fluids 6, Vol. 8, 1994, pp. 2558–2560.
10. Lin, J.C. & Rockwell, D., “Instantaneous Structure of a Breaking Wave,” Phys. Fluids, Vol. 6, 1994, pp. 2877–2879.
11. Lin, J.C. & Rockwell, D., “Evolution of a Quasi-Steady Breaking Wave,” J. Fluid Mech., Vol. 302 , 1995, pp. 29–44.
12. Longuet-Higgins, M.S., “Capillary Rollers and Bores.” J. Fluid Mech., Vol. 240, 1992, pp. 659–679.
13. Hornung, H.G.; Willert C.E. & Turner, S., “The Flow Field Downstream of a Hydraulic Jump,” J. Fluid Mech., Vol. 287, 1995, pp. 299–316.
14. Willert, C.E.; & Gharib, M., “Digital Particle Image Velocimetry,” Exp. Fluids, Vol. 10, 1991, pp. 181–193.
15. Cox, C.S., “Measurements of Slopes of High-Frequency Wind Waves,” J. Marine Res., Vol. 16, 1958, pp. 199–225.
16. Longuet-Higgins, M.S., “The Generation of Capillary Waves by Steep Gravity Waves,” J. Fluid Mech., Vol. 16, 1963, pp. 138–159.
17. Rood, E.P., “Interpreting Vortex Interactions with a Free Surface,” Trans. ASME I: J. Fluid Engng., Vol. 116, No. 1, 1994a, pp. 91–94.
18. Rood, E.P., “Free Surface Vorticity,” chapter 17 in Fluid Vortices, S.Green (ed.), Kluwer Academic Publishing, Norwell, MA 1993, in review.
19. Gharib, M. & Weigand, A., “Experimental Studies of Vortex Disconnection and Connection at a Free Surface,” Submitted to J. Fluid Mech., 1995
20. Longuet-Higgins, M.S., “Shear Instability in Spilling Breakers,” Proc. R. Soc. Lond. A, Vol. 446, 1994, pp. 399–409.