A Hybrid Approach to Capture Free-Surface and Viscous Effects for a Ship in a Channel
V.Bertram (Institut für Schiffbau, Germany) S.Ishikawa (Mitsubishi Heavy Industries, Japan)
Abstract
The flow about a Series-60 (CB=0.6) in a channel is computed by a new hybrid approach to capture most of the free-surface and viscous effects. First, a fully nonlinear wave resistance code computes the potential free-surface flow predicting the squat. Then the Reynolds-averaged Navier-Stokes equations are solved using the Baldwin-Lomax turbulence model. This step uses the squat predicted in the first step and the velocities at the lateral boundary of the RANSE domain, which spans only a small part of the channel width. The free-surface deformation is still neglected. An integrated propeller model interacts automatically with the RANSE computations. Results for flow details agree well with experiments for deep water and reproduce qualitatively all influences of the shallow water. Remaining differences are explained mainly by not capturing the free-surface deformation in the second step.
1.
Introduction
Consider a ship moving steadily ahead in the center of a channel of constant depth and width at a subcritical depth Froude number ![]() where U0 is the ship speed, g=9.81m/s2, and h the channel depth. The flow about the ship is steady except for turbulent fluctuations. It is considerably influenced by the shallow water. The influence of the channel walls is for usual channel geometries of secondary importance. Resistance and sinkage increase strongly near the critical depth Froude number, trim may change its sign. These global changes reflect changes in local flow details such as the wave pattern or the pressure distribution on the hull. The 20th ITTC [1] surveys measurements of global and local flow details for a Series-60 (CB=0.6) in a channel. A correct computational prediction of the pressures at channel bottom or the flow in the aft region of the ship is difficult, because both viscous and free-surface effects play an important role.
where U0 is the ship speed, g=9.81m/s2, and h the channel depth. The flow about the ship is steady except for turbulent fluctuations. It is considerably influenced by the shallow water. The influence of the channel walls is for usual channel geometries of secondary importance. Resistance and sinkage increase strongly near the critical depth Froude number, trim may change its sign. These global changes reflect changes in local flow details such as the wave pattern or the pressure distribution on the hull. The 20th ITTC [1] surveys measurements of global and local flow details for a Series-60 (CB=0.6) in a channel. A correct computational prediction of the pressures at channel bottom or the flow in the aft region of the ship is difficult, because both viscous and free-surface effects play an important role.
Classical approaches following e.g. Sretensky [2] or Inui [3] focus on the prediction of wave resistance and wave pattern. They usually do not capture e.g. the influence of squat on the flow field and neglect all viscous effects. We refer to Lap [4] and Tuck [5] for a more comprehensive review of classical and semi-empirical approaches. More recently, Rankine singularity methods (RSM) have been applied to compute shallow-water flows about ships, using SHIPFLOW [6], [7], [8], REVA in Nantes [9], [10], panel codes of the IfS in Hamburg [11] to [17], and Yasukawa's code [18]. Delhommeau [10], Bertram, [15] to [18], and Yasukawa [18] include also side-wall effects for ships in channels. Bai [19] used a finite-element approach for simplified hull forms. The Duisburg Model Basin VBD [20] investigates various methods including an finite-volume Euler solver around a river cargo vessel in a channel. All these methods still neglect viscosity. Linear RSM ([13, [18]) and methods based on volume grids ([19], [20]) do not account for squat. Thus they improve hardly results compared to classical methods in most cases.
Cura uses a different approach calculating the flow for a Series-60 in a channel, [21], [22]. His RANSE (Reynolds-averaged Navier-Stokes equations) solver captures viscous effects but neglects free-surface effects, namely squat and trim. Cura predicts the pressure at the channel bottom quite accurately and discovers an error in published measurements, [1], [23], which ”most probably explains previous differences between computations and […] measurements”. Remaining discrepancies are attributed to turbulence modelling, large grid cell distortion due to the wide, but shallow channel, and the neglect of free-surface effects.
We will present a combined numerical approach to capture most of these remaining effects. In a first step, a nonlinear Rankine source method will predict squat and trim for a ship in a channel. In a second step, a RANSE solver will use a grid for a ship fixed at the predicted squat and trim. The lateral extent of the grid will be considerably smaller than the actual channel. The velocities at the lateral boundary of the RANSE computational domain will be determined by the Rankine source code. However, the free-surface elevation will still be neglected assuming a flat undisturbed surface instead.
2.
Computational Procedure
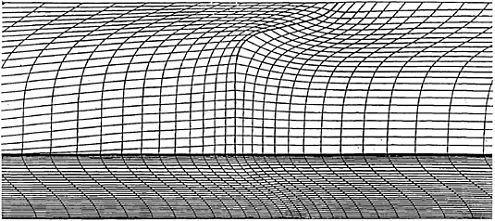
The flow is assumed to be symmetrical with respect to the hull center plane coinciding with the center plane of the channel. The problem is solved in two steps. In the first step, the inviscid free-surface flow in the channel is computed by a Rankine singularity method (RSM). Linear source panels are distributed above a finite section of the free surface. The panels are numerically evaluated by approximating them by a four-point source cluster, [24]. On the hull and the channel side wall, higher-order panels (parabolic in shape, linear in strength) are distributed. Mirror images of the sources at the channel bottom enforce that no water flows through the channel bottom. The nonlinear free-surface boundary condition is met in an iterative scheme that linearizes differences from arbitrary approximations of the potential and the wave elevation, Fig.1, [12]. The radiation and open-boundary conditions are enforced by shifting sources versus collocation points on the free surface. [25] gives more details on the method.
We describe now the automatic grid generation for the free-surface grid. The base 'wave length' is taken as ![]() The upstream end of the grid is 1.5 · max(0.4Lpp,λ) before FP for shallow water. (For infinite water, the factor is 1.0 instead of 1.5). The downstream end of the grid is max(0.6Lpp,λ) behind AP. The outer boundary in transverse direction BG is 0.35 of the grid length for unlimited flow, but taken at the channel wall (0.8L in our case) for a ship in a channel. The intended number of panels per wave length is 10. The intended number of panels in transverse direction is (BG–Δx)/(1.5Δx)+1, where Δx is the grid spacing in longitudinal direction. However, if the intended number of free-surface panels plus the number of hull panels exceeds 2500, the grid spacing in x- and y-direction is increased by the same factor until this condition is met. The innermost row of panels uses square panels, the rest of the panels is rectangular with a side ratio (Δy/Δx) of approximately 1.5. The panels follow a 'grid waterline'. This is the upper rim of the discretized ship (1.5m above CWL in our case) which is modified towards the ends to enforce entrance angles of less than 31°. The channel wall grid follows the free-surface grid in longitudinal direction. In vertical direction the number of panels is the next integer to (h–Δx)/(2Δx)+1, but at least two. The uppermost row uses square panels. The free-surface panels are desingularized by a distance of Δx.
The upstream end of the grid is 1.5 · max(0.4Lpp,λ) before FP for shallow water. (For infinite water, the factor is 1.0 instead of 1.5). The downstream end of the grid is max(0.6Lpp,λ) behind AP. The outer boundary in transverse direction BG is 0.35 of the grid length for unlimited flow, but taken at the channel wall (0.8L in our case) for a ship in a channel. The intended number of panels per wave length is 10. The intended number of panels in transverse direction is (BG–Δx)/(1.5Δx)+1, where Δx is the grid spacing in longitudinal direction. However, if the intended number of free-surface panels plus the number of hull panels exceeds 2500, the grid spacing in x- and y-direction is increased by the same factor until this condition is met. The innermost row of panels uses square panels, the rest of the panels is rectangular with a side ratio (Δy/Δx) of approximately 1.5. The panels follow a 'grid waterline'. This is the upper rim of the discretized ship (1.5m above CWL in our case) which is modified towards the ends to enforce entrance angles of less than 31°. The channel wall grid follows the free-surface grid in longitudinal direction. In vertical direction the number of panels is the next integer to (h–Δx)/(2Δx)+1, but at least two. The uppermost row uses square panels. The free-surface panels are desingularized by a distance of Δx.
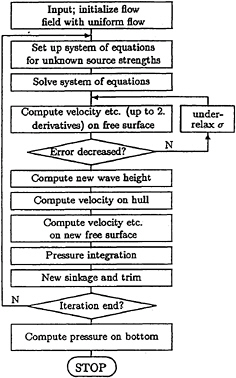
Fig. 1: Flow chart of iterative solution
In a second step, the viscous flow around the ship is solved. The ship is assumed fixed at the squat calculated in the first step. The deformation of the water surface is neglected and the water surface substituted by a flat symmetry plane. The computational domain does not extend in lateral direction to the channel walls. Instead, the inviscid velocities of the first step are taken as boundary condition on the lateral boundary. The RANSE solver is based on Kodama's method, [26]. It solves the continuity equation including a pseudo-compressibility term and the three momentum equations for incompressible turbu-
lent flows. These equations are discretized in space by cell-centered finite volumes. The inviscid fluxes are evaluated by a third-order upwind scheme (MUSCL) with the flux difference-splitting method. The viscous fluxes are determined by central differences. The algebraic Baldwin-Lomax model accounts for turbulence, [27]. [29] gives more details on the method.
The propeller effect is considered by applying an equivalent body force in the right-hand side of the RANSE. Our RANSE solver with propeller effect is based on Hinatsu's method, [29]. This considers the body force in both thrust direction and rotative direction. The propeller force distribution is estimated by Yamazaki 's [30] an infinite-blade propeller theory. The distribution obtained by this method depends on the propeller inflow and has to determined by an iterative procedure:
-
Solve the RANSE for the ship without propeller
-
Calculate the wake distribution at the propeller plane
-
Define the required propeller thrust as ship resistance minus corrective towing force
-
Calculate the propeller force distribution using a propeller program with inflow and required thrust (as computed above) as input data
-
Solve the RANSE with equivalent body forces
-
If the resistance is equal to the required thrust, end the calculation. If not, calculate the new propeller inflow by subtrating the propeller induced velocity from the wake distribution at the propeller plane and go back to step 3)
This cycle is actually performed every 10 outer iterations of the RANSE computation. No problems with convergence were ever observed.
An H-O type grid is generated using Kodama's implicit geometrical method, [31]. An initial algebraicly generated hull grid is modified so as to satisfy requirements of orthogonality, smoothness, clustering towards the ends, and minimum spacing. Grid lines are clustered towards bow and stern profiles in streamwise direction, and towards the hull in radial direction. Bow and stern profiles are followed by vertical grid lines avoiding the step curve approximation of Cura, [21], [22]. The horizontal lines are approximately orthogonal to the vertical grid lines, and also to both the bow and stern profiles.
3.
Test Case: Series-60
The method was applied to a Series-60 ship (CB=0.6, L=6.096m, λ=1:20). Results are compared to experimental data of the Duisburg Model Basin VBD. The lateral wall of the towing tank lies 0.8L from the center plane. Experiments were performed for water depth-to-draft ratios h/T=3.2, 2.0, 1.5, 1.2. We computed the cases given in Table I, Fig.2. We denote the case h/T=3.2 as 'deep' water, h/T=1.5 as ‘shallow' water.
Table I: Computed cases for Series-60
|
h/T |
Fn |
Fnh |
Rn |
|
3.2 |
0.15 |
0.363 |
7.0 · 106 |
|
1.5 |
0.15 |
0.530 |
7.0 · 106 |
|
3.2 |
0.16 |
0.387 |
7.5 · 106 |
|
1.5 |
0.16 |
0.565 |
7.5 · 106 |
|
3.2 |
0.18 |
0.436 |
8.4 · 106 |
|
1.5 |
0.18 |
0.636 |
8.4 · 106 |
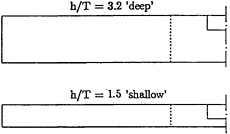
Fig. 2: Computed cases for Series-60 at Fn=0.15; dotted line RANSE grid boundary
503 elements discretized the hull up to a height of 0.23 T above the CWL, Fig.3. The free-surface grid extended 0.8L in lateral direction (to the channel wall), 0.6L ahead of FP and 0.5L behind AP. 96 · 19=1824 elements were used to discretize this area. This discretization resolve the wave pattern coarsely, but is deemed sufficient to capture effects relevant for squat and induced pressures. 96·2=192 elements were used to discretize the channel wall for h/T=1.5, 96 · 3=288 elements for h/T=3.2.
Figs.4 show the RANSE grid for h/T=1.5. The grid extended 0.5L ahead of FP and L behind AP. The lateral extent was 0.2L. 100·24·50=120000 cells were used in total. The computations assumed a kinematic viscosity of v=1.01 · 10–6m2/s and a water density of ρ=1000kg/m3.
4.
Resistance test simulations
Local flow details of the first-step RSM computation like wave pattern, Fig.5, pressure on hull, and wave profile showed no irregularities. Free-surface grid variations gave almost exactly the same results.
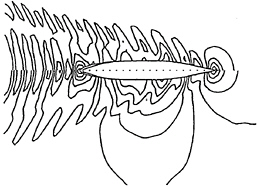
Fig. 5: Wave pattern for Fn=0.15 at h/T=3.2 (top) and h/T=1.5 (bottom)
Table II gives the computed and measured squat for Fn=0.15. The computations capture the squat well. Measurements of various towing tanks, [1], show considerable scatter of measured squat for h/T=1.5, ranging from ΔT/L=0.00236 to 0.00326. Our computed result of 0.00269 lies well within this bandwidth. The difference of 7% between measured (VBD) and computed squat may be due to instationary flow effects in the experiments (VBD in personal communication), but neglect of the boundary layer may also contribute.
Table II: Sinkage and trim (positive for bow immersion) for Series 60 at Fn=0.15
|
Fn=0.15 |
||||
|
experiment |
RSM |
|||
|
h/T |
ΔT/L |
θ |
ΔT/L |
θ |
|
3.2 |
0.00118 |
0.00050 |
0.00120 |
0.00040 |
|
1.5 |
0.00285 |
0.00083 |
0.00269 |
0.00087 |
|
Fn=0.16 |
||||
|
experiment |
RSM |
|||
|
h/T |
ΔT/L |
θ |
ΔT/L |
θ |
|
3.2 |
0.00139 |
0.00058 |
0.00135 |
0.00051 |
|
1.5 |
0.00348 |
0.00116 |
0.00326 |
0.00107 |
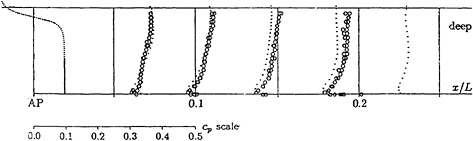
The pressure at the channel bottom is dominated by free-surface effects, namely the primary wave system with its long wave trough along the ship lengths. Towards the ends, the pressure at the channel bottom shows local maxima. The aft maximum is less pronounced due to viscous effects. RANSE and RSM solution are blended with RSM solutions taken between ±0.4L, RANSE solution otherwise. The two solutions coincide in an intermediate region so that the blended solution is smooth. The pressure on the channel bottom is captured well for 'deep water', Fig.6. For 'shallow water', the tendency is captured well including a local maximum amidships, Fig.7. The difference between experiments and computations is 7%. For comparison, linear results of the RSM code (first iterative step) are also given. The hybrid CFD approach improves both the prediction of the pressure minimum (due to the consideration of squat and local wave trough) and the aft pressure maximum (due to capturing viscous effects). We attribute the remaining differences to the underpredicted squat which in turn might be due to a not fully stationary flow in experiments.

Fig.6: Pressure coefficient CP along center line on channel bottom at Fn=0.15; h/T=3.206; experiments (·), hybrid CFD (•)
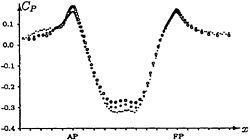
Fig.7: Pressure coefficient CP along center line on channel bottom at Fn=0.15; h/T=1.5; experiments (·), hybrid CFD (•), linear RSM (○)
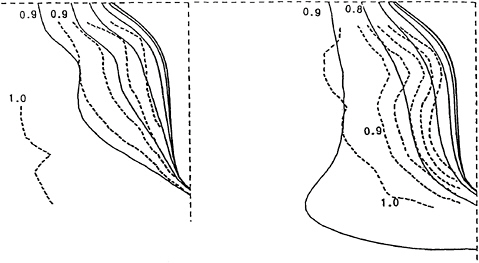
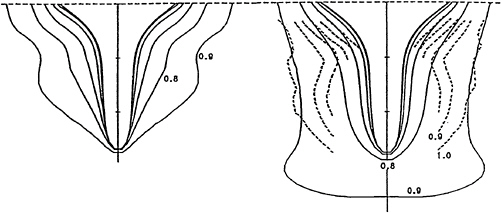
Fig.8 shows contour lines of the axial velocity for Fn=0.18, Rn=8.4 · 106. Unfortunately only very few data were measured close to the hull. Subsequently, the inner contour lines of the experimental results cannot be very reliable. The original plots, [1], [23], do not reflect the quality of the measured data due to a poor plotting procedure. We therefore plotted our own curves based on the data supplied by VBD. In this way we wanted to exclude differences due to the employed plotting algorithms. Experiments and computations agree well for h/T=3.2.
Shallow water strongly changes the experimental contour lines. They are inflated at the lower regime and get closer to the hull in the upper regime which makes their overall circumferential contour smoother. The computations capture this behaviour only qualitatively. The widening of the contour lines in the lower regime is overpredicted. Cura' s [21], [22] RANSE computations show the same effect. Cura suspected as reason for his discrepancies: ”The overprediction of widened contour lines in the lower regime is probably due to the neglected free-surface effects.
Especially the sinkage leads to higher blockage, thus to higher local velocities and contour lines closer to each other.” However, our results indicate that including the sinkage does not remove the discrepancies. Cura's results agree better with experiments than ours. Maybe the strong wave trough over large part of the ship increases the blockage, but we are surprised that this still effects the flow so far aft. Turbulence modelling is a popular scapegoat. But for such a slender hull, it should not have such a large impact on the contour lines. Cura uses a different turbulence model and his results are quite similar to ours. This indicates that differences are rather due to the physical model (neglect of free surface deformation) or differences between computational methods and experiments as such. Computations including the free-surface deformation and further model tests, preferably from other towing tanks or with larger model scales, might give more insight into this phenomenon. With the data presently available, we cannot explain the differences between computations and experiments completely.
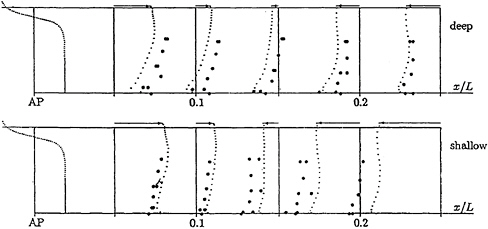
Fig.9a shows the computed pressure coefficient on 5 cross sections in the aftbody for Fn=0.16, Rn=7.5 · 106. (No experimental data were available for Fn=0.15). Shallow water induces strong low pressure over an extended region of the ship. The integral value of this effect is the increased squat. The three-dimensionality of the flow for deep water is shown by the curved pressure lines in the bilge region. Shallow water makes the flow rather two-dimensional. The pressures are nearly constant at each cross section. This agrees qualitatively well with all ITTC experiments, [1]. For deep water, experiments of VBD. and our computations show differences in the order of ΔCP=0.02. Various numerical tests produced only little differences in the computed results. We compared results for Fn=0.16, Rn=3.2 · 106 with experiments of the University of Iowa, [32]. The different Reynolds number has virtually no effect on the computational results, Fig.9b. Our results agree well with the Iowa experiments. The differences between the Iowa and VBD measurements, but also the differences between measurements on port and starboard for the VBD measurements alone, are an indication of the margin of uncertainty for the experimental results. Measuring pressure on the hull is difficult and no criticismn of the experimenters is implied. We just want to point out that in the aftbody apparently the computations are already within the margin of uncertainty of available experiments.
For shallow water, only VBD measurements are available. Agreement is good for the two aftmost sections. For the third section (x/L=0.15), the VBD measurements differ considerably between port and starboard. Computations agree well with measurements for one side. For the fourth and fifth section, the experimental pressures are noticably lower than computed pressures. This is to be expected: Our viscous computations capture a numerically predicted squat, but not the deformation of the water surface. The strong wave trough for shallow water gives an additional blockage effect over the central part of the ship that leads to higher velocities and lower pressures. To capture this effect, the RANSE grid generator would have to incorporate the wave elevation predicted by the RSM code. At present, our grid generator does not have this capability.
Integrating the pressures and shear stresses gives the resistance coefficient (without wave resistance) based on S0=L2/5.83. The RANSE computations integrated the pressure over the whole ship hull (including squat, excluding local wave deformation). The increase in resistance for shallow water is predicted correctly. However, the resistance is overestimated, Table III. The agreement is good for deep water, better than usually for fuller hulls, because the Series-60 is a slender hull with no flow separation in the aftbody. Subsequently the frictional resistance dominates and this is predicted relatively accurately by RANSE codes. We contribute the perfect agreement though to fortunate error cancellation. For shallow water, the overestimation in resistance is considerable. This is qualitatively expected. We neglect the deformation of the free surface in the viscous computation. This has two effects:
-
The actual wetted surface is smaller than the wetted surface in the computation.
-
The blockage effect is underpredicted. In reality the flow is faster, the boundary layer thinner.
A crude correction for the first effect is possible: We computed the actual wetted surface with the RSM
code. The ratio of the actual wetted surface to wetted surface assumed by the RANSE computation is 0.9945 for both water depths. So, this effect is not significant. Better quantitative agreement then requires a RANSE grid that follows the free surface deformation. This could be achieved either by a hybrid approach or by free-surface RANSE computations.
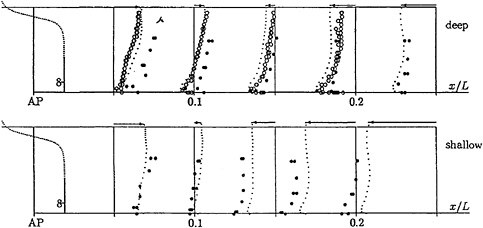
Fig. 11: Pressure distribution for propulsion test, Fn=0.16, • exp. VBD (Rn=7.5 · 106), ○ exp. Iowa (Rn=3.2 · 106), · CFD (Rn=7.5 · 106)
Table III: Computed (w/o wave resistance) and measured resistance coefficients
|
Fn |
Rn |
h/T=3.2 |
h/T=1.5 |
|
|
CFD |
0.15 |
7 · 106 |
3.86 · 10–3 |
5.79 · 10–3 |
|
Exp |
0.15 |
7 · 106 |
3.86 · 10–3 |
4.67 · 10–3 |
The employed turbulence model might also contribute considerably to the error. The Baldwin-Lomax model inherently assumes that there is only one maximum in the flow profile for the product of wall distance and magnitude of vorticity at that point. This assumption already requires some care for deep water cases, as more than one local maximum may appear, e.g. [33]. For shallow water, a second maximum definitely will appear close to the channel bottom. We confirm Graf who investigated the two-dimensional flow around barges on shallow water, [34]. Maybe the Baldwin-Lomax turbulence model is generally unsuited for flows between two walls. In any case, we share the wide consensus that CFD methods are not yet accurate enough to predict resistance with practical accuracy.
5.
Propulsion test simulations
The simulations for propulsion test required some assumptions, but as far as possible the conditions supplied by VBD were used: Table IV gives the propeller data used in the computations. The propulsion tests were performed for the ship self-propulsion point. A corrective towing force was applied based on ITTC-57 and CA=0.0002.
Fig. 10 shows the contour lines of the axial velocity for Fn=0.18, Rn=8.4 · 106. The qualitative effect of the propeller is captured as expected: The contour lines are getting closer to the hull compared to the resistance test, see Fig.8. At the considered station (5% before AP), the port/starboard asymmetric influence of the propeller is still very small. The quantitative agreement resp. disagreement between computed and measured contour lines is similar to the resistance test. Fig.11 shows the computed pressure coefficient on 5 cross sections in the aftbody for Fn=0.16, Rn=7.5 · 106. As the different Reynolds number was proven to have no significant effect for the resistance test, we plotted Iowa and VBD results this time in one figure. The star-board/port asymmetry of the pressure due to the propeller is at the considered stations negigibly small. So we plotted only the starboard computational results. The propeller accelerates the flow shifting the pressure generally to lower values. The computation not only reproduces this effect as expected, it also agrees well with experiments quantitatively. Only for the sections closer to amidships, the same differences as for the resistance test are apparent for the same reasons as discussed above.
Table IV: Propeller data (λ=1:20)
|
propeller diameter |
209.5mm |
|
boss ratio |
0.19 |
|
P/D |
1.04 |
|
Ae/A0 |
0.565 |
|
height over keel |
160mm |
|
position before AP |
1%L |
|
blades |
4 |
|
Blade Geometry |
|
|
r [m] |
chord length [m] |
|
0.021348 |
0.05060 |
|
0.032328 |
0.05714 |
|
0.041114 |
0.06136 |
|
0.051346 |
0.06486 |
|
0.062326 |
0.06649 |
|
0.073306 |
0.06510 |
|
0.083538 |
0.05969 |
|
0.095983 |
0.04388 |
|
0.099066 |
0.03460 |
|
0.104750 |
0.0 |
|
Propeller open-water data |
||
|
J |
KT |
KQ |
|
0.4 |
0.301 |
0.0481 |
|
0.5 |
0.263 |
0.0429 |
|
0.6 |
0.223 |
0.0373 |
|
1.09 |
0.0 |
|
6.
Conclusions
The hybrid approach computing first squat and potential flow field and then the viscous flow improves the quality of results and saves computational time for shallow water applications. A nonlinear potential flow code may be already sufficient for cases where only the pressure on the channel bottom is of interest. Discrepancies remain for the pressure on the hull in the middle section of the ship and the computed resistance. These discrepancies could be reduced by taking the free-surface deformation into account.
Acknowledgement
The research was performed during a stay of V.Bertram as a visiting, scientist of MHI R&D Center in Nagasaki sponsored by the German Research Association (DFG). The authors are grateful for the assistance of VBD, namely Dipl.-Ing. A.Gronarz, for updated data on measurements. We thank H.Sato for his assistance for the RANSE computations.
References
1. ITTC ( 1993), ”Report on cooperative experimental program in shallow water,” 20th Int. Towing Tank Conf., Resistance and Flow Committee, San Francisco
2. Sretensky, L.N. ( 1937), ”A theoretical investigation of wave resistance,” Joukovsky Central Institute for Aero-Hydrodynamics Rep. 319 (in Russian)
3. Inui, T. ( 1954), ”Wave-making resistance in shallow water sea and in restricted water with special reference to its discontinuities,” J. Soc. Nav. Arch. of Japan 76, pp. 1–10.
4. Lap, A. ( 1972), ”Ship resistance in shallow and restricted water,”, 13th Int. Towing Tank Conf., Appendix 5 to Report of Resistance Committee, Berlin/Hamburg
5. Tuck, E.O. ( 1978), ”Hydrodynamic problems of ships in restricted water,” Ann. Rev. Fluid Mech. 10, pp. 33–46.
6. Ni, S.Y. ( 1987), ”Higher order panel method for potential flows with linear or nonlinear free surface boundary conditions,” Ph.D. thesis, Chalmers Univ. of Technology, Sweden
7. Kim, K. and Choi, Y. ( 1993), ”A numerical calculation of free surface potential flow field and of ship wave resistance in shallow water by fully nonlinear wave theory,” 2nd Japan Korea Workshop, Osaka, pp. 111–120.
8. Kim, K., Choi, Y., Jansson, C., and Larsson, L. ( 1994), ”Linear and nonlinear calculations of the free surface potential flow around ships in shallow water,” 20th Symp. Naval Hydrodyn., Santa Barbara
9. Maissonneuve, J. and Delhommeau, G. ( 1991), ”A computer tool for solving the wave resistance problem for conventional and unconventional ships,” 3rd Int. Conf. CADMO, Key Biscaine
10. Delhommeau, G. ( 1993), ”Wave resistance code REVA,” 19th WEGEMT school on Num. Simulation of Hydrodyn., Nantes
11. Söding, H., Bertram, V., and Jensen, G. ( 1989), ”Numerical computation of squat and trim of ships in shallow water, ” STG-Yearbook 83, Springer, pp. 42–48. (in German)
12. Jensen, G., Bertram, V., and Söding, H. ( 1989), ”Ship wave-resistance computations,” 5th Int. Conf. Num. Ship Hydrodyn., Hiroshima, pp. 593–606.
13. Kux, J. and Müller, E. ( 1992), ”Shallow-water influence on ship flows demonstrated for a Series-60 ship, CB=0.6,” STG-Yearbook 86, Springer, pp. 367–389. (in German)
14. Bertram, V. ( 1994), ”Shallow water effects for SWATH ships,” 9th Int. Workshop Water Waves and Floating Bodies, Kuju
15. Zibell, H.G. and Bertram, V. ( 1994), ”Influence of the channel effect on resistance and flow field of a river cargo vessel,” Binnenschiffahrt 49/17, pp. 34–38. (in German)
16. Bertram, V. and Jensen, G. ( 1992), ”Side wall and shallow water influence on potential flow,” 8th Int. Workshop Water Waves and Floating Bodies, Val de Reuil
17. Bertram, V. and Yasukawa, H. ( 1995), ”Inviscid free-surface computations for a Series-60 in a channel,” 4th Symp. Nonlinear and Free-Surface Flows, Hiroshima, pp. 13–16.
18. Yasukawa, H. ( 1989), ”Calculation of the free surface flow around a ship in shallow water by Rankine source method,” 5th Int. Conf. Num. Ship Hydrodyn., Hiroshima, pp. 643–655.
19. Bai, K.J. ( 1977), ”A localized finite element method for steady three dimensional free surface flow problems,” 2nd Int. Conf. Num. Ship Hydrodyn., Berkeley, pp. 78–87.
20. Pagel, W.; Rieck, K.; Grollius, W.; Gronarz, A. ( 1995), ”Experimental and theortical-numerical flow investigations for river cargo ships,” VBD-Report 1366, Duisburg (in German)
21. Cura, A. ( 1994), ”Influence of shallow water on the flow around a slender ship hull, ” 15th Duisburg Koll. Schiffstechnik/Meerestechnik, Univ. Duisburg, pp. 78–96. (in German)
22. Cura, A. ( 1995), ”Influence of water depth on ship stern flows,” Ship Techn. Res. 42/4, pp. 193–197.
23. Binek, H., Ter Jung, G., and Müller, E.
( 1992), ”Resistance and flow characteristics of ships with CB=0.6 on shallow water,” VBD-Report 1320, Duisburg Model Basin, Duisburg, Germany (in German)
24. Bertram, V. ( 1990), ”Fulfilling open-boundary and radiation condition in free-surface problems using Rankine sources,” Ship Techn. Res. 37/2, pp. 47–52.
25. Hughes, M. and Bertram, V. ( 1995), ”A higher-order panel method for steady 3-d free-surface flows,” IfS-Report 558, Univ. Hamburg, Germany
26. Kodama, Y. ( 1992), ”Computation of ship's resistance using a NS solver with global conservation—Flat plate and Series 60 (Cb=0.6) hull,” J. Soc. Naval Arch. Japan 172, pp. 147–156.
27. Baldwin, B. and Lomax, H. ( 1978), ”Thin layer approximation and algebraic model for separated turbulent flows prediction code,” AIAA Paper 78–257
28. Ishikawa, S. ( 1994), ”Application of CFD to estimation of ship's viscous resistance—A series of full hull forms,” Trans. West-Japan Soc. of Naval Arch. 87, pp. 81–92.
29. Hinatsu, M.; Kodama, Y.; Fujisawa, J.; Ando, J. ( 1994), “Numerical simulation of flow around a ship hull including a propeller effect,” Trans. West-Japan Soc. Naval Arch. 88, pp. 1–12. (in Japanese)
30. Yamazaki, R. ( 1966), ”On the theory of screw propellers in non-uniform flows”, Memoirs of the Faculty of Engineering, Kyushu Univ., Vol 25/2
31. Kodama, Y. ( 1991), ”Grid generation around a practical ship hull form using the implicit geometrical method,” J. Soc. of Naval Arch. Japan 169, pp. 27–38. (in Japanese)
32. Toda, Y., Stern, F., and Longo, J. ( 1991), ”Mean-flow measurements in the boundary layer and wake and wave field of a series-60 CB=.6 ship model for Froude numbers .16 and .316,” IIHR Rep. 352, Univ. of Iowa
33. Bertram, V. ( 1994), ”Numerical shiphydrodynamics in practice,” IfS-Report 545, Univ. Hamburg, Germany (in German)
34. Graf, K. ( 1992), ”Calculation of viscous flow around barge-like ship hulls,” Ship Techn. Res. 39/3, pp. 107–117.
DISCUSSION
H.Kajitani
Kumamoto Institute of Technology, Japan
May I congratulate the authors on an impressive paper which describes a hybrid method to simulate the force and flow around a ship in a shallow channel? The blending of RANSE after RSM seems quite effective by the reason that we can consider how the inviscid and viscid flow characteristics are playing their own important roles on the flow. From this point of view, we should have expected if possible a more detailed and step-by-step explanation though we admit a new tendency toward quick, short, and symbolic way of the presentations.
The authors compare the wave patterns in the deep and shallow water cases. However, the wave angle spreading out from bow (or even from stern) seems to be unchanged between deep water and shallow water. This if, of course, due to the low Fn case. I have much interest in widening of the wave pattern at high Fn (or Fnh=0.64) in shallow water case how early or late it comes out.
In Table II, the measured and evaluated (RSM) sinkage and trim are compared which show a so well coincidence. But I'm afraid whether there is room to accept viscous effect. If you evaluate the sinkage force by RANSE, you might get a pronounced downwards local frictional force on the ship fore part, and less effect around the aft part, you may obtain a more closer evaluation. In this case, however, trim by bow moment is also increased. With regard to trim moment, shear stress on the ship bottom surface does not have its counter part, so trim by bow is mainly caused by this frictional force and the towing height has decisive effect both on measurement and evaluation. I would like to know the towing height applied both in experiment and evaluation.
Regarding pressure coefficient Cp along the centerline of the channel bottom (Fig.7), the prediction by CFD seems to be a little less estimate. In advanced RANSE procedures, the trim and sinkage at the latest iteration are included in the next calculation. Even though the authors' RANSE free surface grid does not seem to follow or express the local depression of mean free surface around the midship region. This means a relaxed flow continuity around midship, which implies a less prediction of the velocities also a less evaluation of the Cp. These have a decisive effect
on the resistance evaluation (Table III). In this connection, it is hard to accept the overestimated resistance coefficient in shallow water case. The authors' second reason (2 under prediction of blockage effect…), if corrected by taking the effect of free surface depression into account, may work out a further resistance increment. So we need a more careful approach.
Propulsion test simulation is, I believe, a challenging problem which seems to be yet at the beginning stage. In this case, to check the dipping at AP (usually measured at this station) seems to be a good index whether the simulation is done well or not. I appreciate very much your comments about this including measured results.
AUTHORS' REPLY
The considered depth Froude number does not yet lead to a considerable widening of the wave contour angle. However, the method is capable of capturing this phenomenon as demonstrated previously for an inland water vessel at depth Froude number 0.9 [16].
The sinkage is not very strongly affected by either viscous effects or the towing force. However, the remarks of Prof. Kajitani concerning their influence on trim are qualitatively correct. The towing force may be incorporated in the RSM but no information for the experimental condition was available. So we did not include this option. Tentative initial computations for the deep-water case showed only small influence of changing the towing force between still-water line and propeller height. The effect on trim is expected to increase with shallow water. However, as far as pressures on the channel bottom are concerned, the main influence will be sinkage. As the computations are already within the margin of uncertainty of the experiments for sinkage and trim, we did not focus our efforts on a further improvement of the method in the ability to predict trim and sinkage.
We agree with Prof. Kajitani that we should focus instead on improving the resistance prediction which at present does not satisfy our expectations. Small differences of trim and sinkage affect the accuracy of the resistance prediction, especially for shallow water. So, in order to improve the resistance prediction to the required degree, we may need a free-surface RANSE solver with sinkage and trim effect. As the problem of insufficient resistance prediction is shared by many other colleagues, it appears that we will need considerable more shared research worldwide before we see consistently accurate resistance predictions for real ship geometries, especially for the more complicated shallow-water hydrodynamics.
The propulsion test simulations predicted trim and sinkage using the RSM without propeller action, i.e., the same trim and sinkage as for the resistance test. Admittedly this is crude, but it is better than the usual practice of taking the zero-speed design floating condition. We do not have measured results in addition to the ones published with the kind permission of the Duisburg Towing Tank. We share Prof. Kajitani's wish for further details to validate our computational procedures and hope that maybe ITTC may provide in the future such data.