Shock Waves in Cloud Cavitation
C.Brennen, G.Reisman, Y.-C.Wang (California Institute of Technology, USA)
ABSTRACT
This paper describes experimental and computational investigations of the dynamics of clouds of cavitation bubbles. Recent studies have confirmed that the interactions between bubbles as they are manifest in the dynamics of bubble clouds lead to the generation of very large impulsive pressures which, in turn, cause substantial enhancement of the radiated noise and the material damage which results from this form of cavitation.
The experimental program focuses on cloud cavitation formed on the suction surface of a hydrofoil, both static and oscillating. Piezo-electric transducers mounted at a series of locations on the suction surface measured very large positive pressure pulses with amplitudes of the order of tens of atmospheres and with durations of the order of tenths of milliseconds. Two distinct types of pressure pulse were identified from high-speed films: “local pulses” which are registered by individual transducers and appear to be associated with the propagation of localized bubbly shocks and “global pulses” which result from larger scale, coherent collapses of bubble clouds. The experiments investigate the effects of reduced frequency, cavitation number and tunnel velocity on the magnitude of these pressure pulses.
The computational component continues the earlier work of Wang and Brennen (1, 2), which presented numerical solutions of the growth and collapse of a spherical cloud of bubbles. This confirmed the idea put forward by Mørch and his coworkers who speculated that collapse of the cloud involved the formation of a bubbly shock wave on the surface of the cloud and that inward propagation and geometric focussing of this shock would lead to very large localized pressure pulses. Here we review how the radiated acoustic pulses depend on the governing parameters such as the bubble population density, the cavitation number and the ratio of the bubble size to the cloud size.
Understanding such bubbly flow and shock wave processes is important because these flow structures propagate the noise and produce the impulsive loads on nearby solid surfaces in a cavitating flow. How these shocks are formed and propagate in the much more complex cloud geometry associated with cavitating foils, propeller or pump blades is presently not clear. However, by combining the computational and experimental observations, we suggest some specific mechanisms which may be active in the dynamics and acoustics of these more complex flows.
1.
NOMENCLATURE
|
A |
Radius of the bubble cloud |
|
A0 |
Initial radius of the bubble cloud |
|
c |
Chord length of foil (m) |
|
Cp |
Pressure coefficient, |
|
Cpmin |
Minimum pressure coefficient |
|
D |
Reference body size |
|
f |
Frequency (Hz) |
|
I |
Acoustic impulse (Pa.s) |
|
k |
Reduced frequency, ωc/2U |
|
p |
Fluid pressure (Pa) |
|
p0 |
Upstream reference pressure (Pa) |
|
pa |
Radiated acoustic pressure (Pa) |
|
pv |
Vapor pressure |
|
r |
Dimensionless Eulerian radial coordinate |
|
r0 |
Dimensionless Lagrangian coordinate |
|
R |
Bubble radius |
|
R0 |
Initial radius of the bubble |
|
t* |
Time (s) |
|
t |
Dimensionless time, Ut*/R0 |
|
tp |
Duration of low pressure perturbation |
|
T |
Period of foil oscillation (s) |
|
U |
Reference velocity of the flow (m/s) |
|
Vbmax |
Maximum total volume of bubbles in the cloud |
|
α |
Void fraction of the bubbly mixture |
|
α0 |
Initial void fraction of bubbly mixture |
|
β |
Cloud interaction parameter, |
|
η |
Bubble population per unit liquid volume |
|
ρ |
Density of the liquid |
|
σ |
Cavitation number, |
|
µe |
Effective dynamic viscosity of the liquid |
|
ω |
Foil oscillation frequency (rad/s) |
|
ωn |
Natural frequency of single bubbles |
2.
INTRODUCTION
In many cavitating flows of practical interest one observes the periodic formation and collapse of a “cloud” of bubbles. This temporal periodicity may occur naturally as a result of bubble-filled vortical structures or it may be the response to a periodic disturbance imposed on the flow. Common examples of imposed fluctuations are (a) the interaction between rotor and stator blades in a pump or turbine or (b) the interaction between a ship's propeller and the non-uniform wake created by the hull. Much recent interest has focused on the dynamics and acoustics of finite clouds of cavitation bubbles because of the very destructive effects which are observed to occur when such clouds form and collapse in a flow (see, for example, Knapp (3), Bark and van Berlekom (4), Soyama et al. (5)). Many authors such as Wade and Acosta (6), Bark and van Berlekom (4), Shen and Peterson (7, 8), Bark (9), Franc and Michel (10), Le et al. (11), Kubota et al. (12, 13), Hart et al. (14), McKenney et al. (15), Reisman et al. (16) and de Lange et al. (17) have studied the complicated flow patterns involved in the production and collapse of a cavitating cloud on a hydrofoil.
Analytical studies of the dynamics of cavitation clouds can be traced to the work of van Wijngaarden (18) who first attempted to model the behavior of a collapsing layer of bubbly fluid next to a solid wall. Later investigators explored numerical methods which incorporate the individual bubbles (Chahine (19)) and continuum models which, for example, analyzed the behavior of shock waves in a bubbly liquid (Noordzij and van Wijngaarden ( 20), Kameda and Matsumoto (21)) and identified the natural frequencies of spherical cloud of bubbles (d'Agostino and Brennen (22))). Indeed the literature on the linearized dynamics of clouds of bubbles has grown rapidly (see, for example, Omta (23), d'Agostino et al. (24, 25), Prosperetti (26)). However, apart from some weakly non-linear analyses (27, 28, 29) only a few papers have addressed the highly non-linear processes involved during the collapse of a cloud of bubbles. Chahine and Duraiswami (30) have conducted numerical simulations using a number of discrete bubbles and demonstrated how the bubbles on the periphery of the cloud develop inwardly directed re-entrant jets. However, most clouds contain many thousands of bubbles and it therefore is advantageous to examine the non-linear behavior of continuum models.
Another perspective on the subject of collapsing clouds was that introduced by Mørch, Kedrinskii and Hanson (31, 32, 33). They speculated that the collapse of a cloud of bubbles involves the formation and inward propagation of a shock wave and that the geometric focusing of this shock at the center of cloud creates the enhancement of the noise and damage potential associated with cloud collapse. Recently Wang and Brennen (1, 2) have used the mixture models employed earlier by d'Agostino et al. (22, 24, 25) to study the non-linear growth and collapse of a spherical cloud of bubbles. A finite cloud of nuclei is subjected to a temporary decrease in the ambient pressure which causes the cloud to cavitate and then collapse. The calculations clearly confirm the view of cloud collapse put forward by Mørch and his co-workers. In the present paper, we present some further information from spherical cloud calculations.
How bubbly shocks are formed and propagate in the much more complex and non-spherical geometries associated with cavitating foils, propeller or pump blades is presently not very clear. The present experiments have allowed identification of some specific shock structures whose details remain to be resolved and modelled.
3.
EXPERIMENTS
This section describes an experimental investigation of the large unsteady and impulsive pressures which are experienced on the suction surface of a
hydrofoil as a result of cloud cavitation. Both stationary and oscillating foils are studied Earlier measurements of noise produced by cloud cavitation are characterized by pressure pulses of very short duration and large magnitude (4, 7, 8, 9, 11, 15, 16). Previous experiments in the present series have described measurements of the acoustic signature of the cavitating cloud and related that to the observations of the unsteady cavitation (15); we have also explored the dependence of the sound magnitude on the cavitation number, σ, reduced frequency, k, and total air content (16).
The present experiments used piezo-electric transducers to measure unsteady pressures at four locations along the chord of the foil and at two locations along the walls of the tunnel test section. These transducers measured very large positive pressure pulses with amplitudes of the order of tens of atmospheres and with durations of the order of tenths of milliseconds.
Two distinct types of pressure pulse were identified. “Local” pulses occurred at a single transducer location and were randomly distributed in position and time; several local impulses could be recorded by each transducer during an oscillation cycle. On the other hand, “global” impulses were registered by all the transducers almost simultaneously. Correlation of the transducer output with high speed movies of the cavitation revealed that they were produced by a large scale collapse of the bubble cloud. The location of the global impulses relative to the foil oscillation impulses was quite repeatable and produced substantial far-field noise. The high speed movies also showed that the local impulses were caused both by crescent-shaped regions of low void fraction and by small bubbly structures. These regions appear to be bounded by bubbly shock waves which are associated with the large pressure pulses.
The paper also quantifies the effect of reduced frequency, cavitation number and tunnel velocity on the strength of the pressure pulses by presenting the acoustic impulse for a range of flow conditions. The reduced frequency is an important parameter in the determination of the total impulse level and the local and global pulse distribution. Large impulses are present on the foil surface even at cavitation numbers which do not result in large levels of acoustic radiation or global impulse. The total impulse increases almost universally with increasing tunnel velocity.
4.
PROCEDURE
The experiments were conducted in the Low Turbulence Water Tunnel (LTWT) at Caltech, a closed-circuit facility with test section dimensions of 30.5cm×30.5cm×2.5m (35). A modified NACA 0021 hydrofoil (thickness increased between the mid-chord and the trailing edge) with a rectangular planform, a chord of 15.2cm and a span of 17.5cm, was reflection-plane mounted in the floor of the test section as described in Hart et al. (14). A 750w DC motor is connected to the foil by a four-bar linkage such that it oscillates in pitch about an axis near the center of pressure, 0.38 of a chord from the leading edge. The mean angle of attack, the oscillation amplitude and frequency (up to 50Hz) are adjustable. An optical shaft encoder mounted to the DC motor provides a digital signal which was used to correlate the foil motion with the acoustic measurements and the high speed movies.
The unsteady pressures generated by the cavitation on the hydrofoil were measured by several transducers. A PCB model HS113A21 piezo-electric pressure transducer (bandwidth 100kHz, face diameter 3mm) was mounted flush with the floor of the test section, 5cm downstream of the trailing edge of the foil (this is later denoted by #F). Another HS113A21 transducer was mounted in the tunnel ceiling at approximately the same axial location. Four PCB model 105B02 pressure transducers (bandwidth 50kHz) were recess-mounted inside the foil at locations 26% span from the foil root and 30%, 50%, 70% and 90% chord from the leading edge (denoted respectively by #1 through #4). By driving a transmitting hydrophone with a voltage impulse, the resonant frequencies of the transducer cavities were determined to be about 35kHz. These values are in good agreement with the Helmholtz resonant frequency of 38kHz calculated for the recess. Great care was taken to avoid the presence of air bubbles in the cavities and the impulse response testing was able to confirm their absence by detecting any change in the cavity resonant frequency. All data taken by the foil transducers was digitally low pass filtered at 20kHz to avoid any effect of cavity resonance. The transmitting hydrophone was also used along with a second receiving hydrophone to confirm the manufacturer's calibration of the foil transducers. The output signals from all six transducers were low pass filtered at 45kHz (to avoid aliasing) and recorded digitally at a sampling rate of 100kHz.
A good measure of the magnitude of the collapse pulses contained in the transducer output is the
acoustic impulse, I (36, 37), defined as the area under the pulse or
(1)
where t1 and t2 are obtained from a threshold crossing method to identify the beginning and end of the pulse. A threshold of 20kPa was used for the floor and ceiling transducers while 200kPa was used for the foil surface transducers.
High speed movies with a framing rate of 500fps were taken to assist in the interpretation of the pressure transducer output. These movies were synchronized with the unsteady pressure measurements by triggering a timing light simultaneously with data acquisition commencement.
The data presented here were obtained from 40 samples at each operating condition where a single sample is defined by either one oscillation cycle or a 0.066s time period in the case of the static foil experiments. The mean angle of attack was 5°, the oscillation amplitude was 5°. The foil was fixed at an angle of attack of 5° during the static foil experiments. Experiments were performed at cavitation numbers of 0.85, 0.95, and 1.05, at tunnel velocities of 7.5m/s, 8m/s and 8.5m/s and at reduced frequencies of 0, 0.76, 1.00 and 1.22. The total air content was was 9.3ppm for the oscillating foil experiments and 8.2ppm for the static foil experiments.
6.
CAVITATION STRUCTURE
A typical set of output signals from the transducers is shown in figure 1 which represents a single foil oscillation cycle with the origin corresponding to the maximum angle of attack. The output signals are characterized by very large amplitude pressure pulses of very short duration. As exemplified by figure 1, the magnitudes of these pulses are of the order of tens of atmospheres with typical durations of the order of tenths of milliseconds. As previously described by Reisman et al. (16), the radiated acoustic pressure also contains pressure pulses which are illustrated by the bottom trace in figure 1. The magnitude of these pulses measured by the transducer in the tunnel floor is only on the order of one atmosphere. The closest approximation to the far field pressure is that measured by the transducer in the ceiling of the tunnel test section; this also contains impulses, but these pulses were of less than 10kPa in amplitude. Although these
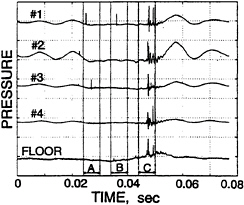
Figure 1: Typical transducer output during a single foil oscillation cycle. The top four traces are from the foil surface transducers and are numbered from the leading edge. The bottom signal is from the transducer mounted in the tunnel floor. The vertical axis scale is 1 MPa/div. for the foil surface transducers and 100 kPa/div. for the floor transducer. This typical data is for σ=0.95, k=0.78, U=8m/s.
far field measurements are affected by both the directional dependence of the ceiling transducer and the tunnel test section acoustics, it is clear that there are order of magnitude differences in the amplitudes of the pulses measured on the foil, near the cavitating region and in the far field, respectively.
The low frequency variation present in the signal prior to the 0.025 s mark and after the 0.05s mark was also observed at high cavitation numbers when the foil was fully wetted. This part of the signal is probably the result of stresses in the foil which are communicated through the transducer casings. This speculation is supported by the virtually instantaneous propagation of the low frequency disturbance and by the observation of similar signals even when the foil was oscillating in air.
Two different types of pressure pulses were identified and can be illustrated by figure 1. The pulses occurring before the 0.04s mark are randomly distributed in time and space and are not repeated from cycle to cycle. We refer to these as local pulses. The pulses located between the 0.04s and 0.05s marks occur virtually simultaneously, are of
higher amplitude and are repeated each cycle. We refer to these as global pulses; they produced substantial far-field noise and the location of the global impulses relative to the foil oscillation was quite re-peatable.
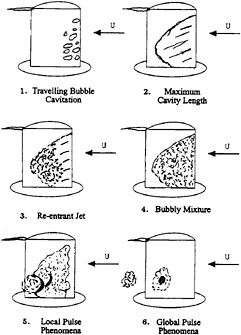
Figure 2: Cavitation structures observed during a single oscillation cycle. The angle of attack increases from sketch 1 to a maximum at sketch 2 and then decreases to a minimum at sketch 5.
The distinction between these two types of pressure pulse can be further elucidated by examining the high speed movies. These movies indicate that local pulses are caused by local disturbances in the cavitation structure while global pulses are generated by a larger scale cloud cavitation collapse.
The various stages of the cavitation observed during a single oscillation cycle are depicted in figure 2. Inception occurs in the tip vortex and is soon followed by travelling bubble cavitation in the area of Cpmin. As the angle of attack increases, the bubbles coalesce into a single attached cavitation sheet which attains its maximum length as the angle of attack reaches a maximum. At this point, a re-entrant liquid jet penetrates the attached cavity from the downstream edge and propagates toward the leading edge of the foil. This re-entrant jet mechanism was first described by Knapp (3) and further explored in the work of Lush and Skipp (38), Kubota et al. (13), and de Lange et al. (17). The current observations, however, indicate that the process which occurs after the passage of the re-entrant jet is critical since the large pressure pulses are detected after the jet has reached the foil leading edge. The re-entrant jet breaks up the attached sheet cavity into a bubbly mixture which detaches from the foil surface and accelerates downstream. Local disturbances in the bubbly mixture are then observed and these structures have been correlated with the production of local pressure pulses, as explained in further detail below. Finally, the remains of the sheet cavity form a cloud of bubbles that undergo a coherent collapse as they are convected downstream. As shown later in this paper, this collapse results in only a slight change in the cloud radius but a large change in void fraction which propagates from the cloud perimeter to the cloud center.
Three specific intervals during the oscillation cycle are indicated in figure 1. Time interval A contains a local pulse in foil surface transducer #3. The cause of this pulse can be deduced from the high speed movie frames in figure 3. The downstream edge of the crescent shaped region of low void fraction indicated by the arrow passes over transducer #3 between the two frames. The existence of this type of transient flow structure is a common occurrence during the detachment of a cavitation cloud from a sheet cavity as noted by Shen and Peterson (7), Bark (9), and McKenney and Brennen (15). Examination of other high speed movies indicates the presence of a local pulse whenever the downstream edge of such a low void fraction structure passes over a transducer, and this observation is consistent with those of Shen and Peterson (7). The transducer located near the trailing edge is an exception to this rule, but the cavitating region might be separated from the foil surface at this location. The boundaries of these low void fraction regions are observed to move either in the upstream or downstream direction relative to the bubbly flow as the region expands. We emphasize that the crescent-shaped regions and their associated pressure pulse were observed with both the stationary and oscillating foil.
Time interval B and the corresponding movie frames of figure 4 contain a second kind of local pulse phenomena. The local pulse in the output from transducer #1 corresponds to the passage of
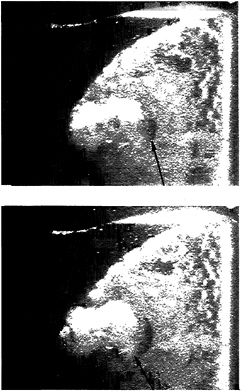
Figure 3: Crescent shaped flow structure of low void fraction. Consecutive high speed movie frames taken during time interval A of figure 1.
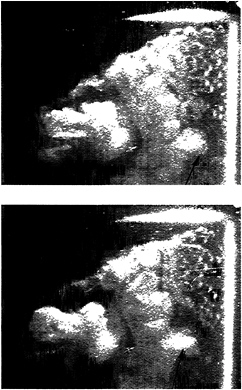
Figure 4: Local pulse generated by a small bubbly structure. Consecutive high speed movie frames taken during time interval B of figure 1.
the upstream boundary of a local cavitation cloud indicated by the arrow in figure 4. Other movie and pressure data also show the presence of a local pulse when the upstream edge of a small bubbly structure passes the transducer. These local structures are created when the sheet cavity detaches from the foil. As with the first type of local pulse, this second type is observed during a transition from a region of high void fraction to a region of low void fraction. The transitions which cause both types of local pulses are discrete and geometrically coherent.
Region C of figure 1 and the frames of figure 5 are representative of a global pulse. The cavitation cloud just upstream of the foil trailing edge undergoes a rapid and complete collapse between the two frames of figure 5. The collapse of this region radiates a pressure pulse which is detected by all of the foil transducers and the transducer located in the tunnel floor. It should be noted that this cloud collapse is similar to that calculated by Wang and Brennen (1, 2) in that it does not involve large changes in the overall dimensions of the cloud; rather collapse involves large changes in the void fraction within the cloud.
A typical set of output signals from the transducers during the static foil experiments is shown in figure 6. The magnitude of the observed pulses is much lower than those measured while the foil was oscillating; they were typically only a few atmospheres in amplitude. There was a substantial reduction in the radiated noise, and only local events were observed. No global pulses were produced when the foil was stationary. The shedding of bubble clouds from the downstream edge of the attached cavity was not characterized by any par-
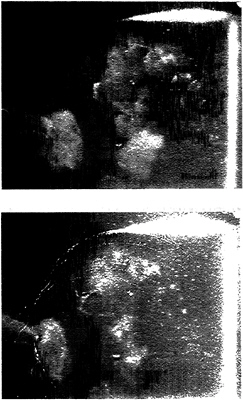
Figure 5: Global cloud collapse. Consecutive high speed movie frames taken during time interval C of figure 1.
ticular frequency; rather the clouds were detached in a continuous process.
7.
IMPULSE MEASUREMENTS
The experimental results depicted in figures 7 through 11 illustrate the variation of the average acoustic impulses with reduced frequency, cavitation number and tunnel velocity for both the static and the oscillating foil. In each figure the calculated impulses are presented for both the global and local pressure pulses detected by the four foil mounted transducers and the transducer located in the tunnel test section floor. Each average acoustic impulse presented in the figures is based on data collected during 40 individual foil oscillation cycles.
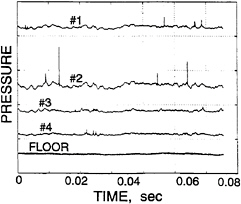
Figure 6: Typical transducer output during static foil experiments. The top four traces are from the transducers mounted on the foil and are numbered from the leading edge. The bottom signal is from the transducer mounted in the tunnel floor. The vertical axis scale is 500 kPa/div. for the foil surface transducers and 50 kPa/div. for the floor transducer. This typical data is for an angle of attack of 5°, σ=0.85, U=8m/s.
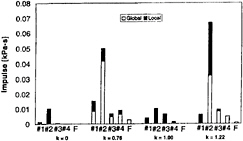
Figure 7: Effect of the reduced frequency, k, on the impulse, I. Data for σ=0.95 and U=8m/s.
Figure 7 illustrates the variation in the magnitudes of the local and global impulses with reduced frequency at a constant cavitation number, σ, and tunnel velocity, U. Note that, with the exception of #2 at k=1.22, the magnitudes of the local
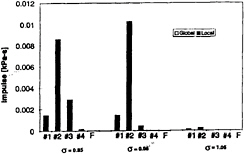
Figure 8: Effect of cavitation number, σ, on the impulse, I. Data for the static foil at an angle of attack of 5° and U=8m/s.
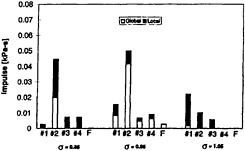
Figure 9: Effect of the cavitation number, σ, on the impulse, I. Data for the oscillating foil with k=0.76 and U=8m/s.
impulses are quite independent of the reduced frequency and are therefore similar for the static and oscillating foils. On the other hand global impulses are virtually non-existent with the static foil under the conditions of figure 7. On the oscillating foil, there appears to be a broad range of reduced frequencies around unity in which the coherent collapses associated with global pulses are triggered. As seen in figure 7, there also appear to be specific frequencies like k=0.76 and k=1.22 which seem to produce the maximum global impulses. This general pattern of variation with reduced frequency is similar to that seen in the radiated noise by McKenney and Brennen (15) and Reisman et al. (16); note that the radiated noise measured by the floor transducer is only substantial when global pulses are present. We also note from figure 7 that the spatial distribution of the measured impulses is similar for all reduced frequencies; they tend to be larger at mid-chord where the sheet cavitation breaks up and collapses.
Figures 8 and 9 illustrate the variations in the impulses with the cavitation number, σ, for the static and oscillating foils, respectively. With the static foil the local impulses appear rather suddenly when σ is reduced below about 1.00. The largest impulses occur near transducer #2, close to the cavity closure region; however, as σ is decreased to 0.85 the values at #3 increase as the cavitation collapse extends to that location. Le et al. (1993) also noted that the largest pulses on their static foil occurred near cavity closure.
When the foil is oscillating, the global impulses produced are also very sensitive to changes in cavitation number with the largest global impulses occurring in the middle of the cavitation number range. A similar effect was detected in the radiated impulses by McKenney and Brennen (15) and Reisman et al. (16), but the occurrence of cloud cavitation in the present experiments is more sensitive to changes in σ, perhaps due to the larger thickness of the present foil.
It is important to note that extremely large local pressure pulses occur at cavitation numbers which do not produce global shocks. An average local acoustic impulse in excess of 0.025 kPa.s is observed on #2 in figure 9 at σ=0.85. This flow condition is characterized by sheet cavitation which extends well beyond the trailing edge of the foil and does not produce large radiated pressure pulses outside of the cavitating region.
Both with the static foil and with the oscillating foil (at high cavitation numbers), large local impulses occur on the foil surface without any subtstantial radiated impulse being registered by the floor transducer. This suggests that significant cloud cavitation damage could occur on a foil which is not exhibiting large acoustic radiation. Conversely, global pulses always produce subtantial radiated noise which is registered by the floor transducer.
The effects of the magnitude of the tunnel velocity are illustrated in figures 10 and 11 for the static and oscillating foils, respectively (in the latter case, since the foil oscillation frequency was held constant at 12.7 Hz, there is also a small variation in the reduced frequency as the tunnel velocity changes). With the static foil, the local impulses increase rapidly with increasing velocity as one would expect since cavitation noise normally scales with the velocity raised to some large power.
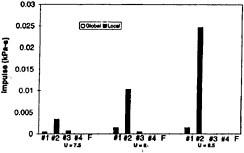
Figure 10: Effect of tunnel velocity, U, on the impulse, I. Data for a fixed angle of attack of 5° and σ=0.95.
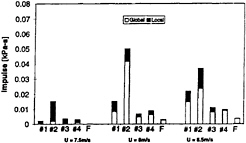
Figure 11: Effect of the tunnel velocity, U, on the impulse, I. Data for σ=0.95 and 0.72<k<0.81.
Note again the predominance of events near transducer #2. The imposition of oscillation changes this pattern. Note in figure 11, that the total impulse increases as the tunnel velocity is increased at constant σ. This occurs at every measuring location with the single exception of the value measured by the #2 transducer at U=8.5m/s. The almost universal increase is primarily due to a growth in the global acoustic impulse. Unlike the behavior with the static foil, the local impulse magnitudes remain fairly constant as the tunnel velocity is changed.
8.
GLOBAL PULSE PROPAGATION
By examining the time delays in the global pulse signals from the five transducers (four foil surface
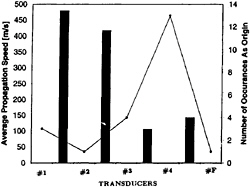
Figure 12: Speed of propagation and location of the origin of the global pressure pulses. Data for σ=0.95, k=0.76, U=8m/s.
and the floor transducer) it was possible to extract some information on the location of the origin of the global pulses and on the speed of propagation of that pulse. This was accomplished by measuring the time intervals between peak occurances in the transducer outputs for 41 events observed at one particular flow condition. The results of these calculations are shown in figure 12. The bar graphs represent the speeds of propagation between neighbouring transducers as calculated from the observed time intervals (the one on the right is the calculated speed between #4 and the floor transducer, #F). In all cases, the propagation speeds are a fraction of the sonic speed in either the pure liquid or pure vapor phase. The speeds calculated for the first two intervals are approximately 3.5 times as fast as those measured for the two downstream intervals. This difference is consistent with the void fraction distribution observed immediately after global cloud collapse. As shown in figure 2 and the photographs, the void fraction increases sharply downstream of the third foil transducer since the sheet cavtiation remains have been carried away from the leading edge of the foil prior to the global cloud collapse.
The approximate origins of the global pulses were calculated by noting which transducer registered the earliest global pulse. The results of this tabulation are depicted by the line in figure 12. The global pulses most frequently originated near the fourth foil transducer; this is consistent with the high speed movie observations.
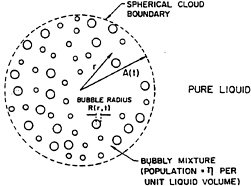
Figure 13: Schematic of a spherical bubble cloud.
9.
THEORETICAL ANALYSES
We turn now to some results obtained by studying the dynamics and acoustics of cavitating clouds of bubbles. The investigations incorporate the interactive effects that the cavitating bubbles have on themselves and on the pressure and velocity of the liquid flow by coupling the conventional mass and momentum equations for the flow with the Rayleigh-Plesset equation for the bubble radius. The model is non-barotropic but homogeneous and neglects, for simplicity, the relative motion between the bubbles and the liquid. The basic equations are same as those used earlier by d'Agostino and Brennen (22, 24, 25) except that all the nonlinear terms are retained.
10.
DYNAMICS OF A SPHERICAL CLOUD
We examine the dynamics of a spherical cloud of bubbles in an unbounded liquid which is at rest at infinity (figure 13). The pure liquid is assumed incompressible, with a density ρL. Since relative motion and the mass transfer between the two phases are neglected, it follows that if the population of bubbles per unit liquid volume, η, within the cloud, is uniform initially and if there is no coalescence or break-up then η is both constant and uniform within the cloud.
Some typical numerical results for the response of the spherical cloud are shown in figures 14 through and 18. These assume the properties typical of R0=100µm bubbles in a water flow at 20°C with a velocity of U=10m/s. An effective liquid viscosity, µe, is employed in the Rayleigh-Plesset equation in order to model all the contributions to the bubble damping (39). The cloud is assumed to originate from a cloud of nuclei in equilibrium and to be convected through a simple sinsoidal pressure depression whose depth is given by Cpmin and whose duration is defined by tp (consequently the length, D, of the low pressure region is given by D=Utp). Results were obtained for various cavitation numbers, σ, and initial void fractions, α0; other important paramters are A0/R0, D/R0, Cpmin, etc.
The characteristic cloud dynamics were found to be strongly dependent on the “cloud interaction” parameter, ![]() When β ≫ 1, that is at larger void fraction, bubble growth is severely restrained due to the strong bubble/bubble interaction effect. Under these circumstances the bubble growth rate within the cloud is quite uniform and all bubbles away from a near-surface region grow to about the same maximum size, as illustrated in figure 14.
When β ≫ 1, that is at larger void fraction, bubble growth is severely restrained due to the strong bubble/bubble interaction effect. Under these circumstances the bubble growth rate within the cloud is quite uniform and all bubbles away from a near-surface region grow to about the same maximum size, as illustrated in figure 14.
Figure 14 presents typical bubble time histories for β ≫ 1 at various Lagrangian locations within the cloud, from the surface, r0=A0, to the cloud center, r0=0. The shielding of the interior bubbles by the outer shell of bubbles is readily apparent in these results (see also 23, 25, 30). Note the formation and inward propagation of a shock wave whose typical structure is illustrated in figure 15. This structure which involves a series of rebounds and secondary collapses, is very similar to that of the gas/liquid shocks investigated by Noordij and van Wijngaarden (20) and Kameda and Matsumoto (21). The pressure pulse increases in amplitude as the shock propagates inwards and is focussed geometrically. Thus the pulse is large when the shock reaches the center of the cloud. The time history of the radius of the cloud is shown in figure 16. Note that, unlike single bubbles, the cloud radius, A(t), only decreases to a size marginally smaller than its equilibrium size during the collapse process. On the other hand, when β is of order unity or less, the bubbles tend to behave as they would in an infinite fluid and, as illustrated in figure 17 (for which β ≈ 3), the behaviour of the cloud is quite different under these circumstances. Then collapse occurs first at the cloud center and propagates out as an innocous expansion wave. The resulting acoustic impulse is much smaller than when β » 1. Other parameters such as the ratio of initial bubble size to cloud size, R0/A0, and the ratio
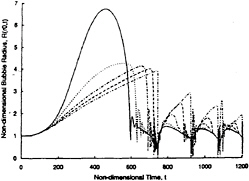
Figure 14: The time history of the dimensionless bubble size at five different positions in the cloud; r0=0 (dash-dot-dot line), r0=0.5A0 (dashed line), r0=0.7A0 (dash-dot line), r0=0.9A0 (dotted line), and r0=A0 (solid line). Parameters used are σ=0.45, Cpmin=–0.75, α0=3%, A0=100, and D/A0=5 (corresponds to tp=500).
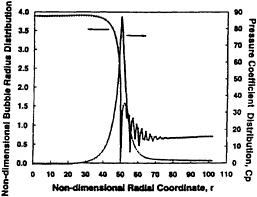
Figure 15: The bubble size distribution and pressure coefficient in the cloud as a function of the cloud radius at the dimensionless time, t=733.56, for the case of figure 14.
of the initial cloud size to the dimension of the low pressure region, A0/D, were exercised in order to explore the range of possible phenomena.
Wang and Brennen (1, 2) also examined the acoustic consequences of the shock wave. The normalized acoustic far-field noise, pa, was calculated
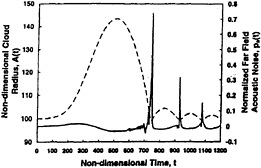
Figure 16: The time history of the dimensionless cloud radius, A/R0 (dashed line), and the far field cloud acoustic noise (solid line) for the case of figure 14.
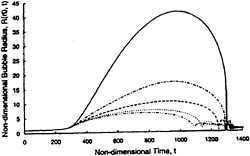
Figure 17: The time history of the dimensionless bubble size at five different positions in the cloud; r0=0 (dash-dot-dot line), r0=0.3A0 (dotted line), r0=0.5A0 (dashed line), r0=0.7A0 (dash-dot line), and r0=A0 (solid line). Parameters used are α0=0.03%, D/A0=10 or tp=1000. Other parameters as in figure 14.
from the volumetric acceleration of the cloud using
(2)
where the normalizing length scale was chosen to be the length of the low pressure region, D. The first shock focus, which induces a large volumetric acceleration in the far-field cause a very large peak in the radiated acoustic noise as illustrated in figure 16.
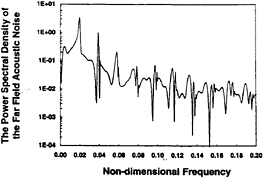
Figure 18: A non-dimensional power spectral density of the far field acoustic noise. In this case, the lowest cloud natural frequency of cloud is about 0.02. The natural frequency of a single bubble is 0.158.
16 The magnitudes of the subsequent peaks in each cloud collapse and rebound cycle may decay rapidly or slowly, depending on the collapse mode of the cloud. After several cycles, the cloud begins to oscillate at its natural frequency (22, 25).
A typical non-dimensional power spectral density of the acoustic noise is shown as a function of dimensionless frequency in figure 18. This spectrum exhibits the f–2 behavior for the frequency range below 0.25 (25kHz) which is typical of cavitation noise (see, for example, Arakeri and Shangumanathan (40), Blake et al. (41)). Other cases exhibited a f–n behavior with n in the range of 0.5 → 2. Some spectra also have large peaks at the natural frequency of the cloud and its higher harmonics. These are contributed by the regular oscillations of the cloud which can occur toward the end of the collapse and rebound process. In the case of figure 18, the first natural frequency of cloud is about 0.02 (2kHz) whereas the natural frequency of a single bubble in the cloud is 0.158 (15.8kHz).
The acoustic impulses (see equation (1)) from calculations using a wide variety of parameter choices (45 permutations) are found to be linearly correlated with the maximum total volume of the bubbles in the cloud normalized by the length of the low pressure perturbation, Vbmax/(0.5D)3, as shown in figure 19. However, we should note that Vbmax/(0.5D)3 decreases with increasing cavitation number and with increase in the initial void fraction, α0.
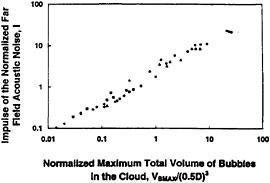
Figure 19: The impulse of the normalized far field acoustic noise correlated with the normalized maximum total volume of bubbles in the cloud at different ratios of the length scale of the low pressure perturbation to the initial radius of the cloud, D/A0, (31.25=solid Δ, 15.625=+, 10=◇, 5=solid ☐, 3.125=×, 1=Δ, 0.5=•).
Thus it would appear that an understanding of the collapse shock dynamics and acoustics has important consequences and implications for the scaling of cloud cavitation noise and damage.
11.
CAVITATION CLOUD COLLAPSE
Thus we have seen how a shock wave develops as part of the non-linear collapse of a spherical cloud of cavitation bubbles. The focusing of shock produces very high pressures at the center of the cloud and then causes rebound of the cloud. The volumetric acceleration induces a large pulse in the far-field noise. Moreover, there are further but weaker shocks which arrive at the center and thus produce a train of acoustic impulses which, eventually, lead to a regular oscillation of the cloud at the first cloud natural frequency. These results suggest that shock focusing may be one of the major mechanisms for the enhanced noise and damage potential associated with cloud cavitation.
The characteristic cloud dynamics are shown to be strongly dependent on the parameter ![]()
![]() where α0 is the initial void fraction, A0 is the initial cloud radius and R0 is the initial bubble radius. Two modes of collapse have been identified. At large values of this parameter, the collapse involves the formation of an inward propagating shock wave which initially forms
where α0 is the initial void fraction, A0 is the initial cloud radius and R0 is the initial bubble radius. Two modes of collapse have been identified. At large values of this parameter, the collapse involves the formation of an inward propagating shock wave which initially forms
at the surface of the cloud. This shock dominates this first mode of collapse and strengthens rapidly due to geometric focusing and the coupling of the bubble dynamics with the flow. In this mode, a large pulse in the far-field noise is produced by the arrival of the shock at the cloud center. Moreover, there are further but weaker shocks which arrive at the center and thus produce a train of acoustic impulses which, eventually, leads into a regular oscillation of the cloud at the first cloud natural frequency.
A different mode of collapse occurs at low values of β. Then the shielding effects of the outer bubbles causes the bubbles in the core of the cloud to grow to a smaller maximum size and to collapse first. This creates an outward moving collapse front and a very different mode of collapse than occurs at high β. At intermediate values, we observe cases where collapse first occurs at an intermediate radius and collapse fronts then propagate both outward and inward from this location.
We have also correlated the far-field acoustic impulse produced in all these cases with the parameters of the problem. It was found that the impulse is strongly correlated with the maximum total volume of bubbles in the cloud. Moreover, this total volume decreases with increasing cavitation number and with increasing void fraction. It also varies with D/A0 where D is the typical length of the low pressure perturbation.
12.
DISCUSSION
This paper has examined the large positive pressure impulses which occur on the surface of a hydrofoil during cloud cavitation; both static and oscillating foils were investigated. The pulses were shown to have magnitudes on the order of tens of atmospheres with typical durations of the order of tenths of milliseconds. Pressure pulses of similar magnitude were observed by Le et al. (11), who measured pulse magnitudes of up to 7 M Pa on a stationary foil at σ=0.81, U=12m/s and an angle of attack of 4.8°. Their experiments used flush-mounted transducers with face diameters of 1mm and bandwidths over 300kHz.
However, these pulse magnitudes are significantly greater than those measured by Shen and Peterson (7) who detected pulses with magnitudes comparable to the dynamic pressure, (up to 110kPa). There are at least two explanations for this discrepancy. Both the amplitude of foil oscillation (up to 1.55°) and the mean angle of attack (3.25°) were significantly less than those of the current experiments. Also, the transducers used by Shen and Peterson (7) had a bandwidth of only 2kHz. The short duration impulses measured in our experiments have a broadband frequency content with substantial contributions above 2kHz.
The radiated pulse magnitudes measured by Bark (9) and Bark and van Berlekom (4) were on the order of tens of kPa, but these were measured off the foil surface. These are similar to our far field measurements but are significantly smaller than the impulse amplitudes measured by the transducer mounted in our water tunnel floor. This reduction in amplitude may be attributed to the significantly lower velocities of the Bark and van Berlekom experiments which were performed at 5m/s. It should be noted that our surface pressure measurements are several orders of magnitude lower than the massive impulses observed by Avellan and Farhat (34) which averaged 900MPa in amplitude with extreme values as high as 2200MPa.
High speed movies indicated the presence of a re-entrant jet which, as previously described by Knapp (3) and a number of recent investigators, penetrates the sheet cavity as the cavity reaches its maximum length. The jet then breaks the cavity into a bubbly mixture which detaches from the foil surface. In the present study, pressure pulses of either type were only detected after the passage of the re-entrant jet.
Furthermore, an examination of the movies led to the identification of two distinct types of pressure pulses. “Local” pulses, which are registered by a single transducer, are randomly distributed in time and space and are not repeated from cycle to cycle. Local pulses are caused at a given transducer location by the passage of either crescent-shaped regions of low void fraction or small bubbly structures. In either case, they are observed during a transition from a region of high void fraction to a region of low void fraction. The crescent-shaped regions are similar to the “depressions in the cavity surface” noted by Shen and Peterson (7) and the “deep inward buckling of the cavity interface” observed by Bark (9). The discrete boundaries of the crescent-shaped regions and the motion of these boundaries relative to the bubbly flow suggest that these boundaries are bubbly shock waves. The collapse of vapor bubbles within these waves could explain the large pressure impulses measured on the foil surface.
On the other hand, “global” pulses, which occur
almost simultaneously on all four transducers, are of higher amplitude, radiate substantial far field noise and are repeated at the same point of each oscillation cycle. Global pulses are caused by large scale cloud cavitation collapse and were not observed on the static foil.
By calculating the acoustic impulse, a quantitative measure of the effect of reduced frequency, k, cavitation number, σ, and tunnel velocity on the strength of the pressure pulses was obtained. The reduced frequency is an important parameter in the determination of the total impulse level and the local and global pulse distribution. The cavitation number has a significant effect on the global impulse strength, but large impulses are still present on the foil surface at values of σ where acoustic radiation is minimal and global pulses are rare or non-existent. The changes with tunnel velocity were significantly different for the stationary and oscillating foils. The local impulses on the stationary foil increased greatly with tunnel velocity and the global impulses on the oscillating foil did likewise. However, the local impulses on the oscillating foil did not change so dramatically with tunnel velocity. We also note that the spatial distribution of the impulse measurements, while highly influenced by the cavitation number, are virtually independent of the reduced frequency and tunnel velocity.
It seems clear that both the local and global surface pressure pulses could contribute to foil damage. Indeed, the very large magnitudes of these surface impacts could be responsible for the foil damage reported by Morgan (42), who observed trailing edges bent away from the suction surface and toward the pressure surface.
In order to shed some light on the experimental observations we have included results from calculations of the dynamics and acoustics of a spherical bubble cloud. These clearly confirm that shock wave formation is an integral part of the collapse of such a cloud provided the cloud interaction parameter, β, is of order one or greater. Fundamentally, this requires either the initial void fraction, α0, or the ratio of cloud size to bubble size, A0/R0, be sufficiently large and this, in turn, is qualitatively in accord with the observation that cavitation must be quite extensive for the cloud phenomenon to be manifest. There is also a cautionary lesson to be drawn from the theoretical analysis. This concerns the scaling of cloud cavitation phenomena. Even if the nuclei have the same size, population and void fraction in the model and prototype, the cloud cavitation effects could be much larger in the prototype due to the larger value of β.
Of course, most clouds are far from spherical. But, nevertheless the collapse of all or part of non-spherical clouds will produce points at which shock waves focus to produce large radiated pulses. However, it is not currently clear what three-dimensional forms the propagating shocks might take in the highly non-uniform bubbly environments which occur in real flows. The experimental observations do suggest that the bubbly region near the surface may act as a wave-guide for the propagation of the crescent-shaped shock structures associated with local impulses. But much clearly remains to be understood regarding these structures and their consequences.
ACKNOWLEDGEMENTS
We wish to thank John Van Deusen and Rodney Rojas for their help in fabricating the foil. The authors are also very grateful for the assistance provided by Amir Alagheband, Amy Herr, Don Kwak, Tricia Waniewski and Cecilia Lin. We are also deeply appreciative of the support of the Office of Naval Research who sponsored this research under grant number N00014–91-J-1295.
REFERENCES
1. Wang, Y.-C. and Brennen, C.E., “Shock wave development in the collapse of a cloud of bubbles,” ASME Cavitation and Multiphase Flow Forum, 1994.
2. Wang, Y.-C. and Brennen, C.E., “The noise generated by the collapse of a cloud of cavitation bubbles, ” ASME Symp. on Cavitation and Gas-Liquid Flows in Fluid Machinery and Devices, 1995, FED-Vol. 226, pp. 17–29.
3. Knapp, R.T., “Recent investigation on the mechanics of cavitation and erosion damage, ” Trans. ASME, 1955, pp. 1045–1054.
4. Bark, G. and van Berlekom, W.B., “Experimental investigations of cavitation noise,” Proc. 12th ONR Symp. on Naval Hydrodynamics, 1978, pp. 470–493.
5. Soyama, H., Kato, H. and Oba, R., “Cavitation observations of severely erosive vortex cavitation arising in a centrifugal pump,” Proc. Third I.Mech.E. Int. Conf. on Cavitation, 1992, pp. 103–110.
6. Wade, R.B. and Acosta, A.J., “Experimental observations on the flow past a plano-convex hydrofoil, ” ASME J. Basic Eng., 1966, Vol. 88, pp. 273–283.
7. Shen, Y. and Peterson, F.B., “Unsteady cavitation on an oscillating hydrofoil,” Proc. 12th ONR Symp. on Naval Hydrodynamics, 1978, pp. 362–384.
8. Shen, Y. and Peterson, F.B., “The influence of hydrofoil oscillation on boundary layer transition and cavitation noise,” Proc. 13th ONR Symp. on Naval Hydrodynamics, 1980, pp. 221–241.
9. Bark, G., “Developments of distortions in sheet cavitation on hydrofoils,” Proc. ASME Int. Symp. on Jets and Cavities, 1985, pp. 215–225.
10. Franc, J.P. and Michel, J.M., “Unsteady attached cavitation on an oscillating hydrofoil,” J. Fluid Mech., 1988, Vol. 193, pp. 171–189.
11. Le, Q., Franc, J.M. and Michel, J.M., “Partial cavities: global behaviour and mean pressure distribution, ” ASME J. Fluids Eng., 1993, Vol. 115, pp. 243–248.
12. Kubota, A., Kato, H., Yamaguchi, H. and Maeda, M., “Unsteady structure measurement of cloud cavitation on a foil section using conditional sampling,” ASME J. Fluids Eng., 1989, Vol. 111, pp. 204–210.
13. Kubota, A., Kato, H. and Yamaguchi, H., “A new modelling of cavitating flows—a numerical study of unsteady cavitation on a hydrofoil section” J. Fluid Mech., 1992, Vol. 240, pp. 59–96.
14. Hart, D.P., Brennen, C.E. and Acosta, A.J., “Observations of cavitation on a three dimensional oscillating hydrofoil, ” ASME Cavitation and Multiphase Flow Forum, 1990, FED-Vol. 98, pp. 49–52.
15. McKenney, E.A. and Brennen, C.E., “On the dynamics and acoustics of cloud cavitation on an oscillating hydrofoil,” Proc. ASME Symp. on Cavitation and Gas-Liquid Flows in Fluid Machinery and Devices , 1994, FED-Vol. 190, pp. 195–202.
16. Reisman, G.E., McKenney, E.A. and Brennen, C.E., “Cloud cavitation on an oscillating hydrofoil,” Proc. 20th ONR Symp. on Naval Hydrodynamics, 1994, pp. 78–89.
17. de Lange, D.F., de Bruin, G.J. and van Wijngaarden, L., “On the mechanism of cloud cavitation—experiment and modelling,” Proc. 2nd Int. Symp. on Cavitation, 1994, pp. 45– 49.
18. van Wijngaarden, L., “On the collective collapse of a large number of gas bubbles in water, ” Proc. 11th Int. Conf. Appl. Mech., Springer-Verlag, Berlin, 1964, pp. 854–861.
19. Chahine, G.L. “Cloud cavitation theory,” Proc. 14th ONR Symp. on Naval Hydrodynamics, 1982, p. 51.
20. Noordij, L. and van Wijngaarden, L., “Relaxation effects, caused by relative motion, on shock waves in gas-bubble/liquid mixtures,” J. Fluid Mech., 1974, Vol. 66, pp. 115–143.
21. Kameda, M. and Matsumoto, Y., “Structure of shock waves in a liquid containing gas bubbles,” Proc. IUTAM Symp. on Waves in Liquid/Gas and Liquid/Vapour Two-Phase Systems, 1995, pp. 117–126.
22. d'Agostino, L. and Brennen, C.E., “On the acoustical dynamics of bubble clouds,” ASME Cavitation and Multiphase Flow Forum, 1983, pp. 72–75.
23. Omta, R., “Oscillations of a cloud of bubbles of small and not so small amplitude, ” J. Acoust. Soc. Am., 1987, Vol. 82, pp. 1018–1033.
24. d'Agostino, L. and Brennen, C.E., “Acoustical absorption and scattering cross-sections of spherical bubble clouds,” J. Acoust. Soc. of Amer., 1988, Vol. 84, No.6, pp. 2126–2134.
25. d'Agostino, L. and Brennen, C.E., “Linearized dynamics of spherical bubble clouds,” J. Fluid Mech. , 1989, Vol. 199, pp. 155–176.
26. Prosperetti, A., “Bubble-related ambient noise in the ocean,” J. Acoust. Soc. Am., 1988, Vol. 84, pp. 1042–1054.
27. Kumar, S. and Brennen, C.E., “Non-linear effects in the dynamics of clouds of bubbles,” J. Acoust. Soc. Am., 1991, Vol. 89, pp. 707–714.
28. Kumar, S. and Brennen, C.E., “Harmonic cascading in bubble clouds,” Proc. Int. Symp. on Propulsors and Cavitation, Hamburg, 1992, pp. 171–179.
29. Kumar, S. and Brennen, C.E., “Some nonlinear interactive effects in bubbly cavitating clouds,” J. Fluid Mech., 1993, Vol. 253, pp. 565–591.
30. Chahine, G.L. and Duraiswami, R., “Dynamical interactions in a multibubble cloud,” ASME J. Fluids Eng., 1992, Vol. 114, pp. 680–686.
31. Mørch, K.A., “On the collapse of cavity cluster in flow cavitation,” Proc. First Int. Conf. on Cavitation and Inhomogenieties in Underwater Acoustics, Springer Series in Electro-physics, 1980, Vol. 4, pp. 95–100.
32. Mørch, K.A., “Cavity cluster dynamics and cavitation erosion,” Proc. ASME Cavitation and Polyphase Flow Forum, 1981, pp. 1–10.
33. Hanson, I., Kedrinskii, V.K. and Mørch, K.A., “On the dynamics of cavity clusters,” J. Appl. Phys., 1981, Vol. 15, pp. 1725–1734.
34. Avellan, F. and Farhat, M., “Shock pressure generated by cavitation vortex collapse,” ASME Int. Symp. on Cavitation Noise and Erosion in Fluid Systems, 1989, FED Vol.-88, pp. 199–125.
35. Gates, E.M., “The influence of freestream turbulence, freestream nuclei populations, and a drag-reducing polymer on cavitation inception on two axisymmetric bodies,” PhD thesis, Cal. Inst. of Tech., 1977.
36. Ceccio, S.L. and Brennen, C.E., “Observations of the dynamics and acoustics of travelling bubble cavitation, ” J. Fluid Mech., 1991, Vol. 233, pp. 633–660.
37. Kuhn de Chizelle, Y., Ceccio, S.L. and Brennen, C.E., “Observations, scaling and modelling of travelling bubble cavitation ”, J. Fluid Mech., 1995, Vol. 293, pp. 99–126.
38. Lush, P.A. and Skipp, S.R., “High speed cine observations of cavitating flow in a duct,” Int. J. Heat Fluid Flow, 1986, Vol. 7, pp. 283–290.
39. Chapman, R.B. and Plesset, M.S., “Thermal effects in the free oscillation of gas bubbles,” ASME J. Basic Eng., 1971, Vol. 93, pp. 373–376.
40. Arakeri, V.H. and Shanmuganathan, V., “On the evidence for the effect of bubble interference on cavitation noise,” J. Fluid Mech., 1985, Vol. 159, pp. 131–150.
41. Blake, W.K., Wolpert, M.J. and Geib, F.E., “Cavitation noise and inception as influenced by boundary-layer development on a hydrofoil,” J. Fluid Mech., 1977, Vol. 80, pp. 617–640.
42. Morgan, W.B., personal communication, 1995.
















