Numerical Investigation on the Turbulent and Vortical Flows Beneath the Free Surface Around Struts
U.-C.Jeong, Y.Doi, K.-H.Mori (Hiroshima University, Japan)
Abstract
Characteristics of turbulent and vortical flows around free surface piercing struts are numerically and experimentally investigated. Three dimensional Reynolds averaged Navier-Stokes and continuity equations are used for the numerical simulation. The LES method with the external disturbance is used to simulate the turbulent flow on the free surface. The governing equations are discretised by a finite different method in a body and free surface fitted curvilinear co-ordinate system. To investigate the curvature effect of the bow, four different struts having NACA0005, NACA0008, NACA0012, and NACA0024 sections are used.
The results show that vorticity production is required on the curved free surface to satisfy the no-shearing stress condition. The no-shearing stress condition is significantly important. The vorticity, whose strength is proportional to the free surface curvature, leads the generation of the vortical motions beneath the free surface in front of the bow. The bow with a larger curvature intensifies the concave curvature of the free surface and generates stronger vorticity than a smaller one. Above a certain velocity, the vortical motions become intensive and the free surface fluctuates with a high frequency around a bow. The proposed LES method can reveal the existence of the free surface turbulence which is observed in experiments prior to the overturning waves.
1
Introduction
Free surface flow around a surface piercing blunt bow is one of the most complicated phenomena in the field of ship hydrodynamics because of various nonlinear characteristics. Many researchers have studied the bow breaking wave with the hope of understanding how it affects the resistance of a ship.
Baba[1] proposed wave breaking resistance as a new component of a ship resistance. He could provide quantitative evidence of a resistance component due to wave breaking around the bow through measuring head-loss by wake survey method. Taneda and Amamoto[2] explained the bow breaking wave as a vortex motion. They called it ”necklace vortex” to distinguish from the horseshoe vortex which was mainly generated by the boundary layer flow around the body mounted on the plate. They also reported that this necklace vortex was strongly affected by the Froude number while the horseshoe vortex was affected by the Reynolds number.
Since then, many investigations have been made to clarify the mechanism of the bow wave breaking both experimentally and theoretically. However, the so-called bow breaking wave and necklace vortex are not so simple and the mechanism has not yet come to knowledge. Miyata et al.[3] and Grosenbaugh and Yeung[4] showed an oscillatory motion of bow wave front which occurred when a certain critical speed was exceeded. However, it may be difficult to say that their findings are general characteristics of bow waves because they used two-dimensional floating bodies. Miyata et al.[ 3] also explained that overturning of waves generated a necklace vortex of which intensity depended on the strength of the overturning motion. Moreover, they reported that the vorticity generated by the breaking waves spread forward by the movement of wave front and backward by diffusive effect.
All the studies mentioned above is mainly concerned to the “broken” waves. However, to make clear the phenomena it may be necessary to study the early stage where the breaking is apt to occur. Honji[ 5] and Kayo and Takekuma[6] experimentally showed the existence of a vortical motion beneath the free surface around the bow at a very low Froude number even though no significant bow waves were generated. Patel et al.[7] explained the phenomenon
assuming the balance of a surface tension and a normal component of a viscous stress.
Mori[8] discussed the free surface flows before the wave breaking took place. He divided the flow into three stages; the development of the free surface shear layer, the formation of the necklace vortex and the production of unsteady turbulent free surface flow. It was called ”sub-breaking waves” as a free surface turbulent flow in distinction from spilling or plunging breakers. He also deduced that the free surface curvature played a role to generate a vorticity on the curved free surface and the vorticity could be one of the sources of the necklace vortex. The theoretical background of the free surface shear layer was also given by Batchelor[9].
Mori and Shin[10] simulated the sub-breaking wave generated by two-dimensional submerged hydrofoil. They used experimental results to set the free surface boundary condition strictly. Mori and Lungu[11] simulated two-dimensional sub-breaking waves directly by imposing a disturbance for vertical velocity component while Coleman[12] used a disturbance of pressure on the free surface. The role of these disturbances might be a kind of a trigger for the transition to the turbulent flow and it might be assumed as a source that maintains the turbulence on the free surface.
Main objective of the present study is to make clear the characteristics of the flow at the early stage of bow wave breaking around surface piercing struts, especially the effect of the vorticity generated on the free surface on the vortical and turbulent flows beneath the free surface. To simplify the problem, the surface tension is excluded in the present investigations. Numerical investigations are made by solving the Reynolds averaged Navier-Stokes(NS) and continuity equations by finite difference method(FDM). Several computations are performed to investigate the effects of computational and physical parameters, for examples, grid dependency, the effects of the Reynolds and Froude numbers, free surface treatment and so on. To investigate the curvature effect of the bow, four different struts having NACA0005, NACA0008, NACA0012, and NACA0024 sections are used(called NS05, NS08, NS12 and NS24 respectively hereafter). The fluctuated free surface flows called sub-breaking waves are also studied by Large Eddy Simulation(LES). Some computed results are compared with the experimental results.
2
Observation of Bow Wave Patterns
An observation of bow wave patterns was performed for NS08, NS12 and NS24 models at the circulating water channel(CWC) of Hiroshima University. The length and draft of the models were 0.8m and 0.4m respectively. Experimental arrangement is shown in Fig.1. The wave patterns were photographed under the CWC. The striped-screen was fixed above the free surface to make the pictures clear. To remove a surface tension, a surfactant was used[13].
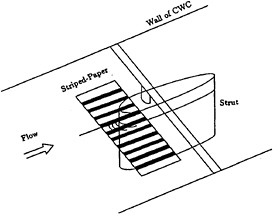
Fig. 1 Experimental set-up.
Fig.2 shows a schematic view of the bow wave on the center plane. The ”Zone-I” where the free surface has smooth concave curvature is the part ahead of the bow wave. Through a sharp change of the curvature, the flow enters ”Zone-II” where the flow can not be stable any more. A border of these two zones is ”wave front” where the curvature has a maximum[8].
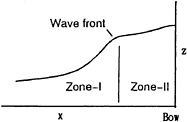
Fig. 2 Schematic view of bow wave.
Fig.3 shows the bow wave pattern of NS12 at Fn=0.15. No clear waves are observed. However, at Fn=0.20 as shown in Fig.4, the wave front is observed surrounding the bow. Increasing the oncoming velocity(Fn=0.25), the wave front appears clearly and the position moves away from the bow(Fig.5). At those Froude numbers, no significant features of turbulence appear on the free surface.

Fig. 3 Picture of free surface flow of NS12, Fn=0.15, Rn=2.3·105.

Fig. 4 Same as Fig.3, Fn=0.20, Rn=3.1·105.

Fig. 5 Same as Fig.3, Fn=0.25, Rn=3.9·105.
Fig. 6 shows the bow wave patterns at Fn=0.30 for three models. The Reynolds number is 4.60×105. The free surface flows of NS08 and NS12 seem to be quite complicated and turbulent in ”Zone-II” which can be called sub-breaking wave[8]. The wrinkles of NS08 and NS12 are more intensive than NS24 around the bow. The flow of NS24 looks still gentle. Here, a question may appear; why the intensity of the free surface wrinkles of NS08 is much stronger than that of NS24 although the bow of NS24 is much blunter?
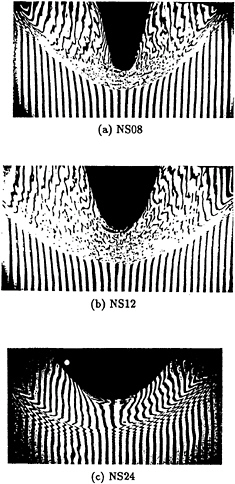
Fig. 6 Pictures of free surface flows of NS08, NS12 and NS24, Fn=0.30, Rn=4.6 ·105.
Similar experiments were carried out by Mori[8]. He used two models which were a circular cylinder and an elliptic strut. He showed that the elliptic strut generated more intensive wrinkle, which was a kind of free surface instability, than that generated by the circular cylinder at the same speed although the necklace vortex of the circular cylinder was more intensive than that of the elliptic strut. He explained that the reason might be the different free surface curvatures in front of the bows.
The detail discussions on the effect of bow curvature will be made by a numerical simulation in chapter 5.
3
Computational Method
3.1
Governing equations
Three dimensional incompressible Reynolds averaged Navier-Stokes and continuity equations are employed for the present numerical study. These governing equations are written as follows;
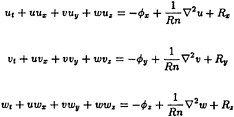
(1)
ux+vy+wz=0 (2)
(3)
where u, v and w are the velocity components in (x,y,z)-directions in the Cartesian co-ordinate system as shown in Fig.7; x in the uniform flow, y in the lateral and z in the vertical directions respectively. The origin is located at the leading edge of the strut on the undisturbed free surface. Subscripts represent partial differentiations with respect to the referred variables except Rx, Ry and Rz which are Reynolds stress components. Fn, Rn, ϕ, p, Pat and k are Froude number, Reynolds number, modified pressure, pressure, atmospheric pressure and turbulent energy respectively. All the variables are normalized by a uniform velocity(U0) and the length of strut(L).
The Reynolds stress terms can be expressed as follows;
Rx={vt(ux+ux)}x+{vt(uy+vx)}y+ {vt(uz+wx)}z
Ry={vt(uy+vx)}x+{vt(vy+vy)}y+ {vt(vz+wy)}z
Rz={vt(ux+wx)}x+{vt(vz+wy)}y+ {vt(wz+wz)}z (4)
The turbulence model for the flow with the free surface around ship like body is complicated and not well developed yet. The Baldwin-Lomax(BL) turbulence model[14] and its modification by Renze et al.[15] are widely used in CFD fields for the simplicity. However, Degani and Schiff[16] pointed out that the difficulty encountered in applying the BL model to bodies with crossflow separation was that of properly evaluating the eddy-viscosity in outer layer. Thus, they modified the BL model to calculate the eddy-viscosity in crossflow separation region. According to some numerical and experimental results, separated re-circulating flows exist on the free surface around shoulder part of the blunt body above a certain velocity [17,18]. Thus, in this study, the modified BL model(MBL) proposed by Degani and Schiff is used to simulate the turbulent flow around the body and it is assumed that the turbulent flow starts at x=0.1.
On the other hand, the SGS model[19] is introduced around bow to simulate the turbulent free surface flow at a high Froude number. This will be discussed in chapter 6.
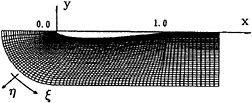
Fig. 7 Co-ordinate systems and generated grid near body on horizontal plane(NS12).
3.2
Numerical algorithm
The basic concept of the solution algorithm is based on the MAC method. A finite difference method
is represented on a regular grid system. So all the variables are defined on the grid nodes. The first order difference form of the time derivatives in NS equations is used for an explicit advancement in time. The convective terms in NS equations are discretised by the third order upwind scheme(equation(5)). All the other spatial derivatives are discretised by the second order central difference scheme.
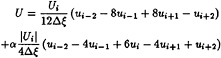
(5)
where α=1.0 is used as a standard coefficient.
3.3
Grid generation
A numerical co-ordinate transformation is introduced into the body fitted co-ordinate system to simplify the computational domain and to facilitate the implementation of boundary conditions. C-H type grid is employed for the present computation. C-type grid is generated by using geometrical method[20] and the whole grid system is obtained by stacking them in the vertical direction algebraically. The grid topology near the body on a horizontal plane and the curvilinear co-ordinate system are shown in Fig.7. The ζ-axis of the body fitted co-ordinate system coincides with the z-axis. The grid lines are clustered near the body and the free surface to simulate properly the free surface and viscous interaction.
4
Boundary Conditions
4.1
Free surface conditions
The free surface location can be calculated to satisfy a kinematic condition which represents that the fluid particles of the free surface always remain on it. In the present study, the following Euler-type kinematic condition is used.
ht+uhx+vhy–w=0 (6)
where h(x,y,t) is the wave height and the subscripts represent partial differentiations with respect to the referred variables. The equation(6) is discretised by the first order forward scheme for the time integration and the third order upwind scheme for other terms.
On the other hand, the velocity and pressure can be calculated by an equilibrium of stresses on the free surface as follows;
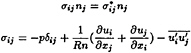
(7)
where σij, ![]() nj and δij are fluid stress tensor, external stress tensor, unit outward normal vector to the free surface and Kronecker delta respectively in the Cartesian co-ordinate system.
nj and δij are fluid stress tensor, external stress tensor, unit outward normal vector to the free surface and Kronecker delta respectively in the Cartesian co-ordinate system.
Assuming no-shearing stress and excluding the surface tension, the equation(7) can be rewritten as follows;
σijnjni=Pat (8)
σijnjti=0 (9)
where ti is unit tangential vector to the free surface. Finally, the following equations can be used as a dynamic free surface boundary condition assuming that the normal component of the viscous and Reynolds stresses are negligibly small.
(10)
2uxnx+(uy+vx)ny+(uz+wx)nz=0
(vx+uy)nx+2vyny+(vz+wy)nz=0
(wx+uz)nx+(wy+vz)ny+2wznz=0 (11)
where, h, nx, ny and nz are wave height and (x,y,z)-components of the unit outward vector normal to the free surface respectively. Solving equation(11), on the free surface the velocity components can be calculated.
The no-shearing stress condition leads a generation of vorticity on the free surface[9]. The axis of the vorticity is perpendicular to the streamwise direction and the strength of the vorticity is
ω=2ksqs (12)
where, ks and qs are the curvature of streamline and streamwise velocity on the free surface respectively. Equation(12) means that the curvature of the free surface can generate the vorticity if the streamwise velocity is not zero.
A zero-gradient extrapolation for the velocity is commonly used on the free surface because of the simplicity. In the present study, the above two approaches are compared.
4.2
Other boundary conditions
On the body surface, no-slip condition is applied for the velocity and Neumann-type condition for the pressure. On the other hand, it is difficult to treat the intersection of the free surface and solid body strictly because the region is a kind of a singular region [ 21]. In the present study, no-slip condition is used for the velocity while the wave elevation on the body is linearly extrapolated using neighboring wave heights calculated by the kinematic free surface boundary condition. The pressure in this singular region is obtained by the dynamic free surface boundary condition directly.
In half-C type grid systems used in this study, there are two symmetry planes which are forward center plane and wake center plane. On the symmetry plane, the flow is assumed to be symmetric.
A uniform velocity and zero wave elevation are applied on the inflow boundary.
Sometimes, improper boundary conditions give some numerical troubles such as reflection or oscillation of waves on the outlet boundary. However, a simple zero-gradient extrapolation can be acceptable to investigate the flow near the body because the outer boundary or the grid arrangement around the far field region does not affect so much the flow near the body when the computational domain is large enough[22]. In the present numerical study, a simple zero-gradient extrapolation is used on the outlet boundary.
5
Numerical Simulations of Vortical Motions
5.1
Computational conditions
Several computations are performed for the four different struts as mentioned in chapter 1 which are NS05, NS08, NS12 and NS24 models. Computational conditions for the standard cases are listed in Table 1. These conditions are chosen through various test computations to investigate the effect of grid density, time increment and so on.
In the present computations, the flow is accelerated from a rest condition to the uniform velocity. The flow acceleration affects the bow wave formations; a sudden acceleration may lead strong oscillatory motion or overturning of wave around a bow. In order to avoid such a strong wave breaking, the flow is slowly accelerated up to nondimensional time T=5.0 in the present computations.
To validate the present computations, the computed wave profile is compared with the experimental one for NS12(Fig.8). The experiment was carried out at the circulating water channel of Hiroshima University. The length and draft of the strut are 0.15m and 0.50m respectively. Wave profiles on the body surface were measured by making use of an image processing system developed at Hiroshima University[23]. To remove the surface tension, a surfactant was also used[13]. The computed results give good agreement with the experimental one except near the wave trough. The reason of this difference may be that the flow around shoulder part of the blunt model is not steady including strong separated flow called shoulder wave breaking[17,18].
Table 1. Computational conditions for standard cases.
|
Rn=5000 |
Rn=105 |
|
|
Grid numbers |
||
|
- ξ-direction |
91 |
110 |
|
- η-direction |
45 |
60 |
|
- ζ-direction |
20 |
20 |
|
Min. grid spacings |
||
|
- Δξ |
0.005 |
0.005 |
|
- Δη |
0.002 |
0.0005 |
|
- Δζ |
0.0015 |
0.0006 |
|
Time increment |
0.001 |
0.00025 |
|
Computational domains |
–2.0≤x≤4.0 0.0≤y≤2.0 –1.0≤z≤hmax |
|
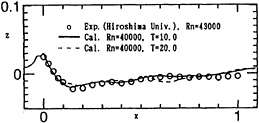
Fig. 8 Comparison between computed and measured wave profiles on the body surface; NS12, Fn=0.25.
5.2
Vortical motions around bows
First, the effect of the dynamic free surface boundary condition is investigated. According to the equation(12), the vorticity can be generated to satisfy the no-shearing stress condition. However, the zero
gradient extrapolation is often used because of the simplicity. Fig.9 shows the distributions of the computed velocity and vorticity on the center plane for two different treatments of the dynamic free surface boundary conditions for NS05 at Fn=0.30 and Rn=5000. In case of the zero-gradient extrapolation, the computed wave height at the bow is almost the same value as the position head at the stagnation point for inviscid fluid. On the other hand, the introduction of the no-shearing stress condition makes the counter-clockwise vorticity more intensive and the wave height decreases. This means that the energy accumulated around the wave crest is consumed by the generation of the vorticity.
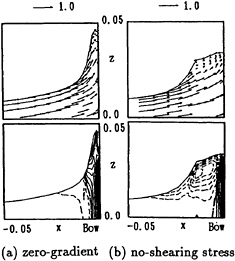
Fig. 9 Computed velocity and vorticity (ωy) distributions for two different treatment of dynamic free surface boundary condition; NS05, Fn=0.30, Rn=5000, T=15.0 (contour interval=10.0).
In case of a lower Froude number flow(Fn=0.25), however, there is no significant difference between the two results as shown in Fig.10.
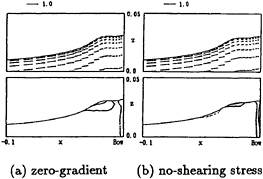
Fig. 10 Same as Fig.9; NS12, Fn=0.25, Rn=5000, T=15.0 (contour interval=10.0).
From these results, it can be pointed out that the no-shearing stress condition on the free surface plays an important role to produce a vortical motion where the free surface curvature is large. The computations neglecting the no-shearing stress may lead misunderstanding of the phenomena. Thus, all the computations are performed taking into account the no-shearing stress condition hereafter.
Fig.11 compares the computed and experimented free surface flows between three models. The Reynolds numbers for the computation and experiment are 1.0×105 and 3.8×105 respectively. The wave front lines, which are defined in Fig.2, are clearly shown in both computed and experimented results except NS24. The computed distances between the leading edge(x=0.0) and the wave front on the center plane are about 0.03L(x=–0.03) and 0.04L(x=–0.04) for NS08 and NS12 respectively (L: length of the strut). It can be noted that the flow field around bow is almost steady both in the experimental and computed results when the Froude number is less than 0.25. The overall computed flow patterns are good agreement with the experimental results.
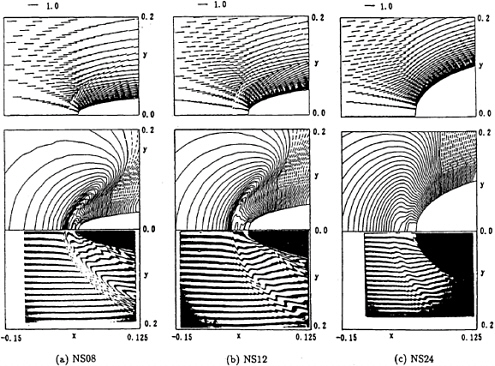
Fig. 11 Comparison of computed and experimented free surface flows; NS08, NS12 and NS24, Fn=0.25, (upper; computed, Rn=1.0·105, down; experimented, Rn=3.9·105).
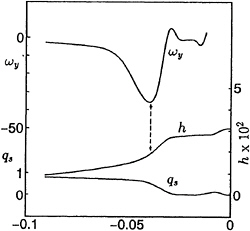
Fig. 12 Relation between vorticity(ωy), wave profile(h) and streamwise velocity(qs) on the free surface on the center plane; NS12, Fn=0.25, Rn=1.0·105.
The relation between the vorticity(ωy), wave height(h) and the streamwise velocity(qs) on the free surface is shown in Fig.12. The peak of the vorticity is located on the free surface having concave curvature as indicated by the dotted arrow. According to the no-shearing stress condition(equation(12)), the vorticity on the free surface can be expressed as a product of the free surface curvature and the streamwise velocity. Although the wave front has a larger curvature than that of the concave surface, the vorticity is smaller at the wave front because the streamwise velocity becomes smaller around there. This is the reason why the counter-clockwise vorticity occupies the region in front of the bow.
The comparison of the vorticity(ωy) and velocity distributions for the three models is shown in Fig.13.
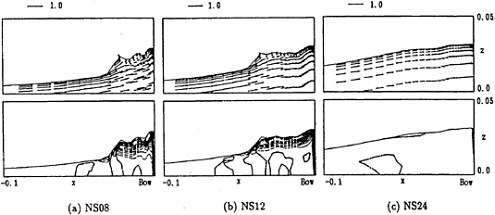
Fig. 13 Computed velocity and vorticity(ωy) distributions on the center plane in front of bows; NS08, NS12 and NS24, Fn=0.25, Rn=1.0·105, T=15.0 (contour interval=10.0).
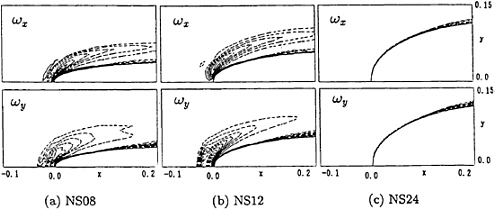
Fig. 14 Computed vorticity(ωx,ωy) distributions beneath the free surface around bows; NS08, NS12 and NS24, Fn=0.25, Rn=1.0·105, T=15.0 (contour interval=10.0).
The model with large curvature(NS08) generates the most intensive vorticity which is induced by the free surface curvature. The peaks of the vorticity are located beneath the free surface around the wave front for each models except NS24. In case of NS24, however, there are no such vortical motions because the free surface is enough smooth. These results can give some explanations to the experimental findings as shown in Fig.6; the bow with a larger curvature(NS08) generates more intensive wrinkles than that with the smaller one(NS24).
Fig.14 shows the vorticity distributions on the
horizontal plane beneath the free surface around the bows at Rn=105 and Fn=0.25. The distance from the free surface is 0.003. The vorticity surrounding the bow, the so called ”necklace vortex”, is more intensive for NS12 than for NS08, although the strength of the vorticity in front of bow is not larger. These results show the same tendency with the results by Mori[8] as mentioned in chapter 2. However, in case of NS24, there are no such clear necklace vortex motions. The reason is that the free surface flow of NS24 is premature to generate the vortex motions at this Froude number.
From these results, It can be concluded that the bow shape has strong relation with the free surface curvature, especially concave shape, which is responsible for the vortical flows around the bow.
5.3
Grid dependency
Fig.15 shows the effect of grid density in the vertical direction around the free surface for NS12 at Rn=105 and Fn=0.25. The computations are performed for the three different minimum grid spacings( Δζ) of 0.0003, 0.0006 and 0.0012. The minimum grid spacing and the grid density in the normal direction to the body surface are kept almost same. In case of Δζ=0.0012, the vortical motions do not fully develop while they develop well for the other two cases and almost the same results are obtained.
It can be concluded that the grid density around the free surface is one of the important computational parameters; coarse grid can not detect the vortical flows beneath the free surface.
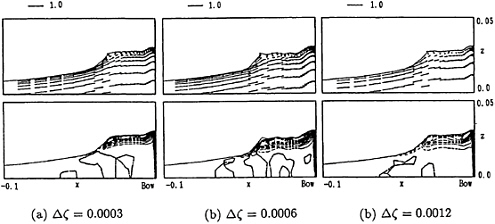
Fig. 15 Grid dependency of the vortical flows on the center plane, NS12, Fn=0.25, Rn=1.0·105, T=15.0 (contour interval=10.0).
6
Large Eddy Simulation of Sub-Breaking Waves
6.1
Computational conditions
One of the important characteristics of the sub-breaking waves is the intensive fluctuations of the free surface such as the turbulent flow in the boundary layer flow on a solid body[8]. The shear flow in the boundary layer developed on a body plays a role as a trigger for the transition to the turbulent flow and it may be assumed as a source that maintains the turbulence. Although the situation is a little different in case of the free surface flow, there exists boundary layer on the free surface which may induce the free surface turbulence.
As shown in Fig.6, the free surface flows of NS08 and NS12 are quite complicated. The situation can be assumed under the sub-breaking condition. In order to detect the sub-breaking waves, Large Eddy Simulation(LES) is performed for NS12 at Fn=0.30 and Rn=105. The basic equations for LES are given through a space averaging operation and they can be expressed in the same forms as equations(1) –(4).
The Sub-Grid Scale(SGS) turbulence model[19] is introduced for the simulation. So, in the computation at high Reynolds and high Froude numbers, two turbulence models are used together. One is the modified Baldwin-Lomax model(MBL) to simulate the flow in the boundary layer on the body and the other is the SGS model for the sub-breaking wave. The combination of these two models is sketched in Fig.16. The eddy-viscosity is smoothly changed in the streamwise direction through the intermediate region(INT) where the eddy-viscosity is calculated by the mean of SGS and MBL. To reduce an artificial viscosity, α=0.5 is used in equation(5).
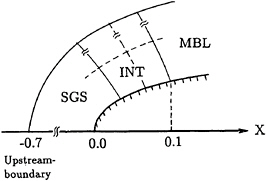
Fig. 16 Combination of two different turbulent models.
In the present numerical study, the following numerical disturbance is introduced to generate the fluctuations on the free surface.
w′=β · (0.5 · u) (13)
where β is a random constant(–1.0≤β≤1.0) and u is the calculated velocity of x-component.
This disturbance is added in the region of SGS as indicated in Fig.16 only for two successive time steps after T=4.0.
Although a sufficient fine grid system and a small time increment are necessary to simulate the fluctuations directly with SGS turbulence model, it is hard to use satisfactory computational parameters because of a restriction of the memory size and the computing time. To avoid the difficulties, a smaller computational domain is used in the present sub-breaking computation. The computational domain and condition are tabulated in Table 2.
Table 2. Computational condition for Large Eddy Simulation of sub-breaking wave.
|
Rn=105, Fn=0.30 |
|
|
Grid numbers |
|
|
- ξ-direction |
72 |
|
- η-direction |
60 |
|
- ζ-direction |
20 |
|
Min. grid spacings |
|
|
- Δξ |
0.005 |
|
- Δη |
0.0005 |
|
- Δζ |
0.0006 |
|
Time increment |
0.0001 |
|
Computational domains |
–0.7≤x≤1.5 0.0≤y≤0.7 –1.0≤z≤hmax |
6.2
Results and discussions
Fig.17 shows the computed and observed flow patterns on the free surface around bow at Fn=0.30. The Reynolds numbers of the computation and experiment are 1.0×105 and 4.6×105 respectively. The distances between the wave front and the bow(x=0.0) are about 0.05L(x=–0.05) and almost the same for the both.
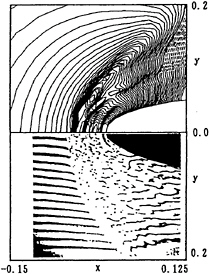
Fig. 17 Comparison of computed and experimented free surface flows; NS12, Fn=0.30, (upper; computed, Rn=1.0·105, down; experimented, Rn=4.6·105).
The computed fluctuations in ”Zone-II” are not so clear and small comparing with the experimental result. The reason may be that the grid system is still not so fine enough to simulate the wrinkles.
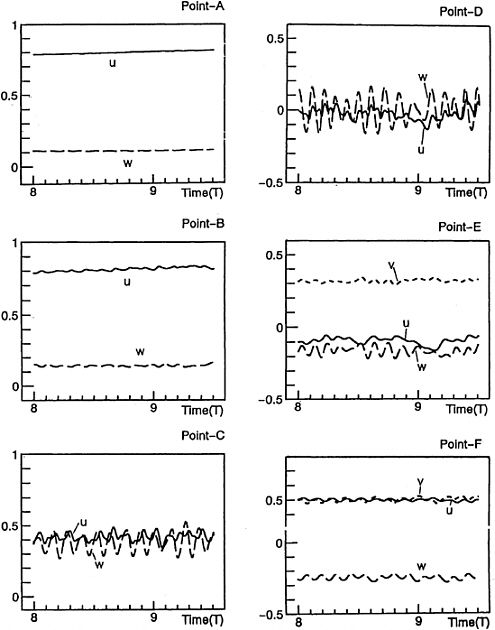
Fig.18 shows the computed velocity and vorticity(ωy) distributions on the center plane at T=10.0. It must be noted that the flow around the bow is still fluctuating. Although there are slight reverse flows in the bow wave field, they are not followed by overturning wave. Several peaks of the free surface exist in the ”Zone-II”. The characteristics of the turbulence on the free surface are investigated at the six points around bow as shown in Fig.19.
Fig.20 shows the time histories of velocity components through T=8.0–9.5 at the six points. Although the initial disturbance is imposed all the domain around the bow including the point A, the fluctuations disappear at there. The velocity remains almost constant. The velocity fluctuates slightly at point B where the concave curvature of the free surface appears. The fluctuations become intensive at point C which is just outside of the wave front and the free surface curvature is larger. It can be considered that the instability of the free surface starts there. At point D, the amplitude of the fluctuations of the velocity components becomes larger and the u-component is less than zero. This result indicates that the free surface flows at point D is turbulent and reverse flows exist there. The fluctuations become gradually weak at points E, and F. At point E, the u-component is still negative and it is a positive at point F. The reverse flow on the free surface disappears after the point E.
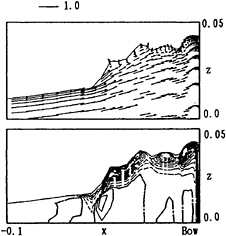
Fig. 18 Computed velocity and vorticity(ωy) distributions on the center plane in front of bows; NS12, Fn=0.30, Rn=1.0·105, T=10.0 (contour interval=10.0).
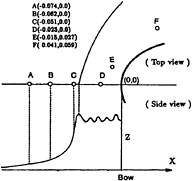
Fig. 19 Schematic view of bow wave and the definition of six points for investigation of turbulent quantities.
Fig.21 shows the distributions of time averaged velocity components in depthwise direction at points A and D. The velocity is averaged for 15000 time steps from T=8.0 to 9.5.
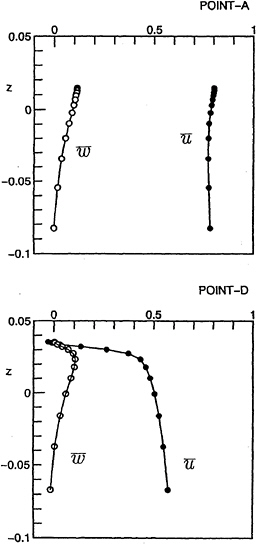
Fig. 21 Computed mean velocity distributions at points A and D; NS12, Fn=0.30, Rn=1.0·105.
At point D where the flow is fully turbulent the strong defect of the u-component exists close to the free surface while w-component has small defect. On the other hand, there is no such a velocity defect at point A where the free surface flow is laminar. These results are found in the experimental results by Mori[8] who measured the velocity components in front of a elliptic strut and a circular cylinder under the sub-breaking condition.
Fig.22 shows the computed Reynolds stress components at point D. The cross component ![]() is almost zero on the free surface because the no-shearing stress condition is imposed on the free surface. On the other hand, other components become larger on the free surface. This is the same tendency with the experimental results by Mori[8].
is almost zero on the free surface because the no-shearing stress condition is imposed on the free surface. On the other hand, other components become larger on the free surface. This is the same tendency with the experimental results by Mori[8].
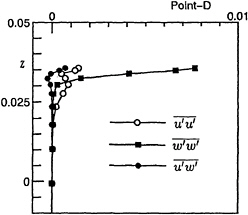
Fig. 22 Computed Reynolds stress distributions at points D; NS12, Fn=0.30, Rn=1.0·105.
Fig.23 shows the turbulent energy profiles in depthwise direction at points A and D. At point A, the turbulent energy is almost zero while, at point D, it is intensive on the free surface and it abruptly becomes weak at the depth of 0.02L from the free surface.
We can point out that the free surface turbulent flow referred to the sub-breaking wave generated without overturning waves. The numerical simulations neglecting the turbulence may lead a misunderstanding of the phenomena.
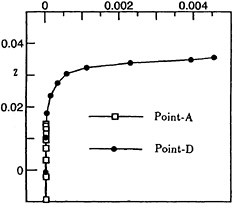
Fig. 23 Computed turbulent energy distributions at points A and D; NS12, Fn=0.30, Rn=1.0·105:
7
Concluding Remarks
Some characteristics of the turbulent and vortical flows around the free surface are numerically and experimentally investigated. Four different struts are used to investigate the curvature effect of the bow.
Findings through the present study are summarized as follow;
-
The no-shearing stress condition on the free surface is important to generate the vorticity beneath the free surface. And the vorticity induces vortical motions beneath the free surface when the free surface curvature is large.
-
The proposed LES method reveals the existence of the free surface turbulence called sub-breaking wave which is not followed by overturning waves.
-
The bow with a larger curvature intensifies the concave curvature of the free surface and generates a stronger vorticity than the bows with smaller curvature.
-
Grid density around the free surface is one of the important computational parameters; coarse grid can not detect the vortical flows beneath the free surface.
The authors express a lot of thanks to Dr. S.Ninomiya, research associate at Hiroshima University, for his kind support in experiments.
References
[1] Baba, E.: A New Component of Viscous Resistance of Ship, Journal of the Society of Naval Architects of Japan, Vol. 125, pp.23–34, 1969.
[2] Taneda, S. and Amamoto, H.: The Necklace Vortex of the Ship, Bulletin of Research Institute for Applied Mechanics, Kyushu Univ., No.31, pp.17–28, 1969 (in Japanese).
[3] Miyata, H., Kajitani, H., Shirai, M., Sato, T., Kuzumi, S. and Kanai, M.: Numerical and Experimental Analysis of Nonlinear Bow and Stern Waves of a Two-Dimensional Body (4th Report)-Simulation of Breaking Waves and Experimental Analysis , Journal of the Society of Naval Architects of Japan, Vol.157, pp.15–33, 1985.
[4] Grosenbaugh, M.A. and Yeung, R.W.: Nonlinear Bow Flows-An Experimental and Theoretical Investigation, Proceedings of 17th Symposium on Naval Hydrodynamics, Hague, Netherlands, pp.195–214, 1988.
[5] Honji, H.: The Necklace Vortex of the Ship, Bulletin of Research Institute for Applied Mechanics, Kyushu Univ., No.43, pp.11–17, 1975 (in Japanese).
[6] Kayo, Y. and Takekuma, K.: On the Free Surface Shear Flow related to Bow Wave-Breaking of Full Ship Models, Journal of the Society of Naval Architects of Japan, Vol. 149, pp.11–20, 1981.
[7] Patel, V.C., Landweber, L. and Tang, C.J.: Free-Surface Boundary Layer and the Origin of Bow Vortices, 2nd International Symposium on Ship Viscous Resistance, Gotenburg, Sweden, pp.23:1–23:13, 1985.
[8] Mori, K.: Necklace Vortex and Bow Wave around Blunt Bodies, Proceedings of 15th Symposium on Naval Hydrodynamics, Hamburg, Germany, pp.303–317, 1984.
[9] Batchelor, G.K.: An Introduction to Fluid Dynamics, Cambridge University Press, pp.364–366, 1970.
[10] Mori, K. and Shin, M.S.: Sub-Breaking Wave: Its Characteristics, Appearing Condition and Numerical Simulation , Proceedings of 16th Symposium on Naval Hydrodynamics, Hague, Netherlands, pp.499–511, 1988.
[11] Mori, K. and Lungu, A.: Sub-Breaking Wave and Its Numerical Simulation with Turbulent Characteristics, Proceedings of 9th International Symposium on Ocean Waves and Floating Bodies, Kyushu, Japan, pp.143–146, 1994.
[12] Coleman, R.M.: Nonlinear Calculation of Breaking and Non-Breaking Waves Behind a Two-Dimensional Hydrofoil , Proceedings of 16th Symposium on Naval Hydrodynamics, Berkeley, USA, pp.51–62, 1986.
[13] Maruo, H. and Ikehata, H.: Some Discussions on the Free Surface Flow around the Bow, Proceedings of 16th Symposium on Naval Hydrodynamics, Berkeley, USA, pp.65–77, 1986.
[14] Baldwin, B.S. and Lomax, H.: Thin Layer Approximation and Algebraic Model for Separated Turbulent Flows, AIAA Paper 78–257, 1978.
[15] Renze, K.J., Buning, P.G. and Rajagopalan, R. G.: A Comparative Study of Turbulence Models for Overset Grids, AIAA Paper 92–0437, 1992.
[16] Degani, D. and Schiff, L.B.: Computation of Turbulent Supersonic Flows around Pointed Bodies Having Crossflow Separation, Journal of Computational Physics, 66, pp.173–196, 1986.
[17] Pogozelski, E., Katz, J., Huang, T.: Flow Structure around a Surface-Piercing Blunt Body, Proceedings of 20th Symposium on Naval Hydrodynamics, Santa Barbara, USA, pp.117A–117G, 1994.
[18] Zhang, Z.J. and Stern, F.: Wave-Induced Separation, Forum on Advances in Numerical Modeling of Free Surface and Interface Fluid Dynamics, 1995 ASME IMECE, San Francisco, USA, 1995.
[19] Deardorff, J.W.: A Numerical Study of Three Dimensional Turbulent Channel-Flow at Large Reynolds Numbers, Journal of Fluid Mechanics, 41, pp.453–480, 1970.
[20] Kodama, Y.: Three Dimensional Grid Generation around a Ship Hull Using the Geometrical Method, Journal of the Society of Naval Architects of Japan, Vol. 164, pp.1–8, 1998.
[21] Farmer, J., Martinelli, L. and Jameson, A.: Multigrid Solution of the Euler and Navier-Stokes Equations for a Series 60 Cb=0.6 Ship Hull for Froude Numbers 0.160, 0.220 and 0.316 (Program 1: Navier-Stokes Formulation), Proceedings of CFD WORKSHOP TOKYO 1994, Vol. 1, pp.56–65, 1994.
[22] Hinatsu, M.: Numerical Simulation of Unsteady Viscous Nonlinear Waves Using Moving Grid System Fitted on a Free Surface, Journal of the Kansai Society of Naval Architects of Japan, No.217, pp.1–11, 1992.
[23] Ninomiya, S., Mori, K., Hosokawa, M.: Measurements of Wave Height by Visualizing Air-Side Free-Surface and Illuminating the Wetted Surface of Hull through Water, Journal of the Society of Naval Architects of Japan, Vol. 174, pp.129–135, 1993 (in Japanese).
DISCUSSION
R.W.Yeung
University of California at Berkeley, USA
I would like to congratulate the authors for a very interesting paper on a subject area that complements and extends our work in the Seoul Symposium (Yeung and Ananthakrishnan [1]). Perhaps the authors are not aware of this work. In our paper, as well as a related publication (Aananthakrishnan and Yeung [2]), we have systematically investigated the effects of the free-surface boundary condition (free-slip, no slip, clean, or with surface contaminants) on the vortical structures below the free surface. Even though our works were two-dimensional, I feel what is stated in the present paper, in regard to the need to apply the zero-stress condition, has already been established in our earlier works. Our investigations and solutions covered a large range of scenarios.
As to qualitative features of the bow-flow results, the present authors ' thick-body results (corresponding to NS24) are consistent with the limiting behavior of our (two-dimensional) blunt bow solution. However, the intensification of cross-stream vorticity due to an increase in waterline curvature (Fig.9b and 13b) seems to suggest the presence of a (steady state) stagnation point on the free surface located between the clockwise and counter-clockwise vortices. Is this really physically plausible? If so, what would the topology of such a flow be like?
Another question that comes to mind concerns the accuracy of computations. In Fig.15, the authors demonstrated that a grid density Δξ=.0003 was needed to capture the surface and vortical details, while most of the computations utilize a grid spacing effectively almost 10 times larger (see Table 1). This fact, coupled with a grid aspect ratio (horizontal to vertical) of almost 10 can easily lead to inaccuracies. Perhaps the authors can comment on this difficulty, particularly in connection with the large artificial viscosity arising from a scheme like Eqn. (5).
My final remark concerns the LES and MBL modeling of the free surface. It appears to rather ad hoc as these models were established on the ground that the flow had no free boundaries. Given that the authors are convinced that the no-stress free-surface condition is an important one, it seems inconsistent to utilize such models. Perhaps it is not surprising that the mean values of computed and measured velocities differ significantly in Figure 21.
REFERENCES
[1] Yeung, R.W. and Ananthakrishnan, P. “Vortical flows with and without a surface-piercing body,” Proc. 19th Symp. Naval Hydrodyn., Seoul, Korea, 1992.
[2] Ananthakrishnan, P. And Yeung, R.W. “Nonlinear interaction of a vortex pair with clean and surfactant-covered free surfaces,” Wave Motion, 19, pp. 343–365, 1994.
AUTHORS' COMMENTS
We would like to thank you for the remarks and comments.
The need to apply the zero-shear stress condition on the free surface was already discussed by Mori [8]. It was concluded the free-surface curvature was one of the sources for the shear flow and vortical motion beneath the free surface. So far as we understood, it was concluded that the free-surface vorticity generated by free-surface curvature was rather weak in the paper for Profs. Yeung and Ananthakrishnan.
The clockwise vorticity around the bow shown in Figs.9b and 13b does not indicate a vortex but a shear flow on the body. The dominant vortical motion is counter-clockwise. As Prof. Yeung pointed out, there is a stagnation point on the free surface because a weak reverse flow is observed on the free surface.
The grid density high aspect ratio of the grid arrangement leads to inaccuracies when the flow is not parallel to the grid. In the present computation, the flow beneath the free surface is almost parallel to grid where the aspect ratio is high. The situation is the same as the flow simulation of the boundary layer developed on a solid surface.
LES was originally developed for the simulation of homogeneous turbulence. Successful implementation of LES for a turbulent flow with no free boundary such as a solid wall is achieved through a special modification of SGS modeling near wall. In the present simulation for a free-surface turbulence, Smagorinsky's closure is applied without a