Calculations of Pressure Fluctuations on the Ship Hull Induced by Intermittently Cavitating Propellers
Y.-Z.Kehr, C.-Y.Hsin, Y.-C.Sun (National Taiwan Ocean University, Taiwan)
Abstract
The object of this work is to develop a numerical method to calculate the hull surface forces induced by cavitating propellers. In this paper, a method based on the numerical model developed by Breslin, is presented. In this method, the effective wake is calculated by the method developed by Huang and Groves, and later modified by Wilson, Van Houten and Kerwin. MIT-PUF-3A is then used to analyze the unsteady flow around propellers in the effective wake, and to compute the propeller induced potentials on the hull surface. A potential based higher order panel method is used to calculate the flow around the ship hull including the propeller influences. In this higher order panel method, a second order panel geometry is used, and a second order normal dipole is distributed on each panel. An internal Dirichlet boundary condition is imposed at each panel that the total potential on the body inner surface is set to be zero. The pressure fluctuations on the hull surface can then be calculated from solutions of the dipole strength by applying Bernoulli's equation. In this paper, the pressure fluctuations generated by propellers on a flat plate and on a ship hull are presented, and the computational results are compared with experimental data.
1
Introduction
When propellers work in the wake of hulls, the nonuniform inflow results in both the unbalanced bearing forces and pressure fluctuations on the hull surface. The latter one is especially serious when the propeller is cavitating. In this paper, a method of predicting the pressure fluctuations on hull surface by a cavitating propeller is presented.
The problems caused by propeller induced pressure fluctuations on hull surface brought naval architects' attentions in 1970's. At that time, loadings on propellers have been dramatically increased due to the demands of higher speed commercial ships. Some serious structure failures due to vibrations were occurred on these high speed ships, and it was found that most of these vibrations were caused by propellers generated exciting forces. Since then, the topics of reducing propeller generated vibrations have been investigated and studied by various institutes and researchers. Recently, NTOU (National Taiwan Ocean University) has begun a series of studies to understand propeller generated vibrations. These researches include better designs of the stern hull forms which may reduce the nonuniformity in the wake, designs of highly skewed propellers which can help to reduce propeller generated vibrating forces, development of new sections for reducing cavitations, establishment of skills of measuring pressure fluctuations on hull surfaces, and development of a numerical prediction model for propeller generated pressure fluctuations. This prediction model which has been developed for the past two years is described in this paper.
The present method is based on the numerical model developed by Breslin, etc. [2], however, the ship hull is completely simulated by a higher order panel method. In the present work, the effective wake is first calculated by a method developed by Huang and Groves [5], and later modified by Wilson, Van Houten and Kerwin [16],[2]. MIT-PUF-3A is then used to analyze the unsteady flow around propellers in the effective wake, and to compute the propeller induced potentials on the hull surface. Finally, a potential based higher order panel method is used to calculate the flow around
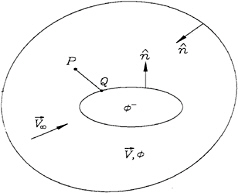
Figure 1: Internal and external flow domain defined in the equation (2)
the ship hull including the propeller influences. In this panel method, a quadratic dipole distribution is distributed over each panel on the body surface, and an internal Dirichlet boundary condition is imposed at the control point of each panel. The pressure fluctuations on the hull surface can then be calculated from solutions of the dipole strength by applying Bernoulli's equation.
2
Representation of the Ship Hull
In order to calculate the propeller generated pressure fluctuations, we need first to develop a numerical method to represent the ship hulls. In the present work, the free surface effect is approximated by a positive or negative hull image. Therefore, it is equivalent to solving the flow around submerged bodies. Hess and Smith [4] first developed a velocity based panel method to calculate the flow around a submerged body. In their method, the source singularities are distributed over the body surface, and the Neumann boundary condition is imposed for solutions. In the present work, the flow around a ship hull is analyzed by a higher order, potential based panel method. A dipole sheet is distributed on the surface of hull, and an internal Dirichlet boundary condition is imposed.
2.1
Governing Equation
Assuming the flow around, the body is incompressible, inviscid, and irrotational, namely, potential flow, then the governing equation of this flow is the Laplace's equation:
![]() 2
2![]() =0 (1)
=0 (1)
where ![]() is the velocity potential.
is the velocity potential.
If we let ![]() to be the external flow velocity potential, and
to be the external flow velocity potential, and ![]() ˉ to be the internal flow velocity potential (Figure 1), then from Lamb [13], and Kerwin, etc.[10], we have the following equation:
ˉ to be the internal flow velocity potential (Figure 1), then from Lamb [13], and Kerwin, etc.[10], we have the following equation:
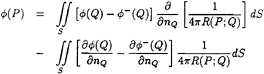
where P is a field point in the flow field, Q is a point on the body surface, and R is the distance between P and Q. In equation (2), we can interpret the term [![]() (Q)–
(Q)–![]() ˉ(Q)] as a dipole strength, and the term
ˉ(Q)] as a dipole strength, and the term ![]() as a source strength. Most of panel methods used in the fluid dynamics area are based on equations derived from equation (2) with a proper boundary condition imposed [6].
as a source strength. Most of panel methods used in the fluid dynamics area are based on equations derived from equation (2) with a proper boundary condition imposed [6].
2.2
Boundary Condition
When solving the problems of non-lifting bodies, velocity based panel methods are commonly used. That is, a source sheet is distributed on the body surface, and the Neumann boundary condition is imposed.
(3)
If we define the total potential as the sum of the inflow potential, ![]() ∞, and the perturbation potential,
∞, and the perturbation potential, ![]() , then, we can rewrite equation (3) as follows:
, then, we can rewrite equation (3) as follows:
(4)
where ![]() is the total velocity.
is the total velocity.
However, for the convenience of calculating the pressure fluctuations on the hull surface, a potential based panel method which a dipole sheet distributed on the body surface is preferred [2]. As we know, the normal velocity is continuous through a dipole sheet, therefore,
(5)
We can let the velocity potential at the inner surface to be –![]() ∞, and the total inner potential thus becomes to be zero. This is the internal Dirichlet boundary condition we are going to use. From the above statements, equation (2) can be rewritten as:
∞, and the total inner potential thus becomes to be zero. This is the internal Dirichlet boundary condition we are going to use. From the above statements, equation (2) can be rewritten as:
(6)
where ![]() +
+![]() ∞=Φ is the total potential, and it can also be interpreted as the dipole strength, µ. Equation (6) is therefore the dipole only formulation derived from equation (2).
∞=Φ is the total potential, and it can also be interpreted as the dipole strength, µ. Equation (6) is therefore the dipole only formulation derived from equation (2).
If a point P is on the external surface, then equation (6) becomes:
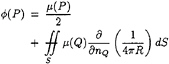
(7)
Similarly, we will ge the following equation if P is on the inner surface:
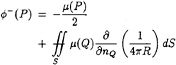
(8)
If we apply the internal Dirichlet boundary condition (total internal potential to be zero), then it becomes,
(9)
The dipole strength, µ, can be solved from equation (9). The velocities and pressure distribution thus can be obtained by taking the gradients of velocity potentials.
2.3
Higher Order Panel Method
In the present work, a higher order panel method based on Johnson [8],[7] is used. In this method, both the panel geometry and the dipole strength are of the second order. The panel geometry is approximated by a quadratic surface, and can be described by
ζ(ξ,η)=aξ2+bη2 (10)
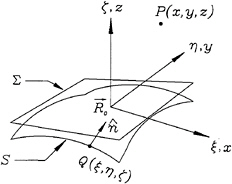
Figure 2: The coordinate system of the panel geometry used in the present method.
after several coordinate transformations. Please refer to Johnson [8] [3] for the detailed descriptions of modeling panel geometries. Figure 2 shows the local coordinate system of a panel. The second order dipole strength thus can be described in terms of the local coordinate system (ξ,η):
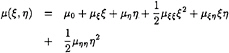
(11)
where coefficients µ0,µξ,µη,µξξ,µξη,µηη are determined from dipole strength at control points of neighboring panels through a fitting process. In the present method, 9 panels (8 neighboring panels and the self panel) are used for this fitting process by the least squares method. By introducing this quadratic dipole strength into the governing equation, and calculating the induced potentials, a linear system is finally obtained for the solutions of the dipole strength at the control point of each panel. The dipole strength coefficients can then be calculated, thus the dipole strength distribution can be obtained from equation (11) (see Appendix).
2.4
Numerical Solutions
The velocity potentials on the surface of a sphere in a uniform flow (Figure 3) are calculated by this potential based higher order panel method, and the results are compared with both the exact
Figure 3: A sphere with its discretized geometry
solutions and numerical solutions from a velocity based panel method.
Since the solutions of a sphere are symmetrical, only one fourth of the sphere geometry is discretized and used for the calculations. Figure 4 shows the relative computational errors in percentage of a sphere with 18 panels/quadrant (6 panels in the θ direction, and 3 panels in the z direction). It shows that the results are satisfactory, and even the maximum error is less than 1%. The relative error is defined as the difference between the computational result and the exact solution. However, if we use a velocity based panel method with a linear source distribution on each panel, then 40 panels (8 panels in the θ direction, and 5 panels in the z direction) are needed to obtain the same accuracy (Figure 5). Figure 5 shows the comparison of the results from a constant source panel method, a linear source panel method and the present method. It shows that the present method gives the most accurate results, and the computational time of the present method is about the same as the linear source panel method by the same given number of panels. In this potential based panel method, velocities can be calculated by taking the gradients of the solved potentials (dipole strength). Figure 6 shows the calculated velocity distributions on the sphere surface by different panel methods compared to the exact solutions. In this figure, velocity distribution is directly calculated from the induced velocities for the source (velocity based) panel method. However, the velocity distribution is calculated from potentials by a finite difference method for the dipole (potential based) panel method.
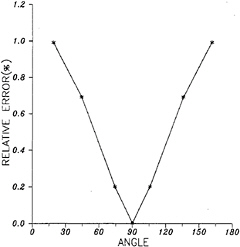
Figure 4: Relative errors of the total potentials of a sphere in the uniform flow calculated by the present higher order panel method, and totally 18 panels are used at each quadrant.
This panel method is also used to calculate Series 60 ship hulls (CB=0.6 and CB=0.82) to make further comparisons between the potential based and velocity based panel methods. Results show that both methods generate very similar results [3].
3
Solutions of the Intermittently Cavitating Propellers
In the present method, MIT-PUF-3A is used to calculate potentials on the hull surface induced by intermittently cavitating propellers. We have discussed how ship hulls are modeled by a higher order panel method in the last section, and we will briefly introduce how PUF-3A simulates propeller effects.
3.1
Calculation of the Effective Wake
When we calculate the flow field around propellers, a ship model wake measured in the towing tank is usually used to be the inflow. This velocity distribution is purely generated by the ship hull without the consideration of propellers, and this is so
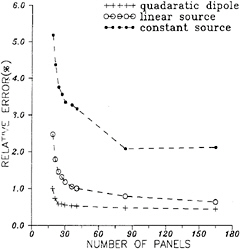
Figure 5: The maximum errors of the total potentials of a sphere in the uniform flow calculated by different panel methods for different numbers of panels.
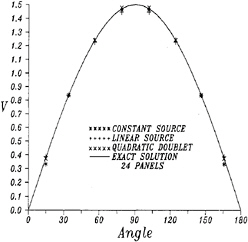
Figure 6: Velocity distribution calculated by different panel methods compared to the exact solutions.
called “nominal wake”. However, the interaction between a propeller and a ship hull will change the wake distribution, and the modified wake distribution is called the “effective wake”. In order to calculate the pressure fluctuations generated by propellers in the wake of hulls accurately, we need first to calculate the “effective wake”. Numerical solutions of Navier-Stokes equations can certainly provide a relatively accurate effective wake distribution. However, in the present method, a simple approach used by PUF-3A is adopted. This approach is based on the model established by Huang and Groves [5], and later modified by Wilson, Van Houten and Kerwin [16],[2].
Huang and Groves' model is used to calculate the effective wake of bodies of revolution in an incompressible, irrotational flow field. It assumes that the axial velocity gradient is small compared to the radial velocity gradient as in a boundary layer, and that the energy in a stream tube is constant. In order to apply this model to the non-axisymmetric flow, such as a ship hull wake, Wilson, Van Houten and Kerwin made the following assumptions [16],[2]:
-
“The circumferential gradient in the nominal wake is due to radial vortex lines convecting downstream with the mean velocity field” ,
-
“The radial vortex lines change only in length and move inward as the flow contracts. Their circumferential points remain steady”.
Therefore, one can find the following relationship from the vorticity equation:
(12)
where ![]() and
and ![]() are the radial vorticities of the effective wake and nominal wake, Ue and Ux are the axial effective velocity and axial nominal wake velocity, Δreff and Δrnom are the length of a vortex filament in the effective wake and nominal wake. Therefore, the Fourier coefficients of the velocities can be obtained.
are the radial vorticities of the effective wake and nominal wake, Ue and Ux are the axial effective velocity and axial nominal wake velocity, Δreff and Δrnom are the length of a vortex filament in the effective wake and nominal wake. Therefore, the Fourier coefficients of the velocities can be obtained.
Figure 7 and Figure 8 show the nominal wake measured in the towing tank and the effective wake calculated by PUF-3A of an 1100 TEU container ship built by CSBC (China Ship Building Corporation). Figure 7 shows circumferential distributions of the nominal wake and the effective wake at 0.7 propeller radius. Figure 8 shows radial distributions of the average nominal wake and the average effective wake. The calculated model mean effective wake of this case is 0.298, and it is very
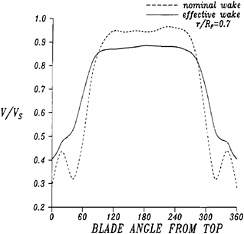
Figure 7: Circumferential distributions of the nominal wake and the effective wake of the CSBC 1100 TEU container ship at 0.7 propeller radius.
close to the value from a model propulsion test, 0.308.
3.2
Numerical Solutions of Propellers
Once the effective wake has been calculated, it can be input as the inflow of propellers. PUF-3A, a vortex lattice method based on the lifting surface theory, is used to solve propeller unsteady flow problems. The “unsteady flow” here actually means the propeller inflow varies spatially, such as the circumferentially nonuniform flow in the hull wake. However, it is equivalent to unsteady flow problems for propeller sections moving in this circumferentially varying inflow. Therefore, we can treat each angular position that propeller rotates to as a time step. An efficient time march scheme is adopted by PUF-3A to solve the unsteady flow problems in the time domain. PUF-3A also includes the calculations of cavitation extensions, and field point induced potentials. The detailed theory and schemes behind PUF-3A are described in [ 11],[12],[9],[2], and we will not repeat here.
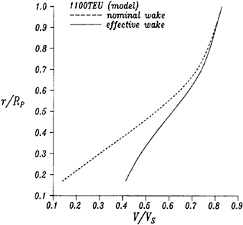
Figure 8: Radial distributions of the average nominal wake and the average effective wake of the CSBC 1100TEU container ship.
4
Propeller Generated Pressure Fluctuations
The calculations of the propeller generated pressure fluctuations include the considerations of the ship hull, propellers and the water surface (free surface.). As described in the last two sections, the solutions of the ship hull problems can be obtained by a panel method. On the other hand, propellers in the wake of hulls can be calculated by a lifting surface vortex lattice method. Once we include the free surface effect, the propeller induced potentials on the hull surface can be computed by coupling these methods. The induced pressure fluctuations then can be obtained by applying the Bernoulli's equation.
In the present method, the free surface effect is approximated by the hull images. For the low frequency free surface, the free surface boundary condition is approached by the zero frequency free surface condition (rigid surface boundary condition). That is, the normal derivative of the perturbation velocity potential should be zero on the free surface.
(13)
In order to satisfy this boundary condition, a positive hull image to the water plane is used, and the influence of the propeller on the hull sur
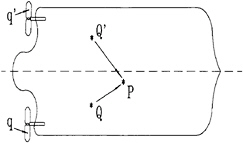
Figure 9: Depiction of the double hull with a propeller and its image
face should include the positive image of that propeller. The “positive image” means that the dipole strength at each panel on the “image hull” surface is the same as its corresponding panel on the “real hull” surface. Therefore, the solutions of the ship hull problems include the hull, the hull image, a propeller, and the propeller image. On the other words, for each panel on the hull surface, the total induced potentials include these from the hull, from the image hull, from the propeller, and from the image propeller.
Therefore, if we define the propeller induced potentials as ![]() pr, then the solutions of the dipole strength on the hull surface panels can be obtained by solving the following equation:
pr, then the solutions of the dipole strength on the hull surface panels can be obtained by solving the following equation:
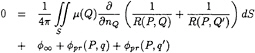
(14)
where P represents a field point on the hull surface, and Q,Q′ represent points on the hull surface and on the image hull surface, q and q′ represent points on the propeller and on its image as shown in Figure 9.
For the high frequency free surface, the perturbation velocity potential should be zero on the free surface.
![]() =0 (15)
=0 (15)
In order to satisfy this boundary condition, a negative hull image to the water plane is used, and the influence of the propeller on the hull surface should include the negative image of that propeller. The “negative image” means that the dipole strength at each panel on the “image hull” surface has the same magnitude as its corresponding panel on the “real hull” surface but with a different sign.
Therefore, the solutions of the dipole strength on the hull surface can be obtained by solving the following equation:
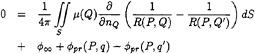
(16)
The potential solution is a function of position and time, therefore, it can be expressed as a Fourier series:
(17)
where P again represents a point on the hull surface, Ck is the Fourier coefficient, NH is the total number of Fourier series terms, and ω is the rotational speed of a propeller.
The pressure distribution on the hull surface thus can be calculated by using the Bernoulli's equation:
(18)
The ![]() term can be directly calculated from equation (17):
term can be directly calculated from equation (17):
(19)
and the total velocities can be calculated by making the gradients of potentials. Therefore, we can obtain the time varying pressure distribution on the hull surface. Again, this time varying pressure distribution can be represented as a Fourier series:
(20)
where Fk is the kth Fourier coefficient. A commonly used nondimensional parameter Kp is then defined as
(21)
Table 1: Geometric parameters of propeller 1242
|
r/R |
P/D |
c/D |
f0/C |
t0/D |
|
0.29 |
0.9469 |
0.1780 |
0.0253 |
0.0528 |
|
0.40 |
1.0530 |
0.2460 |
0.0253 |
0.0383 |
|
0.50 |
1.1498 |
0.3089 |
0.0266 |
0.0314 |
|
0.60 |
1.1690 |
0.3717 |
0.0225 |
0.0247 |
|
0.70 |
1.1150 |
0.4346 |
0.0153 |
0.0186 |
|
0.80 |
1.0192 |
0.4386 |
0.0095 |
0.0132 |
|
0.90 |
0.8961 |
0.2868 |
0.0058 |
0.0085 |
|
0.95 |
0.8172 |
0.1745 |
0.0021 |
0.0061 |
|
1.00 |
0.7281 |
0.0277 |
0.0001 |
0.0017 |
(There are no rake and no skew for this propeller)
5
Computational Results
In this section, we will show computational results from the present method.
5.1
Pressure Fluctuations on a Flat Plate Generated by Propellers
The calculations of propellers generated pressure fluctuations on a flat plate are similar to those of propellers generated pressure fluctuations on ship hulls. However, because the geometry is flat, the potentials at each panel induced by the plate itself will only come from the self panel. It can also be shown that the dipole strength on the flat plate equals to twice of the propeller induced potential plus the inflow potential, 2(![]() pr+
pr+![]() ∞). Therefore, the flat plate case can be used to check the calculations of cavitating propellers and pressure fluctuations.
∞). Therefore, the flat plate case can be used to check the calculations of cavitating propellers and pressure fluctuations.
In 1973, Weitendorf [15] published a series of experimental data of the pressure fluctuations on a flat plate measured in a cavitation tunnel. We will compare the computational results by the present method with these experimental data. The propeller we select is the propeller 1242, and it is a 5-blade propeller with geometric parameters shown in Table 1. We will show the calculated pressure fluctuations, KP, on the plate (at a/R=0.352) generated by this propeller in a nonuniform flow, and more computational results can be seen in [14]. Figure 10 shows the depiction of the propeller and the flat plate, and the wake data can be obtained from [15]. Figure 11 to Figure 14 show the comparisons between computational results and experimental data of propeller 1242 in a nonuniform inflow at different tunnel pressures. One can find
Figure 10: Depiction of the relative positions of the propeller and the flat plate.
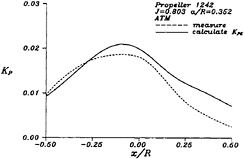
Figure 11: Comparison between the computational KP and the experimental values for propeller 1242 in a nonuniform inflow. The tunnel pressure is at the atmospheric pressure.
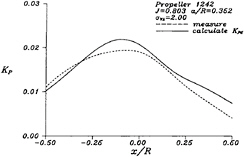
Figure 12: Comparison between the computational KP and the experimental values for propeller 1242 in a nonuniform inflow. The tunnel pressure is at the cavitation number σVA=2.0.
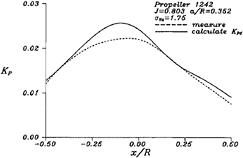
Figure 13: Comparison between the computational KP and the experimental values for propeller 1242 in a nonuniform inflow. The tunnel pressure is at the cavitation number σVA=1.75.
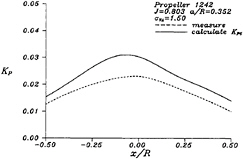
Figure 14: Comparison between the computational KP and the experimental values for propeller 1242 in a nonuniform inflow. The tunnel pressure is at the cavitation number σVA=1.5.
that the difference between the computational KP and the experimental value increases as the cavitation number decreases. This may be caused by the linear approximation of the cavity thickness in PUF-3A.
Figure 15: Discretized geometry of the ship hull used for the calculations. 900 panels are distributed on the hull surface.
5.2
Pressure Fluctuations on a Ship Hull Generated by Propellers
We then compute the pressure fluctuations on a ship hull generated by a cavitating propeller. The computational case we use here is the same case presented in Breslin, etc. [2]. The dimensions of this RO/RO ship model are listed in [2], and the propeller is designed at a speed of 22 knots and RPM of 126. In Breslin etc.'s paper, only lines of the stern part are provided. Therefore, a fake front part of the hull form is made, and is faired with the stern part. Figure 15 shows the panelized geometry of this ship hull with 900 panels. Figure 16 shows the nominal wake, and Figure 17 shows the calculated effective wake, and the model mean effective wake coefficient we calculate is 0.35. It is larger than the full-scale mean effective wake coefficient, 0.29 [2], and this is reasonable since the model mean effective wake should be greater than the full-scale mean effective wake. The propeller calculations show that the mean value of KT is 0.179, and it is very close to the experimental KT,0.182. The advance ratio, JA, is 0.580, and it is the same as the one obtained from the experiment. Figures 18
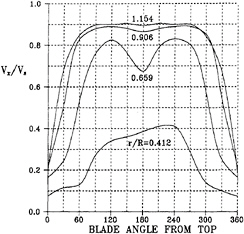
Figure 16: Nominal wake of the model test
and 19 show the computed cavitation extensions and cavitation volumes. The computed cavitation extensions near zero degree and before seem to be larger than those of the model test. However, we are not able to make the comparisons of the cavitation volumes since the measured data are not available. We know that PUF-3A assumes the cavitation occurs when the pressure on the propeller surface is less than the vapor pressure, and this assumption is more similar to the full-scale phenomenon. Also, Blake, Kerwin, etc. [1] point out that the scale effect of the sheet cavitation of a conventional model propeller geometry (as presented in this paper) shows delayed inception due to bubble dynamics. Therefore, the computational results are reasonable since cavitation extensions on a full-scale propeller should be larger than those measured by the model test for conventional propeller geometries.
Figure 20 shows the contour plot of KP at the blade frequency for zero-frequency free surface (rigid surface), and Figure 21 shows the contour plot of KP at the blade frequency for high-frequency free surface. It can be seen that the calculated pressure fluctuations at the high frequency free surface condition are lower than those at the rigid surface condition, especially for regions near the free surface. Table 2 then shows the calculated KP and measured KP [2]. The computational results at Gage 3 are apparently larger than the measured values for both the blade frequency and twice blade frequency. However, the computational results may be reasonable due to the following rea
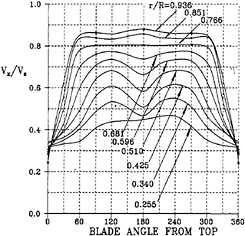
Figure 17: Effective wake calculated by PUF-3A.
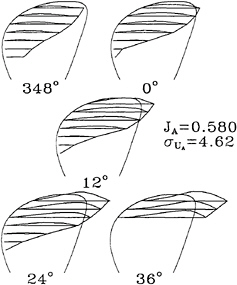
Figure 18: Computed cavitation extensions at 5 different representative angular positions
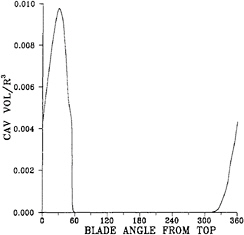
Figure 19: Calculated cavitation volumes.
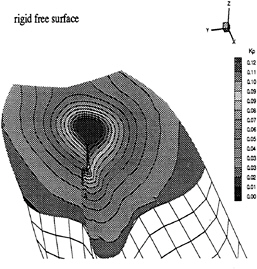
Figure 20: Contour plot of the blade frequency KP at the zero-frequency free surface (rigid surface) condition. Only the pressure fluctuations near the stern are shown here.
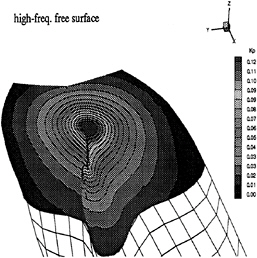
Figure 21: Contour plot of blade frequency KP at the high-frequency free surface condition. Only the pressure fluctuations near the stern are shown here.
sons: First, the pressure fluctuation at Gage 3 was measured by a hydrophone, and this hydrophone was placed outside the hull surface (Figure 8 of [2]). Therefore, we can expect that the ratio of KP at the measured point to the point just above it and on the hull surface, where KP is calculated, should be between 0.5 and 1.0. Form Table 2, we can see that the ratios are 0.650 and 0.585 for high-frequency free surface and rigid surface respectively, and both are within the range of 0.5 and 1.0. Secondly, the calculated results of pressure fluctuations generated by propellers in a model wake should be larger than those in a full-scale wake because the high wake zone of the model wake is wider than that of the full-scale wake. The location of this high wake zone is at the 12 o'clock direction of the propeller, therefore, the influence will be only on Gage 3, not on Gage 4 and Gage 5 whose locations are further away from the high wake zone. Our computational results agree with this statement when referring to Figure 9 in [2] and Figure 17 in [1]. For results at Gage 4 and Gage 5, the comparisons between the calculated values and the measured values are closer. The differences between the rigid surface results and the high-frequency free surface results are larger than those of Gage 3, and it is because that the free surface effect is strong at these two points. The computational results of twice blade
frequency KP are all larger than the measured values, and this is because the calculated cavitation extensions are larger than those of model tests.
Table 2: Comparison of measured and computational 2KP for the blade frequency and twice blade frequency under two water surface conditions.
6
Conclusions
In this paper, the flow field around a ship hull and its propeller is solved by coupling a higher order potential based panel method and a lifting surface vortex lattice method. The advantages of this method are: First, potentials on the ship hull surface can be directly calculated, and the computational time is less than a velocity based panel method since only one scalar term (potential) rather than three components of velocities needed to be computed. Secondly, the propeller induced potentials can be directly added to potentials on the ship hull surface. Thirdly, the ![]() term in the Bernoulli's equation can be easily calculated by differentiating the solved potentials in time. Finally, this higher order panel method has been proved to be more accurate than a low order panel method at the same given computational time.
term in the Bernoulli's equation can be easily calculated by differentiating the solved potentials in time. Finally, this higher order panel method has been proved to be more accurate than a low order panel method at the same given computational time.
The unsteady flow around a propeller is analyzed by MIT-PUF-3A. By investigating the computational results, it is found that the cavitation extensions calculated by PUF-3A are overestimated for conventional model propeller geometries when comparing to the model test results. This may be due to the cavity model in PUF-3A is corresponding to the full-scale.
The computational results have been compared with the experimental data. For pressure fluctuations on a flat plate generated by propellers in a nonuniform inflow, the computational results agree well with the experimental data for cavitation numbers higher than 1.5. For cavitation numbers lower than 1.5, the pressure fluctuations have been overestimated. For pressure fluctuations on a ship hull, the differences between the computed and measured values are relatively large at the point above the propeller. However, the differences can be explained, and the reasons are described in the paper. The comparisons between computed and measured values at other points are good.
For future works, the pressure fluctuations at the actual measured point of Gage 3 (outside the shil hull) should be calculated to confirm our inferences. The effective wake should be calculated by a more accurate method such as solving the Navier-Stokes equations. Finally, the computed hydrodynamic results should be incorporated with structure and vibration calculations.
Acknowledgment
This work was supported by the National Science Council, Taipei, and the project number is NSC-85– 2611-E-019–018. Additional support was provided by China Ship Building Corporation, Keelung, under project CSBC-RD-0372. The authors would like to thank Mr. Y.-H Lee at NTOU, Mr. J.-T.Chen and Mr.S.-K.Chou at USDDC for their assistances in generating hull panels.
References
[1] William K.Blake, Justin E.Kerwin, K. Meyne, E.Weiendorf, and J.Frisch. Design of apl c-10 propeller with full-scale measurements and observations under service conditions. In Transactions, SNAME, 1990.
[2] J.P.Breslin, R.J.Van Houten, J.E.Kerwin, and C-A Johnsson. Theoretical and experimental propeller-induced hull pressures arising from intermittent blade cavitation, loading, and thickness. Trans. SNAME, 90, 1982.
[3] H.-F.Chen. The application of higher order doublet panel method on computation of ship potential flow field (in Chinese). Master's thesis, Department of Mechanical and Marine Engineering, National Taiwan Ocean University, June 1995.
[4] J.L.Hess and A.M.O.Smith. Calculation of nonlifting potential flow about arbitrary three dimensional bodies. Journal of Ship Research, vol 8(no 2), September 1964.
[5] T.T.Huang and Groves N.C. Effective wake: theory and experiment. In 13th Symposium on Naval Hydrodynamics, Tokyo, October 1980.
[6] B.Hunt. The mathematical basis and numerical principles of the boundary integral method for incompressible potential flow over 3-d aerodynamic configurations . In Numerical Methods in Applied Fluid Dynamics, pages pp 49– 135, Academic Press, 1980.
[7] F.T.Johnson. A General Panel Method for the Analysis and Design of Arbitrary Configrations in Incompressible Flows. Technical Report CR-3079, NASA, 1980.
[8] F.T.Johnson, F.E.Ehlers, and P.E.Rubbert. A higher order panel method for general analysis and design applications in subsonic flow. In Proceedings of fifth International Conference on Numerical Methods in Fluid Dynamics, Springer Verlag, 1976.
[9] J.E.Kerwin and D.S.Greeley. Numerical Method for the Calculation of Field Point Potential Due to a Cavitating Propeller: MIT-PUF3FPP Program Documentation and Listings. Technical Report 83–11, MIT, Department of Ocean Engineering, June 1983.
[10] J.E.Kerwin, S.A.Kinnas, J-T Lee, and W-Z Shih. A surface panel method for the hydrodynamic analysis of ducted propellers . Trans. SNAME, 95, 1987.
[11] J.E.Kerwin and C-S Lee. Prediction of steady and unsteady marine propeller performance by numerical lifting-surface theory. Trans. SNAME, vol 86, 1978.
[12] S.A.Kinnas. A Numerical Method for the Analysis of Cavitating Propellers in a Nonuniform Flow, MIT-PUF-3 Program Documentation. Technical Report 83–7, MIT, Department of Ocean Engineering, June 1983.
[13] Sir Horace Lamb. Hydrodynamics. Cambridge University Press, sixth edition, 1932.
[14] Y.-C.Sun. Calculations of the exciting forces at a flat plate induced by an intermittently cavitating propeller (in Chinese). Master's thesis, Department of Naval Architecture, National Taiwan Ocean University , June 1995.
[15] E.A.Weitendorf. Experimentelle untersuchungen der durch kavitierende propeller erzeugten druckschwankungen. SCHIFF UND HAFEN, Jahrgang 25. Heft 11, November 1973.
[16] H.B.Wilson and R.J.Van Houten. A Program for Interpolation, Smoothing, Fourier Analysis, and Effective Wake Estimation of Propeller Inflow Fields: MIT-WKPROC Program Documentation and Listings . Technical Report 83–8, MIT, Department of Ocean Engineering, June 1983.
Appendix
Solutions of the Quadratic Dipole Strength Coefficients
As described in equation (11), the quadratic dipole strength distribution on the body surface, λ(ξ,η,ζ) , can be expressed in terms of the local coordinate system, (ξ,η), on the projection plane Σ (Figure 2):
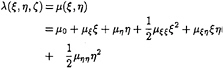
(22)
The coefficients µ0,µξ,µη,µξξ, µξη,µηη are determined from dipole strength at control points of neighboring nine panels (8 neighboring panels and the self panel) through a fitting process. If we now define λk as the dipole strength on the control point of the kth neighboring panel, then we can expressed the dipole strength of these 9 panels as follows:
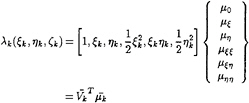
(23)
where k=1,2,…9. By the least squares, we have the array [![]() ]:
]:
(24)
Equation (24) shows that the dipole strength at each panel is determined by neighboring ND panels (ND=9 here). By substituting the above equations into the governing equation (equation (9)), we can obtain the induced potentials at a point P by the panel that Q is located. Assuming the point Q is at panel j, and the field point P is at panel i , then the induced potential at P by panel j, φij, can be expressed as follows:
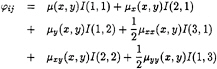
(25)
where,
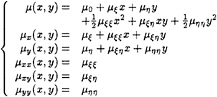
(26)
and
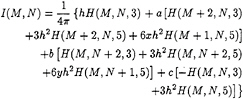
where c=ax2+by2–z0, and a and b are defined in equation (10). The I and H integrals are defined in Johnson [7].
The internal Dirichlet boundary condition specifies the total internal potential to be zero, and the induced potential at a point i on the inner surface by panel j, ![]() can be obtained from equations (25),(26),
can be obtained from equations (25),(26),
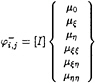
(27)
where
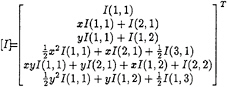
(28)
Notice that the dipole coefficient array can be related to the dipole strength from equation (23):
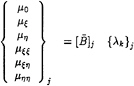
(29)
where {λk}j stands for the dipole strength array of ND neighboring panels to panel j, and
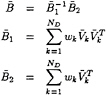
The discretized governing equation with the boundary condition thus becomes
(30)
where NP is total number of panels. ![]() ∞ can be obtained by the product of the inflow velocity and the position vector of the panel control point.
∞ can be obtained by the product of the inflow velocity and the position vector of the panel control point.
(31)
Substituting equations (27) and (29) into equation (30), then we have
(32)
After transferring the local panel indices to the global panel indices of λ and rearranging coefficients, we can get the following matrix form:
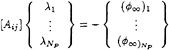
(33)
Solutions of this matrx will be the dipole strength at the control point of each panel. Therefore, the dipole strength coefficients can be obtained from equation (29), and the dipole strength distribution at each panel can be calculated by equation (23).
DISCUSSION
C.-A.Johnsson
SSPA Maritime Consulting AB, Sweden
I could make several comments to this interesting paper, but I have to limit myself to a short discussion of different boundary conditions.
The authors claim that the hydrophone does not have the same “mirror” effect as the flushmounted transducers. Comparative tests made at SSPA on a flat plate indicated, however, no significant differences between the transducers in this respect and therefore we used a hydrophone in one of the positions in order to increase the frequency range.
In connection with the investigation reports in the authors' Ref. [2], it was argued that the phywood roof with water above and below is more or less nonreflecting and thus does not correspond to the rigid surface case. This discussion is summarized in [D2] in which Prof. Breslin concludes that the appropriate conditions are the mean value between the free surface and rigid cases. In this particular case, the difference between the two cases is however much smaller than the differences between the calculations in the authors' paper and those from their Ref. [2], which is evident from Fig. D1. The latter are most likely due to differences in the peripheral volume variations obtained by the two calculations, which are not that large. Thus, Fig.D1 gives an indication of the degree of accuracy that can be expected from calculations of this kind.
The influence of the height and shape of the stern wave is not considered in the calculations. An indication about this influence is obtained by Fig. D2 which is based on measurements on the class of ships considered in the paper. It is evident from this figure that the Froude number is even more important than the draught. Having these results in mind, we at SSPA decided to concentrate on empirical methods for estimating the influence of the free surface rather than on theoretical methods. The first results of these efforts were published in [D2].
REFERENCES
D1. Breslin, J.P. and Andersen, P. “Hydrodynamics of Ship Propellers,” Cambridge Ocean Technology Series 3, Cambridge 1994.
D2. Johnsson, C.-A. “Simple Methods for First Estimate of Propeller Induced Pressure Fluctuations and Vibration,” PRADS 83, Tokyo and Seoul 1983.
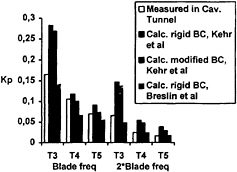
Figure D1: SSPA RO-RO ship model. Calculated and measured pressure fluctuations at three transducer positions in the stern
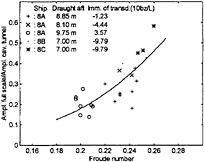
Figure D2: Comparison of pressure fluctuations in model and full scale. Blade frequency
AUTHORS' REPLY
The authors would first like to thank Mr. Johnsson for his valuable comments. Mr. Johnsson did point out some key points in this paper. Mr. Johnsson may be right about the effect of the hydrophone position. The authors will continue to investigate if the hydrophone extruded outside the ship having any influence on the pressure fluctuations.
Regarding the difference between the computations results presented in the paper and carried out by Breslin and Andersen [D1], the authors have carefully investigated the results and conclude that this difference can be explained.
First, we know that the ship effective mean wake is 0.29, and the model nominal mean wake is 0.436. The model effective mean wake calculated is 0.35 by the present paper, and 0.254 by [2]. Therefore, the result calculated by the present paper is more reasonable since the model effective mean wake should be higher than the ship effective mean wake. When authors use the effective wake distribution calculated by [2], the magnitudes of pressure fluctuations calculated decrease as expected. However, they are still higher than those calculated by [2] (as in Figure 1). This is apparently because the ship hull is modeled differently by two methods. Anyhow, we have to point out that the computations of the effective wake distributions in the present paper are rough due to the simplicity of the model.
Because the pressure fluctuations measured in SSPA cavitation tunnel were clearly smaller than those of the full scale, SSPA took the average of the max 5% as the measured values to have a better correlation with the full scale. This however may suggest that the experimental data are too low. On the other hand, as described in the paper, the computational results are supposed to be larger since it is according to the model effective wake distribution instead of the full scale effective wake distribution. This is also supported by the investigation of Blake et al. [1], in which they found that the surface forces calculated or measured by the model wake distribution were larger than those at the full-scale condition. The experimental results in HYKAT by Friesch, et. Al., [R1] (Fig.15) also showed the same tendency.
The figure Mr. Johnsson presented about the influence of the height and shape of the stern wave is very interesting. The authors will include a free-surface calculation to consider these effects in the future.
REFERENCE
[R1] J.Friesch, C.Johannsen, and H.G.Payer. Correlation studies on propeller cavitation making use of a large cavitation tunnel. Trans. SNAME, 100: pp. 65–92, 1992.
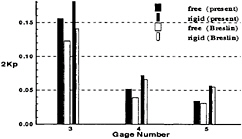
Figure 1: Calculated pressure fluctuations by the present method and by Breslin et al. at the blade frequency. Both methods use the same effective wake distribution.
















