12
Combustion Fluid Mechanics: Tools and Methods
Gerard M. Faeth
Department of Aerospace Engineering
University of Michigan
ABSTRACT
Current understanding and methods of modeling combusting fluid flows are briefly reviewed, emphasizing liquid-fueled buoyant turbulent diffusion flames that are of interest for developing more fire-safe aviation fuels. Liquid fuel/air combustion in both spray flames and pool fires is discussed, considering laminar diffusion flames, buoyant turbulent noncombusting flows, buoyant turbulent diffusion flames, and turbulent sprays and spray flames.
INTRODUCTION
Post-crash fires caused by the ignition of jet fuel released from damaged fuel systems are an important problem of aircraft fire safety. In particular, fuels with improved fire safety are needed to reduce injuries, loss of life, and the loss of property associated with post-crash aircraft fires. Naturally, a good understanding of the properties of liquid-fueled fires burning in air is a prerequisite for developing fire-safe fuels. Current knowledge about the combustion and fluid-flow phenomena of fires, as well as about available methods of predicting fire properties, are discussed briefly, with emphasis on the burning of liquid fuels both as sprays and pools. The following topics are discussed in turn: laminar diffusion flame structure, buoyant turbulent noncombusting flows, buoyant turbulent diffusion flames, and turbulent sprays and spray flames.
LAMINAR DIFFUSION FLAMES
Modeling Laminar Diffusion Flames
Post-crash aircraft fuel fires are invariably turbulent; nevertheless, an understanding of steady laminar flames is a prerequisite for understanding the complex, unsteady, three-dimensional combusting flow phenomena of turbulent flames. Many contemporary models treat turbulent flames as a collection of distorted laminar flames using laminar flamelet concepts. Thus, consideration of combustion fluid mechanics begins with understanding the properties of laminar flames, examining methods of modeling laminar flames, understanding laminar diffusion flame structure, and conceptualizing laminar diffusion flamelets.
Except for a few cases associated with flame ignition and attachment, laminar flames are either nonpremixed (diffusion) flames, where the supplies of fuel and oxidant are separated prior to combustion (e.g., a kerosene lamp flame), or premixed flames, where the fuel and oxidant have been combined before combustion (e.g., a laboratory Bunsen burner flame). Post-crash aircraft fuel fires either involve fuel sprays produced by ruptured fuel lines and fuel tanks to yield spray flames, or liquid fuel spread along aircraft surfaces and the ground to yield pool fires. In both cases, the most representative corresponding laminar flame is a laminar diffusion flame; therefore, this flame configuration will be emphasized, considering both models and experiments.
Contemporary methods of modeling laminar diffusion flames emphasize detailed fluid mechanics, transport, and chemical reaction mechanisms. The fluid mechanics and transport aspects of these models are usually based on the CHEMKIN family of computer codes developed by Kee et al. (1986, 1989, 1990, and 1991). These codes allow for effects of multicomponent transport, including thermal diffusion, and variable thermochemical and transport properties under ideal gas approximations that are appropriate for approximating flames at atmospheric pressure. One-dimensional steady calculations are typically based on available detailed chemical reaction mechanisms that provide information about the hundreds of reversible reactions needed to model complex hydrocarbon-fuel/air combustion chemistry (see Chelliah et al., 1992, for typical examples). In spite of relatively uncompromising treatments of fluid mechanics, transport, and chemical reactions, however, these models frequently ignore radiation, which affects temperature distributions in flames, even though radiation can be treated using available technology (Faeth et al., 1989). Other limitations of detailed models of laminar diffusion flames are discussed below.
Laminar Diffusion Flame Structure
An example of the structure of a heterogeneous liquid-fueled laminar diffusion flame burning in air is illustrated in Figure 12-1. Measured concentrations of major gas species and temperature (Kent and Williams, 1975), along with corresponding predictions (Chelliah et al., 1992), are plotted as a function of distance along the axis of an opposed-jet diffusion flame involving liquid n-heptane and air at a modest strain rate. The results illustrate the main features of laminar diffusion flames proposed by Burke and Schuman nearly 70 years ago: fuel vapor (C7H16) and oxygen (O2) diffuse from opposite sides toward a flame sheet where they react so that the concentrations of saturated combustion products (CO2 and H2O) and the temperature reach maximum values; subsequently, heat flows away from the flame sheet and preheats the fuel and oxygen streams and also provides enough heat to vaporize the fuel at the liquid surface. A more complete chemical reaction mechanism used for the predictions illustrated in Figure 1, however, captures features not considered by Burke and Schuman or other classical models, e.g., the decomposition of the fuel into CO and H2 and the leakage of small concentrations of O2 to the fuel-rich side of the flame.
Although the agreement between the predictions and the measurements illustrated in Figure 12-1 is encouraging, there are many problems that must be resolved before the structure of even very simple laminar diffusion flames can be reliably predicted. First of all, fuel-decomposition chemistry is not known very well for the heavy hydrocarbons present in aircraft fuels. More importantly, laminar diffusion flames of hydrocarbon fuels in air generally involve processes of soot chemistry that are not understood well enough to make predictions regarding concentrations of soot precursors and soot of comparable accuracy to those in Figure 12-1.

FIGURE 12-1 Measured and predicted structure of a laminar liquid-fueled diffusion flame. Measurements and predictions from Kent and Williams (1975) and Chelliah et al. (1992).
This is unfortunate because soot is an obvious feature of hydrocarbon-fueled fires and must be considered for accurate predictions of emissions of toxic materials and flame radiation (Köylü et al., 1991). But, concentrations of soot precursors and soot are relatively small in diffusion flames, which tends to mitigate the penalty of ignoring these properties for some purposes (Sunderland et al., 1995). Finally, full chemical reaction mechanisms are too computationally intensive at the present time for making tractable calculations in more than one independent variable. Various approximate methods have been developed to avoid these difficulties.
Laminar Diffusion Flamelet Concepts
Numerous reduced chemical reaction mechanisms have been proposed to provide computationally tractable ways of treating the multidimensional time-dependent laminar diffusion flames to be used in developing laminar flamelet concepts for turbulent flames. For present purposes, however, an effective way to model soot-containing hydrocarbon-fueled flames is needed, which is beyond the capabilities of current detailed reaction mechanisms. Fortunately, a reasonably effective alternative has been found.
The conserved-scalar formalism, combined with the laminar flamelet concept, has proven to be a reasonably effective way to treat soot-containing hydrocarbon-fueled turbulent diffusion flames (Bilger, 1976; Faeth, 1983, 1987, and 1996; Gore and Faeth, 1988a, 1988b). This approach is based on an extension of Burke and Schuman's ideas about laminar diffusion flames developed by Bilger (1976). In particular, Bilger noticed that scalar properties in soot-containing laminar diffusion flames could be correlated effectively in terms of the extent of mixing (usually represented either by the local mixture fraction, defined as the fraction of mass in a sample that originated in the fuel, or the local fuel-equivalence ratio). This behavior was observed for wide ranges of flame sheet combustion rates, or flame strain rates, in spite of the effects of finite reaction rates associated with fuel decomposition and soot chemistry. These correlations have been termed state relationships, and they are applied to turbulent flames by assuming that turbulent flames correspond to wrinkled laminar flames (Bilger, 1976).
Numerous measurements of state relationships for both liquid and gaseous hydrocarbon-fueled laminar diffusion flames have been reported (see Bilger, 1976; Faeth and Samuelsen, 1986; Gore and Faeth, 1988a, 1988b; Sivathanu and Faeth, 1990, for typical examples). Recent predictions using detailed chemical reaction mechanisms for laminar opposed-jet diffusion flames justify this behavior over strain rate ranges extending from near zero up to quenching conditions for nonsoot-containing flames (Lin and Faeth, 1991). This behavior is explained by the strong nonlinearity of reaction rates with temperature so that the flame structure changes
very little prior to abrupt extinction as strain rates are increased. Nevertheless, corresponding results for soot-containing flames have not been reported.
Although the laminar flamelet concept clearly is very helpful, the need for measurements in laminar flames to provide state relationships for soot-containing hydrocarbon-fueled flames is a significant limitation. Fortunately, universal state relationships have been found for hydrocarbon/air diffusion flames that circumvent this difficulty. A universal state relationship for the concentration of CO2 in diffusion flames is illustrated in Figure 12-2, where the universal state relationship function defined by Sivathanu and Faeth (1990), (ψi, is plotted as a function of the local fuel-equivalence ratio based on measurements for a variety of fuels and flame strain rates (see original sources for the details of these flames). The universal functions were motivated by the expectations of chemical equilibrium at fuel lean conditions; clearly, the equilibrium predictions illustrated in Figure 12-2 support this hypothesis. Although finite rate effects cause significant departures from equilibrium at fuel rich conditions, these departures are fortuitously universal. Thus, universal state relationships and laminar flamelet concepts provide a reasonable treatment of scalar properties in soot-containing diffusion flames pending improved understanding of finite-rate effects associated with fuel decomposition and soot chemistry, as well as the development of increased computer capabilities that will make consideration of detailed chemistry in practical calculations computationally tractable. The next problem involves predicting mixing levels (mixture fractions) within the buoyant turbulent flows of interest for post-crash fires.
BUOYANT TURBULENT NONCOMBUSTING FLOWS
Modeling Buoyant Turbulent Flows
Post-crash fires are reasonably represented by liquid-fueled buoyant turbulent diffusion flames. Given state relationships to find scalar properties in diffusion flames, methods of predicting mixing levels in liquid-fueled buoyant turbulent diffusion flames must be addressed. We must first understand noncombusting single-phase buoyant turbulent flows for the present before we address complications due to combustion and multiphase flow.
Several methods are commonly used to model noncombusting single-phase buoyant turbulent flows. Integral models are the simplest approach and are often used to treat unit flow processes (e.g., fire plumes, flows along ceilings, etc.) in comprehensive models of fires in structures. This approach is less attractive, however, for the open flames in post-crash fuel fires, and integral models will probably not be widely used to assist the development of fuels with improved fire safety. Thus, integral methods will not be considered here.
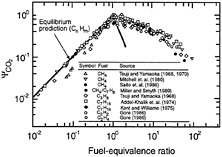
FIGURE 12-2 Measured universal state relationship for carbon dioxide species concentrations in laminar hydrocarbon-fueled diffusion flames. Source: Sivathanu and Faeth, 1990.
Turbulence models and numerical simulations of turbulence, however, should be of interest for fuel development and have already been applied to open liquid-fueled turbulent diffusion flames typical of post-crash fires (Tieszen et al., 1996).
The following discussion will begin with consideration of self-preserving flows that can be helpful for evaluating predictions of models of buoyant turbulent flows. The description and the findings of turbulence models and numerical simulations will then be considered.
Self-Preserving Buoyant Turbulent Flows
Many classical stationary turbulent flows become self-preserving sufficiently far from the source that effects of source disturbances are lost, and properly scaled flow properties become independent of the distance from the source. Such self-preserving flows are fundamentally important because they simplify the interpretation of scaled flow properties even though few flows reach these conditions in the real world. Self-preserving flows also are valuable for testing models of turbulent flows because source disturbances are avoided while modest streamwise development rates (in scaled variables) enhance numerical accuracy.
As discussed by Dai and Faeth (1995, 1996) and Dai et al. (1994, 1995a, 1995b), self-preserving buoyant turbulent flows have only been reliably established for round buoyant turbulent plumes. The development of these flows toward self-preserving behavior is illustrated in Figure 12-3 where mean mixture fractions, &fbar;, are plotted as a function of radius, r, normalized by streamwise distance from the virtual origin of the flow, (x-xo), for various values of (x-x o) normalized by the source diameter, d. Self-preserving variables are used for this plot (see Dai et al., 1994) for specification of all notation. Near the source, scaled profiles of &fbar; clearly vary with
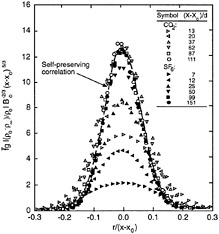
FIGURE 12-3 Measured mean mixture fraction distributions for round buoyant turbulent plumes plotted in terms of self-preserving variables. Source: Dai et al., 1994.
(x-x0)/d, however, once (x-x0)/d > 80, the scaled profiles become universal indicating that self-preserving behavior has been achieved. These results showed that self-preserving plumes were present farther from the source, were narrower in terms of r/(x-x0), and had larger mean scaled property values near the axis than was previously thought (Dai et al., 1994, 1995a, 1995b). This finding has significant implications for modeling flows.
Turbulence Model Predictions
Various properties of round self-preserving buoyant turbulent plumes have been used to evaluate models of buoyant turbulent flows. An example for the scaled self-preserving mean streamwise velocity, U, is plotted as a function of r/(x-x0) in Figure 12-4. These results involve the turbulence model predictions of Dai and Faeth (1995) and Pivovarov et al. (1993), along with the measurements of Dai et al. (1995a), Shabbir (1987), Ogino et al. (1984), Nakagome et al. (1979), and George et al. (1977). All these measurements were originally thought to represent self-preserving behavior, but this behavior has only been established for the recent findings of Dai et al. (1995a). In order to match the earlier measurements of U with their predictions, Pivovarov et al. (1993) were forced to increase substantially the well-known modeling constant, Cm, from its standard value; in contrast, the new measurements of U by Dai et al. (1995a) were in excellent agreement with predictions using standard turbulence modeling constants—resolving earlier criticism of the use of turbulence models. All other mean properties behaved the same way (Dai and Faeth, 1995).
Although the agreement between recent measurements and turbulence model predictions of mean properties in self-preserving round buoyant turbulent plumes is encouraging, corresponding predictions of turbulence properties are less satisfactory. An example of this behavior is illustrated in Figure 12-5, where measurements of the turbulent Prandtl/Schmidt number, σT, for self-preserving conditions are plotted as a function of scaled radial distance. The measurements show that σT progressively decreases from the axis to the edge of the flow rather than remaining constant at σT = 0.7 as prescribed by the most widely used turbulence models. Similar difficulties were encountered with other turbulence model predictions of turbulence quantities, even when using relatively advanced higher-order turbulence models. This raises questions about the capabilities of turbulence models to predict the properties of rapidly developing complex turbulent flows typical of post-crash fires, where good predictions of turbulence properties are necessary for making reasonable predictions of mean properties. Thus, pending
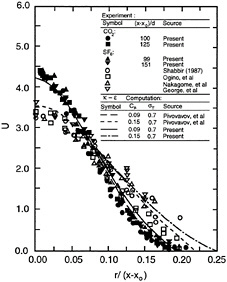
FIGURE 12-4 Measured and predicted profiles of mean streamwise velocities for self-preserving round buoyant turbulent plumes. Source: Dai et al., 1994.
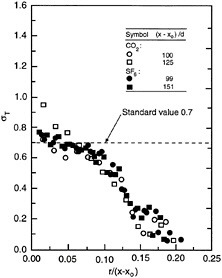
FIGURE 12-5 Measured turbulent Prandtl/Schmidt numbers for self-preserving round buoyant turbulent plumes. Source: Dai et al., 1995b.
well documented improvements in turbulence models for buoyant turbulent flows, measurements should be used as baselines for turbulence model predictions.
Numerical Simulations of Turbulence
Turbulent flows formally satisfy known three-dimensional time-dependent governing equations; therefore, direct numerical simulations potentially offer a model-free way of predicting the properties of buoyant turbulent flows. Unfortunately, the range of length and time scales of practical turbulent flows will far exceed available computational capabilities for the foreseeable future. Thus, simulations must either involve some level of modeling, typically modeling or approximating the small-scale features to yield a large-eddy simulation (LES), or limiting considerations to low Reynolds number quasi-like turbulence in order to gain insight about the properties of turbulence. Using either approach, these methods are of interest for modeling aspects of post-crash fires and have already been used for this purpose (see Tieszen et al., 1996). Thus, some awareness of this methodology is needed and is addressed in the following based on the computations of large fire plumes in a crossflow due to Baum et al. (1994).
The simulations of Baum et al. (1994) begin several fire diameters from the source where temperature variations are modest, where radiation can be ignored, and where the fire can be adequately characterized by release rates of heat and particulate matter. Although the computations involve the complete unsteady equations of conservation of mass, momentum, and energy, they are approximated by a two-dimensional time-dependent flow under the assumption that the component of the fluid velocity in the direction of the ambient wind is constant and equal to the wind speed. The calculations also do not extend to the smallest scales of the actual flow but are truncated by assuming a constant eddy viscosity that is three orders of magnitude larger than the actual viscosity of air. This limits small scale resolution to 5m to 15m, which is acceptable for the very large fire plumes considered in this study. Baum et al. (1994) should be consulted for other details concerning the model and the numerical method; the computer code is an adaptation of an approach used by McGrattan et al. (1994) to model enclosure fires.
The numerical simulations of Baum et al. (1994) were evaluated based on experiments of crude oil combustion in a crosswind by Evans et al. (1993). The experiment considered in the calculations involved a 204 MW fire source in a 4 m/s crosswind with an atmospheric lapse rate of -9.2K/km. Some typical results are illustrated in Figure 6 as plots of the measured (symbols) and predicted (solid line) center-line plume trajectory. The comparison between predictions and measurements is quite encouraging in view of the fact that these methods do not require the use of empirical turbulence modeling constants. This highlights the importance of the effects of large scale features on the mixing properties of buoyant turbulent plumes. Other examples of this and similar methodologies can be found in references cited by Baum et al. (1994), McGrattan et al. (1992), and Tieszen et al. (1996).
BUOYANT TURBULENT DIFFUSION FLAMES
Modeling Buoyant Turbulent Diffusion Flames
Modeling buoyant turbulent diffusion flames involves merging methods of finding the scalar properties of flames with methods for predicting the properties of noncombusting flows. Some typical approaches to this problem follow; methods of predicting flame radiation properties will be deferred for the present.
The most widely used methods of predicting the structure of buoyant turbulent diffusion flames exploit the k-e or k-e-g families of turbulence models (Bilger, 1976; Lockwood and Naguib, 1975). Bilger (1976) discusses the advantages of mass-weighted (Favre) averaged properties, although the quantitative effect of the averaging procedure is generally
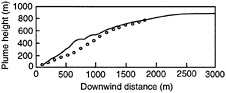
FIGURE 12-6 Measured and predicted trajectory of the center-line of a plume for a round 204 MW fire source in a 4 m/s cross-flow with a -9.2 K/km lapse rate. Symbols denote measurements and line denotes predictions.
Source: Baum et al., 1994.
quite modest for flames. Model constants are usually drawn from classical measurements for turbulent boundary layers and frequently employ gradient diffusion approximations that are known to be questionable for complex turbulent flows (Bilger, 1976; Gore and Faeth, 1988a, 1988b; Holen et al., 1991; Lockwood and Naguib, 1975). Calculations for more complex flows such as KAMELEON typically are based on the SIMPLEC method of Patankar and Spalding (Holen et al., 1991; Tieszen et al., 1996).
The two main methods for predicting scalar properties within buoyant turbulent diffusion flames are the conserved-scalar approach, and the eddy-dissipation or eddy-breakup approach. The conserved-scalar approach exploits state relationships for scalar properties, as discussed by Bilger (1976). The studies of Gore and Faeth (1988a, 1988b) represent typical examples of this approach for hydrocarbon-fueled buoyant turbulent diffusion flames. Concentrations of major gas species were found from state relationships obtained from measurements in laminar diffusion flames (discussed in connection with Figure 12-2). A state relationship for temperature was computed from this information while allowing for the relatively large fractions of combustion energy that are radiated from soot-containing flames. State relationships for soot concentrations were also used in these calculations, based on measurements in laminar flames, although later work shows that this procedure is questionable because of fundamental differences between soot processes in laminar and turbulent flames (see Faeth et al., 1989; Sunderland et al., 1995, for discussions of this issue). Finally, prescribed probability density functions of mixture fractions were used to compute mean and fluctuating values of mixture fractions found from solution of the governing equations; the results of Gore and Faeth (1988a, 1988b) used the clipped-Gaussian probability density function although the specific form of the function used does not seem to be very critical as long as it has at least two moments (Lockwood and Naguib, 1975).
The other main method for finding scalar properties in buoyant turbulent diffusion flames is based on eddy dissipation or eddy-breakup concepts. The studies of Holen et al. (1991) and Tieszen et al. (1986) represent typical examples of this approach. These methods involve the use of Burke/Schuman-like state relationships in conjunction with various approximations to treat finite-rate reactions, including the production and oxidation of soot. Unfortunately, current understanding of fuel-decomposition and soot reaction processes in diffusion flames is not highly developed, which severely limits capabilities for making reliable predictions of the structure of soot-containing flames. Thus, no method of treating the scalar properties of buoyant turbulent diffusion flames provides reliable estimates of soot concentrations, which are crucial for making accurate estimates of flame radiation properties.
Turbulent Diffusion Flame Structure
Two examples of turbulent diffusion flames will be considered: a buoyant turbulent round jet diffusion flame, which provides a well-defined and readily reproducible flame configuration, and a pool fire in an enclosure, which is more representative of practical fire environments. The results include measurements and predictions, with the predictions involving both the conserved scalar and eddy-dissipation methods.
Representative measurements and predictions of properties along the axis of a soot-containing buoyant turbulent round jet diffusion flame by Gore and Faeth (1988b) are illustrated in Figure 12-7. Predictions of scalar properties are based on the conserved scalar approach and include both mass-weighted (Favre) and conventional time averages. As discussed by Faeth and Samuelsen (1986), the differences between these averages is not very significant for predicting scalar properties. The structure of mean properties in turbulent diffusion flames is only qualitatively similar to the structure of laminar diffusion flames (see Figures 12-1 and 12-7). For the turbulent flame illustrated in Figure 12-7, mean fuel and oxygen concentrations are smallest, and mean combustion product concentrations are largest, in a reaction zone (a flame-containing region) for dimensionless streamwise distances, x/d, in the range 60 to 90. Unlike the laminar diffusion flame in Figure 12-1, however, there is considerable overlap of mean fuel and oxygen concentrations. This overlap is caused by laminar flamelets shifting back and forth along the axis in the flame-containing region, i.e., although fuel and oxygen do not coexist at a point, they both appear because given locations in the flame-containing region have finite residence times in the fuel-lean and fuel-rich portions of laminar flamelets.
Measurements and predictions of mean properties shown in Figure 12-7 are in reasonably good agreement, including proper treatment of the overlap between fuel and oxygen and the presence of large concentrations of CO at fuel rich-conditions due to partial oxidation of the fuel. This behavior is typical of the performance of the conserved-scalar formalism
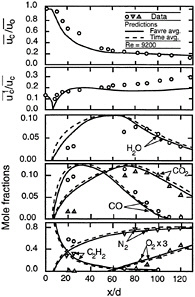
FIGURE 12-7 Measured and predicted properties of a round buoyant turbulent acetylene/air diffusion flame. Source: Gore and Faeth, 1988b.
when combined with state relationships. The main deficiency of these predictions involves predictions of velocity fluctuations in the plume region of the flow beyond the flame-containing region. This problem is caused by deficiencies of the simple k-e-g turbulence model used by Gore and Faeth (1988b), which does not properly account for buoyancy/turbulence interactions in the plume. Unfortunately, existing advanced turbulence models offer little improvement of this deficiency (Dai and Faeth, 1995). As discussed earlier, relatively poor predictions of turbulence properties are typical of most turbulence models for buoyant turbulent flames and are a concern when these methods are used to treat complex flows where rates of flow development are strongly influenced by turbulence levels.
Representative measurements and predictions of the properties of+ a diffusion flame in an enclosure, based on the eddy-dissipation approach of Holen et al. (1991), are illustrated in Figure 12-8. Results shown include measured and predicted mean temperatures at two conditions (averages for the floor and for the enclosure) as a function of time as the fire develops. The agreement between measurements and predictions for this rather complicated fire environment is quite good; predictions of other properties of the enclosure fire were also quite good. Nevertheless, many aspects of the model used for these predictions require additional study and more detailed evaluation than is possible using the comprehensive properties of enclosure fires.
Modeling Flame Radiation
Flame radiation causes heating of materials in flame environments, which affects fire spread and growth rates. Radiation heat transfer is particularly important for soot-containing hydrocarbon-fueled flames because large fractions (as much as 60 percent) of the chemical energy release are radiated to the surroundings by a continuum of radiation from soot (Faeth et al., 1989). Current methods of modeling flame radiation are described next before representative measurements and predictions of radiation for buoyant turbulent diffusion flames are considered.
Reviews of available methods of predicting radiation in turbulent flame environments are presented by Faeth et al. (1989), Gore and Faeth (1988a, 1988b), Gore et al. (1987), and references cited therein. Naturally, information about the scalar structure of flames is a prerequisite for making radiation predictions, and it is assumed in the following description that the necessary properties, based on flame structure predictions that have already been discussed, are known. Issues that must be addressed include consideration of the spectral properties of radiation, the method used to estimate soot concentrations, and the treatment of turbulence/radiation interactions.
Practical flames exhibit significant effects of both gasband radiation and continuum radiation from soot. These effects are important because of the wide temperature variations of practical flames and the tendency of the largest soot concentrations to be associated with the highest-temperature regions of the flows. Predictions of soot concentrations in
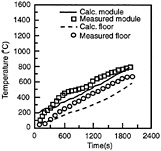
FIGURE 12-8 Measured and predicted temperatures for a rectangular liquid pool fire burning in air within an enclosure. Source: Holen et al., 1991.
flames have already been discussed. Current methods range from state relationships for soot volume fractions (Gore and Faeth, 1988a, 1988b) to empirical soot reaction expressions (Holen et al., 1991); neither approach is well established so that accurate estimates of soot concentrations in flames are probably the greatest limitation for making accurate estimates of flame radiation. Finally, buoyancy/turbulence interactions increase mean radiation levels as much as two to three times the estimates based on mean scalar properties in flames (Faeth et al., 1989); therefore, accurate treatment of these effects is also important. The radiation treatment by Holen et al. (1991) employs the gray gas approximation and uses mean properties as the basis of predictions while ignoring turbulence/radiation interactions, which is typical of the simplest models of flame radiation. At the other end of the spectrum, the methods used by Gore and Faeth (1988a, 1988b) are reasonably comprehensive and attempt to treat non-gray gas properties and the effects of turbulence radiation interactions; this approach is described next.
Predictions of scalar properties for the flames studied by Gore and Faeth (1988a, 1988b) have already been discussed in connection with Figure 12-7. As noted there, state relationships were used for all scalar properties, including soot concentrations, while a k-e-g turbulence model was used to find the distributions of mean and fluctuating mixture fractions. The prescribed clipped-Gaussian mixture fraction probability density function then yielded predictions of scalar property distributions following the conserved-scalar formalism (Lockwood and Naguib, 1975). Radiation predictions were made by first computing spectral radiation intensities for particular paths through the flames and then integrating these results over wavelength and direction in order to estimate radiant heat fluxes. These computations were made ignoring scattering, which is reasonable for typical soot particles and gases in the infrared portion of the spectrum of interest for flame radiation.
These predictions involved solving the equation of radiative transfer for given radiation paths, using the Goody statistical narrow-band model with the Curtis-Godson approximation for inhomogeneous gas paths. The computation considered the gas bands of CO2, H2O, CO, the fuel, and continuum radiation from soot (Ludwig et al., 1973). These calculations are straightforward when effects of turbulent fluctuations are ignored, based on mean scalar property predictions along the radiation path. Effects of turbulent fluctuations were also considered based on a stochastic method where distributions of mixture fractions through the flames were numerically simulated using classical statistical time-series methods. Scalar properties along the paths were then found from the state relationships and spectral radiation intensities were predicted as before for each realization of mixture fractions along the path. Sufficient realizations were considered to compute statistically-significant radiation properties (Faeth et al., 1989).
Flame Radiation Predictions
Methods of predicting the radiation properties of buoyant turbulent flames have been evaluated with reasonably good success for a variety of soot-free and soot-containing flames (Faeth et al., 1989; Gore and Faeth, 1988a, 1988b; Gore et al., 1987). The results of Gore et al. (1987) are of interest for present purposes because they demonstrate capabilities of handling large-scale fires typical of post-crash fires. Present considerations will concentrate on the findings of Gore and Faeth (1988a) instead, however, because they illustrate radiation properties for flames with reasonably large soot concentrations, typical of liquid fuel fires.
Typical predictions and measurements of the radiation properties of round soot-containing buoyant turbulent diffusion flames (based on Gore and Faeth, 1988a) are illustrated in Figure 12-9. These conditions involve an ethylene/air flame at atmospheric pressure with a heat release rate of roughly 30 kW and a mean luminous flame height of roughly 500 mm. Spectral radiation intensities are shown as a function of wavelength for horizontal paths through the axis of the flame at various heights above the burner exit. The gas bands of water vapor and carbon dioxide can be seen, but the spectra are clearly dominated by continuum radiation from soot,
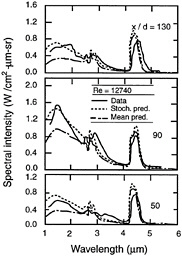
FIGURE 12-9 Measured and predicted spectral radiation intensities for horizontal paths through the axis of acetylene-fueled round buoyant turbulent diffusion flames burning in air. Source: Gore and Faeth, 1988b.
which reaches a maximum intensity near 1500 nm. Not surprisingly, radiation intensities also reach maximum values near the mean luminous flame height, although radiation levels in the plume are still reasonably large. Two predictions are shown, a mean property prediction and a stochastic prediction allowing for turbulence/radiation interactions. As noted earlier, turbulence/radiation interactions significantly increase radiation levels compared to estimates based on mean scalar properties. Nevertheless, differences between the two predictions are comparable to the uncertainties of estimates of soot concentrations and the levels of continuum radiation from soot. Thus, a limited understanding of soot processes in the buoyant turbulent diffusion flames is probably the greatest impediment to making accurate estimates of radiation from practical flames at the present time.
TURBULENT SPRAYS AND SPRAY FLAMES
Modeling Sprays
Sprays and spray flames are an important aspect of post-crash fires. Aircraft fuel is dispersed during crashes by ruptured fuel lines and fuel tanks, by aerodynamic effects due to the motion of the aircraft or wind relative to the aircraft over liquid-fuel streams created by ruptures, and also by splashing or drop formation due to turbulent primary breakup of liquid fuel spilling from ruptured fuel tanks onto aircraft surfaces or the ground. All these effects enhance mixing between the air and the liquid fuel, which creates regions capable of rapid combustion either as premixed flames or as intense spray diffusion flames. Naturally, fuel modifications that would inhibit the formation and mixing of liquid fuels as sprays will tend to enhance resistance to the initiation of post-crash fires. Thus, it is likely that consideration of fuel atomization and spray combustion will be an important aspect of the development of fuels with improved fire safety. Motivated by these considerations, the current understanding of turbulent sprays and spray flames is briefly reviewed beginning with a discussion of contemporary methods of modeling sprays, emphasizing processes in dilute sprays where liquid volume fractions are small, where processes of drop breakup have ended, and where the dispersed phase consists of polydisperse spherical drops. Primary and secondary drop breakup are then considered, prior to a discussion of spray structure and evaluations of predictions with available measurements.
The present discussion of the structure and modeling of sprays is brief, but more details can be found in articles by Chen and Davis (1964), Dai et al. (1997), Faeth (1983, 1987, 1996), Grant and Middleman (1966), Hsiang and Faeth (1992, 1993, 1995), Shearer et al. (1979), Ruff et al. (1991), Shuen et al. (1983), Solomon et al. (1985a, 1985b, 1985c), Tseng et al. (1992), Wu and Faeth (1993, 1995), Wu et al. (1992, 1995), and references cited therein. Some of the generic properties of sprays can be considered in a simple way by studying the properties of an ideal spray where spray atomization immediately yields infinitely small gas-and liquid-phase elements (small drops and bubbles). In these circumstances, the assumption that both phases have the same velocity and temperature and are in thermodynamic equilibrium can be adopted so that the flow can be analyzed using the locally-homogeneous flow (LHF) approximation of multiphase flow theory (Faeth, 1983). This implies that the multiphase flow acts like a single-phase flow but with a more complex equation of state. Then the flow can be analyzed using the conserved-scalar formalism combined with state relationships for scalar properties under the laminar flamelet concept.
Typical spray state relationships under the LHF approximation, providing scalar properties as a function of mixture fraction, are plotted in Figure 12-10. The results are for an n-pentane spray burning as a diffusion flame in air at normal temperature and pressure (NTP), drawn from Mao et al. (1980, 1981). The state relationships for sprays under the LHF approximation are qualitatively similar to state relationships for gas-fueled hydrocarbon/air diffusion flames, with maximum temperatures and combustion product concentrations at a flame sheet condition where the mixture is stoichiometric. The main difference between the state relationships for sprays and those for gaseous fuels involves the
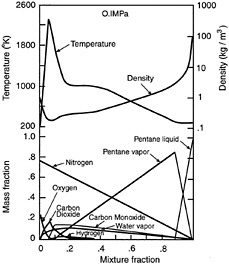
FIGURE 12-10 Predicted state relationships for major gas species for an n-pentane spray burning in air at atmospheric pressure. Source: Mao et al., 1980.
presence of liquid and the large density variation of the flow at large mixture fractions. The results illustrated in Figure 12-10 show that the presence of liquid is limited to mixture fractions of greater than 0.9 while combustion phenomena associated with the maximum temperature region are limited to mixture fractions of less than 0.1, which is typical of most practical combusting sprays. Thus, most spray phenomena occur at relatively cool conditions, remote from combustion phenomena, so that they can be studied without considering the effects of evaporation and combustion as a realistic first approximation—a practice that has been widely adopted by workers in the field (Faeth, 1996).
Although the LHF approximation is helpful for gaining insights into spray properties, numerous evaluations show that LHF models tend to overestimate the rate of development of sprays, indicating that the effects of separated flow are important (Faeth, 1983, 1987, 1996). Continuum formulations provide one approach to treating separated flow, but they are not used widely for sprays because of problems of computational efficiency for dilute dispersed flows.
Discrete-element formulations are probably the most popular separated flow treatments of sprays. These treatments typically involve a Eulerian formulation for the continuous phase, a Lagrangian formulation to track the motion and transport of representative drop groups through the flow, and terms from both formulations to treat interphase transport (Faeth, 1983, 1987). There are two main discrete-element formulations: deterministic separated flow (DSF) where dispersed phase (drop)/turbulence interactions are ignored; and stochastic separated flow (SSF) where drop/turbulence interactions are considered. The DSF approach is not very realistic, however, because drop motion is limited to deterministic trajectories prescribed by their initial conditions and mean gas properties throughout the dispersed flow field. As a result, DSF predictions exhibit unphysical laminar-like behavior where drops collect in low velocity regions.
The SSF methods involve treatment of gas-phase properties very similar to single-phase turbulent diffusion flames, using either the conserved-scalar formalism and state relationships as a function of gas-phase mixture fractions or eddy-dissipation (or eddy-breakup) methods to treat gas-phase scalar properties. Because of limitations on computational tractability, these models integrate over processes on the scale of drop sizes and assume a quasi-steady interphase transport of mass, momentum, and energy. Interphase transport typically involves consideration of particle inertia, drag forces, virtual mass forces, Bassett history forces, body forces, Magnus forces, and Saffman lift forces (Faeth, 1983, 1987). The variation of drop properties (drop life histories) are computed for a statistically significant number of drops throughout the flow, and these results are used to provide the dispersed-phase source terms needed for computations of continuous-phase properties.
Three main drop/turbulence interactions are of interest for SSF models: the dispersion of drops by turbulence; the modification of continuous-phase turbulence properties by transport from drops; and the modification of interphase transport rates by turbulence fluctuations. Current treatments of drop dispersion by turbulence have received significant attention; they involve numerical simulations of turbulence using a variety of approximate methods or, more recently, statistical time series techniques (Faeth, 1987). Given a simulation of the time-varying properties of the continuous-phase, corresponding predictions of drop life histories in this environment are straightforward. These methods also tend to compensate for the effects of turbulence fluctuations on interphase transport rates, at least for fluctuations at scales larger than drop sizes, which are generally the most important for combusting sprays. The earliest SSF simulations of drop dispersion were based on interactions between drops and a succession of uniform-property integral-scale-sized eddies, with eddy velocities found by random selections from the probability density functions of velocities, which were determined using k-e-g turbulence model predictions. Subsequent work has been based on more sophisticated statistical time series simulations of continuous-phase flow properties although turbulence models are still most often used to find flow properties within complex turbulent combusting spray environments (Faeth, 1987, 1996).
In contrast to information about the effects of turbulent dispersion, current information about the modification of turbulence properties by drops is very limited. Fortunately, these effects do not have a large impact on the gross properties of dilute sprays. The effects of turbulence on interphase transport have received significant attention but are not very important compared to other uncertainties about analyzing sprays. Thus, a limited understanding of drop atomization, or breakup properties, is the greatest limitation for making accurate predictions of the properties of spray flames. This issue will be considered next before discussing overall predictions of spray structure.
Drop Breakup
Processes of liquid atomization or drop breakup are important for reliable modeling of sprays. In particular, accurate estimation of drop breakup is crucial because these properties establish the initial conditions for the rest of the flow. In addition, spray processes tend to be quite sensitive to initial drop sizes (or atomization quality) because drop transport rates tend to be proportional to drop diameter squared (Faeth, 1983, 1987, 1996). Finally, recent work has confirmed traditional ideas that sprays involve the primary breakup of liquid columns and sheets to form large irregular ligaments and drops, which subsequently break up into smaller round drops by secondary breakup (Ruff et al., 1991). These two breakup mode will be discussed, in turn, emphasizing the mechanisms most relevant to sprays associated with post-crash fires.
Recent observations have highlighted the importance of flow properties at the beginning of atomization on the near-injector structure of sprays and the nature of primary breakup (Faeth, 1996; Ruff et al., 1991; Wu and Faeth, 1993, 1995; Wu et al., 1992, 1995). In fact, experiments with high velocity liquid jets injected into still air at atmospheric pressure have shown that the absence of vorticity and liquid turbulence at the jet exit entirely inhibits primary breakup and yields a stable liquid stream very similar to liquid cutting jets (Wu et al., 1995). Similar experiments show that the aerodynamic effects of liquid jets in still gases remain small for liquid/gas density ratios greater than 500 (Wu and Faeth, 1993). This behavior is logical because solid surfaces generate the liquid vorticity needed to produce drops by primary breakup more effectively than low density gases.
Past observations of primary breakup suggest that an important mechanism of primary breakup for post-crash fires involves the turbulent primary breakup mechanism. This mechanism has been studied for liquid jets injected into still air with fully-developed turbulent pipe flow at the jet exit (Wu and Faeth, 1993, 1995; Wu et al., 1992). These studies were intended to study practical pressure atomized sprays, but the primary breakup of liquid jets from ruptured fuel lines should be similar. More recent work has involved wall jets, where a turbulent boundary layer grows along the wall, the surface of the wall jet becomes roughened as it is approached by the outer edge of the growing turbulent boundary layer, and drop formation by the turbulent primary breakup mechanism begins once the kinetic energy of turbulent eddies near the liquid surface exceeds the surface-tension energy required by drops of comparable size (Dai et al., 1997). Past studies of the turbulent primary breakup of wall jets were motivated by the primary breakup in the bow waves of ships and hydrofoils. However, the mechanism is analogous to the primary breakup process of liquid fuels spilling along the surfaces of an aircraft or along the ground in connection with a post-crash fire.
Past studies of the turbulent primary breakup of free jets and wall jets have established criteria for the onset and end of drop formation at the liquid surface and for the variation of drop size and velocity distributions after turbulent primary breakup as functions of conditions along the liquid surface (Dai et al., 1997; Wu and Faeth, 1993, 1995; Wu et al., 1992). These studies have shown that drop size distributions after turbulent primary breakup satisfy the universal root normal distribution function with the ratio of the Sauter mean diameter (SMD) to the mass median diameter (MMD) equal to 1.2; therefore, this two-parameter distribution function is fully defined by the SMD alone. It was also found that mean and fluctuating drop velocities after turbulent primary breakup are independent of drop size and approximate local mean and fluctuating velocities near the liquid surface.
An example of the properties of turbulent primary breakup in a round liquid jet in still gases, with fully-developed turbulent pipe flow at the jet exit, is illustrated in Figure 12-11 (taken from Wu and Faeth, 1993). The SMD after turbulent primary breakup, normalized by the radial integral scale of
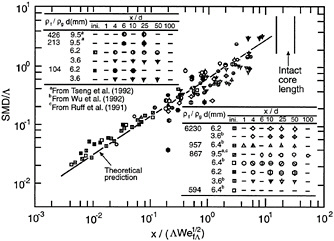
FIGURE 12-11 Measured SMD after turbulent primary breakup of round liquid jets in still air with fully developed turbulent pipe flow at the jet exit. Source: Wu and Faeth, 1993.
the liquid turbulence, Λ, is plotted as a function of distance along the liquid surface, x, and a characteristic Weber number, WefΛ. Measurements taken from Tseng et al. (1992), Wu et al. (1992), Ruff et al. (1991), and Wu and Faeth (1993) are plotted in the figure for a variety of liquid/gas density ratios, rf/rg, and jet exit diameters, d, along with a theoretical prediction based on a simplified phenomenological analysis of the primary breakup process. It is evident that an excellent correlation is achieved with good agreement between predictions and measurements; similar findings have been obtained for turbulent primary breakup in wall jets (Dai et al., 1997). These results also show that predictions of liquid jet intact lengths by Chen and Davis (1964) are a logical outcome of drop formation by turbulent primary breakup reaching the diameter of the liquid jet itself. In spite of this progress, however, information about the rate of drop formation by primary breakup, as well as effects of drops enhancing turbulent primary breakup by falling back into the liquid surface, are not well understood, which will limit capabilities to quantitatively model sprays formed by turbulent primary breakup during post-crash fires.
Other studies of nonturbulent and turbulent primary breakup processes have shown that dispersed phases near liquid surfaces actually are quite dilute, with liquid volume fractions less than 0.1 percent (Ruff et al., 1991; Faeth, 1996). This implies that well developed models of dilute dispersed-flows and sprays can be applied to so-called ''dense-spray" regions near liquid surfaces. In addition, primary breakup by known nonturbulent and turbulent mechanisms yields drops that are intrinsically unstable to secondary breakup; therefore, secondary breakup clearly is an important factor in determining drop sizes in sprays.
Past studies of secondary breakup have been reviewed in several recent papers (Faeth, 1996; Hsiang and Faeth, 1992, 1993, 1995). Most existing studies of secondary breakup have been limited to drops subjected to shock-wave disturbances that simulate a step change of the local gas velocity relative to the drop; this condition is of interest because it approximates the environment of a drop after primary breakup. Most past studies of secondary breakup have been limited to liquid/gas density ratios greater than 500, which fortunately corresponds to drops in post-crash flames. In these circumstances, drop breakup involves bag, multimode, and shear breakup regimes, as drop Weber numbers increase. The jump conditions for these breakup regimes, giving drop size and velocity distributions, have been resolved (Hsiang and Faeth, 1992, 1993, 1995). Similar to primary breakup, the drop size distributions satisfy the universal root normal distribution function with MMD/SMD = 1.2, although drop velocity distributions are rather complex functions of drop sizes due to varying drop drag properties with drop size. The surprising feature of the findings is that drop sizes after secondary breakup are strong functions of liquid viscosity but are relatively independent of the surface tension. This behavior is the opposite of the behavior of drop sizes after turbulent primary breakup (Figure 12-11) where drop sizes are a strong function of surface tension but are relatively independent of liquid viscosity!
Although past work has supplied the jump conditions needed to estimate secondary breakup properties, these results suggest that secondary breakup should be treated as a rate process rather than by jump conditions, in some instances (Hsiang and Faeth, 1995). For example, secondary drop breakup times are tb = (5–6)(rf/rg)1/2do/uo, where do and uo are the initial drop diameter and relative velocity. Unfortunately, these times often are not small compared to drop residence times in dense spray regions. Secondary drop breakup processes can also extend more than 100 do, which is also not small for practical sprays. This implies that secondary breakup should be treated as a rate process rather than by jump conditions in some instances. Unfortunately, available information about the rate aspects of secondary breakup is very limited, which limits capabilities for modeling this potentially important spray process (Faeth, 1996).
Spray Predictions
Available models of simple turbulent dispersed flows are computationally tractable and reasonably effective. Numerous studies attempting to evaluate various models of nonevaporating, evaporating, and combusting sprays have been reported (see examples in Faeth, 1983, 1987, 1996; Mao et al., 1980, 1981; Ruff et al., 1991; Shearer et al., 1979; Shuen et al., 1983, 1985; Solomon et al., 1985a, 1985b, 1985c; Tseng et al., 1992; and references cited therein. A representative evaluation of spray models follows to illustrate the methodology.
The spray model evaluation to be considered involves a nearly monodisperse, round-turbulent-particle-laden jet, injected vertically downward, which was one of several examples considered by Shuen et al. (1983, 1985). The initial conditions of this flow were well documented to provide mean and fluctuating velocities of both phases and the mass flux distribution of the dispersed phase. Subsequent measurements of these properties were carried out over the flow field in order to evaluate the predictions. One model evaluated by the measurements involved using the LHF approximation in conjunction with the conserved-scalar formalism and state relationships analogous to Figure 12-10 to treat the multiphase flow. A second approach involved an SSF model with the turbulence structure approximated by random integral-sized eddies. In both cases, the continuous phase was treated using a conventional k-e-g turbulence model with standard turbulence model constants that had been well established based on measurements in turbulent single-phase flows.
A typical plot of the measured and predicted structure of the round-turbulent-particle-laden jets from Shuen et al.
(1985) appears in Figure 12-12. These results refer to spherical glass particles having an SMD of 0.119 mm and a ratio of the mass flow rate of particles to the mass flow rate of air, LR = 0.2, at a streamwise position of x/d = 20; results at other conditions were similar. Parameters plotted on the figure include radial profiles of mean particle mass flux, G, streamwise particle velocity, &ubar; p, streamwise and cross-stream particle velocity fluctuations, &ubar;´ p and &vbar;´p, and particle turbulence kinetic energy, kp, with the subscript c denoting center-line quantities. Because separated-flow effects are important for the large particles present in this flow, the LHF predictions vastly overestimate the rate of development of the flow. Predictions of the SSF model, however, are quite satisfying, including good predictions of the fluctuating properties of the particles. Thus, the rather simple stochastic simulation of particle trajectories used by Shuen et al. (1985) appears to capture the most important particle turbulence interactions in this flow.
Evaluating models of sprays involving polydisperse effects, evaporation, and combustion becomes progressively more challenging as requirements for both measurements and model predictions increase. Some typical examples involving reasonably well-defined initial conditions include the results

FIGURE 12-12 Measured and predicted mean and fluctuating particle properties in a round turbulent particle/air jet in still air at NTP. Source: Shuen et al., 1985.
for round turbulent nonevaporating and evaporating sprays from Solomon et al. (1985a, 1985b, 1985c); however, there are numerous other examples in the literature (Faeth, 1983, 1987, 1996). It is generally agreed that the structure of sprays can be predicted reasonably well, given a good prescription of initial and boundary conditions, using typical contemporary spray models. Thus, the major limitation of this technology involves the proper definition of initial conditions, especially reliable definitions of atomization properties.
REFERENCES
Baum, H.R., K.B. McGrattan, and R.G. Rehm. 1994. Simulation of smoke plumes from large pool fires. Pp. 1463–1469 in 25th International Symposium on Combustion held July 31–August 5, 1994, at the University of California in Irvine, California. Pittsburgh, Pa.: The Combustion Institute.
Bilger, R.W. 1976. Turbulent jet diffusion flames. Progress in Energy and Combustion Science 1:87–109.
Chelliah, H.K., M. Bui-Pham, K. Seshadri, and C.K. Law. 1992. Numerical descriptions of the structure of counterflow heptane-air flames using detailed and reduced chemistry with comparison to experiments. Pp. 851–857 in 24th International Symposium on Combustion held July 5–10, 1992, at the University of Sydney in Sydney, Australia. Pittsburgh, Pa.: The Combustion Institute.
Chen, T.-F., and J.R. Davis. 1964. Disintegration of a turbulent water jet. Journal of Hydraulic Division 90HYI:175–188.
Dai, Z., and G.M. Faeth. 1995. Evaluation of approximate models of buoyant turbulent flows. Pp. 141–146 in Proceedings of International Conference on Fire Research and Engineering, held in September 11–14, 1995, in Orlando, Florida. Boston, Mass.: Society of Fire Protection Engineers.
Dai, Z., and G.M. Faeth. 1996. Measurements of the structure of self-preserving round buoyant turbulent plumes. Journal of Heat Transfer 118(2):493–495.
Dai, Z., L.-K. Tseng, and G.M. Faeth. 1994. Structure of round, fully-developed, buoyant turbulent plumes. Journal of Heat Transfer 116(2):409–417.
Dai, Z., L.-K. Tseng, and G.M. Faeth. 1995a. Velocity statistics of round, fully-developed buoyant turbulent plumes . Journal of Heat Transfer 117(1):138–145.
Dai, Z., L.-K. Tseng, and G.M. Faeth. 1995b. Velocity/mixture-fraction statistics of round, self-preserving buoyant turbulent plumes. Journal of Heat Transfer 117(4):918–926.
Dai, Z., L.-P. Hsiang, P.-K. Wu, and G.M. Faeth. 1997 (in press). Spray formation at the free surface of turbulent bow sheets. Pp. 197–211 in Proceedings of the 21st Symposium on Naval Hydrodynamics held June 24–28, 1996, in
Trondheim, Norway. Washington, D.C.: National Academy Press.
Evans, D.D., W.D. Walton, H.R. Baum, and K.A. Notarianni. 1993. In-situ burning of oil spills: Meso-scale experiments. Pp. 593–658 in Proceedings of the 16th Arctic and Marine Oil Spill Program Technical Seminar held June 7–9, 1993, in Calgary, Canada. Edmonton, Alberta: Environment Canada.
Faeth, G.M. 1983. Evaporation and combustion in sprays. Progress in Energy and Combustion Science 9:1–76.
Faeth, G.M. 1987. Mixing, transport and combustion in sprays. Progress in Energy and Combustion Science 13:293–345.
Faeth, G.M. 1997 (in press). Spray combustion phenomena. Proceedings of 26th International Symposium on Combustion held July 28–August 2, 1996, at Universita Frederico II, Napoli, Campi Phlegraci, Italy. Pittsburgh, Pa.: The Combustion Institute.
Faeth, G.M., and Samuelsen, G.S. 1986. Fast-reaction non-premixed combustion. Progress in Energy and Combustion Science 12:305–372.
Faeth, G.M., J.P. Gore, S.G. Chuech, and S.-M. Jeng. 1989. Radiation from turbulent diffusion flames. Annual Review of Numerical Fluid Mechanics and Heat Transfer 2:1–38.
George, W.K., Jr., R.L. Alpert, and F. Tamanini. 1977. Turbulence measurements in an axisymmetric buoyant plume. International Journal of Heat and Mass Transfer 20:1145–1154.
Gore, J.P., and G.M. Faeth. 1988a. Structure and spectral radiation properties of turbulent ethylene/air diffusion flames. Pp. 1521–1531 in 21st International Symposium on Combustion held August 3–8, 1986, at the Technical University in Munich, West Germany. Pittsburgh, Pa.: The Combustion Institute.
Gore, J.P., and G.M. Faeth. 1988b. Structure and radiation properties of luminous turbulent acetylene/air diffusion flames. Journal of Heat Transfer 110(1):173–181.
Gore, J.P., G.M. Faeth, D. Evans, and D.B. Pfenning. 1987. Structure and radiation properties of large-scale natural gas/air diffusion flames. Fire and Materials 10:161–169.
Grant, R.P., and S. Middleman. 1966. Newtonian jet stability. American Institute of Chemical Engineering Journal 12:669–678.
Holen, J., M. Brostrom, and B.F. Magnussen. 1991. Finite difference calculation of pool fires. Pp. 1677–1683 in 23rd International Symposium on Combustion held July 22–27, 1990, at the University of Orleans, Orleans, France. Pittsburgh, Pa.: The Combustion Institute.
Hsiang, L.-P., and G.M. Faeth. 1992. Near-limit drop deformation and secondary breakup. International Journal of Multiphase Flow 18(5):635–652.
Hsiang, L.-P., and G.M. Faeth. 1993. Drop properties after secondary breakup. International Journal of Multiphase Flow 19(5):721–735.
Hsiang, L.-P., and G.M. Faeth. 1995. Drop deformation and breakup due to shock wave and steady disturbances. International Journal of Multiphase Flow 21(4):545–560.
Kee, R.J., G. Dixon-Lewis, J. Warnatz, M.E. Coltrin, and J.A. Miller. 1986. A fortran computer code package for the evaluation of gas-phase, multicomponent transport properties. SAND 86-8246. Albuquerque, N.M.: Sandia National Laboratories.
Kee, R.J., J.A. Miller, G.H. Evans, and G. Dixon-Lewis. 1989. A computational model of the structure and extinction of strained, opposed flow, premixed methane-air flames. Pp. 1479–1494 in 22nd International Symposium on Combustion held on August 14–19, 1988, at the University of Washington in Seattle, Washington. Pittsburgh, Pa.: The Combustion Institute.
Kee, R.J., F.M. Rupley, and J.A. Miller. 1990. The CHEMKIN thermodynamic data base. SAND 87-8215B. Albuquerque, N.M.: Sandia National Laboratories.
Kee, R.J., F.M. Rupley, and J.A. Miller. 1991. CHEMKIN II: A fortran chemical kinetics package for the analysis of gas phase chemical kinetics. SAND 89-8009B. Albuquerque, N.M.: Sandia National Laboratories.
Kent, J.H., and F.A. Williams. 1975. Extinction of laminar diffusion flames for liquid fuels. Pp. 315–325 in 15th International Symposium on Combustion held on August 25–31, 1974 , in Tokyo, Japan. Pittsburgh, Pa.: The Combustion Institute.
Köylü, Ü.Ö., Y.R. Sivathanu, and G.M. Faeth. 1991. Carbon monoxide emissions from buoyant turbulent diffusion flames. Pp. 625–634 in Fire Safety Science: Proceedings of the 3rd International Symposium, G. Cox and B. Langford, eds. London: Elsevier Applied Science.
Lin, K.-C., and G.M. Faeth. (Unpublished). Structure of laminar permanently-blue opposed-jet ethlene-fueled diffusion flames. Submitted to Combustion and Flame.
Lockwood, F.C., and A.S. Naguib. 1975. The prediction of the fluctuations in the properties of free, round jet, turbulent diffusion flames. Combustion and Flame 14(1):109–124.
Ludwig, C.B., W. Malkmus, J.E. Reardon, and J.A. Thomson. 1973. Handbook of infrared radiation from combustion gases. NASA SP-3080. Washington, D.C.: National Aeronautics and Space Administration.
Mao, C.-P., G.A., Szekely, Jr., and G.M. Faeth. 1980. Evaluation of a locally homogeneous flow model of spray combustion. Journal of Energy 4(2):78–87.
Mao, C.-P., Y. Wakamatsu, and G.M. Faeth. 1981. A simplified model of high pressure spray combustion. Pp. 337–347 in 18th International Symposium on Combustion held on
August 17–22, 1980, at the University of Waterloo in Waterloo, Canada. Pittsburgh, Pa.: The Combustion Institute.
McGrattan, K.B., R.G. Rehm, and H.R. Baum. 1994. Fire-driven flows in enclosures. Journal of Computational Physics 110:285–291.
Nakagome, H., and M. Hirata. 1977. The structure of turbulent diffusion in an axisymmetrical thermal plume. Pp. 367–372 in Heat Transfer and Turbulent Buoyant Convection, D.B. Spalding and N. Afgan, eds. New York: McGraw-Hill.
Ogino, F., H. Takeuchi, I. Kudo, and T. Mizushima. 1980. Heated jet discharged vertically in ambients of uniform and linear temperature profiles. International Journal of Heat and Mass Transfer 23:1581–1588.
Pivovarov, M.A., H. Zhang, D.E. Ramaker, P.A. Tatem, and F.W. Williams. (1993). Similarity solutions in buoyancy-controlled diffusion flame modelling. Combustion and Flame, 92(3):308–319.
Ruff, G.A., L.P. Bernal, and G.M. Faeth. 1991. Structure of the near-injector region of non-evaporating pressure-atomized sprays. Journal of Propulsion and Power 7(2):221–230.
Shabbir, A. 1987. An experimental study of an axisymmetric turbulent buoyant plume and evaluation of closure hypotheses. Ph.D. dissertation. Buffalo, N.Y.: State University of New York.
Shearer, A.J., H. Tamura, and G.M. Faeth. 1979. Evaluation of a locally homogeneous flow model of spray evaporation. Journal of Energy 3(5):271–278.
Shuen, J.-S., L.-D. Chen, and G.M. Faeth. 1983. Evaluation of a stochastic model of particle dispersion in a turbulent round jet. AIChE Journal 29(1):167–170.
Shuen, J.-S., A.S.P. Solomon, Q.-F. Zhang, and G.M. Faeth. 1985. Structure of particle-laden jets: measurements and predictions. AIAA Journal 23(3):396–404.
Sivathanu, Y.R., and G.M. Faeth. 1990. Generalized state relationships for scalar properties in nonpremixed hydrocarbon/air flames. Combustion and Flame 82(2):211–230.
Solomon, A.S.P., J.-S. Shuen, Q.-F. Zhang, and G.M. Faeth. 1985a. Measurements and predictions of the structure of evaporating sprays. Journal of Heat Transfer 107(3):679–686.
Solomon, A.S.P., J.-S. Shuen, Q.-F. Zhang, and G.M. Faeth. 1985b. Structure of nonevaporating sprays: I. Near-injector conditions and mean properties. American Institute of Aeronautics and Astronautics Journal 23(10):1548–1555.
Solomon, A.S.P., J.-S. Shuen, Q.-F. Zhang, and G.M. Faeth. 1985c. Structure of nonevaporating sprays: II. Drop and turbulence properties. American Institute of Aeronautics and Astronautics Journal 23(11):1724–1730.
Sunderland, P.B., Ü.Ö. Köylü, and G.M. Faeth. 1995. Soot formation in weakly buoyant acetylene-fueled laminar jet diffusion flames burning in air. Combustion and Flame 100(1/2):310–322,
Tieszen, S.R., V.F. Nicolette, L.A. Gritzo, J.K. Holen, B. Murray, and J.L. Moya. 1996. Vortical structures in pool fires: observation, speculation, and simulation. SAND 96-2607. Albuquerque, N.M.: Sandia National Laboratories.
Tseng, L.-K., P.-K. Wu, and G.M. Faeth. 1992, Dispersed-phase structure of pressure-atomized sprays at various gas densities. Journal of Propulsion and Power 8(6):1157–1166.
Wu, P.-K., and G.M. Faeth. 1993. Aerodynamic effects on primary breakup of turbulent liquids. Atomization and Sprays 3(3):265–289.
Wu, P.-K., and G.M Faeth. 1995. Onset and end of drop formation along the surface of turbulent liquid jets in still gases. Physics of Fluids A 7(11):2915–2917.
Wu, P.-K., L.-K. Tseng, and G.M. Faeth. 1992. Primary breakup in gas/liquid mixing layers for turbulent liquids. Atomization and Sprays 2(3):295–317.
Wu, P.-K., R.F. Miranda, and G.M. Faeth. 1995. Effects of initial flow conditions on primary breakup of nonturbulent and turbulent round liquid jets. Atomization and Sprays 5(2):175–196.
13
Fundamentals of Fuel Ignition and Flammability
William A. Sirignano
University of California at Irvine
ABSTRACT
Three fundamental model configurations related to aviation fuel safety are discussed: flame spread above liquid fuel pools, the ignition of gaseous combustible mixtures by hot projectiles, and the ignition and flame propagation of fuel spray/air mixtures. Potential advantages of a two-fuel strategy are identified. The need for further research is identified.
INTRODUCTION
The purpose of this paper is to outline aspects of ignition and flammability related to aircraft safety. The combustion characteristics of aviation fuels and other combustible liquids (e.g., hydraulic and lubricating fluids) will be analyzed in three configurations that could arise from accidents or hostile actions. Because aviation fuels are designed to ignite and burn easily in a combustor, their undesired ignition and burning in other configurations is very difficult to prevent, and makes them a significant fire hazard.
Three fundamental models are discussed below. First, flame spread above liquid fuels is discussed as a significant danger in accidents that result in liquid fuel forming a pool that can be ignited in various ways. Second, the ignition of gaseous combustible mixtures by hot moving particles is analyzed. Hot particles or fragments could result from a breakup of parts in an accident or from projectiles delivered for hostile purposes. Third, a ruptured fuel tank can release a fuel spray/air mixture, which can be easily ignited. In the final section, some potential advantages of a two-fuel strategy are discussed.
IGNITION AND FLAME SPREAD ABOVE A LIQUID FUEL POOL
Figure 13-1 shows the important features of flame spread above a liquid fuel pool. For aviation fuels, the practical interest involves fuels below the flash-point temperature that must be preheated and vaporized before they will mix with oxygen and burn. In this scenario, the flame preheats the fuel. Heating and vaporization become a rate-controlling factor causing the flame to propagate much more slowly than it would through a premixed combustible gas formed from the same fuel.
Flames propagate faster over liquid fuels than solid fuels with similar thermal properties. Thermocapillary convection is the major reason for the difference. A surface shear stress results from the variation in surface tension (caused by the variation in surface temperature). This results in convective heat transfer ahead of the flame (Sirignano, 1972; Schiller and Sirignano, 1996; Schiller et al., 1996).
Understanding flame spread over a fuel pool is a complicated problem because this is an unsteady, multidimensional, multiphase phenomena with many length and time scales and exchanges of mass, momentum, and energy between the phases. The heat transfer results in temperature and density variations through both the liquid and gas phases. Consequently, buoyancy of air produces convection in both phases. The advancing flame causes local gas expansion producing another convective effect. The buoyant air flow and thermocapillary convection are opposed and tend to produce a recirculation zone. However, when the hot gas expands sufficiently, it can destroy any recirculation zone.
In the lower range of initial liquid temperatures (T0), the flame pulsates (alternately accelerates and decelerates) as it propagates. At higher initial temperatures, the flame propagates at a uniform rate. (See Figure 13-2.) The amplitude and period of the pulsations decrease as T0 rises. The domain size (δflow) for liquid motion ahead of the flame also decreases as T0 rises. The size of the gas-phase recirculation cell is directly related to the magnitude of δflow and both become negligible in the uniform flame spread regime.
Figure 13-3 shows the pulsation cycle for a spreading flame. As the flame accelerates, the expansion of hot gas increases, destroying the recirculation zone. When the flame begins to decelerate because of the limited availability of fuel vapor, expansion of the hot gas expansion is reduced and the recirculation zone reforms. As the concentration of fuel vapor in the recirculation zone increases, the flame accelerates again, consuming the available fuel vapor and destroying

FIGURE 13-1 Basic configuration for flame spread above a liquid pool. Source: Schiller et al., 1996.
the recirculation zone. Analyses by Schiller et al. (1996) showed that many parameter variations besides T0 can change uniform flame spread to pulsating flame spread or vice versa. Essentially, the flame spread becomes pulsating as the flammability limit is approached and uniform spread can no longer
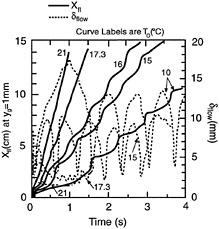
FIGURE 13-2 Effect of initial fuel temperature (T0) on spread rate and domain size (δflow) for liquid motion. Source: Schiller et al., 1996.
be sustained. Average pulsating spread rates are lower than uniform spread rates.
IGNITION OF GASEOUS COMBUSTIBLE MIXTURES
A hot projectile moving through a combustible gaseous mixture has the same effect as a combustible gas flowing around a hot body. Heat is transferred by conduction to the gas; if the temperature rise is sufficient, oxidation rates result in ignition and the establishment of a flame. Figure 13-4 presents a schematic drawing of this phenomenon describing the local flow approximations employed. Namely, the viscous flow produces a boundary layer, and a wake is approximated using two zones: a stagnation flow region and a zero pressure gradient ("flat plate") region. The near wake is approximated using a mixing layer.
At issue is whether an element of combustible gas flowing past the hot body receives enough heat to cause ignition. The amount of heat received and the likelihood of ignition increase with increasing temperature and length of the projectile, and decrease with increasing relative velocity (residence time of the gas in the projectile vicinity). If the gas in the boundary layer over the projectile does not ignite, it might still ignite in the near wake, which can recirculate hot gases and sustain a flame.
Figure 13-5 shows the limits for ignition. Ignition in the stagnation flow region requires higher temperatures and/or lower velocities than ignition in the zero pressure gradient region. If ignition does not occur in the boundary layer, it might occur in the mixing layer between the near wake with
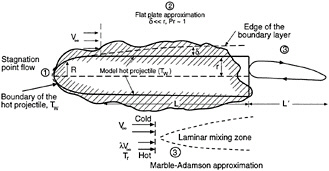
FIGURE 13-4 Schematic diagram of the flow field approximations used around a hot projectile ignition.
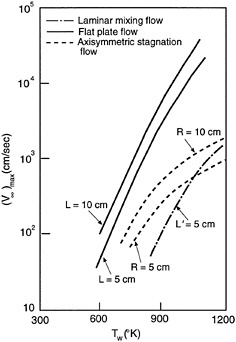
FIGURE 13-5 Variation along the limit of the relative velocity of the hot projectile with projectile temperature (Tw) and projectile characteristics (L or R) or near wake length (L´). Source: Sharma and Sirignano, 1970.
its recirculating hot gases and the external flow. Once ignition occurs, a flame is established that can spread through and consume the gaseous mixture.
SPRAY IGNITION AND FLAME PROPAGATION
The ignition and flame propagation of fuel spray/air mixtures are substantially different from ignition of and flame propagation through gaseous combustible mixtures. The major factor for the differences is the fine structure associated with spatial variations in gas properties on a length scale as small as the distance between neighboring droplets.
Ignition and flame propagation each require heating and vaporization of the droplets and mixing of the fuel vapor with air before chemical reaction can occur. Intuition might indicate that ignition of or flame propagation through a spray always occurs at a slower rate when compared to a gaseous mixture at the same mixture ratio. For certain mixture ratios and for certain initial droplet sizes, however, ignition can be faster and/or flame speeds can be higher for the spray. The major factors causing this difference are variations in temperature and concentrations in the fine structure together, and the nonlinear dependence of the reaction rate on temperature and concentrations.
Figure 13-6 shows that the ignition delay does not always decrease as initial droplet size decreases. Ignition delay is plotted against a normalized mixture ratio (the equivalence ratio [Er] equals unity for a stoichiometric mixture). At lean fuel conditions, the ignition delay is smaller for a certain, finite, initial droplet size than for a prevaporized, premixed gas. Therefore, creating larger initial droplets is not necessarily safer.
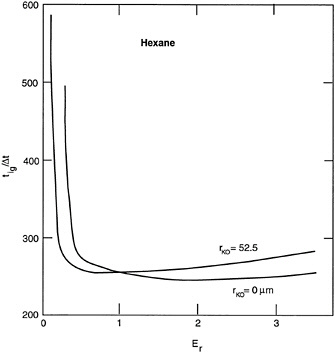
FIGURE 13-6 Ignition time delay versus equivalence ratio (normalized mixture ratio) and initial droplet radius. Source: Aggarwal and Sirignano, 1984.
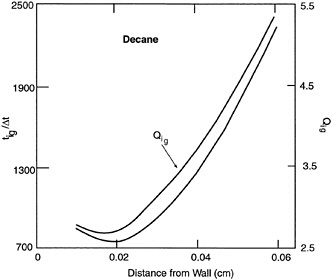
In some situations (see Figure 13-7), the same type of nonlinearities and fine structure lead to a situation whereby the ignition rate may not increase as a droplet moves closer to an ignition source. In Figure 13-7, ignition energy (Qig) and ignition delay are plotted against distance from a hot wall. Minima of those values are shown at specific, finite initial fuel droplet sizes.
In practical situations, a polydisperse spray has a distribution of initial droplet sizes. An average droplet size is used to represent the distribution; d32, an average droplet diameter based on the ratio of volume to surface area, is a common choice. Aggarwal and Sirignano (1986) showed that d20, an average based solely on surface area of the spray, was a better average value for predicting ignition. Figure 13-8 shows that the calculations based upon a monodisperse spray with the d20 value agree better with results for a bidisperse spray than calculations with the d32 value. Smaller droplets in the distribution tend to influence ignition more than larger droplets because they have more surface area per unit volume (or per unit mass).
A spray flame has a complex structure, with both diffusion flame characteristics and premixed flame characteristics. Some vaporization of fuel and mixing of the vapor with air can occur ahead of the flame; as the flame propagates, this gaseous mixture can be burned. However, sufficiently large droplets can pass through the flame and continue to vaporize and mix behind the flame. This can result in a fuel-rich gaseous mixture with fuel vapor that diffuses towards the flame region, where it mixes with oxygen and reacts.
Figures 13-9 and 13-10 show the results of the unsteady propagation of a spray flame. In Figure 13-9, the fuel vapor mass fraction ahead of the flame (traveling to the right) increases with time as a result of prevaporization. Because the calculation is for a closed volume, vaporization causes an increase in pressure and temperature ahead of the flame (see
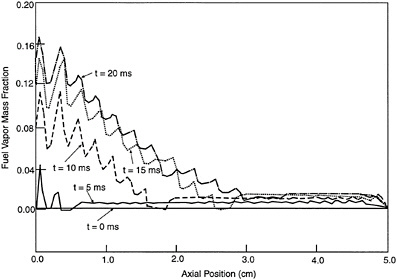
FIGURE 13-9 Fuel vapor mass fraction versus axial position at various times. Source: Aggarwal and Sirignano, 1985.
Figure 13-10). The local peaks of fuel vapor mass fraction and minima of temperature occur at the discrete droplet positions as a result of mass and energy exchange between droplets and surrounding gas. A comparison of Figures 13-9 and 13-10 shows that fuel vapor mass fraction is largest well behind the flame-front (the region of a sharp increase in temperature) so that, to a large extent, burning occurs as a diffusion flame. However, because of prevaporization, the flame also has some of the characteristics of a premixed flame.
The nonlinear character of the reaction rate plus the fine structure in Figures 13-9 and 13-10 lead to the nonintuitive behavior of the flame speed, which does not continually increase as droplet size decreases. Instead, a maximum speed, which is greater than the premixed flame speed, is reached at a finite droplet size. (See Aggarwal and Sirignano, 1985.)
TWO-FUEL STRATEGY
The challenge is to create a liquid fuel that burns very efficiently after injection into the engine combustor but burns considerably less efficiently when released accidentally. So far, no such fuel has been developed, but two new possibilities could be explored. One is a fuel with a strong pressure sensitivity that burns poorly at atmospheric conditions but extremely well at elevated pressure (personal communication from Thor Eklund, William J. Hughes Technical Center, FAA, June 1996). Another possibility is the development of a two-fuel (or multifuel) strategy.
Some liquid fuel combinations burn better when they are blended before injection into a combustor than when they are injected separately into the same combustor, although many fuel combinations do the opposite. Previous studies (Delplanque et al., 1990; Delplanque et al., 1991) considered the advantages and disadvantages of blending fuel for incinerating hazardous waste. Some of those concepts might be applicable to aviation fuel. The goal is to find fuels that can be contained in separate tanks on board an airplane and blended on board at a limited rate before being injected into the engine. Delplanque et al. (1990, 1991), in studies of benzene (or toluene or monochlorobenzene) burned with hexane (or decane), found that improvements in overall burning efficiencies sometimes resulted from blending before injection.
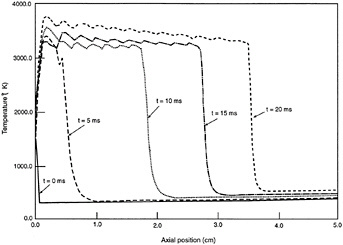
FIGURE 13-10 Gas temperature versus axial position at various times. Source: Aggarwal and Sirignano, 1985.
CONCLUDING REMARKS
The information presented herein does not lead directly to a practical solution of the very difficult aviation fuel safety problem. It is intended to provide fundamental scientific information, to encourage further research, and to provoke interest in improvements in safety.
In general, the models identified above have not been fully studied. Further study on the sensitivity of fuel to property changes might, for example, indicate a path towards improvements. The effects of inhibitors or quenching mechanisms could be added to the models to aid in the development of practical solutions. This author believes that notable improvements in safety will probably be generated by a combination of modifications rather than by a single engineering achievement. Therefore, a broad range of studies on the fuel safety problem must be initiated and sustained.
REFERENCES
Aggarwal, S.K., and W.A. Sirignano. 1984. Ignition of fuel sprays. Deterministic calculations for idealized droplet arrays. Pp. 1773–1780 in Proceedings of the 20th International Symposium on Combustion, held August 12–17, 1984, at the University of Michigan, Ann Arbor, Michigan. Pittsburgh, Pa.: The Combustion Institute.
Aggarwal, S.K., and W.A. Sirignano. 1985. Unsteady spray flame propagation in a closed volume. Combustion and Flame 62(1):69–84.
Aggarwal, S.K., and W.A. Sirignano. 1986. Ignition of polydisperse sprays: Importance of D20. Combustion Science and Technology 46:289–300.
Delplanque, J.P., R.H. Rangel, and W.A. Sirignano. 1991. Liquid-waste incineration in a parallel-stream configuration: Effect of auxiliary fuel. Pp. 164–186 in Dynamics of Deflagrations and Reactive Systems: Heterogeneous Combustion, Progress in Astronautics and Aeronautics Vol. 132, A.L. Kuhl, J.C. Leyer, A.A. Borisov, W.A. Sirignano, eds. Washington, D.C.: American Institute of Aeronautics and Astronautics.
Delplanque, J.P., R.H. Rangel, and W.A. Sirignano. 1991. Liquid-waste incineration in a parallel-stream configuration: Parametric study. Pp. 877–894 in Proceedings of the 23rd International Symposium on Combustion, held July 22–27, 1990, at the University of Orleans, Orleans, France. Pittsburgh, Pa.: The Combustion Institute.
Schiller, D.N, and W.A. Sirignano. 1996. Opposed-flow flame spread across n-propanol pools. Proceedings of the 26th International Symposium on Combustion, held July 28–
August 2, 1996, at Universita Frederico II, Napoli, Campi Phlegraci, Italy. Pittsburgh, Pa.: The Combustion Institute.
Schiller, D.N., H.D. Ross, and W.A. Sirignano. 1996. Computational analysis of flame spread over alcohol pools. Combustion Science and Technology 118(4–6):205–258.
Sharma, O.P., and W.A. Sirignano. 1969. Ignition of stagnation point flow by a hot body. Combustion Science and Technology 1(2):95–104.
Sharma, O.P., and W.A. Sirignano. 1970. On the ignition of a premixed fuel by a hot projectile. Combustion Science and Technology 1(6):481–494.
Sirignano, W.A. 1972. A critical discussion of theories of flame spread across solid and liquid fuels. Combustion Science and Technology 6(1–2):95–105.
14
Post-Crash Fuel Dispersal
Sheldon R. Tieszen
Sandia National Laboratories
ABSTRACT
This paper is brief overview of work done over the last several decades in determining what happens to jet fuel in aircraft fuel tanks on impact with the ground. Fuel dispersal is discussed in terms of overall crash dynamics, and impact regimes are identified. In a generic sense, the types of flow regimes are identified, and general descriptions of the processes are given. Examples of engineering level tools, both computational and experimental, that are used for analyzing the complex environments are presented. Finally, the concept of risk-based decisions is discussed as a quick way of identifying requirements for developing preventive or mitigation strategies, such as antimisting agents.
INTRODUCTION
Large energies are involved when an aircraft crashes into the ground. Gross take-off weights for large transport or bomber aircraft can be on the order of 105 kg. With flight velocities in the 10s to 100s of meters per second, the kinetic energy of impact (1/2mV2) can be on the order of 109 J. The fuel contained in the wing tanks of an aircraft can be in the 104 to 105 kg range. The typical energy in jet fuel that can be liberated on combustion is 4.3 x 107 J/kg. Therefore, the amount of energy available is on the order of 1012 J. These energies are substantial by almost any measure, and the energy available from combustion is potentially several orders of magnitude higher than the kinetic energy on impact.
Because of the energies involved, a crash can result in the destruction of both materials and personnel. Statistics show the magnitude of the effect (The Boeing Company, 1996). From 1959 through 1995, 65 percent of accidents that resulted in damage to the aircraft beyond economic repair also resulted in fatalities. Over the same period, less than 4 percent of accidents resulting in substantial but repairable damage resulted in fatalities. From 1991 to 1995, 71 percent of the fatalities were from loss of control in flight or controlled flight into terrain. Other statistics indicate that for ''crash-survivable" accidents, 40 percent of deaths are caused by fire (20 percent of all fatalities) (FAA, 1991). Because of the high energy content of jet fuel and keeping in mind statistics that attest to the effect of fire, understanding the behavior of jet fuel in the post-crash environment is important, even in the presence of ground-based fuel in the impact area.
The role of fuel dispersal in the post-crash environment can best be described if the crash environment is viewed as a process, albeit an undesirable one. At the most abstract level, as shown in Figure 14-1, the crash process can be thought of as a set of initial conditions (crash scenarios) that lead to a set of undesirable events (combustion modes), that lead to a set of unfortunate consequences (death and adverse environmental impact). Two generic strategies are available for interrupting these undesirable processes. These are prevention, keeping the undesirable event from occurring, and mitigation, minimizing the consequences of the accident.
In the context of the process shown in Figure 14-1, fuel dispersal plays two major roles. The first role is within the process description itself. Jet fuel is a major source of combustible material in a crash environment and, therefore, must be tracked from the moment of impact until it is either consumed by fire or it has traveled sufficiently far from the aircraft that it no longer represents a significant hazard.
Because jet fuel is a major contributor to post-crash fires and fires are a major cause of deaths, it is only natural to seek a preventive strategy by changing the makeup of the fuel. Obviously, the ideal solution would be to have a fuel that burns with great vigor in an engine but absolutely will not combust anywhere else. Until someone creates this idealistic fuel, less effective fire prevention strategies must be employed.
Before one can begin to develop preventive or mitigative strategies for an undesirable process, one must first define the process to the extent that concrete design objectives for the preventive and mitigative strategies can be set. Although this statement is obvious, its importance cannot be overemphasized. The need to minimize costs places higher emphasis on fixing an undesirable process than on defining it. However, attempts to fix a process without a quantitative understanding of how the solution will affect the process can lead to higher overall costs and less than optimal results. Unfortunately, the more complex and nonlinear the process, the more difficult it
FIGURE 14-1 Dual role of fuel dispersal from a process perspective.
is to quantify it and, hence, the less likely it is that development of a preventative or mitigative strategy will be successful. Aircraft crash sequences are very complex, nonlinear processes.
In general terms, fire prevention strategies attempt to separate one key element of fire from the other two. The three key elements are fuel, air, and an ignition source. Because air is ubiquitous, separating air from the other two elements is questionable, except in specific situations like the in-flight inerting of fuel tanks. Thus, either the ignition sources or fuel must be separated from the other two. An example of an ignition source strategy is to cover a runway with foam prior to landing if it appears that a crash is likely. However, not much can be done to eliminate ignition sources completely because hot running engines are required for aircraft flight, and hot brakes are likely in sliding accident. The separation of fuel from the other two fire elements has taken two general forms, improvements to fuel tank structural integrity (improving crashworthiness) and a long running attempt to develop an antimisting agent for jet fuel.
Fuel dispersal in the context of an aircraft crash is discussed in the next section (followed by qualitative descriptions of the processes involved in fuel dispersal). Tools for adressing fuel dispersal are then described, including engineering computational and experimental tools, followed by a description of risk-based decisions as applied to this problem. Because the flow regimes for fuel are numerous, the scope of this paper is limited to qualitative descriptions and the tools shown are meant to be representative, rather than comprehensive. Because of the broad nature of the flow regimes, it is not possible to cover the extensive fundamental research in fluid mechanics that underpins our understanding of them, and no attempt is made to do so in this paper.
FUEL DISPERSAL IN THE CONTEXT OF A CRASH
Figure 14-2 shows an aircraft impact as a series of processes that are a function of time. These processes fit within the overall description in Figure 14-1. From the time of impact until the aircraft motion is terminated, tremendous energy is being dissipated. During a routine landing, this energy is dissipated into the brakes, tires, and, through thrust-reversers, into the air. In a crash, this energy can be further dispersed in abrasion of the fuselage or other parts that are skidding along the ground or in large-scale deformation upon impact with a solid object, all of which can produce either sparks or hot surfaces for ignition. If impact energies are sufficiently high, loss of fuel containment may result. For example, a fuel tank may fracture and begin to leak, resulting in fuel dispersal. The actual processes involved in fuel dispersal will be discussed in the next section.
Energy dissipation processes create the initial conditions for a fire (discussed with respect to Figure 14-1). The role of preventive strategies is to interrupt these processes. For a specified impact regime, such as a "crash-survivable" regime, the effect of preventive strategies is to prevent fire by preventing fuel, air, and an ignition source from occupying the same spot in space simultaneously.
If fuel vapor, fuel droplets, or sheets of fuel on the ground come into contact with an ignition source, then ignition can occur and fire can spread. In a general sense, fire spread can be thought of as a continuous ignition process with the existing fire acting as the ignition source. Thus, a large fireball that results from the ignition of a fine mist becomes a very strong ignition source for spread of the fire to discontinuous fuel segments via the radiative transfer of heat. Potential ignition sources range in duration and scale from a large fireball,
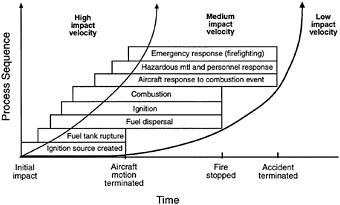
FIGURE 14-2 Processes involved in aircraft crashes as a function of time. The impact velocity regime are defined in Figure 14-3.
which would last for several seconds, to fragmenting engine parts and brakes, which can remain hot for several minutes, to small sparks, which may exist for just milliseconds (Tilston, 1989). Once the fire has spread, combustion continues until the fuel is depleted or effective firefighting measures are initiated. Combustion processes can take several modes depending on the state of the dispersed fuel. The modes range from a fireball to a fire above a continuous liquid pool, either stagnant (called a "pool fire") or replenished (called a "spill fire"), to a fire above soil saturated with fuel (called a "dirt fire").
The ignition and combustion processes form the combustion modes for a fire. The role of mitigative strategies is to interrupt these processes in such a way that the spread of fire into the cabin area is blocked or the thermal/toxic consequences of the fire on humans and/or hazardous cargo (chemical, biological, or nuclear) is reduced. An example of a mitigative strategy is the use of fire-and smoke-resistant interior materials (National Research Council, 1995).
The consequences of a fire are both thermal and chemical (toxic). The aircraft provides some protection to occupants inside depending on the damage and the environmental conditions, such as wind. In general, the consequences of a crash can be impact trauma, thermal trauma, or both. The term crash-survivable typically means that humans can survive the impact trauma. Crash-survivable conditions for hazardous material containers or for nuclear weapons are usually much broader than for humans. Therefore, the term can be confusing unless the object to which it applies is specified.
Regimes can also be categorized by considering the character of the basic process as a function of impact velocity. This method of categorization is shown in Figure 14-3. While this categorization yields less insight on the ratio of impact to thermal survivability, it yields more insight on physical processes that occur in an accident. Accidents can be broadly characterized as "sliding out" accidents or "augering in" accidents (Kuchta and Clodfelter, 1985; Tieszen, 1995) depending on their "normal" impact velocity, the velocity perpendicular to the surface. At low normal impact velocities, a plane lands safely. Above a certain normal impact velocity, in the case of landing gear failure, for example, the plane crosses into the medium impact velocity regime. At medium normal impact velocities, a crash can be characterized as a slide-out, i.e. the plane slides along the ground. The fuel tanks can be damaged in this regime but are not fragmented. Fuel dispersal results from leakage from the damaged tanks. Ignition may result in a small to moderate fireball. After the aircraft comes to rest, pouring fuel can cause a long duration spill fire. At higher impact velocities, the plane and fuel tanks are fragmented as the plane augers in. The fuel disperses in a large splash, and ignition results in a large fireball. Fuel remaining on the ground burns as a pool or dirt fire.
The distinction between medium and high impact regimes is somewhat arbitrary. However, for reference, Wittlin (1987) concludes that a distributed-load wing impact (such as striking a low hill or mound with the wing) between 60 and 72 m/sec will devastate the wing fuel tanks. For concentrated loads (such as a telephone pole), the velocity at which the wing tanks will be destroyed is even lower, 33 to 41 m/sec, depending on the type of obstacle. Because jet flight speeds are well above this range, any impact into the side of a steep
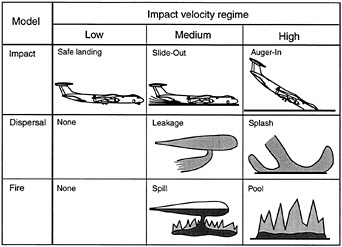
FIGURE 14-3 Classification of crashes by impact velocity.
mountain or building can be considered a high velocity impact. Airports are increasingly being surrounded by the growth of cities, in part because of the commercial opportunities near airports. Considering that almost 50 percent of fatalities already occur during landing and take off (The Boeing Company, 1995), a significant increase in vertical surfaces (i.e., buildings) may mean a significant increase in high velocity impacts. The ratio of ground to aircraft fatalities may also increase with time.
The impact velocity regimes shown in Figure 14-3 can be qualitatively mapped onto the timing of the crash processes shown in Figure 14-2. The higher the impact velocity, the sooner each process begins.
Fuel Dispersal Processes in Medium Velocity Impacts
The crash-survivable regime for humans is wholly within the medium velocity impact range. The principal study of this regime has been the long running FAA program on the development of antimisting kerosene, which ended in 1986 (Yaffee, 1986). The program conducted a dozen full scale tests between 1965 and 1984. The structural damage to fuel tanks and the efficacy of crash resistant designs can be found in Nissley and Heid (1964), Buckson, et al. (1965), Schauerman (1971), Hackler (1972), and Wittlin (1987). Studies characterizing antimisting fuels can be found in Ahlers (1970), Miller and Wilford (1971), Russell (1971), Rockow and Shaw (1972), Faul (1978), Salmon (1981), Mahood and Talley (1982), and Parikh, et al. (1983). Other programs to evaluate crashworthiness have also been conducted within the Department of Defense community (see for example, Shaw [1971] and Johnson, et al. [1989]).
Only a small number of direct measurements of fuel dispersal without an antimisting agent are available. A summary of the data directly related to the physical processes involved in fuel dispersal can be found in Tieszen (1995). The processes involved in fuel dispersal in the medium impact velocity regime are shown in Figures 14-4 and 14-5.
Figure 14-4 shows the dispersal stages prior to ignition of the fuel. Initially, upon impact with the ground, the fuel in the tank is subject to inertial loads because of rapid deceleration of the aircraft on impact (in addition to the gravitational force). The fuel sloshes around in the tanks to adjust to the time-varying inertial force. Because the fuel mass is usually many times the wing mass, the inertia of the fuel and its compressibility are important in determining the impact dynamics of the fuel tank and influenced the damage from the impact. If a fuel tank is punctured or torn, inertial and gravitational forces create a flow out of the tank. The rate of leakage will be proportional to the damage (hole area) and the forces present.
The next stage of dispersal occurs as the balance of forces on the fuel emerging from the tank changes. The fuel stream is subject to a free pressure boundary just outside the damaged tank. During a slide-out accident, there is relative motion between the aircraft and the surrounding air. As a result, the
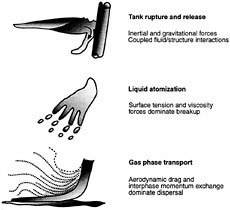
FIGURE 14-4 Stages of pre-ignition fuel dispersal in the medium-impact velocity regime.
total pressure against the fuel stream changes rapidly as it traverses the boundary layer between the tank surface and the free stream. Because of the destabilizing processes of aero-dynamic drag and because of turbulence within the fuel itself, a sequence of breakup processes begins that results in the atomization of some fraction of the fuel. Initially, drops are shed from the liquid column. Under certain flow regimes, the whole column can break up into sheets, ligaments, and drops. Surface tension is the primary force resisting breakup. However, the breakup process occurs in the presence of regions of high spatial and temporal gradients, so rate dependent forces, such as viscosity, which retards breakup, can affect the outcome. The process by which a continuous liquid jet becomes atomized is called primary breakup.
An in-depth description of breakup processes can be found in Lefebvre (1989). Recent studies showing the effect of turbulence in the liquid phase can be found in Wu, et al. (1992), Wu and Faeth (1993), Wu, et al. (1995), and Wu and Faeth (1995). The two distinct flow streams in this stage of dispersal are airborne droplets, which result from the primary breakup, and the residual fuel stream, which continues to fall until it reaches the ground.
The next stage of dispersal of the airborne droplets involves secondary breakup and interphase momentum exchange with the air. Secondary breakup occurs if the drops are large and the velocity difference between the drops and the gas is high. The secondary breakup process has traditionally been viewed as a balance between inertial forces and surface tension. If there are many small drops, then they can coalesce into larger droplets.
The final size distribution of drops is important because it affects the rates of interphase momentum exchange, which occurs continuously from the time drops separate from the fuel stream. The momentum transfer distance can be quite short for small droplets; larger droplets can travel many meters. Given sufficient travel distance without impacting a solid surface, droplets eventually reach an equilibrium velocity relative to air as a result of gravitational acceleration. Although the transfer of momentum from the fuel stream to the air is dissipative, it does not imply a total loss of momentum. Rather the air acquires the momentum and transports the drops. As a result of interphase momentum exchange, a spray can be transported via turbulent air motion over large volumes of space.
Depending on the amount of damage to the fuel tank and the slideout velocity, the fuel flowing from the tank may not be atomized to the point that it is significantly deflected by the air. The fuel stream, both as a continuous column and as discontinuous, partially atomized segments, can continue to fall under the influence of gravity until it reaches the ground. Not all of the fuel that reaches the surface as a liquid stream remains on the surface. Some droplets may splash off the surface back into the air, depending on the impact velocity and liquid turbulence levels (Errico, 1986; Lienhard et al., 1992; Bhunia and Lienhard, 1994a, 1994b; Tieszen, 1995).
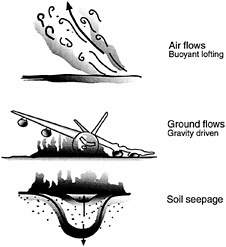
FIGURE 14-5 Stages of post-ignition fuel dispersal in the medium-impact velocity regime.
Depending on the velocity of the fuel stream hitting the ground, the flowing liquid can be either faster than the gravity wave speed on the free surface, i.e., supercritical, or slower than the gravity wave speed, i.e., subcritical. If it is supercritical, a hydraulic jump will follow, which reduces the velocity to subcritical. The subcritical fluid will continue to spread over the terrain. At this point, the fuel spread rate is governed by several factors, including gravity, the slope of the terrain, inertia of the existing fluid, and viscous drag on the solid surface (Didden and Maxworthy, 1982; Huppert, 1982; Lister, 1992). Soil porosity will also affect the spread rate and size of the spill.
Fire can only occur in the presence of fuel, air, and an ignition source. A criterion for ignition can be thought of as the instantaneous overlap of the geometric regions for which ignition energies are present and for which an ignitable spray volume or liquid fuel stream is present. Viewed in this manner, determining ignition requires time-dependent, spatial tracking of energy sources and fuel streams for simultaneous co-location (and accounting for action-at-a-distance mechanisms, such as radiative heating). Determining the ignition of spray requires tracking the concentration and size of drops, which must be sufficient to initiate ignition and propagate flames. The key parameter for the liquid stream is spatial distribution. If ignition sources and fuels can be kept separate for all points in space and for all points in time during the accident transient, then there will be no fire.
Figure 14-5 shows the stages of fuel dispersal after ignition of the fuel. Ignition of the mist can result in a fairly sizable fireball that results in radiant heating of nearby fuel surfaces. Fireballs radiate energy for anywhere from a few seconds to tens of seconds, depending on the mass (Dorofeev et al., 1991). Because of the buoyancy induced by combustion, the fireball will rise, and the combusting mist will be elevated with it. In this manner, fireballs quickly consume fuel. However, they also provide a large ignition source for fuel that might not otherwise be ignited. In addition to radiative heat transfer, a fireball can spread flames back along the fuel mist to the fuel source, if the fuel mist has no discontinuous or nonflammable regions. The flame can then anchor onto the spill point on the aircraft.
Depending on the amount of damage to the fuel tank and the amount of fuel in the tank at the time of the accident, fuel may continue to drain long after the aircraft comes to rest. If ignition occurs in the fuel on the ground, flame spread can result in the propagation of flames back to the source, if the fuel spill has no discontinuous or nonflammable regions. The flame can then anchor onto the spill point on the aircraft.
After the aircraft comes to rest, the flow of liquid from the tanks will primarily be gravity driven. However, fire induced heating of the tanks may produce residual pressures that can contribute to the rate at which the fuel leaks from the tank. The size of the fire will be limited by the balance between the rate of evaporation caused by the fire and the spill rate (Cline and Koenig, 1983).
Besides flowing over the ground, fuel can flow into the ground, if the ground is porous and if the pores are not saturated with water. In addition to gravity, fuel is pulled into porous ground by capillary pressure that is a function of pore size. Because of capillary pressure, fuel that has flowed into the ground is not necessarily safe from being evaporated by and contributing to the fire. In this case, evaporation from the fire dries the surface of the soil and fuel under the dry layer is pulled up against the force of gravity by capillary forces to evaporate and feed the fire. Very long duration fires can be sustained this way.
Fuel Dispersal Processes in High Velocity Impacts
The high velocity impact regime has received less attention than the medium velocity regime. The lack of interest in this regime is not due to a lack of accidents occurring in this regime but to the fact that human survival in this impact regime is problematic. The primary source of data for this regime has been U.S. Department of Defense studies, the most recent of which is the Defense Special Weapons Agency (DSWA) Fuel-Fire Technology Base program, which has sponsored studies of post-crash fuel dispersal (Tieszen, 1995; Tieszen and Attaway, 1996) and fires in post-crash environments (Gritzo et al., 1995, 1996; Nicolette et al., 1995; Tieszen et al., 1996b). The primary goal of these studies is to characterize the post-crash environment to the extent that it affects nuclear weapon safety. Rather than trying to develop preventive engineering measures as the FAA has done, the DSWA program was intended to increase understanding of the crash process so risk-assessment compatible models could be developed. Risk assessments place significant time constraints on models because tens of thousands of scenarios are often run to establish statistical significance. As a result, the models focus only on dominant physical mechanisms.
The primary difference between the medium impact velocity regime and the high impact velocity regime is that aircraft tend to slide out in the medium velocity regime and auger in the high velocity regime. The dividing line between the regimes is continuous and therefore somewhat arbitrary. Figure 14-6 shows examples near the boundary between the regimes. On the medium velocity impact side of the regime, damage to the fuel tanks increases as impact velocity increases. For example, a heavily damaged wing may separate from the fuselage and tumble down range, leaking fuel in the process. This type of accident begins to be indistinguishable from the high-speed impact in which the wing is fragmented on impact, and the fuel and fragments are thrown forward from the impact.
FIGURE 14-6 Transition from medium-to high-impact velocity regimes. A tumbling wing splashing fuel forward of an impact point becomes indistinguishable from a fragmentation impact.
Figure 14-7 shows the stages of fuel dispersal in the high impact velocity regime. In many respects, the flow regimes are not qualitatively different from flow regimes in the medium impact velocity range, although there are quantitative differences. Note that in many cases, the angle of impact, not just the velocity, determines whether or not the impact is of the high normal impact velocity type. The impact of any aircraft at any flight speed against the side of a steel building will result in fragmentation of the aircraft and augering in to the building.
Upon initial impact with the ground, the fuel in the tank will be subject to inertial loads caused by the rapid deceleration of the aircraft on impact. The compressibility not only of the fuel mass but also of the surface that is impacted is important. If the surface is sufficiently hard, such as a concrete runway, there may not be craters. If the surface is sufficiently soft, such as a plowed field, then there will certainly be craters. Studies have shown (Tieszen, 1995; Tieszen and Attaway, 1996) that there is a distinct difference in the dispersal characteristics of crashes into cratering and non-cratering surfaces. This difference illustrates the effect of inertial coupling and compressibility on the problem.
The next stage of dispersal occurs as the fuel emerges from the ground surface or crater. Just as in the medium impact velocity regime, the fuel stream in the high velocity regime is subject to a free pressure boundary. Because of the destabilizing processes of aerodynamic drag and turbulence within the fuel itself, breakup processes begin, which results in complete atomization of the fuel leaving the surface. Surface tension is the primary force resisting breakup. However, the breakup process occurs in regions of high spatial and temporal gradients, so rate dependent forces, such as viscosity, which retards breakup, can affect the outcome. The fuel that leaves the surface is likely to be completely atomized because of the large scale and high velocity associated with the impact

FIGURE 14-7 Stages of fuel dispersal in the high-impact velocity regime.
(Tieszen and Attaway, 1996). However, not all the fuel in the tank leaves the surface in an accident that involves craters. More than 50 percent of the fuel can remain in the crater, depending on the angle of impact (Tieszen and Attaway, 1996).
As a result of the energies involved in impact and the intermixing of aircraft fragments with fuel, ignition is very likely in cratering impacts. In the high velocity regime, it is very difficult to employ any mitigative strategy to prevent ignition by maintaining physical separation of the fuels and ignition sources. Given ignition, the airborne fuel spray causes a large fireball and is consumed. In the medium impact velocity regime, the presence of the fireball significantly increases the probability of ignition and, in this sense, is considered to be detrimental. In the high impact velocity regime, when ignition is virtually guaranteed by intermixing, the fireball is a quick way of burning off the fuel. Often hazardous cargoes are sufficiently hardened so that fireball heat lasting seconds to tens of seconds will not damage the cargo.
Long duration fires present a more serious consequence and can be of two types. If the fuel in the crater is in the form of a continuous liquid pool, then the fire will be a pool fire. If the fuel pool is or becomes discontinuous as a result of seepage into porous soil, then the fire can be sustained off the evaporation from the soil and is a dirt fire. The location, intensity, and duration of this fire relative to hazardous cargo containers has been the principal concern in this type of accident.
Engineering Tools for Post-Crash Fuel Dispersal
Computational and experimental tools that have been applied to fuel dispersal problems are briefly addressed in this section. The purpose is not to be comprehensive but to give the reader a feeling for the types of tools and their uses. As has been discussed, the range of multiphase flow regimes that can result from fuel dispersal is extremely broad. For this reason, space does not permit a discussion of fundamental research tools and results. Tools and issues for four stages of dispersal are briefly covered, tank damage/destruction, fuel atomization, interphase momentum exchange, and ground flows.
The initial stage of fuel dispersal involves tracking the fluid out of the tank. Typically, compressibility is important. Computationally, the tool of choice for many years for this type of problem has been the transient, multidimensional hydrocode. An example of the use of the CTH computer code on a fuel dispersal problem is given in Gardner (1990). A new approach has recently been developed that can easily be coupled to standard finite-element based approaches, which are now the norm for structural dynamics (Attaway et al., 1994). The new approach is called "smooth particle hydrodynamics" (SPH). Although SPH has not yet been completely accepted for general fluid mechanics work, it has many advantages for short duration, high strain rate impacts (such as a gridless formulation that allows large mesh deformation without entanglement).
Figure 14-8 shows a sample two-dimensional calculation (Tieszen et al., 1996). Shell elements representing the wing
FIGURE 14-8 Example of numerical simulation tool for the impact stage of dispersal. Example of two-dimensional SPH calculation. Source: Tieszen et al., 1996a.
skin can be used in the same formulation as the gridless integration points. Both the fuel in the wing and the soil in the near impact region employ the smooth particle integration points. Although SPH allows for differing formulations of equation of state, the time step must be very short to take into account the effects of compressibility. For this and other reasons, SPH is not particularly suitable for tracking fluid beyond the impact and breakup of the tank into the atomization regime.
Figure 14-9 is a photograph of a small gas gun that was used to test the suitability of the SPH approach for liquid/soil impacts (Tieszen and Attaway, 1996). The facility depicted is representative of the facilities in federal laboratories used to study impacts. Very few of these facilities have been used directly for dispersal studies, but many could be modified to cover the range needed for investigating dispersal. The U.S. Department of Defense (all services), the U.S. Department of Energy, and the U.S. Department of Transportation also have impact facilities, ranging in size from several feet long (Figure 14-9) to large sled tracks that run for miles (for example, at White Sands Missile Range, at Naval Air Warfare Center-China Lake, and at Sandia National Laboratories). Most facilities use high-speed cinematography and can record high-speed digital data, such as data from strain gages. The author knows of no transient measurements of the characteristics of fuel leaving the tanks in any tests.
The second stage of fuel dispersal, atomization, is still not understood sufficiently to have been examined computationally at relevant scales and velocities. The principal reason for the lack of an engineering computational tool for this stage (in the author's opinion) has been the differences in length scales. The minimum cross-sectional diameter of a wing, near the wing root, is a significant fraction of a meter. To capture fuel tank breaks and liquid flow from the tank, length scales on this order are required. At the same time, surface tension acts over submillimeter length scales (as evidenced by the distribution of drop sizes from simple pressurized atomization, which range down into the hundreds of micrometers in

FIGURE 14-9 Example of impact facility for studying the impact stage showing liquid impact into soil to determine dispersal. Model wing chord is 0.084 m and impact at 45¹ and 64 m/s. Source: Tieszen and Attaway, 1996.
diameter). Therefore, to be relevant to the engineering problem and to resolve the range of surface tension forces, a spectrum of at least four orders of magnitude (from submillimeter to meter) for each spatial dimension must be run. In three dimensions, this would require 1012 grid points, a very large number by any standard, particularly for a transient, multiphase flow problem.
In many situations the length scale problem can be resolved by placing dense grid points only in regions that require it. This strategy may be used to solve the present problem as well, but as the fuel surface begins to break up, the regions that require high grid density will quickly grow, and the location of break up will change as a function of time. To the author's knowledge, no computational tool directly addresses the problem. Perhaps with the new "teraflop" level of computing hardware, it will be possible to modify existing tools to conduct two-dimensional simulations of the breakup process. It is anticipated that fully transient problems with 108 grid points will be within the capability of the early teraflop level machines.
In an experimental sense, substantial progress has been made in the commercialization of hardware that can characterize drop size. Commercial hardware vendors include Malvern, Insitec, Dantec, and Aerometrics. 1 Available instruments can characterize drop size and, in some cases, velocity. Unfortunately, they are most applicable in flow regimes near the end of the primary breakup stage and into the interphase transfer stage. For various reasons, they have increasing trouble in the primary breakup stage. Experimental diagnostics in the primary breakup phase is still being investigated at the laboratory scale, and, in the author's opinion, this situation will continue. Even though engineering scale tests could be conducted in the impact facilities mentioned above, the relevance of the tests would be limited by the level of diagnostics that could be brought to bear.
The third stage of fuel dispersal, interphase momentum exchange, has even broader length scale ranges than the breakup stage. However, as the overall density of the fuel phase decreases relative to the gas phase, it is possible to treat the liquid phase as dispersed within the continuous gas phase. Computationally, the drops are treated as subgrid models by size classes, allowing for breakup, coalescence, and interphase momentum exchange, in an engineering sense. Figure 14-10 shows a sample calculation of a dispersal of decane droplets (Glass, 1990). The computational tool is a modification of the KIVA-II code, one of several products of the T-3 group at Los Alamos National Laboratories that can be used for this application.
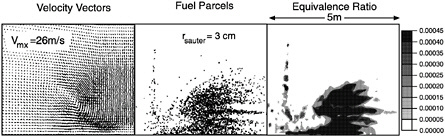
FIGURE 14-10 Example of a numerical simulation tool for the study of the interphase momentum exchange stage using a modified version of the KIV A-II code. Source: Glass, 1990.
Experimentally, the interphase momentum exchange can be studied in engineering environments in the impact facilities mentioned above. Figure 14-11 shows a test from a medium-scale study of an impact on a runway in which the fragmentation of the airframe was ignored (Tieszen, 1995). Drop size diagnostics were not used in the study, but the footprint of the spray was determined by mass collection as a function of position from the point of impact. The mass was collected by rapidly deploying absorbent media. All of the commercial drop size measurement devices work well in the interphase momentum exchange regime.
Tools are available for the study of ground-based flows in the final stages of dispersal prior to ignition. Computationally, commercial tools like Flow 3D2 can be used to track slow moving free surface flows over terrain. Experimentally, flows can be measured at any number of university hydrology laboratories at the appropriate scales.
Post-ignition flows are very difficult to model computationally. The author is not aware of any computational fire models that couple free-surface flow solutions simultaneously with the fire. Computational fire models with fuel spray models are being developed but to the author's knowledge they had not been quantitatively demonstrated at the time of this paper. There are numerous fire test facilities in the U.S. Department of Defense (all services), the U.S. Department of Energy, and the U.S. Department of Transportation. However, the environments are so difficult to work in that the quantitative measurement of fuel dispersal characteristics during fire transients has received very little attention.
RISK-BASED DECISION
Given the current state of knowledge and the available tools, one may ask how one can design a preventive or mitigative strategy to minimize the consequences of fuel firesin the post-crash environment in a cost-effective manner. The answer involves work in two areas. For a given strategy, such as the strategy pursued by the FAA for antimisting kerosene, one must first develop design criteria and then develop the strategy to meet them.
The development of design criteria implies that the post-crash dispersal process is sufficiently understood to permit quantitative assessment. However, from the previous discussion it is obvious that although the dispersal processes in the postcrash environment are qualitatively understood, there is not enough information to predict the effect of a preventive strategy (say a fuel viscosity change) on the dispersal characteristics. This lack of knowledge implies that fundamental work must still be done to characterize the post-crash dispersal environment.
The goal of a risk-based decision is to produce design criteria based on risk reduction targets (Bohn, 1992). The methodology is very similar to probabilistic risk assessment (PRA) methodologies. In a PRA the goal is to analyze an existing process to determine the overall risk and the major contributors to that risk. PRA is based on data from three sources, historical data, deterministic subprocess models, and expert elicitation. A risk-based decision differs in that the process to be studied is new. One of the strengths of a risk-based decision is that it can be used (1) to define the physical processes that need to be understood to make changes at the system level, (2) to identify the uncertainties in the process models and sensitivity to uncertainties at a system level, and (3) to conduct cost-benefit analyses to determine the trade-offs for a given preventive or mitigative strategy.
For a risk-based decision, historical data, such as accident frequency, can be used as inputs to the process (provided, of course, that the frequency of accidents is not modified by the process modification), but the sequence of events that occurs with a preventive or mitigative strategy in place (say a modified-viscosity fuel) must be specified by one or more deterministic models. The deterministic models must be designed

FIGURE 14-11 Example of impact facility for studying the impact stage showing liquid impact into a runway. Source: Tieszen and Attaway, 1996.
so that the effects of the new design strategy can be propagated through the model to the consequence of interest, say passenger deaths from fire. For example, for a modification of fuel viscosity, there might be one model for the effect of viscosity on drop size distribution of the atomized spray, one for the effect of drop size distribution on the size and location of the combustible spray cloud, one for the effect of the cloud size and location on ignitability, and so forth to passenger deaths. The models must be valid over the range of crash parameters for which they will be exercised (medium and high impact regimes).
In an ideal world with perfect knowledge of all physical processes, this type of strategy would not be difficult to implement. However, in practice it is very difficult. For example, some of the physical processes may not have been quantified or may be very difficult to quantify. Under these conditions, it is not possible to design deterministic models for physical processes without additional fundamental research to describe the physics, which requires considerable time and resources.
Historically, in the absence of a clear physical description of the physical processes involved, engineering judgment has been based on the best available knowledge. The risk-based decision process can be used to focus such expert judgments along the lines of the required models. Engineering judgment from individuals with relevant expertise can also be used to estimate effects, based on the best available knowledge. The initial estimate of the effects could be used to guide the development of experiments and models.
This development path, although initially tenuous because of the engineering judgments, would lead to design criteria on a system-wide level. As the process is better understood from the data and models, the estimate of effects would become stronger and more defensible, i.e., less engineering judgment-based and more science-based. The process could be continuously refined to reduce engineering judgment until a satisfactory level of scientific defensibility is reached. At all stages of refinement, uncertainty estimates could be tracked, including uncertainty estimates based on the expert judgment.
In the author's opinion, this would be the most cost-effective way of determining the necessary fundamental research to complete a study, and would allow the most resources to be focused on the development of specific preventive or mitigative strategies. Once all processes are known, the risk based decision process can also be used to decide if a preventive or mitigative strategy makes sense on a cost-benefit basis. To make this decision, cost estimates for research, development, and implementation must be generated, as well as estimates of the expected savings based on the number of deaths prevented (from insurance data, for example). Cost-benefit analyses for different strategies can be conducted without insurance data.
Using a systems strategy, such as a risk-based decision process, the effect of a preventive measure can be tracked throughout any defined process. For example, if a modification in viscosity could be made to the fuel just before impact, only the postcrash environment would need be considered. If the modification was made as the fuel was pumped onto the aircraft, then the effect of the change would have to be tracked through all processes the fuel is used for, from lubrication to combustion. In this way, the positive effects of the modification in the postcrash environment could be balanced against negative effects in other processes.
CONCLUSIONS
Much has been learned about post-crash fuel dispersal processes in the last few decades, both from programs directed at understanding this environment and from fun
damental research in fluid mechanics. In general terms, the processes of fuel dispersal can be qualitatively described, but in many cases, quantitative predictions of effects are beyond our capabilities. Tools, both experimental and computational, have been developed and applied to the dispersal problem and will continue to be developed and improved with time. In designing a preventive or mitigative strategy, the crash process must be understood well enough to develop quantitative design criteria. Risk-based decisions represent one approach that might achieve this goal. However, quantitative descriptions will not come easily because the postcrash environment involves a myriad of complex, coupled, and nonlinear processes that are, by their very nature, difficult to describe quantitatively.
ACKNOWLEDGMENTS
This review was performed at Sandia National Laboratories, a multiprogram laboratory operated by Sandia Corporation, a Lockheed Martin Company, for the U.S. Department of Energy (under contract DE-AC04-94AL85000).
REFERENCES
Ahlers, R.H. 1970. Investigation of Two Methods for Improving the Crashworthiness of Integral Fuel Tanks. FAA-RD-70-56. Atlantic City, N.J.: Federal Aviation Administration Technical Center.
Attaway, S.W., M.W. Heinstein, and J.W. Swegle. 1994. Coupling of the smooth particle hydrodynamics method with the finite element method. Nuclear Engineering and Design 150:199–205.
Bhunia, S. K., and J.H. Lienhard. 1994a. Splattering during turbulent liquid jet impingement on solid targets. American Society of Mechanical Engineers Journal of Fluids Engineering 116:338–344.
Bhunia, S.K., and J.H. Lienhard. 1994b. Surface disturbance evolution and the splattering of turbulent liquid jets. American Society of Mechanical Engineers Journal of Fluids Engineering 116:721–727.
The Boeing Company. 1996. Statistical Summary of Commercial Jet Aircraft Accidents. Seattle, Wash.: Commercial Airplane Group.
Bohn, M.P. 1992. Decision Making under Uncertainty: An Investigation into the Application of Formal Decision-Making Methods to Safety Issue Decisions. SAND 92-1547. Albuquerque, N.M.: Sandia National Laboratories.
Buckson, W., W. Schlegel, and I.R. Smith. 1965. Design, Development, and Evaluation of a Crash-Resistant Fuel System Installation. FAA-ADS-27. Atlantic City, N.J.: Federal Aviation Administration Technical Center.
Cline, D.D., and L.N. Koenig. 1983. The transient growth of an unconfined pool fire. Fire Technology. 19(3):149–162.
Didden, N., and T. Maxworthy. 1982. The viscous spreading of plane and axisymmetric gravity currents. Journal of Fluid Mechanics 121:347–362.
Dorofeev, S.B., D.I. Matsukov, V.P. Sidorov, A.A. Efimenko, A.S. Kochurko, M.S. Kuznetsov, A.K. Pereverzev, V.A. Avenyan, and B.B. Chaivanov. 1991. Experimental Investigation of Thermal Burning Effect from Burning Fuel-Rich Clouds. IRIS-91/3. Moscow: Scientific Research and Development Organization Industrial Risk.
Errico, M. 1986. A Study of the Interaction of Liquid Jets with Solid Surfaces. Ph.D. thesis. San Diego, Calif.: Department of Chemical Engineering, University of California.
Faul, I. 1978. An Investigation into Jet, Droplet, and Spray Behaviour of Safety Fuels. Technical Report 78131. Farnborough, U.K.: Royal Aircraft Establishment.
FAA (Federal Aviation Administration). 1991. Air Safety Research Plan. Atlantic City, N.J.: FAA Technical Center.
Gardner, D.R. 1990. Near-Field Dispersal Modeling for Liquid Fuel-Air Explosives. SAND 90-0686. Albuquerque, N.M.: Sandia National Laboratories.
Glass, M.W. 1990. Far-Field Dispersal Modeling for Fuel-Air Explosive Devices. SAND 90-0528. Albuquerque, N.M.: Sandia National Laboratories.
Gritzo, L.A., V.F Nicolette, D. Murray, J.L. Moya, and R.D. Skocypec. 1995. Wind-induced interaction of a large cylindrical calorimeter and an engulfing JP-8 pool fire. Pp. 269–274 in Proceedings of the Symposium on Thermal Sciences in Honor of Chancellor Chang-Lin Tien held November 14, 1995, at the University of California in Berkeley, California. Urbana, Ill.: University of Illinois Press.
Gritzo, L.A., V.F. Nicolette, S.R. Tieszen, and J.L. Moya. 1996. Heat transfer to the fuel surface in large pool fires. Pp. 701–712 in Transport Phenomenon in Combustion: Proceedings of the 8th International Symposium on Transport Phenomena in Combustion, S.H. Chan, ed. Washington, D.C.: Taylor and Francis.
Hackler, L.W. 1972. Wing Leading Edge Fuel Tank Impact Tests. FAA-RD-72-83. Atlantic City, N.J.: Federal Aviation Administration Technical Center.
Huppert, H.E. 1982. The propagation of two-dimensional and axisymmetric viscous gravity currents over a rigid horizontal surface. Journal of Fluid Mechanics 121:43–58.
Johnson, N.B., S.H. Robertson, and D.S. Hall. 1989. Aircraft Crash Survival Design Guide Volume 5. Aircraft Post-Crash Survival. USAAVSCOM TR 89-D-22E. Fort Eustis, Va.: U.S. Army Aviation Research and Technological Activity.
Kuchta, J.M. and R.G. Clodfelter. 1985. Aircraft Mishap Fire Pattern Investigations. AFWAL-TR-85-2057. Wright Patterson Air Force Base, Ohio: Air Force Wright Aeronautical Laboratories.
Lefebvre, A.H. 1989. Atomization and Sprays. New York: Hemisphere Publishing.
Lienhard, J. H., X. Liku, and L.A. Gabour. 1992. Splattering and heat transfer during impingement of a turbulent liquid jet. Journal of Heat Transfer 114:362–372.
Lister, J.R. 1992. Viscous flows down an inclined plane from point and line sources. Journal of Fluid Mechanics 242:631–653.
Mahood, L., and R.L. Talley. 1982. Correlation of flammability test data on antimisting fuels. DOT/FAA/CT-82/29. Atlantic City, N.J.: Federal Aviation Administration Technical Center.
Millar, R.E., and S.P. Wilford. 1971. Simulated Crash Fire Tests as a Means of Rating Aircraft Safety Fuels. Technical Report 71130. Farnborough, U.K.: Royal Aerospace Establishment.
National Research Council. 1995. Fire-and Smoke-Resistant Interior Materials for Commercial Transport Aircraft. National Materials Advisory Board NMAB-477-1. Washington, D.C.: National Academy Press.
Nicolette, V.F, L.A. Gritzo, J.L. Moya, and S.R. Tieszen. 1995. Comparison of large JP4- and JP8-fueled pool fires. Pp. 461–466 in Proceedings of the International Conference on Fire Research and Engineering held September 10–15, 1995, in Orlando, Florida. Boston, Mass.: Society of Fire Protection Engineers.
Nissley, P.M., and T.L. Heid. 1964. Structural Design for Fuel Containment under Survivable Crash Conditions. FAA-ADS-19. Atlantic City, N.J.: Federal Aviation Administration Technical Center.
Parikh, P., R. Fleeter, and V. Sarohia. 1983. Antimisting Fuel Breakup and Flammability. DOT/FAA/CT-82/149. Atlantic City, N.J.: Federal Aviation Administration Technical Center.
Rockow, R.A., and L.M. Shaw. 1972. Crashworthiness of safe fuels. Pp. 1–13 in Proceedings from Gas Turbine and Fluids Engineering Conference and Products Show held March 26–30, 1972, in San Francisco, California. New York: American Society of Mechanical Engineers.
Russell, R.A. 1971. Small-Scale Impact Tests of Crash-Safe Turbine Fuels. FAA-RD-71-49. Atlantic City, N.J.: Federal Aviation Administration Technical Center.
Schauerman, H.P. 1971. Crash Resistant Fuel Systems Demonstration and Evaluation. FAA-RD-71-27. Atlantic City, N.J.: Federal Aviation Administration Technical Center.
Salmon, R.F. 1981. Wing Spillage Tests Using Antimisting Fuel. FAA-CT-81-11. Atlantic City, N.J.: Federal Aviation Administration Technical Center.
Shaw, L.M. 1971. Safety Evaluation of Emulsified Fuels. USAMRDL Technical Report 71-29. Fort Eustis, Va.: U.S. Army Mobility Research and Development Laboratory.
Tieszen, S.R. 1995. Fuel Dispersal Modeling for Aircraft-Runway Impact Scenarios. SAND 95-2529. Albuquerque, N.M.: Sandia National Laboratories.
Tieszen, S.R., and S.W. Attaway, 1996. Fuel Dispersal in High-Speed Aircraft/Soil Impact Scenarios. SAND 96-0105. Albuquerque, N.M.: Sandia National Laboratories.
Tieszen, S.R., S.W. Attaway, J.W. Swegle, and A.M. Slavin. 1996a. Transient, high-speed, liquid impact into soft soil. Computer Modeling and Simulation in Engineering 1:79–106.
Tieszen, S. R., V.F. Nicolette, L.A. Gritzo, J.K. Holen, D. Murray, and J.L. Moya. 1996b. Vortical Structures in Pool Fires: Observation, Speculation, and Simulation. SAND 96-2607. Albuquerque, N.M.: Sandia National Laboratories.
Tilston, J.R. 1989. The Stability of Fuel Fires. AGARD-CP-467. Farnborough, U.K.: Royal Aerospace Establishment.
Wittlin, G. 1987. Fuel Containment Concepts: Transportation Category Airplanes. DOT/FAA/CT-87/18. Burbank, Calif.: Federal Aviation Administration.
Wu, P.-K., L.K. Tseng, and G.M. Faeth. 1992. Primary breakup in gas/liquid mixing layers for turbulent liquids. Atomization and Sprays 2(3):295–317.
Wu, P.-K., and G.M. Faeth. 1993. Aerodynamic effects on primary breakup of turbulent liquids. Atomization and Sprays 3(3):265–289.
Wu, P.-K., R.F. Miranda, and G.M. Faeth. 1995. Effects of initial flow conditions on primary breakup of nonturbulent and turbulent round liquid jets. Atomization and Sprays 5(2):175–196.
Wu, P.-K., and G.M. Faeth. 1995. Onset and end of drop formation along the surface of turbulent liquid jets in still gases. Physics of Fluids Series A 7(11):2915–2917.
Yaffee, M.L. 1986. Antimisting Fuel Research and Development for Commercial Aircraft: Final Summary Report. DOT/FAA/CT-86/7. Atlantic City, N.J.: Federal Aviation Administration Technical Center.