| This page in the original is blank. |
Appendix A Perspectives on Risk, Risk Assessment, and Risk Management
This appendix is provided to develop a context for understanding risk assessment results. The initial sections deal with fundamental concepts of risk, risk assessment, and risk management. The latter sections explain in technical terms the meaning of the risk measures used for the DCD/TOCDF QRA.
Terminology and Definitions
This section provides definitions of terms used in the report, as well as terms used in the risk assessments. When appropriate, examples are provided.
Hazard is a possible source of danger.
Receptors are people, environmental components, or physical property exposed to a hazard.
Exposure is an opportunity for a hazard and a receptor to interact, creating an at risk situation.
Risk is the possibility or probability that an undesirable outcome (e.g., damage, injury, or fatality) might result during, or as a consequence of, an activity or event that involves a hazard.
Risk assessment is a process focused on assembling and integrating relevant data to provide a quantitative (numerical) estimate of the probability of a particular outcome or range of outcomes.
Risk management is a decision making process focused on balancing alternative strategies and consequences associated with risk reduction and a process for implementing those decisions.
Voluntary risk is a risk that is known and understood (either quantitatively or qualitatively) by an individual(s) who has decided to accept that risk. Examples are sunbathing, driving an automobile, or smoking cigarettes.
Involuntary risk is a risk that may or may not be known or accepted by an individual but is imposed upon him. Examples are air pollutants emanating from a chemical manufacturing facility or from automobiles on a busy highway and radon seeping into basements from underlying bedrock.
Risk Assessment: an Illustrative Example
Risk
Consider a concrete sidewalk with a large, vertically displaced crack in it. The crack presents a hazard (source of danger) to receptors (people) who are exposed to it (i.e., people who use the sidewalk) because there is a possibility that they may trip over the crack. Thus, there is a risk to users of the cracked sidewalk. If such an event occurs (actual exposure), the sidewalk user may fall and be injured, or even killed (risk consequences). Users who are aware of the crack and choose to use the sidewalk are subjecting themselves to voluntary risk; users who are unaware of the crack and use the sidewalk (e.g., on a dark night) are subjected to involuntary risk . Voluntary users may choose to step over the crack (risk management ). Ultimately, the owner of the sidewalk may choose to
repair the crack and eliminate the risk altogether (again, risk management).
This simple example is qualitative in nature because it acknowledges the existence of a risk but does not consider the probability (or chance) of an actual event. In many situations, qualitative knowledge that a risk exists is sufficient for understanding and decision making (e.g., jaywalking on a busy street). Other situations, such as the destruction of chemical weapons, require in-depth understanding and quantitative analysis because of their complexity.
Extending the Example to Risk Assessment
A risk assessment is a process for developing quantitative (numerical) estimates of risk. In its simplest (generic) form, a risk assessment can be viewed as a four-step process. (Note that the NRC (NRC, 1983, 1994) and others have proposed alternative formulations.)
Hazard identification is the first step in the process, and as the term implies, it is concerned with documenting a hazard or hazards associated with a particular condition.
Consequence evaluation considers each hazard and the magnitude and likelihood of possible impacts on the receptor. A thorough analysis of failure or event sequences that can lead to the consequence allows estimates of both the likelihood and magnitude of the failure. For risk assessments involving toxic hazards, consequence evaluation is frequently referred to as dose-response evaluation, i.e., the evaluation of the human health effects from various doses of specific toxic materials.
Exposure assessment is an attempt to quantify the magnitude of possible (or actual) exposures, the pathways for exposure, the duration of exposures, and the size and nature of exposed population(s).
Risk determination combines the results of the consequence evaluation and exposure assessment to generate quantitative estimates of risk for each hazard and for all exposed populations.
The example of a cracked sidewalk illustrates the risk assessment process:
Hazard identification is a straightforward process that involves the simple visual observation of the fact that a tripping hazard exists because of the large, vertically displaced crack in the sidewalk. Consequence evaluation is somewhat more involved because it requires that consideration be given to all possible outcomes of a person actually tripping over the crack. A partial list of possible outcomes, in order of increasing severity, follows:
- person trips, loses balance, recovers
- person trips, bruises toe
- person trips, sprains ankle
- person trips, falls, breaks wrist
- person trips, falls, strikes head, dies
This is a simple set of possibilities. One could posit a more complex set of events, such as one person starts to trip, and a second person trips while trying to help the first. One of the two people falls into the path of a bicycle rider who falls off the bicycle. Fault trees are used to keep track of complex risk events.
Given a knowledge of the risk consequences, one can assign probabilities to the consequences of interest for purposes of risk assessment. In this example, death will be used as the consequence of interest. Death is often chosen as the consequence of interest in risk assessments because it can be clearly defined. If injuries are included, they might range from minor injuries to serious injuries that require longer periods of recovery. Sources of probabilities of occurrence can be either actual data (historical data from similar situations) or assumed values. In this example, the risk assessor would need to know: (1) the percentage of sidewalk users who actually trip over the crack; (2) how many of those who trip fall; (3) how many of those who fall hit their heads; and (4) how many of those who strike their heads die as a result. Sometimes no precisely relevant data are available. In those cases data may come from similar situations, theoretical models, or experts with relevant experience.
The goal of risk assessment is to produce realistic results that reflect the existing uncertainties. Often, "conservative" (upper limit) values are used to simplify problems. Conservative values set an upper bound on risk (i.e., the actual risk is expected to be less than these values); often an upper limit is sufficient for effective decision making. For the sake of simplicity, simple assumptions will be used in the example.
The most conservative answer to the question of the
percentage of sidewalk users who would trip over the crack would be 100 percent. But empirical knowledge tells us that this is unrealistic. A more realistic (but still conservative) number might be one in 50 sidewalk users (2 percent). Another assumption will be used to answer the second question, i.e., how many of those who trip will fall. Here, the assumption is that half of those who trip will fall (i.e., one in two). For the third question, how many of those who fall hit their heads, the assumption is one in 10; and for the fourth question, how many of those who strike their heads will die as a result, it is assumed that the chance of death from striking one's head on a sidewalk is one in 1,000.
Exposure assessment could establish that 10,000 different people might use the sidewalk at one time or another (based on nearby population data) and that the average is 1,000 people per day. (At this phase of the risk assessment, it might be necessary to further characterize the exposed population in terms of age, sex, weight, height, physical condition, etc., to make a truly comprehensive assessment because any one or any combination of these factors could influence the outcome.) The magnitude of the exposure is identical in this example for all exposed individuals because the crack is stationary and the size is constant.
To summarize, hazard identification, consequence evaluation, and exposure assessment have established the following:
- A hazard exists for users of the cracked sidewalk.
- Ten thousand people are potentially exposed to the hazard at some time (e.g., over a period of a year or two).
- One thousand people are exposed to the hazard each day.
- One person in 50 who use the sidewalk will actually trip.
- One in two individuals who trip will actually fall.
- One person in 10 of the individuals who fall will strike his or her head.
- One person of the 1,000 individuals who strike their heads will die as a result.
Risk determination, the final step in the risk assessment process, integrates the preceding information and develops a quantitative estimate of actual risk to sidewalk users. The probability (chance) that a user of the cracked sidewalk will trip, fall, and die can be developed by multiplying the probability of tripping (1 in 50) by the probability of falling (1 in 2) by the probability of striking one's head (1 in 10) and by the probability of dying from striking one's head (1 in 1,000). The result of this multiplication is 1 × 10-6, or 1 in 1 million. In other words, mathematically the probabilities can be expressed:
.02(1 in 50) × .5 (1 in 2) × .1 (1 in 10) × .001 (1 in 1,000) = .000001 (1 in 1,000,000)
One interpretation of the result is that the probability is 1 in 1 million that an individual will die as a result of using the cracked sidewalk (individual risk). This probability is the same as the risk for a single use of the sidewalk by an individual. Another interpretation of the risk estimate is that 1 in 1 million people who use the sidewalk can be expected to die as a result (societal risk). Exposure assessment data (1,000 sidewalk users per day) can be used to calculate the probability of death per unit of time (day, week, month, year, etc.). This calculation yields an average of one death every 1,000 days (2.7 years) or 0.37 deaths per year or 0.001 deaths per day (other measures of societal risk). Several other probabilities or risk estimates could also be calculated.
This example involves a situation where an exposed hazard (the crack in the sidewalk) actually exists. In many situations, risk assessments must determine the probability that an internal or external event will create a new hazard or release a constrained hazard. These events are called initiating events. In the case of the cracked sidewalk, initiating events could be tree roots growing under the sidewalk, freezing and thawing during the winter causing the sidewalk to crack and buckle, or an earthquake.
To continue the example, assume that seismological data indicate that the frequency of earthquakes of sufficient magnitude to cause a sidewalk to buckle in the homeowner's geographical region is one in every 100 years. It may be further assumed that the chance of a homeowner's sidewalk buckling is 1 in 10 (as opposed to some other sidewalk) as the result of an earthquake.
When the risk estimate is considered in the light of initiating events that could produce the hazard, the overall probability becomes about 1,000 times less or 1 in 1 billion. Alternatively, one may think in terms of two related probabilities: (1) the probability of a hazardous
condition being produced of 1 in 1,000; and (2) the probability of death from the hazard of 1 in 1 million, which is manifest only if the initiating event occurs.
Extending the Example to Risk Management
The selection of risk measures to be presented as the output of the risk assessment process depends on the objectives of the risk assessment. Ideally, the results of risk assessments are used by interested and potentially affected parties to make judgments and risk management decisions.
Continuing the example, suppose the sidewalk in question is a residential sidewalk and the owner of the residence is aware of the risk assessment results. The homeowner may decide that a risk of 1 in 1 million is acceptable and decide to do nothing. Conversely, he or she may decide to engage in a risk management program to reduce the risk to sidewalk users.
Among the risk management options would be posting signs to warn sidewalk users of the hazard, roping off the cracked area and requiring users to detour around it, building a ramp over the crack, or repairing the damaged area. Each of these options is accompanied by its own risks. For example, people who walk around the crack may trip over a tree root or step off a curb and sprain an ankle.
Risk Assessment for A Complex Facility
This simple example helps to put the basic ideas of risk assessment in focus. However, it can be deceptive because, in the real world, especially in complex situations where quantitative risk assessments are used, neither the risks nor the useful models of risks nor the presentation of results is this simple. To move from the simple example to the models and results for the DCD/ TOCDF operation requires more precise (mathematical) notions of probability, uncertainty, risk, and risk analysis. It also requires more complex models and carefully developed data, rather than simple assumptions, to describe the risk. This section includes expanded ideas for risk assessments and an overview of current risk assessment and risk management practices. Details of the risk modeling techniques used for DCD/TOCDF, along with a summary of the results from the DCD/TOCDF-specific risk assessments, can be found in Chapter 2. The following two sections, Probability and Uncertainty: A Modem Tower of Babel, and Hazard, Safeguards, and Risk, are for readers interested in the technical details that underpin the methods and results of risk analysis. They explain the meaning of the risk measures (see Chapter 2 of the main report) used for DCD/TOCDF in technical terms.
Probability and Uncertainty: A Modern Tower of Babel
The concepts of probability and uncertainty are relatively straightforward and are the basic vocabulary of risk assessment. However, the language describing these concepts has become confused and garbled, primarily because people use them to describe different concepts or use different words to describe the same concept. It is tempting to ignore all this and invent a new language, but that has been done several times in the past and has only contributed to the problem. To begin with a word, consider probability. Is probability (P) a measurable quantity from the real world or a way to calibrate an internal, mental, state of knowledge? Does it matter?
The notion of probability as a measurable parameter of the physical world (or at least as the subject of a conceptual experiment) is known as the relative frequency interpretation of probability. In this view, the probability of failure (PF) has been represented as
where F is the number of failures in n trials, i.e., the probability of an event is interpreted as the relative frequency of occurrence of that event in the long run. This concept has been known as probability, classical probability, frequentist probability, and frequency. It is now possible to construct mathematical formalisms to examine the behavior of random variables in a wide range of contexts (Cramér, 1946; Fisher, 1990; von Mises, 1957).
The second notion of probability requires acknowledging that, even if an objective, real world probability exists ''out there,'' it may never be measured precisely. There is an element of uncertainty due to lack of knowledge. In this sense, probability becomes a structured scale (over the range of 0 to 1) that calibrates state of knowledge in a meaningful way. Various researchers
have provided methods for constructing and calibrating this scale (de Finetti, 1974; Jaynes, 1996). With this scale, probability becomes a measure of what is in our heads rather than a measure of what is "out there." This concept has been known as probability, personal probability, subjective probability, prevision, degree of belief, Bayesian probability, and state of knowledge (de Finetti, 1974; Jaynes, 1983; Jeffreys, 1961; Lindley, 1965; Savage, 1954). This view of probability has led to the development of methods for treating decision making under conditions of uncertainty and for addressing a wide range of open-ended physical problems where substantial uncertainty exists, i.e., most physical problems risk assessment attempts to address.1
Finally, does all this matter? Sometimes, when substantial facility-specific data are available, for example, either way of thinking leads to the same numerical results. Sometimes the difference matters very much, both numerically and philosophically. The battle over the correct interpretation of probability has been raging for more than 100 years (Kriiger, Daston, and Heidelberger, 1990). At times, it has been a bitter conflict. Even though the two kinds of uncertainty are not difficult to tell apart, the protagonists have managed to ignore each other's ideas, often demonstrating only that "If you accept my definition of probability, then my opponent's calculations of probability are flawed." Two great opponents in this debate, R.A. Fisher and H. Jeffreys, vigorously debated the philosophies underlying their theories and then calculated the same results because each was wise enough to recognize the requirements of the specific problem at hand and adapt his methods to accommodate the proper question (Lane, 1980).
In a recent attempt to reconcile these conflicts, several prominent workers in quantitative risk assessment (also called probabilistic risk assessment and probabilistic safety assessment) have suggested a return to unambiguous language. They call the uncertainty associated with the random nature of the events being modeled aleatory uncertainty and the uncertainty associated with the analyst's state of knowledge about the processes that govern that randomness epistemic uncertainty . The aleatory uncertainty captures variability that is observed but is beyond the explanation of the physical models used in the analysis. The epistemic uncertainty allows for our lack of knowledge (i.e., lack of observation).
If these two types of uncertainty are combined improperly, the result can be an underestimation of epistemic uncertainty (Mosleh et al., 1994). One example from the DCD/TOCDF QRA pointed out by the Expert Panel "is the variability in inventory that results from the operational practice of loading the container handling building for nighttime operation, which was handled as an uncertainty in the inventory. This, however, is a random factor with respect to the initiating event occurrence, and would be better reflected as an aleatory distribution on the source term" (MITRETEK Systems, 1996). The DCD/TOCDF QRA has adopted aleatory/epistemic language for uncertainty and uses the word probability in all cases (frequency and state-of-knowledge concepts).
Form of the Results
The results of analyses that support risk assessment include, in the language of the DCD/TOCDF QRA, probabilities of certain events (e.g., the frequency of initiating events, such as dropping munitions, are expressed as probabilities over the relevant agent destruction campaigns). Figure A-1 illustrates two types of presentation. Type 1 is a point estimate, i.e., a single number that characterizes the result. Here the point estimate of the probability is the mean value ("the probability" to many practitioners). The mean value is the weighted sum of all possible values (the integral is for continuous distributions) and is considered the most appropriate point estimate for summary purposes. Other point estimates include the median (the 50th percentile, for which half of the possible values lie below the median and half above) and the 95th percentile (95 percent of the possible values lie below and 5 percent above).
In Figure A-1, the Type 2 presentation is the full expression of uncertainty. The Type 2 curve is known as a density function, where the probability of lying in any interval is the integral over that interval. The point estimates discussed above are summary "statistics" calculated from the density function.
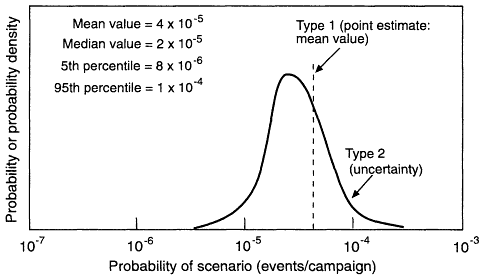
Figure A-1
Form of the results: scenario probability.
Figures A-2a and A-2b illustrate the differences in representation of aleatory and epistemic uncertainties. Figure A-2a is a representation of pure epistemic uncertainty. Here some event will either surely happen (p = 1) or fail to happen (p = 0) under certain conditions. Because it cannot happen only some of the time, only two values are possible: yes (p = 1) or no (p = 0). Therefore, the density function has two spikes, one at p = 0 and one at p = 1. Although there is only one correct answer, there is state-of-knowledge uncertainty about which one is correct. As a specific example, identical stacks of munitions will either fall or remain standing following identical shaking in response to a particular earthquake. Suppose that current knowledge from observations and calculations (the particular earthquake and shaking have not yet occurred) is that the state-of-knowledge probability is 0.3 that a particular stack will not fall (p = 0) and a complementary probability of 0.7 that it will (p = 1). (In terms of a density curve, this amounts to a Dirac delta function of value 0.3 at 0 on the scale of probability of the event "stack does not fall.") This is pure epistemic uncertainty. Once the
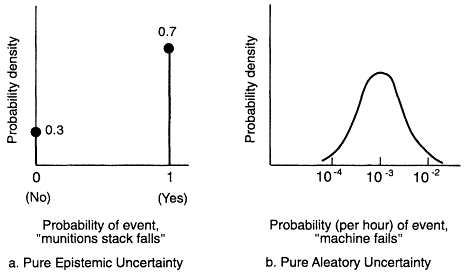
Figure A-2
Aleatory and epistemic uncertainty.
particular earthquake and shaking occur, it will be known with certainty either that the stack falls or that it remains standing. No uncertainty remains.
Figure A-2b is an example of pure aleatory uncertainty. Here an event will happen only some of the time under particular conditions. The resulting probability density curve represents the fraction of the time (relative frequency) that the event occurs (e.g., a particular machine fails during one hour of operation). In the figure, the most likely value is 1 × 10-3/hr. However, randomness among similar machines means that some fail at a rate of 1 × 10-4/hr and some as often as 1 × 10-2/hr.
Finally, pure aleatory and epistemic cases are rare (or may never occur), which has given rise to the strident arguments from those whose work is aimed at solving one problem or the other. Consider the example of stacks of munitions subjected to an earthquake. There are many reasons the uncertainty of this problem does not disappear following the "experiment" of encountering a particular earthquake and shaking. There is an element of randomness in the construction and positions of the stacks that will affect their response to the shaking. Some parameters of the earthquake that affect shaking cannot be modeled and tracked within a quantitative risk assessment (e.g., vertical and horizontal displacement, frequency, and time history), and other intractable factors link shaking to the earthquake itself. Alternatively, consider the aleatory failure rate for the machine. Machines fail in particular ways after particular shocks and stresses. Increased knowledge and modeling of these factors could reduce the randomness. At the same time, even if absolutely identical machines could be constructed, they would be installed in different facilities by different workers, operated under different conditions, and maintained by workers following local policies. Thus, state of knowledge is embedded in most, if not all, cases that at first appear to be purely aleatory.
Hazard, Safeguards, and Risk
A hazard was defined earlier as a possible source of danger. A material may be a hazard because it is toxic to receptors (e.g., a chemical agent), because its potential energy (chemical, mechanical, electrical, or nuclear) could be released causing direct or indirect harm to receptors (e.g., an explosive reaction or an earthquake that topples a stack of munitions), or because its presence could cause the receptors' own activity to lead to harm (e.g., crack in the sidewalk that causes a passerby to trip and fall). The attributes of a hazard must be characterized and may be possible to control, such as mass, toxicity, energy content, shape, and size. However, the presence of a hazard does not guarantee harm.
Safeguards2 stand between hazards and receptors. The term safeguards is used here to describe any physical or procedural barrier (designed or natural) that protects receptors from a hazard. Chemical agents may be stored in sturdy steel ton containers, making exposure to workers or the public quite unlikely. A large propane tank, potentially subject to destructive earthquakes, can be maintained with a limited volume of propane to minimize the tank's structural response to the earthquake, thereby reducing the chance of rupture and subsequent explosion. A chemical processing facility can be located far from large population centers. Signs, lights, and physical barriers can warn walkers of the presence of a crack in the sidewalk. Thus, safeguards can be introduced to control risk. The risk (chance of an undesired outcome) is a function of both the hazard and the safeguards.
Simple risks can be analyzed qualitatively. In the sidewalk example, even the simple analysis may be perceived as tutorial overkill. No one needs to calculate the probability of death from tripping to know that they should protect their neighbors from this hazard and repair the crack. But this example can quickly become complicated. An organization that owns miles of sidewalks may not even know a crack has developed, or, although they know that cracks must exist, they may not know if cracks severe enough to pose a hazard exist or where they are. In this situation, quantitative notions of risk and hazard can provide managers with useful information for controlling the risk to neighbors, employees, and residents. They will need to characterize cracks that pose a hazard (e.g., by length, breadth, and vertical displacement). They will need to examine the range of initiating events that can cause cracks (e.g., growth of tree roots, thawing-freezing cycles, trucks crossing sidewalks) and the probability of each event.
They will need to define the risk in terms of probabilities and consequences. In other words, they will need to perform a risk analysis and present the results in quantitative form. If the organization communicates its concern to neighbors and sets up a simple system for reporting cracks to a central location, a good source of information will be available.
The situation is substantially more complicated for a large chemical processing facility, such as the TOCDF, where there are numerous hazards in many locations and where a variety of processing activities may provide hazards with multiple pathways to workers and the public. Simultaneously, these hazards can be affected by a wide range of safeguards.
The first requirement in analyzing complex situations is to define risk in a way that will be meaningful to managers, individuals (workers and the public), and emergency planners. Historically, the first risk measure proposed for risk studies was the "expected consequences." This widely used measure is the basis (limit or requirement) specified in many environmental regulations and is the sole product of most health risk assessments. Expected consequences are a mathematical construct rather than a characteristic of specific accidents. The expected risk is defined as
where x is the consequences, ƒ(x) is the probability density function, and ƒ(x)dx is the probability that x lies in the small region between x and x+dx. (Note that in the case of discrete consequences, such as fatalities, the mathematics become discrete rather than continuous, i.e., 2.5 deaths is meaningless). Because of this formulation, it is sometimes said that
risk = probability times consequences
To understand this measure, consider a clone of DCD/TOCDF (i.e., consider a hypothetical, very large set [millions or billions] of identical DCD/TOCDF sites [including the nearby population and surroundings]). If the millions of identical sites were operated for their actual lifetimes (estimated as 7.1 years) and if all the accidents causing deaths at all the sites in the clone were tabulated, then the average number of deaths over the millions of sites would be the "expected fatalities" from operating DCD/TOCDF. This average is typically very small, perhaps one-third of a death or 1/10,000 of a death, or even less, because in a well-designed facility, accidents involving fatalities are extremely unlikely. The expected risk is an average over all possibilities rather than a result that is "expected" in the ordinary sense. Moreover, there is only one DCD/ TOCDF and, if it has an accident at all, that accident will have one outcome, and that outcome will not be the "expected'' number of fatalities. It will be one specific outcome from the range of possible outcomes (e.g., no deaths, 1 death, 10 deaths, or perhaps 100 deaths).
Although the risk measure, expected consequences, is often used, it may not be an adequate measure of risk. It does provide a rough summary of the level of risk posed by a facility. However, because it is a high-level average, many important details are obscured. Note that the following three facilities would have the same "risk," in terms of the expected number of deaths, i.e., 0.0045 or 1/220:
- a facility with risk "dominated" by one accident that would kill 300,000 people with a probability of 1.5 × 10-8 of that accident occurring over the lifetime of operation (i.e., it almost certainly will not occur, but, if it does, it will overload local medical facilities, destroy nearby communities, damage the economic base of an entire state, and be an internationally recognized disaster)
- a second facility with risk dominated by two accidents: one that would kill one person with a probability of 5 × 10-4 (very unlikely, but such events have happened); a second one with only a 1 percent chance of killing one person and a probability of 0.4 (this accident is about as likely as tossing heads with a coin, but the consequences are as unlikely as death during a medical operation with general anesthesia; overall, accidents of this severity are commonplace)
- a third facility whose risk is dominated by one accident that would kill 10 people with a probability of 4.5 × 10-4
These three risks have the same number of expected fatalities, but they are in fact very different risks, both in terms of the likelihood that they will occur and in terms of the magnitude of the impact if they occur. Presenting the risk in terms of
risk = probability and consequences
rather than the probability times consequences summary of expected consequences, provides a more thorough understanding and improves the chances of effective risk management.
A display format for summarizing the presentation of probability and consequences is known as the risk curve or risk profile. For fatalities, the risk profile displays the probability of an accident involving "x or more" fatalities as a function of x, the number of fatalities. The three risk profiles for the three simple results above are all shown on Figure A-3.
Moving from the simple examples with one or two dominant accidents to a risk assessment of a complex site/facility like DCD/TOCDF means the risk curve will be more complex. To address the more complex situation, it helps to lay out the risk in a general format. See Kaplan et al. (1981) for further explanation of the notation used below. In this format, risk is simply the answer to three questions:
- What are the scenarios that can cause damage? Call each one Si.
- What is the frequency of the scenario? Call it Φi.
- What are the consequences? Call them Xi.
-
The answers to those questions come in the following form:

and the risk is
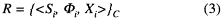
which includes So = "As Planned Scenario"
So a risk assessment is a list of all triplets <Si, Φi, Xi>. The art of risk assessment is in structuring the scenarios in a way that facilitates analysis and computation. The tools for this process include logic modeling (discussed in Chapter 2) and mechanistic calculations based on science and engineering. Uncertainty enters this picture in terms of completeness (have all the important scenarios been identified), in terms of frequency (events per year), and in terms of consequences. Completeness can be directly addressed in limited scope risk assessments in several ways, including making allowances for scenarios that are knowingly omitted (Bley, Kaplan, and Johnson, 1992).
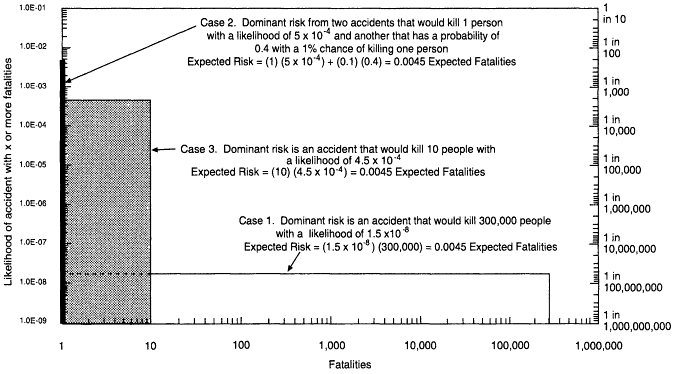
Figure A-3
Risk profiles with the same expected risk.
For full scope risk assessments, every effort is made to be complete by structuring a search for initiating events, by reviewing histories at similar facilities, by examining accident calculations, and by extensive reviews. Uncertainty in the consequences is generally considered by breaking up the range of possible consequences into a number of discrete possibilities, then subdividing the scenarios into many subscenarios, each with its own consequences. Following this process, all the uncertainty is contained in the estimate of the frequency or probability of the scenarios. At this point, consistent with the language of the DCD/TOCDF QRA, replace the frequency in equation (3) with the probability over the appropriate campaigns (Pi).
A large-scale risk assessment like the DCD/TOCDF QRA develops a very large number of scenarios. An easy way to understand the presentation of results, called a risk curve or a risk profile, is to think of the list of scenarios above, ![]() as a table in which the scenarios are rearranged in the order of increasing consequences:
as a table in which the scenarios are rearranged in the order of increasing consequences:
Add a fourth column showing the cumulative probability (Pi), i.e., uppercase P, as shown in Table A-1. Note that
so that Pi can be considered the probability of exceedance (the probability that the consequences are equal to or greater than the associated Xi).
When the points <Xi, Pi> are plotted in Figure A-4, the result is a staircase function. Next note that the scenarios in Table A-1 are really categories of scenarios.
TABLE A-1 Scenario List with Cumulative Probability
|
Scenario |
Probability |
Consequences |
Cumulative Probability |
|
S1 |
P1 |
X1 |
P1 = P2+p1 |
|
S2 |
P2 |
X2 |
P2 = P3 + P2 |
|
• |
• |
• |
• |
|
• |
• |
• |
• |
|
• |
• |
• |
• |
|
S1 |
P1 |
X1 |
P1 = P1+1+p1 |
|
• |
• |
• |
• |
|
• |
• |
• |
• |
|
• |
• |
• |
• |
|
SN-1 |
PN-1 |
XN-1 |
PN-1=PN+PN-1 |
|
SN |
PN |
XN |
PN =PN |
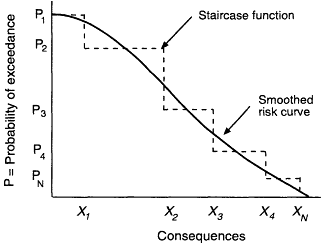
Figure A-4
Risk curve.
For example, the "munitions drop" event actually includes a large number of slightly different scenarios, each resulting in slightly different consequences. Thus, it could be argued that the staircase function should be regarded as a discrete approximation to a nearly continuous reality. If a smooth curve is drawn though the staircase, that curve can be regarded as representing the actual risk, and it is called the risk curve or risk profile.
Thus the meaning of the risk profile is clear. Turning to Figure A-5, the Type 1 (point value) risk curve is familiar. Here P1 is the probability that the consequences are equal to or greater than the consequence X1. The Type 2 risk profile addresses uncertainty. Here there is a family of risk curves (or a risk surface). Now the authors are P3 confident (perhaps 95 percent) that consequences X1 or greater are no more likely than P1,3. They are P2 confident (perhaps 50 percent) that consequences X1 or greater are no more likely than P1,2. Finally, they are only p1 confident (say 5 percent) that consequences X1 or greater are no more likely than P1,1 (i.e., there is a 95 percent chance that they happen more often).
In most QRA studies at least two classes of consequences are considered—acute and latent health effects. Acute health effects involve immediate injuries and deaths. Immediate injuries associated with agent release at the TOCDF tend to be minor, reversible effects of very low-level exposures to nerve agent (e.g., watery eyes and runny noses). In comparison to deaths and latent cancer effects, immediate injuries are minor
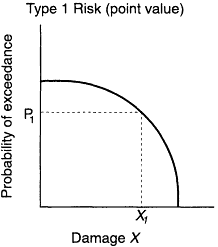
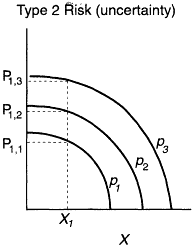
Figure A-5
Form of the results: risk profiles.
and are not reported in the DCD/TOCDF QRA. The most severe latent health effects are possible cancers from exposure to mustard. These cancers, if not properly treated, can become deaths many years later. Risk profiles shown in the main report are associated with immediate (acute) fatalities.
Some General Classes of Risk Analysis
The risk assessment, as developed above, is in the general format used in a QRA. It attempts to be complete, in the sense that the QRA attempts to quantify all scenarios that substantially contribute to the risk measures of interest to those who have chartered the study and to address all uncertainties. Not all QRAs are full-scope studies. In some QRAs, the analysis addresses only internal events or only external events. In many QRAs, the analysis addresses only accidents. Historically, this has been because the risk of death and serious injury to the public, which result only from accidents, has been the focus of the QRAs. The DCD/TOCDF QRA addresses both internal and external events, but only accidents involving agent. For the TOCDF, the risks from normal (non-agent) emissions and minor upset conditions are addressed in the health risk assessment (HRA).
HRAs generally involve a simplification of the basic model described above. Typically, they only examine risks from normal operation and mild upset conditions. The scope of HRAs has been prescribed by the Environmental Protection Agency (EPA), and, therefore, an HRA is rule-driven, rather than science-driven. Although there has been some criticism of this approach (NRC, 1994), it does have some advantages. Criteria are established defining what must be analyzed, how it must be analyzed, and the standards that must be met. This approach allows for a simpler analysis than a full risk assessment. Uncertainties are replaced by using conservative upper limit assumptions on releases of hazardous materials. Even with these conservative requirements, facilities can be engineered to meet EPA limits for releases of cancer-producing chemicals, and there seems to be wide acceptance of the HRA approach. Difficult questions of substantial uncertainty, such as the body's response to very low doses and the possibility and consequences of rare accidents, are not addressed. Questions of values and policy are embedded in the requirements and are, therefore, not revisited for every new application.
QRAs and HRAs are similar in many ways. Both could be called facility-centered risk assessments in that they focus on a single facility and are performed to manage (or regulate) that facility. Both evaluate the impact of facility operations on nearby populations and property. (Sometimes the QRA, like the DCD/TOCDF QRA, also evaluates the impact on workers.) Both are used to manage risk by changing facility design or operation and by managing emergency response practices. The primary differences are the types of risks that are examined and the treatment of uncertainty. The QRA examines accidents (and normal releases, if they contribute substantially to risk); the HRA examines
normal releases and mild upset conditions. For DCD/ TOCDF, the QRA focuses mainly on agent releases, while the HRA is concerned with emissions resulting from the destruction of agent and munitions. The QRA attempts to calculate a realistic result, including uncertainty, which permits management to consider the best estimate of the effects of changes on risk. The HRA calculates an upper limit on releases and health effects, forcing management to meet a pass/fail criteria.
Perception and Risk Assessment
In the past several decades, risk assessment and risk management have become major factors in making decisions involving potentially adverse consequences to society. During this period, risk-related concerns have also permeated the public consciousness. Because meaningful measures of risk can now be generated, people and organizations are being asked to take increased responsibility for the risks they impose upon themselves and others.
More awareness of the risk of an activity does not necessarily translate into an understanding that can be quantified. People may place different values on particular risks, depending on their personal views. Often, the perception of risk by significant segments of the general population has not progressed beyond the level of intuitive feelings based on personal experiences, culture, and mass media coverage (Piller, 1991). Whether risks have been quantified in terms of consequences and frequency of potential occurrence (e.g., one chance in 6,000 per year of being killed in an automobile accident in the United States) or are only vaguely perceived as detrimental influences to an individual, a family, or a community, the political and societal implications need to be examined in an orderly manner.
People have different ideas about which risks are acceptable. Some people may smoke but be afraid of skiing, or vice versa. These are voluntary risks that allow people to choose based on their personal perceptions of risks and benefits. Risks of certain diseases and natural disasters are largely involuntary, although people may take some preventive measures. Involuntary risks associated with a wide range of industrial activities are managed by society through codes, standards, regulations, economic considerations, and responsible behavior. For hazardous chemicals, such as pesticides or highly flammable or toxic materials, a high level of risk analysis is often desirable. For example, in the DCD/TOCDF QRA, each phase of activity is analyzed to determine how accidents might be initiated and progress.
Risk communication is a separate discipline. Risk analyses are very large integrated studies that can be difficult to understand. They involve many different kinds of expertise, modeling, and calculation. Expert input, often in the form of assumptions, is required to limit the scope of the modeling and to permit the models to include information on the boundaries of scientific knowledge. Communicating the content and results of risk assessments in ways that can be understood, that clarify the uncertainties, and that draw a fine distinction between facts and policies has proven to be difficult. Since the publication of the Reactor Safety Study (U.S. NRC, 1975) (the first full nuclear plant QRA, which was widely criticized for the presentation of results in the summary report), extensive research has been done on communicating risk results (NRC, 1989).
Effective communications have been hampered because three traditions (QRA, HRA, and risk communication) are involved, each with its own history, practitioners, and literature. Although some attempts have been made to reconcile them, including the formation of a technical society, the Society for Risk Analysis, they have remained largely separate. The same can be said of the world of practice. The three traditions have progressed rather independently of each other but have converged in the Army' s Chemical Stockpile Disposal Program.
Earlier recommendations of the Stockpile Committee have urged that the risk assessments be integrated and combined with an effective risk communication and public involvement program to ensure that interested parties, such as the public, local and national government entities, and the Army, all understand the risks involved in continued storage and alternative methods of destruction. The present report reviews and comments on the QRA and HRA studies performed for DCD/TOCDF and on the tools established for managing the risk. This report provides perspectives on how the studies can be viewed and used in an integrated way. The committee hopes this report will help
interested parties understand how to interpret and use the results of the risk analyses of DCD/TOCDF and other sites/facilities.
Risk Management
For a chemical agent and munitions disposal facility and its associated storage site, risk assessments of accidents (e.g., a dropped rocket), transients or upsets (e.g., stack agent release), and normal operations can be developed at different levels of detail depending on the available information and the intended use of the results. For example, the TOCDF HRA is a screening risk assessment based on conservative assumptions (overestimates) about emissions and is intended to demonstrate that the risk is below permit requirements. The TOCDF QRA is a detailed, site-specific risk assessment (best estimate and full statement of uncertainty) intended to evaluate and facilitate management of the risks associated with accidents involving agent.
Risk assessments are intended to provide a quantifiable scientific basis for managing facility design and operations. Once the whole spectrum of risks has been quantified, it is possible to evaluate issues, such as whether or not maintenance of a spare piece of equipment has a significant impact on operational safety. A risk management plan that lays out the process for using risk assessment information within the overall plant management structure is essential to taking full advantage of a thorough risk assessment.
Risk management addresses such matters as proper interactions between managers responsible for controlling risks and the individuals on site and off site who are responsible for emergency preparedness and accident mitigation. A risk assessment identifies the major causes of risk and can be useful for developing options to reduce risk. For example, the risk assessment may be used for ordering the sequence of destroying particular weapons to reduce the stockpile risk as quickly as possible. Other areas where a risk management plan uses the results of a risk assessment in decision making include the management of change, performance evaluation, and incident investigation. Conversely, the information that derives from risk management can be used to refine and enhance the accuracy of a risk assessment. A more thorough discussion of the risk management process is given in the next section.
Risk Management Process
Risk management can be described as the process by which risks are understood and controlled. All affected parties have roles to play in the risk management process at DCD/TOCDF. The Army is responsible for managing the chemical stockpile and its destruction. However, the Army's contractors, individual workers, local governments, and the affected public must all participate for the process to proceed efficiently and safely (NRC, 1996a). Risk management usually involves the following steps:
- understanding the risk (including identifying major contributors to risk)
- suggesting alternative ways to reduce risk
- evaluating risk reduction alternatives
- selecting preferred alternatives (including implementing decisions)
Step 1: Understanding the Risk
Understanding the results of risk assessment implies more than knowing the summary numerical results of the QRA and HRA. Understanding also requires knowing the details, including the assumptions, simplifications, and omissions, of the analyses. The results must be viewed in the full context of the risk assessment, as well as in the context of the actual safety performance of the plant. This must be accompanied by a thorough understanding of explicit and implicit uncertainties.
Understanding the results of the risk assessment also means knowing the significant contributors to risk, i.e., knowing how improved performance can reduce risk and how degraded performance can increase risk. The possible benefits are listed below:
- Managers and workers can develop options for reducing risk or for ensuring that risk does not increase. They can also consider how proposals for change affect risk.
- Workers, emergency response personnel, and others can better understand their personal risks and how best to protect themselves and each other.
- Emergency preparedness managers can focus their planning and training programs on the most important scenarios or sources of risk to the surrounding communities.
- State and local officials can provide more informed oversight in their decision making.
- Everyone can participate knowledgeably in the risk management process.
For example, risk from seismic events was found to be the dominant contributor to the risk of fatalities at DCD/TOCDF. The Army has modified operating practice to reduce one of the major seismic contributors (see Example 1 in Chapter 3). Emergency preparedness officials of the Chemical Stockpile Emergency Preparedness Program should also be aware of the nature of seismic risks and keep them in mind when developing and implementing their response plans.
The DCD/TOCDF QRA and HRA reports provide sufficient detail for understanding the risks associated with the Army's Chemical Stockpile Disposal Program (U.S. Army, 1996; Utah DSHW, 1996). See Chapter 2 for a summary of this information, which has also been presented in public meetings near the Tooele site.
Step 2: Suggesting Alternative Ways to Reduce Risk
Risk can be reduced through effective changes of equipment, activities of plant personnel, and emergency response capabilities. uncertainties in calculated risks can be reduced by better understanding the factors affecting risk. Some examples of risk reduction alternatives follow.
Changes to Plant Hardware
These are obvious responses to risks involving plant equipment. These changes are often costly, however, and may involve retraining workers; therefore, other alternatives should also be considered, which may turn out to be more effective. Changes to plant hardware have been considered at the TOCDF and several have been implemented (see Examples 1 and 2 in Chapter 3).
Changes to Plant Procedures
Operating, maintenance, and emergency procedures, as well as related off-site emergency response procedures, can be effectively modified and improved to reduce risk. Care must be taken to ensure that neither the training of personnel nor the level of performance is adversely affected by frequent or poorly analyzed procedural changes.
Changes to Emergency Response Capabilities
Plans, preparations, and mitigation activities by the Chemical Stockpile Emergency Preparedness Program and other emergency response organizations can be revised or restructured to deal more effectively with the major identified contributors to risk. The relative risks associated with alternative responses can also be assessed.
Changes in Management Philosophy and Incentives
These can involve a wide range of activities. For example, changes in training that increase the knowledge and improve the skills or behavior of on-site and off-site personnel can improve performance. Another example would be changes in the criteria for performance evaluation and compensation that could alert both managers and workers to the relative importance of certain factors, such as safety, environmental performance, and productivity.
Changes in philosophy include management response to errors or other failures. If management response is punitive, then mistakes will be covered up. If the management goal is a high level of safety and environmental performance, and if sharing problems and near misses is seen as an opportunity for learning and improvement, then safer operations are more likely to result (Chess, Greenberg, and Tumuz, 1995; Ochsner, Chess, and Greenberg, 1995).
Changes in Organizational Culture
Management can also be proactive in establishing a culture throughout the organization that strives for the continuous improvement of safety and environmental performance in all aspects of operation.
Improvements in Knowledge to Reduce Calculated Risks
Reducing uncertainties often has a tendency to reduce calculated average risks because the average is
strongly affected by possibilities associated with upper uncertainty bounds. Efforts to reduce calculated risks typically involve improvements in basic scientific knowledge and improvements in risk modeling.
Improved Basic Knowledge. Options for gathering or developing new information include extending the review of the scientific literature, eliciting opinions from experts, making more accurate mechanistic calculations, performing experiments and tests to determine new scientific information, and focusing analyses of performance data to find new insights into the behavior and interactions of plant conditions and workers.
Improvements in Risk Modeling. Risk models necessarily involve simplifications, approximations, and assumptions. Improvements in risk modeling are usually possible if analysts can refine their models by replacing worst-case assumptions with detailed analyses. In the initial phase of a risk assessment, it is often necessary to use conservative models that overestimate risks, expending the effort to be more accurate only on those parts of the analysis that have a significant impact on results. Thus initial estimates may exaggerate some risks. In some cases, additional risks are discovered through detailed analyses, especially if the range of possible uncertainties was not carefully considered. Improved data are also possible once a facility begins operations (e.g., the Johnston Atoll Chemical Agent Disposal System or the TOCDF) because models can be refined using facility-specific data rather than data from similar facilities.
Step 3: Evaluating Risk Reduction Alternatives
For every proposed change (in design, equipment, or procedures), it is necessary to assess the impact of the change on safety, ease of operation, environmental performance, public and worker health, short-term and long-term economic costs and benefits, schedules, regulatory compliance, political and public acceptability, and flexibility to respond to future mandated or voluntary changes (OTA, 1995). Changes that may have a significant impact on safety, health, or the environment need to be carefully assessed so that tradeoffs and changes in risk are well understood. Changes can be suggested by managers, operators, inspectors, and other interested parties, and are often required by regulators. Evaluations are influenced by costs, schedules, and advances in technology.
Step 4: Selecting Preferred Alternatives
When considering alternatives for risk reduction, it is appropriate to consider making no change as an option, or at least as a yardstick, for comparison. The decision process involves matters of fact (e.g., changes in risk as calculated in the risk assessments); limitations on the facts (e.g., assumptions, approximations, and uncertainties); and matters of policy (e.g., how safe is safe enough, who should pay, and the value of tradeoffs). There is no easy formula for weighing these factors, especially when tradeoffs are involved. However, failure to give fair consideration to all of these factors can be a recipe for controversy and failure. Public participation is especially important when scientific facts and policy issues must be balanced. Who decides and through what processes decisions will be made involve extremely complex questions. In a given situation, the dynamic interaction of factors, such as legislative mandates, organizational philosophy, and public awareness and organizational involvement, dictate the basic framework of the answers to these questions.
In the past 15 years, formal tools for managing risk at technological facilities have substantially improved. Risk assessments and risk management systems are described in the literature for a variety of facilities in the electric utility, aerospace, transportation, and chemical process industries (NRC, 1996b). Technical conferences often devote numerous sessions to risk management and risk-based or risk-informed regulation. Risk-based regulations are founded on risk assessments; risk-informed regulations consider risk information along with other factors. Conference proceedings include many examples of risk management processes for a variety of industries (e.g., Vesely et al., 1995). Some risk limits are regulation driven. RCRA Part B regulations, for example, set limits on normal process releases from combustors. The U.S. Nuclear Regulatory Commission is about to issue new safety evaluation reports and standard review plans that formally implement a risk-informed regulation process for nuclear power plants as part of its previously announced policy on using risk analysis in regulation (U.S. NRC, 1995).
References
Bernstein, Peter L. 1996. Against the Gods: The Remarkable Story of Risk. New York: John Wiley & Sons.
Bley, D.C., S. Kaplan, and D.H. Johnson. 1992. The Strengths and Limitations of PSA: Where We Stand. Reliability Engineering and Systems Safety 38. Belfast, Northern Ireland: Elsevier Science Publishers Ltd.
Chess, C., M. Greenberg, and M. Tumuz. 1995. Organizational learning about environmental risk communication. Society and Natural Resources 8: 57-66.
Cramér, Harald. 1946. Mathematical Methods of Statistics. Princeton, N.J.: Princeton University Press.
de Finetti, Bruno. 1974. Theory of Probability: A Critical Introductory Treatment. New York: John Wiley & Sons.
Feller, William. 1968. An Introduction to Probability Theory and Its Applications. 3rd ed. New York: John Wiley & Sons.
Fisher, R.A. 1990. Statistical Methods, Experimental Design, and Scientific Inference. New York: Oxford Science Publications.
Jaynes, E.T. 1983. Confidence intervals versus Bayesian intervals (1976). R.D. Rosenkrantz (ed). E.T. Jaynes: Papers on Probability, Statistics and Statistical Physics, pp. 149-209. Dordrecht, Holland: D. Reidel.
Jaynes, E.T. 1996. Probability Theory: The Logic of Science. Unpublished manuscript. St. Louis, Mo.: Washington University. ftp://bayes.wustl.edu/pub/Jaynes/book.probability.theory/pdf
Jeffreys, Harold. 1961. Theory of Probability. 3rd ed. Oxford, U.K.: Clarendon Press.
Kaplan, S., and B.J. Garrick. 1979. On the use of a Bayesian reasoning in safety and reliability decisions—Three examples. Nuclear Technology 44 (July): 231-245.
Kaplan, S., G. Apostolakis, B.J. Garrick, D.C. Bley, and K. Woodward. 1981. Methodology for Probabilistic Risk Assessment of Nuclear Power Plants (PLG-0209). Newport Beach, Calif.: Pickard, Lowe and Garrick, Inc.
Kriiger, L., L.J. Daston, and M. Heidelberger, eds. 1990. The Probabilistic Revolution. Vol. 1. Ideas in History. Vol. 2. Ideas in the Sciences. Cambridge, Mass.: MIT Press.
Lane, David A. 1980. Fisher, Jeffreys, and the Nature of Probability. In S.E. Fienberg and D.V. Hinkley, eds. R.A. Fisher: An Appreciation, pp. 148-160. Berlin, Heidelberg: Springer-Verlag.
Lindley, D.V. 1965. Introduction to Probability and Statistics from a Bayesian Viewpoint: Probability and Inference. 2 vols. New York: Cambridge University Press.
MITRETEK Systems. 1996. Report of the Risk Assessment Expert Panel on the Tooele Chemical Agent Disposal Facility Quantitative Risk Assessment. McLean, Va.: MITRETEK Systems.
Mosleh, A., N. Siu, C. Smidts, C. Liu., eds. 1994. Proceedings of Workshop I in Advanced Topics in Risk and Reliability Analysis—Model Uncertainty: Its Characterization and Quantification. NUREG/CP-0138. Washington, D.C.: U.S. Nuclear Regulatory Commission.
NRC (National Research Council). 1983. Risk Assessment in the Federal Government: Managing the Process. National Research Council. Committee on the Institutional Means for Assessment of Risks to Public Health. Washington, D.C.: National Academy Press.
NRC. 1989. Improving Risk Communication. National Research Council. Committee on Risk Perception and Communication. Washington, D.C.: National Academy Press.
NRC. 1994. Science and Judgment in Risk Assessment. National Research Council. Committee on Risk Assessment of Hazardous Air Pollutants. Washington, D.C.: National Academy Press.
NRC. 1996a. Public Involvement and the Army Chemical Stockpile Disposal Program. National Research Council. Committee on Review and Evaluation of the Army Chemical Stockpile Disposal Program. Washington, D.C.: National Academy Press.
NRC. 1996b. Understanding Risk: Informing Decisions in a Democratic Society. National Research Council. Committee on Risk Characterization. Washington, D.C.: National Academy Press.
Ochsner, M., C. Chess, and M. Greenberg. 1995. Case Study: Du Pont's Edgemoor Facility. Pollution Prevention Review 6(1): 65-74.
OTA (Office of Technology Assessment). 1995. Environmental Policy Tools. Washington, D.C.: U.S. Government Printing Office.
Piller, Charles. 1991. The Fail-Safe Society: Community Defiance and the End of American Technological Optimism. Los Angeles, Calif.: University of California Press.
Savage, Leonard J. 1954. The Foundations of Statistics. New York: John Wiley & Sons.
U.S. Army. 1996. Tooele Chemical Agent Disposal Facility Quantitative Risk Assessment. SAIC-96/2600. Aberdeen Proving Ground, Md.: U.S. Army Program Manager for Chemical Demilitarization.
U.S. NRC (U.S. Nuclear Regulatory Commission). 1975. Reactor Safety Study. WASH-1400, NUREG-75/014. Washington, D.C.: U.S. Nuclear Regulatory Commission.
U.S. NRC. 1995. Federal Register 60FR42622. September 29, 1995. PS-AD-35 to PS-AD-42. Washington, D.C.: U.S. Nuclear Regulatory Commission.
Utah DSHW (Division of Solid and Hazardous Waste). 1996. Tooele Chemical Demilitarization Facility Screening Risk Assessment. EPA I.D. No. UT5210090002. Salt Lake City, Utah: Utah Department of Environmental Quality.
Vesely, W.E., J.W. Chang, E.J. Butcher, and A.C. Thadani. 1995. Risk Management Strategies—Qualitative and Quantitative Approaches. Pp. 869-876 in Proceedings of the International Conference on Probabilistic Safety Assessment Methodology and Applications, Seoul, Korea, November 26-30, 1995. Taejon, Republic of Korea: Korea Atomic Energy Research Institute.
von Mises, R. 1957. Probability, Statistics and Truth. New York: Dover Publications.


















