This paper was presented at a colloquium entitled “Genetics and the Origin of Species,” organized by Francisco J.Ayala (Co-chair) and Walter M.Fitch (Co-chair), held January 30–February 1, 1997, at the National Academy of Sciences Beckman Center in Irvine, CA.
Genes, peoples, and languages
L.LUCA CAVALLI-SFORZA
Department of Genetics, School of Medicine, Stanford University, Stanford, CA. 94305–5120
ABSTRACT The genetic history of a group of populations is usually analyzed by reconstructing a tree of their origins. Reliability of the reconstruction depends on the validity of the hypothesis that genetic differentiation of the populations is mostly due to population fissions followed by independent evolution. If necessary, adjustment for major population admixtures can be made. Dating the fissions requires comparisons with paleoanthropological and paleontological dates, which are few and uncertain. A method of absolute genetic dating recently introduced uses mutation rates as molecular clocks; it was applied to human evolution using microsatellites, which have a sufficiently high mutation rate. Results are comparable with those of other methods and agree with a recent expansion of modern humans from Africa. An alternative method of analysis, useful when there is adequate geographic coverage of regions, is the geographic study of frequencies of alleles or haplotypes. As in the case of trees, it is necessary to summarize data from many loci for conclusions to be acceptable. Results must be independent from the loci used. Multivariate analyses like principal components or multidimensional scaling reveal a number of hidden patterns and evaluate their relative importance. Most patterns found in the analysis of human living populations are likely to be consequences of demographic expansions, determined by technological developments affecting food availability, transportation, or military power. During such expansions, both genes and languages are spread to potentially vast areas. In principle, this tends to create a correlation between the respective evolutionary trees. The correlation is usually positive and often remarkably high. It can be decreased or hidden by phenomena of language replacement and also of gene replacement, usually partial, due to gene flow.
The first book of population genetics I read was Genetics and the Origin of species, by Theodosius Dobzhansky, and it was basic for my understanding of the subject. I later had the chance of knowing Dobzhansky personally and sharing results of my early, relevant research with him. He greatly encouraged me to continue this line of work, and I am happy to share in this opportunity to honor his fundamental contributions.
The first tree of evolution based on gene frequencies of living humans was published 34 years ago. It was based on genetic distances among 15 populations, 3 per continent, calculated from 5 blood group systems, with a total of 20 alleles (1). The number of genes used was admittedly small, but it was practically impossible to get more information at that time. The only major correction of that early tree that became necessary later was to change its root. This was not too surprising, since locating the root is notoriously the most difficult problem. The standard solution today, usually possible with DNA markers, is to add an external group (an “outgroup”), practically chimpanzees.
Table 1 shows a matrix of genetic distances among continents based on six times as many markers (2). The type of genetic distances used—of which there exist a great many— is usually of little importance. But for a tree representation to be acceptable, the evolutionary hypothesis used for drawing the tree must be correct. The simplest hypothesis is that the evolutionary rate is the same across all branches of the tree, and the evolution is independent in all branches [i.e., there are no (important) genetic exchanges among them or similar conditions creating correlations among branches after their origin]. This can be tested on the matrix, since on the basis of this simple hypothesis the distances should be the same, apart from statistical error, in each column (3).
There is one important exception to the rule in Table 1, namely that in the first column of the matrix Europe shows a shorter distance from Africa than do all the other continents. The difference is statistically significant and is consistently found with all markers, ranging from “classical” ones based on gene products [blood groups and protein polymorphisms (1)] to DNA markers such as restriction polymorphisms (4) and microsatellites (5). For incompletely understood reasons, discussed later, mtDNA trees of non-African populations are not as informative as desired.
This exception to good “treeness” of the data (3) is most probably responsible for the difference of results using two classes of methods for fitting trees. One of them, unweighted pair-group method with arithmetic mean, is made popular by its practical convenience and by the similarity of its results with those of the statistically most satisfactory method, maximum likelihood, on the assumption of constant evolutionary rates. The tree is shown in Fig. 1a near that obtained with another method most popular these days, neighbor joining (Fig. 1b). The most important difference is in the position of Europe, which with neighbor joining branches out first after the splitting of Africans and non-Africans and with maximum likelihood is the last but one.
What we know of the occupation of different continents (1) shows that West Asia was first settled around 100,000 years ago, although perhaps not permanently. Oceania was occupied first from Africa, more or less at the same time as East Asia (both probably having been settled by the coastal route of South Asia), and then from East Asia both Europe and America were settled, the latter certainly from the north, via the Bering Strait (then a wide land passage). The dates are approximately known, and the genetic distances corresponding to the splits in the unweighted pair-group method with arithmetic mean tree (or approximately the averages of appropriate columns and other entries in Table 2; see also ref. 1) are in reasonable agreement with them. This is indicated by the approximate constancy of the ratios D/T (genetic distance/ time of first settlement) in Table 2. There is a marked uncertainty in the time of occupation of the Americas, and genetic data suggest the earlier dates are correct. But if very
© 1997 by The National Academy of Sciences 0027–8424/97/947719–6$2.00/0 PNAS is available online at http://www.pnas.org.
Table 1. Genetic distances among major continents or continental areas, based on 120 classical polymorphisms
|
|
Africa |
Oceania |
East Asia |
Europe |
|
Oceania |
24.7 |
|
||
|
East Asia |
20.6 |
10.0 |
|
|
|
Europe |
16.6 |
13.5 |
9.7 |
|
|
America |
22.6 |
14.6 |
8.9 |
9.5 |
small groups of people were responsible for the initial settlement, as suggested also by other considerations, genetic drift may have been especially strong and the time of settlement, calculated from genetic distances, will be in excess.
One reasonable hypothesis is that the genetic distance between Asia and Africa is shorter than that between Africa and the other continents in Table 1 because both Africans and Asians contributed to the settlement of Europe, which began about 40,000 years ago. It seems very reasonable to assume that both continents nearest to Europe contributed to its settlement, even if perhaps at different times and maybe repeatedly. It is reassuring that the analysis of other markers also consistently gives the same results in this case. Moreover, a specific evolutionary model tested, i.e., that Europe is formed by contributions from Asia and Africa, fits the distance matrix perfectly (6). In this simplified model, the migrations postulated to have populated Europe are estimated to have occurred at an early date (30,000 years ago), but it is impossible to distinguish, on the basis of these data, this model from that of several migrations at different times. The overall contributions from Asia and Africa were estimated to be around two-thirds and one-third, respectively. Simulations have shown
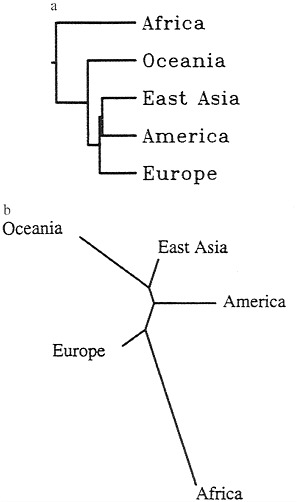
FIG. 1. (a) Tree derived from data in Table 1 by unweighted pair-group method with arithmetic mean. (b) Tree from same data by neighbor joining. Note the difference in the location of the branch leading to Europe.
Table 2. Genetic distances averaged from Table 1 corresponding to the nodes of the tree of Fig. 1a and therefore to the settlement of continents from Africa, and the probable time of occurrence of these settlements on the basis of archeological data
(7) that this hypothesis explains quite well the discrepancy between trees obtained by maximum likelihood and neighbor joining.
Genetic Dating of Population Separations
All molecular dating methods used thus far depend on the use of dates from paleontology, and the above results are no exception. These dates are unfortunately subject to modification as new results accumulate. Moreover, the statistical error affecting the dates calculated on the basis of available genetic results is high. One of the first dates given for the first branching in the evolution of modern humans, the separation of Africans and non-Africans, was first estimated by mtDNA at 190,000 years with a large error interval, not well ascertained statistically (8). The result was heavily criticized (e.g., ref. 9). This ball, park estimate, however, was confirmed by an independent, more detailed assessment (143,000±18,000) based on the full sequencing of the mtDNA of three individuals (10).
It should be noted that estimates such as those obtained with mtDNA, based on the first time of occurrence of mutations, are in excess by an unknown amount with respect to the time of division of populations, e.g., of separation from the mother colony of a party of migrants (11). The difference is difficult to estimate, especially in the absence of knowledge of the migration pattern at the time of early colonization of continents.
An alternative method does not depend on external reference times. Provided that the mutation rate of genes is known, it is possible to estimate the time of separation of two populations given the total genetic difference accumulated between them. This is especially easy for microsatellites, because the square of the average difference in number of repeats between two populations is equal to twice the mutation rate times the time of separation of the populations (with generation as a time unit). If the populations are at equilibrium for drift, the result is independent of drift (12). The squaring of the difference of the number of repeats is easily understood, considering that the model used assumes a random walk at a constant rate, with an equally probable increase or decrease of one repeat at every mutation. In a random walk, the average displacement is proportional to the square root of time. The mutation rate for dinucleotide microsatellites in vivo has been estimated at 1/2,000 (12), and therefore with a generation time of around 25 years there is one mutation in each branch every 50,000 years. Higher mutation rates might be even more satisfactory for generating accurate estimates.
The microsatellite mutation rate method might need correction if mutation rates are sensitive to environmental conditions, if some mutations were responsible for the increase of more than one repeat at a time, if the mutation process were not symmetric, and in other ways. Research is ongoing to test the effect of these conditions.
The method could be employed also for single nucleotide polymorphisms, but only if their mutation rate was much higher than is ordinarily the case. If might be sufficiently high
in the case of some fingerprints with an extremely high number of alleles.
The first estimate gave a separation time of the first migrants out of Africa of 146,000 years ago, very close to the date obtained with the mtDNA full sequence. This was based on results with 30 microsatellites (5). More recent results (L.Jin, unpublished work) with 100 microsatellites gave an earlier date. The accuracy of mutation rate estimates and the full understanding of the mutation process will be essential for completely satisfactory accuracy of the dates obtained by this method. More work will be necessary to validate these results, but the “absolute” nature of the dating method is a basic advantage. It is reassuring that the dates of settlement of the various continents thus obtained tend to agree with predictions based on archaeological observations (12).
Geographic Versus Historic Analysis
Tree analysis is an attempt at reconstructing history of population movements and separations. Its success depends on the choice of populations and markers. In principle, populations of approximately similar size are better suited to analysis. It is essential that the number of markers be large and that results be independent of the markers used. Even under best conditions, however, tree analysis cannot go very far in understanding the genetic factors behind the evolutionary processes.
A geographic approach is an important alternative. When applied to a single gene or allele, it favors the study of the places of origin of mutations, the possibility of their repeated occurrence, and the nature of the selective factors involved in their spread, if any. But drift and migration can be best traced by the joint study of many genes, and the shape of trees is mostly directed by these two evolutionary factors. A method that proved especially useful is a geographic study by principal components (PCs) or related techniques (1, 13). It partitions the total variation into independent, additive components, ordered by their relative importance in determining the total variation observed. As for trees, many genes are necessary, and observations must be spread as regularly as possible over the area being analyzed; as for trees, the best check of the validity of the conclusions is their independence from the markers employed: that is, their reproducibility with different sets of markers.
Applications to the various continents have detected many different hidden patterns, each of which seems to have a precise historical or prehistorical explanation. Thus, in Europe, the most important hidden pattern (the first PC) has an extremely high correlation with the history of the spread of agriculture from the Middle East in the period 10,000–6,000 years B.P. (Fig. 2). Other lesser hidden patterns include: a migration to the north, probably across the northern Urals, of a population speaking a Uralic family language currently still spoken in Europe by Lapps, Finns, Hungarians, and some other populations; a migration from the region below the Urals and above the Caucasus to most of Europe, which was hypothesized by two different archaeologists to have carried Indo-European languages to Europe; the Greek expansion of the first millennium B.C. and earlier; the Basque speaking region in the western part of the Pyrenees. In general, this analysis has detected in almost every major region a variety of demic expansions, almost always due to some important technological development favoring the generation of new or more food, or improving transportation, or political power (14).
It is of particular interest that, whereas all autosomal variation is in agreement with the spread of people from the Middle East toward Europe (and also in other directions), an analysis of the mtDNA variation has shown an essentially flat genetic surface, with a minor ripple in the Basque region (15). By contrast, two Y chromosome alleles showing great variation in Europe have a geographic distribution in excellent agreement with the autosomal data (16). These observations have two possible, noncompeting explanations. It is already clear from other data that the Y chromosome variation shows geographic clustering much higher than mtDNA and probably higher than autosomes (17–19), so that the geographic distribution of Y chromosome variants is more highly focussed. This indicates that males are genetically less mobile than females, probably because at marriage they migrate a shorter distance on average than females. There are anthropological observations that marriage is mostly patrilocal or virilocal, also among hunter/gatherers and in addition, there is female “hypergamy,” i.e., females can marry into higher social classes, usually those of conquerors, where they enjoy a higher fertility. Another explanation is that, for reasons mostly not understood, variation among non-African populations for mtDNA is much lower than for African populations. Heteroplasmy of mtDNA might perhaps be high enough that mutants show a conspicuous segregation lag, so that all populations that expanded from Africa have not had the time to segregate most of the new mutants originated after their migration from Africa. Moreover, Europe has a genetic variation in general about three times less than that of other continents (1). All of these reasons make mtDNA variation in Europe especially small and practically undetectable in the conditions in which it was tested by Richards et al. (15). They may also contribute to the poor discrimination among all or most non-African populations observed in mtDNA trees (20).
Genetic and Linguistic Evolution
A tree of 42 world populations was reconstructed on the basis of some 110 genetic polymorphisms and compared with the incomplete, but nevertheless remarkable, knowledge of the similarities between the languages spoken by the corresponding aboriginal populations (21). The linguistic classification used was largely derived from work by Greenberg and published by Ruhlen (22). Sixteen linguistic families were mapped. The correspondence between the genetic tree and the linguistic tree was remarkable, even if five disagreements were noted. The correlation thus found was statistically significant at a very high probability level with two independent methods (23, 24).
Unfortunately, only the lowest branches of the linguistic tree are known. Many linguists do not accept similarities established between more divergent languages and the trees based on them. Even some of the lower branches and taxa established in ref. 22 are not accepted by some linguists, i.e., Greenberg’s three major American families. Differences in methodology account largely for these discrepancies. As discussed by Greenberg (25), distant linguistic relationships need special approaches.
Fig. 3 shows the comparison of the genetic and the linguistic trees (21). We observed the following regularities:
(i) There are fewer families in the linguistic tree than there are populations in the genetic tree and, therefore, there is on average more than one genetic population per linguistic family. It is usually true that the genetic similarity between populations belonging to the same linguistic family is high, as expressed by their having a common node in the genetic tree, with a low position in the tree hierarchy. This rule is violated only in a few cases in Fig. 3, and we will discuss especially three of them: Lapps, Ethiopians, and Tibetans. Lapps speak a Uralic family language but associate genetically with Indo-European-speaking populations. Ethiopians are genetically African and linguistically Afro-Asiatic, a language family spoken predominantly by Caucasoids. Tibetans are genetically northern Chinese, but linguistically they associate with the southern Chinese, who belong to another genetic node.
It is easy to understand the origin of these exceptions. Lapps probably migrated to northern Europe from a region east of
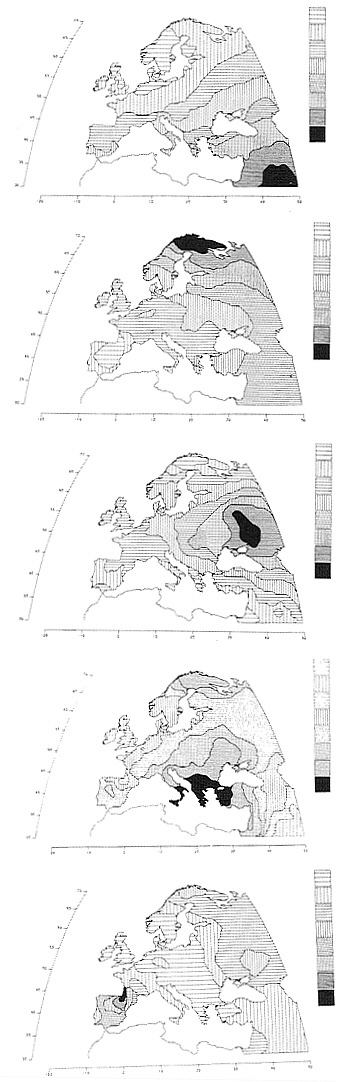
FIG. 2. Hidden patterns in the geography of Europe shown by the first five principal components, explaining respectively 28%, 22%, 11%, 7%, and 5% of the total genetic variation for 95 classical polymorphisms (1, 13, 14). The first component is almost superimposable to the archaeological dates of the spread of farming from the Middle East between 10,000 and 6,000 years ago. The second principal component parallels a probable spread of Uralic people and/or languages to the northeast of Europe. The third is very similar to the spread of pastoral nomads (and their successors) who domesticated the horse in the steppe towards the end of the farming expansion, and are believed by some archaeologists and linguists to have spread most Indo-European languages to Europe. The fourth is strongly reminiscent of Greek colonization in the first millennium B.C. The fifth corresponds to the progressive retreat of the boundary of the Basque language. Basques have retained, in addition to their language, believed to be descended from an original language spoken in Europe, some of their original genetic characteristics. (From ref. 1, with permission of Princeton University Press, modified.)
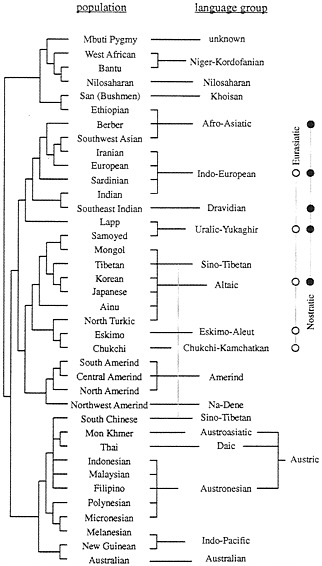
FIG. 3. Coherence between a genetic tree derived from 42 populations with 120 classical polymorphisms (Left) and what is known of the linguistic tree (Right), including two recently reconstructed superfamilies (shown at the extreme right). (From ref. 23.)
the Urals and spoke local languages, related to those of the Samoyeds. In contact with northern Europeans in northern Scandinavia they hybridized extensively with them. Having now more than 50% European genomes, on average, they associated with other Europeans in the genetic tree, but maintained their original languages(s).
The Ethiopians genotype is more than 50% African. It is difficult to say if they originated in Arabia and are therefore Caucasoids who, like Lapps, had substantial gene flow after they migrated to East Africa, or if they originated in Africa and
had substantial gene flow from Arabia, but not enough to pass the 50% mark. We are not helped by knowledge of the origin of Afro-Asiatic languages, which are by far the most common ones spoken in Ethiopia but are also spoken in North Africa, Arabia, and the Middle East.
It is known from historical records that Tibetans migrated from northern China to Tibet. Genetically they are associated with the northern Chinese (not shown in the tree of Fig. 3), Koreans, and Japanese (shown in the tree), but northern Chinese are genetically distinct from southern Chinese. Almost all Chinese today speak Sino-Tibetan languages, which were imposed on all of China at the time of its unification, beginning 2,200 years ago.
(ii) Some linguists have shown that a few of the families given in the tree associate in superfamilies, three of which are indicated in Fig. 3, on the right side. Two of them, Nostratic and Eurasiatic, are rather similar, having about one-half of the families forming them in common; their existence has been inferred by different authors who have used very different methods, and it seems reasonable to assume that the two superfamilies will eventually merge into a larger one. Another linguist has added to Nostratic the recently formed Amerind family (22). It is truly remarkable that the union of Nostratic plus Eurasiatic plus Amerind includes practically the whole major cluster of the genetic tree, which collects together Caucasoids, Northern Mongoloids, and Amerinds. Another superfamily present in Ruhlen’s classification, Austric, also joins populations that are very similar genetically.
At this point one may want to consider why these results, although superficially astonishing, are not unexpected. There are some common evolutionary factors to both linguistic and genetic evolution that are responsible for the observed congruence, and there are also good reasons for possible exceptions. In the spread of modern humans, many groups underwent splits, the two moieties settling in different areas. When these were sufficiently remote that isolation of the splinters was complete, i.e., there was no later migratory exchange, the moieties underwent inevitably genetic differentiation; they also underwent inevitable linguistic differentiation. There was thus a parallelism established between the history of the two phenomena, and very probably both differentiations tended to increase with the time of separation, although at different rates and with different regularities.
Even if the separation of two or more populations was not complete but there remained enough migration between them to reduce differentiation (genetic and/or linguistic), some divergence both at the genetic and at the linguistic level would certainly occur. We have evidence that both genetic distance and also linguistic distance are highly correlated with geographic distance. An increase of the latter decreases cross-migration and increases the rate of both genetic and linguistic differentiation.
We thus expect both genetic and linguistic processes of differentiation to mirror the same basic historical sequence of events or to follow common geography. But inevitably there are reasons the parallelism cannot be perfect. Exceptions could arise in two different ways: language or gene replacement.
(i) Language Replacement. Languages can be replaced entirely (or almost). There has not been a systematic study of this important historical phenomenon. Renfrew (26) has hypothesized three possible mechanisms, which can be reduced to two, pooling the second and third of those he proposed. I will use different names from Renfrew’s, which seem to me to be easier to understand:
(a) Domic expansions, in which an area is occupied by a population increasing demographically at a relatively fast rate. This mechanism was called by Renfrew “demographic-subsistence models.” The area may have been initially uninhabited, as in the earliest migrations to New Guinea, Australia, and the Americas, but in most other circumstances there were earlier settlers who usually spoke a different language. When the later settlers came in large numbers, the earlier ones were sometimes completely suppressed. Tasmania and the Caribbean are such cases. The suppression of Australian aboriginals was only partial, and so was that of American natives, although 95% of the original population of the Americas was killed through disease and war (27). In some other cases early settlers were able to survive without losing their language. Examples are Basques, Lapps, Eskimos, Khoisans. Here the expansions were connected with the development of early agriculture (i.e., for Europe, West Asia, and North Africa, from the Middle East and for Central and South Africa with the Bantu expansion). These prehistoric expansions tied with agriculture were probably more peaceful and usually outnumbered local aborigines, who were hunter/gatherers (some of them still are). Especially if later settlers were in large numbers, they brought their own genes and languages. But in almost all of these cases there was some degree of intermarriage between earlier and later settlers, and in the areas where some kind of this outbreeding occurred, there was likely to develop a discrepancy between language and average genotype.
(b) Subjection of a tribe or nation, by conquest or by economic and social control. This includes Renfrew’s “elite dominance” and “power collapse” (26).
In conquest by people with superior military power or skills there is usually no complete destruction of the subdued nations, but simply their submission and exploitation. After the development of agriculture, the earlier occupants are usually very numerous and retain a high majority after the invasion; genetically, there is then little change, except that the new masters reserve for themselves the positions of power and thus form the new aristocracy. A new strong genetic stratification of social classes is thus generated. The overall gene pool change maybe modest, but will depend on two factors: the proportions of demographic contributions to the population of aborigines and newcomers and also on their relative growth rates, which may be unequal. The newcomers, especially if they are few and powerful, are likely to retain for themselves the best resources and have higher growth rates. Hypergamy, sex differential migration as discussed above, will complicate the final picture.
The new masters are likely to impose their language and thus generate a local discrepancy between the genetic and linguistic pictures. This, however, does not always take place. Even the most extensive demic expansions or conquests were not always effective in totally eradicating all of the languages spoken locally. In general, some relic languages survive in some peripheral areas of their original distribution after expansions of people speaking other languages. There are examples in refuge areas that survived the spread of Indo-European languages to Europe (Basque), northern Pakistan (Burushasky), India (Dravidian languages), and the Caucasus (Caucasian languages); interestingly, they may all belong to a family (Eurasian, different from Eurasiatic) that was spread more than 20,000 years ago to the whole area of Europe, Asia, and America. It has been suggested that this superfamily spread to all of Eurasia at the time of the first occupation of Europe, 40,000 years ago (27).
(ii) Gene Replacement. This can be determined by continued gene flow from neighbors. We have seen examples, e.g., Lapps, Ethiopians. There is one major difference between the two mechanisms: language replacement is mostly an all-or-none phenomenon, at least for a large part of the vocabulary and phonology, and almost without exception for structural rules. Gene replacement instead can be completely gradual. A classic example of gene replacement are Black Americans (not represented in the tree of Fig. 3, which includes only aboriginal people), who notoriously have a lighter skin color than Black Africans, their ancestors. This is especially true in the northern States. Genetic analysis shows that African Americans have on
average 30% of their gene pool from European (White American) genes (28). This partial replacement took place over about 300 years of contact, and it is calculated that, if it was constant in time, there must have been about 3% of mixed unions per generation. Laws assured that the child of mixed parentage would be considered Black. Only individuals with a very low proportion of Black ancestry (or of skin color) would be able to “pass” as White. With gene flow continuing at that same rate, only about 30% of the original gene constitution would remain on average after 1,000 years since the beginning, and about 9% after 2,000 years (1).
Gene and language replacement can to some extent blur the congruence expected between the two types of evolution, but not completely. The accumulation of further genetic and linguistic data will facilitate the study of the relationship between the two evolutions, making it easier to use the genetic tree for predicting the history of linguistic evolution. Charles Darwin had precisely anticipated this development in his first book, The Origin of Species, published in 1859. But the opposite can also happen, and we look forward to linguistic data for ideas about still undetected genetic relationships. Above all we need an increase in genetic data, which modern molecular techniques such as microsatellite analysis and chip hybridization make possible and unusually powerful. The generation of a world collection of stored DNAs for distribution to scientists is the aim of the Human Genome Diversity Project, the feasibility of which is currently being investigated by the National Research Council and by the National Science Foundation.
1. Cavalli-Sforza, L.L., Menozzi, P. & Piazza, A. (1994) The History and Geography of Human Genes (Princeton Univ. Press, Princeton, NJ).
2. Cavalli-Sforza, L.L. (1996) Genes Peuples et Langues (Odile Jacob, Paris).
3. Cavalli-Sforza, L.L. & Piazza, A. (1995) Theor. Popul. Biol. 8, 127–165.
4. Mountain, J.L., Lin, A.A., Bowcock, A.M. & Cavalli-Sforza, L.L. (1992) Philos. Trans. R. Soc. London B 377, 159–165.
5. Bowcock, A.M., Ruiz-Linares, A., Tomfohrde, J., Minch, E., Kidd, J.R. & Cavalli-Sforza, L.L. (1991) Nature (London) 368, 455–457.
6. Bowcock, A.M., Kidd, J.R., Mountain, J.L., Hebert, J., Carotenuto, L., Kidd, K.K. & Cavalli-Sforza, L.L. (1991) Proc. Natl. Acad. Sci. USA 88, 839–843.
7. Ruiz-Linares, A., Minch, E., Meyer, D. & Cavalli-Sforza, L.L. (1993) The Origin and Past of Modern Humans as Viewed from DNA (World Sci., Singapore), pp. 123–148.
8. Cann, R.L., Stoneking, M. & Wilson, A.C. (1987) Nature (London) 325, 31–36.
9. Templeton, A.R. (1993) Am. Anthropol. 95, 51–72.
10. Horai, A., Hayasaka, K., Kindo, R., Tsugane, K. & Takahata, N. (1995) Proc. Natl. Acad. Sci. USA 92, 532–536.
11. Nei, M. (1987) Molecular Evolutionary Genetics (Columbia Univ. Press , New York).
12. Goldstein, D.B., Ruiz-Linares, A., Cavalli-Sforza, L.L. & Feldman, M.W. (1995) Proc. Natl. Acad. Sci. USA 92, 6723–6727.
13. Menozzi, P., Piazza, A. & Cavalli-Sforza, L.L. (1978) Science 201, 786–792.
14. Cavalli-Sforza, L.L. Menozzi, P. & Piazza A. (1993) Science 259, 639–646.
15. Richards, M., Corte-Real, H., Forszter, P., Macaulay, V., Wilkinson-Gerbots, H., Demain, A., Papiha, S., Hedghes, R., Bandelt, H.J. & Sykes, B. (1996) Am. J. Hum Genet. 59, 185–203.
16. Semino, O., Pasarino, G., Brega, A., Fellous, M. & Santachiara-Benerecetti, A.S. (1996) Am. J. Hum. Genet. 59, 964–968.
17. Seielstad, M.T., Hebert, J.M., Lin, A.A., Underhill, P.A., Ibrahim, M., Vollrath, D. & Cavalli-Sforza, L.L. (1994) Hum. Mol. Genet. 3, 2159–2161.
18. Underhill, P.A., Jin, L., Zeman, R., Oefner, P.J. & Cavalli-Sforza, L.L. (1996) Proc. Natl. Acad. Sci. USA 93, 196–200.
19. Ruiz-Linares, A., Nayar, K., Goldstein, D.B., Hebert, J.M., Seielstad, M.T., Underhill P.A., Feldman, M.W. Cavalli-Sforza, L.L. (1996) Ann. Hum. Genet. 60, 401–408.
20. Mountain, J.L., Hebert, J.M., Bhattacharyya, S., Underhill, P.A., Ottolenghi, C., Gadgil, M.Cavalli-Sforza, L.L. (1995) Am. J. Hum. Genet. 56, 979–992.
21. Cavalli-Sforza, L.L., Menozzi, P., Piazza, A. & Mountain, J.L. (1988) Proc. Natl. Acad. Sci. USA 85, 6002–6006.
22. Ruhlen, M. (1991) A Guide to the Languages of the World (Standord Univ. Press, Stanford, CA).
23. Cavalli-Sforza, L.L., Minch, E. & Mountain, J.L. (1992) Proc. Natl. Acad. Sci. USA 89, 5620–5624.
24. Penny, D., Watson, E.E. & Still, M.A. (1993) Syst. Biol. 42, 382–4.
25. Greenberg, J.H. (1987) Language in Americas (Stanford Univ. Press, Stanford, CA).
26. Renfrew, C. (1987) Archeology and Language (Cambridge Univ. Press, Cambridge, U.K.).
27. Diamond, J. (1997) Guns, Germs and Steel (Norton, New York).
28. Cavalli-Sforza, L.L. & Bodmer, W. (1971) The Genetics of Human Populations (Freeman, San Francisco).






