This paper was presented at a colloquium entitled “Genetics the Origin of Species,” organized by Francisco J.Ayala (Co-chair) and Walter M.Fitch (Co-chair), held January 30–February 1, 1997, at the National Academy of Sciences Beckman Center in Irvine, CA.
A demographic approach to selection
(demographic genetics/natural selection/Drosophila pseudoobscura)
WYATT W.ANDERSON*† AND TAKAO K.WATANABE‡
*Genetics Department, University of Georgia, Athens, GA 30602–7223; and ‡Department of Applied Biology, Kyoto Institute of Technology, Kyoto 606, Japan
ABSTRACT The concepts of demography provide a means of combining the ecological approach to population growth with the genetical approach to natural selection. We have utilized the demographic theory of natural selection developed by Norton and Charlesworth to analyze life history schedules of births and deaths for populations of genotypes in Drosophila pseudoobscura. Our populations illustrate a stable genetic equilibrium, an unstable genetic equilibrium, and a case of no equilibrium. We have estimated population growth rates and Darwinian fitnesses of the genotypes and have explored the role of population growth in determining natural selection. The age-specific rates of births and deaths provide insights into components of selection. Both viability and fertility are important components in our populations.
Genetics and the Origin of Species (1) became the cornerstone of the modern synthesis of evolutionary biology because it showed how genetics fits into the processes of evolution, filling the major gap in Darwin’s theory. Dobzhansky was strictly Darwinian in his approach to evolution, and he summarized the available research on genetic changes under natural selection early in the first edition of his book. Although there had been many studies of natural selection by the middle of the 1930s, there had been relatively few studies showing how selection had changed the genetic composition of populations. Dobzhansky’s own pioneering studies on selection in natural and experimental populations of Drosophila were some years away. Each succeeding edition (the second in 1941 and third in 1951) of Genetics and the Origin of Species, as well as the successor book of 1970, Genetics of the Evolutionary Process (2), had an expanded coverage of natural selection as more studies of genetic changes under selection were published.
One theme that emerges in these successive editions is an increasing attention to the concept of Darwinian fitness, of the ways in which genotypic differences in survival and reproductive success bring about selective changes in gene frequencies. Late in his life, Dobzhansky summarized his views on Darwinian fitness in an essay, “On Some Fundamental Concepts of Darwinian Biology” (3), that formed the basis of his discussion of this topic in Genetics of the Evolutionary Process. In particular, he turned to a demographic analysis to relate the Darwinian fitness of genotypes to ecological fitness parameters at the population level, such as the intrinsic rate of increase, r. He proposed that r measured the adaptedness of populations, by which he meant their state of adaptation for population growth. A series of experimental studies by Dobzhansky and his colleagues (4–7) and Ayala and colleagues (8–10) explored this demographic approach to natural selection. One set of studies compared r values measured in populations that were genetically monomorphic or polymorphic for chromosomal inversions. Dobzhansky (see refs. 2 and 11 for summaries) had shown earlier that these inversions were under powerful selection in both nature and the laboratory. Later studies by Mueller and Ayala (12, 13) have explored the use of population growth rates as fitness measures and clarified the mechanisms by which population density affects natural selection (14, 15).
The 1970s brought not only Genetics of the Evolutionary Process but also the beginnings of a new stage in the demographic analysis of natural selection. Anderson and King (16) used life history tables of longevity and fecundity to represent the fitness of genotypes in computer simulations of selection. Cavalli-Sforza and Bodmer (17) employed what they termed “genetic demography” to analyze the fitnesses of human genotypes. Brian Charlesworth, beginning in 1970 (18), combined an analytical study of models with computer simulations to develop a comprehensive theory of selection in age-structured populations. His demographic theory brings together the approaches to population processes that had been, for the most part, treated separately by population ecologists and population geneticists. Its strength lies in joining the ecology and genetics of populations in the way envisioned in the previous decade by Dobzhansky. Charlesworth (19) included in his studies the evolution of life histories, continuing the development of a central topic in evolutionary ecology. Life history strategies (20) and the evolution of senescence (21, 22) are two related areas that have attracted considerable attention.
Charlesworth (18) rediscovered the basic demographic theory of natural selection that had been formulated nearly a half-century earlier by the British mathematician H.T.J. Norton (23). It is interesting to note in passing that Norton had been one of the first people to calculate gene frequency changes under simple models of selection (24). Charlesworth (see ref. 19) went on to greatly expand and extend this demographic theory. The basic Norton-Charlesworth theory establishes the conditions for genetic equilibrium at a single locus when the viability and fertility of genotypes are described by life history tables of longevities and fecundities at all ages, and it shows how the genotypic fitnesses at equilibrium are defined. For the genotype with alleles Ai and Aj, the longevities lij(x) and fecundities mij(x) at age x define an rij that is the intrinsic rate of increase of a population whose members all have this genotype’s life history schedule of births and deaths. This rij is calculated as the root of the demographic equation ![]() . For a single locus with two alleles, there will be a stable genetic equilibrium if and only if r11 < r12 > r22. The equilibrium gene frequency, however, is determined by the demographic functions
. For a single locus with two alleles, there will be a stable genetic equilibrium if and only if r11 < r12 > r22. The equilibrium gene frequency, however, is determined by the demographic functions ![]() , where r is
, where r is
© 1997 by The National Academy of Sciences 0027–8424/97/947742–6$2.00/0 PNAS is available online at http://www.pnas.org.
the intrinsic rate of increase of the entire Mendelian population at genetic equilibrium. These Wij values serve as Darwinian fitnesses of the genotypes in determining equilibrium gene frequencies, as in the discrete-generation model: p1=(W12− W22)/(2W12−W11−W22). For a stable genetic polymorphism, r is calculated as the root of the equation (W12−1)2=(W11− 1) (W22−1).
There have been only a few experimental determinations of genotypic life histories to which this basic demographic theory of selection has been applied. Charlesworth (19) cites only the study of genotypes in Tribolium castaneum by Moffa and Costantino (25). We have obtained life history schedules of longevity and fecundity for three sets of genotypes in D. pseudoobscura, and we present below an analysis of selection on them.
MATERIALS AND METHODS
Chromosomal variants of D. pseudoobscura were chosen as a realistic and practical genetic system for demographic analysis. Natural populations of this species contain an array of inversions on the third chromosome. These inversions segregate as units, just as if they were alleles at a single locus, because crossing over is effectively suppressed within the inverted regions in heterozygotes for the inversions (2). Indeed, crossing over is nearly eliminated over the entire third chromosome in many combinations. The inversions contain linkage blocks of genes much like those thought on theoretical grounds to be the true units of selection (26). Frequencies of these inversions are regulated by selection in nature, and some of these changes can be reproduced in laboratory populations (2, 11). Selection is often intense, as we should expect for genetic units comprising a 10th of the genome. Differences in selection are consequently easier to measure, and the values obtained are more accurate. Four inversions were used in these experiments: Arrowhead (AR), Chiricahua (CH), Pikes Peak (PP), and Standard (ST).
AR/AR, AR/CH, and CH/CH Under Nearly Optimal Conditions. The first set of data comes from a study by Nickerson and Druger (27). These authors extracted seven AR and seven CH chromosomes from a population cage begun with chromosomes collected at Pinon Flats, Mount San Jacinto, CA. These strains were intercrossed, both within each inversion type and between the two, to yield the AR/AR, AR/CH, and CH/CH flies used in the experiment. For each chromosomal genotype, or karyotype, 10 replicate groups of 5 females and 8 males were placed in glass vials, each of which contained a spoon of blackened, yeasted food. The spoons were replaced, with fresh ones every 24 hr, at which time dead females were counted and removed. The eggs on each spoon were counted, and fecundity was recorded as eggs/female/day. Longevity of preadult life stages was measured as egg-to-adult viability. For each karyotype, 20 groups of 50 eggs were placed in half-pint culture bottles and the number of adults emerging in each bottle was recorded. Longevity of adults was measured on groups of 25 females and 25 males in half-pint culture bottles; at 2-day intervals the flies were transferred to new bottles and the number of dead females were recorded. Twenty replicate bottles were studied for each karyotype. All tests were conducted at 25°C, under nearly optimal conditions. The experiment was continued for 58 days, until all fecundities dropped to zero. Nickerson and Druger did not record the average time spent in preadult life stages, but, fortunately, the development times of karyotypes from cage populations started with the same AR and CH chromosomes from Pinon Flats have been studied by others (6, 7).
AR/AR, AR/PP, and PP/PP Under Nearly Optimal Conditions. Ten strains of AR and 10 of PP from collections at Black Forest, 10 miles north of Colorado Springs, CO, were utilized. Marvin Wasserman isolated these chromosomes in 1970, and we conducted our experiment shortly thereafter, in 1971–1972. Crosses were made among all strains of each chromosomal type and between strains of the two types, so that no fly, whether a homokaryotype or a heterokaryotype, was homozygous for any one ancestral inversion. Longevity and fecundity were measured, as in ref. 7, simultaneously on groups of three females and three males in small, glass creamers, each containing approximately 5 ml of blackened food. A glass chimney plugged with cotton was taped to each creamer, and a drop of yeast solution was added before use. Twenty replicates were set up for each karyotype, and all cultures were kept at 25°C. Every 24 hr each group of flies was transferred to a fresh creamer, the number of dead flies of each sex was recorded, and all eggs in each creamer were counted. Measurements were discontinued after 35 days of adult life, when their effect on the parameters of growth and selection was small. Samples of 50 eggs were cultured in half-pint bottles to estimate development time and preadult viability; 16 replicate cultures were studied for each karyotype.
AR/AR, AR/ST, and ST/ST Under Harsh Conditions. Ten strains of AR and 10 of ST from collections at Mather, CA, in 1959 were employed for measurements of the life history functions l(x) and m(x) under conditions such as those a species might encounter in a harsh environment where population growth was severely restricted. The experiment was conducted exactly as for AR and PP, with two exceptions: five, rather than three, pairs of parents were placed in each creamer, and no yeast was added to the food medium. Thus, the flies suffered greater crowding and they were underfed, if not starved. The daily transfers to new containers did not permit much growth of the yeast and other microorganisms that were transferred on the flies or in their guts. The experiment was continued for 30 days of adult life.
ANALYSIS AND RESULTS
Analysis. The first step is the calculation of rij for each karyotype, because the existence of an equilibrium depends on the relative sizes of these quantities. The rij values are calculated from the life history schedules by numerical solution of the equation ![]() . If either a stable or unstable equilibrium is indicated, then the equilibrium equation for age-specific selection can be used to calculate the population growth rate r. This equation does not apply when no genetic equilibrium is indicated, that is, when r12 is intermediate between r11 and r22. In this case the population will ultimately grow at the highest of the genotypic rij values, and substituting this rij into the formulas defining the Wij values provides a useful first approximation to the Darwinian fitnesses (19).
. If either a stable or unstable equilibrium is indicated, then the equilibrium equation for age-specific selection can be used to calculate the population growth rate r. This equation does not apply when no genetic equilibrium is indicated, that is, when r12 is intermediate between r11 and r22. In this case the population will ultimately grow at the highest of the genotypic rij values, and substituting this rij into the formulas defining the Wij values provides a useful first approximation to the Darwinian fitnesses (19).
The fitnesses are calculated as ![]() for x varying from 1 to G. Here, x=age of adults in days, calculated from eclosion; G=maximal age of organisms in the experiment; and, for genotype AiAj, Dij=mean length of preadult life, lij(x)=probability of survival from zygote to age x, and mij(x)=fecundity as female eggs/female/day. The equilibrium equation is
for x varying from 1 to G. Here, x=age of adults in days, calculated from eclosion; G=maximal age of organisms in the experiment; and, for genotype AiAj, Dij=mean length of preadult life, lij(x)=probability of survival from zygote to age x, and mij(x)=fecundity as female eggs/female/day. The equilibrium equation is ![]()
![]() . Beginning with an initial estimate of the population growth rate, r0, an improved estimate r1 is obtained by Newton-Raphson iteration as r1=r0−Z/(dZ/dt). The formula is applied repeatedly to give successively improved estimates, and convergence is rapid. The Darwinian fitnesses are then computed by substituting the final estimate of r into the formulas for the Wij values. The net reproduction, or expected lifetime fecundity of a female zygote, is calculated as Rij=∑x 1ij(x) mij(x), for x varying from 1 to G. Finally, the equilibrium gene frequency, if it exists, is calculated as p1= (W12−W22)/(2W12−W11−W22).
. Beginning with an initial estimate of the population growth rate, r0, an improved estimate r1 is obtained by Newton-Raphson iteration as r1=r0−Z/(dZ/dt). The formula is applied repeatedly to give successively improved estimates, and convergence is rapid. The Darwinian fitnesses are then computed by substituting the final estimate of r into the formulas for the Wij values. The net reproduction, or expected lifetime fecundity of a female zygote, is calculated as Rij=∑x 1ij(x) mij(x), for x varying from 1 to G. Finally, the equilibrium gene frequency, if it exists, is calculated as p1= (W12−W22)/(2W12−W11−W22).
AR/AR, AR/CH, and CH/CH. Nickerson and Druger very kindly made their original data available to us, and it is
summarized in Table 1. Longevity is given as the probability that a female zygote will live to adult age x in days; lij(0) is the preadult viability (of both sexes). The values of lij(x) were obtained by multiplying the probability that adults survive from eclosion to age x by the preadult viability. Fecundity is given as female eggs/female/day. Fecundity was recorded every day, but longevity was measured every 2 days. Because the longevities changed slowly, we interpolated linearly to obtain values for days between counts. To make the tables manageable, data are given at 2-day intervals initially, and at longer intervals thereafter, but data for each day of life were used in the calculations. Five separate sets of measurements (6, 7) failed to disclose any significant differences among the karyotypes in development time. We have chosen an average value of 14.0 days from this data. The reproductive function V(x)=l(x) m(x) is given for each karyotype in Fig. 1. The area under each curve is the net reproduction, Rij, or expected lifetime fecundity of a female at birth. The Rij curves are triangular functions like those described for Drosophila and other insects (5).
AR/AR, AR/PP, and PP/PP. The fecundities and longevities of the karyotypes are given in Table 2. They are abbreviated as for the previous set of data, but again, all calculations were done with the daily values of longevity and fecundity. Longevities of only females are given, but those of males were nearly the same. Differences in development times were small and statistically nonsignificant. Preadult viabilities were moderately low; we confirmed these values in an independent experiment. The reproductive functions V(x) are shown in Fig. 2. Because the fecundities fluctuated somewhat, three-point moving averages are plotted to emphasize the main trends in the data. Again, the V(x) curves are roughly triangular. The conditions of this experiment were nearly optimal and the lifetime fecundities were high; for example, R was 115 female eggs for the AR/AR females.
AR/AR, AR/ST, and ST/ST. Differences among the karyotypes in development time were small and statistically nonsignificant and, as for AR and PP, male and female longevities were alike. The longevities and fecundities are summarized, in the same manner as for the other sets of data, in Table 3. The
Table 1. Life history data for karyotypes with AR and CH inversions
|
|
AR/AR* |
AR/CH† |
CH/CH‡ |
|||
|
x |
l(x) |
m(x) |
l(x) |
m(x) |
l(x) |
m(x) |
|
0 |
.84 |
0.0 |
.83 |
0.0 |
.81 |
0.0 |
|
2 |
.81 |
0.0 |
.83 |
0.0 |
.79 |
0.0 |
|
4 |
.80 |
3.8 |
.83 |
4.4 |
.76 |
4.3 |
|
6 |
.78 |
10.1 |
.82 |
10.7 |
.74 |
9.1 |
|
8 |
.76 |
14.7 |
.82 |
13.3 |
.72 |
12.7 |
|
10 |
.75 |
17.7 |
.81 |
16.2 |
.70 |
14.7 |
|
12 |
.74 |
18.0 |
.80 |
19.4 |
.68 |
14.1 |
|
14 |
.72 |
13.8 |
.78 |
20.2 |
.66 |
12.4 |
|
16 |
.70 |
12.1 |
.76 |
17.6 |
.63 |
10.5 |
|
18 |
.67 |
10.1 |
.75 |
16.7 |
.60 |
8.7 |
|
20 |
.64 |
9.8 |
.74 |
14.2 |
.58 |
7.3 |
|
22 |
.62 |
7.9 |
.72 |
11.5 |
.56 |
5.7 |
|
24 |
.59 |
6.0 |
.70 |
9.6 |
.53 |
4.7 |
|
26 |
.56 |
7.2 |
.68 |
7.0 |
.50 |
4.1 |
|
28 |
.53 |
6.7 |
.67 |
5.5 |
.47 |
3.2 |
|
30 |
.50 |
5.7 |
.62 |
4.4 |
.45 |
3.0 |
|
35 |
.44 |
2.0 |
.55 |
2.3 |
.39 |
1.6 |
|
45 |
.28 |
0.9 |
.38 |
0.7 |
.23 |
0.5 |
|
55 |
.10 |
0.0 |
.25 |
0.8 |
.09 |
0.0 |
|
x, age of adult in days; l(x), probability of living to age x; m(x), fecundity as female eggs/female/day. *Length of preadult life (D)=14.0 days. †D=14.0 days. ‡D=14.0 days. |
||||||
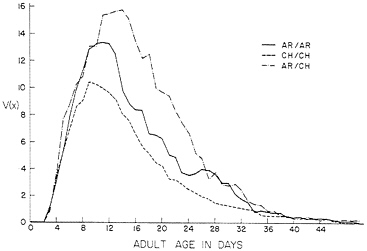
FIG. 1. The reproductive function V(x)=l(x) m(x) for karyotypes bearing AR and CH chromosomes from Pinon Flats, CA. Experimental conditions were nearly optimal.
reproductive functions V(x) are shown in Fig. 3; again, three-point moving averages are plotted to reduce erratic fluctuations. The V(x) functions under these harsh conditions differ noticeably from the triangular curves found for the two sets of karyotypes under nearly optimal conditions.
The results of this demographic analysis for the three sets of data are reported in Table 4. The Wij values as calculated have an average value of 1. To follow convention in reporting fitnesses, we have divided by the heterokaryotype fitness to give relative fitnesses. A stable genetic equilibrium is indicated only for the set of karyotypes bearing combinations of AR and CH chromosomes. The stable age distributions expected for these three karyotypes are nearly the same, and differences between the karyotypes will be small enough that they would disappear under the usual environmental variation.
DISCUSSION
Somewhat to our surprise, the three sets of data illustrate all of the possible outcomes of selection on two alleles: stable genetic equilibrium, unstable genetic equilibrium, and fixation
Table 2. Life history data for karyotypes with AR and PP inversions
|
|
AR/AR* |
AR/PP† |
PP/PP‡ |
|||
|
x |
l(x) |
m(x) |
l(x) |
m(x) |
l(x) |
m(x) |
|
0 |
.60 |
0.0 |
.56 |
0.0 |
.57 |
0.0 |
|
2 |
.60 |
0.0 |
.56 |
0.0 |
.57 |
0.0 |
|
4 |
.60 |
23.6 |
.56 |
21.1 |
.57 |
22.6 |
|
6 |
.60 |
20.7 |
.56 |
21.3 |
.57 |
20.9 |
|
8 |
.60 |
20.2 |
.56 |
21.4 |
.56 |
22.7 |
|
10 |
.60 |
23.2 |
.55 |
20.5 |
.56 |
23.6 |
|
12 |
.60 |
25.8 |
.53 |
23.3 |
.56 |
22.3 |
|
14 |
.60 |
23.3 |
.53 |
17.7 |
.56 |
20.3 |
|
16 |
.60 |
25.1 |
.53 |
21.3 |
.56 |
20.2 |
|
18 |
.59 |
20.1 |
.53 |
16.1 |
.56 |
15.3 |
|
20 |
.59 |
16.4 |
.51 |
15.3 |
.56 |
14.8 |
|
22 |
.58 |
15.9 |
.51 |
16.7 |
.56 |
15.0 |
|
24 |
.53 |
16.6 |
.50 |
17.1 |
.55 |
16.2 |
|
26 |
.50 |
16.3 |
.47 |
13.2 |
.53 |
14.3 |
|
28 |
.46 |
17.0 |
.44 |
12.7 |
.50 |
16.1 |
|
30 |
.44 |
11.1 |
.38 |
11.4 |
.50 |
12.4 |
|
35 |
.36 |
10.0 |
.36 |
12.0 |
.44 |
10.3 |
|
x, age of adult in days; l(x), probability of living to age x; m(x), fecundity as female eggs/female/day. *Length of preadult life (D)=13.66 days. †D=13.63 days. ‡D=13.61 days. |
||||||
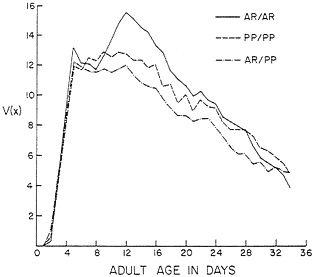
FIG. 2. The reproductive functions V(x)=l(x) m(x) for karyotypes bearing AR and PP chromosomes from Black Forest, CO. Experimental conditions were nearly optimal.
of one allele. The stable genetic equilibrium is a particularly interesting case, because the AR and CH chromosomes at Pinon Flats are part of a balanced polymorphism with annual cycles in frequency of three major inversions (28). In laboratory populations, AR and CH chromosomes from this locality usually reach a stable genetic equilibrium with about 75% AR and 25% CH (29). These chromosomes were extracted from a population cage that was maintained and regularly sampled for 10 1/2 years and subsequently was continued for a total of nearly 14 years (30, 31). Generation time is approximately a month in such population cages. To our knowledge, no other population cage of D. pseudoobscura has been followed as long as this one. Inversion frequencies in this population changed rather rapidly at first and then appeared to be stabilizing at about 36% CH at the end of a year. After year 1, the population was sampled 19 times until its termination at month 166. The frequency of CH fluctuated fairly broadly during this time, ranging between 12% and 33%, with an average value of 24%. This average accords with earlier experiments (29). CH was at a frequency
Table 3. Life history data for karyotypes with AR and ST inversions
|
|
AR/AR* |
AR/ST† |
ST/ST‡ |
|||
|
x |
l(x) |
m(x) |
l(x) |
m(x) |
l(x) |
m(x) |
|
0 |
.46 |
0.0 |
.64 |
0.0 |
.77 |
0.0 |
|
2 |
.46 |
0.0 |
.64 |
0.0 |
.77 |
0.0 |
|
4 |
.46 |
0.3 |
.64 |
0.0 |
.77 |
0.0 |
|
6 |
.46 |
0.5 |
.64 |
0.2 |
.77 |
0.1 |
|
8 |
.44 |
1.1 |
.64 |
0.6 |
.77 |
0.2 |
|
10 |
.44 |
1.1 |
.64 |
0.6 |
.77 |
0.2 |
|
12 |
.44 |
1.2 |
.64 |
0.6 |
.77 |
0.4 |
|
14 |
.43 |
1.3 |
.64 |
1.2 |
.77 |
0.7 |
|
16 |
.43 |
0.5 |
.64 |
0.7 |
.77 |
0.3 |
|
18 |
.42 |
0.3 |
.64 |
0.5 |
.77 |
0.2 |
|
20 |
.41 |
0.8 |
.63 |
0.8 |
.77 |
0.5 |
|
22 |
.40 |
1.0 |
.63 |
0.6 |
.76 |
0.4 |
|
24 |
.39 |
0.7 |
.62 |
1.0 |
.75 |
0.7 |
|
26 |
.38 |
0.7 |
.62 |
1.0 |
.75 |
0.9 |
|
28 |
.38 |
0.6 |
.60 |
0.6 |
.75 |
0.6 |
|
30 |
.35 |
0.4 |
.58 |
0.4 |
.74 |
0.4 |
|
x, age of adult in days; l(x), probability of living to age x; m(x), fecundity as female eggs/female/day. *Length of preadult life (D)=13.10 days. †D=13.22 days. ‡D=13.47 days. |
||||||
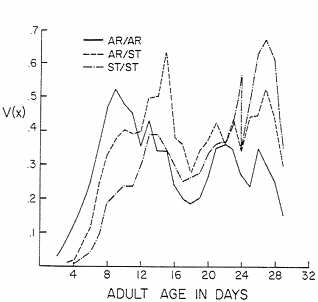
FIG. 3. The reproductive functions V(x)=l(x) m(x) for karyotypes bearing AR and ST chromosomes from Mather, CA. Experimental conditions were harsh.
of 21% when the population was sampled to extract AR and CH chromosomes.
Table 4 shows that the intrinsic rate of increase for an equilibrium population is greater than it would be in a population monomorphic for either AR or CH. These results are consistent with earlier experiments (4, 6, 7) showing that experimental populations polymorphic for AR and CH chromosomes from Pinon Flats produced greater biomass, had higher r values, and were better competitors with another Drosophila species than were populations monomorphic for AR or CH.
The l(x) and m(x) schedules given in Table 1 predict a stable genetic equilibrium because the intrinsic rates of increase for the genotypic life history schedules satisfy the condition r11< r12> r22. The Norton-Charlesworth theory indicates a heterozygote advantage in fitness and an equilibrium frequency of 35% for CH. Frequency changes in the inversions calculated from the genotypic r values fit the observed frequencies in the population cage reasonably well during its first year. The Darwinian fitnesses estimated by demographic theory predict rather well the genetic equilibrium the population approaches during its first year, but they do not explain the lower frequencies of CH in later generations. The fluctuations in inversion frequency indicate that selection was not constant but probably changed in response to external environmental
Table 4. Demographic analysis of selection on three sets of D. pseudoobscura karyotypes
conditions and perhaps to the population’s genetic constitution. The long continuation of the polymorphism for AR and CH in the population cage bears out the prediction of balancing selection based on a fitness advantage of the AR/CH heterozygote.
Decomposing natural selection into its component parts has been one of the most important topics in evolutionary biology during the past few decades (32–34). Two of the most important selection components are viability, or survival, and fertility, which in Drosophila is largely female fecundity and male mating success. A great strength of the demographic theory of selection is that life history tables of l(x) and m(x) represent these selection components in a natural way, and also show their variation with age. Viability or survival between two ages is just the ratio of the longevities at the two. Female fertility is represented by fecundity, but including the male component of fertility is more difficult. Demographic theory is normally formulated in terms of female fecundity alone, because population growth is seldom limited by male fertility. The differential mating success of male genotypes often will not affect population growth, but it will cause changes in gene frequency that reflect natural selection. The demographic model for selection assumes that fertility is alike in the two sexes. If l(x) and m(x) schedules differ in the sexes, the r obtained by averaging the r values separately estimated from male and female l(x) and m(x) schedules will describe the population’s growth rate to a good approximation (19).
Looking down the columns for l(x) and m(x) of the three karyotypes in Table 1, we see a substantial advantage in l(x) and m(x), and the reproductive functions plotted in Fig. 1 show these significant genotypic differences in terms of fecundity adjusted for survival. It is interesting that Druger and Nickerson (30, 31) sampled eggs from the population cage on several occasions and prepared salivary chromosomes from larvae grown under optimal conditions to determine the frequencies of the karyotypes. They also determined the karyotypes of adult flies emerging from cups of food in the population cage. In neither case was there a significant departure from Hardy-Weinberg expectations, and they concluded that the three karyotypes did not differ in preadult viability. The preadult viabilities from their later (27) measurements of l(x) and m(x), given as l(0) in Table 1, do not differ much and show no heterozygote advantage, confirming their earlier (30, 31) conclusions. Although the preadult viabilities of the karyotypes did not differ, the greater l(x) values for AR/CH indicate a substantial heterozygote advantage in viability during the adult life stage.
The fecundity advantage of the heterokaryotype is apparent in early adult life, and becomes pronounced by day 12. It is important to remember that both the demographic equation used to calculate the karyotypic r values and the formula for the Darwinian fitnesses of the karyotypes have the value of V(x) multiplied by what Fisher (35) termed the “discount factor,” e-rx. When r > 0, this discount factor gives greater weight to fecundity contributed by early age classes. When r= 0, the discount factor becomes one and all ages contribute equally to fitness. Thus, for r=0, the Darwinian fitness Wij equals the expected lifetime reproduction Rij. It is this connection between Darwinian fitness and the ecological parameters of population growth that is the special value of the demographic theory of selection.
Charlesworth and Giesel (36) used the demographic theory of selection to show how cycles in population growth rate could drive cycles in gene frequency at a polymorphic locus. Cycles can be caused by environmental factors that affect the longevities and fecundities of all genotypes and ages in the same way, leading to no change in the relative sizes of l(x) and m(x), but rather to an altered population growth rate and in turn to an altered pattern of selection. The cycles of inversion frequency in D. pseudoobscura populations on Mt. San Jacinto (28), where the AR and CH strains used in the experiments were collected, may well be a case in point (19, 36). The fairly broad fluctuations in inversion frequency in the population cage may also be the result of environmental factors that affect population growth, such as temperature, quality of the nutrient medium, mold infection, and mite infestation. Although this scenario is attractive, fluctuations in inversion frequency could be intrinsic properties of these populations, without requiring that environmental changes drive them.
The unstable genetic equilibrium predicted for the AR and PP inversions is not surprising in light of the l(x) and m(x) schedules in Table 2 and the V(x) curves in Fig. 2. The reproductive functions for the karyotypes are only roughly triangular. They rise very steeply, and after V(x) for AR/PP begins to fall, the curve for PP/PP continues upward and levels off before dropping. The V(x) for AR/AR drops a bit after an initial rise and then shows a substantial rise again before dropping off. The heterokaryotype AR/PP is at a clear disadvantage to the homokaryotypes AR/AR and PP/PP. This heterozygote disadvantage is reflected in the unstable equilibrium at 23.3% AR, which would be expected to lead to a decline in frequency of one or the other of the inversions and its eventual loss. The D. pseudoobscura population in Black Forest is polymorphic for AR and PP, and these inversions show seasonal cycles (37). There are no data available on the frequencies of these AR and PP chromosomes in experimental populations, but AR and PP from other localities have not reached balanced polymorphisms in population cages (38). The selective differences between the karyotypes are much smaller for AR and PP than for the karyotypes carrying AR and CH. The demographic analysis suggests that the frequencies of AR and PP would change slowly in experimental populations.
AR and ST chromosomes are normally polymorphic in the natural population at Mather, where these chromosomes were collected. They reach equilibria with slightly higher frequencies of ST than AR in experimental populations and with a pronounced heterozygote advantage in fitness (39). The conditions of our experiment were unusually harsh, as shown by the reduction in net reproduction R by a factor of about 25 (see Table 4). The r values were reduced approximately 3-fold by comparison with the other sets of data. The curves for V(x) were not triangular but showed three pronounced peaks. AR/AR showed a strong advantage early in adult life, followed by a peak for AR/ST and then one for ST/ST near the end of the experiment. AR/ST was intermediate in the karyotypic rates of increase and Darwinian fitnesses, leading to the prediction that there would be no equilibrium but, rather, a steady increase in the frequency of AR. The net reproduction R for the heterokaryotype was greater than that for either homokaryotype, but the growth rate gave additional weight to the early peak of reproduction by AR/AR, giving it a fitness advantage over the other karyotypes.
We have used life history schedules of longevity and fecundity as the basic data for a demographic analysis of selection in three Drosophila populations. The fitness estimates we have obtained, in terms of population growth rates and relative Darwinian fitnesses, make sense in light of what we know about the population genetics of the inversion polymorphism. Two sets of measurements were made under nearly optimal laboratory conditions. From the outset of this study, we wondered whether measurements made under uncrowded conditions would reflect the selection that occurs in crowded population cages, or in nature. Population density is theoretically an important factor in determining fitness (40, 41), but our results indicate that density effects probably do not dominate the selection on the inversions. The D. pseudoobscura inversions are not unique in this respect. Mueller and Ayala (12) found that for Drosophila melanogaster inbred lines, population growth rates at low densities were good indicators
of known fitness differences among the lines, whereas population growth rates at high densities were not.
One of the strong points of estimating fitnesses from life history tables is the focus it gives to female fecundity and, in particular, to the age at which offspring are produced. Unfortunately, our life history tables do not include male mating success, and this omission is a weakness of our approach. We can imagine experiments in which a life history table of longevity and male reproductive success would be generated and then utilized with the female life history table to generate fitness estimates. Such experiments would be difficult to carry out. We believe that the analysis we have presented, although not complete, is a step in the right direction of a demographic approach to fitness and to natural selection.
We thank Drs. Richard Nickerson and Marvin Druger for generously providing us their l(x) and m(x) data on AR/AR, AR/CH, and CH/CH karyotypes, and Dr. Margaret Anderson for help with the calculations. We thank Drs. Daniel Promislow, Mohamed Noor, and Laurence Mueller for their comments on the manuscript, and Dr. Brian Charlesworth for comments on an earlier version.
1. Dobzhansky, T. (1937) Genetics and the Origin of Species (Columbia Univ. Press, New York).
2. Dobzhansky, T. (1970) Genetics of the Evolutionary Process (Columbia Univ. Press, New York).
3. Dobzhansky, T. (1968) Evol. Biol. 2, 1–34.
4. Beardmore, J.A., Dobzhansky, T. & Pavlovsky, O.A. (1960) Heredity 14, 19–33.
5. Birch, L.C., Dobzhansky, T., Elliot, P.O. & Lewontin, R.C. (1963) Evolution 17, 72–83.
6. Dobzhansky, T., Lewontin, R.C. & Pavlovsky, O. (1964) Heredity 22, 169–186.
7. Ohba, S. (1967) Heredity 22, 169–186.
8. Ayala, F.J. (1970) in Essays in Evolution and Genetics in Honor of Theodosius Dobzhansky, eds. Hecht, M.K. & Steere, W.C. (Appleton-Century-Crofts, New York), pp. 121–158.
9. Ayala, F.J. (1969) Can. J. Genet. Cytol. 11, 439–456.
10. Mourao, C.A., Ayala, F.J. & Anderson, W.W. (1972) Genetica 43, 552–574.
11. Anderson, W.W. (1989) Genome 31, 239–245.
12. Mueller, L.D. & Ayala, F.J. (1981) Genetics 97, 667–677.
13. Mueller, L.D. (1988) Proc. Natl. Acad. Sci. USA 85, 4383–4386.
14. Mueller, L.D. & Ayala, F.J. (1981) Proc. Natl. Acad. Sci. USA 78, 1303–1305.
15. Mueller, L.D., Guo, P. & Ayala, F.J. (1991) Science 253, 433–435.
16. Anderson, W.W. & King, C.E. (1970) Proc. Natl. Acad. Sci. USA 66, 780–786.
17. Cavalli-Sforza, L.L. & Bodmer, W.F. (1971) The Genetics of Human Populations (Freeman, San Francisco).
18. Charlesworth, B. (1970) Theor. Pop. Biol. 1, 352–370.
19. Charlesworth, B. (1994) Evolution in Age-Structured Populations (Cambridge Univ. Press, Cambridge, U.K.), 2nd Ed.
20. Stearns, S.C. (1992) Evolution of Life Histories (Oxford Univ. Press, Oxford).
21. Rose, M.R. (1991) Evolutionary Biology of Aging (Oxford Univ. Press, Oxford).
22. Promislow, D.E.L., Tatar, M., Khazaeli, A.A. & Curtsinger, J.W. (1996) Genetics 143, 839–848.
23. Norton, H.T.J. (1928) Proc. Lond. Math. Soc. 28, 1–45.
24. Norton, J.T.H. (1915) in Mimicry in Butterflies, ed. Punnett, R.C. (Cambridge Univ. Press, Cambridge, U.K.), pp. 154–155.
25. Moffa, A.M. & Costantino, R.F. (1977) Genetics 87, 785–805.
26. Franklin, I. & Lewontin, R.C. (1970) Genetics 65, 707–734.
27. Nickerson, R.P. & Druger, M. (1973) Evolution 26, 322–325.
28. Dobzhansky, T. (1943) Genetics 28, 162–186.
29. Wright, S. & Dobzhansky, T. (1946) Genetics 31, 125–156.
30. Druger, M. (1966) Heredity 21, 317–321.
31. Druger, M. & Nickerson, R.P. (1972) Evolution 26, 322–325.
32. Prout, T. (1969) Genetics 63, 949–967.
33. Prout, T. (1971) Genetics 68, 127–149.
34. Christiansen, F.B., Frydenberg, O. & Simonsen, V. (1973) Heredity 73, 291–304.
35. Fisher, R.A. (1958) The Genetical Theory of Natural Selection (Dover, New York). 2nd Ed.
36. Charlesworth, B. & Giesel, J.T. (1972) Am. Nat. 106, 388–401.
37. Crumpacker, D.W. & Williams, J.S. (1974) Evolution 28, 57–66.
38. Pavlovsky, O. & Dobzhansky, T. (1966) Genetics 53, 843–854.
39. Dobzhansky, T. (1948) Genetics 33, 588–602.
40. Anderson, W.W. (1971) Am. Nat. 105, 489–498.
41. Prout, T. (1980) Evol. Biol. 13, 1–68.






