K— Uncertainty in Stock Assessment Methods and Models
Interval Analysis
In much of fisheries science, the assignment of quantitative values to parameters is inexact. Consequently, a measurement is never known certainly, and scientists tend to report measured values as the best estimate and the possible error around the estimate. This is sometimes expressed with the ''plus or minus" convention or as an interval that is believed to contain the actual value. Interval analysis, described in detail by Moore (1966, 1978) and by Alefield and Herzberger (1983), is considered useful for this type of uncertainty projection.
Briefly, interval analysis permits one to circumscribe estimates with bounds, such as a = [al, a2] where al < a2, and to use range arithmetic to propagate uncertainty. A simple example is provided by illustrating the addition of intervals. Suppose we know that M, the instantaneous natural mortality rate, is between 0.2 and 0.4 and F, the instantaneous fishing mortality rate, is between 0.5 and 0.8, and we want an estimate of Z, the total instantaneous mortality rate, as the sum of these two intervals. Interval addition proceeds as follows:
By substitution, we obtain
From the above, we know that the value for Z must be in the interval [0.7, 1.2]. Rules for various other operators, such as subtraction, multiplication, and division, are relatively simple. However, interval analysis is not easy to use in complex calculations. Fortunately, software capable of handling all computational details is available (Ferson and Kuhn, 1994).
Although interval arithmetic is relatively easy to explain and to apply and seems to work regardless of the source of uncertainty, there are some shortcomings. For example, ranges can grow rapidly in some applications, so that the results may lead to overly conservative fishery management advice. In addition, there is an apparent paradox because no exact values are specified, but the end points (bounds) are presumed to be exact. In summary, interval analysis may be appropriate in situations where no repetitive sampling has occurred and no probability is defined.
Fuzzy Arithmetic
Fuzzy numbers have been described by Ferson and Kuhn (1994) as a generalization of intervals that can serve as representations of values whose magnitudes are known with uncertainty. Fuzzy numbers can be thought of as a stack of intervals, each at a different level of presumption (alpha), which ranges from 0 to 1. The range of values is narrowest at alpha level 1, which corresponds to the optimistic assumption about the breadth of uncertainty. More formally, a fuzzy number is defined as a range of values along with a fuzzy set function in [0, 1], which is convex and reaches a maximal value of 1. The function indicates the degree to which a particular value belongs to the set.
This brief discussion is limited to fuzzy arithmetic, which is a derivation of the considerably broader field of fuzzy set theory and fuzzy logic. Fuzzy arithmetic is considered to be a part of possibility theory introduced by Zadeh (1978) and further developed by Kaufmann and Gupta (1985) and Dubois and Prade (1988). Possibility theory is somewhat analogous to probability theory, but it can be carried out under weaker assumptions and thus used when limited experimental or observational information is available. When a complete probabilistic analysis is not desired because of a lack of information about the distributions of parameters, fuzzy arithmetic may still be used to obtain reasonable, but somewhat crude, estimates of the uncertainty being propagated.
An extremely simple example of fuzzy addition follows (Figure K.1). This example adds the fuzzy numbers [B: 2000, 4000, 7000] and [A: 1000, 2000, 5000]. The actual arithmetic operations are performed only on the apex values of these triangular fuzzy numbers; thus, 4000 + 2000 = 6000. The low ranges of the two fuzzy numbers are then added together forming the base of the arithmetic result. In this case, the base of fuzzy 4000 ranges from 2000 to 7000 or 5000. The base of fuzzy 2000 ranges from 1000 to 5000, or 4000. The sum of 5000 and 4000 is 9000. The sum is divided by 2 to yield a quotient of 4500. This value is subtracted from the result of the arithmetic operation on the base number: 6000 minus 4500 in this example. Thus, 1500 becomes the left hand limit of the base. The quotient is then added to the result of the arithmetic operation, namely, 6000 + 4500 = 10500. This number is the right-hand limit of the base. The result of the addition is the fuzzy number [1500, 6000, 10500].
Limited fuzzy logic applications have already been developed in fisheries by Saila (1992), Ferson (1994), and Sakuramoto (1995). However, specific application of fuzzy arithmetic to existing fishery models has not received substantial consideration. As in the case of interval analysis, software for executing fuzzy arithmetic operations is available.* Using fuzzy arithmetic software minimizes the possibility of computational mistakes in complex calculations. In summary, fuzzy arithmetic is possibly an even more effective method than interval analysis for accommodating subjective uncertainty in fishery assessments; its utility should be examined more carefully for future stock assessment applications.
Because of the increasing use of Monte Carlo methods in stock assessment activities, considerably more attention should be given to determining the reliability of Monte Carlo results as a function of uncertainty in the input parameter distributions and in model assumptions. The distinction between objective and subjective uncertainties† should be recognized explicitly. Probability theory could be used to propagate objective uncertainty, and interval analysis or fuzzy arithmetic should be explored as an alternative to Bayesian priors for the propagation of subjective uncertainty in future stock assessment work.
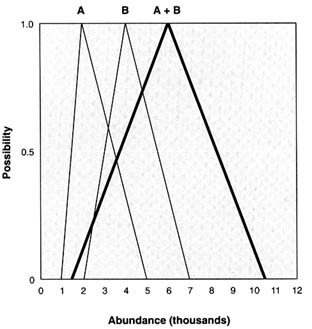
FIGURE K.1 An example of the use of fuzzy arithmetic. The ordinate measures possibility ranging from 0 to 1, and the abscissa shows abundance (in thousands) for the example illustrated in the text. The addition of fuzzy numbers corresponds to the addition of intervals at each possibility level from 0 to 1.



