| This page in the original is blank. |
Variation Risk Management in Product Development
ANNA C. THORNTON
Massachusetts Institute of Technology
Cambridge, Massachusetts
Product development industries are under pressure to decrease both cost and development cycles. In addition, customers are constantly demanding increased quality. As a result, industry is spending significant resources to improve product development processes (PDPs). PDP improvement initiatives have a variety of elements, including simultaneous engineering, variation reduction, quality methods, and integrated product teams. As a part of the Lean Aircraft Initiative and the National Science Foundation's Center for Product Innovation and Development at the Massachusetts Institute of Technology, I have focused on developing tools and methods to assist in the reduction of the effect and magnitude of product variations.
Reducing the effect of variations can have dramatic cost benefits. For example, in the aircraft industry, variability in airframe parts and assemblies influences both cost and quality. Shimming, rework, and repair are major contributors to the labor content of aircraft. In addition, once assembled, variability in wing location as well as steps and gaps between skin panels can increase drag. These problems have strong parallels in the automotive industry.
It is common knowledge that 80 percent of design costs are set in the first 20 percent of a product's definition stage. Early decisions about architecture, assembly processes, and product layout can set a limit on the quality and cost of the final product. In the case of airframes and automotive bodies, fixture design, product decomposition, and assembly methods all affect final product quality (Cunningham et al., 1996; Leyland, 1997). Ideally, early design stages should focus on making tradeoffs between the cost of the product and the ability to achieve the desired product quality.
Many authors have discussed this need and have suggested a variety of tools such as concurrent engineering and design for manufacturing (DFM) techniques (Clark and Fujimoto, 1991; Wheelwright and Clark, 1995). However, the expanded set of tasks is often in conflict with the need to reduce the product development time. I have observed several projects where, because of pressure to deliver a product, tasks such as variation analysis, DFM, and design for assembly (DFA) were jettisoned.
Industry Needs
Based on extended observations and discussions with a range of product development firms, I have identified the need for systematic and quantitative methods to predict yield and manufacturing costs early in the design process. By predicting yields and costs, analysis of alternatives can be made earlier in the design process. However, these methods must operate in an environment where the geometry is not finalized; process capability is uncertain; costs of tooling, rework, and repair are estimated; and the resources available for analysis are limited.
Although this may seem like an impossible goal, the task is simplified because early in the design process designers do not need precise information. What is needed is the ability to predict, with a level of certainty, that option A is more likely to be not as good as option B or that feature C will have the highest rework impact.
Comparing design alternatives involves evaluating multiple optimization criteria. One layout may have a higher labor content but also higher yield rates; another may have less expensive tooling but lower yield rates. The simplest way to make direct comparisons is to reduce the multiple criteria into a single function—cost. Quantitative evaluation of cost and yield is now feasible because cost and process capability databases are being generated within companies and by outside suppliers (Nagler, 1996).
Methods
Current approaches to compare alternatives in the early stages of design have three major shortcomings. First, they predict yield and not total cost. By focusing only on magnitude of yield rather than the overall cost of a product, suboptimal products can be generated. Second, the models required to predict yield are time consuming to generate and often require detailed geometry definition. Third, tools such as Taguchi methods (Taguchi and Clausing, 1990) are limited in their ability to evaluate complex highly coupled systems.
To address these shortcomings, I have developed a set of tools that enable a designer to quickly build a model of a product. Using the model, the costs of labor, tooling, and yield can be evaluated. These tools are based on capturing the key characteristics (KCs) of a product.
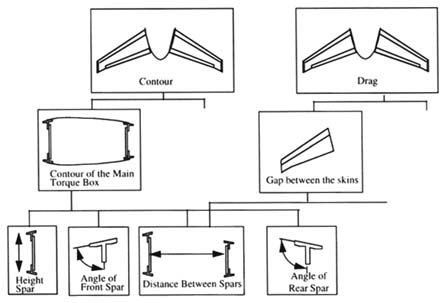
FIGURE 1 KC flowdown for an aircraft wing. Source: Reprinted with permission from the American Society of Mechanical Engineers (Lee and Thornton, 1996b).
Key Characteristics
KCs have been used by a variety of manufacturing organizations, including Boeing, GM, Ford, Chrysler, Xerox, Kodak, Northrop Grumman, McDonnell Douglas, and ITT. KCs are product features, manufacturing process parameters, and assembly features that significantly affect a product's performance, function, and form. KC implementation started in the 1980s and, although these practices are integrated into current design processes in industry, they have been written about predominantly in internal publications (Lee and Thornton, 1996a,b; Thornton, 1996a,b).
KCs can be described in a hierarchical tree structure such as the one in Figure 1. At the top of the tree are the system KCs—the product requirements set by the organization. At the bottom of the tree are the manufactured features. There are often many layers between the system and feature KCs.
I have expanded the typical KC flowdown used in industry to contain a constraint that defines how lower-level KCs combine to create the system-level KC (Lee and Thornton, 1996b). A first-order model of the process capability propagation is used to predict the end yield of the product characteristics by propagating the expected variation at the feature level to the system level (Thornton, 1996b). In addition, the cost of scrap, rework, and repair as well as other costs such as tooling, labor content, and materials can be
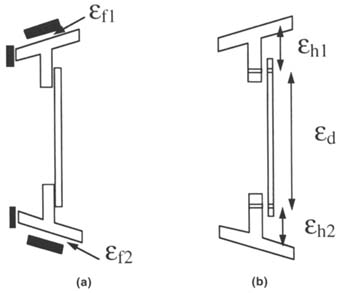
FIGURE 2 Standard method for assembling forward and aft wing spars. (a) Fixtured; (b) Precision. Source: Reprinted with permission from the American Society of Mechanical Engineers (Thornton, 1997).
attached to the general model to enable rapid evaluation of design alternatives. Because of modeling time restrictions and uncertainty in the data, secondary interactions and costs related to other features are not included.
A variety of tools using this representation have been succesfully implemented and tested in industry. The following section provides a simple example of how the KC flowdown and related costs are used to make a direct comparison between two different assembly options in aircraft design. One approach is a traditional assembly requiring fixtures and the other is a newer approach that employs precision features to locate the parts.
Example
Figure 2a shows a simplified version of the standard method for assembling the forward and aft spars for a wing. The fixtured assembly method locates the two cords on hard fixtures by locating the back and upper surface of the cords with the fixtured surfaces. After the cords are located, the web is placed on the surface of the "T." The pieces are match drilled, separated, deburred, sealed, and assembled in the same fixture. Figure 2b shows the precision assembly process. During parts manufacture, holes are drilled in
TABLE 1 Example Cost Tradeoff Between Fixtured Assembly and Precision Assembly
|
|
|
Fixtured Assembly |
Precision Assembly |
|||
|
|
|
Min. |
Max. |
|
Min.Max. |
|
|
Dimensions (expected variation) |
f1 |
0.01 |
0.020 |
h1 |
0.0100.020 |
|
|
f2 |
0.01 |
0.020 |
h2 |
0.010 |
0.020 |
|
|
|
|
|
d |
0.020 |
0.030 |
|
|
Height Variation |
|
0.005 |
0.009 |
|
0.0080.014 |
|
|
Fixture cost |
|
$100k |
$120k |
|
$30k$40k |
|
|
Process cost |
|
$100k |
$110k |
|
$110k$120k |
|
|
Failures/1,000 |
|
3 |
138 |
|
87309 |
|
|
Quality cost |
|
3,600 |
$165k |
|
$104k$307k |
|
|
Total cost |
|
204k |
$395k |
|
$244k$530k |
|
|
Source: Reprinted with permission from the American Society of Mechanical Engineers (Thornton, 1997). |
||||||
each of the cords and in the top and bottom of the web. The holes and surfaces are prepared before assembly. The spars are created by locating the parts using the fixture holes. Some form of nondimensional fixture will be required to support the weight of the parts during assembly.
The dominant key characteristic of the spar assembly is the final height. In the fixtured assembly the feature-level KCs are the errors in the location in the fixture,![]() f1 and
f1 and ![]() f2. In the precision assembly the KCs feature-level are the distance from the top of the cord to the precision holes,
f2. In the precision assembly the KCs feature-level are the distance from the top of the cord to the precision holes, ![]() h1 and
h1 and ![]() h2, and the distance between the holes in the web,
h2, and the distance between the holes in the web, ![]() d. Table 1 shows cost comparisons of the two options using typical data available from the cost and process capability databases.1
d. Table 1 shows cost comparisons of the two options using typical data available from the cost and process capability databases.1
Conclusion
In summary, a set of tools and methods are being developed by the author to predict and mitigate expensive rework, scrap, and repair while balancing other cost drivers in manufacturing processes. These tools use the KC flowdown of a product to focus calculations on those areas likely to have the most significant cost effect on a product. It has been found that first-order analyses are able, even with the uncertainty in process capability and layout, to accurately rank by order high-risk areas and provide a quantitative basis for decision making. The investment in collecting the data and performing the analysis in minimal, thus making use of the tools feasible in the early stages of a design process.
Acknowledgments
The author thanks the U.S. Air Force Wright Laboratory Manufacturing Technology Directorate administering the Advanced Research Projects Agency contracts F33615-94-C-4428 and F33615-94-C-4429, the Boeing Commercial Airplane Group, the Lean Aircraft Initiative, and the Center for Product Innovation and Development.
References
Clark, K. B., and T. Fujimoto. 1991. Product Development Performance: Strategy, Organization, and Management in the World Auto Industry. Boston: Harvard Business School Press.
Cunningham, T. W., R. Mantripragada, D. J. Lee, A. C. Thornton, and D. E. Whitney. 1996. Definition, analysis, and planning of a flexible assembly process. Special session on assembly modeling and its application for concurrent engineering. Proceedings of the ASME Japan/USA Symposium on Flexible Automation, Boston, Mass., July.
Lee, D., and A. C. Thornton. 1996a. Enhanced key characteristics identification methodology for agile design. Proceedings of the Agile Manufacturing Forum , Boston, Mass., March.
Lee, D., and A. C. Thornton. 1996b. The identification and use of key characteristics in the product development process. Proceedings of the ASME Design Engineering Technical Conference: Design Theory and Methodology, Irvine, Calif., August.
Leyland, C. 1997. A Cultural Analysis of Key Characteristic Selection and Team Problem Solving During an Automobile Launch. M.S. thesis. Massachusetts Institute of Technology.
Nagler, G. 1996. Sustaining Competitive Advantage in Product Development: A DFM Tool for Printed Circuit Assembly. M.S. thesis. Massachusetts Institute of Technology.
Taguchi, G., and D. Clausing. 1990. Robust quality. Harvard Business Review 68(1):65–75.
Thornton, A. C. 1996a. Key characteristics. Target 12(5):14–19.
Thornton, A. C. 1996b. Key characteristics: Risk management using modeling and simulation. Massachusetts Institute of Technology, Cambridge, Mass. Internal Working Paper.
Thornton, A. C. 1997. Using key characteristics to balance cost and quality during product development. Proceedings of the ASME Design Engineering Technical Conference: Design Theory and Methodology, Sacramento, Calif., September.
Wheelwright, S. C., and K. B. Clark. 1995. Leading Product Development. New York: Free Press.
NOTE
Multicriteria Evaluation of Manufacturing Performance
ANGELA LOCASCIO
Motorola, Inc.
Schaumburg, Illinois
Manufacturing systems comprise many interacting processes and material flows. Measuring the performance of these complex systems can be difficult. Often, performance is measured by monitoring the processes and materials and then gauging performance by the resulting end-product. In complex manufacturing systems the use of computer integrated manufacturing (CIM) systems permits an enormous amount of data to be gathered during production. Statistical methods have become an essential way to manage this data explosion, yet they may not provide the total solution to measurement of overall factory performance. Measurement methods that focus on processes or material flows alone may not provide an adequate metric for overall manufacturing performance. In addition, with processing times growing and multiple products in process at once, simply counting products as they exit the end of the line may distort factory performance for the products still in production. For these complex manufacturing systems, a more rigorous measurement procedure is needed to consider the individual performance measurements of process and product while providing an overall gauge of manufacturing performance.
Decision analytical methods have been used extensively for project evaluation (e.g., Keeney et al., 1986) and investment and economic decision making (e.g., Boucher and MacStravic, 1991). Some decision analysis applications consider uncertainty and risk in the individual decision criteria (Lavelle et al., 1997). These methods allow the decision maker to balance and trade off competing criteria analytically while representing decision subjectivity mathematically. More recently, decision analysis has been used to improve the process of design (e.g., Thurston, 1991) by modeling competing design
goals and measuring tolerable tradeoffs toward achieving those goals. In this context, constructs such as the von Neumann utility function allow designers to evaluate a candidate design subject to multiple criteria. Just as multicriteria design benefits from decision analysis, a natural extension to other complex systems suggests that decision analysis may be used for multicriteria evaluation of manufacturing performance. Decision analytical methods provide a way of integrating the contributions of multiple performance criteria into a single measure of factory performance.
At Motorola, decision analysis has been used to model complex manufacturing systems and provide a single metric of factory performance. In semi-conductor manufacturing facilities, for example, hundreds of processes and dozens of material flows are tracked simultaneously—making evaluation of factory performance a challenge. Several factors make a performance assessment difficult: (1) products are produced in batches that may require repeated passes at certain processes (reentrant flows); (2) billion-dollar facilities require large work in process to reduce unit costs; and (3) because of product variety and technology type, the total cycle time in the factory may vary from 20 to 40 days. Clearly, current methods that examine only the end-of-line output of a manufacturing system fail to provide an adequate measure of overall system performance. Sophisticated CIM systems monitor and schedule production, tracking hundreds of equipment and material parameters. Still, factory managers may have difficulties in determining how the factory is performing at any given time. By using information from the factory CIM systems, decision analysis allows simultaneous consideration of multiple criteria, such as number of turns, work in process, process yield, queue size, and cycle time at key processes. Preferences are modeled analytically and combined with tradeoff parameters assessed with the certainty equivalent method (Keeney and Raiffa, 1976). These individual criteria data are combined via a multiattribute utility function that permits a measure of total performance of the system. This utility function can be used to more closely monitor and improve factory performance. By deriving the total differential of the utility function, for example, the optimal direction for improvement in performance can be quickly determined. Further, the utility-based performance metric is normalized, which permits easy comparison of performance over different time periods.
Implemented in one Motorola wafer fabrication facility, engineers are using this system to decrease their reaction time to problems in the factory. Prior to installation of this system, problems in performance might have been determined only after several individual performance indicators signaled serious error. With this utility-based performance gauge, reaction time has decreased from days to hours. When the utility function gauge suggests that manufacturing performance is suffering, the tradeoff calculation shows the factory staff where to focus efforts for greatest improvement. Factory engineers report that the quality of
manufacturing decision making is greatly improved now that all factory staff are using the same metric to measure performance, and indirect costs are expected to decrease because of better performance. By using multicriteria decision analysis to integrate traditional methods of measuring and monitoring data, total system performance is greatly improved.
References
Boucher, T. O., and E. L. MacStravic. 1991. Multiattribute evaluation within a present value framework and its relation to the analytic hierarchy process. The Engineering Economist 37(1):1–32.
Keeney, R. L., J. F. Lathrop, and A. Sicherman. 1986. An analysis of Baltimore Gas and Electric Company's technology choice. Operations Research 34(1):18–39.
Keeney, R. L., and H. Raiffa. 1976. Decisions with Multiple Objectives: Preferences and Value Tradeoffs. New York: Wiley.
Lavelle, J. P., J. R. Canada, and J. R. Wilson. 1997. A method for the incorporation of parametric uncertainty in the weighted evaluation multiattribute decision model. Computers and Industrial Engineering 32(4):769–786.
Thurston, D. L. 1991. A formal method for subjective design evaluation with multiple attributes. Research in Engineering Design 3:105–122.
Other Resources
Fishburn, P. C. 1970. Utility Theory for Decision Making. New York: Wiley.
Locascio, A., and D. L. Thurston. 1993. Concurrent optimal design with application to structural dynamics. Journal of Engineering Design 4(4):353–369.
Luce, R. D., and H. Raiffa. 1957. Games and Decisions. New York: Wiley.
Saaty, T. 1980. The Analytic Hierarchy Process. New York: McGraw-Hill. Revised and extended 1988.
von Neumann, J., and O. Morgenstern. 1947. Theory of Games and Economic Behavior, 2nd. ed. Princeton, N.J.: Princeton University Press.
| This page in the original is blank. |












