6
Decision Making
Traditionally, decision theory is divided into two major topics, one concerned primarily with choice among competing actions and the other with modification of beliefs based on incoming evidence. This chapter focuses on the former topic; the latter is treated in detail in the chapters on situation awareness (Chapter 7) and planning (Chapter 8).
A decision episode occurs whenever the flow of action is interrupted by a choice between conflicting alternatives. A decision is made when one of the competing alternatives is executed, producing a change in the environment and yielding consequences relevant to the decision maker. For example, in a typical decision episode, a commander under enemy fire needs to decide quickly whether to search, communicate, attack, or withdraw based on his or her current awareness of the situation. Although perception (e.g., target location), attention (e.g., threat monitoring), and motor performance (e.g., shooting accuracy) are all involved in carrying out a decision, the critical event that controls most of the behavior within the episode is the decision to follow a particular course of action (e.g., decide to attack). The centrality of decision making for computer-generated agents in military simulations makes it critical to employ models that closely approximate real human decision making behavior.
Two variables are fundamental to framing a decision episode: timeframe and aggregation level. Timeframe can vary from the order of seconds and minutes (as in the tactical episode sketched above) to the order of years and even decades (as in decisions concerning major weapon systems and strategic posture). This chapter considers primarily decisions falling toward the shorter end of this range. Second, there are at least two levels of aggregation: entity-level
decisions represent the decisions of a solitary soldier or an individual commanding a single vehicle or controlling a lone weapon system; unit-level decisions represent the decisions made by a collection of entities (e.g., group decisions of a staff or the group behavior of a platoon). This chapter addresses only entity-level decisions; unit-level models are discussed in Chapter 10.
Past simulation models have almost always included assumptions about decision processes, and the complexity with which they incorporate these assumptions ranges from simple decision tables (e.g., the recognize-act framework proposed by Kline, 1997) to complex game theoretic analyses (e.g., Myerson, 1991). However, the users of these simulations have cited at least two serious types of problems with the previous models (see, e.g., Defense Advanced Research Projects Agency, 1996:35-39). First, the decision process is too stereotypical, predictable, rigid, and doctrine limited, so it fails to provide a realistic characterization of the variability, flexibility, and adaptability exhibited by a single entity across many episodes. Variability, flexibility, and adaptability are essential for effective decision making in a military environment. Variability in selection of actions is needed to generate unpredictability in the decision maker's behavior, and also to provide opportunities to learn and explore new alternatives within an uncertain and changing environment. Adaptability and flexibility are needed to reallocate resources and reevaluate plans in light of unanticipated events and experience with similar episodes in the past, rather than adhering rigidly to doctrinal protocols. Second, the decision process in previous models is too uniform, homogenous, and invariable, so it fails to incorporate the role of such factors as stress, fatigue, experience, aggressiveness, impulsiveness, and attitudes toward risk, which vary widely across entities. A third serious problem, noted by the panel, is that these military models fail to take into account known limitations, biases, or judgmental errors.
The remainder of this chapter is organized as follows. First is a brief summary of recent progress in utility theory, which is important for understanding the foundation of more complex models of decision making. The second section reviews by example several new decision models that could ameliorate the stereotypic and rigid character of the current models. The models reviewed are sufficiently formalized to provide computational models that can be used to modify existing computer simulation programs, and are at least moderately supported by empirical research. The next section illustrates one way in which individual differences and moderating states can be incorporated into decision models through the alteration of various parameters of the example decision model. The fourth section reviews, again by example, some human biases or judgmental errors whose incorporation could improve the realism of the simulations. The final section presents conclusions and goals in the area of decision making.
As a final orienting comment, it should be noted that the work reviewed here comes from two rather different traditions within decision research. The first,
deriving from ideas of expected value and expected utility, proposes rather general models of the idealized decision maker. He or she might, for example, be postulated to make decisions that maximize expected utility, leaving the relevant utilities and expectations to be specified for each actual choice situation. Such general models seek descriptive realism through modifications of the postulated utility mechanism, depth of search, and so on within the context of a single overarching model. A second tradition of decision research is based more directly on specific phenomena of decision making, often those arguably associated with decision traps or errors, such as sunk cost dependence. Work in this second tradition achieves some generality by building from particular observations of the relevant phenomenon to explore its domain, moderators, scope, and remedies. In rough terms, then, the two traditions can be seen as top-down and bottom-up approaches to realistic modeling of decision processes. We illustrate in this chapter the potential value of both approaches for military simulations.
SYNOPSIS OF UTILITY THEORY
Utility theory provides a starting point for more complex decision making models. In their pure, idealistic, and elegant forms, these theories are too sterile, rigid, and static to provide the realism required by decision models for military simulations. However, more complex and realistic models, including examples described later in this chapter, are built on this simpler theoretical foundation. Therefore, it is useful to briefly review the past and point to the future of theoretical work in this area.
Expected Value
Before the eighteenth century, it was generally thought that the optimal way to make decisions involving risk was in accordance with expected value, that is, to choose the action that would maximize the long-run average value (the value of an object is defined by a numerical measurement of the object, such as dollars). This model of optimality was later rejected because many situations were discovered in which almost everyone refused to behave in the so-called optimal way. For example, according to the expected-value model, everyone should refuse to pay for insurance because the premium one pays exceeds the expected loss (otherwise insurance companies could not make a profit). But the vast majority of people are risk averse, and would prefer to pay extra to avoid catastrophic losses.
Expected Utility
After the beginning of the eighteenth century, Bernoulli proposed a modification of expected value, called expected utility, that circumvented many of the practical problems encountered by expected-value theory. According to this
new theory, if the decision maker accepts its axioms (see below), then to be logically consistent with those axioms he/she should choose the action that maximizes expected utility, not expected value. Utility is a nonlinear transformation of a physical measurement or value. According to the theory, the shape of the utility function is used to represent the decision maker's attitude toward risk. For example, if utility is a concave function of dollars, then the expected utility of a high-risk gamble may be less than the utility of paying an insurance premium that avoids the gamble. The new theory initially failed to gain acceptance because it seemed ad hoc and lacked a rigorous axiomatic justification. Almost two centuries later, however, Von Neumann and Morgenstern (1947) proposed an axiomatic basis for expected-utility theory, which then rapidly gained acceptance as the rational or optimal model for making risky decisions (see, e.g., Clemen, 1996; Keeney and Raiffa, 1976; von Winterfeldt and Edwards, 1986).
The justification for calling expected utility the optimal way to make decisions depends entirely on the acceptance of a small number of behavioral axioms concerning human preference. Recently, these axioms have been called into question, generating another revolution among decision theorists. Empirical evidence against the behavioral axioms of expected-utility theory began to be reported soon after the theory was first propounded by Von Neumann and Morgenstern (Allais, 1953), and this evidence systematically accumulated over time (see, e.g., early work by MacCrimmon and Larsson, 1979, and Kahneman and Tversky, 1979) until these violations became accepted as well-established fact (see, e.g., the review by Weber and Camerer, 1987). Expected-utility theory is thus experiencing a decline paralleling that of expected-value theory.
A simple example will help illustrate the problem. Suppose a commander is faced with the task of transporting 50 seriously wounded soldiers to a field hospital across a battle zone. First, the transport must leave the battlefield, a highly dangerous situation in which there is an even chance of getting hit and losing all of the wounded (but the only other option is to let them all die on the field). If the transport gets through the battlefield, there is a choice between going west on a mountain road to a small medical clinic, where 40 of the 50 are expected to survive, or going north on a highway to a more well-equipped and fully staffed hospital, where all 50 are expected to survive. Both routes take about the same amount of time, not a significant factor in the decision. But the mountain road is well guarded, so that safe passage is guaranteed, whereas the highway is occasionally ambushed, and there is a 10 percent chance of getting hit and losing all of the wounded.
If a battlefield decision is made to go north to the hospital, the implication is that the expected utility of going north on the paved road (given that the battlefield portion of the journey is survived) is higher than the expected utility of going west on the mountain road (again given that the battlefield portion is survived), since the battlefield portion is common to both options. However,
research suggests that a commander who does survive the battlefield portion will often change plans, decide not to take any more chances, and turn west on the mountain road to the small clinic, violating expected utility.
Why does this occur? Initially, when both probabilities are close to even chance, the difference in gains overwhelms the probability difference, resulting in a preference for the northern route. Later, however, when the probabilities change from certainly to probably safe, the probability difference dominates the difference in gains, resulting in a preference for the western route. Kahneman and Tversky (1979) term this type of result the certainty effect. (The actual experiments reported in the literature cited above used simpler and less controversial monetary gambles to establish this type of violation of expected utility theory, rather than a battlefield example.)
Rank-Dependent Utility
To accommodate the above and other empirical facts, new axioms have been proposed to form a revised theory of decision making called rank-dependent utility theory (see Tversky and Kahneman, 1992; Luce and Fishburn, 1991; Quiggen, 1982; Yaari, 1987). Rank-dependent utility can be viewed as a generalization of expected utility in the sense that rank-dependent utility theory can explain not only the same preference orders as expected utility, but others as well. The new axioms allow for the introduction of a nonlinear transformation from objective probabilities to subjective decision weights by transforming the cumulative probabilities. The nonlinear transformation of probabilities gives the theory additional flexibility for explaining findings such as the certainty effect described above.
Multiattribute Utility
Military decisions usually involve multiple conflicting objectives (as illustrated in the vignette presented in Chapter 2). For example, to decide between attacking the enemy and withdrawing to safety, the commander would need to anticipate both the losses inflicted on the enemy and the damages incurred by his own forces from retaliation. These two conflicting objectives—maximizing losses to enemy forces versus minimizing losses to friendly forces—usually compete with one another in that increasing the first usually entails increasing the second.
Multiattribute utility models have been developed to represent decisions involving conflicting or competing objectives (see, e.g., Clemen, 1996; Keeney and Raiffa, 1976; von Winterfeldt and Edwards, 1986). There are different forms of these models, depending on the situation. For example, if a commander forces a tradeoff between losses to enemy and friendly forces, a weighted additive value model may be useful for expressing the value of the combination. However, a
multiplicative model may be more useful for discounting the values of temporally remote consequences or for evaluating a weapon system on the basis of its performance and reliability.
Game Theory
Game theory is concerned with rational solutions to decisions involving multiple intelligent agents with conflicting objectives. Models employing the principle of subgame perfect equilibrium (see Myerson, 1991, for an introduction) could be useful for simulating command-level decisions because they provide an optimal solution for planning strategies with competing agents. Decision scientists employ decision trees to represent decisions in complex dynamic environments. Although the number of stages and number of branches used to represent future scenarios can be large, these numbers must be limited by the computational capability constraints of the decision maker.
The planning horizon and branching factor are important individual differences among decision makers. For many practical problems, a complete tree representation of the entire problem may not be possible because the tree would become too large and complex, or information about events in the distant future is unavailable or too ill defined. In such cases, it may be possible to use partial trees representing only part of the entire decision. That is, the trees can be cut off at a short horizon, and game theory can then be applied to the truncated tree. Even the use of partial trees may increase the planning capabilities of decision systems for routine tasks.
When decisions, or parts of decisions, cannot be represented easily in tree form, the value of game theory may diminish. Representing highly complex decisions in game theoretic terms may be extremely cumbersome, often requiring the use of a set of games and meta-games.
Concluding Comment
The utility models described in this section are idealized and deterministic with regard to the individual decision maker. He or she is modeled as responding deterministically to inputs from the situation. According to these models, all the branches in a decision tree and all the dimensions of a consequence are evaluated by an individual, and the only source of variability in preference is differences across entities. Individuals may differ in terms of risk attitudes (shapes of utility functions), opinions about the likelihood of outcomes (shapes of decision weight functions), or importance assigned to competing objectives (tradeoff weights). But all of these models assume there is no variability in preferences within a single individual; given the same person and the same decision problem, the same action will always be chosen. As suggested earlier, we believe an appropriate decision model for military situations must introduce variability and adaptability
into preference at the level of the individual entity, and means of doing so are discussed in the next section.
INJECTING VARIABILITY AND ADAPTABILITY INTO DECISION MODELS
Three stages in the development of decision models are reviewed in this section. The first-stage models—random-utility—are probabilistic within an entity, but static across time. They provide adequate descriptions of variability across episodes within an entity, but they fail to describe the dynamic characteristics of decision making within a single decision episode. The second-stage models—sequential sampling decision models—describe the dynamic evolution of preference over time within an episode. These models provide mechanisms for explaining the effects of time pressure on decision making, as well as the relations between speed and accuracy of decisions, which are critical factors for military simulations. The third-stage models—adaptive planning models—describe decision making in strategic situations that involve a sequence of interdependent decisions and events. Most military decision strategies entail sequences of decision steps to form a plan of action. These models also provide an interface with learning models (see Chapter 5) and allow for flexible and adaptive planning based on experience (see also Chapter 8).
Random-Utility Models
Probabilistic choice models have developed over the past 40 years and have been used successfully in marketing and prediction of consumer behavior for some time. The earliest models were proposed by Thurstone (1959) and Luce (1959); more recent models incorporate some critical properties missing in these original, oversimplified models.
The most natural way of injecting variability into utility theory is to reformulate the utilities as random variables. For example, a commander is trying to decide between two courses of action (say, attack or withdraw), but he or she does not know the precise utility of an action and may estimate this utility in a way that varies across episodes. However, the simplest versions of these models, called strong random-utility models, predict a property called strong stochastic transitivity, a property researchers have shown is often violated (see Restle, 1961; Tversky, 1972; Busemeyer and Townsend, 1993; Mellers and Biagini, 1994). Strong stochastic transitivity states that if (1) action A is chosen more frequently than action B and (2) action B is chosen more frequently than action C, then (3) the frequency of choosing action A over C is greater than the maximum of the previous two frequencies. Something important is still missing.
These simple probabilistic choice models fail to provide a way of capturing the effects of similarity of options on choice, which can be shown in the following
example. Imagine that a commander must decide whether to attack or withdraw, and the consequences of this decision depend on an even chance that the enemy is present or absent in a target location. The cells in Tables 6.1a and 6.1b show the percentage of damage to the enemy and friendly forces with each combination of action (attack versus withdraw) and condition (enemy present versus absent) for two different scenarios—one with actions having dissimilar outcomes and the other with actions having similar outcomes.
According to a strong random-utility model, the probability of attacking will be the same for both scenarios because the payoff distributions are identical for each action within each scenario. Attacking provides an equal chance of either (85 percent damage to enemy, 0 percent damage to friendly) or (10 percent damage to enemy, 85 percent damage to friendly) in both scenarios; withdrawing provides an equal chance of either (0 percent damage to enemy, 0 percent damage to friendly) or (0 percent damage to enemy, 85 percent damage to friendly) in both scenarios. If the utility is computed for each action, differences between the utilities for attack and withdraw will be identical across the two tables. However, in the first scenario, the best choice depends on the state of nature (attack if target is present, withdraw of target is absent), but in the second scenario, the best choice is independent of the state of nature (attack if target is present, attack if target is absent). Thus, the first scenario produces negatively correlated or dissimilar outcomes, whereas the second scenario produces positively correlated or similar outcomes. The only difference between the two scenarios is the similarity between actions, but the strong random-utility model is completely insensitive to this difference. Empirical research with human subjects, however, clearly demonstrates a very
TABLE 6.1a Scenario One: Dissimilar Actions
|
Action |
Target Present (.5 probability) |
Target Absent (.5 probability) |
|
Attack |
(85, 0) |
(10, 85) |
|
Withdraw |
(0, 85) |
(0,0) |
|
NOTE: Cells indicate percent damage to (enemy, friendly) forces. |
||
TABLE 6.1b Scenario Two: Similar Actions
|
Action |
Target Present (.5 probability) |
Target Absent (.5 probability) |
|
Attack |
(85, 0) |
(10, 85) |
|
Withdraw |
(0,0) |
(0, 85) |
large difference in choice probability across these two scenarios (see Busemeyer and Townsend, 1993).
Several different types of random-utility models with correlated random variables have been developed to explain the effects of similarity on probabilistic choice, as well as violations of strong stochastic transitivity. Busemeyer and Townsend (1993) and Mellers and Biagini (1994) have developed models for risky decisions. For multiattribute choice problems, Tversky (1972) and Edgell (1980) have developed one type of model, and De Soete et al. (1989) present an alternative approach.
In summary, more recent random-utility models provide an adequate means for producing variability in decision behavior at the level of an individual entity, provided they incorporate principles for explaining the strong effects of similarity on choice. However, these models are static and fail to describe how preferences evolve over time within an episode. This is an important issue for military decision simulations, in which time pressure is a very common and important consideration. Preferences can change depending on how much time the decision maker takes to make a decision. The next set of models includes examples in which preferences evolve over time within an episode.
Sequential Sampling Decision Models
Sequential sampling models of decision making were originally developed for statistical applications (see DeGroot, 1970). Shortly afterwards, however, they were introduced to psychologists as dynamic models for signal detection that explained both the speed and accuracy of decisions (Stone, 1960). Since that time, this type of model has been used to represent the central decision process for decision making in a wide variety of cognitive tasks, including sensory detection (Smith, 1996), perceptual discrimination (Laming, 1968; Link, 1992), memory retrieval (Ratcliff, 1978), categorization (Nosofsky and Palmeri, 1997), risky decision making (Busemeyer and Townsend, 1993; Wallsten, 1995; Kornbrot, 1988), and multiattribute decision making (Aschenbrenner et al., 1983; Diederich, 1997). Most recently, connectionistic theorists have begun to employ these same ideas in their neural network models (see Chapter 5). There is now a convergence of research that points to the same basic process for making decisions across a wide range of cognitive tasks (see Ratcliff et al., 1998).
The sequential sampling model can be viewed as an extension of the random-utility model. The latter model assumes that the decision maker takes a single random sample and bases his or her decision on this single noisy estimate. The sequential sampling model assumes that the decision maker takes a sequence of random-utility estimates and integrates them over time to obtain a more precise estimate of the unknown expected utility or rank-dependent utility.
Formally, the sequential sampling model is a linear feedback system with stochastic inputs and a threshold output response function. Here we intuitively
illustrate how a decision is reached within a single decision episode using this model. Suppose a commander must choose one of three possible actions: attack, communicate, or withdraw. At the beginning of the decision episode, the decision maker retrieves from memory initial preferences (initial biases) for each course of action based on past experience or status quo. The decision maker then begins anticipating and evaluating the possible consequences of each action. At one moment, attention may focus on the losses suffered in an attack, while at another moment, attention may switch to the possibility of enemy detection caused by communication. In this way, the preferences accumulate and integrate the evaluations across time; they evolve continuously, perhaps wavering or vacillating up and down as positive and negative consequences are anticipated, until the preference for one action finally grows strong enough to exceed an inhibitory threshold.
The inhibitory threshold prevents an action from being executed until a preference is strong enough to overcome this inhibition, and this threshold may decay or dissipate over time. In other words, the decision maker may become more impatient as he or she waits to make a decision. The initial magnitude of the inhibitory threshold is determined by two factors: the importance or seriousness of the consequences, and the time pressure or cost of waiting to make the decision.
Important decisions require a relatively high threshold. Thus the decision maker must wait longer and collect more information about the consequences before making a decision, which tends to increase the likelihood of making a good or correct decision. Increasing the inhibitory threshold therefore usually increases the accuracy of the decision. But if the decision maker is under strong time pressure and it is very costly to wait, the inhibitory threshold will decrease, so that a decision will be reached after only a few of the consequences have been reviewed. The decision will be made more quickly, but there will be a greater chance of making a bad decision or an error. Applying these principles, sequential sampling models have provided extremely accurate predictions for both choice probability and choice response time data collected from signal detection experiments designed to test for speed-accuracy tradeoff effects (see Ratcliff et al., 1997)
Not every decision takes a great deal of time or thought according to the sequential sampling model. For example, based on extensive past experience, training, instruction, or a strong status quo, the decision maker may start with a very strong initial bias, so that only a little additional information need be collected before the threshold is reached and a very quick decision is made. This extreme case is close to the recognize-act proposal of Klein (1997).
The sequential sampling model explains how time pressure can drastically change the probabilities of choosing each action (see Figure 6.1). For example, suppose the most important attribute favors action 1, but all of the remaining
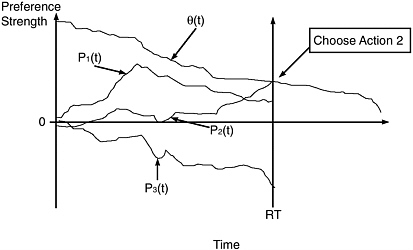
FIGURE 6.1 Illustration of the main ideas of sequential sampling decision models. The vertical axis represents strength of preference, whereas the horizontal axis represents time. The trajectories labeled P1, P2, and P3 represent the evolution of the preference states for actions 1, 2, and 3 over time, and the trajectory labeled theta represents the strength of the inhibitory bound over time. A decision is reached when one of the preference states exceeds the threshold bound, and the first action to exceed this bound determines the choice that is made. In this example, action 2 crosses the threshold first, and thus it is chosen. The vertical line indicated by RT is the time required to make this decision for this example.
attributes favor action 2. Under severe time pressure, the inhibitory threshold is low, and it will be exceeded after a small number of consequences have been sampled. Attention is focused initially on the most important attribute favoring action 1, and the result is a high probability of choosing action 1 under time pressure. Under no time pressure, the inhibitory threshold is higher, and it will be exceeded only after a large number of consequences have been sampled. Attention is focused initially on the most important attribute favoring action 1, but now there is sufficient time to refocus attention on all of the remaining attributes that favor action 2; the result is a high probability of choosing action 2 with no time pressure. In this way, the rank ordering of choice probabilities can change with the manipulation of time pressure.
In summary, sequential sampling models extend random-utility models to provide a dynamic description of the decision process within a single decision episode. This extension is important for explaining the effects of time pressure on decision making, as well as the relation between speed and accuracy in making a decision. However, the example presented above is limited to decisions involving a single stage. Most military decisions require adaptive planning for
actions and events across multiple stages (see, for example, the semiautomated force combat instruction set for the close combat tactical trainer). The models discussed next address this need.
Adaptive Planning Models
Before a commander makes a decision, such as attacking versus withdrawing from an engagement, he or she needs to consider various plans and future scenarios that could occur, contingent on an assessment of the current situation (see also Chapters 7 and 8). For example, if the commander attacks, the attack may be completely successful and incapacitate the enemy, making retaliation impossible. Alternatively, the attack may miss completely because of incorrect information about the location of the enemy, and the enemy may learn the attacker's position, in which case the attacker may need to withdraw to cover to avoid retaliation from an unknown position. Or the attack may be only partially successful, in which case the commander will have to wait to see the enemy's reaction and then consider another decision to attack or withdraw.
Adaptive decision making has been a major interest in the field of decision making for some time (see, e.g., the summary report of Payne et al., 1993). Decision makers are quite capable of selecting or constructing strategies on the fly based on a joint consideration of accuracy (probability of choosing the optimal action) and effort or cost (time and attention resources required to execute a strategy). However, most of this work on adaptive decision making is limited to single-stage decisions. There is another line of empirical research using dynamic decision tasks (see Kerstholt and Raaijmakers, forthcoming, for a review) that entail planning across multiple stages decision, but this work is still at an early stage of development and formal models have not yet been fully developed. Therefore, the discussion in the next section is based on a synthesis of learning and decision models that provides a possible direction for building adaptive planning models for decision making. The models reviewed in this subsection are based on a synthesis of the previously described decision models and the learning models described in Chapter 5. More specifically, the discussion here examines how the exemplar- or case-based learning model can be integrated with the sequential sampling decision models (see Gibson et al., 1997).
The first component is an exemplar model for learning to anticipate consequences based on preceding sequences of actions and events. Each decision episode is defined by a choice among actions—a decision—followed by a consequence. Also, preceding each episode is a short sequence of actions and events that lead up to this choice point. Each episode is encoded in a memory trace that contains two parts: a representation of the short sequence of events and actions that preceded a consequence, and the consequence that followed.
The second component is a sequential sampling decision process, with a choice being made on the anticipated consequences of each action. When a
decision episode begins, the decision maker is confronted with a choice among several immediately available actions. But this choice depends on plans for future actions and events that will follow the impending decision. The anticipated consequences of the decision are retrieved using a retrieval cue that includes the current action and a short sequence of future actions and events. The consequences associated with the traces activated by this retrieval cue are used to form an evaluation of each imminent action at that moment. These evaluations provide the evaluative input that enters into the updating of the preference state, and this evaluation process continues over time during the decision episode until one of the preference states grows sufficiently strong to exceed the threshold for taking action.
In summary, this integrated exemplar learning and sequential sampling decision model produces immediate actions based on evaluations of future plans and scenarios. Although plans and future scenarios are used to evaluate actions at a choice point, these plans are not rigidly followed and can change at a new choice point depending on recently experienced events. Furthermore, because the evaluations are based on feedback from past outcomes, this evaluation process can include adapting to recent events as well as learning from experience.
The model just described represents only one of many possible ways of integrating decision and learning models. Another possibility, for example, would be to combine rule-based learning models with probabilistic choice models (cf. Anderson, 1993) or to combine neural network learning models with sequential sampling decision models. Clearly more research is needed on this important topic.
INCORPORATING INDIVIDUAL DIFFERENCES AND MODERATING STATES
Decision makers differ in a multitude of ways, such as risk-averse versus risk-seeking attitudes, optimistic versus pessimistic opinions, passive versus aggressive inclinations, rational versus irrational thinking, impulsive versus compulsive tendencies, and expert versus novice abilities. They also differ in terms of physical, mental, and emotional states, such as rested versus fatigued, stressed versus calm, healthy versus wounded, and fearful versus fearless. One way to incorporate these individual difference factors and state factors into the decision process is by relating them to parameters of the decision models. The discussion here is focused on the effects of these factors on the decision making process; Chapter 9 examines moderator variables in more detail.
Individual Difference Factors
Risk attitude is a classic example of an individual difference factor in expected utility theory. The shape of the utility function is assumed to vary across
individuals to represent differences in risk attitudes. Convex-shaped functions result in risk-seeking decisions, concave-shaped functions result in risk aversion, and S-shaped functions result in risk seeking in the domain of losses and risk aversion in the domain of gains (see Tversky and Kahneman, 1992). Individual differences in optimistic versus pessimistic opinions are represented in rank-dependent utility theory by variation in the shape of the weighting function across individuals (see Lopes, 1987). Aggressive versus passive inclinations can be represented in multiattribute expected-utility models as differences in the tradeoff weights decision makers assign to enemy versus friendly losses, with aggressive decision makers placing relatively less weight on the latter. Rational versus irrational thinking can be manipulated by varying the magnitude of the error variance in random-utility models, with smaller error variance resulting in choices that are more consistent with the idealistic utility models. Impulsive versus compulsive (or deliberative) tendencies are represented in sequential sampling models by the magnitude of the inhibitory threshold, with smaller thresholds being used by impulsive decision makers. Expert versus novice differences can be generated from an adaptive planning model by varying the amount of training that is provided with a particular decision task.
State Factors
Decision theorists have not considered state factors to the same extent as individual difference factors. However, several observations can be made. Fatigue and stress tend to limit attentional capacity, and these effects can be represented as placing greater weight on a single most important attribute in a multiattribute decision model, sampling information from the most important dimension in a sequential sampling decision model, or limiting the planning horizon to immediate consequences in an adaptive planning model. Fear is an important factor in approach-avoidance models of decision making, and increasing the level of fear increases the avoidance gradient or attention paid to negative consequences (Lewin, 1935; Miller, 1944; Coombs and Avrunin, 1977; Busemeyer and Townsend, 1993). The state of health of the decision maker will affect the importance weights assigned to the attributes of safety and security in multiattribute decision models.
INCORPORATING JUDGMENTAL ERRORS INTO DECISION MODELS
The models discussed thus far reflect a top-down approach: decision models of great generality are first postulated and then successively modified and extended to accommodate empirical detail. As noted earlier, a second tradition of research on decision making takes a bottom-up approach. Researchers in this tradition have identified a number of phenomena that are related to judgmental
errors and offer promise for improving the realism of models of human decision making. Useful recent reviews include Mellers et al. (forthcoming), Dawes (1997), and Ajzen (1996), while Goldstein and Hogarth (1997) and Connolly et al. (forthcoming) provide useful edited collections of papers in the area. Six such phenomena are discussed below. However, it is not clear how these phenomena might best be included in representations of human behavior for military simulations. On the one hand, if the phenomena generalize to military decision making contexts, they will each have significant implications for both realistic representation and aiding of decision makers. On the other hand, evidence in each case suggests that the phenomena are sensitive to contextual and individual factors, and simple generalization to significant military settings is not to be expected.
Overconfidence
An individual is said to be overconfident in some judgment or estimate if his or her expressed confidence systematically exceeds the accuracy actually achieved. For example, Lichtenstein and Fischhoff (1977) demonstrated overconfidence for students answering general-knowledge questions of moderate or greater difficulty; only 75 percent of the answers for which the subjects expressed complete certainty were correct. Fischhoff (1982) and Yates (1990) provide reviews of such studies. More recent work suggests that such overconfidence may be sensitive to changes in the wording and framing of questions (e.g., Gigerenzer, 1994) and item selection (Juslin, 1994). Others have raised methodological concerns (e.g., Dawes and Mulford, 1996; Griffin and Tversky, 1992). The results are thus interesting, but unresolved ambiguities remain.
It would obviously be useful to know the extent to which assessment of confidence should be relied on in military settings. Should a commander discount a confident report of an enemy sighting or a unit commander's assessment of his probability of reaching a given objective on time? More subtly, would overconfidence be reflected in overoptimism about how long a particular assignment will take or in an overtight range of possibilities (see Connolly and Deane, 1997)? Does the military culture encourage overconfident private assessments, as well as overconfident public reports? And should these discounts, if any, be adjusted in light of contextual factors such as urgency and clarity or individual factors such as personality, training, experience, and fatigue? Existing research is sufficient to raise these as important questions without providing much help with their answers.
Base-Rate Neglect
In many settings, an individual must combine two kinds of information into an overall judgment: a relatively stable long-run average for some class of events (e.g., the frequency of a particular disease in a certain target group) and some
specific information about a member of that class (e.g., a diagnostic test on a particular individual). In a classic exploration of this issue by Tversky and Kahneman (1980), subjects were asked to integrate (1) background information on the number of blue and green cabs in town and (2) an eyewitness's report of the color of the cab she saw leaving the scene of an accident. Their primary finding was that the subjects tended to give too much weight to (2) and not enough to (1) in contrast with Bayes' theorem, which the investigators had proposed as the relevant normative rule. As with the overconfidence literature, many subsequent studies have probed variants on the task used by Tversky and Kahneman; see Koehler, 1996, for a review and critique.
Once again, the significance of this phenomenon, if generalizable to military contexts, is obvious. A forward observer may have to judge whether a briefly seen unit is friend or enemy on the basis of visual impression alone. Should he take into account the known preponderance of one or the other force in the area, and if so, to what extent will he do so? Would a decision aid be appropriate? Should training of forward observers include efforts to overcome base-rate neglect, or should such bias be compensated at the command level by training or aiding the commander? Again, it seems unlikely that research will produce simple generalizations of behavioral tendencies that are impervious to the effects of individual differences, context, question wording, training, and so on. Instead, research needs to address to specific settings and factors of military interest, with a view to developing locally stable understandings of phenomena appropriate for representation in models tuned to these specific situations.
Sunk Cost and Escalation Effects
A number of experiments have demonstrated tendencies to persist in failing courses of action to which one has initially become committed and to treat nonrecoverable costs as appropriate considerations in choosing future actions. For example, Arkes and Blumer (1985) showed that theater patrons were more likely to attend performances when they paid full price for their subscriptions than when they received them at an unexpected discount. Staw (1976) used a simulated business case to show that students who made an investment to initiate a course of action that subsequently turned out poorly would invest more in the project at a second opportunity than would those who had not made the initial investment. A considerable amount of laboratory evidence (e.g., Garland, 1990; Heath, 1995) and a modest amount of field evidence (e.g., Staw and Hoang, 1995) are starting to help identify settings in which such entrapments are more and less likely (for reviews see Brockner, 1992, and Staw and Ross, 1989). Despite the obvious relevance to military settings, there is no substantial body of experimental research examining these effects in real or simulated military contexts.
Representation Effects
A central feature of the compendium model known as prospect theory (Kahneman and Tversky, 1979; Tversky and Kahneman, 1992) is that outcomes are evaluated in comparison with some subjectively set reference point and that preferences differ above and below this point. Losses, for example, loom larger than numerically equivalent gains, and value functions in the range of losses may be risk seeking whereas those for gains are risk averse. Since a given outcome can often be framed either as a gain compared with one reference level or as a loss compared with another, outcome preferences are vulnerable to what appear to be purely verbal effects. For example, McNeil et al. (1982) found that both physicians' and patients' preferences between alternative therapies were influenced by whether the therapies were described in terms of their mortality or survival rates. Levin and Gaith (1988) had consumers taste samples of ground beef described as either 90 percent lean or 10 percent fat and found that the descriptions markedly influenced the consumers' evaluations of the product. And Johnson et al. (1993) found that purchase choices for car insurance changed when a price differential between two alternative policies was described as a noclaim rebate on one policy rather than as a deductible on the other. Van Schie and van der Pligt (1995) provide a recent discussion of such framing effects on risk preferences.
The potential relevance to military decision making contexts is obvious. It is commonplace that a maneuver can be described as a tactical repositioning or as a withdrawal, an outcome as 70 percent success or 30 percent failure, and a given loss of life as a casualty rate or a (complementary) survival rate. What needs to be investigated is whether these descriptive reframings are, in military contexts, anything more than superficial rhetorical tactics to which seasoned decision makers are impervious. Given the transparency of the rhetoric and the standardization of much military language, a naive prediction would be that framing would have no substantial effect. On the other hand, one would have made the identical prediction about McNeil et al.'s (1982) physicians, who also work within a formalized vocabulary and, presumably, are able to infer the 10 percent mortality implied by a 90 percent survival rate, but were nonetheless substantially influenced by the wording used. Framing effects, and problem representation issues in general, thus join our list of candidate phenomena for study in the military context.
Regret, Disappointment, and Multiple Reference Points
A number of theorists (Bell, 1982; Loomes and Sugden, 1982) have proposed decision models in which outcomes are evaluated not only on their own merits, but also in comparison with others. In these models, regret is thought to result from comparison of one's outcome with what would have been received under another choice, and disappointment from comparison with more fortunate
outcomes of the same choice. Both regret and disappointment are thus particular forms of the general observation that outcome evaluations are commonly relative rather than absolute judgments and are often made against multiple reference points (e.g., Sullivan and Kida, 1995).
Special interest attaches to regret and disappointment because of their relationship to decision action and inaction and the associated role of decision responsibility. Kahneman and Tversky (1982) found that subjects imputed more regret to an investor who had lost money by a purchasing a losing stock than to another investor who had failed to sell the same stock. Gilovich and Medvec (1995) found this effect only for the short term; in the longer term, inactions are more regretted. Spranca et al. (1991) showed related asymmetries for acts of omission and commission, as in a widespread reluctance to order an inoculation campaign that would directly cause a few deaths even if it would indirectly save many more. The relationships among choice, regret, and responsibility are under active empirical scrutiny (see, for example, Connolly et al., 1997).
Military contexts in which such effects might operate abound. Might, for example, a commander hesitate to take a potentially beneficial but risky action for reasons of anticipated regret? Would such regret be exacerbated by organizational review and evaluation, whereby action might leave one more visibly tied to a failed course of action than would inaction? Studies such as Zellenberg (1996) suggest that social expectations of action are also relevant: soccer coaches who changed winning teams that then lost were blamed; those who changed losing teams were not blamed, even if subsequent results were equally poor. Both internally experienced regret and externally imposed blame would thus have to be considered in the context of a military culture with a strong bias toward action and accomplishment and, presumably, a concomitant understanding that bold action is not always successful.
Impediments to Learning
The general topic of learning is addressed at length in Chapter 5. However two particular topics related to the learning of judgment and decision making skills have been of interest to decision behavior researchers, and are briefly addressed here: hindsight bias and confirmatory search. The first concerns learning from one to the next in a series of decisions; the second concerns learning and information gathering within a single judgment or decision.
Hindsight bias (Fischhoff, 1975; Fischhoff and Beyth, 1975) is the phenomenon whereby we tend to recall having had greater confidence in an outcome's occurrence or nonoccurrence than we actually had before the fact: in retrospect, then, we feel that ''we knew it all along." The effect has been demonstrated in a wide range of contexts, including women undergoing pregnancy tests (Pennington et al., 1980), general public recollections of major news events (Leary, 1982), and business students' analyses of business cases (Bukszar and Connolly, 1987);
Christensen-Szalanski and Fobian (1991) provide an overview and meta-analysis. Supposing the military decision maker to be subject to the same bias, its primary effect would be to impede learning over a series of decisions by making the outcome of each less surprising than it should be. If, in retrospect, the outcome actually realized seems to have been highly predictable from the beginning, one has little to learn. If the outcome was successful, one's skills are once again demonstrated; if it was unsuccessful, all one can do is lament one's stupidity, since any fool could have foreseen the looming disaster. In neither case is one able to recapture the ex ante uncertainty, and one is thus impeded from learning how to cope with the uncertainty of the future.
A second potential obstacle to learning is the tendency, noted by a number of researchers, to shape one's search for information toward sources that can only confirm, but not really test, one's maintained belief. Confirmatory search of this sort might, for example, direct a physician to examine a patient for symptoms commonly found in the presence of the disease the physician suspects. A recruiter might similarly examine the performance of the personnel he or she had actually recruited. Such a search often has a rather modest information yield, though it may increase confidence (see Klayman and Ha, 1987, for a penetrating discussion). More informative is the search for indications that, if discovered, would invalidate one's maintained belief—for example, the physician's search for symptoms inconsistent with the disease initially suspected. Instances of this search pattern might be found in intelligence appraisals of enemy intentions: believing an attack imminent, the intelligence officer might search for, or pay undue attention to, evidence consistent with this belief, rather than seeking out and attending to potentially more valuable evidence that the belief was wrong. Again, there is no specific evidence that such search distortion occurs in military settings, and it is possible that prevailing doctrine, procedures, and training are effective in overcoming the phenomenon if it does exist. As is the case throughout this section, we intend only to suggest that dysfunctions of this sort have been found in other contexts and might well be worth seeking out and documenting in military settings as preparation for building appropriate representations into simulations of military decision makers.
Proposed Research Response
Research on decision behavior embraces a number of phenomena such as those reviewed above, and they presented the panel with special difficulty in forming research recommendations. First, even without a formal task analysis, it seems likely that decision-related phenomena such as these are highly relevant in military contexts and thus to simulations of such contexts. However, research on these topics seems not to fit well with the life-cycle model sketched earlier. That model postulates empirical convergence over time, so that the phenomenon of interest can be modeled with increasing fidelity. Decision behavior phenomena
such as those discussed in this section, in contrast, seem often to diverge from this pattern—starting from an initially strong, clear result (e.g., confidence ratings are typically inflated; sunk costs entrap) and moving to increasingly contingent, disputed, variable, moderated, and contextual claims. This divergence is a source of frustration for those who expect research to yield simple, general rules, and the temptation is to ignore the findings altogether as too complex to repay further effort. We think this a poor response and support continued research attention to these issues. The research strategy should, however, be quite focused. It appears unlikely that further research aimed at a general understanding and representation of these phenomena will bear fruit in the near term. Instead, a targeted research program is needed, aimed at matching particular modeling needs to specific empirical research that makes use of military tasks, settings, personnel, and practices. Such a research program should include the following elements:
-
Problem Identification. It is relatively easy to identify areas of obvious significance to military decision makers for which there is evidence of nonoptimal or nonintuitive behavior. However, an intensive collaboration between experts in military simulations and decision behavior researchers is needed to determine those priority problems/decision topics that the modelers see as important to their simulations and for which the behavioral researchers can identify sufficient evidence from other, nonmilitary contexts to warrant focused research.
-
Focused Empirical Research. For each of the topics identified as warranting focused research, the extent and significance of the phenomenon in the specific military context identified by the modelers should be addressed. Does the phenomenon appear with these personnel, in this specific task, in this setting, under these contextual parameters? In contrast with most academic research programs, the aim here should not be to build generalizable theory, but to focus at the relatively local and specific level. It is entirely possible, for example, that the military practice of timed reassignment of commanders has developed to obviate sunk cost effects or that specialized military jargon has developed to allow accurate communication of levels of certainty from one command echelon to another.
-
Building of Simulation-Compatible Representations. Given the above focus on specific estimates of effects, contextual sensitivities, and moderators, there should be no special difficulty in translating the findings of the research into appropriate simulation code. This work is, however, unlikely to yield a standardized behavioral module suitable for all simulations. The aim is to generate high realism in each local context. Cross-context similarities should be sought, but only as a secondary goal when first-level realism has been achieved.
CONCLUSIONS AND GOALS
This chapter has attempted to identify some of the key problems with the currently used decision models for military simulations and to recommend new
approaches that would rectify these problems. In the top-down modeling tradition, a key problem with previous decision models is that the decision process is too stereotypical, predictable, rigid, and doctrine limited, so it fails to provide a realistic characterization of the variability, flexibility, and adaptability exhibited by a single entity across many episodes. We have presented a series of models in increasing order of complexity that are designed to overcome these problems. The first stages in this sequence are the easiest and quickest to implement in current simulation models; the later stages will require more effort and are a longer-term objective. Second, the decision process as currently represented is too uniform, homogenous, and invariable, so it fails to display individual differences due to stress, fatigue, experience, aggressiveness, impulsiveness, or risk attitudes that vary widely across entities. We have outlined how various individual difference factors or state factors can be incorporated by being related to parameters of the existing decision models.
We have also identified research opportunities and a research strategy for incorporating work in the bottom-up, phenomenon-focused tradition into models of military decision making. The thrust proposed here is not toward general understanding and representation of the phenomena, but toward specific empirical research in military settings, using military tasks, personnel, and practices. Problem identification studies would identify specific decision topics that modelers see as important to the simulations and behavioral researchers see as potentially problematic, but amenable to fruitful study. Focused empirical research would assess the extent and significance of these phenomena in specific military contexts. And simulation-compatible representations would be developed with full sensitivity to specific effect-size estimates and contextual moderators. Model realism would improve incrementally as each of these phenomenon-focused submodels was implemented and tested. Progress along these lines holds reasonably high promise for improving the realism of the decision models used in military simulations.
Short-Term Goals
-
Include judgmental errors such as base-rate neglect and overconfidence as moderators of probability estimates in current simulation models.
-
Incorporate individual differences into models by adding variability in model parameters. For example, variations in the tendency to be an impulsive versus a compulsive decision maker could be represented by variation in the threshold bound required to make a decision in sequential sampling decision models.
Intermediate-Term Goals
-
Inject choice variability in a principled way by employing random-utility models that properly represent the effect of similarity in the consequences of each action on choice.
-
Represent time pressure effects and relations between speed and accuracy of decisions by employing sequential sampling models of decision making.






















