7
Situation Awareness
In everyday parlance, the term situation awareness, means the up-to-the-minute cognizance or awareness required to move about, operate equipment, or maintain a system. The term has received considerable attention in the military community for the last decade because of its recognized linkage to effective combat decision making in the tactical environment.
In the applied behavioral science community, the term situation awareness has emerged as a psychological concept similar to such terms as intelligence, vigilance, attention, fatigue, stress, compatibility, and workload. Each began as a word with a multidimensional but imprecise general meaning in the English language. Each has assumed importance because it captures a characteristic of human performance that is not directly observable, but that psychologists—especially engineering psychologists and human factors specialists—have been asked to assess, or purposefully manipulate because of its importance to everyday living and working. Defining situation awareness in a way that is susceptible to measurement, is different from generalized performance capacity, and is usefully distinguishable from other concepts such as perception, workload, and attention has proved daunting (Fracker, 1988, 1991a, 1991b; Sarter and Woods, 1991, 1995). In fact, there is much overlap among these concepts.
Chapter 4 addresses attention, especially as it relates to time sharing and multitasking. In this chapter we discuss a collection of topics as if they were one. Although each of these topics is a research area in its own right, we treat together the perceptual, diagnostic, and inferential processes that precede decision making and action. The military uses the term situation awareness to refer to the static spatial awareness of friendly and enemy troop positions. We broaden this definition
substantially, but retain the grouping of perceptual, diagnostic, and inferential processes for modeling purposes. While this approach may be controversial in the research community (see, for example, the discussion by Flach, 1995), we believe it is appropriate for military simulation applications. We review several of the definitions and potential models proposed for situation awareness, discuss potential model implementation approaches, outline connections with other models discussed throughout this report, and present conclusions and goals for future development.
We should also note that considerable research remains to be done on defining, understanding, and quantifying situation awareness as necessary precursors to the eventual development of valid descriptive process models that accurately and reliably model human behavior in this arena. Because of the early stage of the research on situation awareness, much of the discussion that follows focuses on potential prescriptive (as opposed to descriptive) modeling approaches that may, in the longer term, prove to be valid representations of human situation assessment behavior. We believe this is an appropriate research and modeling approach to pursue until a broader behavioral database is developed, and proposed models can be validated (or discarded) on the basis of their descriptive accuracy.
SITUATION AWARENESS AND ITS ROLE IN COMBAT DECISION MAKING
Among the many different definitions for the term situation awareness (see Table 7.1), perhaps the most succinct is that of Endsley (1988:97):
Situation awareness is the perception of the elements in the environment within a volume of time and space, the comprehension of their meaning, and the projection of their status in the near future.
Each of the three hierarchical phases and primary components of this definition can be made more specific (Endsley, 1995):
-
Level 1 Situation Awareness—perception of the elements in the environment. This is the identification of the key elements or "events" that, in combination, serve to define the situation. This level tags key elements of the situation semantically for higher levels of abstraction in subsequent processing.
-
Level 2 Situation Awareness—comprehension of the current situation. This is the combination of level 1 events into a comprehensive holistic pattern, or tactical situation. This level serves to define the current status in operationally relevant terms in support of rapid decision making and action.
-
Level 3 Situation Awareness—projection of future status. This is the projection of the current situation into the future in an attempt to predict the evolution of the tactical situation. This level supports short-term planning and option evaluation when time permits.
TABLE 7.1 Definitions of Situation Awareness
|
Reference |
Definitions |
|
Endsley (1987, 1995) |
• Perception of the elements in the environment within a volume of time and space; • Comprehension of their meaning; • Projection of their status in the near future |
|
Stiffler (1988) |
•The ability to envision the current and near-term disposition of both friendly and enemy forces |
|
Harwood et al. (1988) |
• Where: knowledge of the spatial relationships among aircraft and other objects; • What: knowledge of the presence of threats and their objectives and of ownship system state; • Who: knowledge of who is in charge—the operator or an automated system; • When: knowledge of the evolution of events over time |
|
Noble (1989) |
• Estimate of the purpose of activities in the observed situation; • Understanding of the roles of participants in these activities; • Inference about completed or ongoing activities that cannot be directly observed; • Inference about future activities |
|
Fracker (1988) |
• The knowledge that results when attention is allocated to a zone of interest at a level of abstraction |
|
Sarter and Woods (1991, 1995) |
• Just a label for a variety of cognitive processing activities that are critical to dyamic, event-driven, and multitask fields of practice |
|
Dominguez (1994) |
• Continuous extraction of environmental information, integration of this knowledge to form a coherent mental picture, and the use of that picture in directing further perception and anticipating future events |
|
Pew (1995) |
• Spatial awareness; • Mission/goal awareness; • System awareness; • Resource awareness; • Crew awareness |
|
Flach (1995) |
• Perceive the information; • Interpret the meaning with respect to task goals; • Anticipate consequences to respond appropriately |
Additional definitions are given in Table 7.1; of particular interest is the definition proposed by Dominguez (1994), which was specified after a lengthy review of other situation awareness studies and definitions. It closely matches Endsley's definition, but further emphasizes the impact of awareness on continuous cue extraction and directed perception, i.e., its contribution to attention. Note also, however, the effective nondefinition proposed by Sarter and Woods (1995), which reflects the views of a number of researchers in the field. Further expansion on these notions can be found in Flach (1995).
From the breadth of the various definitions, it should be clear that situation awareness, as viewed by many researchers working in the area, is a considerably broader concept than that conventionally held by the military community. The latter view tends to define situation awareness as merely1 spatial awareness of the players (self, blue forces, and red forces), and at that, often simply their static positions without regard to their movements. It is also appropriate to point out the distinction between situation awareness and situation assessment . The former is essentially a state of knowledge; the latter is the process by which that knowledge is achieved. Unfortunately, the acronyms for both are the same, adding somewhat to the confusion in the literature.
Despite of the numerous definitions for situation awareness, it is appropriate to note that "good situation awareness" in a tactical environment is regarded as critical to successful combat performance. This is the case both for low-tempo planning activities, which tend to be dominated by relatively slow-paced and reflective proactive decisions, and high-tempo "battle drill" activities, which tend to be dominated by relatively fast-paced reactive decisions.
A number of studies of human behavior in low-tempo tactical planning have demonstrated how decision biases and poor situation awareness contribute to poor planning (Tolcott et al., 1989; Fallesen and Michel, 1991; Serfaty et al., 1991; Lussier et al., 1992; Fallesen, 1993; Deckert et al., 1994). Certain types of failures are common, resulting in inadequate development and selection of courses of action. In these studies, a number of dimensions relating specifically to situation assessment are prominent and distinguish expert from novice decision makers. Examples are awareness of uncertain assumptions, awareness of enemy activities, ability to focus awareness on important factors, and active seeking of confirming/disconfirming evidence.
Maintenance of situation awareness also plays a key role in more high-tempo battlefield activities (e.g., the "battle drills" noted in IBM, 1993). Several studies have focused on scenarios in which the decision maker must make dynamic decisions under "… conditions of time pressure, ambiguous information,
One aspect of situation awareness, which has been referred to as crew awareness, is the extent to which the personnel involved have a common mental image of what is happening and an understanding of how others are perceiving the same situation. The ideas of distributed cognition, shared mental models, and common frame of reference play a role in understanding how groups can be aware of a situation and thus act upon it. Research in distributed cognition (Hutchins, 1990; Sperry, 1995) suggests that as groups solve problems, a group cognition emerges that enables the group to find a solution; however, that group cognition does not reside entirely within the mind of any one individual. Research on shared mental models and common frames of reference suggests that over time, groups come to have a more common image of a problem, and this common image is more or less shared by all participants. What is not known is how much of a common image is needed to enhance performance and what knowledge or processes need to be held in common.
There is currently a great deal of interest in individual and team mental models (Reger and Huff, 1993; Johnson-Laird, 1983; Klimoski and Mohammed, 1994; Eden et al., 1979; Carley, 1986a, 1986b; Roberts, 1989; Weick and Roberts, 1993; Walsh, 1995). Common team or group mental models are arguably critical for team learning and performance (Hutchins, 1990, 1991a, 1991b; Fiol, 1994). However, the relationship between individual and team mental models and the importance of shared cognition to team and organizational performance is a matter requiring extensive research. Although many problems are currently solved by teams, little is known about the conditions for team success.
MODELS OF SITUATION AWARENESS
A variety of situation awareness models have been hypothesized and developed by psychologists and human factors researchers, primarily through empirical studies in the field, but increasingly with computational modeling tools. Because of the critical role of situation awareness in air combat, the U.S. Air Force
has taken the lead in studying the modeling, measurement, and trainability of situation awareness (Caretta et al., 1994). Numerous studies have been conducted to develop situation awareness models and metrics for air combat (Stiffler, 1988; Spick, 1988; Harwood et al., 1988; Endsley, 1989, 1990, 1993, 1995; Fracker, 1990; Hartman and Secrist, 1991; Klein, 1994; Zacharias et al., 1996; Mulgund et al., 1997). Situation awareness models can be grouped roughly into two classes: descriptive and prescriptive (or computational).
Descriptive Situation Awareness Models
Most developed situation awareness models are descriptive. Endsley (1995) presents a descriptive model of situation awareness in a generic dynamic decision making environment, depicting the relevant factors and underlying mechanisms. Figure 7.1 illustrates this model as a component of the overall assessment-decision-action loop and shows how numerous individual and environmental factors interact. Among these factors, attention and working memory are considered the critical factors limiting effective situation awareness. Formulation of mental models and goal-directed behavior are hypothesized as important mechanisms for overcoming these limits.
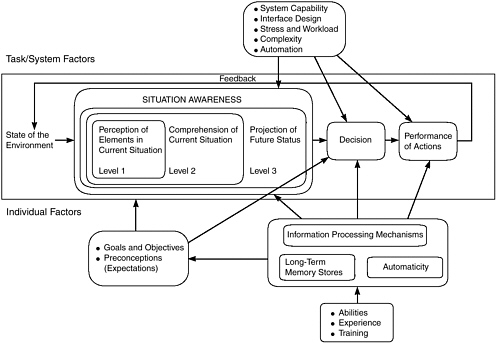
FIGURE 7.1 Generic decision making model centered on the situation awareness process (Endsley, 1995).
Gaba et al. (1995) describe a qualitative model of situation-based decision making in the domain of anesthesiology. An initial stage of sensory/motor processing is concerned with identifying key physiological "events" as presented on the anesthesiology monitors (Endsley's level 1 situation awareness). A second stage of situation assessment focuses on integrating those events to identify potential problems (Endsley's level 2 situation awareness) and anticipated trends into the future (Endsley's level 3 situation awareness). A third stage of decision making includes a "fast" reactive path of precompiled responses (akin to Klein's RPD strategy [Klein, 1989, 1994]) paralleled by a "slow" contemplative path of model-based reasoning about the situation. Both paths then contribute to the next stage of plan generation and subsequent action implementation.
Although descriptive models are capable of identifying basic issues of decision making in dynamic and uncertain environments, they do not support a quantitative simulation of the process by which cues are processed into perceptions, situations are assessed, and decisions are made. Further, we are unaware of any descriptive model that has been developed into a computational model for actual emulation of human decision making behavior in embedded simulation studies.
Prescriptive Situation Awareness Models
In contrast to the situation with descriptive models, few prescriptive models of situation awareness have been proposed or developed. Early attempts used production rules (Baron et al., 1980; Milgram et al., 1984). In these efforts, the situation awareness model was developed as a production rule system in which a situation is assessed using the rule "if a set of events E occurs, then the situation is S." Although this pattern-recognition (bottom-up) type of approach is fairly straightforward to implement, it lacks the diagnostic strength of a causal-reasoning (top-down) type of approach. In the latter approach, a hypothesized situation S can be used to generate an expected event set E*, which can be compared with the observed event set E; close matches between E* and E confirm the hypothesized situation, and poor matches motivate a new hypothesis. Not surprisingly, these early attempts at modeling the situation awareness process using a simple production rule system, going from events to situations, performed poorly because of three factors: (1) they were restricted to simple forward chaining (event to situation); (2) they did not take into consideration uncertainty in events, situations, and the rules linking them; and (3) they did not make use of memory, but simply reflected the current instantaneous event state. More sophisticated use of production rules (e.g., either through combined forward/backward chaining, incorporation of "certainty factors," and/or better internal models) could very well ameliorate or eliminate these problems. Tambe's work on a rule-based model of agent tracking (Taube 1996a, 1996b, 1996c) illustrates just what can be accomplished with this more sophisticated use of production rule systems.
The small unit tactical trainer (SUTT)2 (see Chapters 2 and 8) includes computer-controlled hostiles that behave as "smart" adversaries to evade and counterattack blue forces. Knowledge of the current situation by the computer-controlled hostiles is specified by a number of fairly low-level state variables defining "self" status: location, speed/direction of movement, posture, weapon state, and the like. No attempt is made to model this type of perception/assessment function; rather, the "true" individual combatant states are used directly. State variables defining the status of others are less extensive and focus primarily on detection/identification status and location relative to self, thus following the conventional military definition of situation awareness—positional knowledge of all players in the scenario at hand. Here, an attempt is made to model the perception of these states in accordance with the level 1 situation awareness process postulated by Endsley (1995). The net result is a list of entities, with attributes specifying the observer's knowledge of each (e.g., undetected, detected but unrecognized) and with parameters specifying the state of each (position, and possibly velocity). In the SUTT human behavior representation, situation awareness is modeled as primarily a low-level collection of "events" (identified and located entities), with no attempt made to assess or infer higher-level situations (e.g., "Is this group of individual entities part of an enemy squad?''). Thus actions or plans for actions are necessarily reflexive at a fairly low level (implemented as either rulebases or decision trees), with little abstraction or generalization involved. While this may be adequate for modeling a wide range of "battle drill" exercises in which highly choreographed offensive and defensive movements are triggered by relatively low-level events (e.g., detection of a threat at a particular location), it is unclear how such battle drills can be selected reliably without the specification of an adequate context afforded by higher-level situation awareness processes (e.g., "We're probably facing an entire platoon hiding behind the building"). Certainly it is unclear how more "inventive" situation-specific tactics can be formulated on the fly without an adequate situation assessment capability.
The man-machine integration design and analysis system (MIDAS) was developed by the National Aeronautics and Space Administration (NASA) and the U.S. Army to model pilot behavior, primarily in support of rotorcraft crew station design and procedural analyses (Banda et al., 1991; Smith et al., 1996; see also Chapters 3 and 8). As described earlier in Chapter 3, an agent-based operator model (comprising three basic modules for representing perceptual, cognitive, and motor processing) interacts with the proximal environment (displays, controls) and, in combination with the distal environment (e.g., own ship, other aircraft), results in observable behavioral activities (such as scanning, deciding, reaching, and communicating). Much effort has gone into developing environmental models, as well as perceptual and motor submodels. Work has also gone
Earlier versions of MIDAS (e.g., as described by Banda et al., 1991) relied primarily on a pattern-matching approach to triggering reactive behavior, based on the internal perceptions of outside world states. Recent work described by Smith et al. (1996) and Shively (1997) is directed at developing a more global assessment of the situation (to be contrasted with a set of perceived states), somewhat along the lines of Reece (1996). Again, the focus is on assessing the situation in terms of the external entities: self, friendly, and threat and their locations. A four-stage assessment process (detection, recognition, identification, and comprehension) yields a list of entities and a numeric value associated with how well each entity assessment matches the actual situation. A weighted calculation of overall situation awareness is made across entities and is used to drive information-seeking behavior: low situation awareness drives the attention allocator to seek more situation-relevant information to improve overall awareness. Currently, the situation awareness model in MIDAS does not drive the decision making process (except indirectly through its influence on information-seeking behavior), so that MIDAS remains essentially event-rather than situation-driven. The current structure does not, however, appear to preclude development along these lines.
As discussed in Chapter 2, considerable effort has been devoted to applying the Soar cognitive architecture (Laird et al., 1987; Laird and Rosenbloom, 1990) to the modeling of human behavior in the tactical air domain. Initial efforts led to a limited-scope demonstration of feasibility, fixed-wing attack (FWA)-Soar (Tambe et al., 1995); 3 more recent efforts showed how Soar-intelligent forces (Soar-IFOR) could participate in the synthetic theater of war (STOW)-97 large-scale warfighting simulation (Laird, 1996).
As described in Chapter 3, much of the Soar development effort has been focused on implementing a mechanism for goal-driven behavior, in which high-level goals are successively decomposed into low-level actions. The emphasis has been on finding a feasible action sequence taking the Soar entity from the current situation to the desired goal (or end situation); less emphasis has been placed on identifying the current situation (i.e., situation awareness). However, as Tambe et al. (1995) note, identifying the situation is critical in dynamic environments, in which either Soar agents or others continually change the environment, and hence the situation. Thus, more recent emphasis in Soar has been placed on modeling the agent's dynamic perception of the environment and assessment of the situation.
In contrast with conventional "situated action agents" (e.g., Agre and Chapman, 1987), in which external system states are used to drive reflexive agents (rule-based or otherwise) to generate agent actions, Soar attempts to model the
A brief review of the current Soar effort (Tambe et al., 1995; Laird, 1996; Gratch et al., 1996) indicates that this type of "front-end" modeling is still in its early stages. For example, FWA-Soar (Tambe et al., 1995) abstracts the pilot-cockpit interface and treats instrument cues at an informational level. We are unaware of any attempt to model in Soar the detailed visual perceptual processes involved in instrument scanning, cue pickup, and subsequent translation into domain-relevant terms. However, Soar's "perceptual" front end, although primitive, may be adequate for the level of modeling fidelity needed in many scenarios, but also, more important, could support the development of an explicit situation assessment module, thus providing explicit context for the hundreds or thousands of production rules contained in its implementation.4 As noted below, this functionality in which low-level perceptual events are transformed into a higher-level decisional context, has been demonstrated by Tambe et al. (1995).
Recognizing that situation assessment is fundamentally a diagnostic reasoning process, Zacharias and colleagues (1992, 1996), Miao et al. (1997), and Mulgund et al. (1996, 1997) have used belief networks to develop prescriptive situation awareness models for two widely different domains: counter-air operations and nuclear power plant diagnostic monitoring. Both efforts model situation awareness as an integrated inferential diagnostic process, in which situations are considered as hypothesized reasons, events as effects, and sensory (and sensor) data as symptoms (detected effects). Situation awareness starts with the detection of event occurrences. After the events are detected, their likelihood (belief) impacts on the situations are evaluated by backward tracing the situation-event relation (diagnostic reasoning) using Bayesian belief networks. The updated situation likelihood assessments then drive the projection of future event occurrences by forward inferencing along the situation-event relation (inferential reasoning) to guide the next step of event detection. This approach of using belief networks to model situation awareness is described at greater length below.
Multiagent Models and Situation Awareness
It is relatively common for multiagent computational models of groups to be designed so that each agent has some internal mental model of what other agents know and are doing; see, for example, the discussion of FWA-Soar in Chapter 10.
Situation awareness in these models has two parts—the agent's own knowledge of the situation and the agent's knowledge of what others are doing and might do if the situation were to change in certain ways. To date, this approach has been used successfully only for problems in which others can be assumed to act exclusively by following doctrine (preprogrammed rules of behavior), and the agents continually monitor and react to that environment. Whether the approach is extensible to a more mutually reactive situation is not clear.
ENABLING TECHNOLOGIES FOR IMPLEMENTATION OF SITUATION AWARENESS MODELS
A number of approaches can be taken to implement situation awareness models, from generic inferencing approaches (e.g., abductive reasoning, see, for example, Josephson and Josephson, 1994) to specific computational architectures (e.g., blackboard architectures, Hayes-Roth, 1985). We have selected blackboard systems to discuss briefly here, and expert systems, case-based reasoning, and belief networks to discuss in detail below.
Blackboard systems have been used to model all levels of situation awareness as defined by Endsley (1995). Blackboard system models were initially developed to model language processing (Erman et al., 1980), and later used for many situation assessment applications (see Nii, 1986a, 1986b). In the blackboard approach, a situation is decomposed into one or more hierarchical panels of symbolic information, often organized as layers of abstraction. Perceptual knowledge sources encode sensory data and post it on to appropriate locations of the blackboard (level 1 situation awareness), while other knowledge sources reason about the information posted (level 2 situation awareness) and make inferences about future situations or states (level 3 situation awareness), posting all their conclusions back onto the blackboard structure. At any point in time, the collection of information posted on the blackboard constitutes the agent's awareness of the situation. Note that this is a nondiagnostic interpretation of situation awareness. Other knowledge sources can use this situational information to assemble action plans on a goal-driven or reactive basis. These may be posted on other panels. In a tactical application created for the TADMUS program (Zachary et al., forthcoming), a six-panel model in which two panels were used to construct the situational representation and the other four used to build, maintain, and execute the tactical plan as it was developed.
Expert systems or, more generally, production rule systems, are discussed because they have been used consistently since the early 1980s to model situation awareness in computational behavior models. In contrast, case-based reasoning has not been used extensively in modeling situation awareness; it does, however, have considerable potential for this purpose because of both its capabilities for modeling episodic situation awareness memory and the ease with which new situations can be learned within the case-based reasoning paradigm. Finally,
belief networks (which implement a specific approach to abductive reasoning, in general) are discussed because of their facility for representing the interrelatedness of situations, their ability to integrate low-level events into high-level situations, and their potential for supporting normative model development.
Expert Systems5
An early focus of expert system development was on applications involving inferencing or diagnosis from a set of observed facts to arrive at a more general assessment of the situation that concisely "explains" those observed facts. Consequently, there has been interest in using expert systems to implement situation awareness models.
In typical expert systems, domain knowledge is encoded in the form of production rules (IF-THEN or antecedent-consequent rules). The term expert system reflects the fact that the rules are typically derived by interviewing and extracting domain knowledge from human experts. There have been expert systems for legal reasoning, medical diagnosis (e.g., MYCIN, which diagnoses infectious blood diseases [Buchanan and Shortliffe, 1984], and Internist, which performs internal medicine diagnostics [Miller et al., 1982]); troubleshooting of automobiles; and numerous other domains. Expert systems consist of three fundamental components:
-
Rulebase—a set of rules encoding specific knowledge relevant to the domain.
-
Factbase (or working memory)—a set assertion of values of properties of objects and events comprising the domain. The factbase encodes the current state of the domain and generally changes as (1) rules are applied to the factbase, resulting in new facts, and (2) new facts (i.e., not derivable from the existing factbase) are added to the system.
-
Inference Engine (i.e., mechanical theorem prover)—a formal implementation of one or more of the basic rules of logic (e.g., modus ponens, modus tolens, implication) that operate on the factbase to produce new facts (i.e., theorems) and on the rule base to produce new rules. In practice, most expert systems are based on the inference procedure known as resolution (Robinson, 1965).
The general operation of an expert system can be characterized as a match-select-apply cycle, which can be applied in either a forward-chaining fashion, from antecedents to consequents, or a backward-chaining fashion, from consequents to antecedents. In forward chaining, a matching algorithm first determines the subset of rules whose antecedent conditions are satisfied by the current set of facts comprising the factbase. A conflict-resolution algorithm then selects one rule in particular and applies it to the factbase, generally resulting in the
The majority of current military human behavior representations reviewed for this study implicitly incorporate an expert-system-based approach to situation awareness modeling. The implicitness derives from the fact that few attempts have been made to develop explicit production rules defining the situation.
Rather, the production rules are more often defined implicitly, in a fairly direct approach to implementing "situated action" agents, by nearly equivalent production rules for action, such as6
An explicit situation awareness approach would include a situational rule of the form given by (7.1) above, followed by a decisional rule of the form
This approach allows for the generation of higher-level situational assessments, which are of considerable utility, as recognized by the developers of Soar. For example, Tambe et al. (1995) point out that by combining a series of low-level events (e.g., location and speed of a bogey), one can generate a higher-level situational attribute (e.g., the bogey is probably a MiG-29). This higher-level attribute can then be used to infer other likely aspects of the situation that have not been directly observed (e.g., the MiG-29 bogey probably has fire-and-forget missiles), which can have a significant effect on the subsequent decisions made by the human decision maker (e.g., the bogey is likely to engage me immediately after he targets my wingman). Note that nowhere in this situation assessment process is there a production rule of the form given by (7.2); rather, most or all of the process is devoted to detecting the events (Endsley's [1995] level 1 situation awareness), assessing the current situation (level 2), and projecting likely futures (level 3).
Case-Based Reasoning7
Case-based reasoning is a paradigm in which knowledge is represented as a set of individual cases—or a case library—that is used to process (i.e., classify, or more generally, reason about or solve) novel situations/problems. A case is defined as a set of features, and all cases in the library have the same structure. When a new problem, referred to as a target case, is presented to the system, it is compared with all the cases in the library, and the case that matches most closely according to a similarity metric defined over a subset of the case features called index features is used to solve (or reason further about, respond to) the new problem. There is a wide range of similarity metrics in the literature: Euclidean distance, Hamming distance, the value difference metric of Stanfill and Waltz (1986), and many others.
In general, the closest-matching retrieved case will not match the target case perfectly. Therefore, case-based reasoning systems usually include rules for adapting or tailoring the specifics of the retrieved case to those of the target case. For example, the current battlefield combat scenario may be quite similar to a particular previous case at the tactical level, but involve a different enemy with different operating parameters. Thus, the assessment of the situation made in the prior case may need to be tailored appropriately for the current case. In general, these adaptation (or generalization) rules are highly domain specific; construction of a case-based reasoning system for a new domain generally requires a completely new knowledge engineering effort for the adaptation rules (Leake, 1996). In fact, an important focus of current case-based reasoning research is the development of more general (i.e., domain-neutral) adaptation rules.
A major motivation for using a case-based reasoning approach to the modeling of situation assessment, and human decision making in general, is that explicit reference to individual previously experienced instances or cases is often a central feature of human problem solving. That is, case-specific information is often useful in solving the problem at hand (Ross, 1989; Anderson, 1983; Carbonell, 1986; Gentner and Stevens, 1983). In the domain of human memory theory, such caseor episode-specific knowledge is referred to as episodic memory (Tulving, 1972; see also Chapter 5).
The second major motivation for using the case-based approach is that it is preferable when there is no valid domain model (as opposed to a human behavioral model).8 The state space of most tactical warfare situations is extremely large, thus making construction of a complete and reliable domain model untenable. In the absence of such a domain model, case-based solutions offer an alternative to model-based solutions. Both approaches have their advantages and
disadvantages. Models are condensed summaries of a domain, omitting (i.e., averaging over) details below a certain level. They therefore contain less information (i.e., fewer parameters) and require less storage space and have less computational complexity than case-based approaches. If it is known beforehand that there will never be a need to access details below the model's level of abstraction, models are preferable because of their increased computational efficiency. However, if access to low-level information will be needed, a case-based reasoning approach is preferable.
We are unaware of any military human behavior representations that employ case-based reasoning models of situation awareness. However, we believe this approach offers considerable potential for the development of general situation awareness models and military situation awareness models in particular, given the military's heavy reliance on case-based training through numerous exercises, the well-known development of military expertise with actual combat experience, and the consistent use of "war stories" or cases by subject matter experts to illustrate general concepts. In addition, the ease with which case-based reasoning or case "learning" can be implemented makes the approach particularly attractive for modeling the effects of human learning. Whether effective case-based reasoning models of situation awareness will be developed for future human behavior representations is still an open research question, but clearly one worth pursuing.
Bayesian Belief Networks9
Bayesian belief networks (also called belief networks and Bayesian networks) are probabilistic frameworks that provide consistent and coherent evidence reasoning with uncertain information (Pearl, 1986). The Bayesian belief network approach is motivated directly by Bayes' theorem, which allows one to update the likelihood that situation S is true after observing a situation-related event E. If one assumes that the situation S has a prior likelihood Pr(S) of being true (that is, prior to the observation of E), and one then observes a related event E, one can compute the posterior likelihood of the situation S, Pr(S¦E), directly by means of Bayes' theorem:
where Pr(E¦S) is the conditional probability of E given S, which is assumed known through an understanding of situation-event causality. The significance of this relation is that it cleanly separates the total information bearing on the
probability of S being true into two sources: (1) the prior likelihood of S, which encodes one's prior knowledge of S; and 2) the likelihood of S being true in light of the observed evidence, E. Pearl (1986) refers to these two sources of knowledge as the predictive (or causal) and diagnostic support for S being true, respectively.
The Bayesian belief network is particularly suitable for environments in which:
-
Evidence from various sources may be unreliable, incomplete, and imprecise.
-
Each piece of evidence contributes information at its own source-specific level of abstraction. In other words, the evidence may support a set of situations without committing to any single one.
-
Uncertainties pervade rules that relate observed evidence and situations.
These conditions clearly hold in the military decision making environment. However, one can reasonably ask whether human decision makers follow Bayesian rules of inference since, as noted in Chapter 5, many studies show significant deviations from what would be expected of a "rational" Bayesian approach (Kahneman and Tversky, 1982). We believe this question is an open one and, in line with Anderson's (1993) reasoning in developing adaptive control of thought (ACT-R), consider a Bayesian approach to be an appropriate framework for building normative situation awareness models—models that may, in the future, need to be "detuned" in some fashion to better match empirically determined human assessment behavior. For this brief review, the discussion is restricted to simple (unadorned) belief networks and how they might be used to model the military situation assessment process.
A belief network is a graphical representational formalism for reasoning under uncertainty (Pearl, 1988; Lauritzen and Spiegelhalter, 1988). The nodes of the graph represent the domain variables, which may be discrete or continuous, and the links between the nodes represent the probabilistic, and usually causal, relationships between the variables. The overall topology of the network encodes the qualitative knowledge about the domain.
For example, the generic belief network of Figure 7.2 encodes the relationships over a simple domain consisting of five binary variables. Figure 7.2a shows the additional quantitative information needed to fully specify a belief network: prior belief distributions for all root nodes (in this case just A and B) and conditional probability tables for the links between variables. Figure 7.2a shows only one of this belief network's conditional probability tables, which fully specifies the conditional probability distribution for D given X. Similar conditional probability tables would be required for the other links. These initial quantities, in conjunction with the topology itself, constitute the domain model, and in most applications are invariant during usage.
The network is initialized by propagating the initial root prior beliefs downward through the network. The result is initial belief distributions for all variables
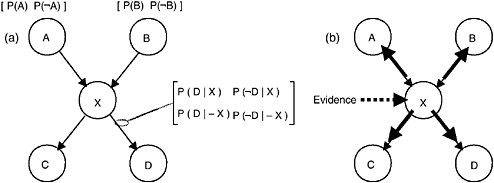
FIGURE 7.2 Belief network components and message passing.
and thus for the domain as a whole. When evidence regarding a variable is obtained, it is applied to the corresponding node, which then updates its own total belief distribution, computed as the product of the prior distribution and the new evidence. The node then sends belief revision messages to its parent and children nodes. For example, Figure 7.2b shows the posting of evidence to X and the four resulting belief revision messages. Nodes A, B, C, and D then update their respective belief distributions. If they were connected to further nodes, they would also send out belief revision messages, thus continuing the cycle. The process eventually terminates because no node sends a message back out over the link through which it received a message.
The major feature of the belief network formalism is that it renders probabilistic inference computationally tractable. In addition, it allows causal reasoning from causes to effects and diagnostic reasoning from effects to causes to be freely mixed during inference. Belief network models can be either manually constructed on the basis of knowledge extracted from domain experts or, if sufficient data exist, learned automatically (i.e., built) by sampling the data. Within the artificial intelligence community, belief networks are fast becoming the primary method of reasoning under uncertainty (Binder et al., 1995).
Note that the evidence propagation process involves both top-down (predictive) and bottom-up (diagnostic) inferencing. At each stage, the evidence observed thus far designates a set of likely nodes. Each such node is then used as a source of prediction about additional nodes, directing the information extraction process in a top-down manner. This process makes the underlying inference scheme transparent, as explanations can be traced mechanically along the activated pathways. Pearl's (1986) algorithm is used to compute the belief values given the evidence.
To illustrate how a belief network model could be used to model the situation assessment of an S-2 staff, Figure 7.3 shows a hypothetical battle scenario in which an enemy motorized rifle division will invade its neighbor to the west. The
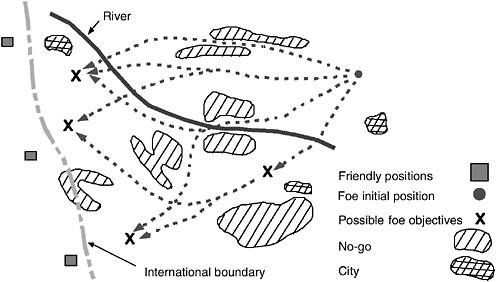
FIGURE 7.3 Hypothetical battle scenario. See text for discussion.
X's and dashed lines represent the friendly S-2's a priori, best hypotheses about possible enemy objectives and paths to those objectives, based on initial intelligence preparation of the battlefield, knowledge of enemy fighting doctrine, and knowledge of more global contexts for this local engagement—for example, that the enemy has already attacked on other fronts, or that high-value strategic assets (e.g., an oil refinery) exist just west of the blue positions. Although not depicted in the figure, the friendly force will, of course, have deployed many and varied sensor assets, such as radio emission monitoring sites, deeply deployed ground-based surveillance units, scout helicopters, and theater-wide surveillance assets (e.g., JSTARS). As the enemy begins to move, these sensors will produce a stream of intelligence reports concerning enemy actions. These reports will be processed by the S-2 staff, who will incrementally adjust degrees of belief in the various hypotheses about enemy positions, dispositions, and so on represented in the system.
Figure 7.4 depicts a simple belief network model supporting blue situation awareness of red activity that might take place under this scenario. It links several lower-level variables that are directly derivable from the sensors themselves to a higher-level (i.e., more abstract) variable, in this case, whether the red force is the main or supporting attack force. The set of values each variable can attain appears next to the node representing that variable.10 For example, the
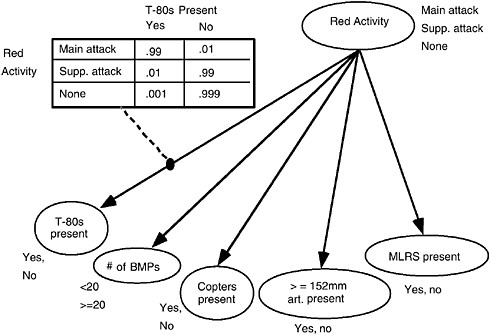
FIGURE 7.4 Belief net linking lower-level and high-level variables. See text for discussion.
The quantitative aspects of this dependence are encoded in a conditional probability table associated with that link, as shown in the upper left portion of Figure 7.4, based on a priori doctrinal knowledge. In the case of discrete-valued variables, a conditional probability table gives the probability of each value, Ci, of the child variable conditioned upon each value, Pj, of the parent variable; i.e., P(C i¦Pj). The conditional probability table of the figure essentially encodes the doctrinal knowledge that, given that a Russian motorized rifle division (MRD) is attacking, its main attack force will almost certainly (i.e., .99) contain T-80s, any support attacks will almost certainly not have T-80s, and it is very unlikely that a stray T-80 (i.e., one not associated with either a main or support attack) will be encountered. Note that qualitative and quantitative knowledge about the interdependencies among domain variables is represented separately in the belief net-
work formalism; qualitative relationships (i.e., whether one variable directly affects another at all) are reflected in the topology (the links), whereas quantitative details of those dependencies are represented by conditional probability tables.
Gonsalves et al. (1997) describe how this model is used to process low-level data on enemy size, activity, location, and equipment coming in during the course of a red attack and how the situation is continually reassessed during the engagement. A related effort by Illgen et al. (1997b) shows how the approach can be extended to model assessment of enemy courses of action and identification of the most likely course of action selected as the engagement unfolds. Research is now under way, as part of the Federated Laboratory effort supported by the Army Research Laboratory, to develop more extensive belief network models of the situation assessment process for a selected brigade-level engagement. Considerable effort is expected to be devoted to validation of developed models through comparison of model predictions with empirical data.
A number of modeling efforts have also been conducted by Zacharias and colleagues to develop belief network-based situation awareness models of Air Force decision makers. Zacharias et al. (1996) first applied belief networks to model pilot situation awareness in counter-air operations, using them to infer basic mission phases, defensive/offensive strength ratios, and appropriate intercept strategies. Zacharias et al. (1996) built upon this work by including additional factors to incorporate more threat attributes, engagement geometry, and sensor considerations. Work is now under way to refine and validate these situation awareness models and incorporate them into self-contained pilot agents (accounting for other aspects of pilot decision making and flight execution) as part of a larger-scale (M versus N) tactical air combat simulator called man-in-the-loop air to air system performance evaluation model (MIL-AASPEM) (Lawson and Butler, 1995). Parallel efforts are also being conducted to use these situation awareness models for driving tactical displays as a function of the inferred tactical situation (Mulgund et al., 1997) and for providing the battlefield commander with tactical decision aids (Mengshoel and Wilkins, 1997; Schlabach, 1997).
Although there is significant activity regarding the use of belief network-based situation awareness models, it should be emphasized that most of this work has been focused on (1) the knowledge elicitation needed to define the subject matter expert's mental model, (2) the computational model implementation, and (3) the generation of simulation-based traces of the inferencing process and the resulting situation-driven activities of the operator model. Little actual validation has been conducted, and experimental efforts to validate the model output with what is actually observed under well-controlled man-in-the-loop simulator experiments are just now beginning.
We believe that a belief network-based approach to modeling situation assessment has considerable potential, but is not without its drawbacks. First, the graphic representation structure makes explicit, to domain experts and developers
alike, the basic interrelationships among key objects and concepts in the domain. However, building these topological structures is not a trivial exercise, nor is the specification of the quantitative probability links between nodes. Second, the event propagation algorithm reflects the continuity of situation assessment—an evidence accumulation process that combines new events with prior situation assessments to evaluate events in the context of the assessed situation. Likewise, the event projection algorithm reflects the continuity of situation awareness—the projection of future events based on the currently assessed situation. However, it should be clear that both propagation and projection are based on normative Bayesian models, which may, in fact, not accurately reflect actual human behavior in assessment (recall the discussion in Chapter 6 on decision making models). Finally, it should be pointed out that much of the functionality achievable with belief networks (e.g., continuous updating of the assessed situation, propagation and projection, normative decision making behavior) may very well be accomplished using other approaches (e.g., forward/backward chaining expert systems incorporating uncertainty factors). Thus it may prove to be more effective to upgrade, for example, legacy production rule systems, rather than to attempt a wholesale replacement using a belief network approach. Obviously the specific details of the model implementation will need to be taken into account before a fair assessment can be made as to the pros and cons of enhancement versus replacement.
RELATIONSHIPS TO OTHER MODELS
This section describes how situation awareness models relate to other models comprising a human behavior representation. In particular, it examines how situation awareness models relate to (1) perceptual models and the way they drive downstream situation awareness, (2) decision making models and the way situational beliefs can be used to support utility-based decision making, (3) learning models and the way situational learning can be modeled, and (4) planning and replanning models and their critical dependence on accurate situation assessment. The section concludes with a pointer to Chapter 9 for further discussion on how situation awareness models can be adapted to reflect the effects of internal and external behavior moderators.
Perceptual Models and Attention Effects
As noted earlier, the effective "driver" of a realistic situation awareness model should be a perceptual model that transforms sensory cues into perceptual variables. These perceptual variables can be associated with states of the observer (e.g., self-location or orientation with respect to the external world), with states of the environment (e.g., presence of vegetation in some region), or with states of other entities in the environment (e.g., threat presence/absence and
location). The perceptual variables may be either discrete (e.g., presence/absence) or continuous (e.g., altitude), and they may be of variable quality, but the key point is to ensure that there is some sort of perceptual model that intervenes between the sensory cues available to the human and the subsequent situation assessment processing that integrates and abstracts those cues. Otherwise, there will be a tendency for the human behavior representation to be omniscient, so that downstream situation assessment processing is likely to be error free and nonrepresentative of actual human assessment behavior. By explicitly modeling perceptual limitations in this fashion, we will be more likely to capture inappropriate assessments of the situation that occur with a "correct" assessment strategy, but an "incorrect" perceptual knowledge base.
A variety of perceptual models could be used to drive a situation awareness model. One that has been used in several modeling efforts conducted by Zacharias and colleagues (1992, 1996) is based on the perceptual estimator submodel of the optimal control model of the human operator developed by Kleinman and colleagues (Kleinman et al., 1971). This is a quantitative perceptual model that transforms continuous sensory cues (e.g., an altimeter needle) into continuous perceived states (e.g., estimated altitude), using a Kalman filter to extract an optimal state estimate from the noisy sensory signal. 11
Several ongoing modeling efforts could benefit from this estimation theory approach to perceptual modeling. For example, Reece and Wirthlin (1996) introduce the notion of "real" entities, "figments," and "ghosts'' to describe concepts that are well understood in the estimation community and would be better handled using conventional estimation theory. Likewise, Tambe et al. (1995) introduce the notion of a "persistent internal state" in Soar; what they mean in estimation theory parlance is simply "state estimate." We suspect that the incorporation of this type of well-founded perceptual model could significantly enhance the realism of Soar's behavior in the face of a limited number of intermittent low-precision cues.
There are, however, at least two problems with this type of perceptual model. The first has to do with its focus on continuous, rather than discrete, states. The continuous-state estimates generated by this type of perceptual model are well suited to modeling human behavior in continuous-control tasks, but not well suited to generating the discrete events typically required by procedure-oriented tasks in which human decision makers engage. Early efforts to solve this problem (e.g., Baron et al., 1980) used simple production rules to effect a continuous-to-discrete transform. More recently, these continuous-to-discrete event transfor-
The second problem associated with a perceptual model based on estimation theory is its focus on the informational aspects of the cue environment. Very little emphasis is placed on the underlying visual processes that mediate the transformation of a cue (say, an altimeter pointer) to the associated informational state (the altitude). In fact, these processes are almost trivialized by typically being accounted for with some simple transfer function (e.g., a geometric transform with additive noise).
To overcome this limitation, one must resort to more detailed process-oriented models. Most of the work in this area has been done in the visual modality, and an extensive literature exists. The following subsections briefly describe four visual perception models that offer potential for driving a situation awareness model and accounting for human perceptual capabilities and limitations in a more realistic fashion. All three are focused on visual target detection and recognition, and all have a common functionality: they take two-dimensional images as input and generate probability of detection (Pd) and probability of false alarm (Pfa) as output. Another commonality is the concept of separating the probability of fixation (Pfix) from the probability of detection (or false alarm) given a fixation (Pdlfix). Pd and Pfa are very relevant to modeling how combatants form a mental picture of what is going on around them because they predict which objects the combatants perceive and how those objects are labeled (target versus clutter).
Night Vision Laboratory Models
The search model developed at the Army Night Vision and Electronic Sensor Directorate (NVESD, formerly known as the Night Vision Laboratory or NVL) is often called the "Classic" model (Ratches, 1976), while the more recent model developed by the Institute for Defense Analysis for NVESD is referred to as the "Neoclassic" model (Nicoll and Hsu, 1995). Further extensions have been developed by others, such as for modeling individual combatants in urban environments (Reece, 1996). The Classic model provides a very simple estimate of Pdlfix : the longer one spends fixating a target, the more likely one is to detect it. Pfix is not modeled (fixation locations are ignored); instead, a single parameter is used to adjust the time-to-fixation manually to fit empirical estimates. The Neoclassic model adds a simple Markov process for modeling eye movements. The eye is assumed to be either in a wandering state, characterized by large random saccades, or in a point-of-interest state, with fixations clustered around target-like
objects. A major drawback of both models is their dependency on empirical estimates, limiting predictive power to the particular situation in which the empirical estimate applies (e.g., a specific type of target, clutter, lighting). Conversely, in simple scenes with no clutter (such as air-to-air or ocean-surface combat), the NVL models can work very well.
Georgia Tech Vision Model
The Georgia Tech Vision model has been in development since the early 1990s at the Georgia Tech Research Institute and has grown to include many specific visual functions relevant to Pfix and Pdlfix. The most recent version has been integrated into a multispectral signature analysis tool called visual electrooptical (VISEO) for the Army Aviation Applied Technology Directorate (Doll, 1997). One of the early psychophysics experiments under the Georgia Tech Vision research project identified experience as the primary determinant of Pfix in visual search tasks for targets in cluttered scenes, even with presentation times as short as 200 milliseconds. While potentially of great importance, this finding needs to be verified independently through more psychophysics experiments, using an eye-tracker and a variety of scenes. The Georgia Tech Vision model also provides a highly detailed representation of the earliest physiological functions of the human visual system, such as dynamics of luminance adaptation due to receptor pigment bleaching, pupil dilation, and receptor thresholds. It is not clear whether this level of detail is appropriate for a model that is ultimately concerned with Pd and Pfa,, especially given the associated computational complexity: a single input image generates up to 144 intermediate equal-size images. For this reason, it is not clear that the Georgia Tech Vision model is well suited for online simulations unless special image processors are used to host it. Benefits, on the other hand, include the potential to identify Pd and Pfa as a function of ambient light level and color and of target attributes such as color, motion, and flicker.
TARDEC Visual Model
The TARDEC Visual Model is a joint effort of the Army Tank-Automotive and Armaments Command Research, Development and Engineering Center and OptiMetrics, Inc. (Gerhart et al., 1995). Its most recent version is known as the National Automotive Center Visual Perception Model (NAC-VPM). The TARDEC Visual Model is a detailed model of Pdlfix combined with use of a simple (NVL Neoclassic-style) Markov process approach to set a time-to-fixation parameter. Hence, the model takes as input a subimage containing just the fixated target (manually segmented by the user). Front-end modules simulate temporal filtering and color opponent separation, enabling input with color and motion. Following modules decompose the image into multiple channels through
multiresolution spatial filtering and orientation selective filtering. A signal-to-noise ratio is then computed for each channel, and the ratios are combined into a single measure of detectability. A strong point of the TARDEC Visual Model is that it has been calibrated to reproduce typical human observer results under a variety of conditions. Its main shortcoming is the lack of Pfix prediction, preventing the use of whole-scene images as input.
Decision Making Models
Chapter 6 describes how the foundations of utility theory can be used to develop a number of deterministic and stochastic models of human decision making. At its simplest level, utility theory predicates that the decision maker has a model of the world whereby if one takes action Ai, under situation Sj, one can expect an outcome Oij with an associated utility12 of Uij, or:
If the decision maker has a belief Bj that situation Sj is true, then the expected utility of action Ai across the ensemble of possible situations (Sj) is
Simple utility theory models the rational decision maker as choosing the "best" action Ai* to yield the maximal EUi. As described in Chapter 6, a number of variants of this utility-based model have been developed to account for observed human decision making.
It should be recognized that there is a close connection between this model of decision making and the situation assessment process, since it is this process that provides the belief values (Bj) for use in the above expected utility calculation, which in turn is the basis for the selection of a best-choice decision option. Clearly, a misassessment of the situation in terms of either the set of possible situations (Sj) or their corresponding likelihoods (Bj) can easily bias the computation of the expected utilities, leading to the inappropriate selection of a non-optimal action Ai.
As discussed in Chapter 6, the human decision maker also often makes decisions consistent with Klein's (1994) RPD, in which action selection immediately follows situation recognition. The majority of human behavior representations reviewed for this study model this process using a simple production rule of the form:
or simply "Select action Ai in situation Sj." As pointed out in Chapter 6, this is merely a special case of the more general utility-based decision model.
Whatever approach is taken to modeling the actual decision making process of action selection, it seems clear that accurate modeling of the situation awareness process deserves close attention if human decisions in the kind of complex military environments under consideration are to be reliably accounted for.
Learning Models
With one exception, the models reviewed here do not incorporate learning. The one exception is Soar, with its chunking mechanism (see Chapter 5). However, as noted in Chapter 5, this capability is not enabled in any of the tactical applications of Soar reviewed for this study. Research in simpler domains has produced Soar models that learn situational information through experience. For example, one system learns new concepts in a laboratory concept-acquisition task (Miller and Laird, 1996), one learns the environmental situations under which actions should be taken in a videogame (Bauer and John, 1995), one deduces hidden situational information from behavioral evidence in a black-box problem solving task (Johnson et al., 1994), and one learns episodic information in a programming task (Altmann and John, forthcoming). Thus, in principle, chunking can be used for situation learning and assessment, but it remains to be proven that this technique will scale up to a complex tactical environment.
As discussed in Chapter 5, exemplar-based or case-based reasoning models are particularly well suited to the modeling of learning because of their simplicity of implementation: new examples or cases are merely added to the case memory. Thus with increasing experience (and presumed learning), case-based reasoning models are more likely to have a case in memory that closely matches the index case, and recognition is more likely to occur in any given situation as experience is gained and more situational cases populate the case library. 13 (See the discussion of exemplar-based learning in Chapter 5 for more detail on learning within the context of a case-based reasoning model.)
Finally, recall that the earlier discussion of belief network models assumed a fixed belief network "mental model"—a fixed-node topology and fixed conditional probability tables characterizing the node links. Both of these can be learned if sufficient training cases are presented to the belief network. To learn the conditional probability tables for a fixed structure, one keeps track of the frequencies with which the values of a given variable and those of its parents occur across all samples observed up to the current time (Koller and Breese,
1997). One can then compute sample conditional probabilities using standard maximum likelihood estimates and the available sample data. Infinite memory or finite sliding-window techniques can be used to emphasize long-term statistics or short-term trends, but the basic approach allows for dynamic conditional probability table tracking of changing node relations, as well as long-term learning with experience.
Planning Models
Planning is described more fully in Chapter 8. The discussion here focuses on how a situation awareness model would support a planning model during both initial planning and plan monitoring.
During the initial planning stage there is a need to specify three key categories of information:
-
Desired Goals—In standard planning jargon, this is the desired goal state. In the U.S. Army, it is doctrinally specified as part of the METT-T (mission, enemy, troops, terrain, and time) planning effort (recall the vignette of Chapter 2). In this case, the desired goal state is specified by the mission and the time constraints for achieving the mission.
-
Current Situation—In standard planning jargon, the current situation is the initial state. In the U.S. Army, it is doctrinally specified by an assessment of the enemy forces (the E of METT-T, e.g., strength, location, and likely course of action), an assessment of friendly troop resources (the first T of METT-T, e.g., their location and strength), and an assessment of the terrain (the second T of METT-T, e.g., trafficability and dependability). Clearly, all these elements are entirely dependent on a proper assessment of the current situation. A failure to model this assessment function adequately will thus result not only in failure to model adequately the initial planning efforts conducted by commander and staff, but also failure to set the proper initial state for the planning process proper.
Once the above categories of information have been specified, the actual planning process can proceed in a number of ways, as discussed in Chapter 8. Whichever approach is taken, however, additional situation awareness needs may be generated (e.g., "Are these resources that I hadn't considered before now available for this new plan?" or "For this plan to work I need more detailed information on the enemy's deployment, specifically, . …"). These new needs would in turn trigger additional situation assessment as a component activity of the initial planning process.14
During the plan monitoring stage, the objective is to evaluate how well the plan is being followed. To do this requires distinguishing among three situations:
(1) the actual situation that reflects the physical reality of the battlefield; (2) the assessed situation that is maintained by the commander and his/her staff (and, to a lesser extent, by each player in the engagement); and (3) the planned situation, which is the situation expected at this particular point in the plan if the plan is being successfully followed.
Stressors/Moderators
The panel's review of existing perceptual and situation awareness models failed to uncover any that specifically attempt to provide a computational representation linking stressors/moderator variables to specific situation awareness model structures or parameters. We have also failed to identify specific techniques for modeling cognitive limitations through computational constructs in any given situation awareness model (e.g., limiting the number of rules that can be processed per unit time in a production rule model; or limiting the number of belief nodes that can reliably be "remembered" in a belief network model, etc.). Clearly, further work needs to be done in this direction if we are to realistically model human situation assessment under limited cognitive processing abilities. This lack, however, does not preclude the future development of models that incorporate means of representing cognitive processing limitations and/or individual differences, and indeed Chapter 9 proposes some approaches that might be taken to this end.
CONCLUSIONS AND GOALS
This chapter has reviewed a number of descriptive and prescriptive situation awareness models. Although few prescriptive models of situation awareness have been proposed or developed, the panel believes such models should be the focus of efforts to develop computational situation awareness submodels of largerscope human behavior representations. As part of this effort, we reviewed three specific technologies that appear to have significant potential in situation awareness model development: expert systems, case-based reasoning, and belief networks. We noted in this review that early situation awareness models, and a surprising number of current DoD human behavior representations, rely on an expert systems approach (or, closely related, decision tables). In contrast, case-based reasoning has not been used in DoD human behavior representations; however, we believe there is a good match between case-based reasoning capabilities and situation awareness behavior, and this approach therefore deserves a closer look. Finally, recent situation awareness modeling work has begun to incorporate belief networks, and we believe that there is considerable modeling potential here for reasoning in dynamic and uncertain situations.
We concluded this review of situation awareness models by identifying the intimate connections between a situation awareness model and other models that
are part of a human behavior representation. In particular, situation awareness models are closely related to: (1) perceptual models, since situation awareness is critically dependent on perceptions; (2) decision making models, since awareness drives decisions; (3) learning models, since situation awareness models can incorporate learning; and (4) planning models, since awareness drives planning.
Short-Term Goals
-
Include explicitly in human behavior representations a perceptual "front end" serving as the interface between the outside world and the internal processing of the human behavior representation. However trivial or complex the representation, the purpose is to make explicit (1) the information provided to the human behavior representation from the external world model, (2) the processing (if any) that goes on inside the perceptual model, and (3) the outputs generated by the perceptual model and provided to other portions of the human behavior representation. Incorporating this element will help make explicit many of the assumptions used in developing the model and will also support "plug-and-play" modularity throughout the simulation environment populated by the synthetic human behavior representations.
-
In future perceptual modeling efforts undertaken for the development of military human behavior representations, include a review of the following:
-
Informational modeling approaches in the existing human operator literature.
-
Visual modeling approaches to object detection/recognition supported extensively by a number of DoD research laboratories.
-
Auditory modeling approaches to object detection/recognition. Developers of perceptual models should also limit the modeling of low-level sensory processes, since their inclusion will clearly hamper any attempts at implementation of real-time human behavior representation.
-
-
In the development of human behavior representations, make explicit the internal knowledge base subserving internal model decisions and external model behaviors. A straightforward way of accomplishing this is to incorporate an explicit representation of a situation assessment function, serving as the interface between the perceptual model and subsequent stages of processing that are represented. Again, the representation may be trivial or complex, but the purpose is to make explicit (1) the information base upon which situation assessments are to be made, (2) the processing (if any) that goes on inside the situation awareness model, and (3) the outputs generated by the situation awareness model and provided to other components of the human behavior representation. At a minimum, incorporating this element will specify the information base available to the decision making and planning functions of the human behavior representation to support model development and empirical validation. This element will also serve as a placeholder to support the eventual development of limited-scope
-
situation awareness models focused primarily on location awareness, as well as the development of more sophisticated models supporting awareness of higher-level tactical situations, anticipated evolution of the situation, and the like. These limited-scope models, in turn, will support key monitoring, decision making, and planning functions by providing situational context. Finally, this explicit partitioning of the situation awareness function will support its modular inclusion in existing integrative models, as described in Chapter 3.
-
Consider taking several approaches to developing situation awareness models, but be aware of the limitations of each. Consider an initial focus on approaches based on expert systems, case-based reasoning, and Bayesian belief networks, but also assess the potential of more generic approaches, such as abductive reasoning, and enabling architectures, such as blackboard systems.
-
For situation awareness models based on expert systems, review techniques for knowledge elicitation for the development of rule-based systems. When developing the knowledge base, provide an audit trail showing how formal sources (e.g., doctrine expressed in field manuals) and informal sources (e.g., subject matter experts) contributed to the final rulebase. In addition, consider using an embedded expert system engine, rather than one developed from scratch. Finally, pay particular attention to how the expert system-based model will accommodate soft or uncertain facts, under the assumption that a realistic sensory/perceptual model will generate these types of data.
-
For situation awareness models based on case-based reasoning, consider using an embeddable case-based reasoning engine. As with an approach based on expert systems, identify how uncertainty in the feature set will be addressed. Finally, consider a hybrid approach incorporating more abstract relations to represent abstract non-case-specific military doctrine, which must somehow be represented if realistic situation assessment behavior is to be achieved in human behavior representations.
-
For situation awareness models based on belief networks, consider using an embeddable belief network engine. As with model development based on expert systems, maintain an audit trail of the way knowledge information sources contributed to the specification of belief network topology and parameter values. A potentially fruitful approach to belief network development at higher echelons may be the formal intelligence analysis process specified by Army doctrine. The top-down specification of intelligence collection planning and the bottom-up integration of intelligence reports suggest that belief networks could be put to good use in modeling the overall process, and perhaps in modeling the internal processing conducted by the human decision makers.
-
Validate all developed situation awareness models against empirical data. Although not reviewed here, there are a number of empirical techniques for evaluating the extent and precision of a decision maker's situation awareness, and this literature should be reviewed before a model validation effort is planned. Model validation efforts have only begun, and considerable work is still needed in this area.
-
Model validation efforts have only begun, and considerable work is still needed in this area.
Intermediate-Term Goals
-
Explore means of incorporating learning into situation awareness models as a means of both assessing the impact of expertise on situation awareness performance and "teaching" the model through repeated simulation exposures. For models based on expert systems, explore chunking mechanisms such as that used in Soar. For models based on case-based reasoning, learning comes as a direct result of recording past cases, so no technology development is required. For models based on belief networks, explore new learning techniques now being proposed that are based on sampled statistics derived from observed situations.
-
Explore means of incorporating the effects of stressors/moderators in situation awareness models. Conduct the behavioral research needed to identify across-model "mode switching" as a function of stressors, as well as within-model structural and/or parametric changes induced by stressors. Conduct concurrent model development and validation to implement stressor-induced changes in situation awareness behavior.
-
Expand model validation efforts across larger-scale simulations.
Long-Term Goals
-
Conduct the basic research needed to support the development of team-centered situation awareness models, looking particularly at distributed cognition, shared mental models, and common frames of reference. Conduct concurrent model development for representing team situation awareness processes.































