II. Learning Challenges
The experience reflected here—the authors' experience and that of the people interviewed—underscore the centrality of the assessment process as a guide to design professional development. Once decisions have been made about the mathematical knowledge and skills that are important to assess, a four-part, cyclical process is used to monitor the quality of assessment data and decisions. Attending to the process helps ensure that important knowledge and skills are being assessed (NCTM, 1995).
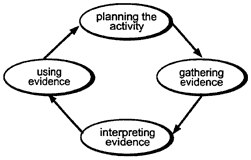
Figure 1.
The Assessment Process
Adapted with permission from Assessment Standards for School Mathematics, NCTM, 1995, p. 4.
The assessment process has proved a powerful model for thinking about student work in mathematics. Used consciously as
a guide to gathering, interpreting, and using evidence, assessment provides a structured way to make values and judgments explicit: What do I think is important for students to learn? What evidence am I going to seek? What meaning do I attach to the evidence I get? How am I going to use the evidence? The assessment process has a simple message about teaching and learning: that a teacher's classroom actions should be based on a thoughtful analysis of student understanding.
Since the introduction of the first set of standards in mathematics in 1989, it has become increasingly evident that, in order to help teachers transform their practice in accordance with standards, professional development must reach levels of need much deeper than the need for information. Working with standards means making decisions that are informed not only by expert information, but also by individual teachers' beliefs, assumptions, and mindsets—all of which affect the interpretation of the information. To be effectively standards-based, therefore, professional
Table 1. Seven core learning challenges
|
Judgment about the quality of mathematics in tasks |
|
|
Challenge 1. |
Reaching consensus about quality when looking at mathematics tasks. |
|
Challenge 2. |
Framing questions and structuring tasks so that what is important and intended is elicited. |
|
Judgment about the appropriateness of tasks |
|
|
Challenge 3. |
Aligning classroom assessment with curriculum, instruction, and external assessment. |
|
Challenge 4. |
Ensuring that tasks involving important mathematics elicit from the broadest range of students what they truly know and can do, and that there are no unnecessary barriers due to wording or context. |
|
Judgment about the quality of student responses |
|
|
Challenge 5. |
Deciding what are reasonable student answers to a problem when there is no one "correct" answer. |
|
Challenge 6. |
Using evidence to make valid inferences about student understanding. |
|
Judgment about consequent actions |
|
|
Challenge 7. |
Determining appropriate actions in light of conclusions from student evidence. |
development must be rich and complex enough to support teachers at the level of judgment as well as the level of receiving and interpreting information. (See, e.g., Ball, 1994; Little, 1993; Schifter and Fosnot, 1993.)
In this regard, professional development based on assessment is not just about assessment content—e.g., the new terminology, techniques, tasks, etc. Teachers engage with the process of assessment, as well. These multiple purposes necessitate more complexity in the design and facilitation of the teachers' learning opportunities, so that they can exercise the judgment and develop the inferencing skills necessary to follow the cycle of the assessment process, from planning to gathering evidence to interpreting evidence to using evidence, and back to further planning. In many assessment work groups, teachers adopt, adapt, and create tasks. As they do so, they are challenged to sharpen and exercise judgment about subject matter, task development, the evidence in student work, and the courses of action implied by student evidence. This section looks at seven core learning challenges we have seen arise in assessment-related professional development. These challenges are organized according the types of professional judgment that teachers may make in response to assessments. (See Table 1 for a summary.)
Judgment about the quality of mathematics in tasks
Though it has not been the norm in staff development to agree on and apply criteria about quality in mathematics, it is difficult to get very deeply into issues of mathematics assessment without being explicit about quality of mathematics tasks and whether a particular task elicits evidence of important mathematical learning.
Challenge 1. Reaching consensus about quality when looking at mathematics tasks.
Challenge 2. Framing questions and structuring tasks so that what is important and intended is elicited.
Ultimately, teachers need to be sure that the tasks they use measure the important mathematics they intend them to measure. This implies some common understanding about mathematical quality. In order for a group of teachers to discuss mathematical quality, there need to be criteria for quality that can be used as dimensions for an informal rating scheme. The point here is not to certify tasks, nor to build an airtight rating scheme. Rather, it is to generate conversations about mathematical quality, so that members of the same teaching community can talk about and listen to opinions about what is important in mathematics.
One option is to focus on the processes involved in doing mathematics. For example, in one teacher-enhancement project2, teachers took the NCTM definition of Mathematical Power and the language in several of NCTM's curriculum standards related to number sense, and used them to build a rating scheme to rank a cluster of tasks concerned with number sense. (For more information on this process, see Bryant and Driscoll, 1998.)
At a teacher institute for a different project3, teachers analyzed the following activity using the Mathematical Power definition along with several aspects of algebraic thinking they had been studying, such as generalizing and building rules to represent functional relations.
|
The post office only has stamps of denominations 5 cents and 7 cents. What amounts of postage can you buy? Explain your conclusion. What if the denominations are 3 cents and 5 cents? 15 cents and 18 cents? What generalizations can you make for stamp denominations m cents and n cents, where m and n are positive integers? |
When reporting back on their work, one group showed what they did on the first part of the task (Figure 2). Another group, aiming more at the generalization prompted by the second part of the task, developed an algorithm.
"Given an amount of money, A, we divide it by the smaller denomination. If the remainder is divisible by the difference between the denominations, then we know we can generate the combination using the given denominations. Example: With 5 cent and 7 cent denominations: Try 129. 129 divided by 5 leaves remainder 4. 4 is divisible by 2, the difference between 7 and 5. So 129 works (5x23 + 7x2 = 129)."
The mathematical-power lens made it possible to discuss the quality of mathematical communication and reasoning in each piece and to measure the potential for conjectures. Thus, the first group looked at the evidence they had that, in the (5, 7) and (3, 5) cases, they could generate all amounts of postage, after a certain point, while the (15, 18) case had consistent gaps. They conjectured that the concept "relatively prime" is a key differentiating
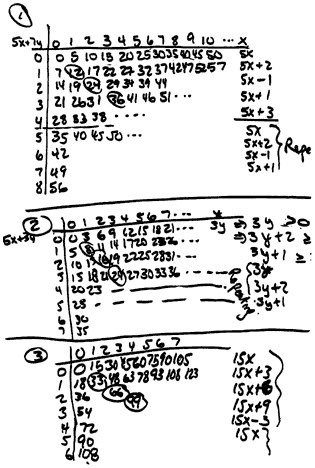
Figure 2.
One solution to the Postage Stamp problem.
factor. Meanwhile, the second group's reasoning could be analyzed to see why the algorithm worked and whether it could be further generalized.
Other schemes for analyzing an activity are possible, which would offer different criteria for analysis. One possibility is to think of quality in mathematics in light of mathematics as a discipline with tradition. For example, one opinion has been offered that there are three criteria for including a piece of mathematics in the curriculum: beauty, historical significance, and utility (Artin, 1995). (Similarly, Thorpe (1989) suggests as criteria for including topics in the curriculum: i. intrinsic value, ii. pedagogical value, and iii. intrinsic excitement or beauty.) Looking at the postage-stamp problem through such a lens, one could focus on the
task's utility, not only in its potential to underscore the power of the relation "relatively prime," but also to foreshadow the importance of linear combinations. Historical significance could be discussed in several ways, including the overarching topic of Diophantine equations. Finally, beauty, which often is experienced when one sees the same concept in different guises, could be discussed in the connection the first group made between the relationship among the rows in the top two tables (captured in their right-hand column) and, respectively, mod 5 and mod 3 systems.
Opportunities to discuss beauty also arise from surprising mathematical results. Groups working on this problem are usually surprised and excited when their evidence leads them to infer that the following statement is true: "For relatively prime stamp denominations p and q, the largest postage amount that cannot be made with combinations of p-stamps and q-stamps is (p-1)(q-1)-1, or pq-(p + q)."
It is not important which particular lens is initially used to discern and discuss the quality of mathematics in a task. It is more important that teachers be afforded opportunities to do mathematics together and to have structured discussions about mathematical quality. Of course, this implies the critical importance of the discussion's facilitator, who must be attentive and prepared, must know the mathematics underlying the tasks, and must be able to introduce relevant viewpoints if they don't arise from the group.
Judgment about the appropriateness of tasks
There are considerable opportunities for teachers to develop their critical skills when weighing the appropriateness of tasks. They can become adept at considering criteria such as student developmental level, available resources and time, and the match between task and purpose. Two particularly important and engaging questions about tasks are whether, as classroom assessments, they are aligned with the curriculum, instruction, and external assessments being used, and how accessible they are to students.
Challenge 3. Aligning classroom assessment with curriculum, instruction, and external assessment.
Challenge 4. Ensuring that tasks involving important mathematics elicit from the broadest range of students what they truly know and can do, and that there are no unnecessary barriers due to wording or context.
|
The small squares are all identical. Their side length is 100 mm. The large squares are also all identical. Show how you can find the side length of a large square without measuring. Give your answer to the nearest millimeter. |
|
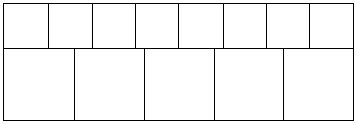 |
Figure 3.
A task on proportion
Adapted from New Standards Project, 1997.
Regarding these challenges, a central feature of assessment reform in recent years has been the variation of mathematics tasks along multiple dimensions. In creating or adapting tasks along these dimensions, it is of course essential to stay mindful of the quality of the mathematics represented and elicited. It is also important to consider the cognitive demands of a task. Is a particular task intended to gauge how well students have mastered a concept like ratio or proportion? Then its problem-solving demands—the requirements for students to plan and carry out an unfamiliar and complex problem solution—should be minimized. For example, the task in Figure 3, adapted from the New Standards Project (1997), allows students to show understanding of the concept of proportion, without demanding much problem solving.
In contrast, the task below involves problem solving, and also challenges students' conceptual understanding of ratio and proportion.
|
Make a two-dimensional paper replica of yourself using measurements of lengths and widths of body parts that are half those of your own body. |
An overarching purpose of teacher assessment groups is to help teachers become more knowledgeable about how to select one form of assessment over another. In this case, if a group of teachers is keen to see how well students understand the concepts of ratio and proportion, then they need to consider the following question: Would the problem-solving demands of the second task—e.g., requiring students to make plans and organizing information—provide less valuable evidence of student learning of the
relevant concepts than the first task? (For further elaboration on task demands, see Neill, 1995, and Balanced Assessment Project.)
Another issue is the accessibility of the task. For example, as interest in standards-based curriculum, instruction, and assessment has grown in recent years, there has been a shift toward greater use of open assessment tasks and instructional activities. Part of the challenge in aligning curriculum, instruction, and classroom assessment is for teachers to be aware of accessibility issues around openness. Tasks can be open in the front to invite multiple entry points; they can be open in the middle to invite multiple pathways to solution; and they can be open in the end to invite multiple solutions and/or extensions. Beyond certain points, however, tasks can be too open if, instead of aiming the students toward what is important, they make it possible for them to concentrate on form instead of substance, or they make it difficult for students to put their solutions into a broader mathematical framework. Open-ended activities can be seductive, in that a wider range of students can gain access to them and, through the variety of exploration paths, develop a high degree of ownership over their work. However, if a task isn't scaffolded in a way that aims students toward important mathematics, then questions can be asked: "Access to what? Ownership over what?" (For opinions regarding the value as well as risk in using open-ended problems, see, e.g., Clarke, 1993 and Wu, 1994.)
There is yet another task-construction caution regarding accessibility: making sure that no students are unwittingly excluded. Assessment tasks—especially more open tasks—often demand that students interpret wording, context, and diagrams as well as what the purpose of the task is and what is important in the underlying mathematics. In particular, the more open a task and the more context-based it is, the more varied and influential are the assumptions students can bring to their interpretation of the task. A task may allow varying, and even conflicting, assumptions to be brought to bear as students interpret. On their part, task writers assume that students are familiar with certain contexts. In addition, those who use the tasks with students assume the students are aware of their intention in presenting the task.
For instance, in a national teacher project4 (Driscoll, In preparation), a team of teachers decided to experiment with relevance of context as a dimension in tasks, on the supposition that students are more likely to engage in relevant tasks. Their experiment
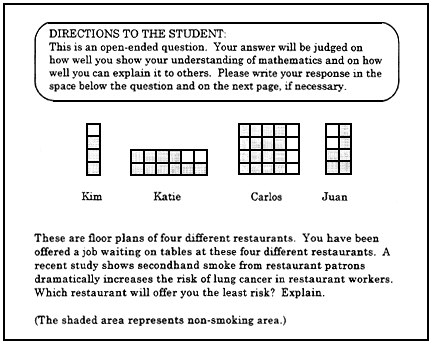
Figure 4.
A task in a new context
Adapted from the California Learning Assessment System.
involved taking a task from CLAS, the California Learning Assessment System, and changing the context from a gameboard to the more politically alive topic of smoking in restaurant. (See Figure 4.) The revised task changed the shaded regions in the diagram from gameboard segments to non-smoking areas, and the students were told, "These are floor plans of four different restaurants. You have been offered a job waiting on tables at these four restaurants. A recent study shows secondhand smoke from restaurant patrons dramatically increases the risk of lung cancer in restaurant workers. Which restaurant will offer you the least risk? Explain."
When the teachers gathered the student work on the revised task, they saw evidence that many students thought that it was just as important in the task, if not more important, to analyze room shape for airflow as it was to deal with raw fractional comparisons. Consequently, many strayed considerably in their responses from the mathematical explanations that the teachers wanted to see. In the end, the experiment and, more importantly, the opportunity to analyze the data together, gave the teachers a chance to enhance their appreciation of the importance of wording and context in mathematics-assessment tasks.
The issue of validity, which refers to the appropriateness of inferences made from information produced by an assessment, is too complex to cover in detail in this document. But the related question, ''Does the assessment tell us what we want to know for each individual student?'' is one that deserves careful attention by teachers in professional-development groups, at the very least so they can be more alert to the many non-mathematical factors, like language and culture, that can get in the way of a student's demonstration of mathematical learning.
"I worry about the language used in how the problem is presented to students, how to make it very clear what they're expected to do, especially if a student is in a testing situation without teacher intervention. I'm concerned with perfecting the skill of making it clear to the student what they are being asked, which is not automatic or easy to do. For example, it's very common that a task ends with 'explain your reasoning or 'justify your conclusions.' I find that too general for my students, at least until they become acclimatized to the problems." Interviewed high-school mathematics teacher
Judgment about the quality of student responses
Among those initiating alternative approaches to mathematics assessment, a frequently recurring realization is that "offering rich problems to students results in getting rich answers. This means that simple marking becomes a thing of the past and that giving students credit for 'the' correct answers becomes a hard job" (Van den Heuvel-Panhuizen, 1994, p. 359). Further, the task may invite a range of mathematical answers. Then it may be more appropriate to ask what is a reasonable, rather than correct, answer—reasonable in light of the assumptions that the students bring and reasonable in a mathematical sense.
Challenge 5. Deciding what are reasonable student answers to a problem when there is no one "correct" answer.
Challenge 6. Using evidence to make valid inferences about student understanding.
Here, again, open-endedness in a problem can have risks as well as advantages, in particular, if the lines of reasonable expectations for student responses are not clear.
For example, teachers in one projects5 have used versions of the so-called Consecutive Sums task in a range of middle-grades and
high-school classrooms. In brief, the challenge to students is to investigate which natural numbers can be written as the sum of consecutive natural numbers (e.g., 15 = 7 + 8), and in how many ways (e.g., 15 = 7 + 8 = 4 + 5 + 6), and to explain any patterns and rules that they infer from their investigations. Questions about what are reasonable answers arise in several ways. As a first example, what is reasonable to expect when students write about the numbers that cannot be expressed as consecutive sums? Some students merely list the numbers: 1, 2, 4, 8, 16, 32, . . . , in some cases adding the observation that "each one is twice the previous number." Other students will identify the set of "powers of 2." Very few students attempt to prove why powers of 2 cannot be expressed as consecutive sums of natural numbers. Again, teachers grapple with the following question: What is reasonable (and at what age level)?
As a second example, when students offer generalized rules, e.g., regarding the different ways a number can be expressed as a consecutive sum, what level of explanation is reasonable? Often, students offer generalizations—sometimes drawing from apparently thoughtful work—with little explanation or convincing argument. (See, e.g., Figure 5.)

Figure 5.
Work on Consecutive Sums
It is possible, as we have seen in several projects, to have productive conversations in mixed groups of middle-grades and high-school teachers regarding expectations at different levels for generalization and convincing argument in student work.
Of critical importance is the readiness for unexpected answers on the part of teachers (and others who look at student work). For instance, it is easy to expect that in the following problem, "rule"
will elicit from students who have had algebra a response that uses equations and/or standard representations of functional relations.
|
Crossing the River. Eight adults and two children need to cross a river. A small boat is available that can hold one adult, or one or two children. Everyone can row the boat. How many one-way trips does it take for them all to cross the river? Can you describe how to work it out for 2 children and any number of adults? How does your rule work out for 100 adults? |
Even among students who have studied algebra, however, their responses sometimes contain no formal algebra. (Figure 6, for example, shows the entire response of a student.) In various groups of teachers, we have found it advantageous to build a discussion around a question: Though it doesn't look like the "algebraic" response you may have used in doing the task, in what ways is this response still reflective of algebraic thinking?
The learning challenges related to judging the quality of student responses suggest the critical importance of two points of emphasis in discussion: purpose and criteria. Teacher inferences about quality must be rooted in discussion about purpose in looking at the student work—especially, the distinction between the purpose of understanding student thinking and the purpose of evaluating student achievement. When teachers examine a piece
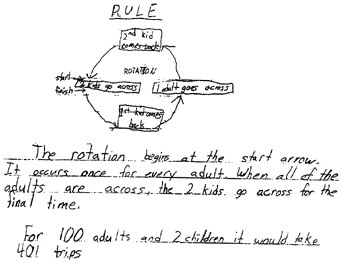
Figure 6.
Work on Crossing the River
of student work, there is often an inclination to score it—to decide if the student "got it." But sometimes student work shows signs that, while the student may have performed at a low level on a task, he or she is thinking in ways that have great potential.
Teachers working together need the opportunity, for a particular mathematics task, to agree on criteria for what are "reasonable" answers, based on a knowledge of the embedded mathematics and of the developmental levels and experiences of the students, and based on expectations for students' mathematical learning that have been established in the broader contexts in which they teach—in particular, through state and local standards and frameworks (Webb, 1997). In professional-development settings, teachers can hone their skills in making inferences about student thinking, strategize on how to talk with students about standards and their progress toward standards, and discuss how to design instruction to move students' understanding forward. In so doing, they can increase the likelihood that assessment will be used to improve teaching and learning and lessen the chances of individual

Figure 7.
More work on Consecutive Sums
teachers wanting to water down assessments because they have concluded their students "can't do this kind of task."
Consider the example in Figure 7, again on Consecutive Sums, in which the student falls well below standards for "describing the shortcuts" and "telling how," but it is easy to infer that there is a well-reasoned procedure underlying the disconnected computations—one that seems based on and works backward from the recognition that three consecutive numbers beginning with n have the sum 3n + 3; four consecutive numbers have the sum 4n + 6; five have the sum 5n + 10; etc.
Not only should teachers agree on criteria, they also should work to calibrate how consistently the criteria are applied across the group. This goal, often referred to as "inter-rater reliability" when the assessment's purpose is evaluation of student achievement, can be accomplished by structuring teacher discussions so that there are frequent opportunities to share, compare, and revise judgments rendered.
Judgment about consequent actions
As mentioned earlier, assessments can be carried out for different purposes. They can aim to inform instruction, or to monitor students' progress toward standards, etc. For each particular purpose, teacher assessment groups can adopt and apply guidelines for what consequent actions should follow their interpretations of student work.
Challenge 7. Determining appropriate actions in light of conclusions from student evidence.
In particular, the enhanced role of teachers in assessment underscores the importance of interpreting student work to craft appropriate classroom responses. Teacher groups can and should learn to analyze a range of student work on a task and to determine points where students need further instruction. Such a process is modeled in the teacher materials from Exemplars (1995), as in the example show in Figure 8. The primary-level task is as follows:
|
Six-Pack of Soda Problem. I often buy cans of soda in a six-pack. If I buy two six-packs of soda each week, how many cans will I buy in a month to recycle? How many six-packs will that be? |
Student responses are provided, with commentary from the teacher who submitted the task and student work, which offers
interpretations of the student work and so models for teachers how they might analyze similar pieces.
Teacher discussions around this analysis can lead to strategies particular to this student, but also, more generally, they can lead to strategies on how to build student capacities for using procedures and for diagrammatic representation.
Teacher groups that stay together for an extended period will notice in student work some key areas where feedback can affect
|
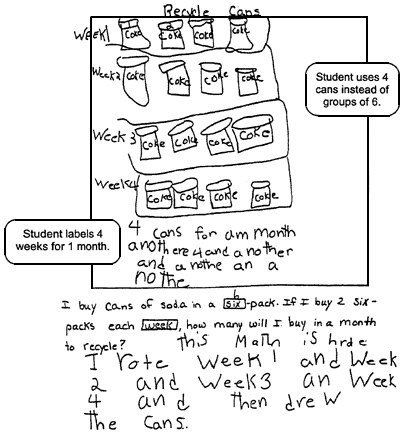 |
|
Commentary. This student started to use a helpful mathematical procedure but didn't carry it through. Even though this student has an understanding of the concept of 6, and verbally stated this while using the models provided, she did not represent this in the diagram and was unable to get close to a solution. |
Figure 8.
Student response to the Six-Pack of Soda problem
Reprinted with permission from Exemplars, 1995, p. 9.

Figure 9.
Stewart's response
Reprinted with permission from Assessment Standards for School Mathematics, NCTM, 1995, p. 35 and from Ruth Cossey, Mills College.
students' progress toward standards. For example, many students have difficulty with the notion of mathematical generalization. The excerpt in Figure 9 from NCTM's Assessment Standards illustrates, and cites one possible strategy for consequent action. It presents the work of a seventh-grader named Stewart, who summarizes, with diagram and statement, his work with pattern blocks to investigate the different ways to increase the size of geometric figures, like squares.
The text comments, "Stewart has clearly identified a pattern of squared numbers but has not expressed his conjecture, 'All squared numbers are the sum of odd numbers,' precisely. The teacher wrote the following note to Stewart and placed it on his report:
Stewart, your work indicates that you know special odd numbers that sum to 16, 1+3+5+7, not just any odd numbers (e.g., 11+5). You need to be more convincing that your pattern will always work. (NCTM, 1995, p. 35)
Most of the mathematics activities in this document, like most of the activities used in our professional-development projects, ask students to construct their responses to mathematical questions. On occasion, however, teachers can benefit from considering the selection, use, and interpretation of more traditional assessments—in particular, multiple-choice items. Discussions about such items can motivate teachers' use of diagnostic questions to uncover patterns of student thinking. For example, the Third National Assessment of Educational Progress presented the following multiple choice item (NAEP, 1983):
|
An army bus holds 36 soldiers. If 1,128 soldiers are being bused to their training site, how many buses are needed? |
Only 24% of a national sample of 13 year-olds chose the correct answer. A common incorrect choice was a non-whole-number answer, such as one of the representations of 31 1/3, the result of dividing 1,128 by 36. This raises several questions, including: How do students make sense of division-with-remainder story problems? Does the choice of an answer that is not a whole number imply the student is working only in a mathematical domain and not considering the story context? Does choosing the wrong answer mean a student isn't trying to make sense, or is making sense in some alternative way?
It would be shortsighted to conclude that the answers to these questions are the same for all students. One study investigated students' sense making in doing a task similar to the one above. Student interviews "revealed that some students, who would have answered incorrectly if the tasks were presented in a multiple-choice format, were able to offer interesting interpretations of their numerical answers. For example, one student spoke of 'squishing in' the extra students, and others suggested ordering minivans rather than a full bus for the extra students" (Silver et al., 1993, p.120).
There is a critical point here for teachers' professional development. Whether the lens on student understanding is an alternative or traditional assessment, student sense making cannot be presumed. As the responses to the bus item indicate, there are cases where the challenge to teachers is to craft appropriate diagnostic actions to determine how students are thinking.
To a great extent, the learning challenges described in this section define the ground of professional development for teachers as they learn to become more effective users of assessment. We have argued that the professional craft of assessment requires more than acquiring information and how-to knowledge; it re-
quires, as well, the honing and exercise of judgment related to the assessment process: from planning to gathering evidence to interpreting evidence to using evidence for decisions about teaching and learning.
|
"But the positive side of that is, they learn more about kids' understanding, more about what they're thinking and not thinking. That's when it becomes assessment that's not separate from instruction, an embedded assessment. Very few people do this or do it well, if assessment is really part of the instruction, then we don't take it separately and the time spent on it is not a separate issue." Mathematics supervisor of large urban district |
The benefits from these efforts can be considerable. For one, teachers find that assessment and instruction can blend together as mutually supportive endeavors. Second, in embracing the various challenges to judgment around the topic of assessment, teacher groups not only build assessment skills; they can integrate the assessment process into other areas of their professional development, as well. In particular, they can improve the habits and norms of professional discourse, make explicit and sharp the mechanisms for drawing inferences about student learning, and build continuous-learning models within staff-development systems. The next section looks at features of planning, organization, and facilitation that make these outcomes possible.


















