This paper was presented at a colloquium entitled “Neuroimaging of Human Brain Function,” organized by Michael Posner and Marcus E.Raichle, held May 29–31, 1997, sponsored by the National Academy of Sciences at the Arnold and Mabel Beckman Center in Irvine, CA.
Functional and structural mapping of human cerebral cortex: Solutions are in the surfaces
DAVID C.VAN ESSEN*†, HEATHER A.DRURY*, SARANG JOSHI‡, AND MICHAEL I.MILLER‡
Departments of *Anatomy and Neurobiology and ‡Electrical Engineering, Washington University, 660 South Euclid Avenue, St. Louis, MO 63110
ABSTRACT The human cerebral cortex is notorious for the depth and irregularity of its convolutions and for its variability from one individual to the next. These complexities of cortical geography have been a chronic impediment to studies of functional specialization in the cortex. In this report, we discuss ways to compensate for the convolutions by using a combination of strategies whose common denominator involves explicit reconstructions of the cortical surface. Surface-based visualization involves reconstructing cortical surfaces and displaying them, along with associated experimental data, in various complementary formats (including three-dimensional native configurations, two-dimensional slices, extensively smoothed surfaces, ellipsoidal representations, and cortical flat maps). Generating these representations for the cortex of the Visible Man leads to a surface-based atlas that has important advantages over conventional stereotaxic atlases as a substrate for displaying and analyzing large amounts of experimental data. We illustrate this by showing the relationship between functionally specialized regions and topographically organized areas in human visual cortex. Surface-based warping allows data to be mapped from individual hemispheres to a surface-based atlas while respecting surface topology, improving registration of identifiable landmarks, and minimizing unwanted distortions. Surface-based warping also can aid in comparisons between species, which we illustrate by warping a macaque flat map to match the shape of a human flat map. Collectively, these approaches will allow more refined analyses of commonalities as well as individual differences in the functional organization of primate cerebral cortex.
The mammalian cerebral cortex contains numerous anatomically and functionally distinct areas arrayed in a complex mosaic across the cortical sheet. Efforts by cortical cartographers to determine the number, arrangement, and internal organization of these areas represent a major thrust in systems neuroscience over the entire 20th century. Nonetheless, a precise and definitive charting of the entire neocortex has yet to be attained for any species. In the human neocortex, classical neuroanatomists identified ≈50 architectonic subdivisions (1). However, the actual number may be 100 or more areas, given the plethora of cortical areas recently discovered in nonhuman primates (2–6) coupled with the disproportionate expansion in cortical surface area in humans compared with nonhuman primates.
The prospects for accurately mapping the arrangement of functionally specialized areas in the human cerebral cortex have been enhanced greatly by recent advances in noninvasive neuroimaging techniques. Positron emission tomography allows localization of activation foci with an accuracy on the order of 1 cm, and functional MRI has even better spatial resolution, comparable to the 3-mm thickness of the cortical sheet. By combining functional MRI with structural MRI, it is possible to map activation patterns precisely in relation to the specific pattern of cortical folds in the same individual.
The ability to chart function at near-millimeter resolution on a cortical sheet whose surface area is ≈80,000 mm2/ hemisphere poses major technical problems in the arenas of data analysis and visualization. The basic challenge is how best to visualize large amounts of complex experimental data with minimal loss of important information about spatial and topological relationships. The problem is compounded by individual variability in cortical structure and function. This variability includes pronounced differences in the pattern of folding, in the size and shape of cortical areas, and in their location relative to these folds. Together, these factors introduce a degree of spatial uncertainty well in excess of the resolution available with current neuroimaging techniques.
To help meet this challenge, new visualization and analysis methods have been developed that emphasize surface representations and surface-based coordinates. Here, we discuss three sets of recently developed tools that collectively offer major advantages over conventional methods that emphasize volume representations and stereotaxic coordinates. The first is surface-based visualization, which includes methods for reconstructing surfaces and changing the shape of the surface to facilitate the analysis of important geometrical and topological relationships. The second involves surface-based atlases, in which reconstructions of particular hemispheres are used as standard substrates for analyzing data obtained from many individuals. The third involves surface-based warping, which uses surface representations to constrain the deformation from a source to a target hemisphere, thereby preserving critical topological relationships when mapping data from individual subjects onto an atlas.
Surface-Based Visualization of Cerebral Cortex
In the most common type of surface reconstruction, the cortex is represented by a wire-frame meshwork running within the cortical sheet (or along its inner or outer margins). Fig. 1A shows a reconstruction of a surface running midway through the cortical thickness of the right hemisphere of the Visible Man (7). The surface was generated from a digitized series of images through an entire brain (8) and has been rendered to show the frontal lobe in beige, the parietal lobe in green, the temporal lobe in blue, and the occipital lobe in pink. This native three-dimensional (3-D) display format, although pro-
© 1998 by The National Academy of Sciences 0027–8424/98/95788–8$2.00/0
PNAS is available online at http://www.pnas.org.
|
|
Abbreviations: 3-D, three-dimensional; STS, superior temporal sulcus. |
|
† |
To whom reprint requests should be addressed. e-mail: vanessen@v1.wust1.edu. |
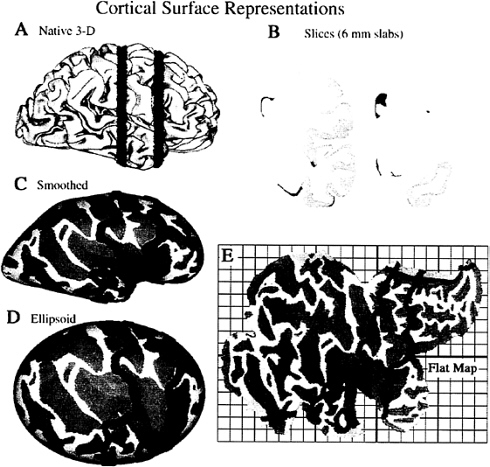
FIG. 1. Surface-based representations of the Visible Man cerebral cortex. (A) Native 3-D view of the right hemisphere, with lobes differently shaded. (B) Two coronal slices (6 mm thick), whose location in the other panels is shown in blue. (C) An extensively smoothed surface. (D) The same surface mapped onto an ellipsoid. (E) A cortical flat map, with selected cuts to reduce distortions. The gridwork surrounding the map defines a surface-based coordinate system, with a grid spacing of 1 map-cm, equivalent to 1 cm along the cortical surface in regions that are not distorted.
viding a familiar view, has several inherent drawbacks. First, sulcal regions are largely occluded from view. Second, dimensions along the image are distorted by foreshortening wherever the surface is oblique to the viewing angle. Third, the stereotaxic coordinate system in which the cortex is embedded does not respect the topology of the cortical surface; points that are close together in 3-D space may be widely separated along the cortical surface.
Surfaces can be modified in several ways to address these problems. The major options include smoothing the surface, cutting it at suitable locations, and mapping it to a geometrically well defined shape. Various combinations of these steps lead to four alternative display formats shown in Fig. 1: slices cut through the hemisphere (shown at two coronal levels in Fig. 1B); an extensively smoothed surface, which makes buried regions visible (Fig. 1C); a geometrically well defined ellipsoidal representation (Fig. 1D); and a cortical flat map (Fig. 1E). Darker shading represents cortex that is buried within sulci in the native 3-D configuration, thereby preserving an explicit representation of cortical geography. For each display format, Table 1 summarizes the tradeoffs between the improvements related to one set of characteristics (visibility, compactness, foreshortening, and parameterization) vs. drawbacks that are introduced, including distortions of surface geometry, topological changes (cuts) in the surface, and shape changes that obscure relationships to the native 3-D configuration.
Slicing a surface into sections, such as the coronal slabs shown in Fig. 1B, reveals buried regions without changing the shape of the surface contours. This format has the advantage of familiarity, insofar as the contours have shapes similar to that shown in standard stereotaxic atlases. Moreover, with computerized reconstructions, it is feasible to slice a given surface in different sectioning planes (e.g., coronal or horizontal). On the other hand, slicing the surface makes it difficult to discern important topological relationships within and between sections. This problem is exacerbated when sections
Table 1. Surface-based display formats for cerebral cortex
are displayed only at sparse intervals, as is generally necessary because slices are not a compact display format.
Buried cortex is brought into full view in three formats that preserve surface continuity: extensively smoothed surfaces, ellipsoidal maps, and flat maps. Extensively smoothed surfaces (9) and ellipsoidal maps preserve all topological relationships across the cortical surface, but they necessarily involve foreshortening around the perimeter, and they require multiple views to see the entire hemisphere. Flat maps are the most compact representation because the entire hemisphere can be seen in a single view, and they have no foreshortening because the surface is planar. However, flat maps do entail the introduction of selected cuts to prevent severe distortions in surface area. Indeed, all of the formats involving shape changes have modest distortions in surface area and in linear dimensions, which are inevitable because the cortex is not simply folded like a sheet of newspaper. Instead, it contains numerous hot spots of high intrinsic curvature (bumps and dents) analogous to the indentations on a golf ball (7). In general, such distortions are not a major drawback because accurate measurements of surface area can be made on the native 3-D surface even when the region of interest has been selected on a different format. Likewise, measurements of distance are best made by calculating geodesics along the native 3-D surface (10).
Mapping the cortex to a geometrically well defined surface (ellipsoidal or planar) allows locations on the surface to be represented by a two-dimensional coordinate system that respects the topology of the cortical surface. Just as latitude and longitude are more useful than volumetric (x, y, z) coordinates for describing locations on the earth’s surface, surface-based coordinates have inherent advantages when describing locations in the cerebral cortex. Either polar or Cartesian coordinates can be used, but polar coordinates are a more natural parameterization for an ellipsoidal surface, and Cartesian coordinates are more natural for flat maps.
Shape changes and cuts tend to obscure the relationship between locations on a deformed surface and the corresponding locations in the native 3-D configuration. The extensively smoothed surface, which has no cuts and is shaped like a lissencephalic primate brain, is the least problematic in this regard. Other formats require more effort to recognize relationships with the native 3-D configuration, but the process is aided by software options for rapidly switching from one format to another while highlighting a particular point or domain of interest. This is illustrated in Fig. 1 by showing the trajectories of the same two coronal slices (blue contours) on each of the display formats.
A Surface-Based Atlas
When comparing experimental data obtained from different subjects, a standard approach is to display results on a common anatomical substrate: an atlas. Some cerebral atlases in current use are based on histological sections or MRI scans through a particular brain that is placed in a standard stereotaxic space, such as the Talairach stereotaxic space (11–13). Other atlases are based on MRI images averaged across many individual brains after initial transformation into stereotaxic space (14, 15). This allows probabilistic descriptions regarding the location of different structures, but it is associated with considerable blurring of gyral and sulcal features because of residual variability in the position of any given sulcus.
Given the advantages of surface representations, it is important to have a cerebral atlas that includes an explicit surface reconstruction. To address this need, we have used reconstructions of the left and right hemispheres of the Visible Man to establish a surface-based human cortical atlas (7, 16). The Visible Man is a reasonable choice for such an atlas because its overall dimensions are similar to those of the Talairach atlas and because the pattern of convolutions for both hemispheres lies within the normal range of a population of normal brains (7, 17). The atlas includes a complete map of major gyri and sulci in each hemisphere and is linked to multiple coordinate systems, including the Talairach stereotaxic space and Cartesian surface-based coordinate systems (cf. Fig. 1).
Many types of experimental data can be visualized conveniently on the Visible Man atlas. Fig. 2 illustrates this by using published results on the functional organization of human visual cortex. The layout of topographically organized visual areas, including primary visual cortex (area V1) and surrounding extrastriate areas V2, V3, VP, V3A, and V4v, is shown on a flat map of the occipito-temporal cortex (Fig. 2A) and on a medial view of the occipital lobe (Fig. 2B). The most likely extent of area V1 in the Visible Man was estimated from a postmortem analysis of the architectonic borders of V1 (7, 18). The boundaries of the extrastriate areas were estimated from their average widths determined in functional MRI studies and displayed on cortical flat maps (19, 20). Although not indicated in Fig. 2, there are significant uncertainties (about ±1 cm) associated with the boundaries of each of these topographically organized areas, mainly because of individual variability in their size and location relative to geographic landmarks.
Complementing these maps of topographically organized areas are studies of regions activated by different aspects of visual processing. Fig. 2C and D show regions implicated in color processing, and Fig. 2E–G summarize the specializations relating to color, motion, form, and spatial relationships. These results are based on positron emission tomography and functional MRI studies that did not include explicit surface reconstructions of the individual subjects from whom the data were acquired. Instead, the data were transformed into Talairach space by using conventional low dimensional warping algorithms (involving only affine transformations), followed by averaging across multiple subjects and reporting the Talairach stereotaxic coordinates for the center of each activation focus. By using these coordinates, each activation focus can be mapped to the nearest point on the Visible Man surface (which
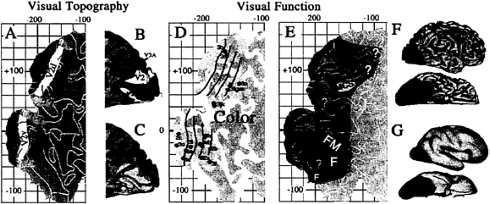
FIG. 2. Functional specialization in human visual cortex. (A) Topographically organized visual areas shown on a flat map of occipito-temporal cortex in the Visible Man. (B) The same areas on a medial view of the occipital lobe. (C) The same regions on a lateral view of the hemisphere. (D) Cortical regions implicated in processing of color. Green dots denote centers of activation foci, and lighter green denotes cortex with the 10-mm uncertainty limit. (E) Cortical regions implicated in the processing of motion (M); form (F); form and color (FC); form and motion (FM); and motion, color, and spatial relations (MCS). Question marks denote additional regions potentially involved in processing of color (green), motion (red), and spatial relations (yellow). (F) The same functional specializations shown on lateral and ventral 3-D views. (G) The same pattern on extensively smoothed surfaces. [Adapted, with permission, from ref. 7 (Copyright 1997, J. Neurosci.)].
itself has been transformed to Talairach space). For example, the distribution of activation foci implicated in color processing are plotted on a cortical flat map (Fig. 2C) and on a medial view of the hemisphere (Fig. 2D). Each green dot on the flat map shows the nearest point on the Visible Man surface to an activation focus reported by Lueck et al. (ref 21; foci 1a–c), Zeki et al. (ref 22; foci 2a–c), or Corbetta et al. (ref 23; foci 3a-n). However, it is deceptive to view only the nearest point on the Visible Man surface because of individual variability that is not compensated by transforming each hemisphere into stereotaxic space.
When a given paradigm is repeated in many subjects, the centers of activation foci are scattered over a considerable range of stereotaxic space, but they mainly lie within 10 mm of the group mean (7, 24, 25). This scatter is mainly attributable to biological variability in the stereotaxic location of activation foci although resolution limits of the neuroimaging techniques presumably contribute to some degree. The light green shading in Fig. 2C and D represents this spatial uncertainty by showing portions of the Visible Man surface that lie within 10 mm of one or another of the reported color activation foci. This represents geographic regions within which these foci probably would have been centered had the experiments been done on the Visible Man.
We extended this type of analysis to 118 activation foci from 12 studies reporting activation foci associated with processing of color, form, motion, and spatial relationships (7). In an intermediate stage of analysis (not illustrated here), all individual foci were superimposed on a single flat map. Fig. 2E and F show summary representations generated from this superposition map, indicating which cortical regions are dominated by a single aspect of visual function and which involve overlap or close interdigitation of multiple functions. For example, the region of the lateral occipito-temporal cortex shaded red is associated largely or exclusively with motion processing (M) whereas the regions of the ventral occipitotemporal cortex shaded blue are associated largely or exclusively with form processing (F). Other regions involve overlap or close interdigitation of foci implicated in more than one function, including form and color analysis (FC, shaded blue-green) in or near areas VP and V4v; form and motion analysis (FM, shaded purple) in a ventro-lateral portion of the occipito-temporal cortex; and motion, color, and spatial analysis (MCS, shaded orange) in or near area V3A in the dorsal extrastriate cortex. Although omitted in Fig. 2, this analysis also revealed numerous activation foci in areas V1 and V2, reflecting the involvement of both areas in multiple aspects of visual processing.
This example demonstrates the utility of a surface-based atlas as a substrate for objective analysis and compact visualization of large amounts of neuroimaging data. However, it also illustrates the limitations associated with the stereotaxic projection method and highlights the need for new methods to reduce spatial uncertainties when mapping data onto the atlas.
Surface-Based Warping
Here, we introduce an approach that uses explicit surface representations to bring one hemisphere into better register with another. It is designed to achieve three general objectives, each motivated by key facts or plausible assumptions regarding cortical structure and function.
1. Surface Topology. A necessary (but by no means sufficient) condition for attaining optimal registration is to preserve surface topology in the mapping from one hemisphere (the source) to another (the target). This requires that neighboring points in the cortex of the source hemisphere always map to neighboring points in the cortex of the target hemisphere (and not, for example, to opposite banks of a sulcus or to locations lying outside the cortical gray matter). This constraint arises because the surface of the cortex (or of any layer within the cortex) is topologically equivalent to a simple disk and because the topological arrangement of cortical areas (areal topology) across the cortical surface is thought to be identical, or at least very similar, from one individual to the next.
2. Point-to-Neighborhood Correspondences. The deformation process aims to improve registration between locations that correspond in function, i.e., that represent the same cortical area and an equivalent location within that area in the source and target hemispheres. However, there are inherent biological limits as well as practical limits in identifying func-
tionally corresponding locations in different hemispheres. The biological limits arise because of individual variability in the size, shape, position, and internal organization of each cortical area. Individual cortical areas can vary in size by at least a factor of two (26, 27), and many areas are characterized by internal compartments, or modules, whose total number and dimensions vary across individuals (28, 29). Accordingly, it is unrealistic to expect functional correspondences to be identified more precisely than within a few millimeters for human cortex. Often, the uncertainty is in the centimeter range because of resolution limits and sparseness in the available functional and structural data. It therefore makes sense to express functional correspondences in terms of “point-to-neighborhood” relationships, in which a given point in one hemisphere is associated not only with the most likely corresponding point in another hemisphere but also with a neighborhood whose extent reflects the degree of spatial uncertainty in this mapping. The deformation algorithm should force registration of corresponding landmarks only to a degree commensurate with this neighborhood size along the cortical surface.
Geographical landmarks provide valuable, albeit indirect, indicators of functional correspondences because the location of many cortical areas is correlated with the pattern of cortical folds. The tightness of this correlation differs from one region to another and tends to be stronger, for example, in the vicinity of primary sensory and motor areas than in most other regions (12, 18, 24). Also, the correlation is generally weaker in the highly convoluted human cortex than in less convoluted species such as the macaque monkey. Both the consistency and the variability of this relationship have a natural explanation in terms of a tension-based mechanism that may drive cortical folding during development (30).
3. Minimize Local Distortions. The functional and geographical landmarks available to guide the registration of any particular pair of hemispheres typically are distributed nonuniformly and often sparsely across the cortical surface. To achieve satisfactory registration of these landmarks, significant compression, expansion, or shearing of cortex in the intervening regions may be necessary. However, it is desirable that such deformations be as smooth and regular as possible because it makes sense to assume similarity in the relative sizes and positions of cortical areas except where there is direct evidence to the contrary.
Surface-based warping offers an attractive general strategy for meeting all three of these objectives. Our approach involves a landmark-based deformation algorithm, in which the surface is modeled as a viscoelastic fluid sheet (31, 32). This approach is analogous to a 3-D viscoelastic model that has been used for high dimensional volume deformations (32–35), but it is computationally much less demanding because of its lower dimensionality. The warping is driven by selected landmarks that are identifiable on both source and target maps and in this respect is analogous to the landmark-based approach of Bookstein (36). As landmarks, we use contours that are drawn explicitly along corresponding locations on the source and target maps, based on geographical and/or functional criteria. The warping algorithm deforms the source map so as to bring the landmarks more closely into register, but its viscoelastic characteristics tend to smooth out local distortions on the map, thereby allowing tradeoffs between these competing objectives.
Some of the issues that arise in judiciously selecting landmarks and in interpreting the results are illustrated in Fig. 3. The top panels (Fig. 3A and B) show cortical flat maps of the left and right hemispheres of the Visible Man, with the left hemisphere map mirror-flipped to facilitate comparison of their shapes. Our objective in this example was to warp the left hemisphere map to match the right hemisphere map by using only geographic landmarks to constrain the deformation.
To insure a complete point-to-point mapping between hemispheres, the warping algorithm requires landmarks along the perimeter of each map, including not only the natural terminations of cortex but also the artificial cuts that were made in geographically corresponding locations in the two hemispheres. As internal geographical landmarks, we used the central sulcus and calcarine sulcus, which are very similar in shape and location on the two maps, and also the cingulate sulcus, whose local irregularities differ in the two hemispheres and was therefore assigned a weighting factor that tolerates less precise registration achieved by the deformation. The deformation grid in Fig. 3C shows the shape changes needed to make the left hemisphere map conform to the shape of the right hemisphere map. Because the warping algorithm insures a diffeomorphic mapping, there are no topological irregularities (tangles) in this deformation field. This satisfies the objective of preserving surface topology, except for the discontinuities tolerated along the cuts. Relative to the original grid size (see Fig. 3 Inset), the deformations involve only modest compression or expansion and relatively little shear except in a few locations.
In Fig. 3D, the right hemisphere and deformed left hemisphere maps are directly superimposed and are color-coded to reveal the degree of geographical registration achieved by deformation. Brown denotes cortex that is buried (Bur.) in both the right and deformed left hemisphere maps; yellow denotes exposed (externally visible) cortex (Exp.) in both maps; and orange and light green denote regions in which exposed cortex on one map overlies buried cortex in the other and thus are not in geographic register. If buried cortex were completely in register between the source and target, the overlay would include only brown and yellow shading. However, this is not possible to achieve because the two hemispheres differ considerably in the topological pattern of buried vs. exposed cortex, i.e. their geographic topology.
As expected, the warping did achieve nearly complete overlap of buried cortex for the central sulcus and calcarine sulcus, whose perimeters were forced to be in tight register, and less overlap along the margins of the cingulate sulcus, where greater misalignment was tolerated. In regions distant from these landmarks, several patterns are evident. The easiest to interpret are regions such as the collateral sulcus, where there is good registration between sulci that are in obvious geographic correspondence. In contrast, in the vicinity of the posterior inferior temporal sulcus, a region known for the variability of its folds (17, 24), the geographic correspondence is much weaker (mainly green and orange instead of brown and yellow in the overlay). Nonetheless, the deformation grid is notably regular in this region, which is desirable if the arrangement of cortical areas is similar on the left and right hemisphere maps despite the marked differences in folding.
Surface-based warping also can reveal unexpected geographic relationships that may be functionally significant. This is exemplified by the region in and around the superior temporal sulcus (STS). The single asterisk in Fig. 3D indicates where the deformed left STS is aligned with the posterior Sylvian fissurein the right hemisphere; the double asterisk indicates where the right STS is aligned with the deformed left anterior occipital sulcus, a sulcus that is altogether absent in the Visible Man right hemisphere. If the left and right STS are occupied by functionally corresponding areas not only in general but in the particular brain of the Visible Man, the geographical misregistration in Fig. 3D would signify an inadequacy of the landmarks used to constrain this particular deformation. However, an alternative interpretation is that there are major left-right differences in the arrangement of cortical areas relative to geographic landmarks in the temporal lobe of the Visible Man, related either to a consistent hemispheric asymmetry or to chance differences in how the cortex was folded in these two hemispheres. To distinguish between

FIG. 3. Surface-based warping from the left to the right hemispheres of the Visible Man. (A) Mirror-flipped flat map of the left hemisphere, with selected sulci labeled, and geographic landmarks used to constrain the deformation shown in black. (B) Equivalently labeled flat map of the right hemisphere. (C) Deformation field associated with a warping of the left hemisphere map to match the right hemisphere map. (D) Overlay of right and deformed left hemisphere maps, color-coded as shown in Inset to indicate buried (Bur.) cortex or exposed (Exp.) cortex in each hemisphere.
such possibilities would require neuroimaging or other functional data that obviously can no longer be obtained for the Visible Man, but this limitation will not apply to future studies that involve cortical reconstructions made from in vivo structural MRI scans.
More generally, surface-based warping should become an important tool in analyzing consistency as well as variability of cortical function and its relation to cortical geography. As progressively more areas and regions of functional specialization become routinely identifiable, they can be added to the repertoire of landmarks that help to constrain surface-based deformations while exploring the functional organization of less well charted regions. Because reconstructing and flattening an entire hemisphere is a major endeavor with current technology, it is worth noting that surface-based warping can be profitably applied at a regional level by warping a map, say, of just the parietal lobe to match the corresponding region of an atlas.
Interspecies Comparisons
Surface-based representations have obvious utility when comparing functional organization across species (19). Fig. 4 illustrates one such example, by using maps of functional organization in the macaque monkey (Fig. 4A) and the Visible Man (Fig. 4B). The macaque map shows the layout of 79 cortical areas identified in the summary partitioning scheme of Felleman and Van Essen (2). Selected visual areas (V1, V2, and V4) are assigned individual colors, as are the inferotemporal complex (IT) and a complex of motion-related areas (M), which includes areas MT, MSTd, and MSTl. These plus the other areas implicated in vision (light blue) together occupy slightly more than half of the macaque neocortex whereas only 20–25% of the human neocortex is known to be visual in function (dark gray in Fig. 4B). This 2-fold difference in relative extent of visual cortex impedes the evaluation of possible homologies, and the problem is exacerbated by the limited utility of geographical landmarks for interspecies comparisons. Although some areas have roughly the same location (e.g., much of V1 lies in the calcarine sulcus), other candidate homologies differ considerably in location (e.g., the motion-related complex, which lies within the STS in the macaque but well posterior to it in humans).
Surface-based warping is well suited for interspecies comparisons because it can preserve surface topology while tolerating highly nonuniform expansion or compression and also allowing functionally irrelevant differences in folding patterns to be ignored. For example, Fig. 4C and D shows a warping
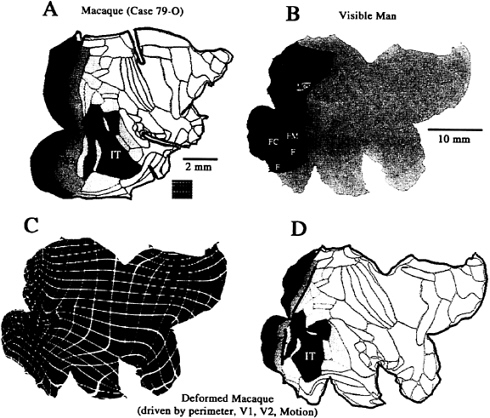
FIG. 4. Surface-based warping from macaque to human cortex. (A) Flat map of cortical areas in the macaque, with visual areas indicated in various colors. (B) Flat map of the Visible Man, with areas and functional specializations for vision indicated. (C) Deformation grid that warps the macaque map to the shape of the human, constrained by the perimeter and selected functional regions. (D) Deformed macaque cortical areas, for comparison with the functional specializations of human visual cortex in B.
from macaque to human cortex, in which the deformation was driven by a combination of geographic landmarks along the perimeter plus several functionally based landmarks (areas V1, V2, and the motion-related complex). Because the normal cuts along the perimeter of the macaque map are fewer and shallower than those in the Visible Man, we added “virtual cuts” extending into the interior of the macaque map to attain better geographical correspondence.
The deformed macaque map is shown with the associated deformation grid in Fig. 4C and with cortical areas in Fig. 4D. As expected from the 10-fold overall disparity in surface area, all regions of the deformed macaque become expanded (note initial grid spacing in Fig. 4A Inset), but the expansion is relatively modest (≈2-fold) for areas V1 and V2, intermediate (≈5-fold) for visual cortex as a whole, and much larger in the temporal and frontal lobes (more than 30-fold in some regions). Consequently, the deformation squeezes macaque V1 and V2 each into only a few percent of total cortex, compared with the ≈10% apiece they occupy in the native configuration. The motion complex is relatively more posterior in human cortex (to the left on the map) compared with its position in the macaque. The deformation brings the macaque inferotemporal complex into register with the larger of the human regions specialized for form analysis (including faces and inanimate forms), thus strengthening the argument for homology between these regions. Likewise, the ventral half of deformed macaque V4 is in register with human ventral V4, consistent with the homology presumed by this terminology. In contrast, dorsal V4 in the deformed macaque map lies over a region of human cortex whose function and topographic organization remains to be elucidated. In this and other regions, it is possible that human cortex contains areas that are altogether absent in the macaque (and in their common ancestor), perhaps reflecting a process analogous to gene duplication at the molecular level (37). Specific hypotheses along such lines can be explored by using surface-based warping after introducing appropriate internal cuts (slits) that allow nonexistent cortex in one species to expand into one or more areas in another species.
Implementation Issues
The various software packages needed for carrying out the various approaches illustrated here are in different stages of
maturity and availability. Surface reconstruction and visualization software (CARET) is now available for Silicon Graphics workstations (http://v1.wustl.edu/caret.html). Digital copies of the Visible Man atlas are available for viewing and analyzing any data of interest, and the atlas is also accessible via an interactive web site (http://v1.wustl.edu/CARETdaemon).
A major impediment to surface-based analyses has been the difficulty in automatically generating accurate surface reconstructions, particularly from high resolution volume representations available using structural MRI. Software for key aspects of this process recently has become available (http://white.stanford.edu/html/teo/mri/mri.html), and additional software is under development in several laboratories. There also has been progress in making robust flattening algorithms available (http://white.stanford.edu/~brian/mri/mrUnfold.html: http://v1.wustl.edu/software.html).
These methods all can be expected to undergo continued refinement that will include qualitative enhancements as well as improvements in speed and robustness. For example, our current surface-based warping algorithm operates only on cortical flat maps. A future objective is to warp ellipsoidal maps rather than flat maps, which will circumvent the limitations imposed by the artificial cuts present on flat maps. Once the warping is done on ellipsoids, it will still be easy to view the results on flat maps that include standard cuts.
The approaches discussed here represent important components of the emerging field of computational neuroanatomy (38, 39). These and related developments will help usher in a new era of high resolution brain mapping, which in turn will greatly improve our understanding of the organization and function of the cerebral cortex in a variety of species, most notably in humans.
We thank Dr. C.H.Anderson for valuable suggestions. This project was supported by National Institutes of Health Grant EY02091 (D.C.V.E), National Science Foundation Grant BIR9424264 (M.I.M.), and joint funding from the National Institute of Mental Health, National Aeronautics and Space Administration, and National Institute on Drug Abuse under the Human Brain Project MHIDA52158.
1. Brodmann, K. (1909) Vergleichende Lokalisationslehre der Grosshirnrinde (Barth. Leipzig, Germany) pp. 1–324.
2. Felleman, D.J. & Van Essen, D. (1991) Cereb. Cortex 1, 1–47.
3. Preuss, T.M. & Goldman-Rakic, P.S. (1991) J. Comp. Neurol. 310, 429–474.
4. Preuss, T.M. & Goldman-Rakic, P.S. (1991) J. Comp. Neurol. 310, 475–506.
5. Carmichael, S.T. & Price, J.L. (1994) J. Comp. Neurol. 346, 366–402.
6. Lewis, J.L (1997) Ph.D. thesis (California Institute of Technology, Pasadena, CA).
7. Van Essen, D.C. & Drury, H.A. (1997) J. Neurosci. 17, 7079–7102.
8. Spitzer, V., Ackerman, M.J., Scherzinger, A.L. & Whitlock, D.J. (1996) J. Am. Med. Inform. Assoc. 3, 118–130.
9. Dale, A. & Sereno, M. (1993) J. Cognit. Neurosci. 5, 162–176.
10. Schwartz, E.L., Shaw, A. & Wolfson, E. (1989) IEEE Trans. Pattern Anal. Mach. Intell. 11, 1005–1008.
11. Talairach, J. & Tournoux, P. (1988) Coplanar Stereotaxic Atlas of the Human Brain (Thieme Medical, New York).
12. Roland, P.E. & Zilles, K. (1994) Trends Neurosci. 17, 458–467.
13. Toga, A.W., Ambach, K.L., Quinn, B., Hutchin, M. & Burton, J.S. (1994) J. Neurosc. Methods 54, 239–252.
14. Andreasen, N.C., Arndt, S., Swayze II, V., Cizadlo, T., Flaum, M., O’Leary, D., Ehrhardt, J.C. & Yuh, W.T.C. (1994) Science 226, 294–298.
15. Evans, A.C., Kamber, M., Collins, D.L. & MacDonald, D. (1994) in Magnetic Resonance Scanning and Epilepsy, eds. Shorvon, S.D., Fish, D.R., Andermann, F. & Bydder, G.M. (Plenum, New York), pp. 263–274.
16. Drury, H.A. & Van Essen, D.C. (1997) Hum. Brain Mapp. 5, 233–237.
17. Ono, M., Kubick, S. & Abernathey C.D. (1990) Atlas of the Cerebral Sulci (Thieme Medical, New York).
18. Rademacher, J., Caviness, Jr., V.S., Steinmetz, H. & Galaburda, A.M. (1993) Cereb. Cortex 3, 313–329.
19. Sereno, M.I., Dale, A.M., Reppas, J.B., Kwong, K.K., Belliveau, J.W., Brady, T.J., Rosen, B.R. & Tootell, R.B.H. (1995) Science 268, 889–893.
20. DeYoe, E.A., Carman, G., Bandetinni, P., Glickman, S., Wieser, J., Cox, R., Miller, D. & Neitz, J. (1996) Proc. Natl. Acad. Sci. USA 93, 2382–2386.
21. Lueck, C.J., Zeki, S., Friston, K.J., Deiber, M.P., Cope, P., Cunningham, V.J., Lammertsma, A.A., Kennard, C. & Frackowiak, R.S.J. (1989) Nature (London) 340, 386–389.
22. Zeki, S., Watson, J.D.G., Lueck, C.J., Friston, K.J., Kennard, C. & Frackowiak, R.S.J. (1991) J. Neurosci. 11, 641–649.
23. Corbetta, M., Miezin, F., Dobmeyer, S., Shulman, G. & Petersen, S. (1991) J. Neurosci. 11, 2383–2402.
24. Watson, J.D.G., Myers, R., Frackowiak, R.S.J., Hajnal, J.V., Woods, R.P., Mazziotta, J.C., Shipp, S. & Zeki, S. (1993) Cereb. Cortex 3, 37–94.
25. McCarthy, G., Spencer, M., Adrignolo, A., Luby, M., Gore, J. & Allison, T. (1995) Hum. Brain Mapp. 2, 234–243.
26. Filiminof, I.N. (1932) J. Psychol. Neurol. 44, 1–96.
27. Van Essen, D.C., Newsome, W.T. & Maunsell, J.H.R. (1984) Vision Res. 24, 429–448.
28. Horton, J.C. & Hocking, D.R. (1996) J. Neurosci. 16, 7228–7339.
29. Olavarria, J.F. & Van Essen, D.C. (1997) Cereb. Cortex 7, 395–404.
30. Van Essen, D.C. (1997) Nature (London) 385, 313–318.
31. Joshi, S.C. (1997) Ph.D. thesis (Sever Institute, Washington University, St. Louis, MO).
32. Joshi, S.C., Miller, M.I. & Grenander, U. (1997) Int. J. Pattern Recog. Artif. Intell., in press.
33. Christensen, G.E., Rabbit, R.D. & Miller, M.I. (1994) Phys. Med. Biol. 39, 609–618.
34. Joshi, S.C., Miller, M.I., Christensen, G.E., Banerjee, A., Coogan, T.A. & Grenander, U. (1995) in Vision Geometry IV, eds. Melter, R.A., Wu, A.Y., Bookstein, F.L. & Green, W.D. (International Society for Optical Engineering, Bellingham, WA), Vol. 2573, pp. 278–289.
35. Christensen, G.E., Rabbit, R.D. & Miller, M.I. (1996) IEEE Trans. Image. Processing 5, 1435–1447.
36. Bookstein, F.L. (1995) Bull. Math. Biol. 58, 313–365.
37. Allman, J. (1990) in Cerebral Cortex, eds., Jones, E.G., Peters, A. (Plenum, New York), Vol. 8A, pp. 269–283.
38. Grenander, U. & Miller, M.I. (1996) Stat. Comput. Graph. 7, 1.
39. Miller, M.I., Banerjee, A., Christensen, G., Joshi, S., Khaneja, N., Grenander, U. & Matejic, L. (1997) Stat. Methods Med. Res. 6, 267–299.








