This paper was presented at a colloquium entitled “Neuroimaging of Human Brain Function,” organized by Michael Posner and Marcus E.Raichle, held May 29–31, 1997, sponsored by the National Academy of Sciences at the Arnold and Mabel Beckman Center in Irvine, CA.
Spatially independent activity patterns in functional MRI data during the Stroop color-naming task
MARTIN J.MCKEOWN*†, TZYY-PING JUNG*, SCOTT MAKEIG‡§, GREG BROWN¶, SANDRA S.KINDERMANN¶, TE-WON LEE*, AND TERRENCE J.SEJNOWSKI*∥
*Howard Hughes Medical Institute, Computational Neurobiology Laboratory, Salk Institute for Biological Studies, La Jolla, CA 92186–5800; ‡Naval Health Research Center, P.O. Box 85122, San Diego, CA 92186–5122; and Departments of §Neurosciences and ¶Psychiatry, School of Medicine, and ∥Department of Biology, University of California at San Diego, La Jolla, CA 92093
ABSTRACT A method is given for determining the time course and spatial extent of consistently and transiently task-related activations from other physiological and artifactual components that contribute to functional MRI (fMRI) recordings. Independent component analysis (ICA) was used to analyze two fMRI data sets from a subject performing 6-min trials composed of alternating 40-sec Stroop color-naming and control task blocks. Each component consisted of a fixed three-dimensional spatial distribution of brain voxel values (a “map”) and an associated time course of activation. For each trial, the algorithm detected, without a priori knowledge of their spatial or temporal structure, one consistently task-related component activated during each Stroop task block, plus several transiently task-related components activated at the onset of one or two of the Stroop task blocks only. Activation patterns occurring during only part of the fMRI trial are not observed with other techniques, because their time courses cannot easily be known in advance. Other ICA components were related to physiological pulsations, head movements, or machine noise. By using higher-order statistics to specify stricter criteria for spatial independence between component maps, ICA produced improved estimates of the temporal and spatial extent of task-related activation in our data compared with principal component analysis (PCA). ICA appears to be a promising tool for exploratory analysis of fMRI data, particularly when the time courses of activation are not known in advance.
Univariate methods for the analysis of functional MRI (fMRI) data typically examine each brain volume element or voxel individually, to determine whether the activity level at that voxel reaches a prespecified criterion for task-related activity. A common criterion is a predetermined level of significance for a statistic, such as the Student t (1) or Kolmogorov-Smirnov (2) statistic, under the null hypothesis that the distribution of a voxel’s values during the behavioral control task is identical to that during performance of the experimental task(s). Correlational analysis (3) determines whether the similarity between a voxel’s time course and a prediction of the task-related modulation, the reference function, exceeds a specified threshold. These methods then assemble individually selected (or “active”) voxels, ignoring statistical relationships between voxels, to create a spatially distributed map demonstrating areas of significant activation.
To enhance the statistical power of standard analysis techniques based on correlation or univariate statistical tests, fMRI experimenters often use alternating task-block designs in which the subject performs two or more tasks successively in alternating 20- to 40-sec blocks. By averaging over a number of task-block cycles, small consistently task-related (CTR) differences in hemodynamic activation can be detected. Isolated stimulus paradigms, such as that employed by Buckner et al. (4), avoid overlapping hemodynamic responses produced by more rapid stimulus presentation rates, but interpretation of the responses still involves averaging responses over many different stimulus presentations.
Averaging over task blocks or individual stimuli assumes stationarity of brain responses and reduces the sensitivity of fMRI analyses to changes in brain activation occurring during only one or more portions of a trial (5). Such transiently task-related (TTR) activations potentially may arise from shifts in subject performance strategy, from variations in subject arousal, attention, or effort, or from changes in brain activation produced by learning or habituation. It is desirable, therefore, to find techniques for analyzing fMRI data that do not involve averaging over trials or blocks and that are capable of detecting TTR activations.
Determining the spatiotemporal extent of transiently or consistently task-related activations by invariate techniques is also problematic because treating each voxel independently ignores relationships between voxels and, hence, between brain regions. Even when activities of voxels in a spatially distributed group individually meet a certain criterion, it cannot necessarily be inferred that the group forms a single processing area. For example, it is possible that the time courses from two voxels each may be both correlated with the reference function for a task above a given threshold, yet be uncorrelated with each other. Complementary multivariate techniques attempt to circumvent this problem by extracting the spatial and temporal structure of distributed brain systems that sum to the measured fMRI signals.
One such technique, principal component analysis (PCA), is commonly used for data decomposition and dimension reduction (6). PCA measures the covariance between all pairs of voxels and then finds the orthogonal spatial maps, or eigenimages, that capture the greatest variance in the data. The first eigenimage represents the combination of voxels explaining the largest source of variance between pairs of voxels, the second eigenimage represents the largest source of residual variance orthogonal to the first eigenimage, and so on. The measured fMRI signals thus can be parsimoniously summarized by projecting them onto a reduced set of the eigenimages, usually those capturing a prede-
© 1998 by The National Academy of Sciences 0027–8424/98/95803–8$2.00/0
PNAS is available online at http://www.pnas.org.
|
|
Abbreviations: TTR, transiently task-related; CTR, consistently task-related; ICA, independent component analysis; fMRI, functional MRI. |
|
† |
To whom reprint requests should be addressed at: Computational Neurobiology Laboratory, Salk Institute for Biological Studies, 10010 North Torrey Pines Road, La Jolla, CA 92037–1099. e-mail: martin@salk.edu. |
termined amount (e.g., >95%) of the variance in the data. However, because performance-related fMRI changes are only a small part of total signal variance, projecting the data onto orthogonal eigenimages capturing the greatest variance in the data may prove ill-suited for detecting task-related activations. In addition, if these involve activations of numerous voxels simultaneously, analysis methods based solely on voxel-pair relationships may not accurately detect the full spatiotemporal extent of the activations.
A decomposition method suitable for detecting task-related activations should be consistent with fundamental neurophysiological principles regarding the spatial extent of neural activity during the performance of psychomotor tasks. The principle of localization (7) implies that each psychomotor function is performed in a small set of brain areas, different for each function. This is based on a large body of empirical knowledge correlating psychomotor deficits with regions of cerebral damage, for example, the characteristic language deficits seen after damage to Wernicke’s and Broca’s areas.
We assume that an appropriate goal for the decomposition of fMRI data into cognitively and physiologically meaningful components is the determination of separate groups of multifocal anatomical brain areas that are coactivated during the acquisition of the fMRI slices throughout the experimental trial. Artifacts secondary to subtle movements (8), machine noise (9), and cardiac and respiratory pulsations (10), which may make up the bulk of variability in the measured fMRI signals, should have spatial patterns of activity separate from the localization of brain areas involved in task-related activation. Specifically, with such a model, each fMRI scan can be considered the sum of a mean activity level at each time point plus activations (or suppressions) belonging to one or more spatially independent components. Each individual component may be described by a graded spatial distribution or map and an associated time course of activation.
Here we use a recently developed statistical technique, independent component analysis (ICA) (11, 12), to determine the three-dimensional brain topographies and time courses of activations associated with spatially independent components that together sum to the measured fMRI signals recorded during the performance of a Stroop color-naming task. Our results suggest that ICA can be used effectively to isolate the spatiotemporal extent of both consistently and transiently task-related activations from artifacts and other sources of variability that comprise the fMRI signals.
Independent Component Analysis
Separating fMRI data into independent spatial components involves determining three-dimensional brain maps and their associated time courses of activation that together sum to the observed fMRI data. The primary assumption is that the component maps, specified by fixed spatial distributions of values (one for each brain voxel), are spatially independent. This means that, if pk(Ck) specifies the probability distribution of the voxel values Ck in the kth component map, then the joint probability distribution of all N components factorizes:
[1]
This is equivalent to saying that voxel values in any one map do not convey any information about the voxel values in any of the other maps. This is a much stronger criterion than merely assuming that map values of voxel pairs from different components are uncorrelated, i.e.,
![]() for all components i≠j, [2]
for all components i≠j, [2]
where M is the number of voxels and Cij is the jth value in the ith component map. This is because Eq. 1 implies that higher order correlations, or polynomial sums of map voxel values, are also zero. For example, for two maps,
[3]
for all natural numbers p and q.
With these assumptions, fMRI signals recorded from one or more sessions can be separated by the ICA algorithm of Bell and Sejnowski (11, 12) into a number of independent component maps with unique, associated time courses of activation. Assuming that the data are mixtures of spatially independent components, the algorithm determines an unmixing matrix, W, from which the component maps and time courses of activation can be computed (see Appendix). The matrix of component map values, C, can then be computed by multiplying the observed data by W,
[4a]
where X is the (row mean-zero) N by M fMRI signal data matrix (N, the number of time points in the trial, and M, the number of brain voxels) obtained by removing the mean signal level from each time point. In matrix notation, this simplifies to:
C=WX. [4b]
Noise in the data is not explicitly modeled, but instead is included in one or more of the components. The number of components determined by the algorithm is equal to the number of input time points in the data. Note that although a nonlinear function is used in the determination of W (described in the Appendix). W still provides a linear decomposition of the data.
To determine whether a given component map is influenced by its requirement to be spatially independent of other maps, the data may be reconstructed with one or more of the components removed and the resultant data matrix may be separated again by using the ICA algorithm (see Appendix).
Methods
A subject volunteer participated in two 6-min trials of a Stroop color-naming task. Each trial consisted of five 40-sec control blocks alternating with four 40-sec experimental task blocks. A 1.5 T General Electric Signa MRI system was used to monitor brain activity by using blood oxygen level-dependent (BOLD) contrast. Ten 64×64 echo planar, gradient-recalled (TR=2,500 msec, TE=40 msec) axial images (5-mm thick, 1-mm interslice gap) with a 24-cm field of view were collected at 2.5-sec sampling intervals, corresponding to 146 images for each slice.
Stimuli spanning a visual angle of 2° by 3° were presented one at a time by overhead projector onto a screen placed at the base of the magnet. In control blocks, the subject was simply required to covertly name the color of a displayed rectangle (red, blue, or green). During experimental Stroop-task blocks, the subject was required to covertly name the discordant color of the script used to print a color name. For example, if the word “green” was presented in blue script, the subject was to covertly “say” the word “blue” without vocalizing or activating the muscles of articulation.
Voxels corresponding to active brain regions were determined by examining their mean signal values. These were found to have a bimodal probability distribution. The local minimum between the two peaks of a third-order polynomial
fitted to the voxel mean-value histogram determined a cutoff value. Voxels with mean signal values above the cutoff value were assumed to represent active brain signals. Voxels with weaker signal means were found to be almost exclusively outside the head and therefore were eliminated from subsequent analyses.
Data were temporally smoothed by using a three-point filter based on a Hanning window (2). The three points were shifted along the window by 250 msec for each successive slice to decrease the time misalignments induced by the successive 250-msec acquisition delays between slices. For each time point, the filtered BOLD signals from all brain voxels were placed into a row of the data matrix after subtracting the mean voxel value for the time point from each voxel.
An ICA algorithm (11, 12) was applied separately to the data matrix from each of the two trials (see Appendix). Around 60 min on an Alphaserver 2100 (Digital Equipment Corporation, Maynard, MA) was required for convergence. For comparison, the eigenimages from each trial were determined by using standard PCA techniques, along with their associated time courses. To explore the effects of higher-order statistics on determining uncorrelated spatial maps, the fourth-order cumulant ICA technique proposed by Comon (13), computationally more expensive than the ICA algorithm (around 390 min of computer time to analyze one trial), was also used to find partially independent maps and associated time courses.
The computed ICA component maps were read into the functional neuroimaging display program MCW AFNI (14) for display and registration with structural T1-weighted MRI brain images for the subject.
Convolving the task block design with a 7.5-sec-long rectangular function (to take into account the lags caused by the hemodynamic response) created a task reference function. The reference function was then correlated with the time courses of the individual voxel time courses and the ICA and PCA components.
To display voxels contributing most strongly to a particular component map, the values in each map were scaled to z-scores. Voxels with absolute z-scores greater than some threshold (e.g., |z|>2) were considered to be the “active” voxels of that component. Negative z-scores indicate voxels whose BOLD signals are modulated opposite to the given time course of activation for the component. (Here, z-scores are used only for descriptive purposes and have no particular statistical significance).
Results
The application of ICA to a 6-min Stroop trial produced 144 component maps and their associated time courses. Some spatial ICA component maps contained multifocal groupings of active voxels, whereas others, typically those explaining the least variance in the data, had diffuse, noise-like, or “speckled” spatial distributions. All component maps had a super-Gaussian distribution of voxel values, i.e., having more values around zero and longer tails compared with a Gaussian distribution of the same variance, resulting in sparse maps after thresholding. Some components were slowly varying, quasi-periodic with a period of ~12 sec, or had sharp changes in their time courses or ring-like spatial distributions suggesting head movements (Fig. 1). These will be described in more detail elsewhere.
Only one component from each trial had a CTR time course closely matching the reference function for the trials (r=0.92 and 0.68) (Fig. 2). In contrast, many principal components had projections that were somewhat correlated with the reference function. The principal components whose projections most correlated with the reference function (r=0.46 and r=0.45) differed both spatially and temporally with the ICA CTR component (Fig. 2). The fourth-order cumulant technique for ICA proposed by Comon (13) provided one component in each trial whose time course was correlated to the reference function (r=0.85 and 0.71) almost the same as that found by the Bell and Sejnowski algorithm for ICA (Fig. 2).
The right column of Fig. 3 superimposes the four 80-sec task cycles of the ICA CTR component for both Stroop trials. Several details of the shape of CTR-component activation were reproducible across experimental/control blocks (Fig. 3). The bottom right plot shows the mean of the eight CTR component task-cycle activations in the two trials, superimposed on one cycle of the reference function. Note that the mean time course of activation was not precisely predicted by the reference function. The CTR component time course suggested that the true hemodynamic response or brain activation during each 40-sec Stroop task block was not constant, but tended to decline after 20 sec on task, and had an unexpectedly long (8-sec) rise time.
Active voxels of these CTR components highly overlapped areas deemed active by standard correlation methods (to be reported elsewhere). Both methods detected activation in Brodmann’s areas 18 and 19 (not involving the calcarine fissure) and in the supplementary motor area and cingulate system. In each of the trials, the ICA method also detected CTR activation in frontal areas including left dorsolateral prefrontal cortex.
In both trials, separating the fMRI data into independent spatial components also produced several components that appeared TTR (Fig. 4). Most often, these showed a marked activation at the onset of one or two of the four Stroop task blocks, especially the first and second blocks (Figs. 1b and 4. in trial 1) or the second and third blocks (in trial 2). In contrast to the CTR components, the most active areas of the TTR components were largely frontal, implying that frontal Stroop task-related activations differed in strength and spatial distribution during and across trials.
Component Removal. To explore whether the TTR components were affected by the ICA requirement that their spatial distributions be independent of the map voxel values of each other and the CTR component, the CTR component was removed from the first trial by using the method described in the Appendix. The resulting reduced-rank data set was then decomposed by ICA applied to eigenimages of the first 100 eigenvectors (explaining 99.99% of data variance).
Removal of the CTR component had varying effects on the recomputed independent component maps. For example, Fig. 5 shows a scatter plot comparing the map voxel values of a suspected artifact (head movement) component in the two ICA decompositions (i.e., before and after the removal of the CTR component using the method outlined in the Appendix). The two spatial distributions are highly similar (r=0.9), suggesting the removal of the CTR component had a minimal effect on the spatial distribution of this component. Similarly, comparisons of map voxel values before and after CTR removal revealed minimal effects on a quasi-periodic component (r=0.97) and a slow head movement component (r=0.82).
Fig. 6a shows a TTR component (Lower Left) whose active area overlapped significantly the active area of the CTR component (Upper). Re-analysis of the data set into spatially independent components with the CTR component removed (Lower Right) yields a component task-related to the second Stroop block, but with mesial frontal active areas. A scatter plot comparing the map voxel distributions of the TTR components before and after the removal of the CTR component reveals significant differences in the component maps (Fig. 6b, r=0.23).
Simulations. A simulation was performed to test the effect of component removal on linearly mixed, spatially independent, and spatially dependent activations. Three simulated activations (one CTR and two TTR) were added to the data from the first trial in brain regions with specified distributions DCTR, DTTR1, and DTTR2 (Fig. 7 Upper). The DCTR (posterior)
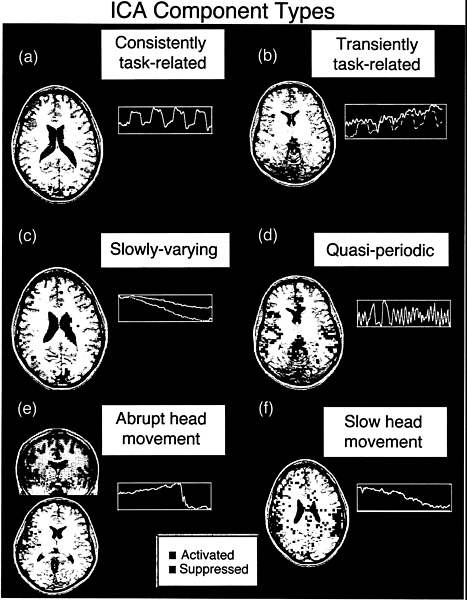
FIG. 1. Different classes of components detected by ICA decomposition of Stroop task fMRI data. (red, z≥2.0; blue, z≤2.0). Negative z values mean those voxels are activated opposite to the plotted time course. (a) Consistently task-related (CTR) component. (b) Transiently task-related (TTR) component. The dotted line shows the time course of the consistently task-related component for comparison. (c) Slowly varying, non-task-related component. The active region for this component was mostly localized to the ventricular system. The lower line shows the mean time course of the active voxels for this component. (d) Quasi-periodic component. This component was largely active in a single slice and had a dominant period of about 12 sec. The spatial distributions of such components were highly reproducible between trials. (e) Suspected abrupt head movement. Note abrupt change in time course, suggesting an abrupt head movement. (f) Component with a “ring-like” spatial structure is suggestive of a head movement.
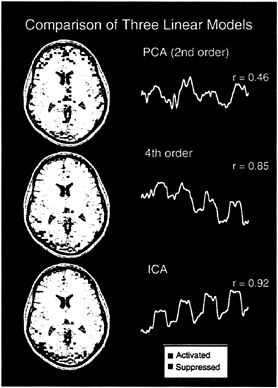
FIG. 2. Comparison of three linear models for analyzing fMRI data. PCA and two versions of ICA were used to linearly separate the data into partially spatially independent maps. The most consistently task-related component determined by each of the three methods from the first trial are shown, along with the correlation coefficient between the associated time courses and the reference function for the behavioral experiment. The ICA algorithm components resembled the task reference function much more strongly than the most highly correlated PCA components.
and DTTR1 (frontal) distributions were highly overlapped for all but the most highly active voxels (Fig. 7). The DTTR2 (parietal) was independent from the other two distributions. An ICA decomposition was performed both before and after removal of DCTR by using the method outlined in the Appendix.
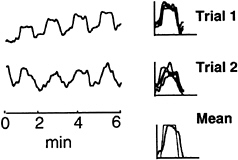
FIG. 3. ICA separated one CTR component for each of the two trials. The right column superimposes the four control/task blocks in each trial on the linearly detrended CTR component. The mean of all eight component activations is shown at the bottom of the right column, superimposed on one cycle of the expected task reference function.
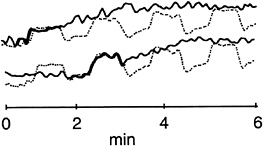
FIG. 4. Examples of activations TTR to the task block design. The CTR component is shown with a dotted line. Bolded portions indicate time periods when TTR activations appear task-related.
ICA decomposition on the data including the simulated activations recovered three components (Fig. 7b) with time courses similar to the added signals. The separated spatial component voxel values (scaled to z-scores) correlated 0.92, 0.54, and 0.99, respectively, with the original simulated distributions DCTR, DTTR1, and DTTR2. Re-computation of the maps after removal of the CTR component with the method outlined in the Appendix resulted in a more accurate separation of the original distributions (r=0.97 and 0.99 with DTTR1 and DTTR2, respectively). Component TTR2 (parietal), with a different spatial distribution to CTR, was largely unaffected by the removal of the CTR component (Fig. 7b and c). Conversely, TTR1, which significantly overlapped with CTR, was recovered more accurately after CTR removal (Fig. 7c).
Discussion
The Stroop color-naming task has long been used for the assessment of patients with closed head injury and frontal lobe lesions (15, 16). Although the brain region affected in closed head injury is typically diffuse, frontal lobes and particularly orbitofrontal cortex are most often affected. Previous PET studies of Stroop task performance reported occipital and medial frontal activation (17). The active participation of frontal areas in the CTR components found by ICA for both Stroop task trials confirm the association of Stroop task performance with frontal activation in this subject. An ICA analysis of data from two other subjects, reported elsewhere
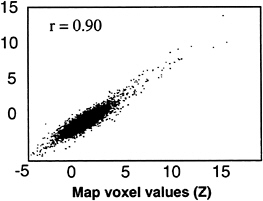
FIG. 5. A scatter plot comparing the map voxel values of a suspected artifact (head movement) component before and after removal of the CTR component. Map voxel values are scaled to z-scores. Note the reproducibility of map voxel values for both the highly active and less-active voxels in each map. Voxel values before CTR removal are shown on the abscissa.
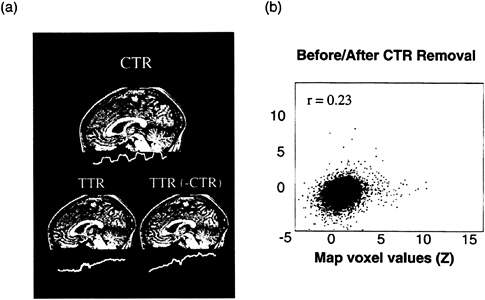
FIG. 6. (a) A marked effect on a TTR component of removing the CTR component. The CTR component for trial 1 (Upper) had areas of activation in predominately posterior regions. The same ICA decomposition revealed TTR activation during the second experimental block (blue rectangle) whose map voxel distribution was constrained by the algorithm to be independent to the CTR component (Lower Left). Application of ICA after the removal of the CTR component (by Eqs. 11–18) again revealed a TTR component with strong mesial frontal activation (Lower Right). (b) Scatter plot showing the effects of removal of the CTR component on a TTR component. Here. CTR-component removal had a significant effect on the map voxel values, in contrast to Fig. 5. Yellow voxels denote activation with the time course shown, and blue voxels denote suppression with the same time course.
(18), was similar. As expected, visual and visual-association areas dominated the active maps of these components. Several features of the time course of the CTR components, including a longer than expected rise time and a trend toward decreasing activation during the second half of each 40-sec Stroop block, were similar in each task block. These features differed from the task reference function used in correlation analyses.
In both trials, separating the fMRI data into independent spatial components also produced several components that appeared TTR. Most often, these showed a marked activation at the onset of one or two of the four Stroop task blocks, especially the first and second blocks (Figs. 1b and 4, in trial 1) or the second and third blocks (in trial 2). The most active areas of the TTR components contained large frontal regions (Fig. 1b), implying that frontal Stroop task-related activations differed in strength and spatial distribution between task blocks. Analysis methods involving averaging over task blocks or trials to detect CTR areas of activation necessarily ignore the possibility of TTR activations, although these may potentially be of considerable interest. Changes in the amount and distribution of frontal activation during cognitive performance reported in several previous PET and fMRI studies have been linked to changes in stimulus novelty (19), verbal fluency (20), verbal suppression (21), working memory (22), visual-spatial attention (23), and language processing (24), all of which may be involved in Stroop task performance.
Our exploratory results suggest that ICA can be used to discover both transient and/or consistently appearing activations, without requiring either their general or precise time courses to be known in advance of the analysis. In particular, details of the time courses of task-related activations found by ICA for our data were unanticipated and might be expected to differ between subjects. Unlike correlational methods, ICA considers all time points individually, without requiring averaging across stimuli or task blocks (5). For these data, as few as 50 time points seemed sufficient to detect details of the CTR and TTR components. Fewer time points would result in fewer components separated by the ICA algorithm, requiring the noise inherent to the data being distributed among the fewer components. Thus, ICA has several advantages compared with other methods of fMRI analysis including correlation and statistical parametric mapping (SPM) (25), in which the time courses and/or spatial extents of anticipated effects must be modeled explicitly before analysis.
To test whether the segregation into occipital CTR and frontal TTR components was in part a consequence of the spatial independence criterion used by the algorithm, we removed the CTR component from the data. ICA decomposition of this new data set gave several TTR components with both frontal and occipital active areas, but left maps unrelated to task activation relatively unaffected (e.g., a component capturing an apparent head movement artifact. Fig. 5). This, coupled with the simulation results, lends support to the original supposition that the spatial patterns of task-related brain activation are spatially independent from the spatial patterns of activity related to artifacts and other physiological processes. Spatial independence of task-related changes from artifact can also be inferred from the observation that the CTR maps had time courses more closely related to the task reference function as stricter criteria for independence between map voxels were applied, from PCA (second order), Comon’s ICA technique (fourth order), to the higher-order ICA algorithm used here (Appendix). However, the fact that some TTR maps were altered by removal of the CTR component suggests that there is some spatial dependence between these task-related components. Further work is needed to determine more clearly the ways in which CTR component removal affects TTR components, as well as methods for assessing the reliability of ICA maps and time courses.
Conclusions
ICA is a new method for analyzing fMRI that is able to separate task-related activations from artifactual and other
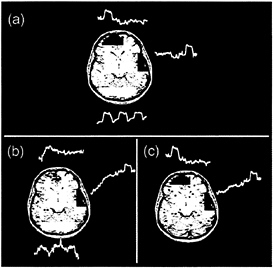
FIG. 7. Simulation depicting the effects of removal of an ICA component on subsequent ICA decomposition. (a) Three simulated activations with different spatial distributions were added to the data set from the first trial. Two of the simulated distributions were highly overlapping for all but the most highly active voxels in anterior and posterior regions (illustrated voxels). The simulated parietal distribution was independent from the other two distributions. (b) After spatial ICA decomposition, the spatial component voxel values for three of the ICA components correlated 0.92, 0.54, and 0.99, respectively, with the distributions of the simulated activations. (c) Removal of the CTR component and reanalysis by ICA resulted in a more accurate separation (r=0.97) of the least-well-separated distribution (frontal). The separated parietal distribution was largely unaffected by CTR removal (r=0.99).
physiological fluctuations in the fMRI signal, including transient brain activity. ICA does not make assumptions about the time courses or spatial extent of activations, and thus appears to be well suited for the detection of both consistently and transiently task-related brain activations as well as separating out artifactual and other physiological processes from fMRI data (8–10). Possibly the greatest promise lies in its potential for separating and measuring multiple neurophysiological processes taking place during learning or other normal and abnormal brain state transitions whose time courses are difficult to predict or measure by other means.
Technical Appendix
The Extended Independent Component Analysis (ICA) Algorithm. Bell and Sejnowski (10, 11) have proposed a simple neural network algorithm for performing ICA. The algorithm iteratively finds a linear transformation, W, that minimizes the statistical dependence between components:
C=WX=WHWSX, [5]
where WS, the “sphering matrix,” is defined.
[6]
and X is the (row mean-zero) N by M fMRI signal data matrix (N, the number of time points in the trial, and M, the number of brain voxels) obtained by removing the mean signal level from each time point. The sphering matrix makes the maps uncorrelated, whereas WH reduces the higher-order correlations between the component maps contained in the rows of C.
Unless otherwise specified, we define W as WHWS. The algorithm attempts to maximize the entropy H() of y, a nonlinear transform by a specified function g() of the computed map matrix. It does this by iteratively updating the elements of WH by using small batches of data vectors drawn at random from {WSX} without substitution, according to
[7]
where ε is a small learning rate and the vector ŷ is composed of elements:
[8]
The ![]() term in Eq. 7 avoids matrix inversion and speeds convergence. During training, the learning rate is reduced gradually until the weight matrix WH stops changing appreciably.
term in Eq. 7 avoids matrix inversion and speeds convergence. During training, the learning rate is reduced gradually until the weight matrix WH stops changing appreciably.
The form of the nonlinearity g() plays an important role in the success of the algorithm. The ideal form for g() is the cumulative density function (c.d.f.) of the distributions of the voxel values in the component maps. In practice, if we choose g() to be a logistic sigmoid function g(C)=(1+exp(–C))–1. as in ref. 11. the algorithm is limited to separating sources with super-Gaussian distributions, but is otherwise relatively insensitive to the exact probability distributions of the component maps. For this choice of g(), ŷ=1–2y.
The ICA learning rule has been extended to components with either sub- or super-Gaussian distributions (26) by approximating the estimated probability density function (p.d.f.) by a fourth-order Edgeworth approximation, as derived by Girolami and Fyfe (27), giving
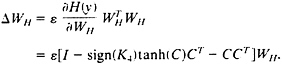
[9]
where K4 is the diagonal matrix of kurtosis values for the computed component map value distributions C, defined by,

[10]
Intuitively, for super-Gaussian components (K4>0), the (sign(K4)) term is an anti-Hebbian rule that tends to push the probability density of C toward sparse distributions, whereas for sub-Gaussians (K4<0), the corresponding term is a Hebbian rule that tends to push the densities of C toward sub-Gaussian distributions.
Component Removal. Removal of one or more component(s) can be accomplished by
[11]
where Wa–1 is the inverse of W with columns corresponding to the component(s) to be removed subsequently set to zero, and Xa is the reconstructed data with the given component(s) removed.
Matrix Xa in Eq. 11 will now be of reduced rank and cannot be separated by the ICA algorithm. Using principal component analysis (PCA) to reduce the dimension of Xa averts this problem:
[12]
where Vp is n by p (p<n) matrix whose columns are the unit length eigenvectors of the covariance matrix, ![]() corre-
corre-
sponding to the p largest eigenvalues, ![]() is transpose of Vp, and Xa is calculated from Eq. 10. Ap is a now smaller but full-rank matrix of eigenimages of Xa. The number p may be taken as the number of eigenvectors required to explain a predetermined proportion of the variance in the original data (e.g., >99%). ICA decomposition of the resulting eigenimages. Ap, gives,
is transpose of Vp, and Xa is calculated from Eq. 10. Ap is a now smaller but full-rank matrix of eigenimages of Xa. The number p may be taken as the number of eigenvectors required to explain a predetermined proportion of the variance in the original data (e.g., >99%). ICA decomposition of the resulting eigenimages. Ap, gives,
Ca=WEAp, [13]
where Ca is the p by n matrix of component maps, and WE is the computed unmixing matrix.
Substituting for Ap from Eq. 11 gives:
[14]
or
[15]
whence
[16]
giving
[17]
since ![]() because eigenvectors are mutually orthogonal. Finding the p time courses (of length n) associated with each of the p maps can now be determined by examining the columns of the matrix,
because eigenvectors are mutually orthogonal. Finding the p time courses (of length n) associated with each of the p maps can now be determined by examining the columns of the matrix,
[18]
The Heart and Stroke Foundation of Ontario, the Howard Hughes Medical Institute, and the Office of Naval Research supported this research.
1. Friston, K.J. (1996) in Brain Mapping, The Methods, eds. Toga, A.W. & Mazziotta, J.C. (Academic, San Diego), pp. 363–396.
2. Press, W.H., Teukolsky, S.A., Vetterling, W.T. & Flannery, B.P. (1992) Numerical Recipes in C: The Art of Scientific Computing (Cambridge Univ. Press, Cambridge, UK).
3. Bandettini, P.A., Jesmanowicz, A., Wong, E.C. & Hyde, J.S. (1993) Magn. Reson. Med. 30, 161–173.
4. Buckner, R.L., Bandettini, P.A., O’Craven, K.M., Savoy, R.L., Petersen, S.E., Raichle, M.E. & Rosen, B.R. (1996) Proc. Natl. Acad. Sci. USA 93, 14878–14883.
5. Kim, S.G., Richter, W. & Ugurbil, K. (1997) Magn. Reson. Med. 37, 631–636.
6. Friston, K.J., Frith, C.D., Liddle, P.F. & Frackowiak, R.S. (1993) J. Cereb. Blood Flow Metab. 13, 5–14.
7. Gardner, E. (1975) Fundamentals of Neurology (W.B.Saunders, Philadelphia).
8. Friston, K.J., Williams, S., Howard, R., Frackowiak, R.S. & Turner, R. (1996) Magn. Reson. Med. 35, 346–355.
9. Weisskoff, R.M. (1996) Magn. Reson. Med. 36, 643–645.
10. Biswal, B., DeYoe, A.E. & Hyde, J.S. (1996) Magn. Reson. Med. 35, 107–113.
11. Bell, A.J. & Sejnowski, T.J. (1995) Neural Comput. 7, 1129–1159.
12. Bell, A.J. & Sejnowski, T.J. (1997) Vision Res. 37, 3327–3338.
13. Comon, P. (1994) Signal Processing 36, 11–20.
14. Cox, R.W. (1996) Comput. Biomed. Res. 29, 162–173.
15. Bohnen, N., Twijnstra, A. & Jolles, J. (1992) Acta Neurol. Scand. 85, 116–121.
16. Ponsford, J. & Kinsella, G. (1992) J. Clin. Exp. Neuropsychol. 14, 822–838.
17. Bench, C.J., Frith, C.D., Grasby, P.M., Friston, K.J., Paulesu, E., Frackowiak, R.S. & Dolan, R.J. (1993) Neuropsychologia 31, 907–922.
18. McKeown, M.J., Makeig, S., Brown, G.G., Jung, T.-P., Kindermann, S.S., Bell, A.J. & Sejnowski, T.J. (1998) Hum. Brain Mapping, in press.
19. Tulving, E., Markowitsch, H.J., Craik, F.E., Habib, R. & Houle, S. (1996) Cereb. Cortex 6, 71–79.
20. Phelps, E.A., Hyder, F., Blamire, A.M. & Shulman, R.G. (1997) Neuroreport 8, 561–565.
21. Nathaniel-James, D.A., Fletcher, P. & Frith, C.D. (1997) Neuropsychologia 35, 559–566.
22. Manoach, D.S., Schlaug, G., Siewert, B., Darby, D.G., Bly, B.M., Benfield, A., Edelman, R.R. & Warach, S. (1997) Neuroreport 8, 545–549.
23. Nobre, A.C., Sebestyen, G.N., Gitelman, D.R., Mesulam, M.M., Frackowiak, R.S. & Frith, C.D. (1997) Brain 120, 515–533.
24. Binder, J.R. (1997) Clin. Neurosci. 4, 87–94.
25. Friston, K.J., Frith, C.D., Liddle, P.F. & Frackowiak, R.S. (1991) J. Cereb. Blood Flow Metab. 11, 690–699.
26. Lee, T.-W. & Sejnowski, T.J. (1997) Joint Symp. Neural Comput., 4th Institute for Neural Computation, UCSD. 7, 132–140.
27. Girolami, M. & Fyfe, C. (1997) in IEEE International Conference on Neural Networks (Houston, TX), pp. 1788–1791.








