Proc. Natl. Acad. Sci. USA
Vol. 95, pp. 13–17, January 1998
Colloquium Paper
This paper was presented at a colloquium entitled “The Age of the Universe. Dark Matter, and Structure Formation,” organized by David N.Schramm, held March 21–23, 1997, sponsored by the National Academy of Sciences at the Beckman Center in Irvine, CA.
Globular cluster ages
RAUL JlMENEZ*
Royal Observatory, Blackford Hill, Edinburgh EH9 3HJ, United Kingdom
ABSTRACT We review two new methods to determine the age of globular clusters (GCs). These two methods are more accurate than the classical isochrone fitting technique. The first method is based on the morphology of the horizontal branch and is independent of the distance modulus of the globular cluster. The second method uses a careful binning of the stellar luminosity function and determines simultaneously the distance and age of the GC. We find that the oldest galactic GCs have an age of 13.5±2 gigayears (Gyr). The absolute minimum age for the oldest GCs is 10.5 Gyr (with 99% confidence) and the maximum 16.0 Gyr (with 99% confidence). Therefore, an Einstein-De Sitter Universe (Ω=1) is not totally ruled out if the Hubble constant is about 65±10 Kms–1Mpc–1.
Galactic globular clusters (GCs) are the best stellar clocks to establish a lower limit to the age of the universe. Nevertheless, a robust age for the oldest GCs is yet to be determined.
GCs are excellent stellar clocks because they fulfill the following properties:
-
All the stars were born at the same time.
-
The population is chemically homogeneous.
-
There has not been any further episodes of star formation that gave birth to new stars, which could cover up the oldest population.
Support for GCs being old comes from two facts: their metallicity is as low as 1/100 of solar and the characteristics of their color magnitude diagram (CMD) are those corresponding to ages larger than 10 gigayears (Gyr), i.e., the stars around the main sequence turn-off (MSTO) have masses lower than 1 M⊙.
Despite the continuous effort carried out during more than 30 years to give a precise value for the age of GCs, the uncertainty in their age still remains at about 4 Gyr. The problem is particularly complicated because age and distance have the same effect on the morphology of the MSTO point. Deficiencies in the input physics combined with the uncertainties in cluster distances and interstellar reddening have made it difficult to determine GC ages with an accuracy better than about 25%.
In this review I present two alternative methods used to derive ages of GCs that are independent of the traditional MSTO fitting. The first method is based on the morphology’ of the horizontal branch (HB) and uses the reddest points in the HB to determine the mass of the stars in the red giant branch (RGB) (1). This method is independent of the distance modulus and therefore is a useful tool to compute systematics in ages determinations by using the traditional MSTO fitting technique. The second of the methods is based on a careful binning of the luminosity function (LF) and determines simultaneously the age and distance of a GC. It therefore is a very useful technique to determine distances to GC independently of the subdwarf fitting and RR-Lyrae techniques. It is also very powerful to determine relative ages of GCs with little error.
In the next sections I describe the traditional isochrone fitting method and the HB morphology and LF methods. I finish with a discussion on the uncertainties of the different methods and the most likely value for the age of the oldest GCs.
The Isochrone Fitting Method
The first (and more obvious) method to compute the age of a GC is to exploit the fact that the locus of the MSTO in the plane Teff vs. L changes with age (mass). In this way one computes different isochrones, i.e., tracks in the plane Teff vs. L at the same time for all masses, with the chemical composition of the GC and finds the better fit to the MSTO region. To do this a very important step is needed: the distance to the GC is necessary to transform the theoretical luminosity into observed magnitudes in different bands, and thus this is where trouble starts. If the distance to the GC is unknown, there is a degeneracy between age and distance. In this way we can simulate a different age by simply getting the GC closer or more distant to us. This is clearly illustrated in Fig. 1 where we plot several isochrones (10, 12, and 14 Gyr) for the GC M5. It transpires from the figure that a vertical translation of any of the isochrones will fit the color-magnitude diagram of M5.
Distances to GCs are very poorly known because it is impossible to get the parallax of individual stars; therefore, ages of GCs are not accurately known by using the isochrone fitting method. Usually, different methods are used to compute distances to GCs: the RR-Lyrae method, the subdwarf fitting method, the tip of the red giant branch, and the LF. The RR-Lyrae method consists of using the known periodluminosity relation for the RR-Lyrae pulsators in the HB. It gives an uncertainty of 0.25 magnitude (mag) in the distance modulus determination, which translates to 3-Gyr error in the age determination. The subdwarf method uses the nearby low-metal subdwarfs to calibrate the distance of GCs; again its uncertainty is about 0.2 mag. The tip of the RGB method uses the fact that stars at the tip of the RGB flash at a well defined luminosity (1); therefore, the tip of the RGB is well defined and can be used as a distance indicator. The LF method, which is explained later, gives more precise distance determination, and the error in the distance is only 0.05 mag. Recently, new parallaxes to local subdwarfs (2) have increased the distance
© 1998 by The National Academy of Sciences 0027–8424/98/9513–5$2.00/0
PNAS is available online at http://www.pnas.org.
|
* |
To whom reprint requests should be addressed, e-mail: raul@roe.ac.uk. |

FIG. 1. The CMD of M5 and three different isochrones. Notice that a vertical shift in any of the nonfitting isochrones (10 and 14 Gyr) will make them fit the observed CMD perfectly well. This is equivalent to a change in the distance modulus.
inferred by the subdwarf method to GCs and therefore reduced the ages of GCs (2).
To circumvent the need for the distance determinations in computing the age, Iben and Renzini (3) proposed an alternative method for deriving ages using the MSTO, the so-called ∆V method. The method exploits the fact that the luminosity of the MSTO, and not only its Teff, changes with mass (age), and also that the luminosity of the HB does not change because the core mass of the He nucleus is the same independently of the total mass of the stars (provided we are in the low mass range), and the luminosity in the HB is provided by the He core burning. Because the method is based on a relative measure (the distance between the HB and the MSTO), it is distance independent. Of course, the method needs the knowledge of at least one GC distance to be zero-calibrated. Unfortunately, the method has a serious disadvantage: the need to know accurately the location of the MSTO point. This turns out to be fatal for the method because it has associated an error of 3 Gyr in the age determination (see Fig. 1 around the MSTO).
Furthermore, all the above methods are affected by three main diseases: the calibration color-Teff, the calibration of the mixing-length parameter (α), and the need to fit morphological features in the CMD (i.e., the MSTO). See Table 2 for a detailed review of all errors involved in the different methods.
The most common ages obtained for the oldest GCs by using the MSTO method are in the 14–18 Gyr range. Nevertheless, an error bar of 3.5 Gyr is associated with all age determinations using the MSTO methods described above.
The Horizontal Branch Morphology Method
We obtained UBVRIJHK photometry of the GCs M22, M107, M72, M5, and M68 at La Silla (Chile) by using the Danish 1.5-m telescope and the ESO 2.2-m telescope. We added to our sample four other GCs: M92, M3, M55, and 47 Tuc.
The spread of stars along the HB is mainly caused by previous mass loss that varies stochastically from one star to another (4). The range of colors where zero-age HB stars are found is a function of metallicity (the “first parameter”) and the range of ZAHB masses. More precisely, the ZAHB color at a given metallicity depends on both the star’s total mass and the ratio of core mass to total mass, but the core mass essentially is fixed by the physics of the helium flash and is quite insensitive to the mass and metallicity. For a given average mass loss, the average final mass is thus a decreasing function of age, which is therefore a popular candidate for the “second parameter” (5), although other candidates such as CNO abundance also have been suggested. A strong case for age as the chief (though perhaps not necessarily the only) second parameter has been made by Lee, Demarque. and Zinn (6), who find a tendency for the clusters to be younger in the outer Galactic halo. Jorgensen and Thejll (7), by using analytical fits to a variety of RGB models and following evolution along the RGB with mass loss treated by Reimers’ formula (8), showed that, for clusters with narrow RGBs (the majority), star-to-star variations in initial mass, metallicity, or mixing-length parameter can be ruled out as a source of the spread along the HB. This leaves as likely alternatives only either variations in the Reimers’ efficiency parameter η (or some equivalent) or a delayed helium flash caused by differential internal rotation. The later alternative would lead to a fuzzy distribution of stars at the RGB tip.
With our data we can analyze these propositions. Assume there was a variation in the total mass at the flash caused by mass loss. The effect on the luminosity at the helium core flash is small ≈0.01 mag, but the effect on the temperature is quite significant ≈110 K. On the other hand, a delayed helium core flash would not produce any effect on the effective temperature but would make stars appear above the theoretical helium core flash in a bin of ≈0.3 mag. Considering that the evolution time in this very last bin would be the same as in the last bin before the theoretical helium core flash, we would expect the same number of stars in these two bins of the diagram. So, for a typical GC we would expect 3–4 stars. Variations in the mass loss certainly will produce variations in the morphology at the red giant branch tip.
Following this strategy we looked at the previous set of observations and counted the number of stars that were expected in every bin of luminosity. By using the set of three clusters where it was possible to distinguish the RGB from the asymptotic giant branch (M72, M68, and M5), we had a relatively good statistical sample to test the theory of a delayed helium core flash. We counted the RGB stars and compared them with the theoretical predictions. To calculate the number of stars expected in every bin of luminosity we used stellar evolutionary tracks to compute the time spent there and then used the fuel consumption theorem (9) to compute the number of stars—the integrated luminosity of the cluster was properly scaled to the area covered by the charged coupled device. We have concluded from the set of observations that there is no GC where there appears to be an extra number of stars populating the RGB beyond the helium core flash (see figure 14 in ref. 1). This argument rules out, to a level of 0.01 M⊙, variations of the core mass at the flash as the cause of HB color variations.
A method that is independent of the distance modulus can be developed, by using the fact that the spread of stars along the HB is mainly because of previous mass loss that varies stochastically from one star to another. It is therefore meaningful to proceed to an analysis of both the right giant branch tip and the HB and to link them together to deduce general properties from morphological arguments.
The procedure that we use to analyze the morphology of the RGB and the HB together and constrain the mass of the stars at the RGB is as follows:
-
Because the vertical position of the RGB depends only on metallicity and α, once the metallicity is known α is the only free parameter. Therefore, we can find a fit for the best value of α, using the vertical position of the RGB.
-
The reddest point of the HB corresponds to zero mass loss and therefore to the most massive stars that are alive in the GC and therefore the oldest.
-
By using HB theoretical models we can determine the mass of the reddest point of the HB. So it is possible to compute stellar tracks for a certain input mass and iterate until the track at the zero age horizontal branch matches the reddest point of the observed HB.
By using the above method, we have analyzed the RGB and HB of eight GCs. For the whole set of GCs the procedure has been the same. Using Kurucz models (10), we know how stars in the HB are distributed in the luminosity-Teff diagram. We then compute their masses by using different grids of HB models. For the case where only oxygen was enhanced we have used the Dorman models (11) to compute the masses, results are presented in Table 1 (column t1). To follow Chieffi et al.’s approach (12) we have used their models with fα=2; the results are marked in Table 1 (column t3). The same set of models has been used for simple solar-scaled metallicities and is given in Table 1 (column t2). Once the mass of the reddest point in the HB has been computed, it is straightforward to get the age of the GC. We have used our grid of models (13) to compute the ages of the cases with Z0 and Z, and the models by Bergush and Vandenbergh (14) to compute the ages of the O-enhanced case. The uncertainty in all age determinations is 2 Gyr.
In Jimenez et al. (1) we analyzed eight GCs using the above method and found that the oldest GCs were not older than 14 Gyr.
The Luminosity Function Method
When the MSTO method is used (both isochrone fitting and ∆V), a different distance modulus can be mimicked with a different mass for the MSTO, and therefore with a different age. This age-distance degeneracy in general leads to an uncertainty in the age of 3 Gyr. On top of this, other uncertainties in the stellar physics lead to an additional uncertainty in the age of about 2 Gyr.
To tackle this problem, we have proposed an alternative method that is independent of the distance modulus (1). Here I review the use of the stellar LF of GCs to break the age-distance degeneracy.
The LF seems to be the most natural observable to try to constrain both age (15, 16), and distance modulus at the same time. The LF is a natural clock because the number of stars in a given luminosity bin decreases with time, because more massive stars evolve more rapidly than less massive ones. The fact that small differences in stellar masses correspond to large differences in evolutionary time explains the power of the LF clock, rather than being a source of uncertainty in getting GC ages (as it is in the MSTO method).
The LF is also a natural distance indicator, because the number of stars in a given luminosity bin depends on the position of the bin.
Stars of different mass evolve along the main sequence at different speeds: the more massive the faster. This means that the number of stars inside a fixed luminosity bin decreases with time. This effect is particularly strong around the subgiant region, so that the whole shape of the LF, and not only its normalization, is changing with time. In other words the ratio
Table 1. Ages for different globular clusters using the HB morphology method
between the number of stars in two different bins in the LF can be used as a clock for GC ages (17, 18).
For a determination of both distance and age, one needs to get from the LF at least two independent constraints, which means three bins in the LF, because one is required for the normalization. A fourth bin is also very useful to check for the completeness of the stellar counts (see Fig. 2).
Therefore the LF method for determining age and distance of GCs consists in the production of four-bin theoretical LFs for GCs, to be compared with their observational counter-parts. This comparison is made for a given chemical composition that is assumed to be known from other methods, like spectroscopy.
The number of bins should not be larger than necessary (four), because each bin should be as wide as possible to reduce the statistical errors in the stellar counts due to uncertainty in the photometry and to the stochastic nature of the stellar mass function. The bins we use are all 1 mag wide, apart from the first one, at the RGB, which is used for the normalization, and may be extended as luminous as possible along the RGB.
The second bin, which is the main constraint for the distance modulus, is positioned between the RGB and the sub-giant branch to partially contain the steepest section of the LF (this gives the sensitivity to a translation in magnitude). The third bin, that is the main constraint for the age, contains the sub-giant branch, because this is the part of the LF that is most sensitive to age. The fourth bin is just next to the third one and typically will include the upper part of the main sequence.
We now summarize the steps of the fitting procedure. We will denote by m2,3 the apparent magnitude separating the second and third bins of the observational LF; by Ni,obs the number of stars in the ith observational bin; by ni,obs the normalized ratio Ni,obs/N1,obs; and by ni,th the corresponding theoretical ratio. m-M is the distance modulus and t is the age.
These are the steps:
-
Determine the metallicity, Z (e.g., from spectroscopy).
-
Choose a grid of ages and distance moduli.
-
For every age, the binning in absolute magnitude is determined by M2,3(t).
-
For every distance modulus m-M, the binning in apparent magnitude is determined by m2,3=M2,3(t)+m-M; this makes it possible to determine n2,obs(t,m-M) and n3,obs(t,m-M).
-
The corresponding theoretical ratios depend on age alone; n2,th=n2,th(t) and n3,th=n3,th(t).
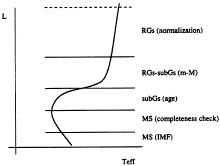
FIG. 2. The bins used in the LF method (see text) to determine age and distance of a GC.
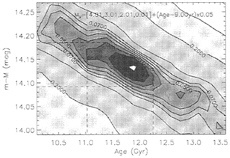
FIG. 3. Distance and age for the low metallicity GC M55 simultaneously determined using the LF method (see text). The contour lines show that the age can be determined with 1 Gyr accuracy and the distance modulus with 0.05 provided the number of stars in the LF can be complete to a level of 4%.
-
Thus, for every combination of age and distance modulus, one can calculate the residual R(t, m-M)= [n2,th(t)-n2,obs(t,m-M)]2+[n3,th(t)-n3,obs(t,m-M)]2.
-
From a contour plot of R(t,m-M), the age and distance modulus may be determined from the minimum, and the contour lines measure the uncertainty.
The procedure to obtain the LF from evolutionary stellar tracks is illustrated in ref. 17. A power law stellar mass function is assumed here, as it was in that work.
We have shown that a careful binning of the stellar LF allows a very precise determination of age and distance of GCs at the same time.
If stellar counts with 5% 1s uncertainties in 1-mag wide bins are available, the age can be determined with an uncertainty of 0.5 Gyr and the distance modulus with an uncertainty of 0.06 mag.
This LF method is therefore an excellent clock for relative ages of GCs and also a very good distance indicator. In other words, its application will provide very strong constraints for the theory of the formation of the galaxy.
In Figs. 3 and 4 we show the result of applying the LF method to the galactic GCs M55 and M5. The plots show contour plots for the error in the determination of the distance modulus and age of M55 (M5) simultaneously. The contour plots correspond to different values for the uncertainty in the number of stars in the LF. As stated above, if stellar counts are within an uncertainty of 5%, then the age is determined with an uncer-
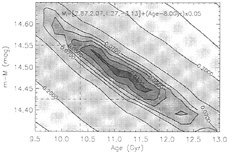
FIG. 4. Same as Fig. 3 but for M5.
Table 2. Errors associated with different methods used to compute the age of the oldest GCs
|
Uncertainties |
MSTO |
HB |
LF |
|
Distance modulus |
25% |
0% |
3% |
|
Mixing length |
10% |
5% |
0% |
|
Color-Teff |
5% |
5% |
0% |
|
Heavy elements diffusion |
7% |
2% |
7% |
|
a-elements |
10% |
5% |
10% |
|
Reddening |
5% |
10% |
0% |
tainty of 0.5 Gyr and the distance modulus with an uncertainty of 0.06 mag.
The age obtained for M55 (12 Gyr) confirms the conclusion of the HB morphology method that GCs are not older than 14 Gyr.
Discussion and Conclusions
Table 2 lists the uncertainties involved in each of the three methods described above to determine GC ages. As already discussed the MSTO method is largely affected by the uncertainty in distance, but uncertainties in the mixing length, diffusion of heavy elements, and in the color-Teff relation are important as well.
The HB method uses the fact that mass loss along the RGB is the chief of the HB morphology. This may seem to introduce an additional uncertainty in the method because mass loss in low-mass stars is unknown. In fact, the only stars used to determine the mass at the RGB are the reddest ones that did not suffer any mass loss. The evolution with mass loss along the RGB was done by using the method developed in Jimenez et al. (1) that describes the mass loss efficiency parameter with a realistic distribution function and minimizes its model dependence. Furthermore, the HB method is insensitive to changes in CNO abundances. The reason for this is that if CNO is enhanced with respect to iron the HB becomes redder, leading to a smaller mass for the reddest point of the HB, but because the stellar clock also goes faster, both effects compensate. The HB morphology method is weakly sensitive to diffusion by heavy elements (J.Mac-Donald, personal communication).
The LF method needs to know the metallicity of the GC. Apart from this, the LF method is the one with the smallest errors among the three methods described here. The biggest advantage of the LF method is that it is insensitive to the mixing-length, reddenning, and color-Teff transformation. Because the LF method is based on counting stars in several bins, it is independent of fitting to morphological features in the observed CMD of the GC. Therefore the LF method is a superb technique to determine relative ages of GCs.
The main conclusions of this paper are:
-
Alternative methods to the traditional MSTO isochrone fitting are important to get a more accurate age (and distance) of the system of galactic GC. The HB morphology and LF methods are more accurate than the traditional MSTO method and overcome many of the uncertainties of the latter.
-
The three methods presented in this paper agree on an age of about of 13 Gyr for the oldest GCs. The minimum possible age is 10.5 Gyr and the maximum 16 Gyr, with 99% confidence.
-
More work needs to be done by using alternative methods to determine more accurately the age of GCs.
1. Jimenez, R., Thejll, P., Jørgensen. U.G., MacDonald, J. & Pagel, B. (1996) Mon. Not. R. Astron. Soc. 282, 926–941.
2. Reid, N. (1997) Astrophys. J. 114, 161–183.
3. Iben, I. & Renzini, A. (1984) Phys. Rep. 105, 329–431.
4. Rood, R.T. (1973) Astrophys, J. 184, 815–824.
5. Searle. L. & Zinn, R. (1978) Astrophys. J. 225, 357–365.
6. Lee, Y., Demarque, P. & Zinn, R. (1994) Astrophys. J. 423, 380–388.
7. Jørgensen, U.G. & Thejll, P. (1993) Astron. Astrophys. 272, 255–263.
8. Reimers, D. (1975) in Problems in Stellar Atmospheres and Envelopes, (Springer, Berlin), p. 229.
9. Renzini, A. & Buzzoni, A. (1986) in Spectral Evolution of Galaxies; Proceedings of the Fourth Workshop, Erice. Italy (Dordrecht D.Reidel, Amsterdam), pp. 211–214.
10. Kurucz, R. (1993) CDROM 13.
11. Dorman, B. (1992) Astrophys. J. Suppl. 80, 701–721.
12. Castellani, V., Chieffi, A. & Pulone, L. (1991) Astrophys. J. Suppl. 76, 911–928.
13. Jimenez, R. & MacDonald. J. (1997) Mon. Not. R. Astron. Soc. 283, 721–732.
14. Bergush, P.A. & Vandenbergh, D.A. (1992) Astrophys. J. Suppl. 81, 163–171.
15. Paczynski, B. (1984) Astrophys. J. 284, 670–674.
16. Ratcliff, S. (1987) Astrophys. J. 318, 196–202.
17. Jimenez, R. & Padoan, P. (1996) Astrophys. J. 463, 17L–20L.
18. Padoan, P. & Jimenez, R. (1997) Astrophys. J. 475, 580–584.





