Proc. Natl. Acad. Sci. USA
Vol. 95, pp. 18–21, January 1998
Colloquium Paper
This paper was presented at a colloquium entitled “The Age of the Universe, Dark Matter, and Structure Formation,” organized by David N.Schramm, held March 21–23, 1997, sponsored by the National Academy of Sciences at the Beckman Center in Irvine, CA.
The age of the universe from nuclear chronometers
J.W.TRURAN
Department of Astronomy and Astrophysics, Enrico Fermi Institute. The University of Chicago, 5640 S. Ellis Avenue, Chicago, IL 60637
ABSTRACT An overview is presented of the current situation regarding radioactive dating of the matter of which our Galaxy is comprised. A firm lower bound on the age from nuclear chronometers of ˜9–10 Gyr is entirely consistent with age determinations from globular clusters and white dwarf cooling histories. The reasonable assumption of an approximately uniform nucleosynthesis rate yields an age for the Galaxy of 12.8±3 Gyr, which again is consistent with current determinations from other methods.
Estimates of the age of the Galaxy, and thereby limits on the age of the Universe, can be obtained by three independent means: (i) the age of the elements by radioactive dating (nucleocosmochronology); (ii) the ages of the globular clusters (the oldest stars in the halo of our Galaxy); and (iii) the ages of white dwarfs from cooling calculations (the age of the Galactic disk?). This paper will focus on radioactive dating, an approach that has played a particularly important role historically.
The presence of naturally occurring radioactive nuclei in Galactic matter testifies to the fact that the age of the elements is finite. To the extent that the long-lived nuclear species of interest are the products of nuclear transformations proceeding in stars and supernovae over the course of our own Galaxy’s history, they can be used to provide a measure of the duration of star formation activity and concomitant nucleosynthesis in the Galaxy. The use of long-lived radioactivities as a mechanism for the determination of a lower limit on the age of the Galaxy has a history that spans much of the 20th century. An early paper by Rutherford (1) outlined the essential features of this science. Subsequently, the defining works in nucleosynthesis theory by Burbidge et al. (2) and Cameron (3) established the nature of the astrophysical r-process of neutron capture, by which the critical long -lived chronometers 187Re, 232Th, 235U, and 238U are synthesized. The task, since then, has been to identify the astrophysical site for the operation of this nucleosynthesis process and to calculate the appropriate rates of production as a function of time over the course of galactic evolution. The early developments of the use of the uranium-thorium chronometers by Fowler and Hoyle (4) and Cameron (5) were based necessarily on rather simple prescriptions for the history of galactic nucleosynthesis. As our understanding of the processes of stellar and supernova nucleosynthesis improved, it became possible to address the problem of nuclear chronology in the context of increasingly realistic models of the chemical evolution of the Galaxy (6–10).
In this paper, we will be concerned with the determination of realistic age constraints from nucleocosmochronology. We will restrict ourselves to the 232Th-238U and 235U-238U chronometer pairs. The use of such other long-lived (t1/2>109 years) radioactivities as 40K, 87Rb, 138La, 147Sm, and 176Lu is constrained by our lack of an adequate knowledge of their nucleosynthesis histories. The long lifetime of 187Re makes the 187Re-187Os chronometer pair an attractive choice for dating galactic nucleosynthesis (11). A major difficulty here, however, is the fact that 187Os is also produced in the s-process. The uncertainties introduced by the subtraction of the s-process contribution to isolate the cosmoradiogenic component are significant. Further complications are associated with the fact that the ß decay rate of 187Re in stellar environments is sensitive to temperature.
Abundance clues to r-process history and the identification of the astrophysical site of r-process synthesis are reviewed in section 1. Critical input to these chronological studies is identified and discussed in section 2. The equations of nucleocosmochronology are presented in section 3, together with a model-independent age determination. In section 4, we obtain lower bounds on the time scale of galactic nucleosynthesis, with the assumption of an early “single event” nucleosynthesis epoch. Observational evidence for a uniform rate of nucleosynthesis, and its implications for the age of the Galaxy, is presented in section 5. The use of the thorium abundance in an extremely metal-deficient halo star for dating purposes is considered in section 6. Discussion and conclusions follow.
1. Abundance Clues to r-Process History. Significant constraints on the site of r-process nucleosynthesis are provided by observations of the heavy element patterns in halo stars. Early abundance studies of metal poor stars [see, e.g., the reviews by Wheeler, Sneden, and Truran (12) and McWilliam (13)] showed that abundances of nuclei normally attributable to the s-process were systematically depleted relative to r-process nuclei. The recognition that the heavy element abundance patterns in extremely metal-deficient stars ([Fe/H]˜-3) involve exclusively r-process products (14) is now strongly supported by spectroscopic studies of an increasing number of such stars. This includes the recent study of the star CS 22892–052 ([Fe/H]=-3.2) by Sneden et al. (15), in which thorium also was detected. HST observations (16) have substantiated further this behavior; with the first detection of platinum, osmium, and lead in a metal-poor halo star, they have shown that nuclei in the r-process peak at mass A˜195 also are formed in solar r-process proportions. In general, excellent agreement with the solar r-process heavy element abundance pattern is obtained, in metal-poor stars, over the entire range of elements from barium to osmium. The level of abundance of thorium in the star CS 22892–052 again confirms that the r-process occurring in the earliest stages of evolution of our Galaxy was generally consistent with that which formed the bulk of the r-process heavy elements in solar system matter; the relative abundance levels in the barium region and immediately beyond, in the mass region A˜195, and in the actinide region are compatible with the corresponding solar ratios. We note that this is true despite the fact that the r-process/Fe ratio in the star CS 22892–052 is ˜10–50 times the solar system value. This does not, however, guarantee that the 232Th abundance in this star can provide a good age estimate.
© 1998 by The National Academy of Sciences 0027–8424/98/9518–4$2.00/0
PNAS is available online at http://www.pnas.org.
The straightforward conclusion to be drawn from these observational behaviors is that r-process nucleosynthesis, and the associated production of the critical actinide nuclear chronometers we have identified, first occurs during the very earliest stages of galactic evolution and, therefore, most likely is associated with the environments provided by the evolution of massive stars (M≈>10 M⊙) and type II supernovae. This supports the viewpoint that the nucleosynthesis history we are probing with the actinide radioactive isotopes is indeed the entire history of the Galaxy. The production history of the 232Th/238U and 235U/238U chronometers produced by the r-process should trace the rate of star formation activity in the Galaxy. This implies that 232Th/238U and 235U/238U chronometer dating should therefore provide an excellent measure of the age of the Galaxy.
2. Age Determinations with r-Process Chronometers. The critical input astrophysical quantities required for dating the epoch of galactic nucleosynthesis include: (i) the abundance ratios characterizing the matter that condensed into meteorites when the solar system formed and (ii) the production ratios of the isotopes of uranium and thorium in the relevant (r-process) nucleosynthesis site.
Abundance determinations for the thorium and uranium isotopes of interest are provided by analyses of meteoritic material. The situation for the 232Th-238U pair is complicated by the chemical differences between the two elements. Anders and Grevesse (17) found the present day value of Th/U to be 3.6, which translates into a primordial solar system ratio (232Th/238U)ss=2.32. This is the value that we have adopted in this paper. We also have used the ratio (235U/238U)ss= 0.317 provided by Anders and Grevesse.
The determination of the critical r-process production ratios (232Th/238U)r-process and (235U/238U)r-process is a sensitive function of both the input nuclear physics and the physical conditions under which the r-process proceeds. There are considerable uncertainties associated with the nuclear properties of the unstable, neutron-rich progenitors of the uranium and thorium isotopes of interest. Determinations of these production ratios available in the literature [see, e.g.. the review articles of Cowan, Thielemann, and Truran (18, 19)] yield values that span a broad range: 1.40 ≤ (232Th/238U)r-process≤ 1.90 and 0.89 ≤(235U/238U)r-process≤1.89. In our subsequent discussions, we have adopted the values (232Th/238U)r-process= 1.65±0.20 and (235U/238U)r-process=1.35±0.30, which represent averages of the values compiled by the above authors.
3. Basic Equations and a “Model-Independent” Age Determination. The equations governing the time evolution of the abundance of a radioactive nuclear species are straightforward. Assuming a homogeneous interstellar medium and instantaneous return of the products of stellar nucleosynthesis into the surrounding gas, the time evolution of species Ni can be written
where ω(t) represents the gain or loss of mass caused by accretion and winds, ψ(t) is the rate of conversion of mass into stars, λi is the decay rate of species i, and Pi is the production rate of species i, per unit mass going into stars.
Assuming no gain or loss of matter (ω(t)=0), the simple cases (which we will use in later sections) of (i) a single event nucleosynthesis history and (ii) a uniform nucleosynthesis rate yield the respective solutions:
and
The astrophysical input to these equations involves the rate of formation of the range of stellar masses within which r-process nucleosynthesis occurs. Although calculations of r-process nucleosynthesis have been carried out for a variety of plausible astrophysical sites [see. e.g., the reviews by Hillebrandt (20) and Meyer (21)], a firm identification of the appropriate environment has become possible only recently. Observations of heavy element abundance patterns in metal-deficient halo stars point strongly to the identification of r-process nucleosynthesis with the environments provided by the evolution of massive stars and supernovae of Type II. In this context, the most promising mechanism of r-process synthesis would appear to be that associated with the neutrino-heated “hot bubble” supernova ejecta (22–23), although an r-process associated with the decompression of cold neutron matter from neutron star mergers (24) provides a viable alternative. An important consequence of the identification of the r-process with such massive stars (M>≈10 M⊙) of short lifetimes (τ< ≈108 years) is that we can reasonably expect that the age we determine from r-process chronometer studies is indeed representative of the age of the Galaxy itself.
The effects of galactic chemical evolution introduce significant complications for age determinations. There is a very substantial literature concerning chemical evolution effects on age dating, including considerations of varied prescriptions for the star formation history, and of the consequences of infall and outflow of gas from the star-forming regions. This literature has been reviewed most recently by Cowan, Thielemann and Truran (18, 19). In general, such age determinations are quite model-dependent.
Meyer and Schramm (25), extending the early work by Schramm and Wasserburg (26). sought to provide a model-independent age determination. In the limit of long-lived chronometers (λT≪1), they derive a simple expression for the age that is approximately independent of galactic evolution effects. In this context, Th/U can be used to provide a firm lower limit, and Re/Os can be used to provide a firm upper limit. When account is taken of the additional constraint that r-process nucleosynthesis must also produce appropriate levels of such shorter lived nuclei as 244Pu (τ1/2=8.2×107 years), Meyer and Schramm (25) arrive at a very firm lower bound on the age of the Galaxy (T+τss)>9.6 Gyr.
4. Lower Bounds on the Age of the Galaxy. Lower bounds on the age of the elements can be obtained by considerations of the long-lived actinide chronometers, on the assumption of a single event nucleosynthesis history. In this section, we will determine limits based on both the 235U/238U and the 232Th/ 238U chronometer pairs.
For the case of the 235U/238U pair, the appropriate equation is
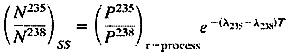
where the primordial solar system ratio is (N235/N238)ss= 0.317 and the r-process production ratio is (P235/P238)r-process= 1.35±0.30. This yields a time scale for the epoch of nucleosynthesis of T=1.75±0.25 Gyr and a limiting age for the Galaxy (T+τss) of
(T+τss)=6.3±0.25 Gyr
We can similarly use the 232Th/238U ratio to arrive at a lower bound on the galactic age. For the case of the 232Th/238U pair, the appropriate equation is
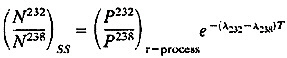
The primordial solar system ratio is (N232/N238)ss=2.32, and the r-process production ratio is (P232/P238)r-process=1.65± 0.20. This yields a time scale for the epoch of nucleosynthesis of T=3.3±1.20 Gyr, and a limiting age for the Galaxy (T+ tss) of
(T+tss)=7.9±1.20 Gyr
We emphasize again that these represent firm lower limits on the galactic age.
5. Implications of a Uniform Nucleosynthesis Rate. The presence of relatively short lived r-process chronometers in primitive solar system matter (e.g., the radioactive isotopes 107Pd, 129I, 182Hf, and 244Pu) constrains the history of r-process synthesis to include significant recent production (a single early r-process event is excluded). The history of star formation and nucleosynthesis activity thus becomes a significant consideration. It was the recognition of this constraint that led Meyer and Schramm (25) to the determination of a lower bound (T+tss)>9.6 Gyr. These authors also concluded that “the effective nucleosynthesis rate was relatively constant over most of the duration of nucleosynthesis…” based on considerations of 244Pu. Wasserburg, Busso, and Gallino (27) recently have argued for such uniform production of the heavy r-process nuclei (A>140) on observational grounds. They find consistency for 182Hf, 244Pu, 235U, 238U, and 232Th, with a uniform nucleosynthesis history.
Given the fact that a rather uniform rate of nucleosynthesis seems most consistent with observations of short-lived r-process chronometers, we can use the 232Th/238U ratio to arrive at an (admittedly) model-dependent age estimate. With the assumption of a constant nucleosynthesis rate over galactic history, the appropriate equation for the case of the 232Th-238U pair is

where, again, the primordial solar system ratio is (232Th/ 238U)ss=2.32 and the r-process production ratio is (232Th/ 238U)r-process=1.65±0.20. This yields a time scale for the epoch of nucleosynthesis of T=8.2±3 Gyr and an age for the Galaxy (T+tss) of
(T+tss)=12.8±3 Gyr
This estimate is intriguingly consistent with galactic age determinations from globular clusters. It also should be noted that an approximately uniform star formation and nucleosynthesis history are consistent with such other observed galactic abundance trends as the relatively “flat” age-metallicity relation for disk stars (28).
6. A Th/Eu Age for a Halo Star. Considerable interest recently has focused on the possibility of a direct determination of the age of an extremely metal deficient (read: extremely old) halo field star, from a knowledge of its thorium abundance (15, 29). In this case, because we have no observational information concerning the abundances of the isotopes of uranium, it is necessary to consider the abundance of thorium relative to some stable r-process species. An obvious choice here is the element europium, the production of which is attributed entirely to the r-process (it is an “r-only” element).
The straightforward determination of the age then proceeds in the following manner. Sneden et al. (15) have found the ratio Th/Eu for the metal deficient ([Fe/H]=-3.2) halo star CS 22892–052 to be (Th/Eu)*=0.219±0.0438. The ratio Th/Eu at the time of formation of the solar system, from the compilation of Anders and Grevesse (17), is (Th/Eu)ss=0.463. With the assumption that the primordial ratio Th/Eu for CS 22892–052 was identical to that of the Sun. we can then obtain an age for the star as (tTh=20.27 Gyr)
0.463exp(-T*/tTh)=0.219
Note that here we have: (i) ignored the uncertainties in the primordial solar system ratio (Th/Eu)ss; (ii) accepted the ± 20% (±0.08 dex) uncertainty quoted by Sneden et al. (15); and (iii) assumed a “steady-state” value for (Th/Eu)ISM over virtually the entirety of galactic history. [That is, we have assumed no evolution of the (Th/Eu)ISM ratio.] Although the value we obtain [and that quoted by Sneden et al. (15) and Cowan et al. (29)] clearly lies in an interesting range, it should be recognized that, even with the consideration of only the quoted abundance uncertainty, the age can only be constrained the range to 11.5–19.7 Gyr. If we assume a ±10% level of uncertainty associated with the Anders and Grevesse (17) value, e.g., (Th/Eu)ss=0.463±0.046, we would rather arrive at an allowed age range 9.3=T=21.6 Gyr.
The assumption that the (Th/Eu)ISM ratio has remained constant over the history of the Galaxy is also considerably uncertain. The fact that the r-process abundances in the metal poor stars are found to be compatible with solar r-process abundances all of the way from barium to platinum is encouraging. It certainly does not allow us to conclude, however, that this is true out through the actinide region. Although theoretical models of the operation of the r-process in these regions can generally reproduce the observed abundance trends, there remain considerable uncertainties in abundance predictions past the A˜190 r-process peak. The fact that the r-process/Fe ratio for the star CS 22892–052 is ˜10–50 times the solar ratio further implies that we are looking at a very early and substantially unmixed phase of galactic evolution; individual supernova r-process episodes might be expected to show greater dispersion in the Th/(light r-element) ratio.
DISCUSSION AND CONCLUSIONS
In general, the observational and theoretical considerations briefly reviewed in this paper allow the following conclusions:
-
The important nuclear chronometers are r-process products.
-
The identification of the r-process site with massive stars, supported by the observations of r-process abundance patterns in halo stars, implies that the critical chronometers for dating the Galaxy were formed early in galactic history and were produced at rates proportional to the star formation rate.
-
Lower bounds on the age of the elements based on the assumption of a single nucleosynthesis event can be obtained from both the 235U/238U and 232Th/238U chronometric pairs, yielding (T+tss)>6.3±0.25 Gyr for 235U/238U and (T+tss)>7.9±1.20 Gyr for 232Th/238U.
-
The very presence of shorter lived r-process chronometers such as 129I, 182Hf, and 244Pu in primitive solar system matter demands some level of recent r-process nucleosynthesis. This will necessarily yield longer age estimates for the epoch of galactic nucleosynthesis than are predicted for a single event model. Meyer and Schramm (25) obtained a firm lower bound (T+tss)>9.6 Gyr. With the assumption of a constant nucleosynthesis rate over the entirety of Galactic nucleosynthesis history, we obtain from consideration of the 232Th-238U chronometer pair an age estimate for the Galaxy of (T+tss)=12.8±3 Gyr.
-
The thorium abundance obtained for the halo star CS 22892–052 by Sneden et al. (15), with the questionable assumption that the primordial ratio Th/Eu for CS 22892– 052 was identical to that of the Sun, yields an age for the star of ˜15.2 Gyr, with an allowed range of ages of ˜10–20 Gyr.
1. Rutherford, E. (1929) Nature (London) 123, 313.
2. Burbidge, E.M., Burbidge, G.R., Fowler, W.A. & Hoyle, F. (1957) Rev. Mod. Phys. 29, 547.
3. Cameron, A.G.W. (1957) Chalk River Rep. 41.
4. Fowler, W.A. & Hoyle, F. (1960) Ann. Phys. 10, 280.
5. Cameron, A.G.W. (1962) Icarus 1, 13.
6. Truran, J.W. & Cameron, A.G.W. (1911) Ap. Space Sci. 14, 179.
7. Reeves, H. (1972) A & A 19, 215.
8. Tinsley, B.M. (1975) Ap. J. 198, 145.
9. Tinsley, B.M. (1980) Fundam. Cosmic. Phys. 5, 287.
10. Clayton, D.D. (1988) MNRAS 234, 1.
11. Clayton, D.D. (1964) Ap. J. 139, 637.
12. Wheeler, J. C., Sneden, C. & Truran, J.W. (1989) ARA & A 27, 279.
13. McWilliam. A. (1997) ARA & A, 35, 503.
14. Truran, J.W. (1981) A & A 97, 391.
15. Sneden, C., McWilliam, A., Preston, G.W., Cowan, J.J., Burris. D.L. & Armosky, B.J. (1996) Ap. J. 467, 819.
16. Cowan, J.J., Sneden, C., Truran, J.W. & Burris, D.L. (1996) Ap. J. 460, L115.
17. Anders, E. & Grevesse, N. (1989) Geochim. Cosmochim. Acta 53, 197.
18. Cowan, J.J., Thielemann, F.-K. & Truran, J.W. (1991a) Phys. Rep. 208, 267.
19. Cowan, J.J., Thielemann, F.-K. & Truran, J.W. (1991b) ARA & A 29, 447.
20. Hillebrandt, W. (1978) Space Sci. Rev. 21, 639.
21. Meyer, B.S. (1994) ARA & A 32, 153.
22. Woosley, S.E., Wilson, J.R., Mathews, G.J., Hoffman, R.D. & Meyer, B.S. (1994) Ap. J. 433, 229.
23. Takahashi, K., Witti, J. & Janka, H.-T. (1994) A & A 286, 857.
24. Lattimer, J.M., Mackie. F., Ravenhall, D.G. & Schramm, D.N. (1977) Ap. J. 213, 225.
25. Meyer, B.S. & Schramm. D.N. (1986) Ap. J. 311, 406.
26. Schramm, D.N. & Wasserburg, G.T. (1970) Ap. J. 162, 57.
27. Wasserburg, G.J., Burro, M. & Gallino. R. (1996) Ap. J. 466, L109.
28. Edvardsson B., Andersen J., Gustafsson B., Lambert D.L., Nissen P.E. & Tomkin J. (1993) A & A 275, 101.
29. Cowan, J.J., McWilliam, A., Sneden, C. & Burris, D.L. (1997) Ap. J. 480, 246.




