Proc. Natl. Acad. Sci. USA
Vol. 95, pp. 2–7, January 1998
Colloquium Paper
This paper was presented at a colloquium entitled “The Age of the Universe, Dark Matter, and Structure Formation,” organized by David N.Schramm, held March 21–23, 1997, sponsored by the National Academy of Sciences at the Beckman Center in Irvine, CA.
Measuring cosmological parameters
WENDY L. FREEDMAN*
Carnegie Observatories, 813 Santa Barbara Street, Pasadena, CA 91101
ABSTRACT In this review, the status of measurements of the matter density (Ωm), the vacuum energy density or cosmological constant (ΩΛ), the Hubble constant (H0), and the ages of the oldest measured objects (t0) are summarized. Three independent types of methods for measuring the Hubble constant are considered: the measurement of time delays in multiply imaged quasars, the Sunyaev-Zel’dovich effect in clusters, and Cepheid-based extragalactic distances. Many recent independent dynamical measurements are yielding a low value for the matter density (Ωm≈0.2–03). A wide range of Hubble constant measurements appear to be converging in the range of 60–80 km/sec per megaparsec. Areas where future improvements are likely to be made soon are highlighted—in particular, measurements of anisotropies in the cosmic microwave background. Particular attention is paid to sources of systematic error and the assumptions that underlie many of the measurement methods.
It is encouraging that very rapid progress is being made in measuring the cosmological parameters that describe the dynamical evolution and the geometry of the Universe. However, despite the considerable advances, the accuracy of cosmological parameters is not yet sufficiently high to discriminate amongst many existing world models with very different implications. Fortunately, there are a number of opportunities on the horizon that will allow us to do so.
In the context of the general theory of relativity, and assumptions of large-scale homogeneity and isotropy, the dynamical evolution of the Universe is specified by the Friedmann equation
where a(t) is the scale factor, ![]() is the Hubble parameter (and H0 is the Hubble “constant” at the present epoch), G is the gravitational constant, ρm is the average mass density, k is a curvature term, and Λ is the cosmological constant, a term that represents the energy density of the vacuum. It is common practice to define the matter density
is the Hubble parameter (and H0 is the Hubble “constant” at the present epoch), G is the gravitational constant, ρm is the average mass density, k is a curvature term, and Λ is the cosmological constant, a term that represents the energy density of the vacuum. It is common practice to define the matter density ![]() the vacuum energy density
the vacuum energy density ![]() and the curvature term
and the curvature term ![]() For the case of a flat universe where k=0, Ωm+ΩΛ=1. The simplest case is the Einstein-de Sitter model with Ωm=1 and ΩΛ=0.
For the case of a flat universe where k=0, Ωm+ΩΛ=1. The simplest case is the Einstein-de Sitter model with Ωm=1 and ΩΛ=0.
Bounds on several cosmological parameters are summarized in Fig. 1 in a plot of the matter density as a function of the Hubble constant, following Carroll et al. (1). Solid lines represent the expansion ages for 10, 15, and 20 billion years (Gyr) in an open (Λ=0) model. The gray box is defined by values of H0 in the range of 40 to 90 km·sec−1·Mpc−1 [1 megaparsec (Mpc)=3.09×1022 m] and 0.15<Ωm<0.4. The
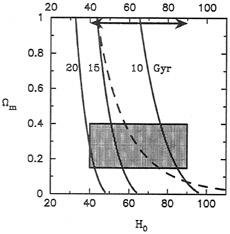
FIG. 1. Ωm versus H0 showing current observational limits on cosmological parameters. Solid lines denote expansion ages for an open (ΩΛ=0) Universe and the broken line denotes an expansion age of 15 Gyr in the case of a flat (ΩΛ≠0) Universe.
solid arrow denotes the same range in H0 for Ωm=1. This plot illustrates the well known “age” problem; namely that for an Einstein-de Sitter Universe (Ω=1, Λ=0), H0 must be less than ≈45 km·sec−1·Mpc−1, if the ages of globular clusters (t0) are indeed ≈15 Gyr. This discrepancy is less severe if the matter density of the Universe is less than the critical density, or if a nonzero value of the cosmological constant is allowed. For example, the broken line indicates an expansion age of 15 Gyr in the case of a flat (Ωm+ΩΛ=1) model for Λ≠0.
A number of issues that require knowledge of the cosmological parameters remain unresolved at present. First is the question of time scales (H0t0) discussed above; possibly a related issue is the observation of red galaxies at high redshift. Second is the amount of dark matter in the Universe. As discussed below, many dynamical estimates of the mass over a wide range of scale sizes are currently favoring values of Ωm≈ 0.25±0.10, lower than the critical Einstein-de Sitter density. And third is the origin of large-scale structure in the Universe. Accounting for the observed power spectrum of galaxy clustering has turned out to be a challenge to the best current structure formation models.
© 1998 by The National Academy of Sciences 0027–8424/98/952–6$2.00/0
PNAS is available online at http://www.pnas.org.
|
* |
To whom reprint requests should be addressed. e-mail: wendy@rmdm.ociw.edu. |
Taking the current data at face value (low Ωm, ages of globular clusters ≈15 Gyr), then even for “low” values of H0, ≈50 km·sec−1·Mpc−1, there appears to be a conflict with the standard Einstein-de Sitter model. One way out of these current difficulties is to introduce a nonzero value of a cosmological constant, Λ. In fact, it is precisely the resolution of these problems that has led to a recent resurgence of interest in a nonzero value of Λ [e.g., Ostriker and Steinhardt (2) and Krauss and Turner (3)]. On the basis of purely theoretical considerations, a very low value of H0 (≤30) could also resolve these issues [e.g., Bartlett et al. (4)]. However, the central critical issues now are (and in fact have always been) testing for and eliminating sources of significant systematic error in the measurements of cosmological parameters. These issues, including also a discussion of age determinations, are discussed in more detail in a very recent review by Freedman (5), and the current text summarizes that discussion.
Ωm— The Matter Density
A wide range of different techniques have been developed for measuring the matter density of the Universe. These techniques apply over a wide range of scales, from galaxy (≈100– 200 kpc), through cluster (Mpc), on up to more global scales (redshifts of a few). Excellent recent articles summarizing measurements of Ωm have been published by Dekel et al. (6) and Bahcall et al. (7). On the scale sizes of galaxies up to clusters of galaxies, matter density estimates have been made by a number of techniques, including mass-to-light ratios, dynamics of satellite galaxies, x-ray measurements, weak lensing. estimates of the baryon fraction, pairwise and peculiar velocities (see refs. 6 and 7 and references therein). Most of these determinations are consistent with a value of Ω= 0.2–0.3. On larger scale sizes (up to 300 Mpc), the situation is less clear. In the measurements of peculiar velocities of galaxies, differences in both the analysis of the Tully-Fisher data, in addition to the models, are leading independent groups to come to very different conclusions, with estimates of Ωm ranging from about 0.2 to 1.3. Understanding the sources of these disagreements is clearly an important goal.
Because lower values of the matter density tend to be measured on smaller spatial scales, it has given rise to the suspicion that the true global value of Ω0 must be measured on scales beyond even those of large clusters—i.e., scales of greater than ≈100 Mpc [e.g., Dekel (8)]. In that way. one might reconcile the low values of Ωm inferred locally with a spatially flat Universe. However, recent studies (7) suggest that the mass-to-light ratios of galaxies do not continue to grow beyond a scale size of about 200 kpc (corresponding to the sizes of large halos of individual galaxies). In their analysis of the dynamics of 16 rich clusters, Carlberg et al. (9) also see no further trend with scale. Hence, currently the observational evidence does not indicate that measurements of Ωm on cluster size scales are biased to lower values than the true global value. Clearly, determining whether there is a smooth component to the matter density on the largest scales is a critical issue that must be definitively resolved.
It is important to keep in mind that all of these methods are based on a number of assumptions. Although in many cases 95% confidence limits are quoted, these estimates must ultimately be evaluated in the context of the validity of their underlying assumptions. It is nontrivial to assign a quantitative uncertainty in many cases, but in fact systematic effects may be the dominant source of uncertainty. They include, for example, diverse assumptions about mass tracing light, mass-to-light ratios being constant, clusters being representative of the Universe, clumping of x-ray gas, nonevolution of type Ia supernovae, and the nonevolution of elliptical galaxies. For methods that operate over very large scales (gravitational lensing and type la supernovae), assumptions about ΩΛ or Ωtotal are currently required to place limits on Ωm.
ΩΛand ΩmLimits
The subject of the cosmological constant Λ has had a long and checkered history in cosmology. There are many reasons to be skeptical about a nonzero value of the cosmological constant. First, there is a discrepancy of ≥120 orders of magnitude between current observational limits and estimates of the vacuum energy density based on current standard particle theory (e.g., ref. 1). Second, it would require that we are now-living at a special epoch when the cosmological constant has begun to affect the dynamics of the Universe (other than during a time of inflation). In addition, it is difficult to ignore the fact that historically a nonzero Λ has been called upon to explain a number of other apparent crises, and moreover, adding additional free parameters to a problem always makes it easier to fit data. Moreover, the oft-repeated quote from Einstein to Gamov about his “biggest blunder” continues to undermine the credibility of a nonzero value for Λ.
However, despite the very persuasive arguments that can be made for Λ=0, there are solid reasons to keep an open mind on the issue. First, at present there is no known physical principle that demands Λ=0. [In fact, supersymmetry provides a mechanism, but it is known that supersymmetry is broken (10)]. Second, unlike the case of Einstein’s original arbitrary constant term, standard particle theory and inflation now provide a physical interpretation of Λ: it is the energy density of the vacuum (e.g., ref. 10). Third, if theory demands Ωtotal=1, then a number of observational results can be explained with a low Ωm and Ωm+ΩΛ=1:
-
For instance, the observed large-scale distribution of galaxies, clusters, large voids, and walls is in conflict with that predicted by the (standard) cold dark matter model for the origin of structure [e.g., Davis et al. (11) and Peacock and Dodds (12).
-
The low values of the matter density based on a number of methods as described above. In addition, the discrepancy between the ages of the oldest stars and the expansion age can be resolved. Perhaps the most important reason to keep an open mind is that this is an issue that ultimately must be resolved by experiment.
The importance of empirically establishing whether there is a nonzero value of Λ cannot be overemphasized. However, it underscores the need for high-accuracy experiments: aspects of the standard model of particle theory have been tested in the laboratory to precisions unheard of in most measurements in observational cosmology. Nevertheless, cosmology offers an opportunity to test the standard model over larger scales and higher energies than can ever be achieved by other means. It scarcely needs to be said that overthrowing the Standard Model (i.e., claiming a measurement of a nonzero value for Λ) will require considerably higher accuracy than is currently available.
In the next section, limits on Λ based on the observed numbers of quasars multiply imaged by galaxy “lenses” are briefly discussed.
Gravitational Lens Statistics
Fukugita et al. (13, 14) and Turner (15) suggested that a statistical study of the number density of gravitational lenses could provide a powerful test of a nonzero Λ. The basic idea behind this method is simple: for larger values of ΩΛ, there is a greater probability that a quasar will be lensed because the volume over a given redshift interval is increased. In a flat universe with a value of ΩΛ=1, approximately an order of magnitude more gravitational lenses are predicted than in a universe with ΩΛ=0 (15). In practice, however, there are a
number of complications: galaxies evolve with time, they contain dust, the properties of the lensing galaxies are not well known (in particular, the dark matter velocity dispersion is unknown), and the numbers of lensing systems known at present is very small (≈20). Moreover, while the predicted effects are very large for ΩΛ=1, because the numbers are such a sensitive function of ΩΛ, it is very difficult to provide limits below a value of about 0.6, given these complicating effects.
Kochanek (16) has recently discussed these various effects in some detail, and he has investigated the sensitivity of the results to different lens models and extinction. His best estimated limits to date are: ΩΛ<0.66 (95% confidence) for Ωm +ΩΛ=1, and Ωm=0.15 (90% confidence) if ΩΛ=0. Significant improvements to these limits could be made by increasing the size of the current lens samples.
Ωmand ΩΛfrom Type Ia Supernovae
The use of type Ia supernovae for measuring cosmological parameters was covered in detail in this colloquium by R. Kirshner [see also Perlmutter et al. (18)].
The obvious advantage of type Ia supernovae is the small dispersion in the Hubble diagram, particularly after accounting for differences in the overall shapes or slopes of the light curves (19–21). In principle, separation of the effects of deceleration or a potential nonzero cosmological constant is straightforward, provided that (eventually) supernovae at redshifts of order unity can be measured with sufficient signal-to-noise and resolution against the background of the parent galaxies. The differences in the observed effects of Ωm and ΩΛ become increasingly easier to measure at redshifts exceeding ≈0.5. In principle, the evolution of single stars should be simpler than that of entire galaxies (that have been used for such measurements in the past).
At the present time, however, it is difficult to place any quantitative limits on the expected evolutionary effects for type Ia supernovae because the progenitors for these objects have not yet been unequivocally identified. Moreover, there may be potential differences in the chemical compositions of supernovae observed now and those observed at earlier epochs. In principle, such differences could be tested for empirically (as is being done for Cepheid variables, for example). It is also necessary to correct for obscuration due to dust (although in general, at least in the halos of galaxies, these effects are likely to be small; a minor worry might be that the properties of the dust could evolve over time). In detail, establishing accurate magnitudes corrected for redshift (K-corrections) for high-redshift supernovae, measuring reddenings, and correcting for potential evolutionary effects will be challenging, although, with the exception of measurements of the cosmic microwave background anisotropies (discussed below), type Ia supernovae may offer the best potential for measuring Ωm and ΩΛ.
Summary of Current Ωmand ΩΛMeasurements
What can be concluded about the value of Ω? Given the available evidence and the remaining uncertainties, plus underlying assumptions at the present time, in my own view the data are still consistent with both an open and a flat Universe. This undesirable situation is very likely to be resolved in the near future with more accurate mapping of the anisotropies in the cosmic microwave background radiation (see below). At this point in time, however, I believe that it is premature either to sound the death knell for (“standard”) inflationary theories or to conclude contrarily that an open Universe is not a viable option.
H0—The Hubble Constant
The requirements for measuring an accurate value of H0 are simple to list in principle, but extremely difficult to meet in practice (e.g., ref. 22). The measurement of H0 to ±1% is not yet possible: however, recent progress (reviewed below) illustrates that a measurement to ±10% is now feasible.
Unfortunately, the methods for measuring H0 cannot be cleanly separated into purely “physical” and “astronomical” techniques, as is sometimes stated. Rather, each method has its own set of advantages and disadvantages. In my view, it is vital to measure H0 by using a variety of different methods to identify potential systematic errors in any one technique. All methods require large, statistically significant samples.
For example, the gravitational lensing method is premised on very solid physical principles (e.g., refs. 23–25). Unfortunately, the astronomical lenses are not idealized systems with well defined properties that can be measured in a laboratory; they are galaxies whose underlying (luminous or dark) mass distributions are not independently known, and furthermore they may be sitting in more complicated group or cluster potentials. A degeneracy exists between the mass distribution of the lens and the value of H0 [e.g., Kundic et al. (26) and Schechter et al. (27) and C.R.Keeton and C.S.Kochanek (personal communication)]. In a similar way, the Sunyaev-Zel’dovich method is sensitive to the clumping of x-ray gas, discrete radio sources, the projection of the clusters, and other astrophysical complications.
Below, progress on H0 measurements based on gravitational lenses, the Sunyaev-Zel’dovich effect, and the extragalactic distance scale is briefly summarized.
Gravitational Lenses
Refsdael (23, 24) noted that the arrival times for the light from two gravitationally lensed images of a background point source are dependent on the path lengths and the gravitational potential traversed in each case. Hence, a measurement of the time delay and the angular separation for different images of a variable quasar can be used to provide a measurement of H0. This method offers tremendous potential because it can be applied at great distances and it is based on very solid physical principles. Moveover, the method is not very sensitive to Ωm and ΩΛ. Some of the practical difficulties in applying this method have already been discussed in the previous section.
A number of new results based on this technique have recently appeared. Estimates of time delay measurements are now available for two systems: 0957+561 [Kundic et al. (26)], and most recently, a new time delay has been measured for PG 1115 [Schechter et al. (27) and Keeton and Kochanek (personal communication)].
In the case of 0957+561, progress has been made on several fronts. On the basis of a new measurement of the time delay by Kundic et al. (26), the model of Grogin and Narayan (28). and new Keck velocity dispersions measurements by Falco et al. (29), the latter authors have recently derived a value of H0 in the range 62–67±8 km·sec−1·Mpc−1 for this system. The velocity dispersion in the lensing galaxy appears to decrease very steeply as a function of position from the center of the galaxy; further higher-resolution measurements will be required to determine the reliability of these faint measurements.
Schechter et al. (27) have undertaken an extensive optical monitoring program to measure two independent time delays in the quadruply imaged quasar PG 1115+080. They fit a variety of models to this system, preferring a solution that yields a value of H0=42 km·sec−1·Mpc−1±14% (for Ω=1). They also considered additional models that yield values of H0 =64 and 84 km·sec−1·Mpc−1. Keeton and Kochanek (17) have
considered a wider class of models for the lensing galaxy and group and conclude that H0=60±17 km·sec−1·Mpc−1 (1σ).
Sunyaev-Zel’dovich Effect and X-Ray Measurements
The inverse-Compton scattering of photons from the cosmic microwave background off of hot electrons in the x-ray gas of rich clusters results in a measurable decrement in the microwave background spectrum (30) known as the Sunyaev-Zel’dovich (SZ) effect. Given a spatial (preferably two-dimensional) distribution of the SZ effect and a high-resolution x-ray map, the density and temperature distributions of the hot gas can be obtained; the mean electron temperature can be obtained from an x-ray spectrum. An estimate of H0 can be made based on the definitions of the angular-diameter and luminosity distances. The method makes use of the fact that the x-ray flux is distance dependent, whereas the Sunyaev-Zel’dovich decrement in the temperature is not.
Once again, the advantages of this method are that it can be applied at large distances and, in principle, it has a straightforward physical basis. As discussed above, some of the main uncertainties with this method are due to potential clumpiness of the gas (which would result in reducing H0), projection effects (if the clusters observed are prolate, H0 could be larger), the assumption of hydrostatic equilibrium, details of the models for the gas and electron densities, and potential contamination from point sources.
To date, a range of values of H0 have been published on the basis of this method ranging from ≈25 to 80 km·sec−1·Mpc−1 [e.g., McHardy et al. (31), Birkinshaw and Hughes (32), Rephaeli (33), and Herbig et al. (34)]. The uncertainties are still large, but as more and more clusters are observed, higher-resolution (two-dimensional) maps of the decrement and x-ray maps and spectra become available, the prospects for this method will continue to improve. At this conference, J.Carlstrom reported on a new extensive survey of lenses being undertaken at both Hat Creek and the Owens Valley Radio Observatory. X-ray images are being obtained with the Röntgensatellite (ROSAT) and x-ray spectra with the Advanced Satellite for Cosmology and Astrophysics (ASCA).
The Cepheid-Calibrated Extragalactic Distance Scale
Establishing accurate extragalactic distances has provided an immense challenge to astronomers since the 1920s. The situation has improved dramatically as better (linear, large-format two-dimensional) detectors have become available, and as several new, promising techniques have been developed. For the first time in the history of this difficult field, relative distances to galaxies are being compared on a case-by-case basis, and their quantitative agreement is being established. Several detailed reviews on this progress have been written [see, for example, the conference proceedings for the Space Telescope Science Institute meeting on the Extragalactic Distance Scale edited by Donahue and Livio (35)].
The Hubble Space Telescope (HST) Key Project on H0 has been designed to undertake the calibration of a number of secondary distance methods using Cepheid variables (36–38). Briefly, there are three primary goals: (i) to discover Cepheids, and thereby measure accurate distances to spiral galaxies suitable for the calibration of several independent secondary methods; (ii) to make direct Cepheid measurements of distances to three spiral galaxies in each of the Virgo and Fornax clusters; and (iii) To provide a check on potential systematic errors both in the Cepheid distance scale and the secondary methods. The final goal is to derive a value for the the Hubble constant, to an accuracy of 10%. Cepheids are also being employed in several other HST distance scale programs [e.g., Sandage et al. (39), Saha et al. (40–42), and Tanvir et al. (43)].
In ref. 44, a comparison of Cepheid distances is made with a number of other methods, including surface-brightness fluctuations, the planetary nebula luminosity function, tip of the red giant branch, and type II supernovae. (In ref. 35 one can find extensive recent reviews of all of these methods by J. Tonry; G.Jacoby; B.F.Madore, W.L.Freedman, and S. Sakai; and R.Kirshner). In general, there is excellent agreement among these methods; the relative distances agree to within ±10% (1σ).
The results of the H0 Key Project have been summarized recently by Freedman et al. (44), Mould et al. (45), and Freedman (5, 22). For somewhat different views, see Sandage and Tammann (46). The remarks in the rest of this section follow Freedman (5, 22). At this midterm point in the HST Key Project, our results yield a value of H0=73±6 (statistical) ± 8 (systematic) km·sec−1·Mpc−1. This result is based on a variety of methods, including a Cepheid calibration of the Tully-Fisher relation, type Ia supernovae, a calibration of distant clusters tied to Fornax, and direct Cepheid distances out to ≈20 Mpc. In Table 1 the values of H0 based on these various methods are summarized.
These recent results on the extragalactic distance scale are very encouraging. A large number of independent secondary methods [including the most recent type Ia supernova calibration by Sandage et al. (39)] appear to be converging on a value of H0 in the range of 60 to 80 km·sec−1·Mpc−1. The longstanding factor-of-2 discrepancy in H0 appears to be behind us. However, these results underscore the importance of reducing remaining errors in the Cepheid distances (e.g., those due to reddening and metallicity corrections), because at present the majority of distance estimators are tied in zero point to the Cepheid distance scale. A 1σ error of ±10% on H0 (the aim of the Key Project) currently amounts to approximately ±7 km·sec−1·Mpc−1 and translates into a 95% confidence interval on H0 of roughly 55 to 85 km·sec−1·Mpc−1.
While this is an enormous improvement over the factor-of-2 disagreement of the previous decades, it is not sufficiently precise, for example, to discriminate between current models of large-scale structure formation, to resolve definitively the fundamental age problem, or to settle the question of a nonzero value of Λ. Before compelling constraints can be made on cosmological models, it is imperative to rule out remaining sources of systematic error to severely limit the alternative interpretations that can be made of the data. The
Table 1. Summary of Key Project results on H0
spectacular success of HST, and the fact that a value of H0 accurate to 10% (1σ) now appears quite feasible, also brings into sharper focus smaller (10–15%) effects that were buried in the noise during the era of factor-of-2 discrepancies. Fortunately, a significant improvement will be possible with the new infrared capability afforded by the recently augmented near-infrared capabilities of HST (the NICMOS instrument). Planned NICMOS observations will reduce the remaining uncertainties due to both reddening and metallicity by a factor of 3.
t0—Ages of the Oldest Stars
The ages of stars can be derived quite independently from the expansion age of the Universe (obtained by integrating the Friedmann equation), and they have long been used as a point of comparison and constraint on cosmology; for example, globular cluster age-dating, nucleocosmo-chronology, and white-dwarf cooling estimates for the Galactic disk. In this volume, reviews of ages are given by Reid (47), Jiminez (48), and Truran (49).
There are many excellent recent reviews covering in great detail the ages obtained for Galactic globular clusters (i.e., from a comparison of observed color magnitude diagrams and theoretical evolution models). There has been a fairly broad consensus that Galactic globular clusters are most likely at least 14–15 Gyr old [e.g. Chaboyer et al. (50), VandenBerg et al. (51), and Shi (52)].
It has not been widely appreciated that the largest uncertainty in the globular-cluster ages results from uncertainties in the distances to the globular clusters. Although the ages of globular clusters are widely regarded as theoretically determined quantities, in the process of determining ages, it is still necessary to interface theory with observation and transform the observed globular cluster magnitudes to bolometric luminosities (by means of an accurate distance scale). Recent subdwarf and RR Lyrae statistical parallax distance calibrations of globular cluster distance moduli have differed by about ≈0.25–0.30 magnitude (e.g., ref. 51). Unfortunately, as emphasized by Renzini (53), small errors in distance modulus (0.25 magnitude or 13% in distance) correspond to 25% differences in age. Even with improved Hipparcos parallax measurements [see the article by Reid in this volume (47)], there are many subtle issues (e.g., reddening, metallicity, photometric zero points) that combine to make it a very difficult problem to measure distances to better than 5% accuracy.
As summarized by Reid (47), if the new Hipparcos subdwarf parallax calibration is confirmed, the ages of globular clusters may be decreased by about 20–30%.
Cosmological Parameters from Cosmic Microwave Background Anisotropies
One of the most exciting future developments with respect to the accurate measurement of cosmological parameters will be the opportunity to measure anisotropies in the cosmic microwave background to high precision [see the reviews by Wilkinson (54) and Bond (55) in this issue of the Proceedings].
The final accuracies in measuring cosmological parameters in cosmic microwave background experiments will of course (again) depend on how well various systematic errors can be controlled or eliminated. The major uncertainties will be determined by how well foreground sources can be subtracted, and probably to a lesser extent, by calibration and instrumental uncertainties. Potentially the greatest problem is the fact that extracting cosmological parameters requires a specific model for the fluctuation spectrum. Currently the estimates of the precisions (i.e., without systematic effects included) are based on models in which the primordial fluctuations are Gaussian and adiabatic, and for which there is no preferred scale. A very different anisotropy power spectrum shape is predicted for defect theories (56), but these calculations are more difficult and have not yet reached the same level of predictive power.
In the observed anisotropy angular power spectrum, the position of the first acoustic peak is very sensitive to the value of Ω0. The determination of other cosmological parameters will also require the measurement of peaks at smaller (arc-minute) angular scales. In general, the ratio of the first to the third peaks is sensitive to the value of value of H0 [e.g., Hu and White (57)]. Excellent sky coverage is critical to these efforts to reduce the sampling variance.
Can the foreground subtraction be accounted for accurately enough to yield final accuracies of 1% or better [e.g., Bond et al. (58)]? There will be foreground contributions due to faint, diffuse Galactic emission. Microwave Anisotropy Probe (MAP) will have five frequency bands ranging from 22 to 90 GHz, allowing both the spectral and spatial distribution of the Galactic foreground to be measured. The Planck Surveyor will have nine frequency channels from 30 GHz to 900 GHz. However, there are many sources of foregrounds whose subtraction is critical: perhaps the greatest unknown is the potential contribution from GHz radio sources, many of which could potentially also be variable sources. In addition there will be foreground contributions due to diffuse emission from external galaxies, dust within galaxies, and bright infrared luminous galaxies. Until these experiments are completed, it will be difficult to assess whether these systematic uncertainties are likely to be small relative to the quoted formal uncertainties. In any event, I believe that both MAP and Planck are likely to revolutionize our understanding of cosmology.
Summary
The current best measurements for the cosmological parameters yield:
|
Ωm≈(0.2–0.4)±0.1 |
(1σ) |
|
H0≈(67–73)±7 km·sec−1·Mpc−1 |
(1σ) |
|
t0≈(14–15)±2 Gyr |
(1σ) |
|
ΩΛ<0.7 |
(2σ) |
The low value for Ωm and relatively high value for H0t0 do not favor the standard Einstein-de Sitter (Ωm=1, ΩΛ=0) Universe; however, this model cannot be ruled out at high statistical significance. Moreover, systematic errors are still a source of serious concern. If the new Hipparcos calibrations are confirmed, the ages of globular clusters may be as low as 10–12 Gyr. Rapid progress is expected in addressing these systematic effects; in particular new data from HST, Hipparcos, and MAP/Planck offer the enticing possibility that some of the cosmological parameters may soon be measured to unprecedented accuracies of ±1–5% within a decade. Let us hope that unexpected systematic errors will not continue to lurk (as they have done historically so many times before) in these future efforts to define the basic cosmological parameters.
The work presented on the Cepheid-based extragalactic distance scale has been done in collaboration with the HST Key Project team on the Extragalactic Distance Scale, and I would like to acknowledge the contributions of R.Kennicutt. J.R.Mould (co-Principal Investigators), S.Faber, L.Ferrarese. H.Ford, B.Gibson, J.Graham, J. Gunn, M.Han, J.Hoessel, J.Huchra. S.Hughes, G.Illingworth, B.F. Madore, R.Phelps, A.Saha, S.Sakai. N.Silbermann, and P.Stetson, and graduate students F.Bresolin. P.Harding. D.Kelson. L.Macri. D. Rawson, and A.Turner. This work is based on observations with the National Aeronautics and Space Administration/European Space Agency HST, obtained by the Space Telescope Science Institute, which
is operated by AURA, Inc., under National Aeronautics and Space Administration Contract 5–26555. Support for this work was provided by the National Aeronautics and Space Administration through Grant GO-2227-87A from the Space Telescope Science Institute.
1. Carroll, S.M., Press, W.H. & Turner, E.L. (1992) Astron. Rev. Astron. Astrophys. 30, 499–542.
2. Ostriker, J.P. & Steinhardt. P. (1995) Nature (London) 377, 600–602.
3. Krauss, L. & Turner, M.S. (1995) Gen. Rel. Grav. 27, 1137–1144.
4. Bartlett, J., Blanchard, A., Silk, J. & Turner, M.S. (1995) Science 267, 980–983.
5. Freedman, W.L. (1997) in Proceedings of the 18th Texas Symposium, eds. Olinto, A., Frieman, J. & Schramm, D. (World Scientific, Teaneck. NJ), in press.
6. Dekel, A., Burstein, D. & White, S.D.M. (1997) in Critical Dialogs in Cosmology, ed. Turok, N. (World Scientific, Teaneck, NJ), in press.
7. Bahcall, N.A., Lubin, L.M. & Dorman, V. (1995) Astrophys. J. Lett. 447, 81–85.
8. Dekel, A. (1994) Astron. Rev. Astron. Astrophys. 32, 371–418.
9. Carlberg, R.G. Yee, H.K.C., Ellingson, E., Morris, S.L., Abraham, R., Gravel, P., Pritchet, C.J., Smecker-Hane, T., Hartwick, F.D.A., Hesser. J.E., Hutchings, J.B. & Oke, J.B. (1997) Astrophys. J. Lett., astro-ph/9611204.
10. Weinberg, S. (1989) Rev. Mod. Phys. 61, 1–22.
11. Davis, M., Efstathiou, G., Frenk, C.S. & White, S.D.M. (1992) Nature (London) 356, 489–494.
12. Peacock, J.A. & Dodds, S.J. (1994) Mon. Not. R. Astron. Soc. 267, 1020–1034.
13. Fukugita, M., Tutamase, T. & Kasai, M. (1990) Mon. Not. R. Astron. Soc. 246, 24p–27p.
14. Fukugita, M. & Turner. E. (1991) Mon. Not. R. Astron. Soc. 253, 99–106.
15. Turner, E. (1990) Astrophys. J. Lett. 365, 43–46.
16. Kochanek, C.S. (1996) Astrophys. J. 466, 638–659.
17. Keeton, C.R. & Kochaneko, C.S. (1997) Astrophys. J. 487, 42–54.
18. Perlmutter, S. Gabi, S., Goldhaber. G., Goobar, A., Groom, D.E., et al. (1997) Astrophys. J. 483, 565–581.
19. Phillips, M. (1993) Astrophys. J. Lett. 413, 105–108.
20. Hamuy. M.M. Phillips, M.M., Maza, J., Suntzeff, N.B., Schommer, R.A. & Aviles, R. (1995) Astrophys. J. 109, 1–13.
21. Reiss, A., Press, W. & Kirshner, R. (1996) Astrophys. J. 473, 88–94.
22. Freedman, W.L. (1997) in Critical Dialogs in Cosmology, ed. Turok, N. (World Scientific. Teaneck, NJ), in press.
23. Refsdael, S. (1964) Mon. Not. R. Astron. Soc. 128, 307–310.
24. Refsdael, S. (1966) Mon. Not. R. Astron. Soc. 132, 101–111.
25. Blandford, R. & Narayan, R. (1992) Astron. Rev. Astron. Astrophys. 30, 311–358.
26. Kundic, T., Turner, E.L., Colley, W.N., Gott, J.R., III, Rhoads, J.E., Wang, Y., Bergeron, L.E., Gloria, K.A., Long, D.C., Malhotra, S. & Wambsganss, J. (1997) Astrophys. J. 482, 75.
27. Schechter, P., Bailyn. C.D., Barr, R., Barvainis, R., Becker, C.M., et al. (1997) Astrophys. J. Lett. 475, 85–88.
28. Grogin, N.A. & Narayan, R. (1996) Astrophys. J. 464, 92–113.
29. Falco, E.E., Shapiro, I.I., Moustakas, L.A. & Davis, M. (1997) Astrophys. J. 484, 70.
30. Zel’dovich, Y.B. & Sunyaev, R.A. (1969) Astrophys. Space Sci. 4, 301–316.
31. McHardy. I.M., Stewart. G.C., Edge, A.C., Cooke, B., Yamashita, K. & Hatsukade, I. (1990) Mon. Not. R. Astron. Soc. 242, 215–220.
32. Birkinshaw. M. & Hughes, J.P. (1994) Astrophys. J. 420, 33–43.
33. Rephaeli, Y. (1995) Astron. Rev. Astron. Astrophys. 33, 541.
34. Herbig, T., Lawrence, C.R. & Readhead, A.C.S. (1995) Astrophys. J. Lett. 449, L5–L8.
35. Donahue, M. & Livio, M.. eds. (1997) The Extragalactic Distance Scale (Cambridge Univ. Press, Cambridge, U.K.).
36. Freedman. W.L., Madore, B.F., Mould, J.R., Hill, R., Ferrarese, L., Kennicutt, R.C., Jr., Saha, A., Stetson, P.B., Graham, J.A., Ford, H., Hoessel, J.G., Huchra, J., Hughes, S.M. & Illingworth, G.D. (1994) Nature (London) 371, 757–762.
37. Kennicutt, R.C., Freedman, W.L. & Mould, J.R. (1995) Astron. J. 110, 1476–1491.
38. Mould, J.R., Huchra, J.P., Bresolin, F., Ferrarese, L., Ford, H.C., Freedman, W.L., Graham. J., Harding, P., Hill, R., Hoessel, J.G., Hughes, S.M., Illingworth, G.D., Kelson, D., Kennicutt, R.C., Jr., Madore, B.F., Phelps, R., Stetson, P.B. & Turner, A. (1995) Astrophys. J. 449, 413–421.
39. Sandage. A., Saha, A., Tammann, G.A., Labhardt, L., Panagia, N. & Macchetto. F.D. (1996) Astrophys. J. Lett. 460, 15–18.
40. Saha, A., Labhardt, L., Schwengeler. H., Macchetto, F.D., Panagia, N., Sandage, A. & Tammann, G.A. (1994) Astrophys. J. 425, 14–34.
41. Saha, A., Sandage, A., Labhardt, L., Schwengeler, H., Tammann, G.A., Panagia, N. & Macchetto, F.D. (1995) Astrophys. J. 438, 8–26.
42. Saha, A., Sandage, A., Labhardt, L., Tammann, G.A., Macchetto, F.D. & Panagia, N. (1996) Astrophys. J. 466, 55–91.
43. Tanvir, N.R., Shjanks, T., Ferguson, H.C. & Robinson, D.R.T. (1995) Nature (London) 377, 27–31.
44. Freedman, W.L., Madore, B.F. & Kennicutt R.C. (1997) in The Extragalactic Distance Scale, eds. Donahue, M. & Livio, M. (Cambridge Univ. Press, Cambridge, U.K.), pp. 171–185.
45. Mould, J.R. (1997) in The Extragalactic Distance Scale, eds. Donahue, M., Livio, M. & Panagia, N. (Cambridge Univ. Press, Cambridge, U.K.).
46. Sandage, A.R. & Tammann, G. (1997) in Critical Dialogs in Cosmology, ed. Turok, N. (World Scientific, Teaneck, NJ), in press.
47. Reid, I.N. (1998) Proc. Natl. Acad. Sci. USA 95, 8–12.
48. Jiminez, R. (1998) Proc. Natl. Acad. Sci. USA 95, 13–17.
49. Truran, J.W. (1998) Proc. Natl. Acad. Sci. USA 95, 18–21.
50. Chaboyer, B., Demarque, P. & Sarajediri, A. (1996) Astrophys. J. 459, 558–567.
51. VandenBerg, D.A., Bolte. M. & Stetson, P.B. (1996) Astron. Rev. Astron. Astrophys. 34, 461–461.
52. Shi, X. (1995) Astrophys. J. 446, 637–645.
53. Renzini, A. (1991) in Observational Tests of Cosmological Inflation, eds. Shanks, T., Banday, A.J., Ellis, R.S., Frenk, C.S. & Wolfendale, A.W. (Kluwer, Dordrecht. The Netherlands), pp. 131–146.
54. Wilkinson, D. (1998) Proc. Natl. Acad. Sci. USA 95, 29–34.
55. Bond, J.R. (1998) Proc. Natl. Acad. Sci. USA 95, 35–41.
56. Turok, E. (1996) Astrophys. J. Lett. 473, 5–8.
57. Hu, W. & White, M. (1996) Astrophys. J. 471, 30–51.
58. Bond. J.R., Efstathiou, G. & Tegmark, M. (1997) Mon. Not. R. Astron. Soc., astro-ph/9702100, in press.






