Proc. Natl. Acad. Sci. USA
Vol. 95, pp. 35–41, January 1998
Colloquium Paper
This paper was presented at a colloquium entitled “The Age of the Universe, Dark Matter, and Structure Formation,” organized by David N.Schramm, held March 21–23, 1997, sponsored by the National Academy of Sciences at the Beckman Center in Irvine, CA.
Cosmic microwave background theory
J. RICHARD BOND*
Canadian Institute for Advanced Research Cosmology Program. Canadian Institute for Theoretical Astrophysics, 60 Saint George Street, Toronto, ON M5S 3H8, Canada
ABSTRACT A long-standing goal of theorists has been to constrain cosmological parameters that define the structure formation theory from cosmic microwave background (CMB) anisotropy experiments and large-scale structure (LSS) observations. The status and future promise of this enterprise is described. Current band-powers in ℓ-space are consistent with a ∆T flat in frequency and broadly follow inflation-based expectations. That the levels are ~(10−5)2provides strong support for the gravitational instability theory, while the Far Infrared Absolute Spectrophotometer (FIRAS) constraints on energy injection rule out cosmic explosions as a dominant source of LSS. Band-powers at ℓ≳100 suggest that the universe could not have re-ionized too early. To get the LSS of Cosmic Background Explorer (COBE)-normalized fluctuations right provides encouraging support that the initial fluctuation spectrum was not for off the scale invariant form that inflation models prefer: e.g., for tilted Λ cold dark matter sequences of fixed 13-Gyr age (with the Hubble constant H0marginalized), ns=1.17±0.3 for Differential Microwave Radiometer (DMR) only; 1.15±0.08 for DMR plus the SK95 experiment; 1.00±0.04 for DMR plus all smaller angle experiments; 1.00±0.05 when LSS constraints are included as well. The CMB alone currently gives weak constraints on Λ and moderate constraints on Ωtot, but theoretical forecasts of future long duration balloon and satellite experiments are shown which predict percent-level accuracy among a large fraction of the 10+ parameters characterizing the cosmic structure formation theory, at least if it is an inflation variant.
THE THEORETICAL AGENDA
Cosmic Microwave Background (CMB) as a Probe of Early Universe Physics
The source of fluctuations to input into the cosmic structure formation problem is likely to be found in early universe physics. We want to measure the CMB [and large-scale structure (LSS)] response to these initial fluctuations. The goal is the lofty one of peering into the physical mechanism by which the fluctuations were generated. The contenders for generation mechanism are (i) “zero point” quantum noise in scalar and tensor fields that must be there in the early universe if quantum mechanics is applicable and (ii) topological defects that may arise in the inevitable phase transitions expected in the early universe.
From CMB and LSS observations we hope to learn the following: the statistics of the fluctuations, whether Gaussian or non-Gaussian; the mode, whether adiabatic or isocurvature scalar perturbations, and whether there is a significant component in gravitational wave tensor perturbations: the power spectra for these modes, ![]() as a function of comoving wavenumber k. Sample initial and evolved power spectra for the gravitational potential
as a function of comoving wavenumber k. Sample initial and evolved power spectra for the gravitational potential ![]() the rms power in each dln k band) are shown in Fig. 1. As the Universe evolves the initial shape of
the rms power in each dln k band) are shown in Fig. 1. As the Universe evolves the initial shape of ![]() is modified by characteristic scales imprinted on it that reflect the values of cosmological parameters such as the energy densities of baryons, cold and hot dark matter, in the vacuum (cosmological constant), and in curvature. Many observables can be expressed as weighted integrals over k of the power specta and thus can probe both density parameters and initial fluctuation parameters.
is modified by characteristic scales imprinted on it that reflect the values of cosmological parameters such as the energy densities of baryons, cold and hot dark matter, in the vacuum (cosmological constant), and in curvature. Many observables can be expressed as weighted integrals over k of the power specta and thus can probe both density parameters and initial fluctuation parameters.
The (linear) density power spectra, ![]() are also shown in Fig. 1. In hierarchical structure formation models such as those considered here, the nonlinear wavenumber kNL(t), defined by
are also shown in Fig. 1. In hierarchical structure formation models such as those considered here, the nonlinear wavenumber kNL(t), defined by ![]() grows as the universe expands. kNL(t) was in the galaxy band at redshift 3 and is currently in the cluster band. At k>kNL(t), nonlinearities and complications associated with dissipative gas processes can obscure the direct connection to the early universe physics. Most easily interpretable are observables probing the linear regime now, k<kNL(t0). CMB anisotropies arising from the linear regime are termed primary; as Fig. 1 shows, these probe 3 decades in wavenumber. LSS observations at low redshift probe a smaller, but overlapping, range. We have hope that z~3 LSS observations, when kNL(t) was larger, can extend the range, but gas dynamics can modify the relation between observable and power spectrum in complex ways. Secondary anisotropies of the CMB (see below), those associated with nonlinear phenomena, also probe smaller scales and the “gastrophysical” realm.
grows as the universe expands. kNL(t) was in the galaxy band at redshift 3 and is currently in the cluster band. At k>kNL(t), nonlinearities and complications associated with dissipative gas processes can obscure the direct connection to the early universe physics. Most easily interpretable are observables probing the linear regime now, k<kNL(t0). CMB anisotropies arising from the linear regime are termed primary; as Fig. 1 shows, these probe 3 decades in wavenumber. LSS observations at low redshift probe a smaller, but overlapping, range. We have hope that z~3 LSS observations, when kNL(t) was larger, can extend the range, but gas dynamics can modify the relation between observable and power spectrum in complex ways. Secondary anisotropies of the CMB (see below), those associated with nonlinear phenomena, also probe smaller scales and the “gastrophysical” realm.
Cosmic Parameters
Even simple Gaussian inflation-generated fluctuations for structure formation have a large number of early universe parameters we would wish to determine (see next section): power spectrum amplitudes at some normalization wavenumber kn for the modes present, ![]() shape functions for the “tilts” [vs(k), vis(k), vl(k)], usually chosen to be constant or with a logarithmic correction—e.g., vs(kn), dvs(kn)/dln k. [The scalar tilt for adiabatic fluctuations,
shape functions for the “tilts” [vs(k), vis(k), vl(k)], usually chosen to be constant or with a logarithmic correction—e.g., vs(kn), dvs(kn)/dln k. [The scalar tilt for adiabatic fluctuations,
© 1998 by The National Academy of Sciences 0027–8424/98/9535–7$2.00/0
PNAS is available online at http://www.pnas.org.
|
* |
e-mail: bond@cita.utoronto.ca. |
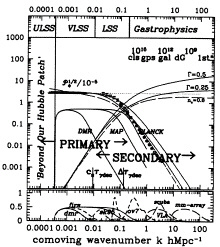
FIG. 1. The bands in comoving wavenumber k probed by CMB primary and secondary anisotropy experiments, in particular by the satellites Cosmic Background Explorer (COBE), Microwave Anisotropy Probe (MAP), and Planck, and by LSS observations are contrasted. Mpc, megaparsec (3.09×1022 m). The width of the CMB photon decoupling region and the sound crossing radius (∆τγdec, csτγdec) define the effective acoustic peak range. Sample (linear) gravitational potential power spectra [actually ![]() ] are also plotted. The region at low k gives the 4-yr Differential Microwave Radiometer (DMR) error bar on the Φ amplitude in the COBE regime. The solid data point in the cluster-band denotes the Φ constraint from the abundance of clusters, and the open data point at 10h−1 Mpc denotes a Φ constraint from streaming velocities (for Ωtot =1, ΩΛ=0). The open squares are estimates of the linear Φ power from current galaxy clustering data by ref. 1. A bias is “allowed” to (uniformly) raise the shapes to match the observations. The corresponding linear density power spectra,
] are also plotted. The region at low k gives the 4-yr Differential Microwave Radiometer (DMR) error bar on the Φ amplitude in the COBE regime. The solid data point in the cluster-band denotes the Φ constraint from the abundance of clusters, and the open data point at 10h−1 Mpc denotes a Φ constraint from streaming velocities (for Ωtot =1, ΩΛ=0). The open squares are estimates of the linear Φ power from current galaxy clustering data by ref. 1. A bias is “allowed” to (uniformly) raise the shapes to match the observations. The corresponding linear density power spectra, ![]() are also shown rising to high k. Models are the “standard” ns=1 cold dark matter (CDM) model (labeled Γ=0.5), a tilted (ns=0.6, Γ=0.5) CDM (TCDM) model, and a model with the shape modified (Γ=0.25) by changing the matter content of the Universe.
are also shown rising to high k. Models are the “standard” ns=1 cold dark matter (CDM) model (labeled Γ=0.5), a tilted (ns=0.6, Γ=0.5) CDM (TCDM) model, and a model with the shape modified (Γ=0.25) by changing the matter content of the Universe.
![]() is related to the usual index, ns, by vs= ns−1.] The transport problem (see below) is dependent upon physical processes, and hence on physical parameters. A partial list includes the Hubble parameter h, various mean energy densities [Ωtot, ΩB, ΩΛ, Ωcdm, Ωhdm]h2, and parameters characterizing the ionization history of the Universe—e.g., the Compton optical depth τC from a reheating redshift zreh to the present. Instead of Ωtot, we prefer to use the curvature energy parameter, Ωk≡1−Ωtot, thus zero for the flat case. In this space, the Hubble parameter h=(Σj(Ωjh2))1/2, and the age of the Universe, t0, are functions of the Ωjh2. The density in nonrelativistic (clustering) particles is Ωnr=ΩB+Ωcdm+Ωhdm. The density in relativistic particles, Ωer, includes photons, relativistic neutrinos, and decaying particle products, if any, Ωer, the abundance of primordial helium, etc., should also be considered as parameters to be determined. The count is thus at least 17. Estimates of errors on a smaller 9-parameter inflation set for the MAP and Planck satellites are given in the final section.
is related to the usual index, ns, by vs= ns−1.] The transport problem (see below) is dependent upon physical processes, and hence on physical parameters. A partial list includes the Hubble parameter h, various mean energy densities [Ωtot, ΩB, ΩΛ, Ωcdm, Ωhdm]h2, and parameters characterizing the ionization history of the Universe—e.g., the Compton optical depth τC from a reheating redshift zreh to the present. Instead of Ωtot, we prefer to use the curvature energy parameter, Ωk≡1−Ωtot, thus zero for the flat case. In this space, the Hubble parameter h=(Σj(Ωjh2))1/2, and the age of the Universe, t0, are functions of the Ωjh2. The density in nonrelativistic (clustering) particles is Ωnr=ΩB+Ωcdm+Ωhdm. The density in relativistic particles, Ωer, includes photons, relativistic neutrinos, and decaying particle products, if any, Ωer, the abundance of primordial helium, etc., should also be considered as parameters to be determined. The count is thus at least 17. Estimates of errors on a smaller 9-parameter inflation set for the MAP and Planck satellites are given in the final section.
The arena in which CMB theory battles observation is the anisotropy power spectrum in multipole space. Fig. 2, which shows how primary Cℓ values vary with some of these cosmic parameters. Here ![]() The
The ![]()
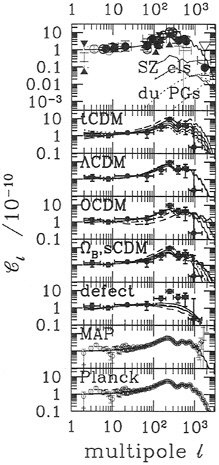
FIG. 2. The anisotropy data for experiments up to March 1997 (top panel) and optimal combined bandpower estimates (lower panels) are compared with secondary ![]() values (top panel) and various primary
values (top panel) and various primary ![]() sequences. The kinematic Sunyaev-Zeldovich
sequences. The kinematic Sunyaev-Zeldovich ![]() is off scale and the thermal SZ is low; compare the primary
is off scale and the thermal SZ is low; compare the primary ![]() values. Dusty emission from early galaxies may lead to high signals, but the power is concentrated at higher ℓ and higher frequency. The next panels are sequences of 13-Gyr models with variations in the following parameters: ns, 0.85 to 1.25 (panel 2 from the top): ΩΛ, 0 to 0.87 (H0 from 50 to 90) (panel 3); Ωk, 0 to 0.84 (H0 from 50 to 65) (panel 4); and ΩBh2, 0.003 to 0.05 (panel 5). Panel 6 shows that sample defect
values. Dusty emission from early galaxies may lead to high signals, but the power is concentrated at higher ℓ and higher frequency. The next panels are sequences of 13-Gyr models with variations in the following parameters: ns, 0.85 to 1.25 (panel 2 from the top): ΩΛ, 0 to 0.87 (H0 from 50 to 90) (panel 3); Ωk, 0 to 0.84 (H0 from 50 to 65) (panel 4); and ΩBh2, 0.003 to 0.05 (panel 5). Panel 6 shows that sample defect ![]() values from Pen, Seljak, and Turok (2) do not fare well compared with the current data;
values from Pen, Seljak, and Turok (2) do not fare well compared with the current data; ![]() values from ref. 3 are similar. Panels 7 and 8 show forecasts of
values from ref. 3 are similar. Panels 7 and 8 show forecasts of ![]() errors for the satellites MAP and Planck.
errors for the satellites MAP and Planck.
values are normalized to the 4-yr DMR(53+90+31) (A+ B) data (4–7). The arena for LSS theory is the ![]() of Fig. 1.
of Fig. 1.
For a given model, the early universe ![]() is uniquely related to late-time power spectrum measures of relevance for the CMB, such as the quadrupole
is uniquely related to late-time power spectrum measures of relevance for the CMB, such as the quadrupole ![]() or averages over ℓ-bands B,
or averages over ℓ-bands B, ![]() and to LSS measures, such as the rms density fluctuation level on the 8 h−1 Mpc (cluster) scale, σ8, so any of these can be used in
and to LSS measures, such as the rms density fluctuation level on the 8 h−1 Mpc (cluster) scale, σ8, so any of these can be used in
place of the primordial power amplitudes in the parameter set. In inflation, the ratio of gravitational wave power to scalar adiabatic power is ![]() with small corrections depending upon vs−vt (5, 8). If such a relationship is assumed, the parameter count is lowered by one.
with small corrections depending upon vs−vt (5, 8). If such a relationship is assumed, the parameter count is lowered by one.
Freedom in Inflation
Many variants of the basic inflation theme have been proposed, sometimes with radically different consequences for ![]() and thus for the CMB sky, which is used in fact to highly constrain the more baroque models. A rank-ordering of inflation possibilities: (i) adiabatic curvature fluctuations with nearly uniform scalar tilt over the observable range, slightly more power to large scales (0.8≤ns≤1) than “scale invariance” (ns=1) gives, a predictable nonzero gravity wave contribution with tilt similar to the scalar one, and tiny mean curvature (Ωtot≈1); (ii) same as t, but with a tiny gravity wave contribution; (iii) same as i but with a subdominant isocurvature component of nearly scale-invariant tilt (the case in which isocurvature dominates is ruled out); (iv) radically broken scale invariance with weak to moderate features (ramps, mountains, valleys) in the fluctuation spectrum (strong ones are largely ruled out); (v) radical breaking with non-Gaussian features as well; (vi) “open” inflation, with quantum tunneling producing a negatively curved (hyperbolic) space which inflates, but not so much as to flatten the mean curvature (dc~(Ha)−1, not >>(Ha)−1, where
and thus for the CMB sky, which is used in fact to highly constrain the more baroque models. A rank-ordering of inflation possibilities: (i) adiabatic curvature fluctuations with nearly uniform scalar tilt over the observable range, slightly more power to large scales (0.8≤ns≤1) than “scale invariance” (ns=1) gives, a predictable nonzero gravity wave contribution with tilt similar to the scalar one, and tiny mean curvature (Ωtot≈1); (ii) same as t, but with a tiny gravity wave contribution; (iii) same as i but with a subdominant isocurvature component of nearly scale-invariant tilt (the case in which isocurvature dominates is ruled out); (iv) radically broken scale invariance with weak to moderate features (ramps, mountains, valleys) in the fluctuation spectrum (strong ones are largely ruled out); (v) radical breaking with non-Gaussian features as well; (vi) “open” inflation, with quantum tunneling producing a negatively curved (hyperbolic) space which inflates, but not so much as to flatten the mean curvature (dc~(Ha)−1, not >>(Ha)−1, where ![]()
![]() (vii) quantum creation of compact hyperbolic space from “nothing” with volume
(vii) quantum creation of compact hyperbolic space from “nothing” with volume ![]() that inflates, with dT~ (Ha)−1, not >>(Ha)−1, and dT of order dc; and (viii) flat (dc =∞) inflating models that are small tori of scale dT with dT a few (Ha)−1 in size. It is quite debatable which of the cases beyond ii are more or less plausible, with some claims that iv is supersymmetry-inspired, others that vi is not as improbable as it sounds. It is the theorists’ job to push out the boundaries of the inflation idea and use the data to select what is allowed.
that inflates, with dT~ (Ha)−1, not >>(Ha)−1, and dT of order dc; and (viii) flat (dc =∞) inflating models that are small tori of scale dT with dT a few (Ha)−1 in size. It is quite debatable which of the cases beyond ii are more or less plausible, with some claims that iv is supersymmetry-inspired, others that vi is not as improbable as it sounds. It is the theorists’ job to push out the boundaries of the inflation idea and use the data to select what is allowed.
LSS Constraints on the Power Spectrum
We have always combined CMB and LSS data in our quest for viable models. Fig. 1 shows how the two are connected. DMR normalization precisely determines σ8 for each model considered; comparing with the ![]() target value derived from cluster abundance observations severely constrains the cosmological parameters defining the models. In Fig. 1, this means the COBE-normalized
target value derived from cluster abundance observations severely constrains the cosmological parameters defining the models. In Fig. 1, this means the COBE-normalized ![]() must thread the “eye of the needle” in the cluster-band.
must thread the “eye of the needle” in the cluster-band.
Similar constrictions arise from galaxy-galaxy and cluster-cluster clustering observations: the shape of the linear ![]() must match the shape reconstructed from the data. The reconstruction shown is from ref. 1. The clustering observations are roughly compatible with an allowed range 0.15≲Γ+vs/2≲ 0.3, where
must match the shape reconstructed from the data. The reconstruction shown is from ref. 1. The clustering observations are roughly compatible with an allowed range 0.15≲Γ+vs/2≲ 0.3, where ![]() characterizes the density transfer function shape. The standard CDM (SCDM) model has Γ≈0.5. To get Γ+vs/2 in the observed range one can: lower h, lower Ωnr (ΛCDM, OCDM), raise Ωer, the density parameter in relativistic particles (1.68Ωγ with three species of massless neutrinos and the photons)— e.g., as in τCDM, with a decaying v of lifetime τd and Γ≈ 1.08Ωnrh(1+0.96(mvτd/keV yr)2/3)−1/2; raise ΩB; tilt vs<0 (TCDM), for standard CDM parameters—e.g., 0.3≤ns≤0.7 would be required. Adding a hot dark matter component gives a power spectrum characterized by more than just Γ.
characterizes the density transfer function shape. The standard CDM (SCDM) model has Γ≈0.5. To get Γ+vs/2 in the observed range one can: lower h, lower Ωnr (ΛCDM, OCDM), raise Ωer, the density parameter in relativistic particles (1.68Ωγ with three species of massless neutrinos and the photons)— e.g., as in τCDM, with a decaying v of lifetime τd and Γ≈ 1.08Ωnrh(1+0.96(mvτd/keV yr)2/3)−1/2; raise ΩB; tilt vs<0 (TCDM), for standard CDM parameters—e.g., 0.3≤ns≤0.7 would be required. Adding a hot dark matter component gives a power spectrum characterized by more than just Γ.
Cosmological Radiative Transport
Cosmological radiative transfer is on a firm theoretical footing. Together with a gravity theory (invariably Einstein’s general relativity, but the CMB will eventually be used as a test of the gravity theory) and the transport theory for the other fields and particles present (baryons, hot, warm, and cold dark matter, coherent fields—i.e., “dynamical” cosmological “constants”, etc.), we propagate initial fluctuations from the early universe through photon decoupling into the (very) weakly nonlinear phase, and predict primary anisotropies, those calculated using either linear perturbation theory (e.g., for inflation-generated fluctuations), or, in the case of defects, linear response theory. The sources driving their development are all proportional to the gravitational potential Φ: the “naive” Sachs-Wolfe effect, Φ/3; photon bunching (acoustic), 1/4(δργ/ ργ), responsible for the adiabatic 1/3(δρB/ρB) effect and the isocurvature effect; linear-order Thompson scattering (Doppler), ![]() with σT the Thomson cross section, ve and n̄e the electron velocity and density, and
with σT the Thomson cross section, ve and n̄e the electron velocity and density, and ![]() the photon direction: the (line-of-sight) integrated Sachs-Wolfe effect,
the photon direction: the (line-of-sight) integrated Sachs-Wolfe effect, ![]() there are also subdominant anisotropic stress and polarization terms. For primary tensor anisotropies, the sources are the two polarization states of gravity waves,
there are also subdominant anisotropic stress and polarization terms. For primary tensor anisotropies, the sources are the two polarization states of gravity waves, ![]() again there are subdominant polarization terms.
again there are subdominant polarization terms.
Spurred on by the promise of percent-level precision in cosmic parameters from CMB satellites (see last section of this paper), a considerable fraction of the CMB theoretical community with Boltzmann transport codes compared their approaches and validated the results to ensure percent-level accuracy up to ℓ~3,000 [Cosmic Background Radiation Archive (COMBA†)]. An important goal for COMBA was speed, since the parameter space we wish to constrain has many dimensions. Most groups have solved cosmological radiative transport by evolving a hierarchy of coupled moment equations, one for each ℓ. Although the equations and techniques were in place prior to the COBE discovery for scalar modes, and shortly after for tensor modes, to get the high accuracy with speed has been somewhat of a challenge. There are alternatives to the moment hierarchy for the transport of photons and neutrinos. In particular, the entire problem of photon transport reduces to integral equations in which the multipoles with ℓ>2 are expressed as history-integrals of metric variables, photon-bunching, Doppler, and polarization sources. The fastest COMBA-validated code uses this method (9).
Secondary Anisotropies
Although hydrodynamic and radiative processes are expected to play important roles around collapsed objects and may bias the galaxy distribution relative to the mass (gastro-physics regime in Fig. 1), a global role in obscuring the early universe fluctuations by late time generation on large scales now seems unlikely. Not too long ago it seemed perfectly reasonable, based on extrapolation from the physics of the interstellar medium to the pre-galactic and intergalactic medium, to suppose hydrodynamical amplification of seed cosmic structure could create the observed Universe. The strong limits on Compton cooling from Far Infrared Absolute Spectrophotometer (FIRAS) (10), in energy δECompton cool/Ecmb=4y<6.0× 10−5 (95% confidence limits), constrain the product fexp![]() of filling factor fexp and bubble formation scale Rexp, to values too small for a purely hydrodynamic origin. If supernovae were responsible for the blasts, the accompanying presupernova light radiated would have been much in excess of the explosive
of filling factor fexp and bubble formation scale Rexp, to values too small for a purely hydrodynamic origin. If supernovae were responsible for the blasts, the accompanying presupernova light radiated would have been much in excess of the explosive
energy (more than a hundredfold), leading to much stronger restrictions (e.g., ref. 5).
Nonetheless significant “secondary anisotropies” are expected. These include: linear weak lensing, dependent on the two-dimensional (projected) tidal tensor, εAB; the Rees-Sciama effect, 2∫l,o,s, ΦNL, dependent upon the gravitational potential changes associated with nonlinear structure formation; nonlinear Thompson scattering, ![]() dependent upon the fluctuation in the electron density δne as well as ve, and responsible for the quadratic-order (Vishniac) effect and the “kinematic” Sunyaev-Zeldovich (SZ) effect (moving cluster/galaxy effect); the thermal SZ effect, associated with Compton cooling, ∫l,o,s, ψK(x)δ(neTe), where ψK(x) is a function of x=Eγ/Tγ passing from −2 on the Rayleigh-Jeans end to x on the Wein end, with a null at x=2.83 (i.e., 1,863 μm or 161 GHz); pregalactic or galactic dust emission, ~∫l,o,s,ψdust(xd)ρd, dependent upon the distribution of the dust density ρd and temperature Td through a function of xd=Eγ/Td.
dependent upon the fluctuation in the electron density δne as well as ve, and responsible for the quadratic-order (Vishniac) effect and the “kinematic” Sunyaev-Zeldovich (SZ) effect (moving cluster/galaxy effect); the thermal SZ effect, associated with Compton cooling, ∫l,o,s, ψK(x)δ(neTe), where ψK(x) is a function of x=Eγ/Tγ passing from −2 on the Rayleigh-Jeans end to x on the Wein end, with a null at x=2.83 (i.e., 1,863 μm or 161 GHz); pregalactic or galactic dust emission, ~∫l,o,s,ψdust(xd)ρd, dependent upon the distribution of the dust density ρd and temperature Td through a function of xd=Eγ/Td.
Secondary anisotropies may be considered as a nuisance foreground to be subtracted to get at the primary ones, but they are also invaluable probes of shorter-distance aspects of structure formation theories, full of important cosmological information. The k-space range they probe is shown in Fig. 1. The effect of lensing is to smooth slightly the Doppler peaks and troughs of Fig. 2. ![]() values from quadratic nonlinearities in the gas at high redshift are concentrated at high ℓ, but for most viable models they are expected to be a small contaminant. Thomson scattering from gas in moving clusters also has a small effect on
values from quadratic nonlinearities in the gas at high redshift are concentrated at high ℓ, but for most viable models they are expected to be a small contaminant. Thomson scattering from gas in moving clusters also has a small effect on ![]() (although it should be measurable in individual clusters). Power spectra for the thermal SZ effect from clusters are larger (11); examples in the top panel of Fig. 2 are for cluster-normalized HCDM and TCDM models, with
(although it should be measurable in individual clusters). Power spectra for the thermal SZ effect from clusters are larger (11); examples in the top panel of Fig. 2 are for cluster-normalized HCDM and TCDM models, with ![]() ~(0.5−1)×10−6. OCDM and ΛCDM models have slightly higher values, but still small—compare the FIRAS constraint. Although
~(0.5−1)×10−6. OCDM and ΛCDM models have slightly higher values, but still small—compare the FIRAS constraint. Although ![]() may be small, because the power for such non-Gaussian sources is concentrated in hot or cold spots the signal is detectable, and has been for two dozen clusters now at the >5σ level.
may be small, because the power for such non-Gaussian sources is concentrated in hot or cold spots the signal is detectable, and has been for two dozen clusters now at the >5σ level. ![]() for a typical dusty primeval galaxy model is also shown, the smaller angle part (arbitrarily normalized) a shot-noise effect for galaxies with dust distributed over 10 kpc, the larger angle contribution associated with clustering. Dusty anisotropies are very likely to be observable with new instrumentation on submillimeter telescopes (e.g., SCUBA on the James Clerk Maxwell Telescope on Mauna Kea). Similar shot-noise spectra are expected for other extragalactic point sources—e.g., radio galaxies.
for a typical dusty primeval galaxy model is also shown, the smaller angle part (arbitrarily normalized) a shot-noise effect for galaxies with dust distributed over 10 kpc, the larger angle contribution associated with clustering. Dusty anisotropies are very likely to be observable with new instrumentation on submillimeter telescopes (e.g., SCUBA on the James Clerk Maxwell Telescope on Mauna Kea). Similar shot-noise spectra are expected for other extragalactic point sources—e.g., radio galaxies.
CMB PARAMETER ESTIMATION, CURRENT AND FUTURE
The Theorists’ Phenomenology of CMB Experiments
We have progressed from the tens of pixels of early ∆T/T experiments through thousands for DMR (4) and SK95 (12), soon tens of thousands for long-duration balloon (LDB) experiments and eventually millions for the MAP (home page http://map.gsfc.nasa.gov) and Planck (ref. 13; home page http://astro.estec.esa.nl/SA-general/Projects/Cobras/cobras.html) satellites. Finding nearly optimal strategies for data projection, compression, and analysis that will allow us to disentangle the primary anisotropies from the Galactic and extragalactic foregrounds and from the secondary anisotropies induced by nonlinear effects will be the key to realizing the theoretically possible precision on cosmic parameters and so to determine the winners and losers in theory space. Particularly powerful is to combine results from different CMB experiments and combine these with LSS and other observations. Almost as important as the end-product is the application of the same techniques to probing the self-consistency and cross-consistency of experimental results.
Much phenomenology is done using few-parameter local models of ![]() —e.g., one with a broad-band power
—e.g., one with a broad-band power ![]() and a broad-band tilt v∆T used for COBE. It has been usual in the COBE literature to denote 1+v∆T by n, inviting confusion with the index for the primordial adiabatic fluctuation power spectrum, ns=1+vs; for SCDM models with Ωk=0 and ΩΛ =0, v∆T≈0.15+vs over the COBE band. It is evident from Fig. 2 that a single power law is a poor fit to the data when the ℓ-range is enlarged,
and a broad-band tilt v∆T used for COBE. It has been usual in the COBE literature to denote 1+v∆T by n, inviting confusion with the index for the primordial adiabatic fluctuation power spectrum, ns=1+vs; for SCDM models with Ωk=0 and ΩΛ =0, v∆T≈0.15+vs over the COBE band. It is evident from Fig. 2 that a single power law is a poor fit to the data when the ℓ-range is enlarged, ![]() -sequences such as the scalar-only tilted CDM sequence with variable ns shown in the second panel of Fig. 2 cover the rise in power suggested by the SK95 data (with ns≥1) while still matching the COBE data well and are therefore of phenomenological as well as obvious theoretical interest.
-sequences such as the scalar-only tilted CDM sequence with variable ns shown in the second panel of Fig. 2 cover the rise in power suggested by the SK95 data (with ns≥1) while still matching the COBE data well and are therefore of phenomenological as well as obvious theoretical interest.
Parameters from the CMB, Current State
Combining CMB anisotropy experiments probing different ranges in ℓ-space improves parameter estimates because of the much extended baseline. Current band-powers, shown in the top panel of Fig. 2, broadly follow inflation-based expectations (the SCDM ![]() is shown underlying them) but may still include residual signals. Lower panels compress the information into nine optimal bandpower estimates derived from all of the current data by A.Jaffe, L.Knox, and me.
is shown underlying them) but may still include residual signals. Lower panels compress the information into nine optimal bandpower estimates derived from all of the current data by A.Jaffe, L.Knox, and me.
Jaffe and I (6) have undertaken full Bayesian statistical analysis of the 4-yr DMR (4), SP94 (14), and SK94/SK95 (12, 15) data sets, taking into account all correlations among pixels in the data and theory. Other experiments were included by using their bandpowers as independent points with the Gaussian errors shown in Fig. 2. We have shown this approximate method works reasonably well by comparing results derived for DMR+SP94+SK95 with the full analysis with those using just their bandpowers (16).
With current errors on the data, simultaneously exploring the entire parameter space of the Cosmic Parameters section is not useful, so we restricted our attention to various subregions of {ΩBh2, Ωcdmh2, Ωhdmh2, Ωkh2, ΩΛh2, vs, vt, σg}, such as {σg, ns, h|fixed t0, ΩBh2}, where Ωk=0 and ΩΛ is a function of ht0 or ΩΛ=0 and Ωk>0 is a function of ht0. The age of the Universe, t0, was chosen to be 11, 13, or 15 Gyr. A recent estimate for globular cluster ages with the Hipparcos correction is 11.5±1.3 Gyr (17), with perhaps another Gyr to be added associated with the delay in globular cluster formation, so 13 Gyr is a good example. We considered the ranges 0.5≤ ns≤1.5, 0.43≤h≤1, and 0.003≤ΩBh2≤0.05. Results are mostly shown for the old “standard” nucleosynthesis estimate ΩBh2=0.0125. We assumed reheating occurred sufficiently late to have a negligible effect on ![]() by no means clear.
by no means clear. ![]() values for sample restricted parameter sequences are shown in Fig. 2. We made use of signal-to-noise compression of the data (by factors of 3) to make the calculations of likelihood functions such as
values for sample restricted parameter sequences are shown in Fig. 2. We made use of signal-to-noise compression of the data (by factors of 3) to make the calculations of likelihood functions such as ![]() more tractable (without loss of information or accuracy).
more tractable (without loss of information or accuracy).
The ns constraints are quite good. If σs is marginalized for the tilted ΛCDM sequence with H0=50, with DMR only, the primordial index is ![]() for scalar perturbations only (no gravity waves, vt=0) and
for scalar perturbations only (no gravity waves, vt=0) and ![]() (with gravity waves and vt=vs), rather encouraging for the nearly scale-invariant models preferred by inflation theory. For the 13-Gyr tilted ΛCDM sequence and H0=50 (and ΩΛ=0) we get
(with gravity waves and vt=vs), rather encouraging for the nearly scale-invariant models preferred by inflation theory. For the 13-Gyr tilted ΛCDM sequence and H0=50 (and ΩΛ=0) we get ![]() for DMR+SK95+SP94,
for DMR+SK95+SP94, ![]() when all of the data are used but SK95 and SP94 (in a bandpower approximation), and
when all of the data are used but SK95 and SP94 (in a bandpower approximation), and ![]() when all of the current data are used; for H0=70 (and ΩΛ=0.66), the numbers are quite similar, with all of the data giving
when all of the current data are used; for H0=70 (and ΩΛ=0.66), the numbers are quite similar, with all of the data giving ![]() And marginalizing over H0 gives
And marginalizing over H0 gives ![]() H0 for fixed age is not that well determined by the
H0 for fixed age is not that well determined by the
CMB data alone. After marginalizing over all ns, we get H0< 75 at 1σ, but effectively no constraint at 2σ.
For the DMR4+SK95+SP94 data, the 15-Gyr sequence with ΩB/t2 fixed at 0.0125 fits better than the 13-Gyr sequence, which in turn fits better than the 11-Gyr sequence for ns≤1. ΩB is not that well determined: if we consider just the 13-Gyr sequence with variable ΩB for ns=1, ΩB~0.17 is preferred, if we allow ns to exceed 1, then a low ΩB is preferred (and ns =1.15): but with all of the CMB data, low ΩB is preferred for ns≥1, high for ns<1. The strong dependence of the position of the acoustic peaks on Ωk means that the OCDM sequence is better restricted: e.g., for the 11-Gyr sequence H0~65 and Ωtot~0.6 is preferred, with either ns marginalized or constrained to be 1. For the 13- and 15-Gyr sequences, smaller H0s but similar Ωtots are preferred.
Parameters from the CMB+LSS, Current State
The first lesson of Fig. 2 is that, in broad brush stroke, smaller-angle CMB data (e.g., SP94, SK95) are consistent with COBE-normalized ![]() values for these models. Although the CMB data alone may soon be powerful enough to offer strong selection, this will definitely not diminish the role that combining LSS and CMB data will play. The approach we used in ref. 6 to add LSS information to the CMB likelihood functions was to design prior probabilities for Γ+vs/2 and
values for these models. Although the CMB data alone may soon be powerful enough to offer strong selection, this will definitely not diminish the role that combining LSS and CMB data will play. The approach we used in ref. 6 to add LSS information to the CMB likelihood functions was to design prior probabilities for Γ+vs/2 and ![]() reflecting the current observations, but with flexible and generous non-Gaussian and asymmetric forms to ensure the priors can encompass possible systematic problems in the LSS data. For example, our choice for
reflecting the current observations, but with flexible and generous non-Gaussian and asymmetric forms to ensure the priors can encompass possible systematic problems in the LSS data. For example, our choice for ![]() was quite flat over the 0.5 to 0.7 range, but fell off below 0.5, although some authors actually prefer such low values.
was quite flat over the 0.5 to 0.7 range, but fell off below 0.5, although some authors actually prefer such low values.
Using only the 4-yr DMR data and these priors we get ![]()
![]() with gravity waves (GW),
with gravity waves (GW), ![]() without for H0=50 TCDM, with values slightly increased when SK95 and SP94 are added. (With Ωhdm=0.2 of the dark matter in massive neutrinos, we get
without for H0=50 TCDM, with values slightly increased when SK95 and SP94 are added. (With Ωhdm=0.2 of the dark matter in massive neutrinos, we get ![]() with GW,
with GW, ![]()
![]() without.) For H0=70 and ΩΛ=0.66, we get
without.) For H0=70 and ΩΛ=0.66, we get ![]() ns=
ns= ![]() The preferred Hubble parameter for the ns=1 sequence is 70±5 (ΩΛ≈0.66).
The preferred Hubble parameter for the ns=1 sequence is 70±5 (ΩΛ≈0.66).
When H0 (range 50 to 100 for the 13-Gyr sequence) is marginalized, the LSS+DMR+SK95+SP94 data give ![]() with GW and a similar number without GW. When all ns are marginalized, we obtain H0=76±4 (ΩΛ≈0.73) with GW, 72±4 (ΩΛ≈0.7) without. When all of the current CMB data are used with the LSS priors,
with GW and a similar number without GW. When all ns are marginalized, we obtain H0=76±4 (ΩΛ≈0.73) with GW, 72±4 (ΩΛ≈0.7) without. When all of the current CMB data are used with the LSS priors, ![]() and H0= 72±3 (ΩΛ≈0.7) are obtained for the GW case,
and H0= 72±3 (ΩΛ≈0.7) are obtained for the GW case, ![]() and H0=70±3 without. (If a fixed ratio Ωhdm/Ωnr=0.2 for two degenerate massive neutrino species is included, then
and H0=70±3 without. (If a fixed ratio Ωhdm/Ωnr=0.2 for two degenerate massive neutrino species is included, then ![]()
![]() and
and ![]() is obtained, thus slightly preferring ΩΛ ~0.3.) For all of the CMB+LSS data, the 13-Gyr open sequence (without massive neutrinos) prefers Ωtot≈0.6 and H0≈54. For the 15-Gyr ΛCDM sequence, the result for ns after marginalization over all H0≥43 (the value for the ΩΛ =0 model) for all CDM plus LSS is
is obtained, thus slightly preferring ΩΛ ~0.3.) For all of the CMB+LSS data, the 13-Gyr open sequence (without massive neutrinos) prefers Ωtot≈0.6 and H0≈54. For the 15-Gyr ΛCDM sequence, the result for ns after marginalization over all H0≥43 (the value for the ΩΛ =0 model) for all CDM plus LSS is ![]() with GW,
with GW, ![]() without; and when ns is marginalized, H0=57±3 (ΩΛ≈0.6) with GW, 54±3 (ΩΛ≈0.5) without.
without; and when ns is marginalized, H0=57±3 (ΩΛ≈0.6) with GW, 54±3 (ΩΛ≈0.5) without.
Should these small error bars be taken seriously? They are driven by just the DMR plus LSS results. I would be rather surprised if σ8 from cluster abundances is drastically revised; and as we have seen, the DMR results are quite robust. The reason the errors are small is typically that the CMB data have a likelihood peaked at high σ8≳1, whereas the LSS data peak at 0.6 or so, so the product is narrow, but with a small likelihood. This asymmetry is not as pronounced for HCDM models with a light massive neutrino, and the model does not require ΩΛ>0, but it does help a bit.
CMB Constraints on Ultralarge-Scale Structure
The “beyond our horizon” land in Fig. 1 is actually partly accessible because long waves contribute gentle gradients to our observables. Constraints on such “global parameters” as average curvature are an example, ![]() though not yet very restrictive. One may also probe whether a huge bump or deficit in power exists just beyond
though not yet very restrictive. One may also probe whether a huge bump or deficit in power exists just beyond ![]() but this has not been much explored. The remarkable non-Gaussian structure predicted by stochastic inflation theory would likely be too far beyond our horizon for its influence to be felt. The bubble boundary in hyperbolic inflation models may be closer and its influence shortly after quantum tunneling occurred could possibly have observable consequences for the CMB. Theorists have also constrained the scale of topology in simple models. We (18) find the torus scale is
but this has not been much explored. The remarkable non-Gaussian structure predicted by stochastic inflation theory would likely be too far beyond our horizon for its influence to be felt. The bubble boundary in hyperbolic inflation models may be closer and its influence shortly after quantum tunneling occurred could possibly have observable consequences for the CMB. Theorists have also constrained the scale of topology in simple models. We (18) find the torus scale is ![]() Mpc from DMR for flat equal-sided three-tori at the 95% confidence limit, slightly better than other groups find since we used full map statistics. The constraint is not as strong if the repetition directions are asymmetric,
Mpc from DMR for flat equal-sided three-tori at the 95% confidence limit, slightly better than other groups find since we used full map statistics. The constraint is not as strong if the repetition directions are asymmetric, ![]() for one-tori from DMR. It is also not as strong if more general topologies are considered—e.g., the large class of compact hyperbolic topologies (18).
for one-tori from DMR. It is also not as strong if more general topologies are considered—e.g., the large class of compact hyperbolic topologies (18).
Parameters from the CMB, Future
Quite an industry has developed forecasting how well future balloon experiments (Maxima, Boomerang, ACE, Beast, Top Hat), interferometers (VSA, CBI, VCA) and especially the satellites MAP and Planck could do in measuring the radiation power spectrum and cosmological parameters if foreground contamination is ignored (13, 19–23), and that is what is done here in Table 1, using the techniques employed in ref. 22; similar results have been obtained in ref. 23. Earlier forecasts made in refs. 21 and 13 were quite influential in the case for MAP and Planck funding. The expected error bars on the power spectrum from MAP and Planck in Fig. 2 show even quite small differences in the theoretical ![]() values, and thus the parameters can be distinguished.
values, and thus the parameters can be distinguished.
We assume models have Gaussian-distributed temperature anisotropies. Among the >17 parameters of the Cosmic Parameters section, we use a restricted 9-parameter space, five densities, {ΩB, Ωnr, Ωhdm, Ωk, ΩΛ}h2, the Compton depth τC, the scalar tilt, ns, the total bandpower for the experiment ![]() in place of
in place of ![]() and the ratio of tensor to scalar quadrupole powers,
and the ratio of tensor to scalar quadrupole powers, ![]() in place of vt, rts is a sensitive function of vt, but it also depends on vs−vt, ΩΛ, etc. (5). In this space, recall that h2=Σj(Ωjh2) is a dependent quantity.
in place of vt, rts is a sensitive function of vt, but it also depends on vs−vt, ΩΛ, etc. (5). In this space, recall that h2=Σj(Ωjh2) is a dependent quantity.
Except for the integrated Sachs-Wolfe effect at low ℓ, the angular pattern of CMB anisotropies now is a direct map of the projected spatial pattern at redshift ~100, dependent upon the cosmological angle-distance relation, which is constant along a line relating Ωkh2 and ΩΛh2 for fixed Ωnrh2. This defines a near-degeneracy between Ωk and ΩΛ broken only at low ℓ. where the large cosmic variance precludes accurate determination of both parameters simultaneously, and other cosmological observables such as type I supernovae at high redshift are needed to break this degeneracy.
Error forecasts depend upon the parameters defining the correct underlying theory. In Table 1 and the lower panels of Fig. 2, untilted SCDM was chosen as the target model, but the values shown are indicative. See ref. 22 for more cases. The table shows how the forecasts work for DMR, using the average noise in the 53+90+31 GHz map for ![]() pix, 60 μK per_2.6° pixel. The channel-weighted noise power (first row) is
pix, 60 μK per_2.6° pixel. The channel-weighted noise power (first row) is ![]() In a 2-parameter tilted sequence, the forecast is for a bandpower with 7% accuracy and ns to ±0.20 accuracy, in agreement with the full analysis of the Parameters from the CMB section above. The number of orthogonal
In a 2-parameter tilted sequence, the forecast is for a bandpower with 7% accuracy and ns to ±0.20 accuracy, in agreement with the full analysis of the Parameters from the CMB section above. The number of orthogonal
Table 1. Sample DMR, NCP, LDB. MAP, and Planck parameter errors, assuming SCDM is the true theory
combinations of parameters that could be determined to better than ±0.1 accuracy was determined by using the full 9-parameter sequences. The north celestial pole (NCP) numbers are SK95-like, for a 9° radius patch. In combination with DMR, the forecast is that two combinations can be obtained to ±0.1, in agreement with the Parameters from the CMB section.
The third column gives errors forecasted for an LDB experiment [using conservative numbers for the bolometer-based TopHat experiment (home page: http://cobi.gsfc.nasa.gov/msam-tophat.html) that took account of excess noise associated with foreground removal]. Other balloon bolometer experiments such as Boomerang (home page: http://astro.caltech.edu/mc/boom/boom.html) and MAXIMA (Millimeter Anisotropy Experiment Imaging Array (home page: http://physics7.berkeley.edu/group/cmb/gen.html) should be able to do as well. High Electron Mobility Transistor (HEMT)-based LDB experiments, such as BEAST (home page: http://www.deepspace.ucsb.edu/research/Sphome.html) using 40-GHz HEMTs, might also achieve similar accuracy. The ℓ-cuts shown for NCP and LDB reflect their limited sky coverage; adding DMR to extend the baseline diminishes the forecasted errors.
We adopt improved specifications especially in beam size, ℓs, for MAP (http://map.gsfc.nasa.gov) and Planck (13) over the original proposal values; these are likely to evolve for Planck. Of the five HEMT channels for MAP, we assume the three highest-frequency channels, at 40, 60, and 90 GHz, will be dominated by the primary cosmological signal (with 30- and 22-GHz channels partly contaminated by bremsstrahlung and synchrotron emission). MAP also assumes 2 yr of observing. For Planck, 14 months of observing and current (proposal-modified) values are used. The HEMT-based LFI specifications are significantly improved; the 100-, 65-, and 44-GHz channels, but not the 30-GHz channel were used. For the bolometer-based HF1, 100, 150, 220, and 350 GHz were used. Dust contamination will certainly affect the 550-and 850-GHz channels.
These idealized error forecasts do not take into account the cost of separating the many components expected in the data, in particular Galactic and extragalactic foregrounds, but there is currently optimism that the Galactic foregrounds at least may not be a severe problem—e.g., see MAP and Planck home pages. There is more uncertainty about the extragalactic foregrounds. We forecast that not far away there will be a day when phenomenological theorists will have optimally analyzed LDBs/VSA/CBI/VCA/MAP/ Planck and delivered the power spectrum and cosmic parameters to wonderful precision. What will it mean? It may not be clear. Take inflation as an example. There will be (undoubtedly optimal) attempts to reconstruct the inflaton’s potential, but all of our CMB and LSS observations actually access only a very small region of the potential, and even this will be fuzzily determined if we allow too much freedom in parameter space. Still, even a fuzzy glimpse is worth the effort. And if the phenomenology teaches us that nonbaroque inflation and defect models fail, the CMB and LSS
data will be called upon to guide us to a new theory of how fluctuations are generated.
1. Peacock, J.A. (1996) preprint astro-ph/9608151.
2. Pen. U.-L., Seljak, U. & Turok. N. (1997) preprint astro-ph/ 9704165.
3. Allen, B., Caldwell, R.R., Dodelson. S., Knox, L., Shellard, E.P.S. & Stebbins, A. (1997) preprint astro-ph/9704160.
4. Bennett, C., Banday, A.J., Gorski, K.M., Hinshaw, G., Jackson, P., Keegstra, P., Kogut, A., Smoot, G.F., Wilkinson. D.T. & Wright, E.L. (1996) Astrophys. J. Lett. 464, 1–4.
5. Bond, J.R. (1996) in Cosmology and Large Scale Structure, Les Houches Session LX, August 1993, eds. Schaeffer, R., Silk, J., Spiro, M. & Zinn-Justin, J. (Elsevier, Amsterdam), pp. 469–674.
6. Bond, J.R. & Jaffe, A. (1996) in Microwave Background Anisotropies, Proceedings of the 31st Rencontre de Moriond, ed. Bouchet, F.R. (Edition Frontières, Paris), pp. 197–208.
7. Bond, J.R. & Jaffe, A. (1997) CITA preprint astro-ph/9610091.
8. Bond, J.R. (1994) in Relativistic Cosmology, Proceedings of the 8th Nishinomiya-Yukawa Memorial Symposium, ed. Sasaki, M. (Universal Academy Press, Tokyo), pp. 23–55.
9. Seljak, U. & Zaldarriaga, M. (1996) Astrophys. J. 469, 437–444.
10. Fixsen, D.J., Cheng, E.S., Gales, J.M., Mather, J.C., Shafer. R.A. & Wright, E.L. (1997) Astrophys. J. 473, 576–587.
11. Bond, J.R. & Myers, S. (1996) Astrophys. J. Suppl. 103, 1–79.
12. Netterfield, C.B., Devlin, M.J., Jarosik, N., Page, L. & Wollack, E.J. (1997) Astrophys. J. 474, 47.
13. Bersanelli, M., Bouchet, F.R., Efstathiou, G., Griffin, M., Lamarre, J.M., Mandolesi, N., Norgaard-Nielson, H.U., Pace, O., Polny, J., Puget, J.L., Tauber, J., Vittorio, N. & Volonte, S. (1996) COBRAS/SAMBA, The Phase A Study for an ESA M3 Mission, preprint.
14. Gundersen, J.O., Lim, M., Staren. J., Wuensche, C.A., Figueiredo, N., Gaier, T.C., Koch, T., Meinhold, P.R., Seiffert, M.D., Cook, G., Segale, A. & Lubin, P.M. (1995) Astrophys. J. Lett., 443, L57–L60.
15. Netterfield, C.B., Jarosik, N., Page, L. & Wilkinson, D. (1995) Astrophys. J. Lett. 455, L69–L72.
16. Jaffe, A.H., Knox, L. & Bond. J.R. (1997) preprint astro-ph/ 9702109.
17. Chaboyer, B., Demarque, P., Krauss, L.M. & Kernan, P.J. (1997) preprint astro-ph/9706128.
18. Bond, J.R., Pogosyan. D. & Souradeep, T. (1996) preprint astro-ph/9702212.
19. Knox, L. (1995) Phys. Rev. D 52, 4307–4318.
20. Tegmark, M. & Efstathiou, G. (1996) Mon. Not. R. Astron. Soc. 281, 1297–1314.
21. Jungman, G., Kamionkowski, M., Kosowsky, A. & Spergel. D.N. (1996) Phys. Rev. Lett. 16, 1007–1010.
22. Bond, J.R., Efstathiou, G. & Tegmark, M. (1997) Mon. Not. R. Astron. Soc., in press; preprint astro-ph/9702100.
23. Zaldarriaga, M., Spergel, D. & Seljak. U. (1997) Astrophys. J., in press; preprint astro-ph/9702157.







