Proc. Natl. Acad. Sci. USA
Vol. 95, pp. 42–46, January 1998
Colloquium Paper
This paper was presented at a colloquium entitled “The Age of the Universe, Dark Matter, and Structure Formation,” organized by David N.Schramm, held March 21–23, 1997, sponsored by the National Academy of Sciences at the Beckman Center in Irvine, CA.
Primordial nucleosynthesis
DAVID N. SCHRAMM*
University of Chicago, 5640 South Ellis Avenue. Chicago. IL 60637, and the National Aeronautics and Space Administration/Fermilab Astrophysics Center, Fermilab, Box 500, Batavia, IL 60510
ABSTRACT With the advent of the new extragalactic deuterium observations, Big Bang nucleosynthesis (BBN) is on the verge of undergoing a transformation. In the past, the emphasis has been on demonstrating the concordance of the BBN model with the abundances of the light isotopes extrapolated back to their primordial values by using stellar and galactic evolution theories. As a direct measure of primordial deuterium is converged upon, the nature of the field will shift to using the much more precise primordial D/H to constrain the more flexible stellar and galactic evolution models (although the question of potential systematic error in 4He abundance determinations remains open). The remarkable success of the theory to date in establishing the concordance has led to the very robust conclusion of BBN regarding the baryon density. This robustness remains even through major model variations such as an assumed first-order quarkhadron phase transition. The BBN constraints on the cosmological baryon density are reviewed and demonstrate that the bulk of the baryons are dark and also that the bulk of the matter in the universe is nonbaryonic. Comparison of baryonic density arguments from Lyman-α clouds, x-ray gas in clusters, and the microwave anisotropy are made.
Big Bang nucleosynthesis (BBN) and the light element abundances are in the middle of a major transformation in approach. The bottom line remains: primordial nucleosynthesis has joined the Hubble expansion and the microwave background radiation as one of the three pillars of Big Bang cosmology. Of the three. BBN probes the universe to far earlier times (~1 sec) than the other two and led to the interplay of cosmology with nuclear and particle physics. Furthermore, because the Hubble expansion is also part of alternative cosmologies such as the steady state, it is BBN and the microwave background that really drive us to the conclusion that the early universe was hot and dense. The new extragalactic deuterium observations not only cement this picture and give added convergence on a value of the baryon density, Ωb, they also enable BBN to become a constraint on stellar and galactic evolution scenarios.
Overview
Although the extragalactic D/H observations naturally have attracted the most attention, it should not be forgotten that recent heroic observations of 6Li, Be and B, as well as 3He and new 4He determinations also have been seen. Let us now briefly review the history, with special emphasis on the remarkable agreement of the observed light element abundances with the calculations. This agreement works only if the baryon density is well below the cosmological critical value. We also will note how a convergence on extragalactic D/H will enable powerful new constraints on stellar and galactic evolution.
It should be noted that a symbiotic connection exists between BBN and the 3 K background dating back to Gamow and his associates, Alpher and Herman. The initial BBN calculations of Gamow’s group (1) assumed pure neutrons as an initial condition and thus were not particularly accurate, but their inaccuracies had little effect on the group’s predictions for a background radiation.
Once Hayashi (2) recognized the role of neutron-proton equilibration, the framework for BBN calculations themselves has not varied significantly. The work of Alpher, Follin, and Herman (3) and Taylor and Hoyle (4), preceding the discovery of the 3 K background, and of Peebles (5) and Wagoner, Fowler, and Hoyle (6), immediately after the discovery, and the more recent work of our group of collaborators (7–14) all do essentially the same basic calculation, the results of which are shown in Fig. 1.
As far as the calculation itself goes, solving the reaction network is relatively simple by the standards of explosive nucleosynthesis calculations in supernovae, with the changes over the last 25 yr being mainly in terms of more recent nuclear reaction rates as input, not as any great calculational insight, although the current Kawano code (14) is somewhat stream-lined relative to the earlier Wagoner code (6). In fact, the earlier Wagoner code is. in some sense, a special adaptation of the larger nuclear network calculation developed by Truran (16, 17) for work on explosive nucleosynthesis in supernovae. With the exception of Li yields and nonyields of Be and B (18), the reaction rate changes over the past 25 yr have not had any major affect [see Yang et al. (13) and Krauss and his collaborators (19, 20), or Copi, Schramm, and Turner (8) for a discussion of uncertainties]. The one key improved input is a better neutron lifetime determination (21, 22). Much improvement has been made in the t(α,γ)7Li reaction rate, but as the width of the curves in Fig. 1 shows, the 7Li yields are still the poorest determined, both because of this reaction and even more because of the poorly measured 3He(α,γ)7Be.
With the exception of the effects of elementary particle assumptions, to which we will return, the real excitement for BBN over the last 25 yr really has not been in redoing the basic calculation. Instead, the true action is focused on understanding the evolution of the light element abundances and using that information to make powerful conclusions. In the 1960s, the main focus was on 4He, which is very insensitive to the baryon density. The agreement between BBN predictions and observations helped support the basic Big Bang model but gave no significant information, at that time, with regard to density. In fact, in the mid-1960s, the other light isotopes (which are, in principle, capable of giving density information) generally
© 1998 by The National Academy of Sciences 0027–8424/98/9542–5$2.00/0
PNAS is available online at http://www.pnas.org.
|
* |
To whom reprint requests should be addressed, e-mail: dns@oddjob.uchicago.edu. |
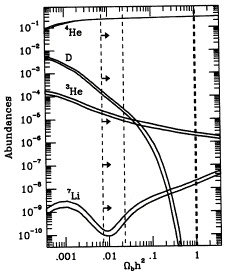
FIG. 1. BBN abundance yields vs. baryon density (Ωb) and ![]() for a homogeneous universe, (h≡H0/100 km/sec per Mpc: thus, the concordant region of Ωbh2~0.015 corresponds to Ωb~0.06 for H0 =50 km/sec per Mpc.) Figure is from Copi, Schramm, and Turner (8). Note concordance region is slightly larger than Walker et al. (9) primarily because of inclusion of possible systematic errors on Li/H. The width of the curves represents the uncertainty due to input of nuclear physics in the calculation. Recent measurements by Buries and Tytler (15) narrow the vertical concordance region toward the high Ωb side.
for a homogeneous universe, (h≡H0/100 km/sec per Mpc: thus, the concordant region of Ωbh2~0.015 corresponds to Ωb~0.06 for H0 =50 km/sec per Mpc.) Figure is from Copi, Schramm, and Turner (8). Note concordance region is slightly larger than Walker et al. (9) primarily because of inclusion of possible systematic errors on Li/H. The width of the curves represents the uncertainty due to input of nuclear physics in the calculation. Recent measurements by Buries and Tytler (15) narrow the vertical concordance region toward the high Ωb side.
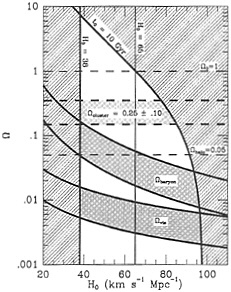
were assumed to have been made during the T-Tauri phase of stellar evolution (23), and so, were not taken then to have cosmological significance. It was during the 1970s that BBN fully developed as a tool for probing the universe. This possibility was in part stimulated by Ryter et al. (24), who showed that the T-Tauri mechanism for light element synthesis failed. Furthermore, 2D abundance determinations improved significantly with solar wind measurements (25, 26) and the interstellar work from the Copernicus satellite (27). [Recent Hubble Space Telescope observations reported by Linsky et al. (28) have compressed the local intersteller medium 2D error bars considerably.] Reeves, Audouze, Fowler and Schramm (29) argued for cosmological 2D and were able to place a constraint on the baryon density excluding a universe closed with baryons. Subsequently, the 2D arguments were cemented when Epstein, Lattimer, and Schramm (30) proved that no realistic astrophysical process other than the Big Bang could produce significant 2D. This baryon density was compared with dynamical determinations of density by Gott, Gunn, Schramm, and Tinsley (31). See Fig. 2 for an updated H0-Ω diagram.
In the late 1970s, it appeared that a complimentary argument to 2D could be developed by using 3He. In particular, it was argued (33) that, unlike 2D, 3He was made in stars: thus, its abundance would increase with time. Unfortunately, recent data on 3He in the interstellar medium (34) has shown that 3He has been constant for the last 5 Gyr. Thus, low mass stars are not making a significant addition, contrary to these previous theroetical ideas. Furthermore, Rood, Bania, and Wilson (35) have shown that interstellar 3He is quite variable in the galaxy, contrary to expectations for a low-mass, star-dominated nu
cleus. However, the work on planetary nebulae shows that at least some low-mass stars produce 3He.Nonetheless, the current observational situation clearly shows that arguments based on theoretical ideas about 3He evolution should be avoided (c.f. Hata et al., ref. 36) where their “crisis” is really about 3He problems (and excessively small assumed uncertainties in 4He),not BBN. Because 3He nowseems not to have a well-behaved history, simple 3He or 3He+D inventory arguments are misleading at best. However, one is not free to go to arbitrary low baryon densities and high primordial D and 3He, because processing of D and 3He in massive stars also produces metals that are constrained (37, 38) by the metals in the hot intra-cluster gas, if not the galaxy. In the near future, this problem with 3He evolution will be constrained severely by the extragalactic D/H. In particular, the Tytler D/H=2.6± 0.6×10−5 is almost identical to the presolar D/H=2.4± 0.4×10−5 (39) and less than a factor of 2 above the current interstellar D/H=1.5±0.1×10−5 (40). This tells us that the production of current metal content of the galaxy did not destroy much 2D. Thisimplies either a very different initial mass function to make the metals, or much primordial infall throughout the history of the galaxy.
It was interesting that the abundances of the other light elements led to the requirement that 7Li be near its minimum of 7Li/H~10−10, which was verified by the Population II (Pop II) Li measurements of Spite and Spite and their group (41–43), hence yielding the situation emphasized by Yang et al. (13) that the light element abundances are consistent over nine orders of magnitude with BBN, but only if the cosmological baryon density, Ωb, is constrained to be around 6% of the critical value (for H0![]() 50 km/sec per Mpc). The Li plateau argument was strengthened further with the observation of 6Li in a Pop II star by Smith, Lambert, and Nissen (44). Because 6Li is much more fragile than 7Li, and yet it survived, no
50 km/sec per Mpc). The Li plateau argument was strengthened further with the observation of 6Li in a Pop II star by Smith, Lambert, and Nissen (44). Because 6Li is much more fragile than 7Li, and yet it survived, no
significant nuclear depletion of 7Li is possible (18, 45, 46). This observation of 6Li now has been verified by Hobbs and Thorburn (47), and a detection in a second Pop II star has been reported. Lithium depletion mechanisms are also severely constrained by the recent work of Spite et al. (48) showing that the lithium plateau also is found in Pop II tidally locked binaries. Thus, meridonal mixing is not causing significant lithium depletion. Recently Nollett et al. (49) have discussed how 6Li itself eventually might become another direct probe of BBN depending on the eventual low energy measurement of the 2D (αγ) 6Li cross-section and on spectroscopy improvements for extreme metal-poor dwarfs. With the new extragalactic D/H, one should be able to turn the 7Li argument around and argue how much depletion and/or what model atmosphere is necessary. It is again clear from this argument that large amounts of depletion did not occur, contrary to the earlier models of Delyannis (50).
Another development back in the 1970s for BBN was the explicit calculation of Steigman, Schramm, and Gunn (51) showing that the number of neutrino generations, Nv, had to be small to avoid overproduction of 4He. [Earlier work (4, 52, 53) had commented about a dependence on the energy density of exotic particles but had not done an explicit calculation probing Nv.] To put this in perspective, one should remember that the mid-1970s also saw the discovery of charm, bottom and tau, so that it almost seemed as if each new detector produced new particle discoveries, and yet, cosmology was arguing against this “conventional” wisdom. Over the years, the limit on Nv improved with 4He abundance measurements, neutron lifetime measurements, and with limits on the lower bound to the baryon density, hovering at Nv≲4 for most of the 1980s and dropping to slightly lower than four just before Large Electron Position Collider (LEP) and Stanford Linear Collider turned on (9, 10, 54, 55). This was verified by the LEP results (ref. 56; see also CERN preprint CERN-PPE/96–183) where now the overall average is Nv=2.99±0.02. A recent examination of the cosmological neutrino limit by Copi et al. (7) in the light of the recent 3He and D/H work shows that the BBN limit remains between three and four for all reasonable assumption options. It should be noted that this limit remains robust despite the uncertainties on 4He systematics, because those uncertainties are still relatively small compared with a ∆Nv of unity, although they are not small compared with significant shifts in Ωb.
The recent apparent convergence of the extragalactic D/H measurements toward the lower values (57, 58) D/H~3× 10−5 is beginning to collapse the ΩB band in Fig. 1 to a relatively narrow strip on the high ΩB side (see arrows). However, such a full collapse at present is probably a bit premature. In any case, it is clear that deuteronomy (the study of deuterium in the cosmos) is a success because: (i) deuterium is clearly cosmological as it is seen in low metalicity and high redshift Lyman-α clouds; (ii) the primordial D/H is higher than the present ISM D/H, as predicted by theory; and (iii) the range of values for primordial D/H, regardless of whether or not the high or low ones win out, is consistent with the range of expectations based on the other light nuclei.
One potential problem that the low D/H, high ΩB solution raises is that the central primordial 4He mass fraction is ~0.23, rather than ~0.245, which the Tytler and Burles (15, 57) D/H value would prefer for concordance. However, as Copi et al. (7) emphasize, systematic uncertainties in Yp cannot rule out such an excursion. But clearly we have to look carefully at 4He.The recent work of Izotov et al. (59) on y~0.24 shows how uncertain the present situation is, but the resolution remains to be found. How high Yp can be and still be consistent with the He observations in extragalactic H-II regions is still quite debatable, although most agree that Yp up to 0.25 is not impossible.
The power of homogeneous BBN comes from the fact that essentially all of the physics input is well determined in the terrestrial laboratory. The appropriate temperature regimes, 0.1 to 1 MeV, are well explored in nuclear physics laboratories. Thus, what nuclei do under such conditions is not a matter of guesswork, but is precisely known. In fact, it is known for these temperatures far better than it is for the centers of stars like our sun. The center of the sun is only a little over 1 keV, thus, below the energy where nuclear reaction rates yield significant results in laboratory experiments, and only the long times and higher densities available in stars enable anything to take place.
Density of Baryons
The bottom line that emerges from the above discussion is that (7)
where h0≡H0/100 km/sec per Mpc. If the Tytler arguments on D/H do indeed hold up, then this will compress toward the high side, say ΩBh2~0.02±0.005. Let us now compare with other ways of estimating Ωb.
Attempts to circumvent the conclusion of homogeneous BBN by invoking a first-order quark-hadron phase transition (60, 61) merely have illustrated the robustness of the conclusions. Fig. 3 illustrates this fact.
Lyman-α Clouds. Recent work by Bi and Davidsen (62), Quashnock and Vanden Berk (63), and Weinberg et al. (64) also argues that the density of gas in the form of Lymon-α clouds at high redshift is consistent with the high end of the BBN range on Ωb. This would appear to resolve the long-time problem of where the “dark baryons” are. It is well known that ΩVISIBLE ≲ less 0.01, which, when compared with ΩBBN, implies that the bulk of the baryons are not associated with stellar material. At least at high redshift this unseen material appears to have been found in these Lyman-α clouds. In conjunction with the Lyman-α clouds, it also should be noted that singly ionized helium is seen in the intergalactic gas, thus supporting the BBN fact that helium is primordial, and also supporting the point that significant numbers of baryons were between galaxies at high redshift (62, 65).
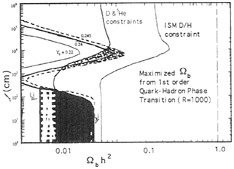
FIG. 3. An assumed first-order quark-hadron phase transition still yields the same allowed range on Ωbh2 when the same abundance constraints are used. The parameter l is the separation of nucleation sites (the most sensitive additional parameter in the calculation). The dotted region is an additional allowed region if lithium is ignored completely. Even then, the constraint on Ωb is within a factor of two of the standard value.
Hot Gas in Clusters. Hot gas has been found in clusters of galaxies by the German satellite ROSAT and the Japanese satellite ASCA. The temperature of the gas can be used to estimate the gravitational potential of the clusters if it is assumed that the gas is vivialized and purely supported by thermal pressure. Similarly, the intensity of the emission can be used to estimate the density of the gas. White et al. (66) have shown that the typical values for x-ray clusters yield a hot gas to total mass ratio MHOT/MTOT of about 0.2. If clusters are representative of the universe as they would be in standard cold dark matter models, and if ΩTOTAL=1, then MHOT/MTOT =Ωb. Even with the spread in MHOT/MTOT in clusters as found by Mushotsky (67), only a marginal overlap is at very low H0 and the high end of Ωb from BBN. Clearly, higher values of ΩBBN are favored by this argument. However, it should be noted that various systematic effects such as: magnetic field pressure in clusters (68), clumping of the hot gas regions, and admixture of hot dark matter (69) all go in the direction of increasing MTOTAL and improving the overlap. Also, if clusters are not fair samples of the universe, then concordance is not needed here. This latter point may be implied by the variations observed by Mushotsky (67), because, if clusters are fair samples, then they all should be giving the same answer. Another way to obtain concordance is if ΩTOTAL<1! All of these caveats tell us that clusters do not represent any “baryon catastrophe,” but they are important to continue to monitor, and it is clear that the overlap is better for higher ΩBBN and requires less variation from the standard assumptions. Regardless of Ωb implied by x-ray gas, the total cluster mass implied is consistent with that implied by dynamics and lensing.
Microwave Anisotropies. The method with the most potential for checking Ωb is the measurement of the acoustic peaks in the microwave background anisotropy at angular scales near 1° or less (70–72). The height of the first doppler (acoustic) peak for gaussian fluctuation models is directly related to ΩBh2, thus a direct check on BBN. Current experiments at the South Pole and at Sasketoon, and by using balloons seem to favor values near the high side of the BBN range, but the present uncertainties are too large to make any strong statements. However, the next generation of satellites, the National Aeronautics and Space Administration’s MAP and the European Space Agency’s PLANCK (formerly COBRAS/ SAMBA) should be able to fix Ωbh2 to better than 10% (if the sky is gaussian), which should provide a dramatic test of BBN.
Dark Matter
The robustness of the basic BBN arguments and the new D/H measurements have given renewed confidence to the limits on the baryon density constraints. Let us convert this density regime into units of the critical cosmological density for the allowed range of Hubble expansion rates. This is shown in Fig. 2. Fig. 2 also shows the lower bound on the age of the universe of 10 Gyr from both nucleochronology and from globular cluster dating (32) and a lower bound on H0 of 38 from extreme type IA supernova models with pure 1.4 M⊙ carbon white dwarfs being converted to 56Fe. The constraint on Ωb means that the universe cannot be closed with baryonic matter. [This point was made over 20 yr ago (73) and has proven to be remarkably strong.] If the universe is truly at its critical density, then nonbaryonic matter is required. This argument has led to one of the major areas of research at the particle-cosmology interface, namely, the search for nonbaryonic dark matter. In fact, from the lower bound on ΩTOTAL from cluster dynamics of ΩTOTAL>0.1, it is clear that nonbaryonic dark matter is required unless H0<40. The need for nonbaryonic matter is strengthened on even larger scales (74). Fig. 2 also shows the range of ΩVISIBLE and shows no overlap is between Ωb and ΩVISIBLE. Hence, the bulk of the baryons are dark.
Another interesting conclusion (32) regarding the allowed range in baryon density is that it is in agreement with the density implied from the dynamics of single galaxies, including their dark halos. The recent Massive Compact Halo Object (MACHO) (75) and Earth Resources Observation Satellite (EROS) (76) reports of halo microlensing may well indicate that at least some of the dark baryons are in the form of brown dwarfs in the halo. However, Gates, Gyuk, and Turner (77) and Alcock et al. (75, 78) show that the observed distribution of MACHOs favors less than 50% of the halo being in the form of MACHOs, but a 100% MACHO halo cannot be completely excluded yet.
For dynamical estimates of Ω, one estimates the mass from ![]() where v is the relative velocity of the objects being studied, r is their separation distance, and G is Newton’s constant. The proportionality constant out front depends on orientation, relative mass, etc. For large systems such as clusters, one uses averaged quantities. For single galaxies v would represent the rotational velocity and r the radius of the star or gas cloud. It is this technique that yields the cluster bound on Ω shown in Fig. 2. It should be noted that the value of ΩCLUSTER~0.25 also is obtained in those few cases where alignment produces giant gravitational-lens arcs. Recent work using weak gravitational lensing by Kaiser (79) also supports large Ω. As Davis (74) showed, if the large-scale velocity flows measured from the IRAS satellite survey are due to gravity, then ΩIRAS≳0.2. For H0>40, ΩCLUSTER already requires ΩTOTAL>ΩBARYON and hence the need for nonbaryonic dark matter.
where v is the relative velocity of the objects being studied, r is their separation distance, and G is Newton’s constant. The proportionality constant out front depends on orientation, relative mass, etc. For large systems such as clusters, one uses averaged quantities. For single galaxies v would represent the rotational velocity and r the radius of the star or gas cloud. It is this technique that yields the cluster bound on Ω shown in Fig. 2. It should be noted that the value of ΩCLUSTER~0.25 also is obtained in those few cases where alignment produces giant gravitational-lens arcs. Recent work using weak gravitational lensing by Kaiser (79) also supports large Ω. As Davis (74) showed, if the large-scale velocity flows measured from the IRAS satellite survey are due to gravity, then ΩIRAS≳0.2. For H0>40, ΩCLUSTER already requires ΩTOTAL>ΩBARYON and hence the need for nonbaryonic dark matter.
An Ω of unity is, of course, preferred on theoretical grounds because that is the only long-lived natural value for Ω, and inflation (80, 81) or something like it provided the early universe with the mechanism to achieve that value and thereby solve the flatness and smoothness problems. Note that our need for exotica is not dependent on the existence of dark galatic halos and that high values of H0 increase the need for nonbaryonic dark matter.
It also is interesting to note that the convergence of Ω on cluster scales at ~0.25±0.1 has important implications. If ΩTOTAL is really unity, it would necessitate clusters not being a fair sample of the universe. Because standard cold dark matter implies cluster scales as fair samples, this would imply a more complex structure formation picture. Options include biasing on cluster scales, a very hot dark matter component, or even a smooth background component such as a Λ0 term, or a vacuum energy from a late-time phase transition (82, 83).
I would like to thank my collaborators, Craig Copi, Ken Nollett. Martin Lemoine, David Dearborn, Brian Fields, Dave Thomas, Gary Steigman. Brad Meyer, Keith Olive. Angela Olinto, Bob Rosner, Michael Turner, George Fuller, Karsten Jedamzik, Rocky Kolb, Grant Mathews. Bob Rood, Jim Truran, and Terry Walker for many useful discussions. I would further like to thank Art Davidsen. Poul Nissen. Jeff Linsky, David letter, Len Cowie, Craig Hogan, Julie Thorburn, Doug Duncan, Lew Hobbs, Evan Skillman, Bernard Pagel, and Don York for valuable discussion regarding the astronomical observations. This work is supported by the National Aeronautics and Space Administration (NASA) and the Department of Energy (nuclear) at the University of Chicago, and by the Department of Energy and NASA Grant NAG5–2788 at Fermilab.
1. Alpher, R.A., Bethe, H. & Gamow, G. (1948) Phys. Rev. 73, 803–804.
2. Hayashi, C. (1950) Prog. Theor. Phys. 5, 224–235.
3. Alpher, R.A., Follin, J.W. & Herman, R.C. (1953) Phys. Rev. 92, 1347–1361.
4. Taylor, R. & Hoyle, F. (1964) Nature (London) 203, 1108–1110.
5. Peebles, P.J.E. (1966) Phys. Rev. Lett. 16, 410–413.
6. Wagoner, R., Fowler, W.A. & Hoyle, F. (1967) Astrophys. J. 148, 3–49.
7. Copi, C.J., Schramm, D.N. & Turner, M.S. (1997) Phys. Rev. D Part. Fields 55, 3389–3393.
8. Copi, C.J., Schramm, D.N. & Turner, M.S. (1994) Science 267, 192–199.
9. Walker, T., Steigman, G., Schramm, D.N., Olive, K. & Kang, H.S. (1991) Astrophys. J. 376, 51–69.
10. Olive, K., Schramm, D.N., Steigman, G. & Walker, T. (1990) Phys. Lett. B 236, 454–460.
11. Schramm, D.N. & Wagoner, R.V. (1977) Annu. Rev. Nuclear Sci. 27, 37–74.
12. Olive, K., Schramm, D.N., Steigman, G., Turner, M. & Yang, J. (1981) Astrophys. J. 246, 557–568.
13. Yang, J., Turner, M., Steigman, G., Schramm, D.N. & Olive, K. (1984) Astrophys. J. 281, 493–511.
14. Kawano, L., Schramm, D.N. & Steigman, G. (1988) Astrophys. J. 327, 750–754.
15. Tytler, D., Fan, X-M. & Burles, S. (1996) Nature (London) 381, 207–209.
16. Truran, J.W. (1965) PhD. thesis (Yale University, New Haven, CT).
17. Truran, J.W., Cameron. A.G.W. & Gilbert, A. (1966) Can. J. Phys. 44, 563–592.
18. Steigman, G., Fields, B.D., Schramm, D.N., Olive, K. & Walker, T. (1993) Astrophys. J. 415, L35–L38.
19. Krauss, L.M. & Romanelli, P. (1990) Astrophys. J. 358, 47–59.
20. Kernan, P. & Krauss, L. (1994) Phys. Rev. Lett. 72, 3309–3312.
21. Mampe, W., Ageron, P., Bates, C., Pendlebury, J.M. & Steyerl, A. (1989) Phys. Rev. Lett A 63, 593–596.
22. Mampe, W., Ageron, P., Bates, C., Pendlebury, J.M. & Steyerl, A. (1993) JETP Lett. (Engl. Transl.) 57, 82–87.
23. Fowler, W.A., Greenstein, J. & Hoyle, F. (1962) Geophys. J.R. Astron. S. 6, 148–220.
24. Ryter, C., Reeves, H., Gradstajn, E. & Audouze, J. (1970) Astron. Astrophys 8, 389–397.
25. Geiss, J. & Reeves, H. (1971) Astron. Astrophys. 18, 126–132.
26. Black, D. (1971) Nature (London) 234, 148–149.
27. Rogerson. J. & York, D. (1973) Astrophys. J. 186, L95–L98.
28. Linsky, J., Brown, A., Gayley, K., Diplas, A., Savage, B., Ayres, T., Landsman, W., Shore, S. & Heap, S. (1993) Astrophys. J. 402, 694–709.
29. Reeves, H., Audouze, J., Fowler, W.A. & Schramm, D.N. (1973) Astrophys. J. 179, 909–930.
30. Epstein, R., Lattimer, J. & Schramm, D.N. (1976) Nature (London) 263, 198–202.
31. Gott, J.R., III, Gunn, J., Schramm, D.N. & Tinsley, B.M. (1974) Astrophys. J. 194, 543–553.
32. Shi, X., Schramm, D.N., Dearborn, D. & Truran, J.W. (1995) Comments Astrophys. 17, 343–360.
33. Rood, R.T., Steigman, G. & Tinsley, B.M. (1976) Astrophys. J. 207, L57–L60.
34. Gloeckler, G. & Geiss, J. (1996) Nature (London) 381, 210–212.
35. Rood, R.T., Bania, T. & Wilson, J. (1992) Nature (London) 355, 618–620.
36. Hata, N., Scherrer, R.J., Steigman, G., Thomas, D., Walker, T.P., Bludman, S. & Langacker, P. (1995) Phys. Rev. Lett. 75, 3977–3980.
37. Copi, C.J., Schramm, D.N. & Turner, M.S. (1995) Astrophys. J. 455, L95–L98.
38. Scully, S.T., Cassé, M., Olive, K.A., Schramm, D.N., Truran, J. & Vangioni-Flam, E. (1996) Astrophys. J. 462, 960–968.
39. Geiss, J. (1997) in Proceedings of International Space Science Institute Workshop on Primordial Nuclei and Their Galactic Evolution (Bern, Switzerland, May 1997), Space Sciences Series of ISSI, ed. de Jaeger, C. (Kluwer, Dordrecht, The Netherlands), in press.
40. Linsky, J. (1997) in Proceedings of International Space Science Institute Workshop on Primordial Nuclei and Their Galactic Evolution (Bern, Switzerland. May 1997), Space Sciences Series of ISSI, ed. de Jaeger, C. (Kluwer, Dordrecht, The Netherlands), in press.
41. Spite, J. & Spite. M. (1982) Astron. Astrophys. 115, 357–366.
42. Rebolo, R., Molaro, P. & Beckman, J. (1988) Astron. Astrophys. 192, 192–205.
43. Hobbs, L. & Pilachowski, C. (1988) Astrophys. J. 326, L23–L26.
44. Smith. V.V., Lambert. D.L. & Nissen, P.E. (1993) Astrophys. J. 408, 262–276.
45. Olive, K. & Schramm, D.N. (1992) Nature (London) 360, 439–442.
46. Lemoine, M., Schramm, D.N., Truran, J.W. & Copi, C.J. (1997) Astrophys. J. 478, 554–562.
47. Hobbs, L. & Thorburn, J. (1994) Astrophys. J. Lett. 428, L25–L28.
48. Spite, M., Nissen, P.E. & Spite, F. (1996) Astron. Astrophys. 307, 172–183.
49. Nollett, K., Lemoine, M. & Schramm, D.N. (1997) Phys. Rev. C., 56, 1144–1151.
50. Delyannis, C.P. (1995) in The Light Element Abundances (Proceedings of an ESO/EIPC Workshop Held in Marciana Marina, Isola d’Elba, May 1994). ed. Crane, P. (European Southern Observatory Astrophysics Svmposia, Springer, Berlin), pp. 395– 409.
51. Steigman, G., Schramm. D.N. & Gunn, J. (1977) Phys. Lett. B 66, 202–204.
52. Schvartzman, V.F. (1969) JETP Lett. (Engl. Transl.) 9, 184–186.
53. Peebles. P.J.E. (1971) Physical Cosmology (Princeton Univ. Press, Princeton).
54. Schramm, D.N. & Kawano, L. (1989) Nucl. Instrum. Methods A 284, 84–88.
55. Pagel, B. (1991) Physics Scripta, T36, 7–15.
56. The LEP Collaborations: ALEPH, DELPHI, L3, and OPAL (1992) Phys. Lett. B 276, 247–253.
57. Tytler, D. (1997) in Space Sciences Series of ISSI (Proceedings of ISSI Workshop on Primordial Nuclei and their Galactic Evolution, Bern, Switzerland, May 1997) eds. Prantos, N., Tosi, M., and von Steiger, R. (Kluwer, Dordrecht, the Netherlands), in press.
58. Hogan, C. (1997) in Proceedings of the 18th Texas Symposium on Relativisitic Astrophysics (World Scientific, Singapore), in press.
59. Thuan, T.X., Izotov, Y.I. & Lipovetsky, V.A. (1996) Astrophys. J. 463, 120–133.
60. Applegate, J.H., Hogan, C.J. & Scherrer, R.J. (1988) Astrophys. J 329, 572–579.
61. Alcock, C.R., Fuller, G. & Mathews, G. (1987) Astrophys. J. 320, 439–447.
62. Bi, H.G. & Davidsen, A.F. (1997) Astrophys. J. 479, 523–542.
63. Quashnock, J.M. & Vanden Berk, D.E. (1997) Astrophys. J., in press.
64. Weinberg, D.H., Miralda-Escué, J., Hernquist, L. & Katz, N. (1997) Astrophys. J. 490, 564–570.
65. Jakobsen, P., Boksenberg, A., Deharveng. J.M., Greenfield, P., Jedrzewski, R. & Paresce, F. (1994) Nature (London) 370, 35–39.
66. White, S.D.M., Navarro, J.F., Evrard, A.E. & Frenck, C.S. (1993) Nature (London) 366, 429–433.
67. Mushotsky, R. (1993) Ann. NY Acad. Sci. 688, 184–194.
68. Kronberg, P.P. (1994) Rep. Prog. Phys. 57, 325–382.
69. Strickland. R. & Schramm, D.N. (1997) Astrophys. J. 481, 571–577.
70. Jungman, G., Kosowsky, A., Kamionkowski, M. & Spergel, D.N. (1996) Phys. Rev. Lett. 76, 1007–1010.
71. Jungman, G., Kosowsky, A., Kamionkowski, M. & Spergel, D.N. (1996) Phys. Rev. D 54, 1332–1344.
72. Scott, D. & White, M. (1995) Gen. Relativ. Gravitation 27, 1023–1030.
73. Reeves, H., Fowler, W.A. & Hoyle, F. (1970) Nature (London) 226, 727–729.
74. Davis, M. (1997) in Proceedings of the 18th Texas Symposium on Relativistic Astrophysics (World Scientific, Singapore), in press.
75. Alcock, C., Akerlof, C.W., Allsman, R.A., Axelrod, T.S., Bennett, D.P., Chan, S., Cook, K.H., Freeman, K.C., Griest, K., Marshall, S.L., Park, H.-S., Perlmutter, S., Peterson. B.A., Pratt, M.R., Quinn, P.J., Rodgers, A.W., Stubbs, C.W. & Sutherland, W. (1993) Nature (London) 365, 621–623.
76. Aubourg, E., Bareyre, P., Bréhin, S., Gros, M., Lachièze-Ray, M. et al. (1993) Nature (London) 365, 623–625.
77. Gates, E., Gyuk, G. & Turner, M. (1995) Phys. Rev. Lett. 74, 3724–3727.
78. Alcock, C., Allsman, R.A., Alves, D., Axelrod, T.S., Becker, A.C., Bennett, D.P., Cook, K.H., Freeman, K.C., Griest, K., Guern, J., Lehner, M.J., Marshall. S.L., Peterson, B.A., Pratt, M.R., Quinn, P.J., Rodgers, A.W., Stubbs, C.W., Sutherland, W. & Welch, D.L. (1995) Astrophys. J. 486, 697–726.
79. Fahlman, G., Kaiser, N. & Squires, G. (1994) Astrophys. J. 437, 56–62.
80. Guth, A. (1981) Phys. Rev. D 23, 347–356.
81. Linde, A. (1990) Particle Physics and Inflationary Cosmology (Harwood, NY).
82. Hill, C.T. & Schramm. D.N. (1985) Phys. Rev. D 31, 564–580.
83. Frieman, J.A., Hill, C.T., Stebbins, A. & Waga, I. (1996) Phys. Rev. Lett. 75, 2077–2080.





