Proc. Natl. Acad. Sci. USA
Vol. 95, pp. 47–52, January 1998
Colloquium Paper
This paper was presented at a colloquium entitled “The Age of the Universe, Dark Matter, and Structure Formation,” organized by David N.Schramm, held March 21–23, 1997, sponsored by the National Academy of Sciences at the Beckman Center in Irvine, CA.
The universe at z>5: When and how did the “dark age” end?
MARTIN J. REES
Institute of Astronomy, Madingley Road, Cambridge. CBS OHA, United Kingdom
ABSTRACT This paper considers how the first subgalactic structures produced the UV radiation that ionized the intergalactic medium before z=5 and the “feedback” effects of the UV radiation on structure formation. The first “pregalaxies” may eventually be detectable by their direct UV emission, with characteristic spectral features at Lyman a; high-z supernovae may also be detectable. Other probes of the intergalactic medium beyond z=5, and of the epochs of reheating and reionization, are discussed, along with possible links between the diffusion of pregalactic metals and the origin of magnetic fields.
The structures in our present universe are the outcome of more than 10 billion years of evolution. Slight irregularities imprinted at very early eras led to increasing contrasts in the density from place to place, until overdense regions evolved into bound structures. Quantitative and detailed (albeit speculative) theories for the origin of the fluctuations (in an ultra-early inflationary phase, or else as the outcome of topological defects, etc.) can now be tested against increasingly detailed and precise data.
The data are of two kinds. (i) CMB fluctuations probe irregularities on scales relevant to observed cosmic structure and on larger scales that are still in the linear regime. The detected photons have (according to most assumptions) propagated almost uninterruptedly since the recombination era, when the universe had been expanding for less than a million years, (ii) The other line of evidence on cosmic structure comes from traditional astronomy. Any acceptable theory must account for the present clustering properties of galaxies and dark matter; it must also match the actual universe at all past eras that can be probed observationally. We have for some years known about quasars with redshifts up to 5. Quasars themselves may be associated with atypical (even exceptional) galaxies, so their intrinsic properties are hard to relate to the general trend of galaxy formation. What has been especially exciting about recent developments is that the morphology and clustering of ordinary galaxies can now be probed out to similar redshifts: the powerful combination of the Hubble Space Telescope (HST) and the Keck Telescope has revealed many galaxies at z>3. Also, the absorption features in quasar spectra (the Lyman forest, etc.) probe the history of the clumping and temperature of a typical sample of the universe on galactic (and smaller) scales.
The mystery lies at still higher redshifts, between (in round numbers) a million years (z=1,000) and a billion years (z= 5). When the primordial radiation cooled below a few thousand degrees, it shifted into the infrared. The universe then entered a dark age, which continued until the first bound structures formed, releasing gravitational or nuclear energy that lit up the universe again. How long did the “dark age” last? We now know that at least some galaxies and quasars had already formed by a billion years. But how much earlier did structures form, and what were they like?
In most cosmological theories, especially those that postulate adiabatic Gaussian irregularities in the early universe, quasars and large galaxies should thin out beyond z=5, but subgalactic structures may exist even at redshifts exceeding 10. I shall discuss the effects of the earliest stars and supernovae— production of UV radiation, nonuniform reheating of the intergalactic medium (IGM), and the production of the first heavy elements—and the implications for observations at ultra-high redshifts. I shall discuss some potential observations that can probe pregalactic era, telling us when the first energy input occurred, and what scale of objects already existed at z> 5. But it may first be useful to summarize our theoretical picture of how the first cosmic structure emerged.
Clustering in Hierarchical Models
Characteristic Scales in Cold Dark Matter (CDM) Models. I will focus on the CDM model. But this is just a “template” for some more general deductions, which essentially apply to any “bottom up” model for structure formation. There is no minimum scale for the aggregation, under gravity, of cold nonbaryonic matter. However, the baryons constitute a gas whose pressure opposes condensation on very small scales. Therefore, the gas does not ‘feel” the very smallest condensations. In the context relevant here, where the dark matter’s gravity dominates, the baryonic Jeans mass is
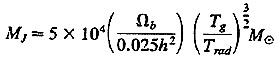
[1]
Only on scales larger than this can baryons promptly condense into bound systems, along with the dark matter. [The proviso “promptly” is nontrivial because, as emphasized by Loeb (private communication), the baryons may be able to condense later into smaller systems.] During the “dark age” the gas became even cooler than the microwave background (i.e., Tg<Trad): if it had cooled adiabatically, with no heat input since recombination, Tg would, at z=10, have been below 5 K. The smallest bound structures, with mass ~MJ, would have virialized at a temperature a few times larger than Tg(z). Larger masses would virialize at temperatures higher by a further factor (M/MJ)1/2. This virial temperature would be reached not solely by adiabatic compression, but also because of a shock, which would typically occur before the radius had decreased by a factor of 2.
These virialized systems would, however, have a dull existence as stable clouds unless they could lose energy and deflate
© 1998 by The National Academy of Sciences 0027–8424/98/9547–6$2.00/0
PNAS is available online at http://www.pnas.org.
due to atomic or molecular radiative processes—clouds that couldn’t cool would simply remain in equilibrium, being later incorporated in a larger scale of structure as the hierarchy built up. On the other hand, clouds that can cool radiatively will deflate. Most cooling mechanisms are more efficient at higher temperatures, as well as at higher densities. Once collapse starts, it proceeds almost isothermally, so that the internal Jeans mass falls as the density rises. A virialized, self-gravitating cloud that can cool radiatively would eventually go into free-fall collapse and (perhaps after a disc phase) fragment into smaller pieces.
Three “cooling regimes” are relevant during successive phases of the cosmogonic process, each being associated with a characteristic temperature.
-
For a H-He plasma the only effective cooling at low temperatures (<104 K) comes from molecular hydrogen. Even this process cuts off below a few hundred degrees; but above that temperature it allows contraction within the cosmic expansion timescale. The H2 fraction is never high, and it is, in any case, not a very efficient coolant—indeed, systems that collapse at z<10 fail to form enough molecules for effective cooling [e.g., see figure 1 of Tegmark, et al. (1)]—but molecular cooling almost certainly played a role in forming the very first objects that lit up the universe
-
If H2 is prevented from forming, so that molecular cooling is ineffective, then a H-He mixture behaves adiabatically unless T is as high as 8,000–10,000°, when excitation of Lyman a by the Maxwellian tail of the electrons provides efficient cooling whose rate rises steeply with temperature. Because of this steep temperature dependence, gas in this regime contracts almost isothermally, so that its Jeans mass decreases as the density rises.
-
The UV from early stars will photoionize some (and eventually almost all) of the diffuse gas. When this happens, the HI fraction is suppressed to a very low level, so there is no cooling by collisional excitation of Lyman lines; moreover, the energy radiated whenever a recombination occurs is quickly canceled by the energy input from a photoionization, so the only net cooling is via bremsstrahlung. The cooling is, in effect, then reduced by a factor of 100 (see, for instance, ref. 2). The minimum temperature (below which there is a net heating from the UV) depends on the UV spectrum and on whether the He is doubly ionized: it is in the range of 20,000–40,000°. (These three regimes refer to a H-He plasma. When heavy elements are present they can dominate the low-T cooling; ionization is still important in suppressing the most efficient channels for cooling.)
The Role of Molecular Hydrogen and the UV Feedback. The role of molecular cooling at early cosmic epochs has been considered by many authors, dating back to the 1960s; recent discussions are given, for instance, by Tegmark et al. (1) and Haiman. Rees, and Loeb (3). The exact efficiency depends on the density and, therefore, on the redshift when the first collapse occurs.
However, even at high redshifts, H2 cooling would be quenched if there were a UV background able to dissociate the molecules as fast as they formed. Photons of hv>11.18 eV can photodissociate H2. as first calculated by Stecher and Williams (4). These photons can penetrate a high column density of HI and destroy molecules in virialized and collapsing clouds. (If the incident spectrum has a nonthermal component extending up to KeV energies, there is a counterbalancing positive feedback because the number of photoelectrons is increased, and this enhances molecule formation.)
Only a small fraction of the UV that ionized the IGM could have been produced in systems where star formation was triggered by molecular cooling. Most must have formed in systems large enough to have been able to cool by atomic line effects. There is then a further transition when the medium breaks through and becomes completely ionized: the UV background intensity gets a boost, because the contributions from remote regions (which dominate in Olbers-type integrals) are less severely attenuated. The UV is then enough to maintain the very high mean ionization implied by transparency of the IGM beyond the Lyman limit. This means that it can maintain high ionization of a cloud until it has either collapsed to an overdensity exceeding the IGM ratio of ions to neutrals or until it becomes self-shielding (which happens at more modest overdensities for large clouds). Until that happens the cooling rate will be reduced by the lack of bound electrons and consequent elimination of the (otherwise dominant) “line” contribution to the cooling.
When this third phase is reached, the thermal properties of the uncollapsed gas will resemble those of the structures responsible for the observed Lyman-forest lines in high-z quasars spectra—these are mainly filaments, draining into virialized systems. Such systems have velocity dispersions of 50 km/sec and are destined to turn into galaxies of the kind whose descendants are still recognizable. I shall return (section 4) to discuss the detectability of these early galaxies.
Evidence for Diffuse Gas at High z
CMB Fluctuations as a Probe of the Ionization Epoch. If the intergalactic medium were suddenly reionized at a redshift z, then the optical depth to Thomson scattering back would be
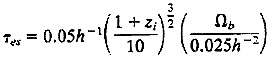
[2]
(the generalization to a more realistic scenario of gradual reionization is straightforward). Even when this optical depth is far below unity, the ionized gas constitutes a “fog” that attenuates the fluctuations imprinted at the recombination era; the photons that are scattered at <zi then manifest a different pattern of fluctuations, characteristically on larger angular scales. This optical depth is consequently one of the parameters that can, in principle, be determined from CMB anisotropy measurements. It is feasible to detect a value as small as 0.1—polarization measurements may allow even greater precision, because the scattered component would imprint polarization on angular scales of a few degrees, which would be absent from the Sachs-Wolfe fluctuations on that angular scale originating at trec.
Twenty-one-centimeter Emission, Absorption, and Tomog raphy. The 21-cm line of HI at redshift z would contribute to the background spectrum at a wavelength of 21 (1+z) cm. This contribution amounts to a brightness temperature of order 0.05 (1+z)1/2. This is very small compared with the 2.7 K of the CMB and smaller still compared with the nonthermal background, which swamps the CMB, even at high galactic latitudes, at the long wavelengths where high-z HI should show up. Nonetheless, inhomogeneities in the HI may be detectable, because they would give rise not only to angular fluctuations but also to spectral structure (5, 6). If the same strip of sky were scanned at two radio frequencies differing by (for example) 1 MHz. the temperature fluctuations due to the CMB itself, to galactic thermal and synchrotron backgrounds, and to discrete sources would track each other closely. Contrariwise, there would be no correlation between the 21-cm contributions, because the two frequencies would be probing “shells” in redshift space whose radial separation would exceed the correlation length. Consequently, it is not necessarily unfeasible to distinguish the 21-cm background, utilizing a radio telescope with a large collecting area. That line radiation allows three-dimensional tomography of the high-z HI renders this a specially interesting technique.
For the 21-cm contribution to be observable, the spin temperature Ts must differ from that of the black-body cosmic background. The gas would be detected in absorption or in emission depending on whether Ts is lower or higher than Trad. The hyperfine levels of HI are affected by the microwave background itself, by collisional processes, and by Lyman α (whose profile is itself controlled by the kinetic temperature). Ts will therefore be a weighted mean of the CMB and gas temperatures.
Before there had been any heat input due to the development of nonlinear structures, the kinetic temperature would be lower than that of the radiation, and the 21 cm would be an absorption feature. In principle, one might be able to detect incipient large-scale structure, even when still in the linear regime, because it leads to variations in the column density of HI, per unit redshift interval, along different lines of sight (5).
When reheating occurs, the situation becomes more complicated (6). The kinetic temperature can rise due to the weak shocking and adiabatic compression that accompanies the emergence of the first (very small scale) nonlinear structure (compare section 2). When photoionization starts, there will also, around each HII domain, be a zone of predominantly neutral hydrogen that has been heated by hard UV or x-ray photons. This latter effect would be more important if the first UV sources emitted radiation with a power-law (rather than just exponential) component.
Because the signal is so weak, there is little prospect of detecting high-z, 21-cm emission unless the signal displays structure on (comoving) scales of several million parsec (Mpc) (corresponding to angular scales of several arc minutes). According to CDM-type models, the gas is likely to have been already ionized, predominantly by numerous ionizing sources, each of subgalactic scale, before such large structures become conspicuous. On the other hand, if the primordial gas were heated by widely spaced, quasar-level sources, each of these would be surrounded by a shell that could feasibly be revealed by 21-cm tomography using, for instance, the new Giant Meter Wave Telescope (7).
Detection of First Galaxies at z ≥ 6 via Lyman α Features
Arguments that ~10 UV Photons Were Generated for Each Baryon. According to most “hierarchical” cosmological models, the UV that reheated and photoionized the IGM before z=5 came from stars that formed in dark matter clumps with total mass greater than 108 solar masses and internal velocity dispersion greater than about 15 km/sec. What is the chance of detecting these ancient stellar systems?
Estimating the cumulative amount of activity at high redshifts is straightforward. The total integrated UV production beyond z=5 must have been enough to ionize the IGM and build up the UV background, whose strength can be inferred directly out to z=5 from models of the Lyman forest, etc. Therefore, we have a firm lower limit to the ionizing UV generated. The total amount could be substantially above this limit, because much could “go to waste” through reprocessing in dense clouds, local absorption in the sources, etc.
A separate estimate of the number of O and B stars at these early eras comes from the heavy element abundance in high-z absorption clouds. The diffuse gas in the Lyman α forest was already enriched to a heavy element abundance z~10−2Z![]() by a redshift z=3. The evidence comes from absorption lines of CIV and other species associated with Lyman α forest lines with NHI≥1014 cm−2 (ref. 8 and references therein). Detailed calculations of the expected column densities of the observed absorption lines, using hydrodynamic simulations of the Lyman α forest and realistic models for the spectrum of the ionizing background (ref. 9: U.Hellsten, R.Dave, L.Hernquist, D.H.Weinberg, and N.Katz, unpublished work), have shown that the carbon abundance needed to reproduce the observations is [C/H]=−2.5. However, the metal abundances are similar to those of Population II stars, where oxygen is the most abundant element and is overabundant by a factor ~2 relative to carbon. With ZΘ=0.02, the metallicity of the Lyman α forest is then Z
by a redshift z=3. The evidence comes from absorption lines of CIV and other species associated with Lyman α forest lines with NHI≥1014 cm−2 (ref. 8 and references therein). Detailed calculations of the expected column densities of the observed absorption lines, using hydrodynamic simulations of the Lyman α forest and realistic models for the spectrum of the ionizing background (ref. 9: U.Hellsten, R.Dave, L.Hernquist, D.H.Weinberg, and N.Katz, unpublished work), have shown that the carbon abundance needed to reproduce the observations is [C/H]=−2.5. However, the metal abundances are similar to those of Population II stars, where oxygen is the most abundant element and is overabundant by a factor ~2 relative to carbon. With ZΘ=0.02, the metallicity of the Lyman α forest is then Z![]() 10−4. This metallicity should be approximately the same as the mean metallicity of the universe at z=3 if the Lyman α forest contains most of the baryons, as is found to be the case in models of structure formation for the Lyman α forest similar to those analyzed in refs. 10 and 11. The mean metallicity of the universe could be significantly lower only if most of the baryons were metal-free and in NHI <1014 cm−2 absorption systems, or in a very diffuse, unobserved intergalactic medium.
10−4. This metallicity should be approximately the same as the mean metallicity of the universe at z=3 if the Lyman α forest contains most of the baryons, as is found to be the case in models of structure formation for the Lyman α forest similar to those analyzed in refs. 10 and 11. The mean metallicity of the universe could be significantly lower only if most of the baryons were metal-free and in NHI <1014 cm−2 absorption systems, or in a very diffuse, unobserved intergalactic medium.
The ratio of the mass of heavy elements ejected by a star to the energy in ionizing photons emitted over the lifetime of the star, as derived from models of stellar evolution and supernova explosions, turns out to be about constant over the relevant mass range 10 M⊙≤M≤50 M⊙, so given a mean metallicity ![]() we can predict the energy in ionizing photons that was emitted for each baryon in the universe. According to Madau and Shull (12), this energy is 0.002
we can predict the energy in ionizing photons that was emitted for each baryon in the universe. According to Madau and Shull (12), this energy is 0.002 ![]() mpc2 per baryon. For
mpc2 per baryon. For ![]() =10−4, 10 ionizing photons were emitted per baryon by the stars that produced the Lyman α forest heavy elements (assuming a mean energy of 20 eV per ionizing photon).
=10−4, 10 ionizing photons were emitted per baryon by the stars that produced the Lyman α forest heavy elements (assuming a mean energy of 20 eV per ionizing photon).
Most of these photons must also have been absorbed by neutral hydrogen. A fraction fi will be absorbed internally, in the galaxies where the emitting stars were formed; the rest should be absorbed after having escaped their original galaxies, in other dense absorbing systems where protons can recombine many times during the reionization epoch (similar to the observed Lyman limit systems). Of the photons that were absorbed internally, about 70% resulted in the production of Lyman α photons. These will then be scattered many times in the host galaxy, until they move to the wings of the Lyman α line and escape. We define fd as the fraction of Lyman α photons that can eventually escape without being absorbed by dust. The mean comoving number density of these Lyman α photons is then 7fifd(![]() _4)nb, where nb is the comoving
_4)nb, where nb is the comoving
The Likely Luminosity of Individual “Galaxies.” The above arguments determine the average surface brightness of the high-redshift sky in the Lyman α emission line or, in other words, the product of the number of galaxies per solid angle and their individual, mean Lyman α flux. But the ease of detection obviously depends crucially on whether the UV background comes from huge numbers of individually ultrafaint systems or (more optimistically) at least in part from systems of higher luminosity. The uncertainty here is much greater—it is essentially tied to the poorly understood efficiency of forming massive stars in low-mass dark matter halos with shallow potential wells.
If star formation were highly efficient in all collapsed halos with velocity dispersion σ≥15 km·s−1, corresponding to the virial temperature T=µσ2/k![]() 104 K, then reionization would take place as soon as the highest-density peaks on the scales of these low-velocity dispersions collapse. For a top-hat spherical region of mass M that turns around when the age of the universe is tf/2, the relation between mass and velocity dispersion is M=23/2/(2πG)σ3tf~109M
104 K, then reionization would take place as soon as the highest-density peaks on the scales of these low-velocity dispersions collapse. For a top-hat spherical region of mass M that turns around when the age of the universe is tf/2, the relation between mass and velocity dispersion is M=23/2/(2πG)σ3tf~109M![]() (σ/20 km·s−1)3(tf/109 yr). If all the baryons turned into stars over a timescale of order of the free-fall time of the halo, the star formation rate would then be 0.3M
(σ/20 km·s−1)3(tf/109 yr). If all the baryons turned into stars over a timescale of order of the free-fall time of the halo, the star formation rate would then be 0.3M![]() yr−1(σ/20 km·s−1)3. For a normal IMF, this can yield a luminosity close to the peak luminosity of a supernova. The Lyman α luminosity from this efficient, rapid starburst
yr−1(σ/20 km·s−1)3. For a normal IMF, this can yield a luminosity close to the peak luminosity of a supernova. The Lyman α luminosity from this efficient, rapid starburst
would be 1052fifd (σ/20 km·s−1)3(fb/0.1), photons per sec−1. The corresponding Lyman α flux at present (for Ω=1 and H0 =70 km·s−1·Mpc−1) is 10−6fifd (σ/20 km·s−1)3(fb/0.1) [1− (1+zf)−1/2]−2 (1+zf)−1 photons per cm−2·sec−1. If the sources that reionized the universe have these characteristics, then we can use the mean Lyman α surface brightness obtained earlier to conclude that the number density of these sources in the sky should be ~1 per arcsec2 for the fiducial numbers we have chosen, and a formation redshift zf~10. The redshift zf should of course depend on the detailed model for the amplitude of the primordial fluctuations on small scales.
The main problem with this scenario is that supernova explosions in galaxies of such low velocity dispersions may well expel the gas before more than a small fraction has turned to stars. This leaves us with two other options regarding the sources of the reionization photons. (i) If just a small fraction of the gas in each object turns to stars before the remainder is expelled in a wind, then each galaxy emits fewer photons. Therefore, more have to form from lower amplitude peaks. The luminosity of each galaxy would be reduced, (ii) Star formation may be so inefficient in the low-escape-velocity halos that reionization has to await the formation of more massive galaxies with σ≤100 km·s−1 (photoionization has little effect on the cooling rate in halos with velocity dispersion σ≤100 km·s−1; see refs. 14 and 15).
Some moderately massive galaxies are in any case expected to form before reionization, because the power spectrum at small scales in cold dark matter models flattens to a slope of about n=−2.7 (so the amplitude of fluctuations decreases very slowly with scale), implying that at the same epoch, halos with σ=70 km·s−1 (with a mass ~40 times larger than halos with σ=20 km·s−1) would be collapsing from 3−σ peaks on this larger scale. In a Gaussian theory, the 3−σ peaks should contain ~10% as much mass as the 2−σ peaks at a fixed epoch; so we see that the mass distribution of these first-generation galaxies should probably extend well above the minimum mass for efficient atomic cooling.
Detectability of Galaxies Beyond the Reionization Redshift zi. What is the chance of detecting these galaxies? Given the mean surface brightness of Lyman α photons derived previously, the surface brightness in the UV continuum follows with little additional uncertainty, because the stars emitting most of the light in the range 1,216 Å<λ≤2,500 Å are also mostly very young stars. For every Lyman α photon produced from ionizing photons there should be ~10 UV continuum photons. The mean surface brightness from all galaxies in the rest-frame UV continuum is 10−6 photons cm−2·sec−1·arcsec−2. The main spectral feature that should identify any such galaxies at z ≥ 5 is a sharp break of the UV continuum at the Lyman α wavelength, due to the Gunn-Peterson trough (16). In addition, the Lyman α emission line may be present, depending on dust absorption and scattering of the Lyman α photons. Notice that the redshift at which the IGM was reionized is only marginally relevant to the presence of the Gunn-Peterson edge, because even if the medium was reionized at z >> 5, we know that the flux decrement caused by the Lyman α forest reaches a factor of 2 at z![]() 4 and grows rapidly with redshift. Thus, the technique of identifying galaxies at z
4 and grows rapidly with redshift. Thus, the technique of identifying galaxies at z![]() 3 from the Lyman continuum break (17, 18) should be replaced by the Gunn-Peterson trough at z ≥ 5 (see refs. 19 and 20 for a careful analysis of the effects of the Lyman α forest on galaxy colors).
3 from the Lyman continuum break (17, 18) should be replaced by the Gunn-Peterson trough at z ≥ 5 (see refs. 19 and 20 for a careful analysis of the effects of the Lyman α forest on galaxy colors).
The mean surface brightness in the rest-frame UV continuum from these galaxies can also be expressed as Sv=6× 10−33 erg cm−2·sec−1·Hz−1·arcsec−2=32AB arcsec−2 (where AB denotes AB magnitudes in the band where the UV continuum is observed). If there is one galaxy per arcsec2 at redshifts zf~10, each galaxy would have an AB magnitude of 32, i.e., about 3 magnitudes fainter than the detection limit in the Hubble Deep Field for the I-band (21). However, as mentioned above, galaxies with a mass 40 times larger would be ~400 times rarer, which still implies a number density of a few galaxies per square arc minute with AB magnitudes of ~28 (with the optimistic assumption of a rapid and efficient starburst in these more massive galaxies).
Detection with ground-based telescopes should be possible at z<6. The Keck telescope can detect point sources to AB magnitudes R<28, and I<27, in a night of observing time [M. Rauch, personal communication; Cohen (23, 24)]. Galaxies up to z=6 can be detected in the I band; for higher redshift, the magnitude limit from a ground-based telescope degrades rapidly due to the high atmospheric background at λ>8,500 Å. The magnitude limit could be improved significantly with adaptive optics. And the HST detects galaxies in the Hubble Deep Field down to I−28.5 (ref. 21). The New Generation Space Telescope (NGST) could image galaxies to AB magnitudes ~31 in the near-infrared and should be able to detect galaxies to a much higher redshift (24) with a much higher number density than has been seen so far. The prospect for detecting the high-redshift galaxies responsible for the enrichment of the Lyman α forest has also been analyzed by Haiman and colleagues (25) and by Cen (R. Cen, unpublished work).
In general, the lensing magnification in rich lensing clusters may be used here to stretch the magnitude limit (see also R.Cen, unpublished work). As an example, a lensing cluster with an Einstein ring radius b=30″ should magnify to A>10 an area of ~30 arcsec2 in the source plane. In the example used above, about 30 galaxies with AB=32 could be in this area, which would be magnified to AB=29.5. Magnified images of high-redshift galaxies should characteristically appear in pairs around the critical lines, in a region that can be predicted from lensing models [see Miralda-Escudé and Fort (26), Kneib et al. (27), and references therein], so this should help in their identification. These numbers indicate that a new deep field (similar to the Hubble Deep Field) imaged with HST in a rich cluster, adding also the H and J filters in the near-infrared, might well identify several galaxies at z>5. In fact, the largest redshift object known at present (at z=4.92) is already a gravitationally lensed galaxy (M. Franx, G.D.Illingworth, D.D.Kelson, P.G. van Dokkum, and K.-V. Tran, unpublished work).
The foregoing discussion has assumed that these high-redshift galaxies would be sufficiently small to remain unresolved. Resolved objects would need to have higher fluxes to be detected, because the detection is limited by the sky background. The likely dimensions of the star-forming regions are ~100 parsec (pc), corresponding to angular sizes ~0.01 arcsec—not resolvable even with NGST.
The Lyman α Emission Line. Another possible way to detect the faint galaxies is to search directly for the Lyman α emission line. As we discussed before, for a normal starburst spectrum we expect ~10% of the UV photons to be in the Lyman α emission line if dust absorption is not important. Therefore, if the sensitivity for detecting galaxies is still limited by the sky background for emission-line searches, the width of the line should be ∆λ/λ<0.01 to allow detection on a shorter time than for the UV continuum. The width of the Lyman α line in emission from a region of neutral gas with column density NHI =1022N22 cm−2 and velocity dispersion σ=10 σ6 km·s−1 is ∆λ/λ![]() 2×10−3(N22σ6)1/3 (28). Thus, the sensitivity of emission-line searches might be, at best, similar to searches for the UV continuum, and of course a much smaller range of redshift is searched because a very narrow band must be used.
2×10−3(N22σ6)1/3 (28). Thus, the sensitivity of emission-line searches might be, at best, similar to searches for the UV continuum, and of course a much smaller range of redshift is searched because a very narrow band must be used.
The Lyman α emission line may be suppressed because of internal dust extinction. In addition, any photon emitted in the blue side of the Lyman α line will be scattered in the surrounding IGM, reducing the strength of the line by a factor of 2. For a galaxy observed when the surrounding IGM is still mostly neutral, even photons on the red side can be scattered because of the damping wing of the Gunn-Peterson trough (34). This width of the damped absorption from the IGM is broader than the emission lines from starburst galaxies, so any
Lyman a emission line should be suppressed by the IGM in any galaxy observed before the reionization. The edge of the Gunn-Peterson trough should be “rounded off” into a characteristic shape (34), except that the inhomogeneity of the IGM may alter the profile (in particular, the presence of a halo of gas accreting on the galaxy may substantially increase the column density contributing to the damped profile from gas at a redshift close to that of the galaxy).
Thus, even though the Lyman a emission line might not be as good a spectral signature as the Gunn-Peterson trough as a technique to search for high redshift galaxies, its presence or absence should be an important diagnostic of the ionization state of the IGM in the neighborhood of any detected galaxy.
A Note on Active Galactic Nuclei (AGNs) and Nonthermal UV Background. AGN formation requires virialized systems with larger masses and deeper potential wells (cf. ref. 29). AGNs may “take over” as the dominant UV source at redshifts below 5 (and the second ionization of He may be delayed until AGNs can provide a power-law contribution to the spectrum), but at higher z, when the H itself was reheated and ionized, OB stars would dominate.
It is worth noting also that the diffuse IGM at redshifts of 3–5 has such a long thermal timescale that it retains a “memory” of its thermal history at even higher redshifts. The adiabat this gas is on at z=5 depends on the value of zi and also on the slope of the UV spectrum. This adiabat can be constrained by observations of weak and narrow lines in the Lyman forest (30, 31).
Very High Redshift Supernovae (and Gamma-Ray Bursts?)
The intergalactic gas was already highly photoionized by z= 5; also, the mean abundance of heavy elements had attained a level about 0.01 solar by that time, this degree of contamination being about what would be expected if the reheating and ionization were due to OB stars (25, 32). It is straightforward to calculate how many supernovae would have gone off, in each comoving volume, as a direct consequence of this output of UV and heavy elements; there would be one, or maybe several per year in each square arc minute of sky (33). These would be primarily of type 2. The typical observed light curve has a flat maximum lasting 80 days. One would therefore (taking the time dilation into account) expect each supernova to be near its maximum for nearly a year. It is possible that the explosions proceed differently when the stellar envelope is essentially metal-free, yielding different light curves, so any estimates of detectability are tentative. However, taking a standard type 2 light curve (which may, of course, be pessimistic), one calculates (33) that these objects should be approximately 27th magnitude in J and K bands even out beyond z=5. The detection of such objects would be an easy task with the NGST. With existing facilities it is marginal. The best hope would be that observations of clusters of galaxies might serendipitously detect a magnified, gravitationally lensed image from far behind the cluster.
As a speculative addendum, note that a few percent of observed gamma-ray bursts may come from redshifts as large as 5: this would be expected if the burst rate, as a function of cosmic epoch, tracks the star-formation rate. At the time of writing, data on optical and x-ray afterglows are still very sparse, but it is at least an exciting possibility that there may be occasional flashes, far brighter than supernovae, from very large redshifts.
The First Stars: Some Uncertainties
The gravitational aspects of clustering can all be modeled convincingly by computer simulations. Now the dynamics of the baryonic (gaseous) component—including shocks and radiative cooling—can be modeled this way as well. But the nature of the simulation changes as soon as the first stars (or other compact objects) form. The first stars exert crucial feedback—the remaining gas is heated by ionizing radiation and perhaps also by an injection of kinetic energy via winds and even supernova explosions. The three uncertainties here are:
-
What is the IMF of the first stellar population? The high-mass stars are the ones that provide efficient (and relatively prompt) feedback. It plainly makes a big difference whether these are the dominant type of stars or whether the initial IMF rises steeply toward low masses, so that very many faint stars form before there is a significant feedback.
-
The influence of the early stars depends on whether their energy is deposited locally or penetrates into the all-pervasive medium that is not yet in contracting systems. The UV radiation could, for instance, be mainly absorbed in the gas immediately surrounding the first stars, so that it exerts no feedback on the condensation of further clumps—the total number of massive stars needed to build up the UV background, and the concomitant contamination by heavy elements, would then be greater.
-
Quite apart from the uncertainty in the IMF, it is also unclear what fraction of the baryons that falls into a clump would actually be incorporated into stars before being reejected. The retained fraction would almost certainly depend on the virial velocity, gas more readily escapes from the shallow potential wells relevant to dwarf galaxies. Ejection is even easier in potential wells so shallow that they cannot confine gas at the photoionization temperature. This effect may lead to a reduced efficiency during the second, as compared with the third, of the three cosmogonic stages discussed in section 2.
All of these three uncertainties would, for a given fluctuation spectrum, affect the redshift at which molecules were destroyed and at which full ionization occurred.
Heavy Elements and Magnetic Fields
If the main UV source is stars, there is inevitably an associated build-up of heavy elements. (In more radical pictures where black holes are involved in the early energy input, this inference doesn’t hold, because the energy supply could be gravitational rather than nuclear.) The question then arises of how this processed gas would be distributed. Would it be confined in the virialized systems, or could it spread through the entire IGM?
The ubiquity of carbon features in intermediate- and high-(N=3.1014 cm-2) column-density systems implies that heavy elements are dispersed broadly enough to have a large covering factor. These absorption systems may be associated with the subgalactic sites of star formation that produce the first heavy elements. The nucleosynthesis sites therefore cannot be too sparse if these elements are, within the time available, to diffuse enough so that they are encountered somewhere along every line of sight through a typical high-column-density cloud. (Moreover, efficient mixing would then certainly imply bulk motions so high that their neglect would be a serious inadequacy in simulations of Lyman a forest formation, etc.) The absorption line data tell us the mean abundance through the relevant cloud. They are compatible with 99% of the material being entirely unprocessed, the heavy elements being restricted to 1% of the material—the early heavy elements need not be thoroughly mixed, but they must have spread sufficiently to have a large “covering factor” in the intermediate- and high-N clouds.
The first stars are important for another reason: they may generate the first cosmic magnetic fields. Moreover, mass loss (via winds or supernovae permeated by magnetic flux) would disperse magnetic flux along with the heavy elements. This flux, stretched and sheared by bulk motions, can be the “seed” for the later amplification processes that generate the larger-scale fields pervading disc galaxies.
Where Are the Oldest Stars?
The efficiency of early mixing is important for the interpretation of stars in our own galaxy that have ultra-low metallicity (33)— lower than the mean metallicity that would have been generated in association with the UV background at z>5. If the heavy elements were efficiently mixed, then these stars would themselves need to have formed before galaxies were assembled. To a first approximation they would cluster nondissipatively, they would therefore be distributed in halos (including the halo of our own galaxy) like the dark matter itself. More careful estimates slightly weaken this inference. This is because the subgalaxies would tend, during the subsequent mergers, to sink via dynamical friction toward the centers of the merged systems. There would nevertheless be a tendency for the most extreme metal-poor stars to have a more extended distribution in our galactic halo and to have a bigger spread of motions.
The number of such stars depends on the IMF. If this were flatter, there would be fewer low-mass stars formed concurrently with those that produced the UV background. If, on the other hand, the IMF were initially steeper, there could, in principle, be a lot of very low mass (macho) objects produced at high redshift. These could provide a few percent of the halo if omega were 1 (and a higher proportion of the =30-kpc inner halo probed by lensing searches); a larger proportion could be provided in a low-density universe.
Most of the small, first-generation galaxies by now should have merged into more massive systems (forming part of the halo population of stars in normal galaxies like the Milky Way), but some could survive until today in galactic halos or even as isolated objects. This may be the explanation of present-day dwarf spheroidal galaxies (34).
Summary
Our general conclusions are relevant to any model in which the initial fluctuations have amplitudes decreasing with scale, so that cosmic structures form “bottom-up.” Such models differ, of course, in the epoch at which “first light” would have occurred. In models with primordial baryon fluctuations (PIB), this may be at z>100; for CDM (primarily discussed here), it is in the range 10–20; and for “mixed dark matter” models, the first structures may form still more recently. Molecular cooling tends to be more efficient at high densities and, therefore, at large redshifts: but in all cases it determines the scale of the first objects that condense out and contribute the first injection of heat into the universe.
The amount of background UV generated per solar-mass of material in these first objects is very uncertain—it depends on the efficiency of star formation, on whether the IMF favors massive stars (or even supermassive objects or black holes), and on how much of the UV is “soaked up” by dense gas within the bound objects themselves. But irrespective of all these uncertainties, the UV background exerts an important feedback on the cosmogonic process, by quenching H2 cooling, long before reaching the level needed to photoionize the entire IGM.
The IGM remained predominantly neutral until a sufficient number of objects above 109((1+z)/10)-3/2M![]() had gone nonlinear. Such systems are massive enough to have virial temperatures above 10,000 K—hot enough for HI line emission to permit very efficient cooling. Most of the O-B stars (or accreting black holes) that photoionized the IGM had to form in systems at least as large as this.
had gone nonlinear. Such systems are massive enough to have virial temperatures above 10,000 K—hot enough for HI line emission to permit very efficient cooling. Most of the O-B stars (or accreting black holes) that photoionized the IGM had to form in systems at least as large as this.
Formation of such systems would have continued unimpeded until ionization was complete; the UV background rises sharply, to a value of order 10-21 ergs per cm-2·Hz-1·ster-1, when the universe becomes, in effect, an HII region. This must have happened before z=5. The only net cooling of a fully photoionized gas comes from bremsstrahlung, which is less effective than the collisionally excited line emission from gas that is only partly ionized. The completion of photoionization may therefore signal another pause in the cosmogonic process, associated with a further increase in the minimum scale that can collapse, and in the efficiency of cooling.
By the epoch z=5, some structures (albeit perhaps only exceptional ones) must have attained galactic scales. But huge numbers of lower-mass systems should already exist at higher redshifts, and we can make quite firm estimates of their integrated UV output. This paper has addressed how we can probe their indirect effects and perhaps even detect them directly.
I am especially grateful to Jordi-Miralda Escude and would also like to thank Zoltan Haiman, Avi Loeb, and Max Tegmark for discussion and collaboration on some of the topics described here.
1. Tegmark, M., Silk, J., Rees, M.J., Blanchard, A., Abel, T. & Palla, F. (1997) Astrophys. J. 474, 1.
2. Efstathiou, G. (1992) Mon. Not. R. Astron. Soc. 256, 43.
3. Haiman, Z., Rees, M.J. & Loeb, A. (1997a) Astrophys. J. 476, 458.
4. Stecher, T.P. & Williams, D.A. (1967) Astrophys. J. Lett. 149, L1.
5. Scott, D. & Rees, M.J. (1990) Mon, Not. R. Astron. Soc. 247, 510.
6. Madau, P., Meiksin, A. & Rees, M.J. (1997) Astrophys. J. 475, 429.
7. Swarup, G. (1996) in Cold Gas at High Redshifts, ed. Bremer, M. (Kluwer, Dordrecht, The Netherlands), 457.
8. Songaila, A. & Cowie, L.L. (1996) Astrophys. J. 112, 335.
9. Rauch, M., Haehnelt. M.G. & Steinmetz. M. (1997) Astrophys. J., in press.
10. Hernquist, L., Katz, N., Weinberg, D.H. & Miralda-Escudé, J. (1996) Astrophys. J. 457, L51.
11. Miralda-Escudé, J., Cen, R., Ostriker, J.P. & Rauch, M. (1996) Astrophys. J. 471, 582.
12. Madau, P. & Shull, J.M. (1996) Astrophys. J. 457, 551.
13. Tytler, D., Fan, X.-M., Burles, S., Cottrell, L., Davis, C., Kirkman, D. & Zuo, L. (1995) in QSO Absorption Lines, ed. Meylan, G. (Springer, Heidelberg), p. 289.
14. Thoul, A. & Weinberg, D.H. (1996) Astrophys. J. 465, 608.
15. Navarro, J.F. & Steinmetz, M. (1997) Astrophys. J. 478, 13.
16. Gunn, J.E. & Peterson, B.A. Astrophys. J. 142, 1633.
17. Guhathakurta, P., Tyson, J.A. & Majewski, S.R. (1990) Astrophys. J. 357, L9.
18. Steidel, C.C., Giavalisco, M., Pettini, M., Dickinson, M. & Adelberger, K.L. (1996) Astrophys. J. 462, L17.
19. Madau, P. (1995) Astrophys. J. 441, 18.
20. Madau, P., Ferguson. H.C., Dickinson, M.E., Giavalisco, M., Steidel, C.C. & Fruchter, A. (1996) Mon. Not. R. Astron. Soc. 283, 1388.
21. Williams, R.E., Blacker, B., Dickinson, M., Van Dyke Dixon, W., Ferguson, H., et al. (1996) Astron. J. 112, 1335.
22. Cohen, J.G. (1995) Keck LRIS Quick Reference Guide (California Polytechnic State University, San Luis Obispo, CA).
23. Cohen, J.G. (1995) The Efficiency of the LRIS in the Spectroscopic Mode (California Polytechnic State University, San Luis Obispo, CA).
24. Mather, J. & Stockman. H. (1996) NASA Report (National Aeronautics and Space Administration, Washington, D.C.).
25. Haiman, Z. & Loeb, A. (1997) Science with the Next Generation Space Telescope (National Aeronautics and Space Administration, Washington, D.C.). in press.
26. Miralda-Escudé, J. & Fort, B. (1993) Astrophys. J. 417, L5.
27. Kneib. J.P., Ellis, R.S., Smail, I.R., Couch, W.J. & Sharples, R. (1996) Astrophys. J. 471, 643.
28. Harrington, J.P. (1973) Mon. Not. R. Astron. Soc. 162, 43.
29. Haehnelt, M. & Rees, M.J. (1993) Mon. Not. R. Astron. Soc. 263. 168.
30. Haehnelt, M. & Steinmetz, M. (1997) Mon. Not. R. Astron. Soc., in press.
31. Miralda-Escudé, J. & Rees. M.J. (1994) Mon. Not. R. Astron. Soc. 266, 343.
32. Ostriker, J.P. & Gnedin. N. (1996) Astrophys. J. 472, 630.
33. Miralda-Escudé, J. & Rees, M.J. (1997) Astrophys. J. 478, L57.
34. Miralda-Escudé, J. & Rees, M.J. (1998) Astrophys. J., in press.






