Proc. Natl. Acad. Sci. USA
Vol. 95, pp. 53–58, January 1998
Colloquium Paper
This paper was presented at a colloquium entitled “The Age of the Universe, Dark Matter, and Structure Formation,” organized by David N.Schramm, held March 21–23, 1997, sponsored by the National Academy of Sciences at the Beckman Center in Irvine, CA.
Particle components of dark matter
JOHN ELLIS
Theoretical Physics Division, European Center for Nuclear Research, CH-1211 Geneva 23, Switzerland
ABSTRACT Particle candidates for astrophysical dark matter are reviewed, with particular emphasis on the lightest supersymmetric particle and the axion. The former is now constrained by accelerator experiments to have a mass above about 40 GeV, and ongoing searches at accelerators, in space, and in underground experiments have a good chance to detect it. A reevaluation of the constraint on the axion from supernova 1987a leaves open an interesting window where it may be detected if it constitutes the galactic halo.
There are many particle candidates for dark matter, which can be considered in two general categories: particles (mainly fermions) that contribute individually to the matter density of the Universe, and bosons that contribute collectively in the form of coherent waves. In this talk I concentrate on one selected candidate in each category: the lightest supersymmetric particle (LSP) and the axion, respectively.
Consider first the generic dependence on mass mX of the possible relic density of a “neutrino” or other electroweakly interacting particle X such as the LSP. For mX<1 MeV, the number density nX is essentially independent of the mass, so that ρX=nXmXαmX. Closure density ρX=ΩXρC:ΩX=1 is exceeded when mX exceeds about 30 eV, and one recovers acceptable densities ΩX<1 only when mX> a few GeV. If the candidate can annihilate through the Z, like the neutrino or the LSP, there is a minimum of the density around mX~mZ/2, after which the annihilation rate slows and the density may rise again to the critical density ΩX=1.
As seen in Fig. 1, experiments at the Large Electron Positron (LEP) Collider have by now explored thoroughly the particles produced by e+ e− annihilation through the Z, at energies corresponding to a cosmological redshift z~2×1014, and the LEP 2 upgrade is now exploring higher energies: Ecm~160 to 200 GeV corresponding to a redshift z~4×1014. They have ruled out dark matter candidates weighing a few GeV and have almost forced us into the region mX>mZ/2, at least for the LSP as we now discuss.
Why Supersymmetry?
The primary theoretical motivation for supersymmetry at accessible energies is provided by the hierarchy problem (1–4): why is mW<<mP the only candidate for a fundamental physics mass scale we have? This question can be reformulated as: why is ![]() ? or alternatively as: why is the Coulomb potential Vc=e2/r in an atom so much larger than the Newton potential VN=GNm2/r, where m≤mW is a typical particle mass? You might reply by asking: why not just set mW<<mP by hand? The problem is that you must contend with the quantum corrections to mW shown in Fig. 2, which are quadratically divergent:
? or alternatively as: why is the Coulomb potential Vc=e2/r in an atom so much larger than the Newton potential VN=GNm2/r, where m≤mW is a typical particle mass? You might reply by asking: why not just set mW<<mP by hand? The problem is that you must contend with the quantum corrections to mW shown in Fig. 2, which are quadratically divergent:
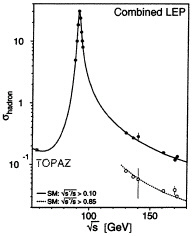
FIG. 1. Measured e+ e− hadron cross sections at LEP and from the lower-energy TOPAZ experiment at Koh-Enerugii Kasokuki Kenkyu Kikou (KEK). At high energies, the measured cross section depends strongly on the cut on the observed energy ![]() that is imposed.
that is imposed.
[1]
where Λ represents a cutoff scale up to which the Standard Model describes physics before breaking down. If Λ~mP, the quantum correction (Eq. 1) is much larger than the small physical value of mW, which can be recovered only by fine-tuning a large bare value for mW so that it can be canceled almost exactly by Eq. 1. This all sounds very unnatural.
The theoretical motivation (1–4) for low-energy supersymmetry (refs. 5–7: for a review see ref. 8) is that the quantum corrections due to virtual bosons and fermions have opposite signs, and hence can be made to cancel (up to mass-difference effects) by postulating pairs of fermions and bosons with identical couplings:
[2]
© 1998 by The National Academy of Sciences 0027–8424/98/9553–6$2.00/0
PNAS is available online at http://www.pnas.org.
|
|
Abbreviations: LSP, lightest supersymmetric particle: LEP, Large Electron Positron; GUT. grand unified theory; CERN, European Center for Nuclear Research. |
|
* |
To whom reprint requests should be addressed, e-mail: john.ellis@cern.ch. |
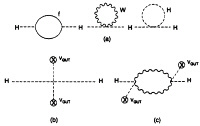
FIG. 2. Potentially large contributions to mH from quadratic divergences in the Standard Model (a), couplings to grand unified theory (GUT) Higgs bosons (b), and logarithmic corrections to the latter (c).
This would be ![]() if the differences between the boson and fermion squared masses
if the differences between the boson and fermion squared masses
[3]
suggesting that the supersymmetric partner particles should be accessible to present or planned accelerators.
The next section discusses in more detail the current lower limit on the lightest neutralino—a mixture of the supersymmetric partners of the photon, Z boson, and neutral Higgs bosons, which is the best candidate for the LSP (9). In addition to these supersymmetric particles per se, even the minimal supersymmetric extension of the Standard Model predicts a rich spectrum of Higgs bosons, with five physical states, of which the lightest must weigh less than about 150 GeV (10–15).
This prediction underlies one of two tentative experimental indications in favor of supersymmetry. As seen in Fig. 3, precision electroweak data favor indirectly a relatively light Higgs boson weighing about 140 GeV with a factor of 2 uncertainty, which is highly consistent with the supersymmetric prediction (16). The second tentative indication comes from measurements of the gauge couplings at LEP and elsewhere shown in Fig. 4. which favor unification in a supersymmetric GUT over a theory without supersymmetry (17– 25). The supersymmetric GUT prediction is ![]()
![]() to 0.232, whereas a minimal nonsupersymmetric GUT predicts sin2θw
to 0.232, whereas a minimal nonsupersymmetric GUT predicts sin2θw![]() 0.21 to 0.22, and the LEP data find sin2θw=0.2315±0.0002.
0.21 to 0.22, and the LEP data find sin2θw=0.2315±0.0002.

FIG. 3. Global fit to the precision electroweak data and Fermilab measurements of mt, compared with the LEP lower limit on mH and the range expected if the Standard Model remains unmodified up to a scale Λ.
These indications are nice, but there still is no smoking “gunino”!
The LSP
The LSP is expected to be stable in many models—and hence present in the Universe today as a cosmological relic from the Big Bang—because of a multiplicatively conserved quantum number called R parity (26), which is +1 for all particles and −1 for all sparticles. Its conservation is related to those of baryon and lepton numbers (B, L), because R=(−1)3B+L+2S, where S is the spin. If B and L are conserved, and thus also R parity, sparticles must always be produced in pairs (e.g., e+ e− →![]() +
+![]() −), heavier sparticles must decay into lighter ones (e.g.,
−), heavier sparticles must decay into lighter ones (e.g., ![]() →μ
→μ![]() ), and the LSP is stable because it has no legal decay modes.
), and the LSP is stable because it has no legal decay modes.
If the LSP had charge or strong interactions, it would bind with conventional matter to form anomalous heavy isotopes. The fact that these have not been seen suggests that the LSP must be electrically neutral and have only weak interactions. Possible scandidates include the sneutrino ![]() of spin 0, the lightest neutralino (partner of the γ, H0, Z) of spin 1/2, and the gravitino of spin 3/2 (the prefix “s” is used to denote the supersymmetric partner of some observed particle). The sneutrino has essentially been excluded by LEP experiments and the underground searches for dark matter discussed later, and the gravitino is expected in many models to be heavier than the lightest neutralino χ, so attention has focused on the χ as the LSP (9).
of spin 0, the lightest neutralino (partner of the γ, H0, Z) of spin 1/2, and the gravitino of spin 3/2 (the prefix “s” is used to denote the supersymmetric partner of some observed particle). The sneutrino has essentially been excluded by LEP experiments and the underground searches for dark matter discussed later, and the gravitino is expected in many models to be heavier than the lightest neutralino χ, so attention has focused on the χ as the LSP (9).
In simple supersymmetric models, neutralinos and charginos X± (partners of the W±, H±) are characterized by three parameters: a primordial gaugino mass m1/2, a Higgs mixing parameter μ, and the ratio tan β of two Higgs vacuum expectation values. The lightest neutralino looks simple in certain limits: as m1/2→0, χ→![]() , and as μ→0, χ→H, though neither of these ideal limits is compatible with the constraints from LEP and other experiments. What makes χ a particularly attractive candidate for cold dark matter is the fact that there are generic domains of parameter space where the relic cosmological density is in the interesting range: 0.1≤Ωχh2≤ 1 (9).
, and as μ→0, χ→H, though neither of these ideal limits is compatible with the constraints from LEP and other experiments. What makes χ a particularly attractive candidate for cold dark matter is the fact that there are generic domains of parameter space where the relic cosmological density is in the interesting range: 0.1≤Ωχh2≤ 1 (9).

FIG. 4. Measurements of sin2θw. Note that the nonsupersyrametric GUT prediction disagrees significantly with the data. The minimal supersymmetric GUT prediction assumes unrealistically that all sparticles (supersymmetric particles) have masses mZ. Realistic spectra give predictions in agreement with the data.
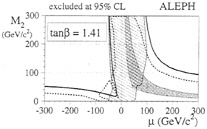
FIG. 5. Interplay of gaugino constraints from LEP 1 (dashed line) and LEP 1.5 (thick solid line χ+χ−, thin solid line χχ′). Notice their complementarity in the μ<0 quadrant.
LEP searches for χ+χ− and χχ′ production in Z0 decay and at higher energies together provide an interesting lower bound on mχ. As seen in Fig. 5, neither LEP 1 nor LEP 1.5 (runs at energies between 130 and 140 GeV) individually provided a bound on mχ, but each excluded “wedges” of parameter space allowed by the other, leading to an experimental bound mχ≥ 12.8 GeV modulo loopholes when tan β~1 and mv is large, and when tan ![]() and mv~60 GeV (27). However, these loopholes could be blocked by using data from other accelerators and/or cosmological and theoretical constraints.
and mv~60 GeV (27). However, these loopholes could be blocked by using data from other accelerators and/or cosmological and theoretical constraints.
Specifically, we have assumed universality for the gaugino and scalar masses (m1/2, m0) at the GUT scale, and required 0.1≤Ωχh2≤0.3, where the lower bound is motivated solely by astrophysical relevance, whereas the upper bound is required to avoid overclosing the Universe. Moreover, physical renormalized parameters such as the Higgs vacuum expectation values and masses are determined by dynamics involving the heavy top quark. The resulting lower bound on mχ as a function of tan β is shown in Fig. 6, where we see that mχ≥ 21.4 GeV on the basis of LEP 1 and LEP 1.5 results (28).
More recently, results from higher-energy LEP 2 runs and 160 and 170/172 GeV have been announced, which can be used to strengthen significantly the LEP lower bound on mχ. The latest chargino searches indicate that mχ±≥80 GeV for
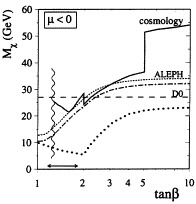
FIG. 6. Phenomenological lower limits on mχ based on LEP 1.5 data, for arbitrary m0, including the AMY result (dotted line), inferred from the Dø gluino search assuming universal gaugino masses (dashed line), assuming scalar-mass universality (dot-dashed line), and applying the cosmological constraint (0.1<Ωχh2<0.3) (solid line).
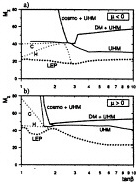
FIG. 7. Lower limits on mχ based on data from LEP 1, 1.5, and 2. The dotted line makes no appeal to extra theoretical assumptions. Lines labeled UHM assume universal scalar masses also for Higgs bosons. The branches labeled “cosmo” and “DM” assume Ωχh2<0.3 and >0.1, respectively. The lines labeled C and H are explained in ref. 29.
mχ±−mχ≥5 GeV, slepton searches indicate that mē±≥70 GeV, and the latest searches for supersymmetric Higgs bosons indicate that mh≥60 GeV. This mass is linked to the other sparticle masses if one assumes scalar-mass universality, and it plays a particularly important role at low tan β. We find that the previous mχ=0 loopholes are excluded without the need for other theoretical inputs. Overall, as seen in Fig. 7, we find (29)
mχ≥40 GeV [4]
and no consistent model if μ<0 and tan β≤1.7, or if μ> 0 and tan β≤1.4. These lower limits on tan β come about because Ωχh2≤0.3 is possible only if m1/2≤400 GeV for tan β≤2, whereas the LEP Higgs limits impose increasingly strong lower limits on m1/2. Future LEP searches at center-of-mass energies up to 190 or 200 GeV should be able to explore mχ= ≤95 GeV, m-ℓ±≤85 GeV and mh≤100 GeV. These should reveal evidence for a neutralino weighing ≤50 GeV and explore all astrophysically interesting models with universal scalar masses and tan β≤3.
In the longer run, the LHC accelerator at the European Center for Nuclear Research (CERN) (operating at an equivalent redshift z~5×1015!) will be able to explore all the mass range (expression 3) expected for supersymmetric particles. Moreover, the range of parameters in which Ωχh2≤1 can be explored by means of several independent experimental signatures. Therefore, we can expect supersymmetric dark matter to be smoked out at the Large Hadron Collider (LHC) if not previously at LEP (see ref. 30 and the information about the LHC Experiments Committee Workshop on Supersymmetry at http://www.cern.ch/Committees/LHCC/SUSY96.html).
The above discussion is in the context of models with universal gaugino masses![]() and scalar masses mq
and scalar masses mq![]() at the GUT scale. The lower limit on the neutralino mass would be affected quantitatively if the gaugino mass universality assumption were relaxed, but not altered qualitatively. On the other hand, if Higgs mass universality is relaxed:
at the GUT scale. The lower limit on the neutralino mass would be affected quantitatively if the gaugino mass universality assumption were relaxed, but not altered qualitatively. On the other hand, if Higgs mass universality is relaxed: ![]() with δi≠0, the preferred neutralino composition might change from being mainly a gaugino to being higgsino-like. In this case, the relic density can be interestingly large only if mχ≤mw, LEP searches already exclude mχ≤70 GeV in this case, and future LEP searches should determine
with δi≠0, the preferred neutralino composition might change from being mainly a gaugino to being higgsino-like. In this case, the relic density can be interestingly large only if mχ≤mw, LEP searches already exclude mχ≤70 GeV in this case, and future LEP searches should determine
the fate of this deviant neutralino option.† Another deviant option is charge-parity (CP) violation in the neutralino sector. This would permit S wave χχ annihilation, which is more efficient, so that larger neutralino masses would be allowed by cosmology (32).
Searches for Dark Matter Particles
Three major strategies for experimental searches for massive cold dark matter particles such as the LSP have been proposed. In calculating the rates for these, it is essential to restrict one’s attention to models with an acceptable relic density: it does not make sense to imagine that our galactic halo is made solely of χ particles if the calculated cosmological density Ωχh2<<0.1. This is a pity, because models with low cosmological densities have large annihilation and scattering cross sections!
Annihilation in the Galactic Halo. Here the underlying idea is that a pair of χ particles make their lonely ways around the galactic halo, they meet and have a one-night stand (annihilate) to produce stable particles such as ![]() , e+, γ, and v that might be detectable in cosmic rays. In addition to restricting one’s attention to models with a plausible cosmological relic density, one must also assume a plausible local halo density ρχ
, e+, γ, and v that might be detectable in cosmic rays. In addition to restricting one’s attention to models with a plausible cosmological relic density, one must also assume a plausible local halo density ρχ![]() 0.3 GeV cm−3. One should then be careful to include all accessible annihilation channels: χχ→ff, VV, HH, HV, . . . , and then use a phenomenological fit for the secondary
0.3 GeV cm−3. One should then be careful to include all accessible annihilation channels: χχ→ff, VV, HH, HV, . . . , and then use a phenomenological fit for the secondary ![]() , e+, γ, or v spectra produced by these primary annihilation products, based, e.g., on a Monte Carlo tuned to fit Z decays (33).
, e+, γ, or v spectra produced by these primary annihilation products, based, e.g., on a Monte Carlo tuned to fit Z decays (33).
Sam Ting, for the Alpha Magnetic Spectrometer (AMS) Collaboration, has shown in a talk at this meeting the ![]() fluxes calculated in a couple of supersymmetric models, compared with existing measurements and the range expected for secondary
fluxes calculated in a couple of supersymmetric models, compared with existing measurements and the range expected for secondary ![]() production by primary matter cosmic rays. He also showed the statistical precision in the flux that could be obtained by flying the AMS experiment on the Space Shuttle. There is a window of opportunity for AMS at low
production by primary matter cosmic rays. He also showed the statistical precision in the flux that could be obtained by flying the AMS experiment on the Space Shuttle. There is a window of opportunity for AMS at low ![]() energies ≤1 GeV. In the longer run, it is planned to fly AMS on the Space Station for several years. This may enable it to detect the modulation of the dark-matter
energies ≤1 GeV. In the longer run, it is planned to fly AMS on the Space Station for several years. This may enable it to detect the modulation of the dark-matter ![]() flux expected due to variations in the solar wind over the 11-year solar cycle. Ting has also shown the corresponding data on e+ in the cosmic rays, compared with a supersymmetric calculation. There used to be some excitement about a possible excess reported by the WIZARD experiment, which could have been explained by supersymmetric dark matter, but this possible excess has now been refuted by the HEAT experiment with larger statistics.
flux expected due to variations in the solar wind over the 11-year solar cycle. Ting has also shown the corresponding data on e+ in the cosmic rays, compared with a supersymmetric calculation. There used to be some excitement about a possible excess reported by the WIZARD experiment, which could have been explained by supersymmetric dark matter, but this possible excess has now been refuted by the HEAT experiment with larger statistics.
Annihilation in the Sun or Earth. The idea here is based on the observation that a dark matter particle on its way through the solar system on a hyperbolic orbit may pass through the Sun or Earth, scatter off some nucleus therein, and lose sufficient recoil energy to become trapped in an elliptic orbit with perihelion (perigee) less than the solar (Earth) radius. Therefore it passes repeatedly through the Sun (Earth), losing more energy through scattering from time to time, and eventually settling into a quasi-isothermal distribution. Because evaporation off the surface of the Sun (Earth) is negligible for mχ≥ a few GeV, the only mechanism for controlling the χ population is annihilation, which would give rise to high-energy (multi-GeV) neutrinos: χχ→v+X. These could be detected in underground experiments, either directly by means of v interactions, or indirectly by means of μs produced by v collisions in the surrounding rock (34).
Underground μ searches already exclude some supersymmetric models, but only those with the largest scattering cross sections, which tend to have also the highest annihilation cross sections, and this study included models with Ωχh2≥0.025 (35). We (36) found that favored supersymmetric models yielded fluxes below the present experimental sensitivites if universal scalar masses were assumed, whereas nonuniversal models could yield larger rates and some might already be excluded. Future experiments such as SuperKamiokande. Baikal, AMANDA, and NESTOR should be able to exclude a larger selection of models.
Dark Matter Scattering on Nuclei. The rates of χ capture in the Sun (Earth) and scattering on nuclei are determined by the amplitudes A(χ(p, n)→χ(p, n)) for scattering on individual nucleons. These are calculated from elementary four-fermion χq→χq scattering amplitudes mediated by the exchanges of heavy quarks such as Z, H, and ![]() , in much the same way as the Fermi four-fermion β-decay interaction is mediated by W exchange. In particular, there is a spin-dependent part that takes the form
, in much the same way as the Fermi four-fermion β-decay interaction is mediated by W exchange. In particular, there is a spin-dependent part that takes the form ![]() in the χ→
in the χ→![]() limit, where the ∆q are the different quark contributions to the proton spin (37). These used to be estimated by using the naive quark model, but recent polarized lepton-nucleon scattering experiments have shown this to be a bad approximation, currently yielding (ref. 38 and references therein)
limit, where the ∆q are the different quark contributions to the proton spin (37). These used to be estimated by using the naive quark model, but recent polarized lepton-nucleon scattering experiments have shown this to be a bad approximation, currently yielding (ref. 38 and references therein)
∆u=0.80±0.04±0.04, ∆d=−0.46±0.04±0.04,
∆s=−0.12±0.04±0.04. [5]
Likewise, there are spin-independent contributions to dark matter scattering, which are proportional to the quark contributions to the nucleon mass. These contributions are coherent and dominant for large nuclei. In Fig. 8 some supersymmetric model calculations are compared with recent upper limits from an experiment using a Xe target (39). We see that the experimental upper limit is getting down into the range where it can discriminate between realistic supersymmetric models, and further improvements can be expected from several groups in the coming years.
Axions
Axions may be considered as an archetype for bosons that contribute coherently to the mass density of the Universe by means of coherent waves. Axions were invented to explain (40, 41) the approximate conservation of parity and charge parity in the strong interactions:
[6]
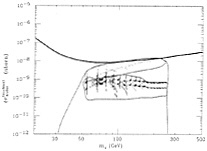
FIG. 8. Comparison of experimental upper limit on direct dark-matter scattering cross section on heavy nuclei with model calculations (39).
|
† |
In this higgsino-like region, quantum corrections to the chargino and higgsino masses are potentially significant (31). |
The θ parameter may be adjusted dynamically to a very small value with the aid of a very light spin-0 boson a with couplings ≈l/fa, where fa is called the axion decay constant:
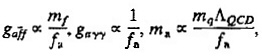
[7]
where ΛQCD is a typical strong-interaction scale. The absence of axions in accelerator experiments tells us that fa≥1 TeV.
One expects (see, e.g., refs. 42 and 43) coherent waves of axions to have formed in the Universe during the quarkhadron phase transition, yielding
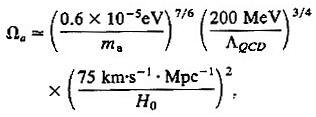
[8]
which is ≥1 if ma ≥10−5 eV—i.e., fa≤1012 GeV. There might in addition be a nonnegligible density of axions radiated from cosmic strings or from other sources. If present, these would strengthen the upper bound on fa.
There are many astrophysical constraints on axions by means of their nonemission from the cores of astrophysical objects. For example, the fact that the Sun radiates photons, not axions, tells us that fa≥107 GeV, and a similar limit is obtained from upper limits on the axio-electric effect induced by axions radiated by the Sun. Moreover, the agreement of observations of other astrophysical objects such as Red Giants and White Dwarfs with standard models constrains fa≥few× 109 GeV.
Part of this window may be closed by observations of supernova 1987a (44). According to the standard theory of type II supernovae, 99% of its binding energy should have been radiated in the form of neutrinos with a characteristic energy of a few MeV, and this theory is consistent with the observation of the Irvine-Michigan-Brookhaven and Kamiokande underground experiments. Any extra energy emission by means of axions would have reduced the total energy radiated in neutrinos and would have shortened the pulse. The other astrophysical limits suggest that any axions created in the core would have streamed freely out.
The dominant axion emission process is usually thought to be NN→NNa bremsstrahlung, with a possible contribution from ππ→πa conversion. The axion-nucleon couplings are related to the ∆q introduced earlier:
Cap![]() 2(−2.76∆u−1.13∆d+0.89∆s−cos2β(∆u−∆d−∆s))
2(−2.76∆u−1.13∆d+0.89∆s−cos2β(∆u−∆d−∆s))
Can![]() 2(−2.76∆d−1.13∆u+0.89∆s−cos2β(∆d−∆u−∆s)).
2(−2.76∆d−1.13∆u+0.89∆s−cos2β(∆d−∆u−∆s)).
[9]
The values (Eqs. 5) of the ∆q determine the Cap and Can with uncertainties that are smaller than many others in axion emission, which is approximately ![]()
![]()
We have recently taken a fresh look at axion emission from supernova 1987a (44), incorporating these latest determinations of the ∆q, studying the possible reduction of a emission by many-body effects, and including the possibility of πa conversion. In particular, we found that nucleon spin fluctuations in the nuclear medium could degrade previous limits by a factor ~2, whereas πa conversion could strengthen the limits by a factor ~3 or 4. Overall, we found (44)
[10]
corresponding to a lower limit
fa≥1010 to 1011 GeV,
with the precise value depending on nuclear uncertainties. This leaves an interesting window of opportunity for axion search experiments.
Conclusion
Cosmology and the theory of structure formation are going through a (pre-)revolutionary period reminiscent of that leading to the establishment of the Standard Model of particle physics. The observation by Cosmic Background Explorer (COBE) of fluctuations ∆T/T in the microwave background radiation reminds me of the discovery of neutral currents. That was suggestive for the Weinberg-Salam model: COBE is suggestive for inflation. Subsequently, many experiments went on to measure sin2θw very precisely, and the microwave background experiments may go on to map out the inflaton potential. The defining moment of the Standard Model revolution was the discovery of the J/ψ and charm, and it was essentially established by the later discovery of the W± and Z0. For me, the corresponding steps now would be the discovery of a cold dark matter particle and/or the discovery of neutrino masses.
To my mind, no theory of structure formation can be regarded as established unless and until the nature of the dark matter has been identified in a laboratory experiment.
Discovery of the LSP, the axion, or a massive neutrino not only would establish a Standard Model of structure formation but also would reveal to us grand unification, supersymmetry, or some other extension of the Standard Model of particle physics. Interesting years of collaboration among cosmologists, astrophysicists, and particle physicists lie before us.
1. Maiani, L. (1980) in Proceedings of the Summer School on Particle Physics, Gif-sur-Yvette, 1979 (IN2P3, Paris), pp. 3–42.
2. ’t Hooft. G. (1980) in Recent Developments in Field Theories, eds. ’t Hooft, G., Kzykson, C., Jaffe. A., Lehmann, H., Mitter, P.K., Singer, I.M. & Stora, R. (Plenum, New York), pp. 135–157.
3. Witten, E. (1981) Nucl. Phys. B188, 513–554.
4. Kaul, R.K. (1982) Phys. Lett. 109B, 19–24.
5. Gol·fand, Y.A. & Likhtman, E.P. (1971) Pis’ma Zh. E.T.F. 13, 323–326.
6. Volkov. D. & Akulov, V.P. (1973) Phys. Lett. 46B, 109–110.
7. Wess. J. & Zumino, B. (1974) Nucl. Phys. B70, 39–50.
8. Fayet P. & Ferrara. S. (1977) Phys. Rep. 32C, 249–334.
9. Ellis, J., Hagelin, J.S., Nanopoulos, D.V., Olive, K.A. & Srednicki, M. (1984) Nucl. Phys. B238, 453–476.
10. Okada. Y., Yamaguchi, M. & Yanagida, T. (1991) Prog. Theor. Phys. 85, 1–6.
11. Ellis, J., Ridolfi, G. & Zwirner, F. (1991) Phys. Lett. B257, 83–91.
12. Ellis, J., Ridolfi, G. & Zwirner, F. (1991) Phys. Lett. B262, 477–484.
13. Haber, H.E. & Hempfling. R. (1991) Phys. Rev. Lett. 66, 1815–1818.
14. Barbieri, R., Frigeni, M. & Caravaglios, F. (1991) Phys. Lett. B258, 167–170.
15. Okada, Y., Yamaguchi, M. & Yanagida, T. (1991) Phys. Lett. B262, 54–58.
16. Ellis, J., Fogli, G.L. & Lisi, E. (1996) Phys. Lett. B389, 321–326.
17. Dimopoulos, S., Raby, S. & Wilczek, F. (1981) Phys. Rev. D24, 1681–1683.
18. Marciano, W.J. & Senjanovic, G. (1982) Phys. Rev. D25, 3092– 3095.
19. Ibán̄ez, L.E. & Ross, G.G. (1982) Phys. Lett. 105B, 439–442.
20. Einhorn. M.B. & Jones, D.R.T. (1982) Nucl. Phys. B196, 475–488.
21. Ellis, J., Kelley, S. & Nanopoulos, D.V. (1990) Phys. Lett. B249, 441–448.
22. Ellis. J., Kelley, S. & Nanopoulos, D.V. (1991) Phys. Lett. B260, 131–137.
23. Langacker, P. & Luo, M. (1991) Phys. Rev. D44, 817–822.
24. Amaldi, U., de Boer, W. & Furstenau, H. (1991) Phys. Lett. B260, 447–455.
25. Anselmo, F., Cifarelli, L., Petermann, A. & Zichichi, A. (1991) Nuovo Cimento 104A, 1817–1834.
26. Fayet P. (1980) in Unification of the Fundamental Particle Interactions, eds. Ferrara, S., Ellis, J. & van Nieuwenhuizen, P. (Plenum, New York), pp. 587–620.
27. ALEPH Collaboration, Buskulic, D., et al. (1996) Z. Phys. C72, 549–559.
28. Ellis, J., Falk, T., Olive. K.A. & Schmitt, M. (1996) Phys. Lett. B388, 97–105.
29. Ellis, J., Falk, T., Olive, K.A. & Schmitt, M., CERN preprint TH/97–105, hep-ph/9705444.
30. Hinchliffe, I., Paige. F.E., Shapiro, M.D., Soderqvist, J. & Yao, W. (1997) Phys. Rev. D55, 5520–5540.
31. Drees, M., Nojiri, M.M., Roy, D.P. & Yamada, Y. (1997) Phys. Rev. D56, 276–290.
32. Falk, T., Olive, K.A. & Srednicki, M. (1995) Phys. Lett. B354, 99–106.
33. Ellis, J., Flores, R.A., Freese, K., Ritz, S., Seckel, D. & Silk, J. (1988) Phys. Lett. B214, 403–412.
34. Ritz, S. & Seckel, D. (1988) Nucl. Phys. B. 304, 877–908.
35. Griest, K., Jungman, G. & Kamionkowski, M. (1996) Phys. Rep. 267, 195–373.
36. Berezinskii, V., Bottino, A., Ellis, J., Fornengo, N., Mignola, G. & Scopel, S. (1996) Astropan. Phys. 5, 1–26, 333–352.
37. Ellis, J., Flores, R.A. & Ritz, S. (1987) Phys. Lett. 198B, 393–402.
38. Ellis, J. & Karliner, M., Lectures at the International School on Nucleon Spin Structure, Erice (1995), CERN preprint TH/95– 334, hep-ph/9601280.
39. Bottino, A., Donato, F., Mignola, G., Scopel, S., Belli, P. & Incicchitti, A. (1997) Phys. Lett. B402, 113–121.
40. Peccei, R.D. & Quinn, H.R. (1997) Phys. Rev. Lett. 38, 1440–1443.
41. Peccei, R.D. & Quinn, H.R. (1997) Phys. Rev. D16, 1791–1797.
42. Turner, M.S. (1990) Phys. Rep. 197, 67–97.
43. Raffelt, G.G. (1990) Phys. Rep. 198, 1–113.
44. Keil, W., Janka, H.-T., Schramm, D.N., Sigl, G., Turner, M.S. & Ellis, J., (1997) Phys. Rev. D56, 2419–2432.






