Proc. Natl. Acad. Sci. USA
Vol. 95, pp. 59–66, January 1998
Colloquium Paper
This paper was presented at a colloquium entitled “The Age of the Universe, Dark Matter, and Structure Formation,” organized by David N.Schramm, held March 21–23, 1997, sponsored by the National Academy of Sciences at the Beckman Center in Irvine, CA.
Direct searches for dark matter: Recent results
LESLIE J. ROSENBERG
Department of Physics and Laboratory for Nuclear Science, Massachusetts Institute of Technology. Cambridge, MA 02139
ABSTRACT There is abundant evidence for large amounts of unseen matter in the universe. This dark matter, by its very nature, couples feebly to ordinary matter and is correspondingly difficult to detect. Nonetheless, several experiments are now underway with the sensitivity required to detect directly galactic halo dark matter through their interactions with matter and radiation. These experiments divide into two broad classes: searches for weakly interacting massive particles (WIMPs) and searches for axions. There exists a very strong theoretical bias for supposing that supersymmetry (SUSY) is a correct description of nature. WIMPs are predicted by this SUSY theory and have the required properties to be dark matter. These WIMPs are detected from the byproducts of their occasional recoil against nucleons. There are efforts around the world to detect these rare recoils. The WIMP part of this overview focuses on the cryogenic dark matter search (CDMS) underway in California. Axions, another favored dark matter candidate, are predicted to arise from a minimal extension of the standard model that explains the absence of the expected large CP violating effects in strong interactions. Axions can, in the presence of a large magnetic field, turn into microwave photons. It is the slight excess of photons above noise that signals the axion. Axion searches are underway in California and Japan. The axion part of this overview focuses on the California effort. Brevity does not allow me to discuss other WIMP and axion searches, likewise for accelerator and satellite based searches; I apologize for their omission.
Most matter in the universe is invisible. The matter we can easily identify—stars, dust, and gas—accounts for perhaps 10% of the mass density of the universe. That this missing mass, dubbed dark matter, exists is well founded. Everywhere this dark matter is expected to manifest itself, it does so. The evidence for the existence of dark matter includes the flat rotation curves of galaxies (even well beyond the clustered luminous stars), flow maps of matter over huge distance scales, and the gravitational shearing of starlight by this missing mass. Today, only a curmudgeon would doubt the existence of dark matter. However, the question of the nature of this dark matter is still open. Thus, a major question in science today is as follows: What is the nature of 90% of matter? The study of a question this profound has many twists and turns and nuances. A good starting point is the wonderful book by Kolb and Turner (1).
The simplest answer, that this dark matter is dark normal matter, runs against the very successful theory of primordial nucleosynthesis. This theory describes the production of light elements during the Big Bang and is in good agreement with observed abundances. In particular, deuterium is weakly bound. Most deuterium is produced in the Big Bang, and later processing in stars mostly depletes the deuterium abundance. Should dark matter be normal matter (that is, made up of baryons), these extra baryons would have broken up deuterium during the Big Bang and this would be reflected in a lesser-then-observed present day deuterium abundance. This same argument applies, though somewhat less strongly, to other light isotopes. Although these nucleosynthesis constraints on the amount of nonbaryonic matter have evolved and been refined over the years, the conclusion seems robust: the missing mass completely in the form of baryons is in conflict with our understanding of the Big Bang. This argues that most of the missing mass is some new exotic form of matter.
A hint as to the kind of exotic form of matter comes from looking at structure in the universe, that is, the pattern of mass scales we see. The structures we see evolved from seeds in the early universe. Should the dark matter have been moving relativistically during the epoch of structure formation (this flavor of dark matter is dubbed HDM, hot dark matter), then structures on relatively small scales would have been hard to sustain. The dark matter would have eroded this high-spatial frequency structure. On the other hand, should dark matter have been moving slowly (dubbed CDM, cold dark matter), then structure could form on small spatial scales. When we look around the galaxy and evaluate how matter is formed into structure, we see that the amount of matter clustered on small spatial scales does not allow for the missing mass to be substantially HDM. The majority of the missing mass must be CDM to not wash out structure. Now, the exact mixture of HDM, CDM, and perhaps a cosmological constant that best fits the data is contentious. However, the need for substantial amounts of CDM seems ubiquitous. The amount of dark matter in our own halo is likewise contentious. There is some irony that the fairly recent discovery of massive compact halo objects (MACHOs) in our halo may cause us to rethink the structure of our galaxy, with result the local density of nonbaryonic matter may actually increase. A recent paper, taking into account the MACHO observations and other constraints, allows for a broad range of densities near Earth, with the most likely nonbaryonic density of 7.5×10-25 g/cm3 (2).
Among the candidates for CDM, the number one favorite among theorists is WIMPs, and the number two is axions. The other CDM candidates for whatever reason are met with less favor. Both these CDM candidates are hard to detect; by its very nature, CDM couples extraordinarily feebly to ordinary matter and radiation. I should emphasize that the focus on WIMPs and axions is a theoretical bias. There is no compelling experimental validation for either theory. To the experimenter, the veracity of the theory that gives rise to WIMPs or axions is untested.
© 1998 by The National Academy of Sciences 0027–8424/98/9559–8$2.00/0
PNAS is available online at http://www.pnas.org.
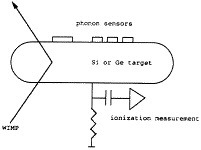
FIG. 1. Principle of the CDMS detector. A Ge or Si crystal is cooled to 20 mK and instrumented with charge and bolometric detectors. A WIMP recoils off a nucleus, releasing phonons (heat) and charge.
Despite the feeble couplings and the lack of evidence for the underlying theories, several experiments are now underway with the sensitivity required to detect directly galactic halo dark matter through its interactions with matter and radiation. These experiments divide into two broad classes: searches for weakly interacting massive particles (WIMPs) and searches for axions. There is a very strong theoretical bias for supposing that supersymmetry (SUSY) is a correct description of nature. WIMPs are predicted by this SUSY theory and have the required properties to be dark matter (3). These WIMPs are detected from the signals of an occasional recoil against nucleons. There are efforts around the world to detect these rare recoils. The WIMP part of this overview focuses on the cryogenic dark matter search (CDMS) underway in California. Axions are predicted to arise from a minimal extension of the standard model that explains the absence of the expected large CP violating effects in strong interactions (4). Axions can turn into microwave photons in the presence of a large magnetic field. It is the slight excess of photons above noise that signals the axion. Axion searches are underway in California and Japan. The axion part of this overview focuses on the California effort. Brevity does not allow me to discuss other WIMP and axion searches, likewise there is not space for accelerator and satellite-based searches; these are important topics and I apologize for their omission.
Searching for WIMPs
SUSY, the theory that predicts WIMPs, is really more a class of theories than a specific theory (4). The theory does not do a very good job of constraining what exactly the WIMP is, nor does it do a very good job of constraining the WIMP mass, nor does it do a very good job of constraining the WIMP couplings. This makes the task of detection more difficult. However, WIMPs too light would have been seen in accelerator experiments. WIMPs too heavy are theoretically disfavored. WIMP masses from perhaps 50 to 10,000 TeV are then reasonable masses to suppose. Also, by positing the WIMPs density to account for the missing mass, one can work backwards to the early universe and roughly infer the strength of the WIMP interactions. Experimenters look for by-products of the occasional recoil of a WIMP against a nucleus. These by-products include charge, light, heat, or some or all of the three. The expected signal levels and signal rates are small. The backgrounds of radioactive decays and cosmic rays are serious.
Several new high-sensitivity detectors are beginning to take data around the world. These include CRESST (cryogenic rare
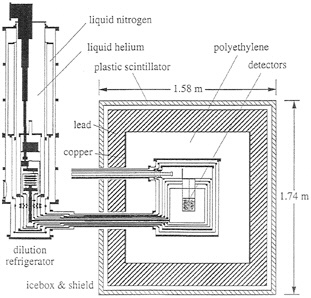
FIG. 2. Sketch of the “icebox” housing the CDMS detectors. The dilution refrigerator is shown to the left. The cold stage temperature is carried within multiple heat shields to the box shown on the right. Removing the refrigerator from the experiment area reduces backgrounds from materials in the refrigerator. The icebox is surrounded by plastic scintillation veto counters, as well as polyethylene neutron absorber.
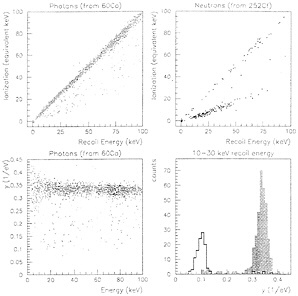
FIG. 3. The response of the 60-g Ge BLIP detector to gamma and neutron sources. (Upper Left) Detector response (vertical axis the ionization, horizontal axis the bolometric recoil energy) to a 60Co source of photons. (Upper Right) Response to a 252Ca neutron source. Notice that neutrons (meant to mimic nuclear recoils) are less efficient ionizers than photons. The lower left shows the 60Co photon-induced charge normalized to the bolometric recoil energy: this is the charge yield per keV of recoil energy. (Lower Right) The charge yield distribution from the neutron and gamma source.
event search with superconducting thermometers) in the Gran Sasso tunnel, Italy; EDELWEISS in the Frejus tunnel, France; CDMS in California; and a University of Tokyo group at Nokogiriyama, Japan. The nuclear targets differ: CRESST has sapphire; EDELWEISS has Ge: CDMS has either Ge or Si: Tokyo has LiF. These operate at deep cryogenic temperatures and require 3He cooling. All are instrumented to look for the heating associated with the nuclear recoil. The EDELWEISS and CDMS efforts in addition are instrumented to look for the associated ionization.
Example WIMP Search
Details of all the current experiments is well beyond the scope of this paper. Instead, I’ll describe in some detail one state-of-the-art WIMP search, the CDMS effort. This collaboration is a group of scientists from Berkeley, Stanford, Santa Barbara, Santa Clara, San Francisco State, Case Western, and elsewhere. The principal of their detector is shown in Fig. 1. A 160-g Si [CDMS calls this FLIP (fast large ionization and phonon detector)] or 60-g Ge [called BLIP (Berkeley large ionization and phonon detector)] crystal is cooled to 20 mK and instrumented with charge and bolometric detectors. A WIMP recoils off a nucleus, releasing phonons (heat) and charge. The charge is collected on electrodes, and the slight heat rise is detected with superconducting sensors. CDMS has two competing internal designs for these sensors: one uses a more conventional neutron transmutation doped (NTD) sensor. Another uses a transition edge sensor (TES) with SQUID (superconducting quantum interference device) readout. The SQUID readout allows the TES to be self-biased at the operating point. They designs differ, also, in their response time and position segmentation.
Assuming the electronics is sensitive to 5 keV or more nuclear recoil, and assuming WIMPs saturate the local nonbaryonic dark matter density, the approximate WIMP recoil rate is expected to be less than one detected recoil per target kilogram per day. Hence the great advantage in simultaneously measuring heat and charge; this allows for discrimination of the rare WIMP recoils from γ and β backgrounds. Going lower in recoil energy threshold increases the detected recoil rate but increases the background rate. Going deeper underground reduces cosmic ray induced backgrounds.
These detectors are mounted in the “icebox”, sketched in Fig. 2. The dilution refrigerator is shown to the left. The cold stage temperature is carried within multiple heat shields to the box shown on the right. Separating the refrigerator from the experiment area reduces backgrounds from materials in the refrigerator. The icebox is surrounded by plastic scintillation veto counters, as well as polyethylene neutron absorber.
This background rejection, by way of the response to gamma and neutron sources (in this case for the 60-g Ge BLIP detector) is shown in the four frames of Fig. 3. Fig. 3 Upper Left shows the detector response (vertical axis the ionization. horizontal axis the bolometric recoil energy) to a 60Co source of photons. Fig. 3 Upper Right shows the response to a 252Ca neutron source. Notice that neutrons (meant to mimic nuclear recoils) are less efficient ionizers than photons. Fig. 3 Lower Left shows the 60Co photon-induced charge normalized to the bolometric recoil energy; this is the charge yield per keV of recoil energy. Fig. 3 Lower Right shows this charge yield distribution from the neutron and gamma source. Notice, at least for these relatively large recoil energies, the separation of neutron (signal-like) and gamma (background-type) recoils. Also notice the distributions are non-Gaussian. At some point, the CDMS group will consider background subtraction from
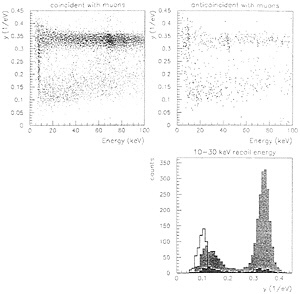
FIG. 4. The in situ response of the 60-g Ge BLIP detector while in the low-background environment of the ice-box. (Upper Left) The charge yield vs. recoil energy in coincidence with a muon signal. The dense horizontal band are photons and electrons associated with the muons traversal The lighter, broader, band just below are likely muon-associated ß’s depositing energy in inefficient regions of the detector. (Upper Right) The same response, except in anti-coincidence with a muon signal. Also shown in the band of charge yield where nuclear recoils are expected to be. (Lower Right) The distribution of charge yield in the recoil energy region between 10 and 30 keV. Three distributions are overlaid: (i) the highest number or counts is from the muon-coincident data. (ii) the filled distribution is the anti-coincident data, and (iii) the neutron calibration is shown at the left.
their signal region; the non-Gaussian nature of the background is what makes this subtraction challenging.
The in situ response of this same 60-g Ge BLIP detector while in the low-background environment of the ice-box is shown in Fig. 4. Fig. 4 Upper Left shows the charge yield vs. recoil energy in coincidence with a muon signal. The dense horizontal band represents photons and electrons associated with the muons’ traversal. The lighter, broader, band just below are likely muon-associated ß’s depositing their energy in inefficient regions of the detector. Fig. 4 Upper Right shows the same response, except in anti-coincidence with a muon signal. Also shown in the band of charge yield where nuclear recoils are expected to be. Notice that low background in the region expected for WIMP nuclear recoils. Fig. 4 Lower Right shows
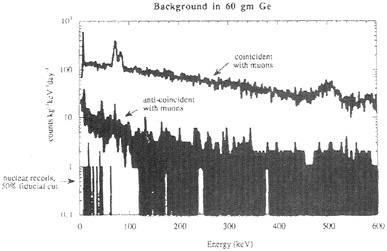
FIG. 5. The background spectrum in the 60-g Ge BLIP detector. The horizontal axis is recoil energy, and the vertical axis is the count rate. The upper distribution is the signal in coincidence with muons; lead fluorescence lines are seen to the left and the 511-keV line is seen at the right. The middle distribution is the signal anti-coincident with muons. The lower distribution to the left is the remaining signal after demanding a charge yield of less than 0.1/eV and removing data from inefficient detector areas.
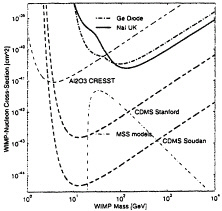
FIG. 6. Preliminary CDMS data in context with other experiments and the expected WIMP signal. The horizontal axis is WIMP mass, the vertical axis is the WIMP cross section. The two curves at the top are existing limits. I estimate their present sensitivity at about or slightly better than the two existing limits; the small sample of CDMS data is already competitive with the long “Ge Diode” production run. Somewhat lower down is “CDMS Stanford” the anticipated ultimate sensitivity of the CDMS detector in the Stanford shallow site. And somewhat lower yet is the “CDMS Soudan” ultimate projected sensitivity at a deep Soudan mine site. The curve “CRESST” is the projected sensitivity of the European sapphire detector. The curve labeled “MSS models” gives an estimate of the expected cross sections for SUSY-motivated WIMPs.
the distribution of charge yield in the recoil energy region between 10 and 30 keV. Three distributions are overlaid: (i) the highest number of counts is from the muon-coincident data, (ii) the filled distribution is the anti-coincident data, and (iii) the neutron calibration is shown at the left.
The background spectrum in the 60-g Ge BLIP detector is shown in Fig. 5. The horizontal axis is recoil energy, and the vertical axis is the count rate. The upper distribution is the signal in coincidence with muons; lead fluorescence lines are seen to the left and the 511-keV line is seen at the right. The middle distribution is the signal anti-coincident with muons. The lower distribution to the left is the remaining signal after demanding a charge yield of less than 0.1/eV and removing data from inefficient detector areas.
These data, in context with other experiments and the expected WIMP recoil signal, are shown in Fig. 6. The horizontal axis is WIMP mass, and the vertical axis is the WIMP cross section. The two curves at the top are existing limits. Although not released by the CDMS collaboration, I estimate their present sensitivity at about or slightly better than the two existing limits. This is impressive, considering the CDMS data is 30 fiducial g with 21-day exposure, and the “Ge Diode” (data from the Oroville detector) result is from 0.9 fiducial kg with 146-day exposure. The small sample of CDMS data is even now competitive with the long “Ge Diode” production run. Somewhat lower down is “CDMS Stanford,” the anticipated ultimate sensitivity of the CDMS detector in the Stanford shallow site. And somewhat lower is the “CDMS Soudan” ultimate projected sensitivity at a deep Soudan mine site. Also notice the curve “CRESST,” the projected sensitivity of the European sapphire detector. The curve labeled “MSS models” gives an estimate for the expected cross sections of SUSY-motivated WIMPs. Notice that current experiments are beginning to push into the region of plausible WIMP couplings.
Searching for Axions
The other broad class of CDM searches look for axions. Axions arise as part of a simple extension of the standard model that explains the lack of expected CP violating effects in strong interactions. The axion would be a pseudoscalar, similar in properties to the neutral pion. Originally, the scale attached to axion physics was taken as the weak scale. This predicted relatively heavy axions (several hundred keV) with couplings to normal matter and radiation that would permit them to be seen in conventional nuclear and particle physics experiments. This weak scale axion was not seen. Theorists then built models attached to much greater energy scales, with correspondingly smaller masses and couplings to matter and radiation. At these

FIG. 7. Regions in the axion mass vs. two photon coupling constant plane excluded by the pilot cavity experiments. Also shown are coupling constants expected in a range (dubbed DFSZ and hadronic) of axion models. The area extending into the hadronic axion region is the expected sensitivity of the U.S. experiment.
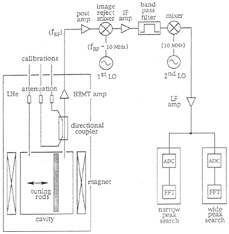
FIG. 8. Sketch of the major components of the U.S. axion search experiment.
large scales, the axion couplings to matter and radiation are incredibly feeble. They are “invisible axions”.
However, axions cannot be too light. Axions acquired their mass at the Quantum Chromodynamics (QCD) scale during the Big Bang. One particular production mechanism— misalignment production—has the total mass density of axions increasing with the axion scale. A sufficiently light axion (say, 1–10 µeV) would dominate the mass density of the universe yet possess couplings so weak as to render them virtually invisible.
With the axionic component of the Universe increasing with the axion scale, and the observation that we do not live in an over-closed universe, we get a rough lower bound on the mass of the axion of a few µeV. An upper bound to the axion mass, around 1 meV, comes from observing 20 neutrinos from SN1987a over tens of seconds in terrestrial experiments. The arrival time distribution does not allow for meV scale axions— these would have efficiently channeled energy out of the supernova and foreshortened the burst. This leaves a window 1–1,000 µeV of plausible axion masses.
In 1983, Pierre Sikivie proposed a technique to detect these invisible axions (5). His technique called for three basic components: a high Q microwave cavity, permeated by a strong static magnetic field, whose rf power is measured by low-noise amplifiers. In the magnetic field, axions can convert into microwave photons, each photon carrying the energy of the axions. The axion signal on the power spectrum is expected to be narrow, with frequency the axion mass, the line width broadened slightly by the virial velocity of axions in the galactic halo. As axions are moving at virial velocities of ߘ10-3, the axion peak should have a line width about 10-6. The power in the axion line will be small, perhaps 10-22 W or less. Two small experiments based on this technique reported results in the 1980’s (6, 7), but with inadequate sensitivity to detect axions.
There are two new experiments underway based on Sikivie’s technique. One, a Kyoto University group, is commissioning an experiment having relatively small cavities, but with exotic and potentially extremely low noise microwave amplifiers. Another group from the Massachusetts Institute of Technology, Lawrence Livermore Laboratory, University of Florida, Berkeley, and Fermilab is now taking data on a large volume cavity.
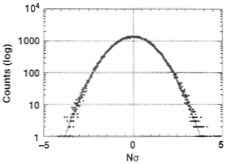
FIG. 9. The distribution of power, in units of standard deviation, about the mean power.
Example Axion Search. This second axion search, operated at the Lawrence Livermore National Laboratory in the United States, is now taking data. The capability of this experiment to either detect axions (with signal-to-noise ratio of 4) or exclude them (at the 97.7% confidence limit) is shown as the region extending into hadronic axion couplings in Fig. 7. The key goals of the experiment are (i) to attain a power sensitivity which is conservatively a factor of nearly 100 improvement over the pilot experiments—achieved by having a big magnet volume and incorporating advances in low noise microwave amplification, and (ii) the potential to search the entire mass range 1.5–12.6 µeV, achieved through filling the magnet volume with multiple higher frequency cavities.
The key parts of the U.S. experiment are sketched in Fig. 8. The experiment features a superconducting magnet with a central field near 8.0T. The experimental volume has inner diameter 50 cm and length 100 cm. Hence, the magnet figure-of-merit B2V is about a factor of 25 better than the pilot experiments from the 1980s. The experimental volume is separated from the magnet cryostat by a cold-vacuum wall. The vacuum wall allows exchanging cavity arrays and electronics while the magnet is energized and for cooling the cavity arrays to below the magnet temperature of 4.2K. The cavity is operated at about 1.3K, a physical temperature somewhat lower than the noise temperatures of the best amplifiers available today in the UHF through S-bands (0.5–3 GHz). The total noise temperature near 4K (physical plus electronic) yields another factor 1.6 in improved sensitivity over the pilot experiments.
The U.S. experiment features arrays of multiple cavities to extend the mass search range. Each cavity is separately tuned by moving dielectric or metallic rods within the cavity, and in this way the experiment will search the range 1.5–12.6 µeV. Additionally, the U.S. experiment looks for possible narrow peaks in the halo axion velocity spectrum. This has the potential to greatly increase sensitivity as the signal to noise power ratio improves with decreasing bandwidth. In the U.S. experiment, there are separate processing paths for the isothermal and narrow peak searches. Data taking started after a shake-down run in January 1995 and has been in continuous operation with >90% duty factor.
For the most part, this experiment records noise. Fig. 9 shows the distribution of power, in units of standard deviation, about the mean power. The data is Gaussian distributed beyond 4s. Occasionally, one detects non-Gaussian deviations. Fig. 10 shows such a deviation. The vertical axis is power in an arbitrary linear scale. The horizontal axis is frequency. Each frequency bin is 125 Hz. The series of spectra arrayed from top to bottom are individual power
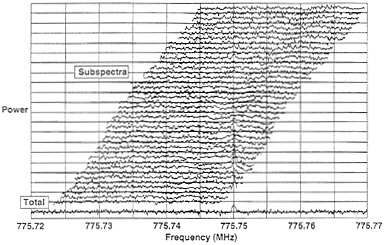
FIG. 10. An obvious spurious peak. The vertical axis is power in an arbitrary linear scale. The horizontal axis is frequency. Each frequency bin is 125 Hz. The series of spectra arrayed from top to bottom are individual power spectra accumulated as the frequency of the cavity was changing. The center of each individual spectrum is the resonant frequency of the cavity. At the very bottom is the weighted sum of these individual power spectra. Notice the peak at 775.75 MHz. By going back and examining the individual spectra, one can see this peak developed off-resonance in each individual spectrum. This 10s peak is therefore unlikely to be an axion; it is probably radio interference entering calibration ports and reflecting off the cavity into the amplifier.
spectra accumulated as the frequency of the cavity was changing. The center of each individual spectrum is at the resonant frequency of the cavity. The spectrum at the very bottom is the weighted sum of these individual power spectra. Notice the peak at 775.75 MHz. By going back and examining the individual spectra, one can see this peak developed off-resonance in each individual spectrum. This 10s peak is therefore unlikely to be an axion, it is probably radio interference entering calibration ports and reflecting off the cavity into the amplifier.
Fig. 11 illustrates the sensitivity of the detector. The horizontal axis is frequency (also, axion mass). The vertical axis to the left is power in watts. The points are the sensitivity of the experiment in a particular frequency bin. The line is
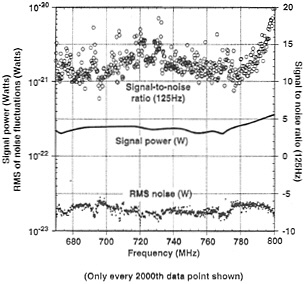
FIG. 11. The sensitivity of the detector. The horizontal axis is frequency (also axion mass). The vertical axis to the left is power in W. The points are the sensitivity of the experiment in a particular frequency bin. The line is the expected power deposited by a “KSVZ” axion should the axion have the corresponding mass. Notice the experiment sensitivity is approaching 10-23 W. well below the line.
the expected power deposited by a “KSVZ” axion should the axion have the corresponding mass. Notice the experiment sensitivity is approaching 10-23 W, well below the line.
Conclusions
Over the last year, WIMP and axion searches became sensitive enough to detect plausible dark matter candidates. The WIMP part of this overview focused on the CDMS effort. The axion part of this overview focused on the California effort. There are numerous other experiments, but brevity did not allow me to discuss them in any detail. This is an exciting time for the dark matter community: should copious amounts of dark matter exist as WIMPs or axions, they could be discovered soon.
I wish to thank Tom Shutt of the Center for Particle Astrophysics, Berkeley, for helpful discussions and for material relating to the CDMS effort.
1. Kolb, E. & Turner. M. (1990) The Early Universe (AddisonWesley, Reading, PA).
2. Gates. E., Gyuk, G. & Turner, M. (1995) Astrophys. J. 449, 123.
3. Jungman, G. & Kamionkowski, M. (1996) Phys. Rep. 267, 195–373.
4. Turner, M. (1990) Phys. Rep. 197, 67–97.
5. Sikivie, P. (1983) Phys. Rev. D 32, 2988–2991.
6. Wuensch, W.U., DePanfilis-Wuensch, S., Semertzidis, Y.K., Rogers, J.T., Melissinos, A.C., Halama, H.J., Moskowitz, B.E., Prodell, A.G., Fowler. W.B. & Nezrick, F.A. (1989) Phys. Rev. D 40, 3153–3167.
7. Hagmann, C., Sikivie, P., Sullivan, D.B. & Tanner, D.B. (1990) Phys. Rev. D 42, 1297–1300.








