Proc. Natl. Acad. Sci. USA
Vol. 95, pp. 67–71, January 1998
Colloquium Paper
This paper was presented at a colloquium entitled “The Age of the Universe, Dark Matter, and Structure Formation,” organized by David N.Schramm, held March 21–23, 1997, sponsored by the National Academy of Sciences at the Beckman Center in Irvine, CA.
Galaxy formation
P.J.E.PEEBLES†
Joseph Henry Laboratories, Princeton University, Princeton, NJ 08544
ABSTRACT It is argued that within the standard Big Bang cosmological model the bulk of the mass of the luminous parts of the large galaxies likely had been assembled by redshift z~10. Galaxy assembly this early would be difficult to fit in the widely discussed adiabatic cold dark matter model for structure formation, but it could agree with an isocurvature version in which the cold dark matter is the remnant of a massive scalar field frozen (or squeezed) from quantum fluctuations during inflation. The squeezed field fluctuations would be Gaussian with zero mean, and the distribution of the field mass therefore would be the square of a random Gaussian process. This offers a possibly interesting new direction for the numerical exploration of models for cosmic structure formation.
Galaxies are not mentioned much in modern studies of structure formation; the emphasis is on phenomena on the smaller mass scales of the Lymanα forest clouds and on the larger scales of the extended dark matter concentrations that might be sites for formation of galaxies and clusters of galaxies. That is, the focus is on simpler problems, involving systems that are not strongly nonlinear and not likely to have been greatly disturbed by star formation. The path is sensible but not a very direct route to the lessons to be drawn from the galaxies.
An important lesson may be found in the high mass densities within galaxies. The mean density within our position in the Milky Way is equivalent to about one proton cm−3, six orders of magnitude greater than the large-scale average. Why is the contrast so big? In the commonly discussed adiabatic cold dark matter (CDM) model, protogalaxies form at relatively low redshift and reach high contrast because they collapse by a large factor. Another possibility is that the mass was assembled at high redshift, when the mean density was larger and the collapse factor thus more modest. In the next section I argue that the latter agrees with the interpretation of rich clusters of galaxies as scaled versions of protogalaxies, and that late assembly is not easy to reconcile with constraints from the physics and astrophysics.
We must take care to distinguish the epochs of formation of star populations from the epoch of assembly of the bulk of the mass (1). If, as the evidence reviewed here suggests, the latter happened early, we likely will have to find an alternative to the adiabatic CDM model for structure formation. The success of the standard picture for the light elements [as discussed by Schramm in this issue of the Proceedings (2)] leads me to stay with the idea that the dominant mass in clusters of galaxies and the outer parts of individual galaxies is nonbaryonic, the commonly discussed CDM. A picture that seems worth exploring is that this CDM is the remnant of quantum fluctuations frozen into a massive scalar field during inflation.
Clusters of Galaxies as Scaled Protogalaxies
We have a remarkably tight set of checks on the mass distribution within a cluster. The gravitational potential well needed to contain the motions of the galaxies agrees with what is needed to contain the intracluster plasma detected by its x-ray emission and by its effect on the thermal background radiation. The gravitational potential also agrees with the observations of gravitational lensing. A useful approximation to the mass distribution is a limiting isothermal sphere with mass M(<r)=2σ2r/G, where σ is the line-of-sight velocity dispersion. Characteristic numbers for clusters are
rcl=1.5h−1 Mpc, σ=750 km s−1, [1]
where rcl is the Abell radius, σ is an rms mean for Abell clusters, Mpc is megaparsecs, and Hubble’s constant is H0=100h km s−1 Mpc−1. The isothermal model also gives a useful first approximation to the mass distribution within the luminous parts of L· spiral galaxies (objects like the Milky Way that contribute the bulk of the luminosity density); characteristic numbers here are
rg=10h−1 kpc, vc=200 km s−1, [2]
where vc is the circular velocity and kpc is kiloparsecs. I have chosen the radius rg to be large enough to include most of the luminosity and enough of the dark halo that, in the standard model for an L· spiral, the contained mass typically is dominated by CDM.
The mass density contrasts within the radii in Eqs. 1 and 2 are:
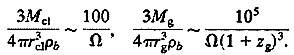
[3]
The cosmic mean mass density is ρb, and the density parameter Ω is the ratio of ρb to the critical Einstein-de Sitter value. The contrast for clusters is evaluated at the present epoch. The contrast for galaxies could be evaluated at redshift zg if galaxies existed then with about the same characteristic mass within the physical radius rg. The fractions of the net mass of the universe within radii rcl and rg in clusters and in galaxies are:
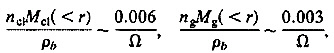
[4]
where ncl and ng are the characteristic number densities of clusters and galaxies. The ratio of the object size to the separation defined by the number density is
© 1998 by The National Academy of Sciences 0027–8424/98/9567–5$2.00/0
PNAS is available online at http://www.pnas.org.
|
† |
To whom reprint requests should be addressed, e-mail: pjep@pupgg.princeton.edu. |
[5]
As in Eq. 3 this ratio could be evaluated at redshift zg if the galaxies were present then.
Gravity is scale-invariant at distances small compared with the Hubble length, and the expansion of the universe is scale-invariant or close to it. If the initial conditions were scale-invariant and we could ignore nongravitational interactions then structure formation would follow a scaling law where the length scale as a function of redshift is set by the spectrum of primeval mass density fluctuations. Eqs. 3–5 show that galaxies at redshift
zg~10 [6]
resemble scaled versions of present-day clusters of galaxies.
We might pause to consider the slope of the power spectrum of density fluctuations that would scale protogalaxies to clusters. The ratio of comoving wavenumbers that enclose the masses defined by Eqs. 1 and 2 is
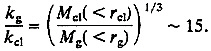
[7]
The ratio of the mean square primeval mass density fluctuations on these two scales is
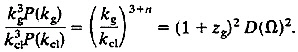
[8]
The power spectrum is assumed to vary as P∝kn. The last expression is the ratio of the gravitational growth factor up to the present for clusters and up to redshift zg for protogalaxies, where D(Ω) is the departure from the Einstein-de Sitter growth factor. In a cosmologically flat model D(Ω) is close to unity, and Eqs. 7 and 8 with zg~10 require n~−1.3. This is not far from the measured slope of the power spectrum on larger scales where the present galaxy distribution is thought to be linearly related to the primeval mass distribution. That is, the scaling picture seems to be consistent with what is known about the present mass distribution.
Substructure shows that there is considerable ongoing merging and relaxation in present-day clusters of galaxies. Within this scaling picture one similarly would expect substantial merging and relaxation at z~10 in young galaxies that are considerably more irregular than they are now. The main point is that because nature manifestly is capable of producing bound mass concentrations on the scale of clusters now it is capable of doing about the same on the scale of galaxies at z=10.
The value for zg from this argument depends on the choice of rg in Eq. 2. A larger radius would yield a smaller value for zg, which in this picture would be interpreted as a characteristic epoch for the assembly of the extended dark halos of spiral galaxies. A substantially smaller value for rg would probe the baryon-dominated parts of galaxies, which certainly can behave differently from the CDM that is assumed to dominate clusters and the outer parts of individual spirals.
The scaling picture would fail if the mass concentration within the Abell radius of a cluster typically were evolving on the scale of the Hubble time, but this is inconsistent with the evidence that clusters are close to dynamical equilibrium at the Abell radius, and that many clusters at z=0.5 have central masses comparable to present-day systems [as discussed in this issue of the Proceedings by Mushotzky (3)]. The picture would fail if the spectrum of primeval density fluctuations were cut off at about the mass of a galaxy: pancake collapse at the cutoff might allow a larger collapse factor than is seen in clusters of galaxies. The point is worth exploring but not relevant to the adiabatic CDM model or the proposed isocurvature variant. I turn now to an issue that could be very relevant, the breaking of scaling by dissipation by gaseous baryons.
Dissipative Galaxy Assembly at Redshift z≤3
If protogalaxies were assembled well after redshift z=10 they would have to have collapsed by a considerable factor to reach the densities characteristic of the bright parts of galaxies. Gaseous baryons can be strongly dissipative, and dissipation can result in strong settling. This is a commonly held basis for the assumption of relatively late galaxy assembly, but some issues should be considered.
Fig. 1 shows models for galaxy assembly at relatively early and late epochs. The curves contain baryonic and total masses
MB=1×1011M⊙, M=6×1011M⊙. [9]
The former is typical of an L· spiral like the Milky Way. The ratio of baryonic to CDM mass is in the range now under discussion (4, 5); the uncertainty in the ratio does not affect these considerations much. The background cosmological model has density and Hubble parameters
Ω=0.3, h=0.7. [10]
If the mass distribution may be modeled as spherical and homogeneous (to avoid orbit crossing) then the relation between the nominal redshift zc at collapse to zero radius and the radius at maximum expansion may be approximated as
[11]
The second expression uses the numbers in Eqs. 9 and 10. The curves in Fig. 1 follow the spherical model through maximum expansion and nearly free collapse to a radius typical of a large spiral galaxy. In a spherical and homogeneous mass distribution the kinetic energy vanishes at maximum expansion, and collapse by a factor of two in radius produces enough kinetic energy for virial equilibrium at density contrast ~100. A real protogalaxy or protocluster likely has appreciable kinetic energy at nominal maximum expansion, which would tend to reduce the collapse factor. Thus it is not surprising that clusters are close to equilibrium at least as far out as the Abell radius
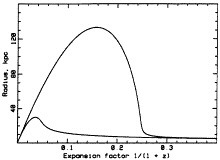
FIG. 1. Scenarios for the assembly of the luminous parts of a galaxy like the Milky Way. The curves show two models for the proper radius of the protogalaxy as a function of the expansion parameter (1+z)−1. The models follow the solution for a spherical mass distribution over the peak and down to a radius characteristic of a large galaxy. Late assembly requires close to free collapse by an order of magnitude in radius. Early assembly requires more modest contraction, consistent with what is observed in the great clusters of galaxies.
at the density contrast in Eq. 3. In the model for late galaxy assembly in Fig. 1, the radius at maximum expansion is 130 kiloparsecs, and the protogalaxy must dissipatively collapse by more than an order of magnitude in radius. Is this reasonable? I offer two points.
First, in models like adiabatic CDM and the isocurvature variant, structure formation is hierarchical: protogalaxies are assembled out of subconcentrations that were assembled out of sub-subconcentrations. If nongravitational dissipation of nonradial motions could cause the baryons in a protogalaxy to collapse nearly freely by a factor of 10 in radius, why would the same effect not have caused strong collapse earlier in major subconcentrations? In the late formation scenario in Fig. 1 that would have produced dwarf galaxies in a group with diameter ~100 kiloparsecs, which would take a long time to merge into something resembling the spheroid component of a large galaxy. The problem is avoided if nonradial motion prevented catastrophic collapse of the major subconcentrations, but the same effect of nonradial motion would have slowed collapse of the protospheroids, contrary to the late formation model in Fig. 1.
Second, the evidence is that in large spirals the rotation curve is close to flat from the inner parts dominated by baryons to the outer parts that are presumed to be dominated by dissipationless CDM. In the late assembly picture, dissipative collapse increases the baryon density by a large factor. The growing potential well would drag CDM with it, but the increase in density has to be much less than for the baryons because the CDM is not allowed to dissipate energy. Why would the large difference of collapse factors for the baryons and the CDM not have produced a Keplerian feature in the rotation curves of spiral galaxies?
Galaxies at High Redshift
The remarkable advances in observations of galaxies at z>1, described in this issue of the Proceedings by Steidel (6), offer valuable clues to the epoch of galaxy assembly. We have to consider the possible difference between the epochs of formation of star populations and of the assembly of the mass, however (1). The peak in the comoving number density of quasars at z~2.5 may be evidence for late galaxy assembly, or instead it could be a measure of the time required for the development of an active galactic nucleus central engine after assembly of the protogalaxy. A peak in the star formation rate is at z~1 (7), but a major contributor is a population of relatively low mass galaxies that since have faded or merged (8); the evidence is that the large spirals and ellipticals are in place at z~1. The small scatter in the color-magnitude relation suggests the stars in ellipticals and the spheroid components of the spirals formed at high redshift. Kauffmann (9) shows that this does not contradict the adiabatic CDM model; the stars can have formed before the ellipticals were assembled. On the other hand, Prochaska and Wolfe (10) show that the damped Lymanα systems at z~3 have the properties expected of rotationally supported gaseous discs; they are reasonable candidates for protodiscs draped around the spheroid bulges in the dark matter halos of protospirals, an example of star formation well after assembly of the mass.
A CDM Model for Early Galaxy Assembly
I turn now to a model for early galaxy assembly within the inflation scenario for the very early universe. These qualitative comments are meant to show that a more detailed assessment by numerical simulations could be interesting.
In early discussions of the inflation scenario people considered two ways homogeneity could be broken. In the first model, quantum fluctuations δø(![]() ) frozen into the field ø whose energy is driving inflation produce adiabatic fluctuations with mass density contrast
) frozen into the field ø whose energy is driving inflation produce adiabatic fluctuations with mass density contrast
δ(![]() )=δρ/ρ
)=δρ/ρ![]() δø(
δø(![]() ). [12]
). [12]
The perturbation to the density is proportional to the perturbation to the field, because |δø|<<|ø|. In simple models for inflation this makes the primeval mass density contrast δ(![]() ) a random Gaussian process characterized by a power spectrum (the Fourier transform of the mass autocorrelation function) that is close to a power law,
) a random Gaussian process characterized by a power spectrum (the Fourier transform of the mass autocorrelation function) that is close to a power law,
Pρ(k)![]() Pø(k)økn. [13]
Pø(k)økn. [13]
The case n=1 first attracted attention because the perturbation to space-time curvature diverges only as the logarithm of k, so the power law can apply to a broad range of scales. In the second model a single-component scalar field ψ that is present during inflation ends up as (or decays into) the present-day CDM. The field is supposed to acquire mass m0, so on scales large compared with the Compton wavelength ![]() the CDM mass distribution well after inflation is
the CDM mass distribution well after inflation is
[14]
Here the mass fluctuations are non-Gaussian.
If inflation is cool, adiabatic departures from homogeneity may be subdominant. Under this isocurvature condition, the net mass distribution is homogeneous at high redshift, and the composition is a function of position. In the model in Eq. 14 the inhomogeneity is the local ratio of mass in the CDM to the mass in all the other components. If ψ(![]() ) is a random Gaussian process with zero mean the autocorrelation function of the mass distribution in the field is
) is a random Gaussian process with zero mean the autocorrelation function of the mass distribution in the field is
[15]
If the power spectrum of ψ(![]() ) is close to a power law,
) is close to a power law,
Pψ(k)![]() kmø, [16]
kmø, [16]
with −3<mψ<0, then the autocorrelation function of ψ(![]() ) is
) is
[17]
and the mass fluctuation power spectrum from Eq. 15 is
Pρ(k)![]() km, m=3+2mø, [18]
km, m=3+2mø, [18]
for mø<−1.5. Continuity requires ξψ(x)→1 at x→0, so Pψ must break from the power law form in Eqs. 16 and 17 at a comoving length x1 shortward of which it might approach the scale-invariant form Pψ![]() Pρ
Pρ![]() k−3. At x→0 the primeval CDM mass density fluctuations in this model are mildly nonlinear, δρ/ρ→21/2 (Eq. 15).
k−3. At x→0 the primeval CDM mass density fluctuations in this model are mildly nonlinear, δρ/ρ→21/2 (Eq. 15).
In simple inflation scenarios the power law indices are n= 1 in the adiabatic model in Eq. 13 and mø=−3 in the isocurvature model in Eq. 18. The demonstration by Efstathiou and Bond (11) that the latter case violates the bounds on the large-scale anisotropy of the thermal cosmic background radiation (CBR) was a significant factor in focusing the attention of the community on the adiabatic case with n=1. The Cosmic Background Explorer measurement of the large-scale CBR anisotropy showed that if Ω=1 the adiabatic power law index has to to be tilted to n<1 to avoid unacceptable small-scale mass fluctuations. Tilt also is possible and surely equally socially acceptable in the isocurvature case; a value mø ~−2.5 gives a reasonable fit to the CBR angular fluctuations and the large-scale mass distribution. The details are presented
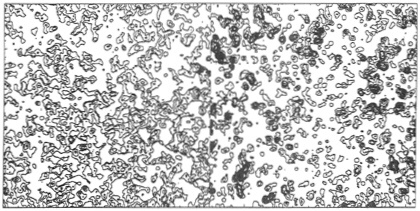
FIG. 2. Mass distributions with power spectrum P![]() k−1.8, smoothed through a spherical window with radius equal to 1.2% of the box width in the figure. The lowest contour is at the mean and the contour interval is one standard deviation. The left side is a realization of a Gaussian process. The right side shows a realization of the CDM distribution in the model in Eq. 14.
k−1.8, smoothed through a spherical window with radius equal to 1.2% of the box width in the figure. The lowest contour is at the mean and the contour interval is one standard deviation. The left side is a realization of a Gaussian process. The right side shows a realization of the CDM distribution in the model in Eq. 14.
elsewhere (12); here I comment on the possible relation of a tilted isocurvature model to the argument for early galaxy assembly.
Fig. 2 compares realizations of the primeval mass distributions in the Gaussian adiabatic and non-Gaussian isocurvature models. The power spectra are the same and give about the same fit to the second moments of fluctuations in the CBR and the large-scale galaxy distribution. In the isocurvature case the figure applies on scales larger than the cutoff x1 (Eq. 17) and smaller than about 300 megaparsecs. (On larger scales the radiation pressure gradient force is not important and the net mass distribution ends up as it began, close to homogeneous, the primeval density fluctuations in the now dominant CDM being replaced with large-scale fluctuations in the distribution of the baryons and radiation. On scales <300 raegaparsecs radiation pressure forces the radiation and baryons to remain nearly homogeneous up to decoupling, leaving the CDM with close to its primeval distribution.) The mass distributions in this figure are constructed from Gaussian realizations with zero means in a cube of 2563 cells, and the figure shows a cut through the cube. For the isocurvature case the Gaussian realization is squared to get the primeval CDM mass distribution, and the mean subtracted. Finally, the distributions are smoothed through a window of radius 3.1 cell widths. The fit to the second moments of the CBR and galaxy distributions requires similar mass fluctuation power spectra extrapolated to the present in linear perturbation theory, but one sees from Fig. 2 that there would be quite different galaxy formation histories in the adiabatic and isocurvature CDM models.
The adiabatic model gives a successful account of the formation and dissipation of the Lymanα forest clouds at z~ 3 (13, 14). In a Gaussian model it is reasonable to think that the galaxies, which are more massive than the clouds, form no earlier, that is, at redshifts <3, which I have argued does not seem reasonable. Three points suggest to me that the isocurvature version looks promising.
First, one sees in the figure that outside the concentrations of prominent upward density fluctuations conditions in the isocurvature case are not greatly different from the general mass distribution in the adiabatic CDM case. For example, in the probability distribution of the mass smoothed through a spherical window, about 90% of the mass is outside windows centered on peaks at δρ/ρ>2σ in the Gaussian and the non-Gaussian cases with the same second moment. The adiabatic and isocurvature models thus might give similar accounts of the Lyα forest at z~ 3. Second, at the same normalization of the power spectrum the prominent upward density fluctuations are a factor of three larger in the isocurvature case, meaning the first generation of galaxies would be assembled at 1+z larger by a factor of about three. This could be consistent with the lower curve in Fig. 1, which we have seen agrees with the scaling relation of rich clusters and protogalaxies. Third the fact that the prominent peaks in the isocurvature case tend to appear in concentrations qualitatively agrees with the clustering of young galaxies (15). At δρ/ρ>6σ the correlation function of peak positions is ![]() at x equal to half the mean interpeak separation xp, and (ξρρ)~ 0.2 at x=xρ. Because the model assumes mass clusters with the galaxies we have to assume that the gravitational growth of clustering has emptied the voids and swept the dwarf galaxies into the concentrations of giants. Whether this could happen without causing the galaxies to cluster too strongly remains to be investigated. Other issues are discussed in ref. 12. It will be interesting to see tests of the issues by the now well developed methods of numerical N-body model simulations of structure formation.
at x equal to half the mean interpeak separation xp, and (ξρρ)~ 0.2 at x=xρ. Because the model assumes mass clusters with the galaxies we have to assume that the gravitational growth of clustering has emptied the voids and swept the dwarf galaxies into the concentrations of giants. Whether this could happen without causing the galaxies to cluster too strongly remains to be investigated. Other issues are discussed in ref. 12. It will be interesting to see tests of the issues by the now well developed methods of numerical N-body model simulations of structure formation.
Concluding Remarks
If the evidence for early galaxy assembly really were as compelling as I have argued why would so many capable people have devoted so much time to the analysis of the adiabatic CDM model? The commonly held opinion is that the evidence for early assembly is not at all compelling, but rather that the recent galaxy assembly predicted by the CDM model is quite reasonable. Numerical N-body simulations of pure gravitational dynamics show the formation of regions with large density contrast, and dissipation by diffuse baryons naturally enhances the contrast. But the conclusions by several groups that the adiabatic CDM model successfully accounts for the properties of the great clusters of galaxies indicates to me that the collapse factor in pure gravitational simulations need not be so large. Dissipation in the baryon component certainly can greatly enhance collapse of a protogalaxy that collects around a single seed mass, but in models for hierarchical assembly of protogalaxies I cannot see how the proposed strong dissipative collapse would not instead produce unacceptably large numbers
of compact groups of dwarf galaxies. It is only fair to admit that my colleagues by and large do not seem to be impressed, however.
The question is being put to observational tests. Key to the argument for early assembly is the idea that present-day clusters of galaxies yield a consistent scaled picture for young galaxies as irregular mass concentrations at redshift z~10. Ongoing advances in observations of the evolution of the clusters back to z=1 will help test this picture and may offer lessons on how protogalaxies evolved. The exploration of the universe at redshifts greater than unity already has given us a remarkably detailed picture of the history of the galaxies—a complex mix of evolution and stability—the meaning of which is under intense discussion. Further advances in observations of the state of the universe at high redshift will be followed with interest by all sides of the debate on how it all began, what it all might mean, and how it all will end.
This work was supported in part by the National Science Foundation.
1. Peebles, P.J.E. (1988) in The Epoch of Galaxy Formation, eds. Frenk, C.S., Ellis, R.S., Shanks, T., Heavens, A.F. & Peacock, J.A. (Kluwer, Dordrecht, the Netherlands), pp. 1–13.
2. Schramm, D.N. (1998) Proc. Natl. Acad. Sci. USA 95, 42–46.
3. Mushotzky, R. (1998) Proc. Natl. Acad. Sci. USA 95, 72–77.
4. Songaila, A., Wampler, E.J. & Cowie, L.L. (1997) Nature (London) 385, 137–139.
5. Tytler, D., Burls, S. & Kirklin, D. (1997) Astrophys. J., in press.
6. Steidel, C.C. (1998) Proc. Natl. Acad. Sci. USA 95, 22–28.
7. Madau. P., Ferguson, H.C., Dickinson, M.E., Giavalisco, M. Steidel, C.C. & Fruchter. A. (1996) Mon. Not. R. Astron. Soc. 283, 1388–1404.
8. Guzmán, R., Gallego, J., Koo, D.C., Phillips, A.C., Lowenthal, J.D., Faber, S.M., Illingworth, G.D. & Vogt. N.P. (1997) Astrophys. J., in press.
9. Kauffmann, G. (1996) Mon. Not. R. Astron. Soc. 281, 487–492.
10. Prochaska, J.X. & Wolfe, A.M. (1997) Astrophys. J. 487, 73.
11. Efstathiou, G. & Bond, J.R. (1986) Mon. Not. R. Astron. Soc. 218, 103–121.
12. Peebles, P.J.E. (1997) Astrophys. J. 483, L1–L4.
13. Hernquist, L., Katz, N., Weinberg, D.H. & Miralda-Escudé, J. (1996) Astrophys. J. 457, L51–L55.
14. Miralda-Escudé, J., Cen, R., Ostriker, J.P. & Rauch, M. (1996) Astrophys. J. 471, 582–616.
15. Cohen, J.G., Cowie, L.L., Hogg, D.W., Songaila, A., Blanford. R., Hu, E.M. & Shopbell, P. (1996) Astrophys. J. 471, L5–L9.





