Proc. Natl. Acad. Sci. USA
Vol. 95, pp. 78–81, January 1998
Colloquium Paper
This paper was presented at a colloquium entitled “The Age of the Universe, Dark Matter, and Structure Formation,” organized by David N.Schramm, held March 21–23, 1997, sponsored by the National Academy of Sciences at the Beckman Center in Irvine, CA.
Cosmic velocity fields and their interpretation
MARC DAVIS
Departments of Astronomy and Physics, University of California, Berkeley, CA 94720
ABSTRACT We review the current status of our knowledge of cosmic velocity fields, on both small and large scales. A new statistic is described that characterizes the incoherent, thermal component of the velocity field on scales less than 2h−1 Mpc (h is H0/100 km·s−1·Mpc−1, where H0 is the Hubble constant and 1 Mpc=3.09×1022 m) and smaller. The derived velocity is found to be quite stable across different catalogs and is of remarkably low amplitude, consistent with an effective Ω~0.15 on this scale. We advocate the use of this statistic as a standard diagnostic of the small-scale kinetic energy of the galaxy distribution. The analysis of large-scale flows probes the velocity field on scales of 10–60 h−1 Mpc and should be adequately described by linear perturbation theory. Recent work has focused on the comparison of gravity or density fields derived from whole-sky redshift surveys of galaxies [e.g., the Infrared Astronomical Satellite (IRAS)] with velocity fields derived from a variety of sources. All the algorithms that directly compare the gravity and velocity fields suggest low values of the density parameter, while the POTENT analysis, using the same data but comparing the derived IRAS galaxy density field with the Mark-III derived matter density field, leads to much higher estimates of the inferred density. Since the IRAS and Mark-III fields are not fully consistent with each other, the present discrepancies might result from the very different weighting applied to the data in the competing methods.
The deviations of the local galaxy distribution from smooth Hubble flow, known as peculiar velocities, can be characterized in a number of ways. On scales of order 1h−1 megaparsec (Mpc; 1 Mpc=3.09×1022 m; h is H0/100 km·s−1·Mpc−1, where H0 is the Hubble constant), the galaxy clustering is known to be highly nonlinear and the peculiar velocities near most galaxies can be expected to be incoherent and random. Details will of course depend on the local environment, but it is of interest to estimate the rms amplitude of the peculiar velocity field averaged over all galaxies. On much larger scales, linear theory should apply and there should exist a well defined velocity field. We discuss the present state of our knowledge of both of these components of peculiar velocity and their comparison to the field predicted on the basis of the observed galaxy distribution. Because this comparison is the best method of measuring the cosmological parameter Ω, it is of considerable interest to fully understand the systematics of the analysis. As we shall see below, the current status of the analysis is somewhat murky.
Small-Scale Fields
For more than a decade, the pair weighted velocity dispersion σ[12](r), employed by Davis and Peebles on the CfA1 survey (1), has been the standard method of estimating the thermal state of the distribution of galaxies. It is well known that this statistic is dominated by the pairs contributed by rare, rich clusters of galaxies and is thus an unstable measure. Its interpretation in terms of the cosmic virial theorem is complicated by the difficulties of evaluating the necessary integral over the three-point correlation function of the mass distribution (2, 3).
Recently Davis, Miller, and White (4) have suggested an alternative measure of the thermal state of the galaxy distribution, which they label σ1. This statistic is the rms motion of galaxies relative to their neighbors within projected cylinders of radius 2h−1 Mpc; it is similar to the traditional σ[12], with the major difference being that each galaxy is given equal weight in the computed distribution function of the redshift separation of neighbors, rather than each pair of galaxies. Either of these statistics is evaluated using only redshift space information, and thus they can be applied to large distant redshift surveys of galaxies. The σ1 measure can be interpreted in terms of a filtered version of the cosmic-energy equation, which is lower order than the cosmic virial theorem, because it depends on an integral of the two-point correlation function ξ, rather than the three-point function ζ. This is much easier to evaluate and is expected to be much more stable in different samples. Indeed, tests of this statistic within mock catalogs and with different samples of real galaxies confirm remarkable stability.
Davis et al. (4) report σ1=96±16 km/s for the Infrared Astronomical Satellite (IRAS) 1.2-Jansky (Jy; 1 Jy=10−26 W·m−2·Hz−1) sample of galaxies, and σ1=130±15 km/s for a redshift sample drawn from the Uppsala General Catalog (UGC) sample of galaxies. Analysis of the Las Campanas Redshift Survey (M.D., H.Lin, and R.Kirshner, unpublished work) leads to similar conclusions as for the UGC, with consistency observed for the six individual slices of the Las Campanas Redshift Survey. This must be compared with results derived from mock catalogs extracted from N-body simulations with nearly identical clustering amplitude. In unbiased Ω=1 simulations, the measured σ1 dispersion is σ1 =325 km/s, nearly three times higher than observed in optically selected galaxy catalogs! If galaxies are unbiased mass tracers, the inferred density parameter from this test is Ω= 0.15±0.02.
This test is important because it measures the thermal environment of a typical galaxy and is not biased by the rare rich clusters of galaxies. It confirms that the quiet thermal environment of a typical galaxy is well constrained and is very different from the hot thermal environment characteristic on small scales in N-body simulations. Such a discrepancy is very difficult to reconcile with high values of the density parameter, with or without bias in the galaxy distribution.
Peebles (5) has long argued that the “coldness” of the local flow of galaxies is a serious problem for high-density models
© 1998 by The National Academy of Sciences 0027–8424/98/9578–4$2.00/0
PNAS is available online at http://www.pnas.org.
of structure formation. Schlegel et al. (6) measure deviations from Hubble flow of only 60 km/s for galaxies within 5 Mpc of the Local Group. Govertano et al. (7) show that candidate Local Groups within high-resolution N-body models never exhibit such cold local flows, either in O=1 or O=0.3 models. Typical local group candidates in their simulations have much higher local velocity dispersions, including objects with blue-shifts, which are not observed for the nearby galaxies outside our own Local Group.
The small-scale “coldness” of the galaxy distribution is well known by alternative expressions: the high “mach number” of the cosmic velocity field (8) or the thinness of the observed sheets of galaxies in redshift space (9). We want to emphasize that the problems presented by such low amplitude peculiar velocities are real and that they indicate a serious gap in our understanding of structure formation.
Large-Scale Flows
On scales greater than 5h-1 Mpc the deviations from Hubble flow are expected to be smaller than the Hubble flow itself, so that in most regions galaxies are physically expanding from each other. In such a situation it is reasonable to expect the velocity field to be largely irrotational. On slightly larger scales, one can expect linear perturbation theory to be a reasonably accurate guide to the expected peculiar velocity field. This is a fortunate circumstance because it allows comparison of the observed deviations from Hubble flow with the flow predicted on the basis of full-sky redshift catalogs of galaxies. The most recently compiled large datasets used in these analyses are the peculiar velocity data of the Mark III consortium (10) and the sample of Tully-Fisher galaxies presented by Giovanelli and colleagues (11). For comparison to the gravity field predicted by the observed galaxy distribution, most recent work has used the full-sky 1.2-Jy IRAS flux limited redshift survey (12), but an optically selected sample of galaxies combined with the IRAS survey has also been used in recent work (J.Baker, M.D., M.Strauss, and O.Lahav, unpublished work).
Recent reviews and methodological details are given by Dekel (13, 14) and by Strauss and Willick (15, 16). Although there are many uses for the peculiar velocity data, the most powerful, model-independent, tests are those that keep phase information. There are two broad categories of tests of this sort, the first of which compares the observed galaxy density field with the mass density field inferred from the divergence of the observed velocity field [also known as POTENT (13, 14)], and the second of which compares the observed velocity field with the gravity field inferred from the galaxy distribution [e.g., the VELMOD analysis (15–17), the inverse Tully-Fisher (ITF) method (18), or the least-action method (19)]. The search for reflex dipole flows [e.g., the local motion relative to brightest cluster galaxies (20) or relative to nearby supernovae (21)] are similar in spirit to the second form of these tests.
The density-density comparison of POTENT is inherently a local comparison, which is a tremendous virtue, because neither the galaxy density field nor the peculiar velocity field are well known at large distance. The velocity-gravity comparison, on the other hand, suffers from coherent errors induced by nonlocality, since the estimated peculiar gravity field at a given point in space is computed by effectively summing over neighbors at all distances, weighted inversely by the square of the distance. Poisson shot noise of the galaxy distribution in one locale therefore generates a coherent error in the gravity field over all space. This nonlocality makes the statistics of the field comparison quite complicated.
It has been argued that this sensitivity to the uncertain far-field galaxy distribution precludes the second class of tests as a useful diagnostic of gravitational instability or as a measure of the cosmic density parameter. For example, comparison of the gravitational dipole for the cosmic microwave background radiation (CMBR) dipole is a difficult, dangerous game (22, 23). The amplitude and direction of the CMBR dipole are rather precisely known, but the coherence of the flow is completely uncertain. How large a region is flowing at 620 km/s along with the Local Group of galaxies? Should a full reflex of this dipole be detectable within 50, 100, or 3,000 Mpc? Without an answer to this question—i.e., an assumption of the nature of the large-scale power spectrum—it is not possible to infer the cosmological density parameter by comparing the CMBR dipole to the gravitational dipole inferred from galaxy catalogs such as the 1.2-Jy IRAS survey.
However, the nonlocality does not apply to all aspects of the velocity-gravity field comparison. Recall Einstein’s gedanken experiment of an observer within an elevator. He cannot distinguish whether he is in an accelerating frame or is stationary in an external gravitational field. If the elevator goes into freefall, he can detect the presence of an external gravitational field only by its tidal influence on the matter within the elevator. Exactly the same considerations apply for the gravitational field estimated from an imperfectly sampled galaxy distribution. A poorly sampled, distant cluster of galaxies will induce coherent errors in the nearby gravity field, but they will be tidal in nature. Working in the Local Group frame of reference rather than the cosmic microwave background frame is conceptually cleaner for this analysis. Recall Newton’s iron sphere theorem, which states that for spherical symmetry, the acceleration of a point at radius r is sensitive only to the mass interior to that point. In terms of a spherical harmonic expansion of the external gravity field, the l=0 component of the field at radius r is insensitive to the mass distribution at R> r. The general solution of the Poisson equation for an exterior mass at radius R leads to an acceleration proportional to (r/R)l-1/R2. Tidal effects are described by l=2, and grow linearly with r, as we know well. But we tend to forget that for the dipole term, l=1, the external field produces an acceleration independent of r, which means that by moving to the freely falling Local Group frame, the l=1 gravity field at radius r is sensitive only to the mass distribution interior to that point (24). This is a critical point, demonstrating why a comparison of the peculiar velocity field with the gravity field, if limited to the monopole and dipole terms, is effectively a local test that is totally insensitive to the matter distribution at large distances.
The ITF method of Nusser and Davis (24) is ideal for this type of comparison, because it allows expansion of the gravity and velocity fields in terms of whatever functional expansion is most convenient. This method expands the radial component of the peculiar velocity field in terms of a set of orthogonal functions, characterized by coefficients that are determined by minimizing the scatter in the linewidth direction for a uniformly calibrated set of Tully-Fisher data. Details are given by Davis et al. (18). The method is merely a filtering tool that can smooth both the gravity and velocity fields to the same resolution, which can be dependent on position; it smoothes the data without binning it, and the derived coefficients of both the gravity and velocity fields, for which one can compute a full covariance matrix, are a complete description of the field to a given resolution. In a typical application, 50–100 coefficients are fit. Tests demonstrate that the method works and recovers the true velocity field with minimal bias. These tests with mock data show that the residual field, the difference of the inferred velocity and gravity fields, has negligible dipole errors, and is dominated by l=2, 3 components due to the dilutely sampled exterior mass field.
As previously discussed in detail (18), the comparison of the IRAS gravity field with the Mark III Tully-Fisher data is not nearly as successful. For no value of the density parameter is it possible to eliminate the dipole residual. The comparison of the modal coefficients demonstrates that for no value of the density parameter are the gravity and velocity fields statisti
cally consistent with each other. Thus, although the qualitative comparison of the two fields is quite impressive, the fields are inconsistent with each other at the 4-s level or worse. A value of ß=0.6 fits best, but it is not an acceptable fit. Until we better understand the reason for the large dipole residual, which grows nearly linearly with redshift, it is premature to use these methods to measure the density parameter. A dipole residual that grows with redshift is not physically reasonable and strongly suggests a calibration error that is nonuniform on the sky, either in the IRAS catalog or in the Mark III database.
Willick et al. (17) report a more successful comparison of the IRAS gravity field to a subset of the Mark III data limited to redshift of 3,000 km/s, vs. the 6,000 km/s limit used by Davis, Nusser, and Willick. Their analysis procedure, VELMOD, is capable of treating the nonlinear, multivalued zones around clusters of galaxies, whereas the ITF method is a redshift space procedure that assumes a single-valued relationship between distance and redshift. The gravity field computed for the ITF procedure is similarly a redshift space algorithm that works only in the linear theory limit. VELMOD does not produce a visual image of the flow field but it yields a maximum likelihood solution for ß=O0.6/b based on a series of IRAS gravity fields. Willick et al. report ß=0.5±0.1, which leads to an inferred density O=0.3 if IRAS galaxies trace the mass distribution (b1=1), or O=0.2 if optical galaxies trace the mass distribution (b0=1). A plot of the ITF inferred velocity and gravity field (for ß=0.5) for this subset of the Mark III data is shown in Fig. 1. Note that the two fields are remarkably well aligned, and that the sign of the predicted vs. observed peculiar velocity matches for virtually every galaxy in the sample. The residual field is also shown, and at this redshift limit, it is not overly dominated by the dipole residual. Perhaps, therefore, the ß value inferred by VELMOD is an acceptable fit.
Similar values for ß emerge from the use of the ITF algorithm and the SFI sample of Tully-Fisher data (11), which has many galaxies and much data in common with Mark III but in which the data were processed somewhat differently. Da Costa et al. (25) report no anomalous dipole residuals in their fits, which seems quite encouraging.
Yet additional, independent confirmation of this relatively low value of ß is given by a direct comparison of the observed vs. predicted peculiar velocities for a sample of 24 supernovae 1A within a redshift limit of 10,000 km/s (26). They find a good fit and a 95% confidence limit in the range 0.15<ß<0.7, a constraint which will tighten as the sample of supernovae with good data increases over the coming years.
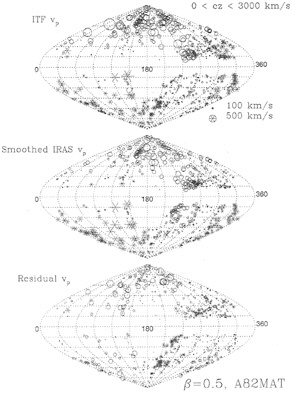
FIG. 1. A full-sky plot of the peculiar velocity field of the Mark III galaxies within 3,000 km/s. Galaxies with positive (negative) peculiar velocity in the Local Group frame are shown as stars (circles) with symbol size proportional to velocity. (Top) ITF peculiar velocity inferred from the Tully-Fisher data. (Middle) IRAS predicted peculiar velocities for these galaxies, assuming ß=0.5, filtered by the same set of functions that were used for the ITF fit. (Bottom) The difference of the ITF and IRAS fields.
On the other hand, the same Mark III and IRAS data, when analyzed by the POTENT procedure, lead to estimates of ß consistent with unity (27), well above the limits from the velocity-gravity field comparisons. The POTENT algorithm has had at least as much validation studies applied to it as any of the competing algorithms, and tests show that it is fully capable of recovering the underlying true value of ß in a noisy field of data. How is it that the same data can lead to such divergent conclusions when analyzed using different procedures?
The answer is currently unknown but might result from the very different weighting applied to the density-density algorithms vs. the velocity-gravity algorithms. In the former case, the procedure is most sensitive to the divergence of the velocity field and is insensitive to the largest scale components of the field. In the Fourier domain, the divergence of velocity is proportional to (k vk), so the highest Fourier modes remaining after the smoothing are given maximal weight. The velocity-gravity algorithms, on the other hand, are seeking the reflex dipole of the motion of the local group and are dominated by the largest wavelength Fourier modes in the volume. Thus the weightings of the alternative procedures could not be more different!
Because, as argued above, the Mark III data do not really fit the predictions of the IRAS inferred gravity field for any value of ß, it should therefore not be a surprise when very differently weighted analyses of the data lead to differing conclusions. The prudent course of action is to work to understand why the fields are so inconsistent, to search for systematic errors in one or both of the fields, and to restrain from drawing overly strong cosmological conclusions until the competing algorithms lead to consistent solutions.
This work was supported by National Science Foundation Grant AST95–28340 and National Aeronautics and Space Administration Grant NAG 5–1360.
1. Davis, M. & Peebles, P.J.E. (1995) Astrophys. J. 267, 465–482.
2. Peebles, P.J.E. (1980) The Large-Scale Structure of the Universe (Princeton Univ. Press, Princeton. NJ).
3. Bartlett, J. & Blanchard, A. (1996) Astron. Astrophys. 307, 1–7.
4. Davis, M., Miller, A. & White, S.D.M. (1997) preprint astro ph/9705224.
5. Peebles, P.J.E. (1993) Principles of Physical Cosmology (Princeton Univ. Press, Princeton, NJ).
6. Schlegel, D., Davis, M., Summers, F. & Holtzman, J. (1994) Astrophys. J. 427, 527–532.
7. Govertano, F., Moore, B., Cen, R., Stadel, J., Lake, G. & Quinn, T. (1997) New Astron. 2, 91–106.
8. Suto, Y., Cen, R.Y. & Ostriker, J. (1992) Astrophys. J. 395, 1–20.
9. Bothun, G., Geller, M.J., Kurtz, M., Huchra, J. & Schild, R. (1992) Astrophys. J. 395, 347–359.
10. Willick, J., Courteau, S., Faber, S., Burstein, D., Dekel, A. & Strauss, M. (1996) Astrophys. J. 457, 460–489.
11. Haynes, M., Giovanelli, R., Heter, T., Vogt, N., Freundling, W., Maia, M., Salzer, J. & Wegner, G. (1997) Astron. J. 113, 1197– 1211.
12. Fisher, K., Huchra, J., Strauss, M., Davis, M., Yahil, A. & Schlegel, D. (1995) Astrophys. J. Suppl. Ser. 100, 69–103.
13. Dekel, A. (1994) Annu. Rev. Astron. Astrophys. 32, 371–418.
14. Dekel, A. (1997), preprint astro-ph/9705033.
15. Strauss, M. & Willick, J. (1995) Phys. Rep. 261, 271–431.
16. Strauss, M. (1996) preprint astro-ph/9610033.
17. Willick, J., Strauss, M., Dekel, A. & Kolatt, T. (1997) preprint astro-ph/9612240.
18. Davis, M., Nusser, A. & Willick, J. (1996) Astrophys. J. 473, 22–41.
19. Shaya, E., Peebles, P. & Tully, B. (1995) Astrophys. J. 454, 15–31.
20. Lauer, T. & Postman, M. (1995) Astrophys. J. 440, 28–47.
21. Riess, A., Press, W. & Kirshner, R. (1995) Astrophys. J. 445, L91–L94.
22. Strauss, M., Yahil, A., Davis, M., Huchra, J. & Fisher, K. (1992) Astrophys. J. 397, 395–419.
23. Juszkiewicz, R., Vittorio, N. & Wyse, R. (1990) Astrophys. J. 349, 408–414.
24. Nusser, A. & Davis. M. (1995) Mon. Not. R. Astron. Soc. 276, 1391–1401.
25. da Costa, L., Nusser, A., Freundling, W., Giovanelli, R., Haynes, M., Salzer, J. & Wegner, G. (1997) preprint astro-ph/9707299.
26. Riess, A., Davis, M., Baker, J. & Kirshner, R. (1997) Astrophys. J. 488, L1–L5.
27. Sigad, Y., Dekel, A., Strauss, M. & Yahil, A. (1997) preprint astro-ph/9708141.




