Proc. Natl. Acad. Sci. USA
Vol. 95, pp. 8–12, January 1998
Colloquium Paper
This paper was presented at a colloquium entitled “The Age of the Universe, Dark Matter, and Structure Formation,” organized by David N.Schramm, held March 21–23, 1997, sponsored by the National Academy of Sciences at the Beckman Center in Irvine, CA.
Globular clusters, Hipparcos, and the age of the galaxy
NEILL REID*
Palomar Observatory, 105–24, California Institute of Technology, Pasadena, CA 91125
ABSTRACT We discuss the impact of the results from the recent Hipparcos astrometric satellite on distance estimates of galactic globular clusters. Recalibrating the clusters not only implies a relatively small change in the distance to the Large Magellanic Cloud, and hence a rescaling of several estimates of the Hubble constant, but also leads to significantly younger cluster ages. Although the data are not yet conclusive, the results so far point to a likely resolution of the apparent paradox of a universe younger than its constituents, without requiring significant modifications to simple cosmological models.
Since the pioneering work of Sandage and Arp, globular clusters have been recognized as providing important sign posts to the history of star formation over the lifetime of the Milky Way. Once it was realized that these clusters had formed during the earliest stages of protogalactic collapse, their potential as galactic chronometers became apparent. In simple terms, find the age of the oldest globular cluster and one has the age of the galaxy; add 0.5 to 1 gigayear (Gyr) and, for most cosmological models, one has the age of the universe.
Recently, this apparently simple calculation has led to a paradox. The availability of charge coupled device (CCD) cameras on large telescopes has made it possible to extend observations of cluster color-magnitude diagrams to stars on the lower main sequence. Given accurate distance estimates, matching those data against the predictions of theoretical models allows one to estimate the age of the cluster from the luminosity (mass) at the main-sequence turnoff. The most extreme metal-poor clusters generally are also found to be the oldest, weighing in at ages of 16–22 Gyr (1, 2). The uncertainties in those ages, which are a result of uncertainties in the underlying stellar physics, were estimated as only ≈15% (3). Thus, T0, the age of the universe, can be deduced as being at least 17 Gyr.
This lower limit is in stark contrast to cosmological estimates, based on the most recent determinations of the large-scale Hubble expansion. The interim value of 77 km·s−1·Mps−1 derived by the Hubble Space Telescope (HST) key project team (4) translates to an age of only 10 Gyr for a closed universe and only 12–13 Gyr for a universe with Ω=0.2 (with Λ=0 in both cases). Even the lower values of H0=50–55 km·s−1·Mpc−1 favored by Sandage et al. (5) can scarcely accommodate a 12-Gyr-old, critical-density universe. These ages lie well outside the formal range of uncertainty estimated for the astrophysically based cluster ages and seemed to imply that more complex cosmological models, with at least a nonzero cosmological constant, were required to reconcile the results from the two techniques.
The crucial point, however, emphasized by Sandage (6), is that the accuracy of the cluster ages depends crucially on the accuracy of the cluster distances. The turnoff mass in globular clusters is close to 1 M⊙, where a small change in mass (luminosity) represents a change in the main-sequence lifetime of 1+Gyr. As we shall describe, the availability of new, high-accuracy trigonometric parallax measurements for a larger sample of nearby halo subdwarfs has permitted a critical reevaluation of the cluster-distance scale. When the recalibrated cluster color-magnitude diagrams are combined with the latest stellar models, it becomes clear that the data are compatible with ages that are significantly younger than had been the norm. Although the age paradox does not vanish utterly, the discrepancy is reduced to a matter of no more than 1 Gyr.
Calibrating Cluster Distances
Main-sequence fitting is one of the classical methods of estimating the distances to globular clusters. In the empirical approach, used originally by Sandage (7), local halo subdwarfs of known distance and abundance are used to define a metal-poor main sequence in the (Mv, (B–V)) plane. If that calibrated sequence is matched against the observed cluster color-magnitude diagram, then the mean offset (V–Mv) gives the distance modulus of the cluster.
Two complications confound the straightforward application of this technique. First, there are relatively few halo subdwarfs within the immediate vicinity of the sun. Second, the (Mv, (B–V)) color-magnitude relation is a function of stellar composition. No more than 1 in 500 stars in a volume-limited sample belongs to the galactic halo. There are only approximately 8,000 F and G dwarfs within 50 parsec (pc) of the sun, so we can expect to find no more than a dozen or so halo subdwarfs with trigonometric parallaxes larger than 20 milliarcsec (mas). Moreover, those few subdwarfs span an abundance range of more than 1 dex, from [Fe/H]=−1 to less than −2.5, and an extreme subdwarf is significantly less luminous than an intermediate-abundance ([Fe/H]=−1.5) subdwarf of the same color. Thus, not only are there only a small number of calibrating stars, but they all lie on different main sequences. Generally, the latter problem is taken into account by using theoretical models to estimate the offset in color as a function of abundance and adjusting each star to define a monometallicity sequence. However, even with those adjustments, only 7–10 subdwarfs were available to calibrate the distances to any given cluster.
Given a scarcity of subdwarfs with precise ground-based parallax measurements, an alternative approach is to match the observed color-magnitude diagrams directly against the theoretical isochrones. However, the latter are computed for the (luminosity, effective temperature) plane and must be trans
© 1998 by The National Academy of Sciences 0027–8424/98/958–5$2.00/0
PNAS is available online at http://www.pnas.org.
|
|
Abbreviations: LMC, Large Magellanic Cloud; Gyr, gigayear; CCD, charge coupled device; pc, parsec; mas, milliarcsec; as, arcsec; mag, magnitude; HST, Hubble Space Telescope. |
|
* |
e-mail: inr@astro.caltech.edu. |
formed to the (Mv, (B–V)) plane to enable comparison with the observations. The accuracy of the necessary transformations, derived from atmosphere models, is crucial, because the steep slope of the main sequence means that any systematic errors in the colors are amplified at least 5-fold in the derived distance modulus. Because most theoretical models fail to match the sun exactly, a direct application of similar models to metal-poor stars is not advisable. Moreover, it is clear from recent high-resolution spectroscopic observations that the abundance pattern in halo subdwarfs differs from that among disk dwarfs. Oxygen, calcium, neon, and other a-rich elements have enhanced abundances relative to iron in halo subdwarfs, reflecting the greater contribution made by Type II supernovae to chemical evolution at early epochs. It is only recently that these detailed differences have been taken into account in model calculations.
Thus, both of these approaches have significant drawbacks: sparse sampling of the (Mv, (B–V)) plane by the empirical data, and zeropoint uncertainties in the theoretical tracks. Given these problems, most recent studies (e.g., ref. 1) have adopted a semiempirical, hybrid approach, using the few subdwarfs with well calibrated distances to determine systematic corrections to the theoretical isochrones, and then matching the corrected, calibrated isochrones against the cluster data. These corrections generally comprise an offset of a few hundredths in the (B–V) colors of the models, with the assumption that the same correction is appropriate at all luminosities. Thus, Bolte and Hogan (1) used the local subdwarfs (primarily the nearest subdwarf, Groombridge 1830 or HD 103095) to estimate that the colors predicted by the Bergbusch and Vandenberg (8) isochrones were too blue by 0.02 magnitudes. Applying this systematic offset to the appropriate-abundance isochrones, Bolte and Hogan matched the theoretical tracks against observations of the classical metal-poor cluster M92 and derived a best-fit age of 15.8±2 Gyr.
Hipparcos and the Local Subdwarfs
Ground-based, parallax measurements can achieve an accuracy of better than 1 mas—but only through the painstaking acquisition of numerous well calibrated CCD frames, extending deep enough to include observations of a sufficient number of faint, distant, positional-reference stars. The nearby F and G subdwarfs, whose parallaxes are essential for main-sequence fitting, have magnitudes of 8 to 10—observable photographically, but not with CCDs, and photographic plates cannot achieve the necessary precision. The Hipparcos satellite was designed to achieve milliarsecond-precision astrometry for stars at these magnitudes and to obtain absolute parallaxes for over 110,000 stars, including almost every star brighter than ninth magnitude.
Hipparcos achieved this goal by using two small telescopes to image widely separated regions of sky onto the same focal plane. In ground-based parallax measurement, one can measure only the parallactic motion of a nearby star relative to the positions of fainter background stars in the same field. Those stars share that same parallactic motion, albeit at a much lower level. Hence, statistical corrections must be applied to the derived relative parallax to correct to an absolute scale. Hipparcos, by measuring the angular separation of stars more than 58° apart on the sky, and at very different parallactic angles, was able to circumvent this problem.
The satellite was launched in 1989 and, despite being left in a highly elliptical orbit through a technical failure, was able to obtain almost 3 years of data. Those raw observations, essentially tens of millions of measured angular separation between pairs of stars from the input catalogue specified in 1985, were then reduced and analyzed separately by two consortia. The final catalogue was completed in late 1996 and will be released to the general community in June 1997 (9). However, astronomers who had requested observations of stars for specific projects (the “1982 PIs”) were given access to subsets of the data in January 1997.
As part of the “1982 PI” release, I received astrometric data for some 2,400 stars from the Lowell observatory proper motion catalogue—stars brighter than 11.5 and with proper motions of at least 0.27 as per year. Among those stars were more than 700 that had photometric and spectroscopic observations by Carney et al. (10) as part of their investigation of local Galactic structure—including more than 100 subdwarfs with abundances [Fe/H]<-1, stars suitable for calibrating globular cluster distances through main-sequence fitting (ref. 10, hereinafter CLLA). However, many of those stars lie at distances of more than 100 pc. where even Hipparcos parallaxes are of relatively low precision. Combining low-precision parallax data in a statistical analysis can lead to significant systematic bias: in any volume-limited sample, there are more stars with small parallax than large parallax, so if a subsample is defined, either implicitly or explicitly, by a parallax limit, then observational uncertainties in the measured parallax will lead to a larger number of stars scattering into the sample from a larger distance than are scattered out of the sample. Hence, the average distance, and the mean luminosity, of the parallax-limited subsample is underestimated.
This statistical bias was quantified originally for a uniform space distribution by Lutz and Kelker (11). Hanson (12) extended the analysis to different spatial distributions and deals with the effect of introducing a magnitude limit (as is the case in the Hipparcos sample). These biases should be corrected for in any statistical analysis, such as main-sequence fitting, but the corrections can amount to more than half a magnitude for a parallax precision less than 20%. Given these concerns, our present analysis is limited to a total of 18 subdwarfs with abundances (from CLLA) of less than -1.3 dex and with parallaxes measured to a precision of better than 12%. The statistical corrections involved are no more than 0.12 mag for an individual star and 0.02 mag in the mean.
Cluster Distances
We have matched the local subdwarf-calibrating stars against fiducial (V, (B–V)) sequences derived for a number of the better-studied globular cluster systems. Rather than rely on theoretical models to determine the color corrections required to adjust each star to match a given cluster abundance, we have limited the analysis to subdwarfs whose abundance is within ±0.25 dex of each cluster in the sample. The cluster abundances were taken from the compilation by Zinn and West (13). This technique limits the calibration to only 7–9 stars per cluster, but the distribution in absolute magnitude is sufficient so that the cluster distances can be determined to a formal distance of ˜5% (±0.1 magnitude). Results for three well studied clusters are shown in Fig. 1, and full details of this first analysis are given by Reid (14).
The most important result is that the distances to the most metal-poor clusters ([Fe/H] ~ -2.0) have been underestimated by at least 10–15% in previous analyses. NGC 6397, long known as the nearest cluster to the sun, turns out to be fully 25% more distant than the conventional estimate, lying at a 2.8 kpc distance. To some extent, this reflects differences between the older, ground-based parallaxes and the new Hipparcos data but is also due partly to an underestimate of the color corrections required to match previously available theoretical isochrones to the observations. Rather than 0.02 mag, the latter corrections amount to at least 0.05 mag for the extreme, metal-poor subdwarfs. [Much smaller corrections are required to match the isochrones predicted by the most recent models calculated by D’Antona et al. (15).)
An immediate consequence of the increased distance to these clusters is that one infers a higher luminosity for the
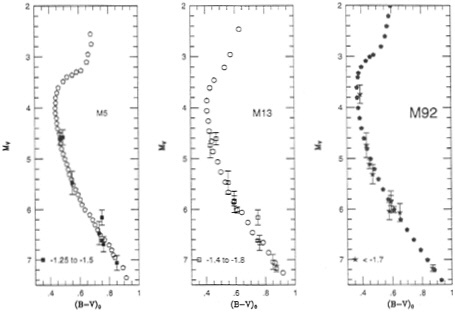
FIG. 1. Main-sequence fitting for three globular clusters: M5, M13, and M92. In each case the cluster color—magnitude diagram has been matched against subdwarfs of the appropriate abundance range (plotted with error bars).
cluster RR Lyrae variables. Both M5 and M92 have substantial and well studied, variable star populations. In M5 ([Fe/H]= -1.4), the mean absolute magnitude is +0.51 mag, with an uncertainty of at least ±0.1 mag; in M92, [Fe/H]=-2.1, Mv =0.15. The Large Magellanic Cloud (LMC) has an extensive population of globular clusters, several of which have a substantial number of RR Lyrae members. Averaging data for five clusters with [Fe/H]=-1.8, the mean apparent magnitude of the variables, corrected for foreground reddening, is 18.98. Given an intrinsic Mv=0.3 mag, the inferred distance modulus of the LMC is 18.68 (53.8 kpc)—slightly higher than the standard value adopted for the HST Distance Scale Key Project, and in good agreement with the results independently derived by Feast and Catchpole (16), who use Hipparcos data to recalibrate the zeropoint of the Galactic Cepheid periodluminosity relation.
These increased distances also have a direct effect on the ages estimated for the metal-poor clusters: increasing the distance modulus by 0.3 mag also increases the turnoff luminosity by 0.3 mag and leads to a correspondingly higher turnoff mass and a younger age. The only method of quantifying these ages is through comparison with theoretical models. Fig. 2 matches the observed turnoff luminosity for eight clusters in our sample against the luminosities predicted by three sets of models: by Bergbusch and Vandenberg (ref. 8, BV92), who include an enhanced oxygen abundance; by Straniero and Chieffi (ref. 17, SC91), whose models include no selective element enhancements and traditional physics; and by D’Antona et al. (ref. 16. DCM), who also include no elemental enhancements but who employ a different treatment of convection and helium diffusion and use the equation of state calculated recently by Rogers et al. (18). It is clear that the ages estimated for even the most metal-poor clusters are younger significantly than the 16–20 Gyr found in previous studies: none of the models implies cluster ages much above 13 Gyr, whereas the D’Antona et al. models are compatible with a galactic age of 11 Gyr and, therefore, T0 of no more than 12 Gyr.
Qualifications and Uncertainties
These results clearly go a long way toward resolving the discrepancy between the astrophysical and cosmological time scales. However, there remain a number of areas of uncertainty, both empirical and theoretical, which will require further attention.
Observationally, there are three important concerns:
-
Scarcity of calibrators. Even with the new Hipparcos data, there are only a small number of extreme subdwarfs ([Fe/H]<-1.7) that have parallaxes measured to sufficient accuracy to be useful as calibrators for metal-poor clusters such as M92. Moreover, several stars with good parallaxes are identified as possible binaries and, therefore, perhaps are significantly overluminous compared with single stars. Observations of additional stars, particularly on the lower main sequence (Mv>5), are essential—but all the available candidates have parallaxes of only a few milliarcseconds and are therefore ourwith the reach of even Hipparcos. The forthcoming Space Interferometry Mission should target a number of local subdwarfs as well as actual members of globular clusters.
-
Metallicity. Abundance determinations based on high-resolution spectroscopy of both field subdwarfs (19) and globular cluster members (20) arrive at systematically different results from the Zinn and West (13) and CLLA calibrations that we have used. Generally, the hires metallicities tend to be
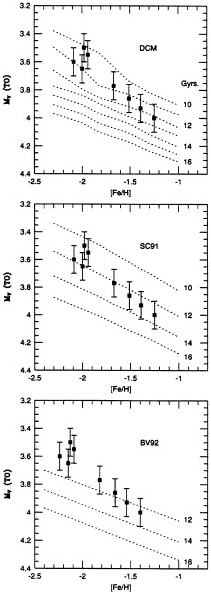
FIG. 2. A comparison between the observed absolute magnitude at the main-sequence turnoff in eight globular cluster systems and the luminosity predicted by the three sets of stellar models discussed in the text. The eight clusters are, from low to high abundance. M92, M15, M30, M68, NGC 6397, M13, MGC 6752, and M5. The cluster abundances have been increased by 0.15 dex in matching against the Straniero and Chieffi (17) and D’Antona et al. (15) models, because neither of the latter two includes enhanced a-element abundances.
-
higher for both subdwarfs and clusters, although the metal-poor globulars are the least affected. Distance determinations using Hipparcos parallaxes and based on the hires calibrations confirm our results (21), but this matter remains a source of uncertainty, particularly because the cluster abundances are derived from red giants rather than main-sequence stars. A direct spectroscopic comparison of cluster and field subdwarfs would clarify the relative-abundance scales. Such observations are within the scope of Keck.
-
Cluster reddening. A change of 0.02 in the foreground reddening due to interstellar dust leads directly to a change of at least 0.5 Gyr in the inferred age of the cluster. Lowering the reddening decreases the inferred turnoff luminosity and increases the age. Some analyses, particularly direct matching to theoretical isochrones, tend to place only loose constraints on the allowed reddening, ignoring the sensitivity of their final results to the value adopted for this parameter. Fortunately, there are several clusters (including M92) where the reddening is well established as being extremely low, so there is little scope for aging the clusters.
There are also theoretical concerns. First, which are the most appropriate set of models? In particular, how reliable is the internal physics in the newest set of models, which give the youngest ages? There are other independent theoretical analyses that indicate ages of 12–14 Gyr for globular clusters, based on the morphology of the color-magnitude diagram. However, one could argue that stellar evolutionary theory mainly has had postdictive, rather than predictive, success in this field— particularly because the new ages fall well outwith the previously quoted ±15% uncertainties.
Second, clearly, the models need to be improved to include the appropriate enhanced abundances for all of the a elements, not only oxygen. These modifications are being made by several groups.
Third, the models must be matched to the data. Theoretically, defining the position of the main-sequence turnoff is straightforward; observationally, one is searching for the bluest point on a nearly vertical sequence defined by a finite number of points that have photometric uncertainties. Extending the observational data to infrared wavelengths can alleviate this problem to some extent. It is easier observationally to define the luminosity at lower or higher luminosities—but matching the models then requires accurate theoretical (effective temperature, color) transformations.
Conclusions
Despite the qualifications cited in the previous section, it is clear that the astrophysical estimates of the age of the galaxy are moving toward lower values. Although it would have been difficult to justify adopting ages as low as 14 Gyr for many clusters in the early years of this decade, it now appears that 14 Gyr represents a generous upper limit to the age of the oldest globular cluster. Considerable work remains to be done to verify the result, but if the latest stellar models are reliable, then our revised distance scale points to a galaxy aged ˜11 Gyr and a universe of age ˜12 Gyr.
One of the prime aims of the Hipparcos project was to set distance determinations on a firmer foundation. It is a credit to the Hipparcos team that, despite the initial problems, the satellite is realizing those aims.
1. Bolte, M. & Hogan, C.J. (1995) Nature (London) 376, 399–402.
2. Chaboyer, B., Demarque, P. & Sarajedini, A. (1996) Astrophys. J. 459, 558–571.
3. Chaboyer, B. (1995) Astrophys. J. 444, L9–L12.
4. Freedman. W.L., Madore, B.F. & Kennicutt, R.C. (1997) The Extragalactic Distance Scale, eds. Donahue, M. & Livio, M. (Cambridge Univ. Press, Cambridge, U.K.).
5. Sandage, A., Saha, A., Tammann, G.A., Labhardt, L., Panagia, N. & Macchetto, F.D. (1996) Astrophys. J. 460, L15–L18.
6. Sandage, A. (1986) Annu. Rev. Astron. Astrophys. 24, 421–458.
7. Sandage, A. (1970) Astrophys. J. 162, 841–872.
8. Bergbusch, P.A. & Vandenberg, D.A. (1992) Astrophys. J. Suppl. 81, 163–220.
9. ESA, (1997) The Hipparcos Catalogue (ESA SP-1200).
10. Carney, B.W., Latham, D.W., Laird. J.B. & Aguilar, L.A. (1994) Astron. J. 107, 2240–2289.
11. Lutz. T.E. & Kelker. D.H. (1973) Publ. Astr. Soc. Pacif. 85, 573–580.
12. Hanson, R.B. (1979) Mon. Not. R. Astron. Soc. 186, 875–896.
13. Zinn, R. & West, M.J. (1984) Astrophys. J. Suppl. 55, 45–66.
14. Reid, I.N. (1997) Astron. J. 114, 161–179.
15. D’Antona, F. Caloi. V. & Mazzitelli, I. (1997) Astrophys. J. 477, 519–534.
16. Feast, M.W. & Catchpole, R.W. (1997) Mon. Not. R. Astron. Soc. 286, L1–L5.
17. Straniero, O. & Chieffi, A. (1991) Astrophys. J. Suppl. 76, 525–616.
18. Rogers, F.J., Swenson, F.J. & Iglesias, C.A. (1996) Astrophys. J. 456, 902–908.
19. Gratton, R.G., Carretta, E. & Castelli, F. (1997) Astron. Astrophys. 314, 191–203.
20. Carretta, E. & Gratton, R.G. (1997) Astron. Astrophys. Suppl. 121, 95–112.
21. Gratton, R.G., Fusi Pecci, F., Carretta, E., Clementini, G., Corsi, C.E. & Lattanzi, M. (1997) Astrophys. J., in press.





