Proc. Natl. Acad. Sci. USA
Vol. 95, pp. 82–84, January 1998
Colloquium Paper
This paper was presented at a colloquium entitled “The Age of the Universe, Dark Matter, and Structure Formation,” organized by David N.Schramm, held March 21–23, 1997, sponsored by the National Academy of Sciences at the Beckman Center in Irvine, CA.
Measuring the topology of the universe
NEIL J. CORNISH*, DAVID N. SPERGELI†‡, AND GLENN D. STARKMAN§
*Department of Applied Mathematics and Theoretical Physics, Cambridge University, United Kingdom: †Princeton University Observatory, Princeton, NJ 08544: and ‡Case Western Reserve University, Cleveland, OH 44106
ABSTRACT Observations of microwave background fluctuations can yield information not only about the geometry of the universe but potentially about the topology of the universe. If the universe is negatively curved, then the characteristic scale for the topology of the universe is the curvature radius. Thus, if we are seeing the effects of the geometry of the universe, we can hope to soon see signatures of the topology of the universe. The cleanest signature of the topology of the universe is written on the microwave sky: There should be thousands of pairs of matched circles. These circles can be used to determine the precise topology and volume of the universe. Because we see hundreds of slices through the fundamental domain of the universe, we can use the microwave observations to reconstruct the initial conditions of the entire universe on the scale of a few megaparsecs.
There is growing evidence that we live in a negatively curved universe. A number of independent arguments suggest that the matter density is significantly less than the critical density: comparisons of density fluctuations and velocity fields (1–3); determination of mass-to-light ratios in clusters (4); measurements of the baryon-to-dark matter ratio in clusters (5–7); the presence of more large scale structure than expected in flat models (8, 9); the need to reconcile the value of the Hubble constant with globular cluster ages (10); and the existence of large numbers of clusters at moderate redshift (11, 12). A number of groups have shown that cold dark matter models with Ω0≃0.3–0.4 are compatible with microwave background measurements and large scale structure (13, 14). Although we cannot rule out the possibility that there is a cosmological constant (see, e.g., ref. 15) that makes the universe flat, recent high redshift supernova observations (16), as well as gravitational lens statistics (17, 18), suggest that this term is small.
There has been growing interest in the possibility that the universe is not only negatively curved, but compact (19–24). Our interest in the topology of the universe was stimulated by the possibility that it may be detectable and by the philosophical attractions of a finite universe (21). This talk reviews some basic concepts in topology and then turns to the possibility of detecting the observational signature of a finite universe.
Topology: A Quick Primer. Physicists assume that the universe can be described as a manifold. Mathematicians characterize manifolds in terms of their geometry and topology. Geometry is a local quantity that measures the intrinsic curvature of a surface. General relativity relates the mass distribution of the universe to its geometry, and, of course, the geometry of the universe determines the dynamics of the mass. Topology is a global quantity that characterizes the shape of space (see, e.g., ref. 25 for a general introduction). General relativity does not at all constrain the topology of the universe.
The relationship between topology and geometry is most familiar in flat space. Cosmologists often consider flat infinite universes; a model that mathematicians denote as R3, which symbolizes a space that is the product of the three orthogonal real lines. A familiar cosmological model that has the same geometry as R3, but a different topology, is the three torus or what mathematician call “T3.” Most cosmological simulations are run on a three torus; if a particle tries to leave the computational cube through one side, it emerges on the opposite side.
There are several different ways of thinking about the topology of a manifold. It is simplest to begin by considering the topology of flat two-dimensional space. One way of thinking about topology is to think about a square with identified sides. This square is the fundamental domain of the topology. Another way of thinking about topology is to glue the sides together to create a donut, a two-dimensional surface embedded in a three dimensional space. Yet another way of thinking about topology is to tile an infinite plane with identical copies of the same fundamental domain.
Cosmologists generally consider three possible geometries for the universe: a positively curved universe, a flat universe, and a negatively curved universe. In standard parlance, closed, critical, and open universes. The latter nomenclature is misleading; negatively curved universes can be either infinite in spatial extent or compact. Both models have the same dynamics and expand forever: Dynamics is determined by geometry. The three-sphere is a space of constant positive curvature, and the pseudosphere is a hyperbolic space with constant negative curvature.
From a topological point of view, negatively curved (hyperbolic) universes are “generic”; most three dimensional manifolds can be viewed as homogenous, negatively curved, and compact [Thurston’s geometrization conjecture (26)]. Cornish, Gibbons, and Weeks (N.J.C., G.Gibbons, and J.R. Weeks, unpublished work) recently have shown that, in the Hartle-Hawking approach to quantum cosmology, the smallest volume manifolds are favored. These smallest volume manifolds are the simplest compact models.
In negatively curved manifolds, the characteristic length is the curvature scale. Thus, throughout the rest of this paper, we will use it as our unit of length. There is an infinite number of distinct compact hyperbolic topologies. There is a fundamental group, usually denoted Γ, associated with each of these topologies. Each of these topologies also has a specific volume (measured in curvature units). We strongly recommend the publicly available SNAPPEA program (http://www.geom.umn.edu) for anyone interested in developing a more intuitive feel for the rich structure of compact hyperbolic topology.
© 1998 by The National Academy of Sciences 0027–8424/98/9582–3$2.00/0
PNAS is available online at http://www.pnas.org.
|
§ |
To whom reprint requests should be addressed, e-mail: dna@astro.princeton.edu. |
One of the intriguing mathematical properties of compact hyperbolic manifolds is that geodesic flows on these manifolds are maximally chaotic and mixing. Because of this property, they are extensively studied by physicists and mathematicians interested in quantum chaos (27, 28). We have speculated that quantum chaos plays an important role in the homogenization of the early universe (21).
Observing the Effects of Topology. How would we know whether we are living in a compact hyperbolic universe? Local observations can only measure the geometry of the universe. We need to look out beyond our own fundamental domain to begin to see the effects of topology. Most cosmologists trying to look for observational signatures of topology have attempted to find replicas of our own galaxy or other familiar objects (rich clusters) (19, 29, 30). In a typical small volume compact hyperbolic universe, the expectation value for the length of the shortest closed geodesic in generic small volume manifolds (volumes <10 say) is between 0.5 and 1 (W.P. Thurston, personal communication). That is, if we randomly select a point in such a manifold, this is the most probable value for the conformal distance to our nearest copy. In a matter dominated universe, the redshift of an object is related to the conformal distance by
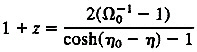
[1]
where η is the conformal lookback time and η0=arccosh(2/Ω0−1) is the present conformal time. For an Ω0=0.3 universe, η0=2.42 and the nearest image of ourselves is likely to lie between a redshift of 0.88 and 2.92. Similarly, if Ω0=0.4, we find η0=2.06, and the nearest copy will typically lie between a redshift of 1.01 and 3.83. These numbers indicate that it will be very difficult to constrain the topology of a hyperbolic universe using direct searches for ghost images of any astrophysical objects. This difficulty is compounded by the evolution of astrophysical objects on much shorter time scales.
Fortunately, observations of the microwave background are potentially a very powerful tool for probing the topology of the universe. The MAP and PLANCK satellites will measure millions of independent points on the surface of last scatter. If we live in a universe in which the distance to our nearest copy is less than the diameter of the last scattering surface then we will see the same position on the surface of last scatter at multiple points on the microwave sky (21, 22). Because the surface of last scatter is a sphere, it will intersect itself along circles. This will lead to pairs of matched circles across the sky. Note that the temperature is not constant along these circles but rather that there are pairs of points along each circle with identical temperatures.
There are several effects that make this signature very difficult to detect in the COBE satellite data. If the universe is negatively curved, then most of the large scale fluctuations are not caused by physics at the surface of last scatter but rather are caused by the decay of potential fluctuations along the line of sight (13). These fluctuations are mostly generated at z< 2, generally within our fundamental domain. Thus, large angular scale measurements are not sensitive to topology. Even without this effect, we will likely need higher resolution maps with higher signal-to-noise to definitively detect the matched circles. The combination of high signal-to-noise and large numbers of independent pixels along each circle significantly reduces the chances of false detections.
Can we detect topology with the MAP data? The number of matched circle pairs is equal to the number of copies of the fundamental cell that can fit inside a ball of proper radius χ= 2η0 (we are approximating the radius of the last scattering surface by the radius of the particle horizon). A fair estimate of the number of cells, Nc, needed to tile this hyperbolic ball is given by the volume ratio,
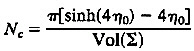
[2]
where Vol(Σ) is the volume of the fundamental domain in curvature units. In a universe with Ω0=0.3, this is a whopping ratio of Nc=25000/Vol(Σ). Considering that there is an infinite number of hyperbolic three manifolds with volumes <3, we have no shortage of model universes that can be seen by this method. Even if Ω0 was as high as 0.95, we would still have an infinite number of manifolds to chose from that would produce at least some matched circle pairs.
How big are these matched circles? Let us consider an infinite hyperbolic universe tiled with copies of our fundamental domain. We can draw the last scattering sphere centered not only around our own location but also around all of our images. The circles arise at the intersections of these spheres. The angular radius, θ, of the circles is set by the radius of the last scattering sphere (~η0) and the conformal distance, ξ, to the appropriate image of the MAP satellite:
[3]
If Ω0=0.3, there will be over 4000/Vol(Σ) circles of radius between 10 and 15°. At its highest frequency, MAP will have a resolution of 0.21°, thus it will measure over 300 independent points along each of these circles. Even at a resolution of 0.5°, where we can use the three highest frequency maps, there are still over 125 independent points along each circle. We are currently simulating the analysis of MAP data using synthetically generating skies: our current results are promising. It appears that MAP has a sufficient signal-to-noise ratio and sufficient resolution to detect topology in a Ω=0.3 universe even if the volume of the fundamental domain is several 10s of curvature volumes.
Once we detected the circles, Weeks (personal communication) showed us that we can use them to determine the topology of the universe. Each pair of circles lies on matched faces of the fundamental cell; thus, each pair of circles gives us an element of the fundamental group Γ. From the list of elements, we can construct the generators of the group. Most small volume universe have only two or three generators. We expect to have many hundreds if not thousands of circle pairs, so constructing the generators from the elements is a highly overdetermined problem. Thus, producing a consistent solution is an extremely powerful check that will help demonstrate that the circles are not random events or artifacts of some pernicious instrumental effect. The Mostow-Prasad rigidity theorem implies that a given topology has a fixed volume measured in curvature units; thus, once we know the topology and the angular size of the circles, we have an independent topological determination of the radius of last scattering surface in units of the curvature radius. This yields an independent measurement of Ω that does not rely on any assumptions about the nature of the primordial fluctuations.
After determining the topology of the universe, we can then proceed onwards and reconstruct the temperature of the photons and the velocity of the baryon photon fluid throughout the entire fundamental domain from the microwave sky. The surface area of the microwave sky is 4πsinh2η0; thus, in an Ω0=0.3 universe, we see ≈400/Vol(Σ) slices through the fundamental domain. Hence, the characteristic distance between slices is only a few comoving megaparsecs. We should be able to reconstruct not only the statistical properties of the initial fluctuations but the actual amplitude and phases of the initial fluctuations on the scale of galaxy clustering. These initial fluctuations can, of course, be integrated forward and compared with the local observed universe. At the end of the analysis, we, in principle, should be able to identify the cold
spot that eventually collapsed to form the Virgo supercluster and other familiar parts of our local universe. Cosmologists are used to thinking of looking out at the universe and measuring the prehistory of other regions of the universe. If we are fortunate enough to live in a compact hyperbolic universe, we can look out and see our own beginnings.
We thank Jeff Weeks and Bill Thurston for deepening our understanding of topology and for helpful comments. D.N.S. is supported by the MAP/MIDEX program. G.D.S. is supported through the National Science Foundation CAREER Grant. N.J.C was supported by Particle Physics and Astronomy Research Council Grant GR/L21488.
1. Strauss, M.A. & Willick, J.A. (1995) Phys. Rep. 261, 271–431.
2. Davis, M., Nusser, A. & Willick, J. (1996) Ap. J. 473, 22–41.
3. Riess, A.G., Davis, M., Baker, J. & Kirshner, R.P. (1997) Ap. J. 488, L1.
4. Bahcall, N.A., Lubin, L.M. & Dorman, V. (1995) Ap. J. 447, L81–L84.
5. White, S.D.M., Navarro, J.F., Evrard, A.E. & Frenk, C.S. (1993) Nature (London) 366, 429–433.
6. Lubin, L.M., Cen, R., Bahcall, N.A. & Ostriker, J.P. (1996) Ap. J. 460, L10–L13.
7. White, D.A., Jones, C. & Forman, W. (1997) Monogr. Nat. R. Astronom. Soc., in press.
8. Da Costa, L.N., Vogeley, M.S., Geller, M.J., Huchra, J.P. & Park, C. (1994) Ap. J. 437, L1–L4.
9. Lin, H., Kirshner, R.P., Shechtman, S.A., Landy, S.D., Oemler, A., Tucker, D. & Schechter, P.L. (1996) Ap. J. 471, 617–635.
10. Spergel, D.N., Bolte, M. & Freedman, W.L. (1997) Proc. Natl. Acad. Sci. USA 94, 6579–6584.
11. Carlberg, R.G., Yee, H.K.C., Ellingson, E., Morris, S.L., Abraham, R., Gravel, P., Hartwick, F.D.A., Hesser, J.E., Hutchings, J.B., Oke, J.B., Pritchet C.J. & Smecker-Hane, T. (1997) J.R. Assoc. Soc. Can. 90, 314–320.
12. Bahcall, N.A., Fan, X. & Cen, R. (1991) Ap. J. Lett. 485, L53–L56.
13. Kamionkowski, M. & Spergel, D.N. (1994) Ap. J. 432, 7–16.
14. Ratra, B., Sugiyama, N., Banday, A.J. & Gorski, K.M. (1991) Ap. J. 481, 22–34.
15. Ostriker, J.P. & Steinhardt, P.J. (1995) Nature (London) 377, 600–602.
16. Perlmutter, S., Gabi, S., Goldhaber, G., Goobar, A., Groom, D.E., et al. (1997) Ap. J. 483, 565–581.
17. Turner, E.L. (1990) Ap. J. 365, L43–L46.
18. Falco, E.E., Kochanek, C.S. & Munoz, J.M. (1997) Ap. J., in press.
19. Gott, J.R., III (1980) Monogr. Nat. R. Astronom. Soc. 193, 153–169.
20. Fagundes, H.V. (1983) Phys. Rev. Lett. 51, 517–520.
21. Cornish, N.J., Spergel, D.N. & Starkman, G.D. (1996) Phys. Rev. Lett. 77, 215–218.
22. Cornish, N.J., Spergel, D.N. & Starkman, G.D. (1996) astro-pk/9708225.
23. Bond, J.R., Pogosyan, D. & Souradeep, T. (1997) Proceedings of the 18th Texas Symposium on Relativistic Astrophysics, eds. Olinto, A., Frieman, J. & Schramm, D. (World Scientific, River Edge, NJ), in press.
24. Levin, J.J., Barrow, J.D., Bunn, E.F. & Silk, J. (1997) Phys. Rev. Lett., in press.
25. Weeks, J.R. (1985) The Shape of Space: How to Visualize Surfaces and Three Dimensional Manifolds (Dekker, New York).
26. Thurston, W.P. (1978) The Geometry and Topology of 3-Manifolds (Princeton Univ. Press, Princeton).
27. Balazs, N.L. & Voros, A. (1985) Phys. Rep. 143, 1109–1240.
28. Gutzweiler, M.C. Physica Scripta T9, 184–192.
29. Lehoucq, R., Lachieze-Rey, M. & Luminet, J.P. (1996) A & A 313, 339–346.
30. Roukema, B.F. & Edge, A.C. (1997) Monogr. Nat. R. Astonom. Soc., in press.



