Proc. Natl. Acad. Sci. USA
Vol. 94, pp. 8292–8299, August 1997
Colloquium Paper
This paper was presented at a colloquium entitled “Carbon Dioxide and Climate Change,” organized by Charles D. Keeling, held November 13–15, 1995, at the National Academy of Sciences, Irvine, CA.
Global air-sea flux of CO2: An estimate based on measurements of sea–air pCO2 difference
TARO TAKAHASHI *, RICHARD A. FEELY †, RAY F. WEISS ‡ , RIK H. WANNINKHOF § , DAVID W. CHIPMAN * , STEWART C. SUTHERLAND * , AND TIMOTHY T. TAKAHASHI ¶
*Lamont–Doherty Earth Observatory of Columbia University, Palisades, NY 10964; †Pacific Marine Environmental Laboratory, National Oceanic and Atmospheric Administration, Seattle, WA 98115; ‡ Scripps Institution of Oceanography, University of California at San Diego, La Jolla, CA 92093; § Atlantic Oceanographic and Meteorological Laboratory, National Oceanic and Atmospheric Administration, Miami, FL 33149; and ¶Ames Research Center, National Aeronautics and Space Administration, Moffett Field, CA 94035
ABSTRACT Approximately 250,000 measurements made for the pCO2 difference between surface water and the marine atmosphere, ∆pCO2, have been assembled for the global oceans. Observations made in the equatorial Pacific during El Nino events have been excluded from the data set. These observations are mapped on the global 4° × 5° grid for a single virtual calendar year (chosen arbitrarily to be 1990) representing a non-El Nino year. Monthly global distributions of ∆pCO2 have been constructed using an interpolation method based on a lateral advection–diffusion transport equation. The net flux of CO2 across the sea surface has been computed using ∆pCO2 distributions and CO2 gas transfer coefficients across sea surface. The annual net uptake flux of CO2 by the global oceans thus estimated ranges from 0.60 to 1.34 Gt-C·yr−1 depending on different formulations used for wind speed dependence on the gas transfer coefficient. These estimates are subject to an error of up to 75% resulting from the numerical interpolation method used to estimate the distribution of ∆pCO2 over the global oceans. Temperate and polar oceans of the both hemispheres are the major sinks for atmospheric CO2, whereas the equatorial oceans are the major sources for CO2. The Atlantic Ocean is the most important CO2 sink, providing about 60% of the global ocean uptake, while the Pacific Ocean is neutral because of its equatorial source flux being balanced by the sink flux of the temperate oceans. The Indian and Southern Oceans take up about 20% each.
Measurements of the atmospheric CO2 concentration indicate that it has been increasing at a rate about 50% of that which is expected from all industrial CO2 emissions. The oceans have been considered to be a major sink for CO2. Hence the improved knowledge of the net transport flux across the air–sea interface is important for understanding the fate of this important greenhouse gas emitted into the earth’s atmosphere ( 1 , 2 , 3 , 4 and 5 ).
A number of different approaches has been used for estimating the role of the oceans as a CO2 sink, yielding a wide range of estimates for the CO2 uptake flux (3). Most commonly used are ocean–atmosphere CO2 cycle models. In these models, ocean circulation is modeled using various schemes ranging from one-dimensional box-diffusion models (4, 5) to three-dimensional ocean general circulation models ( 6, 7 and 8), and biological processes are assumed to be invariant with time and are not explicitly described. These “perturbation” models yield an oceanic uptake of about 2 Gt-C·yr−1 (= 2 × 1015 g of carbon·yr−1), which corresponds to about 35% of the current industrial CO2 emission rate of about 6 Gt-C·yr−1. On the basis of temporal changes of the 13C/12C ratio in atmospheric and oceanic CO2, the annual oceanic uptake of atmospheric CO2 has been estimated to be 1.6 ± 0.9 Gt-C·yr−1 (2, 9). Tans et al. (1) combined the meridional gradient of atmospheric CO2 concentration and the net CO2 flux over the northern oceans to constrain the CO2 budget and concluded that the net uptake of atmospheric CO2 by the global oceans is 1 Gt-C·yr−1 or less and that the northern terrestrial ecosystem is a major CO2 sink. Using an advanced atmospheric general circulation models that includes a more realistic description of turbulent mixing near the ground, Denning et al. (10) concluded that an even greater biospheric CO2 sink is needed in the northern hemisphere. In these studies, the mean annual meridional gradient of atmospheric CO2 was assumed implicitly to be zero during the pre-industrial period. This assumption, however, has been questioned by Broecker and Peng (11) on the basis of the meridional gradient of oceanic CO2 concentrations estimated for the pre-industrial time.
Since global ∆pCO2 data were summarized by Tans et al. (1), the number of observations has been increased significantly as a result of many recent field programs in the United States as well as those in Canada, France, Japan, the Nordic countries, and the United Kingdom (12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37 and 38). In this paper, we present monthly ∆pCO2 distribution maps in 1990 for the global oceans computed using these new data and give estimates for the net CO2 flux over the global oceans obtained using the ∆pCO2 distributions. The magnitude of errors in the mean ∆pCO2 values thus estimated has been estimated and discussed.
Measurements
All of the data used in this study are the results of direct pCO2 measurements made using air–seawater equilibration methods (12, 17, 39, 40). Although the CO2 concentration in equilibrated air was determined using various types of infrared gas analyzers and gas chromatographs, all these measurements are calibrated against the reference CO2/air mixtures of known CO2 concentrations that were determined by C. D. Keeling (Scripps Institution of Oceanography) using his manometric method. The pCO2 value in seawater was obtained using the CO2 concentration, the water vapor pressure at the equilibration temperature and the pressure of equilibrated gas (which is commonly equal to the barometric pressure). It was corrected to the seawater temperature using the difference between in situ and equilibration temperatures and the isochemical temperature effect on seawater pCO2 of 4.23% C−1 (31). The atmospheric pCO2 was obtained using the local mean
|
|
© 1997 by The National Academy of Sciences 0027-8424/97/948292-8$2.00/0 PNAS is available online at http://www.pnas.org. |
value of CO2 concentrations in dry air measured concurrently with the seawater pCO2, barometric pressure, and water vapor pressure at seawater temperature. The sea–air pCO2 difference, ∆pCO2, was computed by subtracting it from the oceanic pCO2 value. Although the non-ideal behavior of CO2 gas due to CO2–CO2 as well as CO2–N2–O2–H2O molecular interactions has been estimated by Weiss and Price (41), its effect is about 1 µatm in the concentration range of CO2. Furthermore, since the corrections are similar for the air and seawater pCO2, the non-ideal effect cancels due to the differencing for ∆pCO2. Therefore, CO2 has been treated as an ideal gas.
The pCO2 database assembled for this study consists of about 250,000 individual measurements made during about 250 expeditions. Many of the observations used have been published in scientific journals and in technical reports (12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37 and 38; 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56 and 57). In addition, many unpublished data in the archives of the authors at the Lamont–Doherty Earth Observatory, the Scripps Institution of Oceanography, the Pacific Marine Environmental Laboratory (National Oceanic and Atmospheric Administration), and the Atlantic Oceanographic and Meteorological Laboratory (National Oceanic and Atmospheric Administration) have been used.
Adjustments and Resampling of the Data
In assembling the global data set for ∆pCO2, the original measurements have been processed through the four steps which are discussed below.
Averaging of the Underway pCO2 Data. There are two sources of pCO2 data in surface waters: those obtained for discrete water samples at each hydrographic station and those obtained semicontinuously (several times per hour) using underway systems. Because the number of the latter measurements far exceeds the number for discrete water sample measurements, the latter would statistically overwhelm the former. To prevent this, we have computed a 6-h mean value (e.g., a mean over 100 km if ship’s speed is 8 knots) for underway measurements and counted this mean with an equal statistical weight as a discrete measurement. This averaging scheme has been shown to represent a spatial variation of pCO2 in seawater even in areas of strong gradients such as the equatorial Pacific.
Exclusion of the Equatorial Pacific Data for El Nino Periods. The objective of this study is to obtain a representative distribution of global ocean ∆pCO2 during non-El Nino periods. Although El Niño Southern Oscillations (ENSO) events could affect a wide range of global meteorological and oceanographic conditions including those in the Southern Ocean (58, 59), the extent of its effects on the carbon chemistry beyond the equatorial Pacific belt has not been documented. Therefore, we have assumed that the effects are limited to the equatorial Pacific between 10°N and 10°S and removed the equatorial Pacific data from the data set for the following El Nino periods, which have been identified on the basis of the Southern Oscillation Index (less than −1.5) and sea surface temperature (SST) changes (NINO3 and NINO4) (59): March 1972–March 1973; May 1976–March 1977; June 1982–June 1983; August 1986–July 1987; October 1991–May 1992; October 1992–October 1993; and April 1994–February 1995.
Through these two processes described above, the original 250,000 individual measurements were reduced to about 16,500 data points; their spatial distribution is shown in Fig. 1. Although the global ocean appears to be well covered over the 12-month period with the exception of the southern Indian Ocean, monthly data distributions (February and August are shown as examples) show large oceanic areas without measurements.
Normalization of ∆pCO2 to the Year 1990 With the exceptions of well-studied areas such as the western North Pacific, the available observations are not sufficient to resolve the interannual variability of ∆pCO2 over the global oceans. Therefore, our approach is to combine all the observations onto a single virtual calendar year (chosen arbitrarily to be 1990). However, since the mean atmospheric CO2 concentration has increased by about 30 ppm from about 326 ppm in 1972 to 356 ppm in 1994, the secular increase in atmospheric CO2 must be taken into consideration when ∆pCO2 data are assembled to represent a single year. In subtropical gyres, vertical mixing of surface layer waters with subsurface waters is limited due to the strong stratification. Hence, as the surface water takes up more atmospheric CO2, the mean pCO2 in surface waters tends to increase with a rate similar to the atmospheric CO2 increase. This has been demonstrated over the Sargasso Sea (60) and over the western North Pacific between 3°N and 35°N along the 137°E meridian by Inoue et al. (21). R.A.F. (unpublished data) analyzed the surface water pCO2 data obtained in the equatorial Pacific along 140°W during the years 1984, 1988, 1990, and 1995, and observed that the surface water pCO2 values have been increasing at a mean rate of 1.3 ± 0.5 µatm·yr−1, which is consistent with the atmospheric rate of about 1.8 ppm·yr−1. This implies that the strong CO2 source in the Pacific equatorial belt is caused by the warming of recently ventilated, colder subsurface waters derived primarily from depths about 100–300 meters. Hence ∆pCO2 values for the temperate gyre and equatorial areas are nearly independent of the year of measurements and thus, those measured in different years may be treated as though those were measured in the same year.
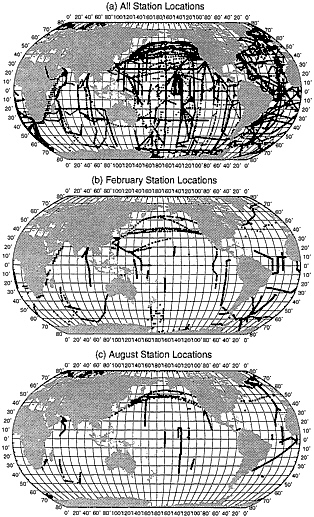
FIG. 1. Locations of ∆pCO2 measurements used in this study. (a) All sample locations, 1960–1995; (b) those in the month of February; and (c) August during the same years.
In contrast to the warm water regime, cold high-latitude surface waters located poleward of the subpolar front are known to convectively mix with deep waters seasonally and thus reflect the chemical characteristics of deep waters, in which anthropogenic effects are diluted. In Fig. 2, the surface water pCO2 data observed in 1974–1979 at Weather Station “P” (50°N, 145°W) in the northeastern subarctic Pacific by Wong and Chan (36) are compared with the 1985–1989 observations by the Lamont–Doherty Earth Observatory group (31, 50) and with the 1986 observations by the Pacific Marine Environmental Laboratory group (25). This shows that, while the atmospheric CO2 concentration increased by about 15 ppm over the 10-year period, an increase in the oceanic pCO2 has not been detectable. Therefore, the sea–air pCO2 difference has increased with time approximately at the mean annual rate for atmospheric CO2 increase, and ∆pCO2 measured in a different year must be corrected for atmospheric CO2 changes that occurred between the time of measurement and the reference year of 1990. Since the annual rate of increase in surface water CO2 depends on the vertical flux of subsurface waters and the duration of exposure time to the atmosphere, surface water pCO2 values in some regions where vertical mixing is weaker and/or air–sea ventilation time is longer may increase at a slower rate. However, relevant observations are not yet available in other subpolar and polar oceanic regions. Therefore, to normalize the observed ∆pCO2 values to the reference year of 1990, we assumed two cases in this study: (i) ∆pCO2 in the cold water regimes increased at the same mean annual rate as atmospheric CO2 and (ii) it increased with one-half the rate of atmospheric CO2. These are named respectively as “full” and “half” atmospheric CO2 increase cases in Table 1 and Table 2. These two normalization schemes are applied to the ∆pCO2 values observed poleward of the subpolar front which are located approximately along 40°N in the North Pacific, 45°N in the North Atlantic, 50°S in the South Atlantic, South Indian, and western Pacific (west of 180°) oceans, and 60°S in the eastern South Pacific Ocean (between 60°W and 180°).
The CO2 concentration in the marine air at a given time and location over the global oceans has been computed using an equation which has been fitted to the mean annual data summarized in refs. 1, 61, and 62 with better than 1 ppm. Because seasonal variation in atmospheric CO2 concentration is represented in the observed ∆pCO2 value by the concurrent measurements of atmospheric and oceanic pCO2, only the effect of the secular increase is considered for correction.
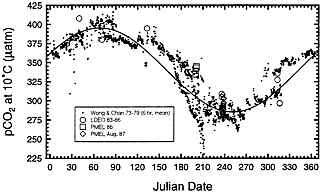
FIG. 2. The pCO2 values observed by Wong and Chan (36) during 1974–1979 in surface waters at or near the Weather Station “P” in the northeastern North Pacific (50°N, 145°W) are compared with more recent measurements by the Lamont–Doherty Earth Observatory during 1984–1989 (31, 53) and the Pacific Marine Environmental Laboratory during 1986–87 (25). The pCO2 values are normalized to a constant temperature of 10.0°C to remove the effect of temperature changes. The solid line indicates a sine curve fitted to the 1974–1979 data.
Resampling of the Data onto a 4° × 5° Grid. For use in the computational scheme of this study, the ∆pCO2 values normalized to the reference year of 1990 must be resampled onto the computational grid which consists of 72 grid points in longitude by 41 in latitude for each of 365 days in time. This amounts to a total of about 750,000 pixels excluding land areas. Although observations made in some areas are sufficient to allow a finer grid locally, the global data set assembled for this study is limited in spatial and time resolutions to allow a finer grid over the entire global oceans. A weighted average, inversely proportional in both space and time, is used to transform about 16,500 ∆pCO2 data onto the 4° latitude × 5° longitude × 365 days grid. Observations within ±4° latitude, ±5° longitude, and ±1 day from the pixel center is utilized to compute a mean pixel value. This liberal resampling algorithm gives sparse data more representation.
Computational Method for Time–Space Interpolation
The data set which has been discussed above represents measurements made at locations and times that were dictated by ship tracks without mathematical regularity. A computational method is needed to interpolate these observations discretized in a 4° × 5° × 365 days grid to construct global ∆pCO2 distribution maps. For this purpose, a finite-difference algorithm based on a lateral two-dimensional transport model developed by Takahashi et al. (63) is used. In the interpolation scheme, all pixel values based on observations are explicitly satisfied, and those in pixels that have no observations are computed.
Transport Equation and Boundary Conditions. The concentration of a chemical property throughout the oceans is governed by advective transport, eddy diffusion, internal sources, and sinks and exchange with the surroundings at the sea floor, the ocean margins, and the air–sea interface. In an interpolation scheme, in which the observations are satisfied, the effects on the surface water property of internal sources and sinks, exchange with atmosphere and upwelling of deep water are considered inherently imbedded in the observed data. Accordingly, the short-term behavior of surface water properties may be approximated using a lateral two-dimensional transport model without sink/source and exchange terms.
The transport equation used for interpolation is:
dS/dt = K ∈2S − (∂S/∂x Vx + ∂S/∂y Vy) and ∇2S = ∂2S/∂x2 + ∂2S/∂y2,
where S is a scalar quantity, Vx and Vy are the local surface water advective velocities, and K is the eddy diffusivity. The implied boundary condition is that there is no material transport across the sea–land interface: on an orthogonal grid, ∂S/∂x = 0 and ∂S/∂y = 0 along the boundaries. The computational domain is joined at the prime meridian, so that the oceans are freely interconnected in the east–west domain. Singularities at the poles are avoided by the presence of the Antarctic continent in the south (>80°S) and the polar ice cap in the north (>84°N) which is assumed to be a land mass. As discussed earlier, data collected in various years are mapped onto a single, virtual calendar year of 1990. Therefore, the computations are numerically joined across the December/January border ensuring continuity of solutions in both space and time. This allows solutions to be obtained iteratively over a single year period.
The finite–difference algorithm required must possess some unusual properties. Due to the temporal and spatial connectivity of the computational matrix, it is essential that the
influence of observed data propagates at the same computational speed both forwards and backwards in time: an average of forward-centered time step about time (t − 1) and backwards-centered time step about time (t + 1) is utilized. The spatial derivatives are second-order accurate and are central differences: ∂S/∂x = (Sx+l − Sx−1)/2∆x and ∂2S/∂x2 = (Sx+l − 2Sx + Sx−1)/(∆x)2. The time increment, dt, is chosen to be 1 day to maintain numerical stability under both diffusion and advection ( 63 ). The recursion relationship is applied over all active nodes (where no observation is available) until convergence is obtained. The convergence criterion is the net aggregate change (R) in the value of S between successive iterations: R = Σ abs[S(x, y, t)i − S(x, y, t)i−1], where x = 180°W through 180°E, y = 80°S through 84°N, and t = day 1 through day 365 and S(x, y, t)i represents the value of the scalar function, S, at a node representing a given position and time at the iteration, i. The solution is considered converged when changes in R fall below 0.1%. Typically, it takes several thousand iterations for the convergence criterion to be satisfied. Although the solutions give daily distributions, monthly mean distributions have been computed and used for the flux estimates.
Advective Field and Eddy Diffusion. For the computation of advective transport, we use the mean monthly surface water advective fields (4° × 5° resolution) of Bryan and Lewis ( 64 ), which have been kindly provided by the Geophysical Fluid Dynamics Laboratory (National Oceanic and Atmospheric Administration, Princeton, NJ). The advective field is changed each month in our computation. While the seasonal variability is small in the Pacific and Atlantic Oceans, currents in the northern Indian Ocean undergo a complete reorganization as a result of monsoon conditions. The lateral eddy diffusivity of surface waters has been estimated to be in a range of 1,000 to 3,000 m2·sec−1 (see refs. 65 , 66 and 67 ) and is assumed in this study to be a constant value of 2,000 m2·sec−1.
Preloading of the Field. To obtain converged solutions rapidly and to constrain the solutions in polar regions where data are very scarce, initial ∆pCO2 values for those pixels that have no measurement are assigned to be equal to the monthly zonal mean of the observed ∆pCO2 values in each of the polar (90° to 54°), subpolar (38° to 54°), temperate (18° to 38°), and tropical (18° to 18°) zones. In addition, the polar pixels with ice fields are assumed to have seasonally varying ∆pCO2 values that are consistent with a limited number of observations made in polynyas and adjacent to ice fields ( 29 , 34 , 44 , 51 , 52 ): for the Arctic pixels with ice, −150 µatm for August, −75 µatm for September, −50 µatm for October, and −35 µatm for the remaining 9 months; for the Antarctic pixels with ice, −85 µatm for February, −10 µatm for January and March, +5 µatm for December and April, and +30 µatm for the remaining 6 months. The CO2 flux is assumed to be zero when a pixel is covered with ice, the flux estimates are not sensitively affected by the choice of preset values. A constant temperature of −1.9°C is assigned to all pixels with ice. Starting with these preloaded field, the interpolation computation was performed using a time step of 1 day. The results obtained after 2,000 iterations are presented in this paper.
Tests for the Interpolated Values
Comparison with Climatological SST. To evaluate the validity of our results, the SST values that have been computed using the measurements made concurrently with ∆pCO2 are compared with the climatological SST compiled by Shea et al. ( 68 ). Consistent with the procedures used for ∆pCO2 interpolation, the temperature field was preloaded using mean monthly values for temperature values measured concurrently with ∆pCO2 in each climatic zone. In Fig. 3a , the difference between the mean monthly SST observed in 4° × 5° pixels and the corresponding climatological SST are plotted against the climatological SST; and in Fig. 3b , the difference between the interpolated value and the corresponding climatological SST is plotted. Fig. 3a shows that the measured temperatures are consistent with the climatological SST yielding a mean difference of −0.07°C (n = 5,780) with a rms deviation of ±1.5°C. The small mean difference indicates that our temperature observations are consistent with the climatological SST.
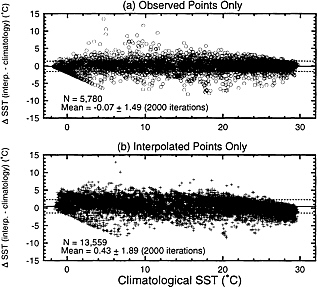
F IG . 3. Comparisons between (a) the mean monthly climatological SST data ( 68 ) and the mean monthly temperatures measured concurrently with ∆pCO2; and (b) the mean monthly climatological SST data and those interpolated for pixels with no measurements. The solid and dashed horizontal lines indicate the mean and rms deviation values, respectively.
Fig. 3b shows that our interpolated temperatures are, on average, warmer than the climatological SST by 0.43 ± 1.89°C. This may be taken as a measure of errors attributable to our computational method and limited time–space database. The temperature dependence of pCO2 in surface waters varies regionally and seasonally from about +3% C−1 in temperate gyres to about −6% C−1 in polar oceans ( 31 ), and is about 3.5% C−1 (in the absolute magnitude) on the average over the global oceans. This gives that the SST error of 0.43°C corresponds to a ∆pCO2 of 5 µatm. If a mean global sea–air CO2 exchange rate of 19 mol·m−2yr−1 ( 69 ), which is consistent with the gas transfer formulation used by Tans et al. ( 1 ), is assumed, this error would correspond to a flux error of about 1 Gt-C·yr−1 or 75% of the net global ocean CO2 flux estimated in this study. Because of the sparseness of time–space coverage, the uncertainty in the global ocean ∆pCO2 depends critically on the availability of observations especially in data poor areas. The error could be reduced significantly by additional seasonal observations especially over the southern mid- and high-latitude oceans.
Sensitivity to the Interpolated ∆pCO2 Values. The sensitivity of the interpolated ∆pCO2 values to the number of observations made along ship’s tracks has been tested by eliminating a measurement from every 10 observations. The interpolated values obtained with 90% of the full database have been compared with those computed using 100% of the database. The effect of this reduction on the interpolated ∆pCO2 is small with a mean difference of −0.01 ± 2.2 µatm and is independent of latitude. Therefore, the estimated ∆pCO2 values over the global oceans are not sensitively affected by the number of measurements made along ship’s tracks.
Distribution of the CO2 Sink/Source Over the Global Oceans
Distribution of ∆pCO2. The mean monthly distribution of sea–air pCO2 difference, ∆pCO2, over the global oceans is
Table 1. Sea–air pCO2 difference (µatm) nomalized to 1990 with the effect of full and half atmospheric CO2 increase for five zones
|
Latitude |
Effect |
Jan. |
Feb. |
March |
April |
May |
June |
July |
Aug. |
Sept. |
Oct. |
Nov. |
Dec. |
Annual |
|
N of 50°N |
Full |
−15.9 |
−10.3 |
−13.7 |
−18.6 |
−28.5 |
−44.9 |
−50.4 |
−51.7 |
−51.3 |
−46.3 |
−39.8 |
−29.1 |
−34.5 |
|
|
Half |
−11.9 |
−6.2 |
−9.6 |
−14.9 |
−25.1 |
−41.4 |
−46.4 |
−46.9 |
−47.2 |
−42.0 |
−35.4 |
−25.0 |
−30.5 |
|
14°N–50°N |
Full |
−16.3 |
−18.6 |
−19.9 |
−20.2 |
−17.4 |
−9.0 |
+2.8 |
+7.6 |
+4.7 |
−1.8 |
−8.3 |
−13.6 |
−9.2 |
|
|
Half |
−15.9 |
−18.3 |
−19.5 |
−19.8 |
−17.0 |
−8.7 |
+3.2 |
+8.0 |
+5.3 |
−1.1 |
−7.8 |
−13.1 |
−8.7 |
|
14°S–14°N |
F/H |
+26.7 |
+27.9 |
+25.9 |
+28.6 |
+28.8 |
+26.1 |
+25.0 |
+23.0 |
+22.3 |
+21.9 |
+23.1 |
+24.6 |
+25.3 |
|
14°S–50°S |
Full |
−3.0 |
−1.0 |
−0.9 |
−2.9 |
−6.8 |
−9.5 |
−11.2 |
−11.9 |
−11.2 |
−10.4 |
−8.9 |
−6.8 |
−7.1 |
|
|
Half |
−2.6 |
−0.6 |
−0.6 |
−2.7 |
−6.5 |
−9.2 |
−10.8 |
−11.4 |
−10.7 |
−9.9 |
−8.4 |
−6.3 |
−6.6 |
|
S of 50°S |
Full |
−13.6 |
−15.0 |
−13.0 |
−6.6 |
−4.5 |
−3.4 |
−3.0 |
−1.5 |
−3.3 |
−5.4 |
−7.3 |
−11.0 |
−7.9 |
|
|
Half |
−12.0 |
−13.2 |
−12.3 |
−6.1 |
−4.1 |
−2.8 |
−2.5 |
−1.1 |
−2.9 |
−5.0 |
−6.9 |
−10.2 |
−7.1 |
|
Global mean |
Full |
+0.7 |
+1.1 |
+0.4 |
+1.1 |
+0.3 |
−0.1 |
+1.3 |
+1.6 |
+0.8 |
−0.4 |
−0.8 |
−0.8 |
+0.4 |
|
|
Half |
+1.3 |
+1.7 |
+0.8 |
+1.4 |
+0.7 |
+0.3 |
+1.8 |
+2.1 |
+1.4 |
+0.3 |
−0.2 |
−0.2 |
+1.0 |
tabulated in Table 1 for the “full” and “half” effects of the atmospheric CO2 increase; and its geographical distribution for the months of February and August 1990 is presented in Fig. 4 a and Fig. 4 b , respectively. During the month of February, the following areas are strong sources for atmospheric CO2 (positive ∆pCO2 values): (i) the northwestern subarctic Pacific (due to winter upwelling), (ii) the entire equatorial Pacific (upwelling), (iii) the eastern subtropical South Pacific (seasonal warming), (iv) the tropical and subtropical South Atlantic (upwelling and seasonal warming), (v) the western equatorial Indian Ocean, and (vi) a few patchy areas near Antarctica (local upwelling). The CO2 sink areas include (i) the temperate gyre areas in the North Pacific and North Atlantic (seasonal cooling), (ii) subpolar and polar areas of the South Atlantic and South Pacific (photosynthesis), and (iii) south and east of New Zealand (photosynthesis). In August ( Fig. 4b ), the strong source areas include (i) the central and eastern equatorial Pacific (upwelling), (ii) the North Pacific temperate gyre (seasonal warming), (iii) the northwestern North Atlantic (warming of the Labrador Current), (iv) Arabian Sea (upwelling), and (v) patchy areas near Antarctica (upwelling). The strong sink areas are as follows: (i) the northern North Atlantic and adjacent subpolar seas (photosynthesis), (ii) the northwestern North Pacific (photosynthesis), and (iii) the temperate regions of the south Indian, Pacific, and Atlantic Oceans (cooling). Over the subpolar and polar Atlantic, Pacific and Southern Oceans, the surface water pCO2 increases during winter due to winter convective mixing, whereas it decreases during summer due to photosynthesis in stratified photic waters ( 31 ).
Table 1 shows that the mean annual ∆pCO2 values (area weighted) for the global oceans are small (+0.4 ≪ + 1 µatm), as are many of the monthly mean values (−0.8 ≪ +2.1 µatm). This means that the global oceans are, as a whole, nearly in equilibrium with atmospheric CO2, although they are locally out of equilibrium by as much as 30%. This suggests that the oceanic uptake of CO2 depends sensitively on the wind speed distribution especially in areas such as subpolar oceans where large negative ∆pCO2 and high wind speeds prevail.
Computation of the Net CO2 Flux Across the Sea Surface. The net CO2 flux (F) across each 4° × 5° pixel area is computed using F = A × E × ∆pCO2, where A is a pixel area, E is mean monthly gas transfer coefficient across the sea surface, and ∆pCO2 is mean monthly sea–air pCO2 difference evaluated for each pixel. Since the E value for CO2 gas is not well known, we consider the following three different functions of wind speed (W): (i) a linear wind speed dependence based on the 14C budget in the atmosphere and oceans ( 1 , 69 ): E (CO2 mol·m−2·yr−1·µatm−1) = 1.6 × 10−2 [W(m·sec−1) − 3.0] and E = 0 when W ≤3.0 (m·sec−1); (ii) a relationship formulated by Wanninkhof ( 70 ) for long-term wind (i.e., his equation 2): E = 1.13 × 10−3·W2; and (iii) a three linear-segment wind speed dependence formulated by Liss and Merlivat ( 71 ): E = 4.8 × 10−4 × W for 0 ≤ W ≤ 3.6 m·sec−1, E = 8.3 × 10−3 (W − 3.39) for 3.6 ≤ W ≤ 13 m·sec−1, and E = 1.7 × 10−2 (W − 8.36) for W ≥ 13 m·sec−1. While i yields the fastest gas transfer rate representing the upper limit, iii yields rates about 50% of the first, representing the lower limit, and ii yields rates about 15% smaller than the first. It is therefore important in the future to improve our understanding of the CO2 gas transfer rate across the sea surface over a wide range of turbulences near the air–sea interface. In this paper, the mean monthly wind speed data compiled for the global oceans ( 72 ) are used to compute the CO2 gas transfer rate constant, and the results of these three relationships are presented and compared.
Net Flux of CO2 Over the Global Oceans.
Fig. 5 shows the distribution of annual CO2 flux and indicates that the equatorial belt of the Pacific and Atlantic is a major CO2 source,

FIG 4. Mean monthly distribution of ΔpCO2 (μatm) for (a) February 1990 and (b) August 1990, estimated using the assumption of full atmospheric CO2 increase. The positive values indicate that the ocean is a source for atmospheric CO2, and the negative values indicate CO2 sinks. The pink lines indicate edges of ice field.
whereas temperate areas of the global oceans and the subarctic Atlantic are major sinks. Table 2 shows that the global ocean CO2 uptake flux ranges from 0.6 to 1.34 Gt-C·yr−1 depending on the gas transfer formulations used. This is about 2 times as large as those estimated by Tans et al. ( 1 ), whereas it is about 30–70% of the estimates of about 2 Gt-C·yr−1 obtained by perturbation models. It, however, overlaps with 1.6 ± 0.9 Gt-C·yr−1 based on 13C/12C distribution in seawater (2, 9).
The mean ocean flux for each of the five latitudinal zones is compared in Table 2 with the results of Tans et al. (1). The northern ocean CO2 uptake estimated by this study is about twice as large as that of Tans et al. (1). This is partially due to more negative ∆pCO2 values resulting from correcting the older data to 1990, and partially due to improvements in the database and time–space interpolation method. While a time resolution of 4 months was used in Tans et al. (1), 1 month is used in this study, allowing a better representation for pCO2 drawdowns during spring phytoplankton blooms. The equatorial CO2 source flux estimated in this study is about 30% smaller than that by Tans et al. (1). This is a result of increased observations especially in the western and central equatorial Pacific by the Japanese (19, 20, 21) and U.S. (13, 16, 25) investigators, respectively. The Southern Ocean CO2 source flux of +0.5 Gt-C·yr−1, which was proposed by Tans et al. (1) to satisfy the observed meridional gradient of the atmospheric CO2 concentration, cannot be supported by the oceanic observations used in this study.
Net CO2 Flux Over the Oceanic Basins. The equatorial zone (14°N to 14°S) of the Pacific is the major oceanic CO2 source area emitting (+0.35 to +0.79 Gt-C·yr−1) about 5 times as much CO2 to the atmosphere than the corresponding areas in the Atlantic and Indian Oceans. On an annual basis, the Atlantic (north of 50°S) is the most important CO2 sink (−0.42 to −0.85 Gt-C·yr−1) because of the temperate and subarctic oceans being strong CO2 sinks and the equatorial belt being a weak source. On the other hand, the Pacific (north of 50°S) as a whole is nearly neutral (+0.04 to −0.02 Gt-C·yr−1) because of the strong equatorial source nearly balancing the strong sinks in the temperate areas. The Southern Ocean (south of 50°S) is a strong sink (−0.15 to −0.3 Gt-C·yr−1), which is comparable to the uptake flux for the temperate oceanic areas.
Each of the Pacific, Atlantic, and Indian basins shows different north–south contrasts. Excluding the Southern Ocean, south of 50°S, the magnitude of the uptake flux for the southern temperate Pacific is similar to that for the northern temperate Pacific. On the other hand, because of strong sink areas in the subarctic oceans, the northern Atlantic sink is about 4 times as strong as the southern temperate Atlantic. On the basis of the flux estimated using the gas transfer coefficient of Tans et al. (1), the north–south flux asymmetry is about 0.6 Gt-C·yr−1 if the Southern Ocean (south of 50°S) is excluded or about 0.45 Gt-C·yr−1 if the Atlantic sector of the Southern Ocean is included. This is comparable to the preindustrial north–south ocean transport of 0.6 Gt-C·yr−1 in the Atlantic proposed by Broecker and Peng (11).
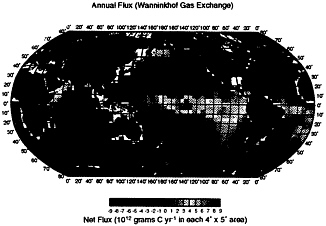
FIG. 5. Mean annual net CO2 flux over the global oceans (in 1012 grams of C per year for each pixel area) computed for 1990 using the gas transfer coefficient formulated by Wanninkhof (70). The effect of full atmospheric CO2 increase is assumed for normalizing observed ∆pCO2 values in high latitude areas to the reference year of 1990. Areas covered with ice (i.e., the poleward of the pink lines in Fig. 4 a and Fig. 4 b ) are assumed to have zero sea–air CO2 flux.
Table 2. Zonal mean sea–air CO2 flux and mean annual ∆pCO2 over the global oceans during 1990
|
|
Net CO2 Flux, Gt-C·yr1 |
|||
|
|
Gas coefficient |
This study |
|
|
|
Zones |
Full |
Half |
Tans et al. ( 1 ) |
|
|
N of 50°N |
TF&T |
−0.45 |
−0.39 |
−0.23 * |
|
(Arctic) |
W |
−0.35 |
−0.31 |
|
|
|
L&M |
−0.22 |
−0.19 |
−0.12 * |
|
14°N–50°N |
TF&T |
−0.72 |
−0.68 |
−0.36 * |
|
(Nort. Temperate) |
W |
−0.55 |
−0.52 |
|
|
|
L&M |
−0.35 |
−0.33 |
−0.18 * |
|
14°N–14°S |
TF&T |
+1.04 |
+1.04 |
+1.30 * |
|
(Tropical) |
W |
+0.72 |
+0.72 |
|
|
|
L&M |
+0.46 |
+0.46 |
+0.65 * |
|
14°S–50°S |
TF&T |
−0.92 |
−0.87 |
|
|
(Sout. Temperate) |
W |
−0.71 |
−0.68 |
|
|
|
L&M |
−0.45 |
−0.42 |
|
|
S of 50°S |
TF&T |
−0.30 |
−0.27 |
+0.5 † |
|
(Antarctic) |
W |
−0.25 |
−0.22 |
|
|
|
L&M |
−0.15 |
−0.12 |
+0.5 † |
|
Global oceans |
TF&T |
−1.34 |
−1.17 |
|
|
|
W |
−1.14 |
−1.01 |
|
|
|
L&M |
−0.71 |
−0.60 |
|
Sources of Errors. The flux estimates are subject to errors from the following five independent sources: (i) the gas transfer coefficients, (ii) the wind speed variability, (iii) the normalization of observations to the reference year of 1990, (iv) the interpolation of limited observations, and (v) skin temperature effect.
-
The estimated flux values, which range from 0.60 to 1.34 Gt-C·yr−1, depend on the choice of sea–air CO2 gas transfer formulations. Hence the error is of a systematic nature and may be reduced if the gas transfer coefficient is better understood in the future.
-
Because the gas transfer coefficient increases with wind speed at an increasingly faster rate, gas exchange rates estimated using mean monthly wind speeds tend to be smaller than those estimated using high-frequency wind speed data with a large wind speed variability. Hence, our flux estimates are likely to represent a minimum value. The mean monthly gas transfer coefficient thus obtained may be underestimated relative to that obtained using high frequency wind data by about −10% on the average, although it could be off by as much as −51% locally depending upon the frequency distribution and magnitude of wind speed variations ( 73 ). Because the variation of wind speed is coupled with that of ∆pCO2 through the interactions between turbulent mixing in upper
-
waters and biological activities, the covariance of wind speed and ∆pCO2 should be taken into consideration in future studies.
-
To correct for interannual changes in the oceanic and atmospheric pCO2 values, the observed ∆pCO2 values have been normalized to a reference year 1990 as explained earlier. The flux values for high latitude oceans computed using the “full” atmospheric CO2 increase are about 10% greater in magnitude than the respective values obtained for the “half” effect ( Table 2 ), and hence the error due to this effect is about ±5%.
-
Errors due to the computational method has been estimated to be about 5 µatm for the mean global ∆pCO2. This corresponds to an error of up to 75% of the flux estimates made using a given gas transfer formulation.
-
∆pCO2 depends on the skin temperature of surface ocean water (49, 74), while the pCO2 has been evaluated at the bulk water temperature in this study. The effect of skin layer cooling on the global CO2 uptake has been estimated to be 0.1–0.6 Gt-C·yr−1 (75). However, the skin temperature may be higher or lower than the bulk water temperature depending upon meteorological and oceanic conditions, and the measurements are limited in space and time. Therefore, its effect on the global ∆pCO2 and flux has been neglected in this study.
Summary and Conclusions
A database for the sea–air pCO2 difference, ∆pCO2, has been assembled using about 250,000 observations made between 1960 and 1995 during 250 expeditions over the global oceans. Observations made in the equatorial Pacific during El Nino events have been excluded. In light of the sparseness of observations over large oceanic areas, the multiyear data have been corrected and combined to represent a single reference year of 1990. These observations have been organized into 4° latitude × 5° longitude × 1 day pixels for 365 days, and interpolated in space and time using a computational scheme based on the diffusive and advective transport of surface water (63).
On the basis of the global distribution of ∆pCO2 values thus computed, a global net ocean uptake of 0.60 to 1.34 Gt-C·yr−1 is obtained for 1990 using three different formulations for the gas transfer coefficient. This is similar to 1.6 ± 0.9 Gt-C·yr−1 estimated on the basis of 13C changes in the atmosphere and ocean (2), but is smaller than about 2 Gt-C·yr−1 based on various ocean–atmosphere perturbation models (3 , 4, 5, 6, 7 and 8). However, it is greater than the estimates based on the atmospheric CO2 distribution and mass balance (1).
The Pacific equatorial belt is the largest oceanic CO2 source to the atmosphere. The temperate oceanic areas of the both hemispheres are the most important sinks, and their uptake fluxes exceed those of high latitude oceans (poleward of the 50° parallel) by a factor of 2 to 3. Among the four ocean basins, the Atlantic Ocean (north of 50°S) is the strongest sink providing about 60% of the total global ocean uptake, whereas the Pacific (north of 50°S) is nearly neutral. The Indian and Southern Oceans contribute about 20% each to the global uptake flux. The uptake flux by the North Pacific is similar to that by the South Pacific, whereas the North Atlantic takes up 0.45 to 0.6 Gt-C·yr−1 more CO2 than the South Atlantic and Southern Ocean combined. This is comparable to the preindustrial oceanic transport of CO2 from the North to South Atlantic estimated by Broecker and Peng (11). Because the results of this study differ significantly from the northern ocean uptake of CO2 used in the analysis of the atmospheric and oceanic data by Tans et al. (1), a global analysis of the CO2 and carbon isotope data in the ocean, atmosphere, and biosphere must be made to evaluate their mutual coherence.
This study has benefited from observations made by many international investigators. We thank the following scientists for their contributions: W. S. Broecker, A. W. Dickson, R. H. Gammon, S. S. Jacobs, Walker Smith, H. Ducklow, W. M. Smethie, D. Martinson, P. Schlosser, J. Sarmiento, D. Wallace, E. Garvey, N. R. Bates, A. H. Knap, T. D. Foster, C. S. Wong, C. D. Keeling, L. Merlivat, C. LeQuere, V. Garcon, C. Provost, W. Roether, H. Y. Inoue, K. Fushimi, A. Watson and J. E. Robertson. We also thank members of our technical staff who ran instruments at sea and on land and processed data in our respective laboratories: J. Goddard, S. Rubin, R. Esmay, F. A. van Woy, P. K. Salameh, P. P. Murphy, K. C. Kelly, L. S. Waterman, Matt Steckley and David Ho. This work was supported by a number of grants from the National Science Foundation, the U.S. Department of Energy, and the National Oceanic and Atmospheric Administration to T.T. at the Lamont–Doherty Earth Observatory and to R.F.W. at the Scripps Institution of Oceanography. R.A.F. and R.H.W. have been supported by the Climate and Global Change Program of the National Oceanic and Atmospheric Administration. We gratefully acknowledge the support and encouragement received from these agencies. This is contribution 5573 of the Lamont–Doherty Earth Observatory.
1. Tans, P. P. , Fung, I. Y. & Takahashi, T. ( 1990 ) Science 247 , 1431–1438 .
2. Quay, P. D. , Tilbrook, B. & Wong, C. S. ( 1992 ) Science 256 , 74–79 .
3. Siegenthaler, U. & Sarmiento, J. L. ( 1993 ) Nature (London) 365 , 119–125 .
4. Oeschger, H. , Siegenthaler, U. & Gugelmann, A. ( 1975 ) Tellus 27 , 168–192 .
5. Broecker, W. S. & Peng, T.-H. ( 1982 ) Tracers in the Sea ( Eldigio , Palisades, NY ).
6. Bacastow, R. & Maier-Reimer, E. ( 1990 ) Clim. Dyn. 4 , 95–125 .
7. Sarmiento, J. L. , Orr, J. C. & Siegenthaler, U. ( 1992 ) J. Geophys. Res. 97 , 3621–3645 .
8. Sarmiento, J. L. , Murnane, R. & Le Quere, C. ( 1995 ) Philos. Trans. R. Soc. London B 343 , 211–219 .
9. Tans, P. P. Berry,J. A. & Keeling R. ( 1993 ) Global Biogeochem. Cycles 7 , 353–368 .
10. Denning, A. S. , Fung, I. Y. & Randall, D. ( 1995 ) Nature (London) 376 , 240–243 .
11. Broecker, W.S. & Peng, T-H. ( 1992 ) Nature (London) 356 , 587–589 .
12. Chipman, D. W. , Marra, J. & Takahashi, T. ( 1993 ) Deep-Sea Res. 40 , 151–169 .
13. Archer, D. E. , Takahashi, T. , Sutherland, S. , Goddard, J. , Chipman, D. , Rogers, K. & Ogura, H. ( 1996 ) Deep-Sea Res. PArt II 43 , 779–808 .
14. British Oceanographic Centre ( 1994 ) BOFS North Atlantic Data Set (CD-ROM) ( British Oceanographic Centre, Bidson Observatory , Birkenhead, Merseyside, U.K. ).
15. Chipman, D. W. , Takahashi, T. , Breger, D. & Sutherland, S. C. ( 1992 ) Investigation of Carbon Dioxide in the South Atlantic and Northern Weddell Sea Areas (WOCE Sections A-12 and A-21) during the Meteor Expedition 11/5, January–March, 1990 ( Lamont–Doherty Geological Observatory , Palisades, NY ).
16. Feely, R. A. , Wanninkhof, R. , Cosca, C. E. , Murphy, P. P. , Lamb, M. F. & Steckley, M. D. ( 1995 ) Deep-Sea Res. Part II 42 , 365–386 .
17. Goyet, C. , Beauverger, C. , Brunet, C. & Poisson, A. ( 1991 ) Tellus B 43 , 1–11 .
18. Goyet, C. & Peltzer, E. T. ( 1994 ) Marine Chem. 45 , 257–266 .
19. Inoue, H. Y. & Sugimura, Y. ( 1988 ) Tellus B 40 , 308–320 .
20. Inoue, H. Y. & Sugimura, Y. ( 1992 ) Tellus B 44 , 1–22 .
21. Inoue, H. Y. , Mastueda, H. , Ishii, M. , Fushimi, K. , Hirota, M. , Asanuma, I. & Takasugi, Y. ( 1995 ) Tellus B 47 , 391–413 .
22. Ishii, M. & Inoue, H. Y. ( 1995 ) Tellus B 47 , 447–460 .
23. Metzl, N. , Poisson, A. , Louanchi, F. , Brunet, C. , Schauer, B. & Bres, B. ( 1995 ) Tellus B 47 , 56–69 .
24. Murphy, P. P. , Feely, R. A. , Gammon, R. H. , Harrison, D. E. , Kelly, K. C. & Waterman, L. S. ( 1991 ) J. Geophys. Res. 96 , 20,455–20,465 .
25. Murphy, P. P. , Kelly, K. K. , Feely, R. A. , & Gammon, R. H. ( 1995 ) Carbon Dioxide Concentrations in Surface Water and the Atmosphere during 1986–1989 NOAA/PMEL Cruises in the Pacific and Indian Oceans ( Oak Ridge Natl. Lab. , Oak Ridge, TN ), Rep. NRNL/CDIAC-75, NDP-047 .
26. Poisson, A. , Metzl, N. , Brunet, C. , Schauer, B. Bres, B. , Buiz-Pino, D. & Louanchi, F. , ( 1993 ) J. Geophys. Res. 98 , 22759–22778 .
27. Poisson, A. , Metzl, N. , Danet, X. , Louanchi, F. , Brunet, C. , Schauer, B. , Bres, B. & Ruiz-Pino, D. ( 1994 ) in The Polar Oceans and Their Role in Shaping the Global Environment , eds. Johannessen, O. M. , Muench, R. D. & Overland, J. E. ( Am. Geophys. Union , Washington, DC ), Geophysical Monograph 85 , pp. 273–284 .
28. Robertson, J. E. , Watson, A. J. , Langdon, C. Ling, R. D. & Wood, J. W. ( 1993 ) Deep-Sea Res. 40 , 409–422 .
29. Rubin, S. , Goddard, J. , Chipman, D. W. & Takahashi, T. ( 1996 ) Antarct. J. USA 31 , 113–115 .
30. Takahashi, T. , Goddard, J. G. , Rubin, S. , Chipman, D.W. & Sutherland, S. C. ( 1993 ) Investigation of Carbon Dioxide in the Central South Pacific Ocean (WOCE Sections P-16C and P-17C) During the TUNES/2 Expedition of the R/V Thomas Washington, July–August, 1991 ( Lamont–Doherty Earth Observatory, Columbia Univ. , Palisades, NY ).
31. Takahashi, T. , Olafsson, J. , Goddard, J. , Chipman, D.W. & Sutherland, S. C. ( 1993 ) Global Biogeochem. Cycles 7 , 843–878 .
32. Wanninkhof, R. , Feely, R. A. , Atwood, D. K. , Berberian, G. , Wilson, D. , Murphy, P. P. & Lamb, M. F. ( 1995 ) Deep-Sea Res. Part II 42 , 387–409 .
33. Watson, A. J. , Robinson, C. , Robertson, J. E. , Williams, P. J. le B. & Fasham, M. J. R. ( 1991 ) Nature (London) 350 , 50–53 .
34. Weiss, R. F. , van Woy, F. A. & Salameh, P. K. ( 1992 ) Surface Water and Atmospheric Carbon Dioxide and Nitrous Oxide Observations by Shipboard Automated Gas Chromatography: Results from Expeditions Between 1977 and 1990 ( Scripps Inst. of Oceanography , La Jolla, CA ), SIO Report 92-11, ORNL/CDIAC-59, NPD-044.
35. Japan Meteorological Agency ( 1994 ) WMO World Data Center for Greenhouse Gases, Sample Issue, CD-ROM ( Japan Meteorological Agency , Tokyo ).
36. Wong, C. S. & Chan, Y.-H. ( 1991 ) Tellus B 43 , 206–223 .
37. Wong, C. S. , Chan, Y.-H. , Page, J. S. , Smith, G. E. , & Bellegay, R. D. ( 1993 ) Tellus B 45 , 64–79 .
38. Karl, D. M. , Tilbrook, B. D. & Tien, G. ( 1991 ) Deep-Sea Res. 38 , 1097–1126 .
39. Broecker, W.S. & Takahashi, T. ( 1966 ) J. Geophys. Res. 71 , 1575–1602 .
40. Wanninkhof, R. & Thoning, K. ( 1993 ) Marine Chem. 44 , 189–204 .
41. Weiss, R. F. & Price, B. A. ( 1980 ) Marine Chem. 8 , 347–359 .
42. Andrie, C. , Genthon, C. & Merlivat, L. ( 1986 ) J. Geophys. Res. 91 , 11741–11755 .
43. Chipman, D.W. , Takahashi, T. & Sutherland, S.C. ( 1986 ) Carbon Chemistry of the South Atlantic Ocean and the Weddell Sea: The Results of the Atlantic Long Lines (AJAX) Expeditions, October 1983–February, 1984 ( Lamont–Doherty Geological Observatory , Palisades, NY ).
44. Chipman, D. W. & Takahashi, T. ( 1990 ) Investigation of Carbon Chemistry in the Weddell Sea Area During the 1986 Winter Expedition of the F/S Polarstern: June 28, 1986–September 16, 1986 ( Lamont–Doherty Geological Observatory , Palisades, NY ).
45. Kelley, J. J., Jr. ( 1970 ) Limnol. Oceanograph. 15 , 80–87 .
46. Kelley, J. J. , Longerich, L. L. & Hood, D. W. ( 1971 ) J. Geophys. Res. 76 , 8689–8693 .
47. Peng, T.-H. , Takahashi, T. , Broecker, W. S. & Olafsson, J. ( 1987 ) Tellus B 39 , 439–458 .
48. Roos, M. & Gravenhorst, G. ( 1984 ) J. Geophys. Res. 89 , 8,181–8,193 .
49. Smethie, W. M. , Takahashi, T. , Chipman, D. & Ledwell, J. R. ( 1985 ) J. Geophys. Res. 90 , 7005–7022 .
50. Takahashi, T. , Goddard, J. , Chipman, D. W. , Sutherland, S. C. & Mathieu, G. ( 1991 ) Assessment of Carbon Dioxide Sink/Source in the North Pacific Ocean: Seasonal and Geographic Variability 1984–1989 ( Lamont–Doherty Geological Observatory , Palisades, NY ).
51. Takahashi T. , Chipman, D. , Schechtman, N. , Goddard, J. & Wanninkof, R. ( 1982 ) Measurements of the Partial Pressure of CO2 in Discrete Water Samples during the North Atlantic Expedition, the Transient Tracers of Oceans Project ( Lamont–Doherty Geological Observatory , Palisades, NY ).
52. Takahashi, T. & Chipman, D. ( 1982 ) Antarctic J. USA 17 , 103–104 .
53. Takahashi, T. , Chipman, D. W. , Smethie, Wm. Jr. , Goddard, J. Trumbore, S. , Mathieu, G. G. & Sutherland, S. C. ( 1985 ) Assessment of Carbon Dioxide Sink/Source in the Oceanic Areas: The Results of 1982–84 Investigation ( Lamont–Doherty Geological Observatory , Palisades, NY ).
54. Takahashi, T. , Olafsson, J. , Broecker, W. S. Goddard, J. , Chipman, D. & White J. ( 1985 ) J. Mar. Res. Institute Reykjavik , 9 , 20–36 .
55. Takahashi, T. , Goddard, J. , Sutherland, S. , Chipman, D. W. , & Breeze, C. ( 1986 ) Seasonal and Geographic Variability of Carbon Dioxide Sink/Source in the Oceanic Areas: Observations in the North and Equatorial Pacific Ocean 1984–1986 and Global Summary ( Lamont–Doherty Geological Observatory , Palisades, NY ).
56. Takahashi, T. , Chipman, D. W. , Goddard, J. , Mathieu, G. & Ma, L.-M. ( 1990 ) in Sea–Air Interaction in Tropical Western Pacific , eds. Chao J.-P. & Young, J.A. ( China Ocean Press , Beijing, PRC ), pp. 511–539 .
57. Takahashi, T. , Goddard, J. , Chipman, D. W. , Sutherland, S. C. & Mathieu, G. ( 1991 ) Assessment of Carbon Dioxide Sink/Source in the North Pacific Ocean: Seasonal and Geographic Variability 1984–1989 ( Lamont–Doherty Geological Observatory , Palisades, NY ).
58. White, W. B. & Peterson, R.G. ( 1996 ) Nature (London) 380 , 699–702 .
59. Trenberth, K. E. & Hoar, T. J. ( 1996 ) Geophys. Res. Lett. 23 , 57–60 .
60. Takahashi, T. , Chipman, D. & Volk, T. ( 1983 ) Proceedings: Carbon Dioxide Research Conference: Carbon Dioxide, Science and Consensus ( U.S. Department of Energy , Washington, DC ), Vol. 2 , Rep. CONF-820970 , pp. 123–145 .
61. Keeling, C. D. & Whorf, T. P. ( 1994 ) in Trends ’93: A Compendium of Data on Global Change , eds. Boden, T. A. , Sepanski, R. J. & Stoss, F.W. ( Carbon Dioxide Information Analysis Center , Oak Ridge Natl. Lab. , Oak Ridge, TN ), Rep. ORNL/CDIAC-65 , pp. 16–26 .
62. Conway, T. J. , Tans, P. P. & Waterman, L. S. ( 1994 ) in Trend ’93: A Compendium of Data on Global Change , eds. Boden, T.A. , Kaiser, D. P. , Sepanski, R. J. & Stoss, F. W. ( Carbon Dixoide Information Analysis Center , Oak Ridge National Laboratory , Oak Ridge, TN ), Rep. ORNL/CDIAC-65 , pp. 41–119 .
63. Takahashi, T. , Takahashi, T. T. & Sutherland, S. C. ( 1995 ) Philos. Trans. R. Soc London B 348 , 143–152 .
64. Bryan, K. & Lewis, L. J. ( 1979 ) J. Geophys. Res. 84 , 2503–2517 .
65. Bretherton, F. P. & Karweit, M. ( 1975 ) Proceedings of Symposium on Numerical Models of Ocean Circulation ( Natl. Acad. of Sci. , Washington, DC ), pp. 237–249 .
66. Thiele, G. , Roether, W. , Schlosser, P. , Kuntz, R. , Siedler, G. & Stramma, L. ( 1986 ) J. Phys. Oceanogr. 16 , 814–826 .
67. Jenkins, W. J. ( 1991 ) J. Phys. Oceanogr. 21 , 1058–1061 .
68. Shea, D. J. , Trenberth, K. E. & Reynolds, R. W. ( 1992 ) J. Clim. 5 , 987–1001 .
69. Broecker, W. S. , Ledwell, J. R. , Takahashi, T. , Weiss, R. F. , Merlivat, L. , Memery, L. , Peng, T.-H. , Jahne, B. & Munnich, K. O. ( 1986 ) J. Geophys. Res. 91 , 10517–10527 .
70. Wanninkhof, R. ( 1992 ) J. Geophys. Res. 97 , 7373–7382 .
71. Liss, P. S. & Merlivat, L. ( 1986 ) in The Role of Air-Sea Exchange in Geochemical Cycling , ed. Buat-Menard, P. ( Reidel , Hingham , The Netherlands ), pp. 113–127 .
72. Esbensen, S. K. & Kushnir, Y. ( 1981 ) The Heat Budget of the Global Ocean: An Atlas Based on Estimates from the Surface Marine Observations ( Oregon State Univ. , Corvalis, OR ), Climatic Research Institute Report 29 .
73. Boutin, J. & Etcheto, J. ( 1991 ) Tellus B 43 , 236–246 .
74. van Scoy, K. A. , Morris, K. P. , Robertson, J. E. & Watson, A. J. ( 1995 ) Global Biogeochem. Cycles 9 , 253–262 .
75. Sarmiento, J. L. & Sundquist, E. T. ( 1992 ) Nature (London) 356 , 589–593 .








