Proc. Natl. Acad. Sci. USA
Vol. 94, pp. 8308–8313, August 1997
Colloquium Paper
This paper was presented at a colloquium entitled “Carbon Dioxide and Climate Change,” organized by Charles D. Keeling, held November 13–15, 1995, at the National Academy of Sciences, Irvine, CA.
Direct observation of the oceanic CO2increase revisited
PETER G. BREWER * , CATHERINE GOYET † , AND GERNOT FRIEDERICH *
*Monterey Bay Aquarium Research Institute, P.O. Box 628, Moss Landing, CA 95039; and †Woods Hole Oceanographic Institution, Woods Hole, MA 02543
ABSTRACT We show, from recent data obtained at specimen North Pacific stations, that the fossil fuel CO2signal is strongly present in the upper 400 m, and that we may consider areal extrapolations from geochemical surveys to determine the magnitude of ocean fossil fuel CO2uptake. The debate surrounding this topic is illustrated by contrasting reports which suggest, based upon atmospheric observations and models, that the oceanic CO2sink is small at these latitudes; or that the oceanic CO2sink, based upon oceanic data and models, is large. The difference between these two estimates is at least a factor of two. There are contradictions arising from estimates based on surface partial pressures of CO2alone, where the signal sought is small compared with regional and seasonal variability; and estimates of the accumulated subsurface burden, which correlates well other oceanic tracers. Ocean surface waters today contain about 45 µmol·kg-1excess CO2compared with those of the preindustrial era, and the signal is rising rapidly. What limits should we place on such calculations? The answer lies in the scientific questions to be asked. Recovery of the fossil fuel CO2contamination signal from analysis of ocean water masses is robust enough to permit reasonable budget estimates. However, because we do not have sufficient data from the preindustrial ocean, the estimation of the required Redfield oxidation ratio in the upper several hundred meters is already blurred by the very fossil fuel CO2signal we seek to resolve.
In a recent paper Ciais et al. (1) described the results of careful measurements of atmospheric CO2 distributions and isotopic ratios. While they noted that “there is still ample room for improvement in this technique,” they concluded that a large northern hemisphere terrestrial CO2 sink existed, and that the oceanic sink at temperate latitudes was small. This is in general agreement with the earlier work of Tans et al. (2) which estimated a minimal oceanic sink.
In contrast, work on the other side of the Pacific Ocean by Tsunogai et al. (3) concludes that the Intermediate waters of the North Pacific form a very large contemporary CO2 sink, and provide oceanic data to support this conclusion. Siegenthaler and Sarmiento (4) have summarized a great deal of work and also conclude that the ocean is indeed an important sink for anthropogenic carbon, but that a “missing sink” is also probably located in the land biota. The differences are large: data presented by Ciais et al. (1) for 1993 indicate that the global oceanic CO2 sink is about 1.15 Gt-C·yr-1; Tans et al. (2) state that “the global ocean sink is at most 1 Gt-C·yr-1.” This is in contrast to oceanic tracer-based data and models which indicate an oceanic sink of >2 Gt-C·yr-1.
How can such differing views hold? And why is there such confusion over what should be a reasonably straightforward oceanic geochemical signal?
The importance of the large oceanic CO2 sink, and the fundamental principles of the chemistry and physics that drive it, have been cited in classic papers over many decades of this century (5, 6 and7), and no flaw in these basic concepts is seen: CO2 remains an acidic gas, we still have a vast and alkaline ocean for it to react with, and the rate of transfer is determined by the large-scale circulation which brings the ocean and atmosphere into contact. Yet the current debate is confusing, and therefore in this paper we re-examine the elementary question of detection of the oceanic CO2 increase, seek to place some limits on the errors involved, and make suggestions for practical steps to reduce the uncertainty. We cannot here resolve the question of the ultimate size of the large-scale integrated ocean burden; but the detection of the fossil fuel CO2 signal by direct measurement, and the determination of its areal extent by careful expeditionary surveys offers the best way to achieve this and those measurements are being accomplished today.
Background
Brewer ( 8 ) first proposed and demonstrated a simple and direct estimate of detection of the oceanic anthropogenic CO2 increase by examination of Geochemical Ocean Sections Study (GEOSECS) data from the South Atlantic Ocean. He corrected contemporary deep observations for the effects of oxidative decomposition of marine organic matter, and the dissolution of carbonates, and derived a value for a corrected pCO2 that was linked to the invasion of the gaseous anthropogenic signal. An extended version of this analysis for North Atlantic waters, based upon Transient Tracers in the Ocean, North Atlantic Study (TTO NAS) data was recently given by Goyet and Brewer (9), who again calculated the invasion term for the fossil fuel CO2 component, and showed a strong correlation of this signal with the F-11 chlorofluorocarbon tracer along the isopycnal surface of Labrador Sea water. Other researchers (10) have adopted this technique with only small variations.
Chen and Millero (11) independently published a somewhat different approach to this interesting problem, and Chen has since published widely on this topic (12, 13). Both the Brewer (8) and Chen and Millero (11) methods involve a simple arithmetic subtraction of the quantities of CO2 gas and alkalinity added to deep waters by respiration and carbonate dissolution once the surface waters are removed from their contact with the atmosphere and begin their century scale sojourn in the abyss. However the two approaches differ importantly in their normalization procedures and in the assumptions necessary to formalize the signal.
This validity of these approximations to recognition of the fossil fuel signal has been the subject of much debate. Broecker et al. (14) attempted to greatly extend the question first posed, and asked whether not just the accumulated amount, but the time record of the CO2 chemistry of the past atmosphere,
|
|
© 1997 by The National Academy of Sciences 0027-8424/97/948308-6$2.00/0 PNAS is available online at http://www.pnas.org. |
could be recovered by inverting the oceanic water mass signals; not surprisingly, they found this to be impractical. Their closing comment, however, is worthy of note: “Once the preanthropogenic CO2 content of the atmosphere has been firmly established by ice core studies . . . then the oceanic distribution of TCO2 can be used to constrain some of the current uncertainties in models for the uptake of fossil fuel CO2 by the ocean.” Since that time the preanthropogenic atmospheric CO2 content has been established as close to 280 µatm, and the fossil fuel signal of ocean surface waters that we seek to identify has continued to rise, so that the surface ocean today contains some 45 µmol·kg-1 of CO2 in excess of that in the preindustrial era.
Wallace (15) has carried out a survey of strategies for monitoring global ocean carbon inventories, and has attempted to assess uncertainties. He comments favorably on the need for providing reliable estimates of the build up of fossil fuel CO2 in the ocean, and notes that the anthropogenic CO2 content of the ocean now ranges from zero (deep waters) to 45 µmol·kg-1 (surface waters) thus providing a useful dynamic range; that individual measurement errors are between 1 and 5 µmol·kg-1; and that the manmade signal is superimposed on a natural background that has to be accurately recovered to use the signal. He notes that “a clear advantage of this approach is that it can provide model-independent estimates of the spatial variability of the excess CO2 distribution which in turn can be used to validate model predictions.”
The mapping of sea surface pCO2 is relatively easy now that superior instrumentation has been developed, and it provides data on the distribution of natural sources and sinks. However, the driving signal for the fossil fuel term is not the natural pattern, but the forced disequilibrium between air and sea resulting from the rapid rate of atmospheric CO2 growth. If the oceanic uptake rate is at the high end of published estimates, then this signal must now have a globally averaged value of about +8 µatm to provide the needed driving force, but its observation on top of a natural background that varies by ±100 µatm is difficult indeed (2), and so far it has not been unequivocally detected.
There is clearly an oceanic fossil fuel signal present, but it is the integrated amount and its time evolution that is hard to assess. Consider the simple large scale problem first: the surface area of the ocean is about 3.6 × 1014 m2. The globally averaged mixed layer depth has been estimated as about 75 m (7), and thus a volume of “fresh” sea water of about 2.7 × 1019 liters·yr-1 is exposed to the atmosphere. Recent work at the Joint Global Ocean Flux Study (JGOFS) Bermuda time series station (16) indicates that the CO2 content of mixed layer waters is increasing at a rate of about 1.7 µmol·kg-1·yr-1. Leaving aside for the moment the question of natural variability versus industrial atmospheric trends, and simply integrating this number from a northern hemisphere temperate gyre, on an ocean wide basis we would find a global uptake of 4.6 × 1013 mol·yr-1, or 0.55 Gt-C·yr-1.
This is broadly consistent with the lower estimates of oceanic uptake of Tans et al. (2) and Ciais et al. (1), and it at once raises the question of how representative are single sites of a global balance, how to obtain a legitimate integrated signal, and how reliable the mean mixed layer (ventilation) depth might be. The average mixed layer depth estimate was derived so as to match the oceanic penetration of bomb radiocarbon over a decade or more; the mean equilibration time for CO2 is about 1 year, and that for 14CO2 is about 10 years, and so the two results are not entirely compatible. For instance, a greater effective mixed layer depth (a winter dominated signal) would increase the CO2 uptake rate significantly over the crude estimate above.
It therefore seems timely to reconsider the problem of detection of the fossil fuel signal in the ocean by direct means, and to examine the concepts and assumptions involved in a more formal way.
Concepts
The relatively small, but rapidly growing, fossil fuel CO2 invasion signal in the ocean is written on top of a large and variable natural background; the problem is to normalize, or remove, or otherwise constrain the background signal so as to reveal the man-made component. The arithmetic turns out to be extraordinarily simple; but the problems that are thereby exposed lie at the root of our field and force us to ask some difficult questions.
In the following discussion we use the notation TC to define the total quantity of CO2 in all its forms (CO2 + H2CO3 + HCO-3 + CO32-) in sea water, and TA to define the total alkalinity.
Carbon dioxide gas is fixed in surface waters by photosynthesis, and returned as mineralized products at depth. This biogeochemical cycle is superimposed on the signal imposed by the physical effects of temperature and salinity distributions, and by any imbalances caused by the slow equilibration rate of CO2 with the atmosphere.
The most commonly used equation to describe the biogeochemical cycle is that given by Redfield (17), and embellished and extended by Redfield et.al.(18):
(CH20)106(NH3)16(H3PO4) + 138O2 <=> 106CO2 + 16NO-3 + HPO2-4 + 122H2O + 18H+.
The assumptions are that in living organic matter the oxidation state of carbon is that of carbohydrate, that nitrogen is present in the amino form, and that phosphorous may be represented as orthophosphate.
This so called “Redfield Ratio” is critical to the problem; note that the addition or removal of CO2 gas during photosynthesis or decay does not change the total alkalinity, but that the companion removal or release of nitrate ion does. As indicated in the notation here, the uptake and release of nitrate ion is equivalent to removal and regeneration of nitric acid and must be accounted for in relating the observed alkalinity to the mass changes from calcium carbonate removal and addition. This was first described by Brewer et al. (19), and shown experimentally for the uptake side of the equation by Brewer and Goldman (20) and Goldman and Brewer (21). The effect of phosphate ion is more complex [see Bradshaw et al. (22) for a detailed account], for it appears in the acidimetric titration of sea water as a proton contributor in two steps; a correction for this of one H+ in the 18 Redfield protons is required here.
There have been many attempts to revise the Redfield equation [e.g., Takahashi et al. (23) and Boulahid and Minster (24)], not normally through the inclusion of additional terms for trace constituents, but in an effort to increase the accuracy of the numerical coefficients for the principal reactants; it is remarkable that such a simple relationship should apparently hold over all the vast area of the earth’s surface covered by the oceans. A recent and very thorough analysis is given by Anderson and Sarmiento (25). They examined the distribution of nutrients upon ˜20 neutral surfaces in the South Atlantic, Indian, and Pacific basins between 400 and 4,000 m depth and produced a revised set of values such that their preferred estimates are
C/N/P/O = 117:16:1:–170.
Thus in the deep ocean the addition of CO2 by respiration can be calculated by observing the oxygen deficit relative to
saturation with the atmosphere, and recourse to the preferred version of the Redfield ratio for the appropriate coefficients.
We should note that the Anderson and Sarmiento (25) selection of a depth interval that excludes data from shallower than 400 m is in part due to the assumed presence in that depth range of the fossil fuel CO2 contamination signal described here. We are thus in a bind, for this is the very zone where the regeneration rates are largest (26), where local deviations from the mean may be expected to occur, and where we are most in need of information. There simply are no reliable data prior to the onset of penetration of fossil fuel CO2, and we must extrapolate through this zone in the best way possible. The oceanic cycles of phosphorus, nitrogen and oxygen have changed far less than that of CO2, and recovery of those ratios would be possible if multiple water mass mixing problems were not so severe.
In surface sea water total alkalinity is observed to be a very well constrained function of salinity: the fossil fuel CO2 burden does not change the total alkalinity, and the seasonal variations are small for the increase in alkalinity from NO3 assimilation is partially offset by the decrease from calcium carbonate formation. Thus we can recognize subsurface addition of CO2 from carbonate dissolution by departures from the salinity to total alkalinity (TA) ratio established for winter time surface waters.
For example Brewer et al. (27) give
TA = 50.56S%0 + 547.0 µmol·kg−1,
from an analysis of Transient Traces in the Ocean (TTO) data from North Atlantic surface waters, and the equivalent regional functions in other ocean basins will be increasingly well constrained in the near future from the Joint Global Ocean Flux Study/World Ocean Circulation Experiment (JGOFS/WOCE) Global Survey data, and from time series data such as that reported by Bates et al. (16). In this paper we will use the relationship
TA = 45.785S%0 + 703.7 µmol·kg−1,
(see Fig. 2), with a standard error of ± 6.2 µmol·kg−1 from our specimen analysis of recent Pacific data.
To establish the CO2 correction for deep waters due to the dissolution of calcium carbonate, and the addition of acidic nitrate ion, we write (using Redfield’s original coefficients for example)
∆TA = ∆TA (CaCO3) + (1 − 18)/138O2.
FIG. 1. Cruise tracks and station locations for WOCE Leg P17N.
Note that we cannot use the observed nitrate ion concentration directly, for there is a significant nonmetabolized fraction (the preformed nitrate), and thus all corrections reduce to a function of the oxygen deficit of the water mass. To establish the deep water correction terms for total CO2, we therefore write
∆TC = 106/138∆O2 + 0.5(∆TA − [(1 − 18)/138 ∆O2]),
which reduces to
∆TC = 0.8297∆O2 + 0.5∆TA
[original Redfield ratios (17, 18)], or
∆TC = 0.738∆O2 + 0.5∆TA
[from Anderson and Sarmiento (25)]. We now have, given the gas solubility data, the information we need to calculate a pair of values for TC and TA at some point at depth that in relates to the chemical properties acquired during ventilation at the surface many years ago. The term representing the initial TC is in effect a tracer of fossil fuel CO2 input written on top of the natural background; it is a surprisingly robust signal and may be analyzed along ventilation surfaces of constant density much as any other tracer. The use of oxidative corrections to derive a quasi-conservative property is not a new concept, and
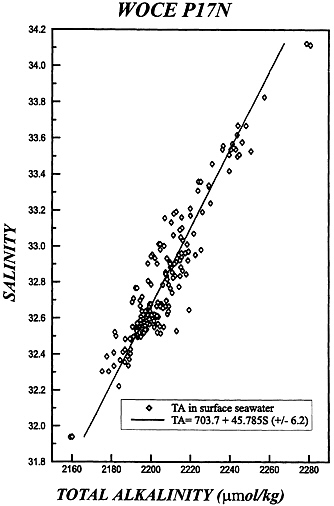
FIG. 2. Correlation between measured values of alkalinity and salinity for surface waters along the WOCE P17N transect. The strong linear correlation is to be expected, and the standard deviation is only ±6 µmol·kg−1.
properties such as “NO” and “PO” for nitrogen and phosphorus have been proposed and used for other purposes (28).
From these two carbonate system properties we can also fully constrain the CO2 system (computing pH and pCO2 and thereby relating the signal to the atmosphere) if we know the thermodynamic constants.
Errors and Sensitivity
Behind this simple scheme lies complexity. Only a few specialists are aware of the details of CO2 chemistry. Let us give some simple examples.
For clarity, we will take as a target a desire to constrain the system to ±10 µatm in pCO2; this represents about 7 years growth in today’s atmospheric signal, and is about 5% of the accumulated fossil fuel change to date. We will see that we may not meet this goal, but it is a useful ready reference point. First, a signal of 10 µatm pCO2 is equivalent to ≈7 µmol·kg−1 in TCO2, and to ≈8 µmol·kg−1 in total alkalinity within the normal range of sea water values. Analytical errors of single samples today are ≈1 µmol·kg−1 in TCO2 and ≈3 µmol·kg−1 in total alkalinity, although improvements are possible.
We need to establish the sensitivity to salinity, and the slope of the alkalinity/salinity line established for surface waters (see Fig. 2) indicates that to constrain the system to ≈10 µatm pCO2 we need to know salinity to ≈0.3%0, which is easily achievable by direct measurement, but a significant problem for remote sensing.
We need to determine the oxygen deficit of subsurface waters; the direct dissolved O2 measurement of deep waters has an error of ≈1 µmol·kg−1 (roughly equivalent to 1 µmol TCO2); however the assumption of atmospheric equilibrium at the time of subduction may not be valid and is very hard to determine. We estimate the error from this source as perhaps 5 µmol·kg−1, equivalent to ≈5 µatm pCO2.
We need to know the Redfield ratio, and this problem was reviewed above. As an aside, we are fortunate that there is very little other chemical ambiguity; species representing the other oxidation states of carbon (e.g., CO and CH4) are present in insignificant quantities. We have shown that the principal correction to total alkalinity, other than carbonate uptake and dissolution, results from changes in the oxidation state of nitrogen and these are well understood; problems of denitrification do occur, but in the Anderson and Sarmiento (25) analysis these are significant only in the range between 1,000 and 3,000 m. The magnitude of other redox changes, such as those from sulfur, are trivial in the oxic ocean.
Oceanic Example
In earlier work (9) on North Atlantic data we have shown significant correlations between the computed invasion term for CO2, and the chlorofluorocarbon (F11) signal. Here we choose, in tribute to Roger Revelle and his love of his home in California, recent data from that region. The data are selected from WOCE Cruise P17N, and the station locations are shown in Fig. 1. We must first determine the correlation between total alkalinity and salinity for this region, and this is shown in Fig. 2. The correlation is remarkable, with a standard deviation of only 6 µmol·kg−1, and it is a tribute to the very careful experimental work accomplished. However, this represents the chemical state of the surface ocean at the time of the observations. The deep waters are formed in late winter at some
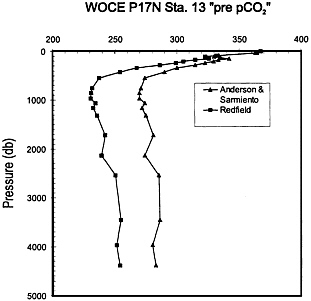
FIG. 3. Specimen calculation of a vertical profile of the partial pressure of CO2 at WOCE P17N Station 13, corrected for the effects of oxidative organic matter decomposition and carbonate dissolution so as to reveal an approximation to the original water mass surface conditions. The corrections resulting from the use of the original (1934) Redfield ratios (17, 18) and the more recent coefficients (1994) of Anderson and Sarmiento (25) are shown: both profiles are computed utilizing the thermodynamic constants of Goyet and Poisson (30). The deep water value of 280 ± 6 ppm given by the Anderson and Sarmiento coefficients is close to the established preindustrial atmospheric level.
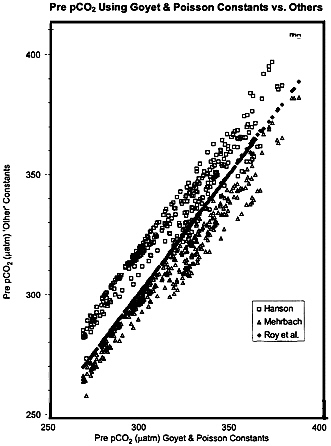
FIG. 4. Comparison of the calculated pCO2 profile from WOCE P17N stations utilizing the thermodynamic constants from several sources. The deep water values are in agreement to about ±10 ppm, but the warmer surface waters show a spread of about ±25 ppm. It is not necessary to use these constants to derive a ∆TCO2 value, but they are required to link calculated changes in oceanic chemical composition to the atmospheric driving signal.
other latitude, and we must find some way of either compensating for this (29) or of estimating the error. Changes due to CaCO3 fluxes are likely to be very small, and the NO3 cycle is likely the dominant concern.
We then simply apply the equations above, and examine the signal. Fig. 3 shows a specimen calculation for WOCE P17N Station 13 off San Francisco. The calculation is run with both the original (1934) Redfield ratio (17, 18) and with the newer (1994) coefficient of Anderson and Sarmiento (25). While the ∆TC function may be calculated without recourse to the thermodynamic constants required for computing the partial pressure, we compute pCO2 here for clarity.
The result shows clearly a consistent signal in the deep water below 500 m close to 280 µatm, and above that depth a rapidly rising signal that converges close to today’s value near the surface. This picture is consistent with all other examinations of this signal and reveals a penetrating tracer related to the fossil fuel perturbation of the chemistry of the upper ocean. Interestingly the original Redfield ratio yields a deep water value about 30 µatm lower than the coefficient of Anderson and Sarmiento (25); we then have to make a value judgment as to the correct signal. In doing so we expose a weakness in our understanding, for although the preindustrial atmosphere and the ocean must have been in gross overall equilibrium, regional disequilibrium in the pCO2 of the deep water at the time of formation is clearly possible. Takahashi et al. (31) have compiled an extensive data set and analysis of seasonal surface ocean pCO2 conditions and find broadly that very large disequilibria do not occur; however, we do not know as well as we would like the initial conditions of water mass formation.
Next we must make a choice of thermodynamic constants to carry out the calculation of pCO2; a recent review is provided by Millero (32). Although work on these constants has proceeded for decades, the choice is still controversial, and as we shall see the differences can be significant.
In Fig. 4 we show results, not just for one station but for the entire WOCE P17N data set, for the initial pCO2 value, calculated with constants from Roy et al. (33), Hansson (34) and Mehrbach et al. (35) relative to the constants of Goyet and Poisson (30). While the deep water values are in agreement to within about ± 10 µatm (close to the target value for discussion in this paper), the surface values with a greater range of temperature and salinity show a spread of about ± 25 µatm; in fact the noise in the estimate resulting from the varying choice of thermodynamic constants for carbonic acid in sea water is about equal to that caused by uncertainty in the Redfield ratio.
The selection of a set of thermodynamic constants for the ocean CO2 system appears in some way at many stages of the variety of experimental protocols and numerical calculations performed by all scientists in this area; there is no uniform international agreement on this, and experimentalists and modelers alike choose their personal preference. It is tempting to conclude from inspecting Fig. 4 that, since oceanic data treated with the constants of Goyet and Poisson (30) and Roy et al. (33) yields closely similar results, then these constants, determined in fully independent experiments, should be preferred. There is, however, not uniform agreement on this point, and it was pointed out in review of this manuscript that if the values for K1 and K2 are considered separately then the apparent agreement is not as good. That is that the impressive agreement shown in Fig. 4 may be the result of a fortunate compensation of positive and negative errors, rather than resulting from absolute accuracy of the values. The net result is that if we are to achieve an increase in our ability to observe
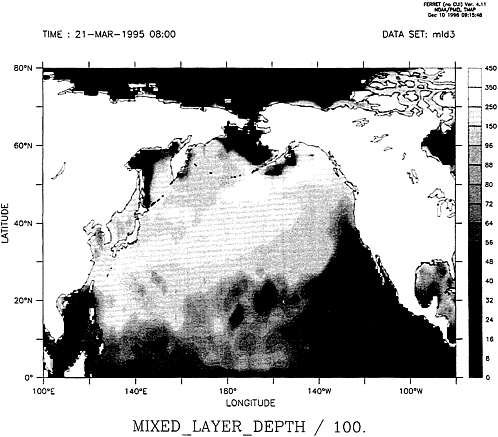
FIG. 5. Image of the calculated mixed layer depth for the North Pacific Ocean for the month of March 1995 from data supplied by the Fleet Numerical Meteorological and Oceanography Center model (37).
and model the oceanic carbon system, then a fundamental improvement in the accuracy of the thermodynamic constants is one of the required steps. This is an exceptionally challenging experimental task.
The calculation of a signal which appears to be very closely related to a direct observation of the accumulated ocean fossil fuel CO2 invasion term, such as the profile given in Fig. 3, seems to be readily achievable. The principal debate is about the levels of accuracy acceptable for such a calculation, and the ultimate goal of integrating the signal on an ocean basin scale and relating the quantities to the global fossil fuel CO2 budget. The subsurface signals revealed are integrals mixed from several water mass sources, and divining the unique surface signature of any one oceanic region will be difficult. Moreover in practice there are strong regional and seasonal sources and sinks of CO2 in the surface ocean, and until we find strategies for dealing with these there will always be room for debate.
Here there is room for optimism; the ability to gain seasonal CO2 data at a remote site has been greatly aided by the recent development of accurate and reliable new sensors that can be mated with buoy technology (36). The ability to predict in real time the mixed layer depth of the ocean has also undergone a revolution through advanced remote observational and computing techniques (37), and the results are now being made available to the civilian community. A specimen global map of calculated mixed layer depths produced by us from data supplied by the Fleet Numerical and Oceanography Center for the month of March 1995, close to the northern hemisphere vernal equinox and probably representing maximum values, is shown in Fig. 5.
Conclusion
The problem of detecting the fossil fuel CO2 signal in sea water is relatively easy. Modifications of the calculation of Brewer (8) or of Chen and Millero (11) all yield a robust signal of about 45 µmol·kg-1 in surface ocean waters today. In the North Pacific Ocean example given here the signal decays with depth, corresponding to the ventilation age of the water masses, and may be traced to about 400-m depth, consistent with deep winter time mixed layer formation in the northwest sector.
The most consistent results are presently obtained by using the oxidative decomposition ratios of Anderson and Sarmiento (25) and the thermodynamic constants of either Goyet and Poisson (30) or Roy et al. (33).
Refining the calculation will require increased knowledge of the Redfield ratio, and of surface winter time total alkalinity values. New sensing and sampling technologies now developed offer every prospect of yielding this information, and of improving estimates of long term ocean CO2 uptake.
The very careful work of the teams of ocean scientists now producing data on the ocean carbon system as part of a coordinated global survey is gratefully acknowledged. This work was supported by a grant to the Monterey Bay Aquarium Research Institute from the David and Lucile Packard Foundation, and by National Aeronautics and Space Administration Grant Earth Observing System (EOS) NAG-232431 to the Woods Hole Oceanographic Institution.
1. Ciais, P. , Tans, P. P. , Trolier, M. , White, J. W. C. & Francey, R. J. ( 1995 ) Science 269 , 1098–1102 .
2. Tans, P. P. , Fung, I. Y. & Takahashi, T. ( 1990 ) Science 247 , 1431–1438 .
3. Tsunogai, S. , Ono, T. & Watanabe, S. ( 1993 ) J. Oceanogr. 49 , 305–315 .
4. Siegenthaler, U. & Sarmiento, J. L. ( 1993 ) Nature (London) 365 , 119–125 .
5. Callendar, G. S. ( 1938 ) Q. J. R. Meteorol. Soc. 64 , 223–240 .
6. Revelle, R. & Suess, H. E. ( 1957 ) Tellus 9 , 18–27 .
7. Oeschger, H. , Siegenthaler, U. , Schatterer, U. & Gugelmann, A. ( 1975 ) Tellus 27 , 168–191 .
8. Brewer, P. G. , ( 1978 ) Geophys. Res. Lett. 5 , 997–1000 .
9. Goyet, C. & Brewer, P. G. ( 1993 ) in Modeling Oceanic Climate Interactions , NATO Series I11 , eds. Willebrand, J. & Anderson, D. L. T. ( Springer , Berlin ), pp. 271–297 .
10. Jones, E. P. & Levy, E. M. ( 1981 ) J. Mar. Res. 39 , 405–416 .
11. Chen, C.-T. & Millero, F. J. ( 1979 ) Nature (London) 277 , 205–206 .
12. Chen, C.-T. ( 1982 ) Deep Sea Res. 29 , 563–580 .
13. Chen, C.-T. ( 1993 ) J. Oceanogr. 18 , 257–270 .
14. Broecker, W. S. , Takahashi, T. & Peng, T.-H. ( 1985 ) Reconstruction of the Past Atmospheric CO2Contents of the Contemporary Ocean: An Evaluation ( U.S. Department of Energy , Washington, DC ), Rep. DOE/OR 857 .
15. Wallace D. W. R. ( 1995 ) Monitoring Global Ocean Carbon Inventories, Ocean Observing System Background Report 5 ( Texas A&M Univ. , College Station ).
16. Bates, N. R. , Michaels, A. F. & Knap, A. H. ( 1996 ) Deep Sea Res. 43 , 347–383 .
17. Redfield, A. C. ( 1934 ) James Johnstone Memorial Volume ( Liverpool Univ. Press , Liverpool, U.K. ), 176–192 .
18. Redfield, A. C. , Ketchum, B. H. & Richards, F. A. ( 1963 ) in The Seas , ed. Hill, M. N. ( Wiley-Interscience , New York ), Vol. 2 , pp. 26–77 .
19. Brewer, P. G. , Wong, G. T. F. , Bacon, M. P. & Spencer, D. W. ( 1975 ) Earth Planet. Sci. Lett. 26 , 81–87 .
20. Brewer, P. G. & Goldman, J. C. ( 1976 ) Limnol. Oceanogr. 21 , 108–117 .
21. Goldman, J. C. & Brewer, P. G. ( 1980 ) Limnol. Oceanogr. 25 , 352–357 .
22. Bradshaw, A. L. , Brewer, P. G. , Shafer, D. K. & Williams, R. T. ( 1981 ) Earth Planet. Sci. Lett. 55 , 99–115 .
23. Takahashi, T. , Broecker, W. S. & Langer, S. ( 1985 ) J. Geophys. Res. 90 , 6907–6924 .
24. Boulahid, M. & Minster, J.-F. ( 1989 ) Mar. Chem. 26 , 133–153 .
25. Anderson, L. A. & Sarmiento, J. L. ( 1994 ) Global Biogeochem. Cycles 8 , 65–80 .
26. Martin, J. H. , Knauer, G. A. , Karl, D. M. & Broenkow, W. W. ( 1987 ) Deep Sea Res. 34 , 267–285 .
27. Brewer, P. G. , Bradshaw, A. L. , Shafer, D. K. & Williams, R. T. ( 1986 ) in The Changing Carbon Cycle: A Global Analysis , eds. Trabalka, J. R. & Reichle, D. E. ( Springer , New York ), pp. 348–370 .
28. Broecker, W. S. ( 1974 ) Earth Planet. Sci. Lett. 23 , 100–107 .
29. Glover, D. M. & Brewer, P. G. ( 1988 ) Deep Sea Res. 35 , 1525–1546.
30. Goyet, C. & Poisson, A. ( 1989 ) Deep Sea Res. 36 , 1635–1654 .
31. Takahashi, T. , Olafsson, J. , Goddard, J. G. , Chipman, D. W. & Sutherland, S. C. ( 1993 ) Global Biogeochem. Cycles 7 , 843–878 .
32. Millero, F. J. ( 1995 ) Geochim. Cosmochim. Acta 59 , 661–677 .
33. Roy, R. N. , Roy, L. N. , Vogel, K. M. , Moore, C. P. , Pearson, T. , Good, C. E. , Millero, F. J. & Campbell, D. M. ( 1993 ) Mar. Chem. 44 , 249–268 .
34. Hansson, I. ( 1973 ) Deep Sea Res. 20 , 461–478 .
35. Mehrbach, C. , Culberson, C. H. , Hawley, J. E. & Pytkowicz, R. M. ( 1973 ) Limnol. Oceanogr. 18 , 897–907 .
36. Friederich, G. E. , Brewer, P. G. , Herlien, R. & Chavez, F. ( 1995 ) Deep Sea Res. 42 , 1175–1186 .
37. Clancy, R. M. & Sadler, W. D. ( 1992 ) Weather Forecasting 7 , 307–327 .






