Proc. Natl. Acad. Sci. USA
Vol. 94, pp. 8335–8342, August 1997
Colloquium Paper
This paper was presented at a colloquium entitled “Carbon Dioxide and Climate Change,” organized by Charles D. Keeling, held November 13–15, 1995, at the National Academy of Sciences, Irvine, CA.
Can increasing carbon dioxide cause climate change?
(global warming/climate sensitivity/climate modeling/greenhouse effect)
RICHARD S. LINDZEN
Building 54, Room 1720, Massachusetts Institute of Technology, Cambridge, MA 02139
ABSTRACT The realistic physical functioning of the greenhouse effect is reviewed, and the role of dynamic transport and water vapor is identified. Model errors and uncertainties are quantitatively compared with the forcing due to doubling CO2, and they are shown to be too large for reliable model evaluations of climate sensitivities. The possibility of directly measuring climate sensitivity is reviewed. A direct approach using satellite data to relate changes in globally averaged radiative flux changes at the top of the atmosphere to naturally occurring changes in global mean temperature is described. Indirect approaches to evaluating climate sensitivity involving the response to volcanic eruptions and Eocene climate change are also described. Finally, it is explained how, in principle, a climate that is insensitive to gross radiative forcing as produced by doubling CO2might still be able to undergo major changes of the sort associated with ice ages and equable climates.
The title suggested for this paper (by Dave Keeling) is tantalizing for its ambiguity. At some level, the answer is philosophically trivial. After all, our knowledge is rarely so perfect that we can say anything is absolutely impossible. In connection with this question we can go a bit further, and state that increasing CO2 is likely to cause some climate change, and that the resulting change will involve average warming of the earth. However, this answer is almost as trivial as the first. The climate is always undergoing change, and if the changes due to increasing CO2 are smaller than the natural variability, then these changes will be of only modest concern except as an exercise in weak signal detection. The more serious question then is do we expect increasing CO2 to produce sufficiently large changes in climate so as to be clearly discernible and of consequence for the affairs of humans and the ecosystem of which we are part. This is the question I propose to approach in this paper. I will first consider the question of whether current model predictions are likely to be credible. We will see why this is unlikely at best. I will then show how we might estimate and bound climate sensitivity both directly and indirectly from existing data. Finally, I will consider the relationship of changes in mean temperature to changes in the structure of climate. It has been suggested that small changes in mean temperature are important because major changes in past climate were associated with major changes in the equator-to-pole temperature difference, but only small changes in the mean temperature. I will argue that the changes in mean temperature may be only residuals of the changes in the meridional temperature distribution rather than the cause.
Current Forecasts
Present projections of the climatic effects of increasing CO2 are based on models of varying degrees of complexity. The relative similarity of all these predictions for the increase in global mean temperature has lent a degree of plausibility to the resulting predictions. We shall, in this section, analyze the nature of these “traditional” results to understand what the physical basis is for the common prediction. In the following section we will examine some of the processes crucial to these predictions to see whether they are known to sufficient accuracy for the purpose of climate predictions. Before doing this, it will be necessary to briefly review the physics of the “greenhouse effect.” Although this process is usually summarized by the assertion that infrared-absorbing gases inhibit the ability of the earth’s surface to emit thermal radiation, and thus force the surface to get warmer, the reality is substantially more complex. Möller and Manabe ( 1 ) made an early start toward understanding this matter. In this one-dimensional study, both radiative and radiative–convective equilibria were calculated using assumed distributions for humidity and cloudiness. The simplistic picture corresponds essentially to radiative equilibrium, for which Möller and Manabe calculated the equilibrium temperature of the surface to be about 350 K, which is 95 K warmer than the black-body temperature of 255 K. When convection is included by introducing a simple convective adjustment, the surface temperature comes down to the observed value of 288 K. Convective adjustment reduced the greenhouse effect by about 75%, by allowing for the fact that radiation is not the only form of heat transfer in the atmosphere. When infrared opacity is high, evaporation and mechanical transport are more efficient ways for the surface to cool. Lindzen ( 2 ) offered a more complete schematic of the realistic operation of the natural greenhouse effect. One begins by recognizing that water vapor, the atmosphere’s main greenhouse gas, decreases in density rapidly with both height and latitude. Surface radiative cooling in the tropics, which has the highest concentration of water vapor, is negligible. Heat from the tropical surface is carried upward by cumulus convection and poleward by the Hadley circulation and planetary-scale eddies to points where radiation can more efficiently transport the heat to space. Where radiation can more efficiently carry the heat depends on the radiative opacity and the motions themselves. In point of fact, without knowing the dynamical heat fluxes, it is clear that one cannot even calculate the mean temperature of the earth. It is interesting, in this regard, to look at model intercomparisons of meridional heat flux, and their comparison with observationally based estimates. An extensive study ( 3 ) shows that such differences reach 2 PW (petawatts). As shall be noted later, this is roughly equivalent to differences in vertical fluxes of about 25 W·m-2—much larger than the 4 W·m-2 change that a doubling of CO2 is expected to produce. A particularly acute example of the problem with dynamic fluxes is revealed when one couples
|
|
© 1997 by The National Academy of Sciences 0027-8424/97/948335-8$2.00/0 PNAS is available online at http://www.pnas.org. |
models for the atmosphere with ocean models. Here, theclimate tends to drift unless one applies so-called flux corrections. Examples of such corrections are given for all the leading models ( 4 ). The corrections have to be applied on a latitude-by-latitude basis, and the magnitude of the correction can be as large as 100 W·m-2. As can be understood from our discussion of the realistic nature of the greenhouse effect, these dynamic fluxes do not represent systematic biases independent of the CO2 forcing; rather they are essential to calculating the response to increased CO2. The issue is not that the forcing due to CO2 is buried within these larger uncertainties, but rather whether we can reckon the response reliable.
The role of water vapor is nonlinear. Assuming 80% relative humidity in a 2-km boundary layer, and a fixed relative humidity above the boundary layer, Fig. 1 shows how, for a given temperature distribution, outgoing long-wave radiative flux varies as one perturbs the relative humidity above the boundary layer [ Fig. 1 was calculated using the radiative transfer code ( 5 ); a similar calculation appears in ref.6 ]. One sees that the effect of a 5% change in relative humidity depends on the base humidity being perturbed. For low base humidities, a 5% change is associated with about 5 W·m-2. For high base humidities, the change is about half of this. For purposes of comparison, the 4 W·m-2, which a doubling of CO2 is expected to produce, is roughly equivalent to a 4–8% change in relative humidity. Note that uncertainties in measurements of humidity are on the order of 20% or more, though things appear to have improved over the past 2 years. We shall look at the improved data soon. However, it is again clear that we are dealing with uncertainties and errors that are large compared with the climatic impact of CO2. Here too, these errors occur in a field that is crucial to calculating the response to CO2, since the water vapor feedback is essentially responsible for the model predictions of large warming due to increasing CO2. Clearly, even superficial agreement between observations and model-derived water vapor would be inadequate to establish the model feedback.
This potentially important positive feedback was first identified by Manabe and Wetherald ( 7 ). Using a simple one-dimensional radiative–convective model, they found that assuming constant relative humidity led to a significantly enhanced response to increased CO2 over what would have been obtained with fixed specific humidity. The point, simply, is that with fixed relative humidity, specific humidity must increase with warming. Upper-level water vapor (above 2–3 km in the tropics) dominates the radiative role of water vapor, despite the fact that most of the atmosphere’s water vapor is found below 800 millibars [1 millibar (mb) = 100 Pa] ( 8 ). Of course, given the nonlinearity of the radiative effect of water vapor, the average radiative response to water vapor is not equal to the response to an average water vapor, and, therefore, one-dimensional studies are inappropriate. However, the results of the above one-dimensional studies remain indicative of general properties.
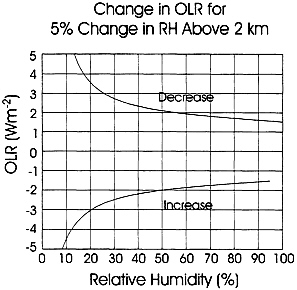
FIG. 1. The changes in outgoing long-wave radiation (OLR) for increase and decrease of 5% in relative humidity above 2 km as a function of the unperturbed relative humidity.
The most useful way of viewing feedbacks is by means of the formula
where fi is the ith feedback factor. For fixed relative humidity, the water vapor feedback factor is about 0.4. This turns out to be much larger than the factors due to clouds and snow in present models. However, as may be seen from the formula, the addition of smaller factors on top of the 0.4 due to water vapor rapidly increase the response. Without the water vapor feedback the impact of model cloud and snow feedbacks would be small ( 2 ).
It is worth reviewing the basis for the assumption of constant relative humidity in ( 7 ). It is based on the crudely observed picture from ref. 9 reproduced in Fig. 2 . It was argued in ( 7 ) that the overall relative humidity varied only between about 30% and 50%, and that the pattern was similar for both winter and summer, suggesting that the atmosphere was attempting to maintain a given relative humidity regardless of temperature. There were, of course, very few measurements available for ref. 9. However, subsequent analyses of radiosonde data showed a fairly similar picture ( 10 ). Unfortunately, the radiosonde data have proven extremely unreliable ( 11 ). In particular, radiosonde data tended to replace readings of very low humidity with relative humidities of 20%. Nevertheless, these primitive observations received a certain amount of credibility insofar as they were consistent with humidities predicted in general circulation models (GCMs). However, recently, the 183-GHz channel on the SSM/T-2 satellite has provided detailed data on the global distribution of relative humidity. Fig. 3 shows a global daily map for relative humidity between 500 and 300 mb for May 5, 1995. We see hugely more variability
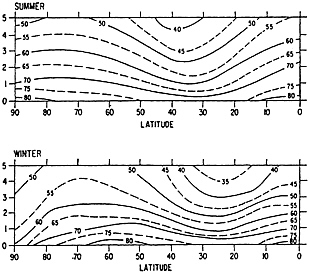
FIG. 2. Latitude (in deg)-height (in km) distribution of relative humidity for both summer and winter (taken from ref. 9).

FIG. 3. Relative humidities in the layer 500–300 mb derived from 183-GHz soundings from SSM/T-2 for May 5, 1995. The color scale for relative humidity is shown below the panel. Figure provided by R. Spencer, National Aeronautics and Space Administration/Huntsville (personal communication).
than was suggested in ref. 9. We also see confined moist regions associated with active convection and comparatively rapid transitions to extremely dry regions away from the convection. Incidentally, this observation resolves a problem in ref. 12, where, in studying the moisture budget of the tropical troposphere, it was found that it was impossible to account for the humidities observed by radiosondes in clear subsiding regions. The satellite data show that these regions are, indeed, dry. Some indication of why current models misrepresent the vertical distribution of humidity is given in ref. 13, where the authors calculated the correlations of interannual variability of humidity at various levels with the variability at the surface for both traditional radiosonde data and for the output of a Geophysical Fluid Dynamics Laboratory (GFDL) GCM. The results are shown in Fig. 4 . In the data, upper-level humidity rapidly decorrelates from surface humidity, while in the model all levels are highly correlated. This strongly points to the likelihood of strong artificial coupling of levels in this model. Judging from the results in ref. 14, similar problems are likely in the Goddard Institute for Space Studies (GISS) model, and they appear to be independent of the choice of convective parameterization. To be sure, there are the already-mentioned problems with radiosonde data which are discussed in detail in ref. 15. Current radiosonde data are much better (though they still display a moist bias in dry regions) and show the decoupling of water vapor behavior above and below the trade inversion much better. Fig. 5 illustrates this. Models also show a tendency to underestimate humidity in moist regions and to overestimate it in dry regions ( 16 ).
There are potential problems with the vertical distribution of temperature as well. For simple radiative convective models, the vertical profile of temperature in the troposphere is essentially fixed. Thus, the response to tropopause level forcing from doubled CO2 must consist in warming throughout the troposphere, including the surface. In principle, warming at the top of the troposphere (without warming at the surface) would be sufficient to balance the forcing. Data indicate a significant degree of independence for temperature changes at different levels ( 17 ). Of course, GCMs do not explicitly assume rigid vertical coupling of temperature in the troposphere; however, it is possible that coupling is stronger than in nature.
The above-described problems with heat fluxes and humidity, as well as the potential problems with vertical structure of temperature, all serve to render model feedbacks extremely uncertain. In view of these problems, it is important to
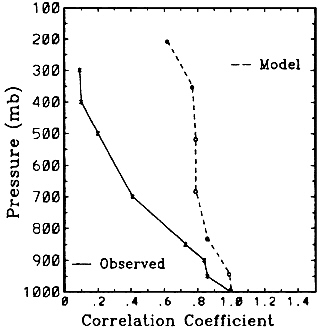
FIG. 4. Correlation of interannual variations in specific humidity with interannual variations in specific humidity at the surface as observed in radiosonde data, and as calculated in a GFDL climate model forced by observed variations in sea surface temperature. [Reproduced with permission from ref. 13(Copyright 1996, American Meteorological Society).]
consider whether there are alternative approaches to determining climate sensitivity.
Observational Determinations of Climate Sensitivity
The purpose of the present section is to assess various approaches to using data to infer climate sensitivity, given that current GCMs are unlikely to be adequate for this task.
Direct Approach. As already noted, a doubling of CO2 is generally taken to imply a forcing at the tropopause of about 4 W·m−2. The question of climate sensitivity amounts to asking how much must the earth’s surface warm to compensate for this forcing. A simplistic approach to the question of climate sensitivity would be to study the temporal variation of globally integrated OLR with varying globally averaged temperature. The ratio of the temperature variations to the variations in OLR would represent the climate sensitivity. However, a priori, naturally occurring changes in global mean temperature on time scales of from weeks to years may not form proper surrogates for warming due to increased CO2 ( 18 ). Another problem with this approach is that OLR is not the sole contributor to the radiative response. In principle, we should look at the change in total radiative flux at tropopause levels. For the tropics, however, OLR in clear sky regions appears to be the dominant contributor to the total flux change ( 19 ). Still another part of the problem is that naturally occurring changes in mean temperature on these time scales are significantly associated with changing regional patterns of warming rather than global warming ( 20 ). Insofar as the water vapor feedback is involved in climate sensitivity, Fig. 1 shows that moisture changes in dry regions are much more important than changes in moist regions. A global change involving an intensification or reduction of existing differences between moist and dry regions can lead to a change in OLR even in the absence of change in mean temperature. It will clearly be necessary to distinguish such changes from those specifically associated with changes in the mean temperature. It should be noted that changing patterns can be associated with changes in circulation and changes in temperature, both of which play a role in the moisture budget ( 12 ). Fig. 3 , in fact, suggests the interesting possibility that the primary feedback process might consist in the change in areal coverage of the very dry regions. Presumably, natural variations include a full range of such possibilities so that observed ratios of average temperature variations to variations in total OLR would show a significant scatter. A primary problem associated with the direct measurement of climate sensitivity will be to distinguish changes in flux associated with changes in mean temperature from those associated with pattern changes not associated with changes in the mean temperature. There is, moreover, no assurance that all changes in mean temperature will be appropriate surrogates for global warming.
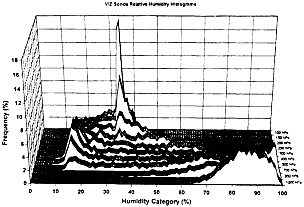
FIG. 5. Histograms of relative humidity at different pressure levels obtained from recent radiosondes at near equatorial stations. Figure provided by R. Spencer (personal communication).
The question of the sensitivity of tropical temperature is an important matter in its own right. In particular, the tropics have distinctly different basic physical balances from those in the extratropics ( 21 ). Tropical sensitivity is also an important factor in global sensitivity. GCM results characteristically indicate no special difference between tropical and extratropical sensitivity to a doubling of CO2. This is seen in Fig. 6 . Although there is enhanced response at polar latitudes, the response is relatively flat from the equator to about 40°. While there are reasons to suppose that the model response in the tropics is excessive, this has been widely argued about and is not essential to the present discussion; it will, however, be important for the discussion in the next section. What is relevant here is that the changing tropical sensitivity has a profound effect on the response to increased CO2 globally. In calculations performed with the Center for Oceans, Land, Atmosphere GCM, it was found that constraining surface temperature in small regions of the tropics was sufficient to substantially reduce the globally averaged response ( 23 ). Moreover, recent work ( 24 ) leads one to conclude that models underestimate the degree of mixing from the tropics to the extratropics, and hence may underestimate the effect of the tropics on the extratropics. In general, therefore, reduced tropical sensitivities will imply reduced global sensitivity, though the extent of the reduction may well be greater than indicated in ref. 23, since models appear to understate the degree of coupling between the tropics and extratropics.
In dealing with the climate sensitivity of the tropics, we are dealing with the sensitivity of a system open not only to changes in top of atmosphere (TOA) radiative forcing but also to changes in meridional flux. This is illustrated in Fig. 7. Sensitivity would essentially be the ratio of average tropical temperature change to change in total flux. However, for the meridional flux, we can be reasonably confident that for increasing temperature, ∆F meridional ≥ 0, provided that we are considering zonal averages over the whole tropics. In this case, if we include only TOA flux changes, we will get an upper bound for sensitivity, as is readily seen from Eq. 2:
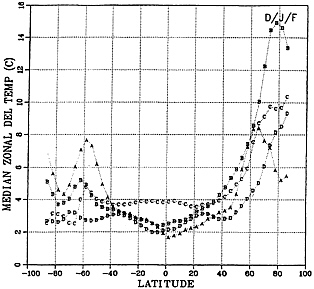
FIG. 6. Meridional distributions of zonally averaged change in surface air temperature due to a doubling of CO2 for December, January, February (A, Community Climate Model; B, GFDL; C, GISS; D, Oregon State University). From ref. 22.
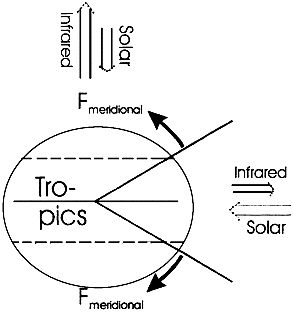
FIG . 7. Schematic illustration of the fluxes relevant to the heat budget of the tropics.
If the average is over only a sector of the tropics, we have no such assurance. This is one of the main problems in ref. 19. The results there are nonetheless both suggestive and instructive. Chou used Earth Radiation Budget Experiment data to assess the changes in net flux over the region (-30° = latitude = +30°, -100° = longitude = +100°) between April 1987 (a warm El Niño year) and April 1985 (a colder La Niña year). The average surface temperature for the region he examined was about 0.3°C warmer in 1987 than in 1985. The change in net flux was about 4 W·m-2. This flux change was almost entirely due to OLR over clear sky regions (as opposed to clear sky OLR, which commonly refers to the calculated OLR that would occur in the absence of clouds). The changes over cloudy regions were dominated by clouds whose infrared and visible effects tended to cancel to a large extent locally, but to an important extent there is also cancellation between different regions. As we see from Fig. 3 , clear sky regions tend to be very dry. The radiative response must be due to drying over these regions, and this is consistent with Chou’s results, which show that the flux changes are almost exclusively restricted to the subsiding region of the Pacific. The explicit drying of already dry regions appears to be more important than net drying. Indeed, there can be moistening of already moist regions and even net moistening while still having a negative water vapor feedback. Taken at face value, this suggests a very low sensitivity for the tropics compared with most GCMs, where a change of about 2°C is associated with 4 W·m-2. Using Eq. 1, this would imply a water vapor feedback factor of about -2 rather than + 0.4, which is typical of current models. However, given that Chou considered only a sector, we do not know if this is an over- or underestimate of the actual tropical sensitivity, since feedbacks require a consideration of complete systems including both convective and subsiding regions, and limited sectors include unknown proportions of each. Indeed, consideration of other months and years can even lead to apparent feedbacks of opposite sign for such limited regions. We also are unable to distinguish pattern changes not directly related to mean temperature from changes that are. It is nonetheless useful to examine any differences between GCM-generated TOA flux changes and those found by Chou for runs using the same sea surface temperatures used by Chou. A preliminary attempt has been made in ref. 25, focusing only on OLR and using the Atmospheric Model Intercomparison Program’s data for various GCMs. This is by no means a test of sensitivities. However, it does provide some information on how a very important component of sensitivity is replicated in models. The results demonstrate that most models overestimated the observed “sensitivity” appreciably (though one, in fact, underestimated it). However, this work did not check in detail as to how much of the difference was due to errors in pattern or to water vapor feedbacks directly, nor did it focus on the OLR in clear regions which dominated Chou’s results. In particular, it would appear from Fig. 4 that a very important consideration ought to be how dry and how large the areal coverage is of the very dry subsiding regions. One important methodological point which emerged from Covey’s study ( 25 ) was that model results for regional “sensitivity” varied pronouncedly from the models’ global sensitivity, indicating rather clearly that what Chou was observing was not global sensitivity. Such a situation is not remedied by considering the statistics of many month pairs as opposed to the use of a single pair by Chou.
Despite the problems in ref. 19, it does point the way toward a proper observational determination of the sensitivity to global forcing. It would consist, at best, in the measurement of the complete TOA flux integrated over the whole earth (averaged over, say, a month) for several years, and the measurement of surface temperature over the same period. One would form the pattern correlation of temperature for each pair of months in the record, as well as the average rms difference of the temperatures and the difference of the globally averaged temperatures. By sorting according to these three quantities, one might, hopefully, be able to disentangle the dependence of flux on both patterns and mean temperature. Presumably the latter would be indicative of the climate sensitivity we are seeking. Comparing pairs of months separately would avoid the problems in averaging associated with the nonlinearity of the effect of water vapor. Performing such a study for tropical latitudes separately would allow some insight into the physical origins of the sensitivity. Of, course, there would remain the problem of whether states differing only in mean temperature formed proper surrogates for global climate change. There is also the problem that total insolation varies with an annual cycle due to the varying distance of the earth from the sun. This may require that comparisons be restricted to the interannual variability of each month. However, none of the quantities needed for such a study require any truly new instruments. Indeed, it appears that the needed data may be marginally available from existing satellites and surface data. The necessary length of record will likely be determined by the need to obtain sufficiently large numbers of month pairs to populate all relevant possibilities. This number of appropriate month pairs is greatly reduced if one cannot find a suitable correction for the varying solar distance. A caveat that requires some consideration is the obvious fact that Chou’s results ( 19 ) suggest how it is possible for OLR to change in response to changes in circulation without accompanying changes in mean temperature. If our question is how much must the earth’s temperature change to compensate for 4 W·m-2 forcing, then Chou’s results show that it is at least physically possible for such compensation to occur without net warming. This should alert us to the possibility that simple definitions of climate sensitivity are by no means guaranteed to be relevant.
It should be mentioned that there have been attempts other than Chou’s to directly measure climate sensitivity. Unfortunately, these generally assumed that local or seasonal changes in temperature could be considered as surrogates for climate change. However, as noted in ref. 12, the warmest regions are associated with convection and high upper level humidities, while dry subsiding regions are associated with cooler temperatures regardless of feedbacks. Thus, a study like that of Raval and Ramanathan ( 26 ) inevitably shows a positive cor-
relation of surface temperature and “enhanced” greenhouse effect. Indeed, should there be a strong negative feedback associated with enhanced drying in subsiding regions (and/or expanded dry regions), such an approach would indicate a spuriously increased water vapor feedback. (This, itself, might lead to a useful test.) A similar problem pertains to the study by Rind et al. ( 27 ). They compared the summer tropics with the winter tropics. However, the summer tropics are associated with ascending moist air, while the the winter tropics are associated with dry subsiding air—again independent of the actual feedback.
Indirect Approach: Volcanic Sequences. It has long been noted that volcanic veils provide a short-term perturber of global temperature. Whether, the climatic response to such perturbations provides a test of climate sensitivity is less clear. The problem was addressed crudely in ref. 28. In that paper, a simple energy balance climate model with a box-diffusion ocean was used. The ocean was taken to have an insulated boundary at 300 m to simulate the effect of upwelling and avoid the problems associated with unbounded oceans. Climate sensitivity was specified. Volcanic veils were assumed to set up within 3 months of eruption and decay with an exponential decay time of 13 months. Diffusion, in such models, is a surrogate for all the processes in real oceans that couple the mixed layer with the thermocline. The coefficient is chosen to match chemical tracer data. This is, of course, extremely crude, but might be adequate for global response to global forcing. Using such a model, it was noted that the response to a volcano during the first 2 years following eruption was, given the uncertainties in both temperature measurements and aerosol optical properties, unable to distinguish between sensitivities ranging (in terms of the equilibrium response to double CO2) from 0.15°C to 6°C. In this connection, it should be noted that a study of the response of the GISS GCM to Pinatubo did mention that it was only a test of the short-term physics in their model ( 29 ). Recently, C. Giannitsis and I have recalculated the response to volcanos with a model that, at least, distinguishes land and sea, tuning the coupling between the two by using the seasonal cycle (R.S.L. and C. Giannitsis, unpublished work). The results, for the purposes of this discussion, are similar to those reported in ref. 28 in that a reasonable correspondence between calculated response and observed response is obtained for a wide range of sensitivities, at least for the first 2 years following eruption. For longer periods, there is an interesting dependence on sensitivity. For low sensitivities, the response rapidly decays to essentially zero. However, for higher sensitivities, there is a rapid decay of the response to about 30% of the maximum response, with the remainder decaying on the ocean response scale, which is very long. The reason for this difference is that climate sensitivity is also a measure of how tightly air and sea temperatures are coupled. High sensitivity is associated with weak coupling, allowing the establishment of significant disequilibration of the sea surface temperature. This was noted in detail in ref. 31. As a practical matter, 30% of the peak response is too small relative to natural variability to be detected. However, it was suggested in ref. 28 that a sequence of strong volcanos occurring over several decades would produce a measurably different response for different sensitivities. Such a sequence did occur between Krakatoa in 1883 and Katmai in 1912, with a noticeable absence of large eruptions until the 1950s. Of course, there is a great deal of uncertainty over the exact strength of the forcing due to these volcanos. Our results were based on what we believe to be the conservative assumption that Krakatoa was no stronger than Pinatubo. The results show that for sensitive climates (>0.6°C for a doubling of CO2), each volcano builds on the residual base of earlier volcanos leading to a substantial long-term cooling (≈0.5°C between 1883 and 1912). For low sensitivity, the response consists in a sequence of essentially independent “blips.” The observed temperature record certainly shows nothing more than isolated “blips.” Given the uncertainties in the volcanic forcing, it would be inappropriate to place undue confidence in this result. However, it is consistent with low sensitivity. The results stem from the long response time associated with large sensitivity, and argue for short response times. It is also possible to reduce response times by assuming lower ocean heat diffusivity. However, this gives rise to larger discrepancies between predictions and observations of temperature change over the past century. The commonly claimed “broad consistency” depends on long ocean delays.
Indirect Approach: Eocene. Fig. 6 suggests another possibility for the indirect estimate of tropical sensitivity. Pastclimates involved marked changes in the equator-to-pole temperature difference. In the case of ice ages, this difference may have been due in part to the increased meridional gradient in radiative forcing due to the increased high-latitude albedo associated with the ice itself. This renders difficult the specification of the forcing that was acting on the tropics. However, for warmer climates, like that of the Eocene, the change in albedo from the present may not have been large, and the reduced equator-to-pole temperature difference almost certainly called for an increased heat flux out of the tropics. At present, this flux is about 5 PW, of which the ocean contributes about 1 PW ( 10 ). It may be estimated that a reduction of the equator-to-pole temperature difference from about 40°C to 20°C will require that the present flux be increased to about 6 PW. Although it is currently popular to seek such changes as arising from shifts in ocean circulation, they can also arise quite readily from changes in atmospheric heat flux. The strength of forcing of atmospheric eddies depends not only on the meridional gradient of radiative forcing but also on the intensity of the tropical Hadley circulation, which supplies the momentum to the unstable subtropical jet. The latter is strongly influenced by both orbital parameters and the distribution of land and sea ( 2 , 32 ), both of which were almost certainly different during the Eocene. Such forcings are potentially much larger than one expects from the net external radiative forcing (especially from orbital variations), and do not, in fact, call for net average external forcing. In any event, a positive ∆F meridional of about 1 PW is equivalent to a ∆FTOA of about 12 W·m−2 for the tropics. This ought to have cooled the tropics, and, indeed, early estimates of Eocene equatorial temperatures indicated that the tropics may have been as much as 5°C cooler than they are today. This is only modestly less than current model sensitivity. However, recent corrections to these early estimates have reduced the equatorial cooling to less than 1°C ( 33 ), which is more in line with the sensitivity estimates based on the sequence of volcanos around the turn of the past century. The response in the extratropics is consistent with meridional temperature structure being significantly determined by dynamic processes rather than detailed radiative responses at each latitude ( 34 , 35 ). Again, there are legitimate questions about this procedure, not the least of which concern the reliability and representativeness of the paleoclimatic data. The role of potentially higher levels of CO2 during the Eocene could have contributed to reduced equatorial cooling, though current assessments ( 36 ) suggest that CO2 levels during the Eocene were only double present values, and such changes would cancel only 4 W·m−2.
The Nature of Past Climate Change
The primary variable in most global warming discussions is global mean temperature. The suggested values for change on the order of 2°C do not, on the face of it, seem catastrophic. However, it is commonly noted that major changes in past climate were, in fact, associated with relatively small changes in global mean temperature, but that the global changes were well correlated with changes in the mean. The basis for these
claims is essentially Fig. 8 , which is based on ref. 37 but is generally attributed to ref. 38. What is shown in this figure is the meridional distribution of surface temperature for various past climates scaled by the change in global mean temperature. The fact that temperatures so scaled seem to lie on a single curve has led to the conclusion that mean temperature determines the meridional distribution uniquely. However, the “universality” of the relation is almost certainly an artifact of the fact that equatorial temperature changes are, according to this curve, very small. Thus, climate changes involving primarily changes in the equator-to-pole temperature difference will inevitably scale approximately with the mean temperature, since changes in the mean temperature are simply a residual of the changes in the equator-to-pole temperature when equatorial temperatures are approximately fixed. If, as suggested by GCM results in Fig. 6 , equatorial temperature changes are not much smaller than extratropical changes, then the “universality” of the curve in Fig. 8 would disappear. In either case, we no longer have any direct relation between global mean temperature and overall climate. This is consistent with the fact that we have no convincing mechanism whereby changes in mean temperature automatically determine the changes in meridional heat flux. At the same time, we do have mechanisms for changing the meridional heat flux even in the absence of changes in the mean external radiative forcing ( 32 ). In view of the above, there appears to be little reason to assume the modest changes in mean temperature that are claimed for increased CO2 will automatically be associated with major global climate change. Similarly, there is no reason to suppose that a climate insensitive to changing CO2 cannot, nonetheless, undergo profound climate change.
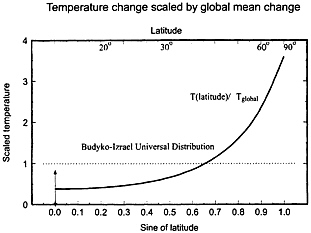
F IG . 8. Universal latitude variation of climate change. Based on ref. 37 .
Conclusion
The brief conclusion of this paper is that current GCMs are inadequate for the purpose of convincingly determining whether the small changes in TOA flux associated with an increase in CO2 are capable of producing significant climate change. However, we may not be dependent on uncertain models to ascertain climate sensitivity. Observations can potentially directly and indirectly be used to evaluate climate sensitivity to forcing of the sort produced by increasing CO2 even without improved GCMs. The observations needed for direct assessment are, indeed, observations that we are currently capable of making, and it is possible that the necessary observations may already be in hand, though the accuracy requirements may be greater than current data provide. Still, the importance of the question suggests that such avenues be adequately explored. Since the feedbacks involved in climate sensitivity are atmospheric, they are associated with short time scales. Oceanic delays are irrelevant, since observed surface temperatures are forcing the flux changes we are concerned with. The needed length of record must be determined empirically. Indirect estimates, based on response to volcanos, suggest sensitivity may be as small as 0.3–0.5°C for a doubling of CO2, which is well within the range of natural variability. This is not to suggest that such change cannot be detected; rather, it is a statement that the anticipated change is well within the range of what the earth regularly deals with. It is further noted that the common assertion that even small changes in mean temperature can lead to major changes in climate distribution is ill-founded and, likely, wrong.
Work reported here was done cooperatively with E. Schneider, C. Giannitsis, and D. Kirk-Davidoff. This work was supported by Grant 914441-ATM from the National Science Foundation and Grant NAGW 525 from the National Aeronautics and Space Administration. Ten percent of this research was funded by the U.S. Department of Energy’s National Institute of Global Environmental Change (NIGEC) through the NIGEC Northeast Regional Center at Harvard University (Department of Energy Cooperative Agreement DEFC03–90ER61010) and through the Computer Hardware, Advanced Mathematics and Model Physics program. Financial support does not constitute an endorsement by the Department of Energy of the views expressed in this article.
1. Möller, F. & Manabe, S. ( 1961 ) Z. Meteorol. 15 , 3–8 .
2. Lindzen, R. S. ( 1993 ) Annu. Rev. Fl. Mech. 26 , 353–378 .
3. Gleckler, P. J. , Randall, D. A. , Boer, R. , Colman, G. , Dix, M. , Galin, V., Helfand, M. , Kiehl, J. , Kichl, A. , Kitch, A. , Lau, W. , Liang, X.-Z. , Lykossov, V. , McAvaney, B. , Miyakoda, K. & Planton, S. ( 1994 ) Cloud-Radiative Effects on Implied Oceanic Energy Transports as Simulated by Atmospheric General Circulation Models , Report No. 15 of the Program for Climate Model Diagnostics and Intercomparisons ( Lawrence Livermore Radiation Laboratory , Livermore, CA ).
4. Gates, W. L. , Cubasch, U. , Meehl, G. , Mitchell, J. & Stouffer, R. ( 1993 ) An Intercomparison of Selected Features of the Control Climates Simulated by Coupled Ocean-Atmosphere General Circulation Models ( World Meteorological Organization , Geneva ), Publ. WMO/TD-No. 574 .
5. Chou, M. D. , Krats, D. P. & Ridgway, W. ( 1991 ) J. Climate 4 , 424–437 .
6. Thompson, S. L. & Warren, S. G. ( 1982 ) J. Atmos. Sci. 39 , 2667–2680 .
7. Manabe, S. & Wetherald, R. T. ( 1967 ) J. Atmos. Sci. 24 , 241–259 .
8. Shine, K. P. & Sinha, A. ( 1991 ) Nature (London) 354 , 382–384 .
9. Telegadas, K. & London, J. ( 1956 ) A Physical Model of Northern Hemisphere Troposphere for Winter and Summer ( Research Div. College of Engineering , New York Univ., New York ), Scientific Report No. 1, Contract AF19(122)-165 .
10. Peixoto, J. P. & Oort, A. H. ( 1992 ) Physics of Climate ( Am. Inst. Phys. , New York ).
11. Elliot, W. P. & Gaffen, D. J. ( 1991 ) Bull. Am. Meteorol. Soc. 72 , 1507–1520 .
12. Sun, D.-Z. & Lindzen, R. S. ( 1993 ) J. Atmos. Sci. 50 , 1643–1660 .
13. Sun, D.-Z. & Held, I. M. ( 1996 ) J. Clim. 9 , 665–675 .
14. DelGenio, A. D. , Lacis, A. A. & Ruedy, R. A. ( 1991 ) Nature (London) 351 , 382–385 .
15. Wade, C. G. ( 1994 ) J. Atmos. Ocean. Tech. 11 , 687–700 .
16. Schmetz, J. & van de Berg, L. ( 1994 ) Geophys. Res. Lett. 21 , 573–576 .
17. Lee, W.-J. & Mak, M. ( 1994 ) J. Atmos. Sci. 51 , 2137–2144 .
18. Lindzen, R. S. , Kirtman, B. , Kirk-Davidoff, D. & Schneider, E. ( 1994 ) J. Climate 8 , 1681–1684 .
19. Chou, M.-D. ( 1994 ) J. Climate 7 , 1684–1692 .
20. Wallace, J. M. , Zhang, Y. & Renwick, J. A. ( 1995 ) Science 270 , 780–783 .
21. Lindzen, R. S. ( 1991 ) Prospects for Tropical Modeling, Proceedings of the European Centre for Medium-range Weather Forecast Conference on Tropical Meteorology, Reading (internal report, available from ECMWF, Shinfield Park, Reading RG2 9AX, U.K.) .
22. MacCracken, M. C. & Luther, F. M. , eds. ( 1991 ) Projecting the Climatic Effects of Increasing Atmospheric Carbon Dioxide ( U.S. Dept. of Energy
, Washington, DC ), pp. 280–319 (available as NTIS, DOE ER-0237 from Natl. Tech. Inf. Service, Springfield, VA) .
23. Schneider, E. K. , Lindzen, R. S. & Kirtman, B. P. ( 1997 ) J. Atmos. Sci. , in press.
24. Stone, P. H. & Nemet, B. ( 1996 ) J. Atmos. Sci. 53 , 1663–1674 .
25. Covey, C. ( 1995 ) Correlation Between Outgoing Longwave Radiation and Surface Temperature as a Measure of Climate Sensitivity: A Model Intercomparison , Report No. 30 of the Program for Climate Diagnostics and Model Intercomparisons (Lawrence Livermore Radiation Laboratory, Livermore, CA) .
26. Raval, A. & Ramanathan, V. ( 1989 ) Nature (London) 342 , 758–761 .
27. Rind, D. , Chiou, E. W. , Chu, W. , Larsen, J. , Oltmans, S. , Lerner,J. , McCormack, M. P. & McMaster, L. ( 1991 ) Nature (London) 349 , 500–503 .
28. Lindzen, R. S. ( 1995 ) in Natural Climate Variability on Decadeto-Century Time Scales , ed. Martinson, D. G. ( National Acad. Press , Washington, DC ), pp. 182–186 .
29. Hansen, J. , Lacis, A. , Ruedy, R. & Sato, M. ( 1992 ) Geophys. Res. Lett. 19 , 215–218 .
30. Budyko, M. I. & Izrael, Y.A. ( 1991 ) in Anthropogenic Climate Change , eds. Budyko, M. I. & Izrael, Y. A. ( Univ. Arizona Press , Tucson ), pp. 277–318 .
31. Hansen, J. , Russell, G. , Lacis, A. , Fung, I. & Rind, D. ( 1985 ) Science 28 , 857–859 .
32. Lindzen, R. S. & Pan, W. ( 1994 ) Clim. Dyn. 10 , 49–57 .
33. Zachos, J. C. , Stott, L. D. & Lohmann, K. C. ( 1994 ) Paleoceanography 9 , 353–387 .
34. Stone, P. H. ( 1978 ) J. Atmos. Sci. 35 , 561–571.
35. Sun, D.-Z. & Lindzen, R. S. ( 1994 ) J. Atmos. Sci. 51 , 757–772 .
36. Sinha, A. & Stott, L. D. ( 1994 ) Global and Planetary Change 9 , 297–307 .
37. Hoffert, M. I. & Covey, C. ( 1992 ) Nature (London) 360 , 573–576 .








