Proc. Natl. Acad. Sci. USA
Vol. 95. pp. 5872–5879, May 1998
Colloquium Paper
This paper was presented at the colloquium “Computational Biomolecular Science,” organized by Russell Doolittle, J.Andrew McCammon, and Peter G.Wolynes, held September 11–13, 1997, sponsored by the National Academy of Sciences at the Arnold and Mabel Beckman Center in Irvine, CA.
A statistical mechanical model for β-hairpin kinetics
VICTOR MUN̄OZ,* ERIC R.HENRY, JAMES HOFRICHTER, AND WILLIAM A.EATON*
Laboratory of Chemical Physics, Building 5. National Institute of Diabetes and Digestive and Kidney Diseases. National Institutes of Health, Bethesda. MD 20892–0520
ABSTRACT Understanding the mechanism of protein secondary structure formation is an essential part of the protein-folding puzzle. Here, we describe a simple statistical mechanical model for the formation of a β-hairpin, the minimal structural element of the antiparallel β-pleated sheet The model accurately describes the thermodynamic and kinetic behavior of a 16-residue, β-hairpin-forming peptide, successfully explaining its two-state behavior and apparent negative activation energy for folding. The model classifies structures according to their backbone conformation, defined by 15 pairs of dihedral angles, and is further simplified by considering only the 120 structures with contiguous stretches of native pairs of backbone dihedral angles. This single sequence approximation is tested by comparison with a more complete model that includes the 215possible conformations and 15×215possible kinetic transitions. Finally, we use the model to predict the equilibrium unfolding curves and kinetics for several variants of the β-hairpin peptide.
As is evident from the presentations at this Colloquium, the continuous discovery of thousands of new gene sequences is producing a revolution in all aspects of protein physics, chemistry, and biology. Foremost among these is the protein-folding problem. C.B.Anfinsen, in his Nobel Prize winning experiments at the National Institutes of Health (1), showed that a denatured protein can refold spontaneously to form a biologically functional (native) structure. From this result. Anfinsen concluded that the information for determining the three-dimensional structure is somehow encoded in the amino acid sequence. This work has led to the realization that it should in principle be possible to calculate the three-dimensional structure of a protein from its amino acid sequence. Calculating the structure from the sequence has become known as the first part of the protein-folding problem and currently engages a large number of theoretical and computational scientists. The second part of the protein-folding problem is to understand how a protein folds. That is, what are the kinetics and mechanism (or mechanisms) of protein folding? This question is in many ways more challenging because for in vitro folding the ultimate answer is a description of the distribution of three-dimensional structures as a function of time, as the polypeptide progresses from a nearly random set of structures to the unique, compact native protein. An additional motivation for kinetic studies is their relation to the evolution of protein sequences. Evolution preserves protein sequences that correspond to structures with functions that are important to the organism. Theoretical studies by Wolynes and coworkers (2) have suggested how rapid folding to the native structure is yet another evolutionary pressure.
The experimental investigation of the kinetics and mechanism of protein folding has been aided by several recent theoretical and technological advances. The theoretical advances include analytical approaches (2–4), simulations of simplified representations of proteins (2, 5–8), and all-atom molecular dynamics calculations (9–11). This work has painted a comprehensive picture of possible general mechanisms and has provided a framework for experimentalists to think more clearly about the problem. It also has helped define questions, design new experiments, and interpret experimental results. Important technological advances include the availability of a great variety of materials from protein engineering and peptide synthesis, the development of more rapid kinetic methods (12,13), and increased computer power. The combination of these advances now permits the development of an “aufbau” approach to protein folding. This approach starts with the investigation of isolated secondary structural elements: α-helices, β-structures. and loops. The relative simplicity of these elements should permit their mechanism of formation to be described in much greater detail than is possible for proteins. Such studies include the development of statistical mechanical models which quantitatively reproduce equilibrium populations and kinetic progress curves. Once the kinetics and mechanism of the elements are understood, it should be possible to investigate structures of increasing size and complexity.
We have begun to study secondary structural elements by using nanosecond-resolved kinetic methods and statisticalmechanical modeling (14). The thermodynamic and kinetic behavior of the α-helix has been studied for more than 40 years (15–20). Only recently, however, have kinetic measurements been made on helices of size and composition comparable with those found in proteins (21–23). Also, early theoretical studies (16, 17) were limited by the lack of computer power, preventing the detailed modeling of experimental kinetic data on helix formation that is now possible (13). The experimental and theoretical study of the kinetics of loops and β-structures is a new subject. Jones et al. (24) and Hagen et al. (25, 26) used a nanosecond photochemical triggering method to study loop formation in cytochrome c by determining the diffusion limited rate for an intramolecular ligand-binding reaction. We also recently reported a thermodynamic and kinetic study of a β-hairpin formed by the 16 C-terminal residues of streptococcal protein G B1 (Fig. 1) (27). This peptide had been shown to adopt the β-hairpin conformation by Blanco et al. (29) using NMR spectroscopy. Our β-hairpin experiments consisted of measuring the thermal unfolding curve for the 16-residue peptide between 273 K and 363 K and measuring the relaxation kinetics following 15-degree nanosecond laser temperature jumps to final temperatures ranging from 288 K to 328 K (27). The three principal experimental results from this study were:
0027–8424/98/955872–8$0.00/0
PNAS is available online at http://www.pnas.org.
|
* |
To whom reprint requests may be addressed: e-mail: vmunoz@helix.nih.gov or eaton@helix.nih.gov. |
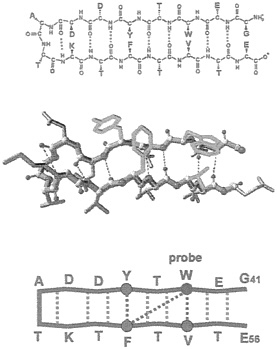
FIG. 1. Chemical, structural, and schematic representations of the β-hairpin. The sequence corresponds to the C-terminal fragment containing residues 41–56 of protein G B1 (28). Dashed lines indicate hydrogen bonds or hydrophobic interactions.
(i) the β-hairpin peptide exhibits two-state behavior in both its equilibrium and kinetics; (ii) the apparent activation energy for the folding rate calculated from the two-state analysis is negative; and (iii) the rate of β-hairpin formation is much (>10-fold) slower than that of the α-helices that have been studied up to now in short peptides.
To explain these results, we used a simple statistical mechanical model which was only briefly described (27). Here, we present a detailed description of the model, test one of its major approximations, and use the model to predict kinetic and equilibrium properties expected for other β-hairpinforming peptides. We shall see that analysis of β-hairpin thermodynamics and kinetics addresses many of the same issues that arise in considering the folding of a small protein.
Description of the Model. Our objective has been to develop a model for protein secondary structure kinetics, which can be used to analyze experimental data and to predict new experiments. In this work, the model is applied to a β-hairpin, but it also can be applied to helices and is readily adapted for more complex structures. We adopt a description, which uses pairs of ϕ,ψ, dihedral angles to define the conformation of each molecule; the complete native structure is formed when all of the residues have native values for these angles. Formation of the native structure is opposed by the loss of conformational entropy and favored by the formation of stabilizing interactions, i.e., hydrogen bonds and hydrophobic interactions (Fig. 1). The model postulates that two groups interact only when all of the dihedral angles of the sequence connecting them are native. This restriction considerably simplifies the model by identifying three-dimensional structures with sequences of peptide bond conformations.
A second simplifying step is to consider only two conformations for the backbone dihedral angles, native and nonnative (in a spirit similar to the “correct” and “incorrect”
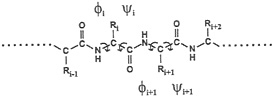
FIG. 2. Choice of dihedral angle pairs for motion in elementary kinetic steps.
parameter of the Zwanzig model; ref. 30). The nonnative conformation of a dihedral angle pair is not a unique conformation but is the set of all conformations that are incompatible with the native structure. An additional feature of the model is that pairs of ϕ,ψ dihedral angles are assumed to rotate between native and nonnative values simultaneously.† We chose the dihedral angles ψ of residue i and ϕ of residue i + 1 (Fig. 2) so that the peptide bond, rather than the residue, is the conformational unit. Formation of a backbone-backbone hydrogen bond is therefore associated with the transformation of one pair of ψi, ϕi+1 angles in each β strand from nonnative to native values.
In our thermodynamic description of the β-hairpin, we consider only three factors. These are the stabilizing effect of the hydrogen bonds between the backbone carbonyl and amide of the N- and C-terminal β strands, the stabilizing effect of the three hydrophobic interactions among the four side chains of the hydrophobic cluster (Fig. 1). and the destabilizing effect of the loss of conformational entropy when fixing pairs of dihedral angles in the native hairpin conformation. Nonnative interactions, such as wrong hydrogen bonds or hydrophobic interactions, are ignored. We also ignore electrostatic interactions among the charged side chains and chain termini (their importance could be assessed by experiments on the ionic strength dependence of the equilibrium and kinetics which have not yet been performed). Each thermodynamic factor is considered to be homogeneous, i.e., independent of side chain and position in the native structure. We assume that the free energies of formation for each of the three hydrophobic interactions, ΔGsc, are identical. Each of the backbonebackbone hydrogen bonds, including the one in the turn region, is assumed to have the same free energy, ΔGhb. The conformational entropy loss for the strand and turn regions also is assumed to be the same (ΔSconf). which is equivalent to assuming that the residues in the turn have a propensity for this conformation equal to the propensity of the strand residues to be in a strand conformation. To further reduce the number of parameters, we assume that the hydrogen bond is purely enthalpic, i.e., ΔGhb=ΔHhb and that the hydrophobic inter
actions are temperature-independent over the temperature range studied.
For the elementary kinetic steps (motion of individual dihedral angle pairs), we choose a transition state that can be described in terms of the equilibrium thermodynamic parameters. It is natural to assume that there is an entropy barrier to forming a native dihedral angle pair, so we equate the entropy of activation to the equilibrium entropy loss. For some steps, native dihedral angle pair formation is not associated with stabilizing interactions, whereas in others it is associated with the formation of hydrogen bonds or both hydrogen bonds and hydrophobic interactions. We assume that all native interactions are broken in the transition state. Also, we include the possibility that these steps have an activation barrier,Eo, in addition to the barriers imposed by the equilibrium free energy changes.
We must next decide how to treat the temperature dependence of the prefactor for these kinetic steps because it will have a significant effect on the height of the potential energy barrier required to fit the kinetic data. In investigating the viscosity-dependence of the conformational relaxation rate of myoglobin, Ansari et al. (31, 32) found that the data could be well-represented by a preexponential factor proportional to 1/(σ +η), where η is the solvent viscosity and σ is the contribution to the effective friction from interacting protein atoms (4 cP in myoglobin). A much greater fraction of the β-hairpin peptide atoms interact with solvent, so we expect σ to be smaller. Simulations of β-hairpin formation by Klimov and Thirumalai (33) suggest a 1/η dependence (σ=0) so, in the absence of direct experimental data, we use a prefactor proportional to 1/η. The net result is that the model is completely defined by only five parameters—three equilibrium parameters, ΔHhb, ΔGsc, and ΔSconf, and the two kinetic parameters, ko (To), the preexponential factor at the reference temperature, and an activation energy, Eo.
A final, major simplifying feature in the model is the single sequence approximation first used by Schellman (34) in describing the helix-coil equilibrium and recently by us in describing helix-coil kinetics of a 21-residue peptide (23). In the single sequence approximation, only species with a contiguous run of native peptide bonds are considered. All other structures are ignored. For the β-hairpin peptide, which has 16 residues (15 peptide bonds), there are 215 (=32,768) possible molecular conformations. The single sequence approximation reduces this number to 121. In helix-coil theory, the justification for the single sequence approximation is the expectation that for short polypeptides there is a low probability of nucleating more than one stretch of helix in any individual molecule. For the β-hairpin, we give the justification a posteriori by comparing with a more complete model in which the approximation is not made.
Partition Functions. The nonnative conformation of the peptide bond (coil, c) is taken as the reference state and assigned a weight of 1. The weight of a peptide bond in the native conformation (hairpin, h) is exp(ΔSconf/R), and the weight for a single stretch of j contiguous native peptide bonds, starting with peptide bond i [i.e., the ψ of residue i and ϕ of residue i +1 (Fig. 2)], is:
wj,i=exp[–(ΔGj,i–jTΔSconf)/RT];
ΔGj,i≡pΔHhb+qΔGsc, [1]
where p is the number of backbone-backbone hydrogen bonds and q is the number of side-chain-hydrophobic interactions in the native stretch. In this model, there are 215 conformations for the 16-residue hairpin arising from all of the possible combinations of hs and cs. The weight of each of these conformations is simply the product of the weights of each of the native stretches that it contains, and the partition function is the sum of the 215 weights.
The model can be greatly simplified by considering only those species which contain a single stretch of native peptide bonds (the “standard” single sequence approximation). This simplification results in a model with only 121 species with the partition function:
[2]
where n+1 is the total number of residues (16 in this β-hairpin). The equilibrium probability of the all-coil conformation is P0,0=1/Q and the equilibrium probability for all other conformations is Pj,i=wj,i/Q.
To test the accuracy of this standard single sequence approximation, we compared the equilibrium curves of the model with and without this approximation in Fig. 3. The approximation significantly overestimates the fraction of folded hairpin. This problem arises because the standard single sequence approximation does not properly account for the entropy of the system, as has been discussed by Qian and Schellman (35) for the helix-coil transition. The population of each of the 32,647 ignored species [such as cchcchcccchcccc with a weight of exp (3ΔS/R)] is quite small, but because their number is large, their contribution to the entropy of the system is significant. In particular, most of the ignored species do not contain significant hairpin structure, and ignoring them underestimates the stability of the unfolded hairpin. The number of species ignored by the standard single sequence approximation grows geometrically with peptide length, precluding its application to molecules of different length.
The underestimation of the entropy can be minimized by defining a “coil” state that includes not only the all c species (ccccccccccccccc) but also all the possible combinations of h and c peptide bonds that do not have just one single native stretch. For all those conformations, we ignore native interactions (even for a species such as ccchhhhhhhhhchc, which has the backbone conformation of the β-turn as well as residues
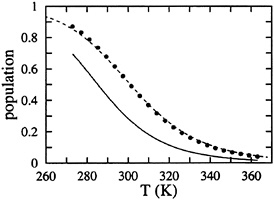
FIG. 3. Comparison of thermal unfolding curve for the β-hairpin predicted by standard single sequence (121 species) and complete (32, 768 species) models. The fractional population of molecules containing the intact hydrophobic cluster is plotted vs. temperature. The points are derived from a two-state analysis of the fluorescence equilibrium curves. The dashed curve is the fit to the data using the standard single sequence (121 state model) partition function (Eqs.1 and 2). The continuous curve is predicted by the 215-state partition function using the parameters from the fit with the standard single sequence model (ΔSconf=–3.09 cal mol–1 K–1, ΔHhb=–0.86 kcal mol–1, ΔGsc=–2.19 kcal mol–1).
Y45 and F52 in position to make a hydrophobic interaction). The weight of the coil state now becomes: where:
[3]
where the second term eliminates the contribution to the coil state by conformations with a single stretch of native peptide bonds (see Eq. 1). The partition function in this “modified” single sequence approximation is:
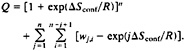
[4]
Rate Equations. To transform the equilibrium description of the model with the modified single sequence approximation into a kinetic model, we begin by assuming that conformations are connected if they can be interconverted by single h→c or c→h transitions. Species that contain a single stretch of native peptide bonds are connected to those other species that contain one more or one less native peptide bond at either end of the stretch. The rate constant for adding native peptide bond i to a native stretch, ki+, is given by:
[5]
where ko is the preexponential factor at the reference temperature To, ηo is the solvent viscosity at To. and Eo is the activation energy for rotation of the peptide bond. The rate constants for removing native peptides bonds i or i+j–1 from a native stretch of length j that starts at residue i (Fig. 2) are given by:
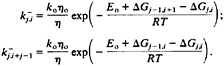
[6]
It is less straightforward to treat the contribution to the overall kinetics of the system of those additional species that now have been included in the coil state. For example, a coil conformation such as cchhhchhccccccc can convert to a single sequence conformation cchhhhhhccccccc by a single c→h transition. We assume that the rate for this process is equal to k6+(Eq. 5) times the probability of finding this particular conformation within the coil state (i.e., exp(5ΔSconf/R)/w0.0 for the above example). We then can define an overall rate that is the summation of the rates for all possible transitions between the coil state and each conformation with a single native stretch. The overall rate for going from the coil state to a conformation with a stretch of j native peptide bonds starting at residue i is given by:
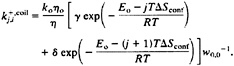
[7]
The overall reverse rate is given by:
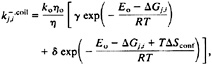
[8]
where
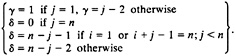
Using these rates (Eqs. 5–8), the population of the 121-molecular species of the model as a function of time is described by the following set of master equations:
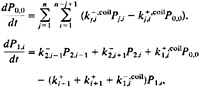
[9]
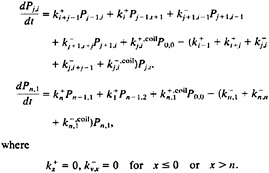
Despite its complexity, this treatment of the kinetics maintains detailed balance. Moreover, it implicitly includes all the kinetic connections involving single h→c or c→h transitions for each of the 120-single sequence species without increasing the size of the rate matrix. The physical description in this approximation is, however, somewhat artificial. For example, our definition of the coil species requires that a c→h transition which does not occur at the end of a native stretch (such as ccchhhhhhhhcccc→ccchhhhhhhhchcc), transforms the molecule back to the coil state instead of closer to the fully formed hairpin. However, an additional single transition (ccchhhhhhhhchcc→ccchhhhhhhhhhcc) returns the molecule to a more complete hairpin conformation.
Test of Modified Single Sequence Approximation. We tested the modified single sequence approximation by comparing it with a “complete” model that considers all 2″(=215=32,678) possible conformations explicitly. To perform the test, we fit the experimental data with the modified single sequence approximation model to obtain parameters that were then used in simulations using the complete model. The fit and simulations of the equilibrium data are shown in Fig. 4a. The equilibrium description is rather similar for both models, in contrast to the standard single sequence approximation (Fig. 3). This result confirms our interpretation that underestimation of the entropy of the unfolded ensemble is the main deficiency in the standard single sequence approximation. In the modified single sequence approximation, however, there is a small overestimation of the fraction of unfolded hairpin. The major contribution to this difference is the small subset of species that has significant β-hairpin structure (including stabilizing interactions) but are counted as species of the coil state (which have no stabilizing interactions) in the modified single sequence approximation.
We also tested the kinetic description with simulations carried out with the complete model, in which there are n2" (=
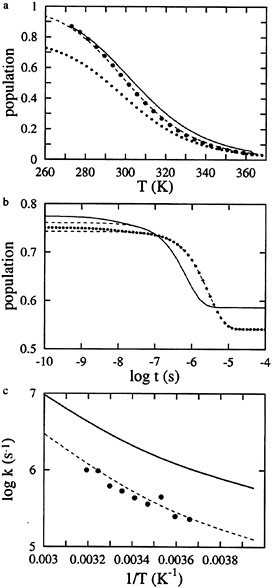
FIG. 4. Comparison of thermal unfolding curves and kinetics for modified single sequence and complete models, (a) Fractional population of the hydrophobic cluster as a function of temperature. Derived from a two-state analysis of fluorescence equilibrium curves (large dots). Fit to the data with the modified single sequence model (Eqs. 3 and 4), producing the parameters ΔSconf=–2.74 cal mol–1 K–1, ΔHhb=–0.96 kcal mol–1, ΔGsc=–1.94 kcal mol–1 (dashed line). Calculated with the complete model using these parameters (continuous line). Fraction of native hydrogen bonds calculated using the model with modified single sequence approximation (dotted line), (b) Simulations of progress curves for the complete model (continuous line) and the model using the modified single sequence approximation (dotted line). The fractional population of the hydrophobic cluster vs. time is plotted following a temperature jump from 283 to 298 K. The dashed lines are single exponential fits to the simulated progress curves at limes >10 ns, the resolution of the T-jump instrument. The fits of the modified single sequence model to the kinetic data were performed using the LSODA routine (36). which incorporates algorithms for solving both stiff and nonstiff systems of equations. The resulting parameters were k0=8.0×108 s–1 and E0=0 (equilibrium parameters same as in a. The equilibrium and kinetic parameters are slightly different from those reported by Mun̄oz et al. (27) for two reasons. One is that in the previous work the viscosity dependence was not included in the preexponential factor, and the second is that in the present work the kinetic and equilibrium data were fit simultaneously, whereas in the previous analysis (27), the equilibrium data were fit independently, (c) Arrhenius plot of relaxation times following 15 degree temperature jumps. The points are the experimental relaxation rates, whereas the dashed curve through the points is obtained from the fit to the data using the modified single sequence model. The continuous curve is obtained from single exponential fits to the kinetic progress curves generated by the complete 215-state model using the kinetic parameters from the modified single sequence model.
49, 520) possible kinetic transitions. Only 450 of those are explicitly included in the modified single sequence approximation model. The fitting to the kinetic experiments with this model was performed by floating its five parameters to produce the best least-squares fit to the observed progress curves for the nine experimental temperature jumps between 288 and 328 K (Fig. 4c). This was carried out using the equilibrium populations at the initial temperatures (before the T-jump) and integrating the rate equations (Eq. 9) by using rate constants evaluated at the final temperatures (after the T-jump). These parameters were then used in kinetic simulations with the complete model. The rate matrix for this model was constructed using an automatic pattern-matching algorithm (E.R.Henry, unpublished data).‡
The results for the two models are very similar, with fluorescence progress curves that can be represented as a biexponential process in each case. There is initially a small amplitude phase, corresponding to very rapid reequilibration among conformations in the global-free energy minima of the folded state, followed by a slower large-amplitude phase, corresponding to crossing of the free energy barrier separating the folded and unfolded states (see Fig. 5 and below). Overall, the agreement between the two models must be considered very good and justifies the use of the modified single sequence approximation. There are, however, significant differences, and the relaxation rates for the major phase (the only one detected experimentally) are about a factor of three faster in the complete model (Figs. 4 b and c). This effect is produced because the modified single sequence approximation ignores the stabilizing interactions in the rates connecting conformations included in the coil state with the conformations in the folded state (with a stretch of seven or more native peptide bonds). For example, the transition cccchhhhhhchccc→cccchhhhhhhhccc is less probable in the simpler model because ignoring the two hydrogen bonds of the starting conformation lowers its population by a factor of 25 [=exp(–2ΔHhb/RT)].
Predictions for Other β-Hairpins. An important consequence of having a statistical mechanical model for β-hairpin formation is that it can be used to make specific predictions that can be tested experimentally. A useful way of examining the results of the model is to consider the free energy as a function of the fraction of native peptide bonds, its natural reaction coordinate (Figs. 5a and 6a). The model postulates that formation of a β-hairpin in the absence of side-chain
|
‡ |
The system of equations is stiff and was integrated using an iterative multi-step backward differentiation formula method (37), as implemented in the CVODE package (36, 38). This algorithm requires the solution of a set of nonlinear algebraic equations by Newton iteration at each time step. Each Newton iteration in turn requires solving an NxN linear system AΔP=residual, where the matrix A is derived from the rate matrix K. For n=32,768, this problem is rather too large to solve using standard methods (39). However, the matrix A is sparse, containing only ≈500,000 nonzero elements of a possible 109. Therefore, an iterative generalized minimal residual method (40) appropriate for large sparse linear systems, as implemented in the CVODE package (36, 38). was used. The performance of the algorithm was improved dramatically in this application by Jacobi (diagonal) preconditioning or very simple block-diagonal preconditioning (40). |
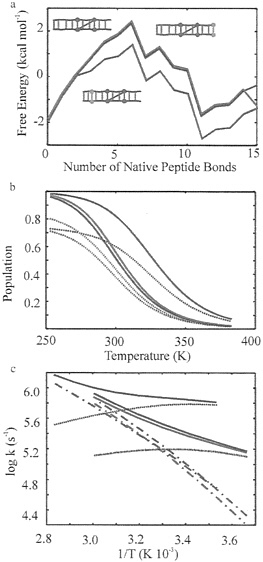
FIG. 5. Prediction of equilibrium and kinetic properties of β-hairpins with additional interactions. Red. original hairpin; blue, hairpin with interaction in the β-turn (residues D47–K50); and green, hairpin with interaction between end residues (residues R41–E56). (a) Free energy profiles (not including kinetic barriers), (b) Population of the hydrophobic cluster (continuous lines) and fraction of hydrogen bonds (dotted lines) for the three hairpins, (c) Arrhenius plot of the kinetics of the three hairpins. Relaxation rates (continuous lines), folding rates (dotted lines), and unfolding rates (dashed-dotted lines). The folding and unfolding rates have been calculated from a two-state fit to the relaxation rates and equilibrium constants generated with the modified single sequence model.
interactions is continuously uphill in free energy because backbone hydrogen bonds do not compensate for the loss in contbrmational entropy of forming native peptide bonds in both β-strands. Side-chain interactions are, therefore, necessary for the stability of the hairpin and determine the position and height of the free energy barrier for hairpin formation. This hairpin is stabilized by a cluster of four hydrophobic side chains (W43, Y45, F52, and V54), making three hydrophobic interactions (Fig. 1). Based on our model, the folding free energy barrier for this hairpin is crossed when the seven central peptide bonds become native and the first hydrophobic interaction (between residues Y45 and F52) is formed.
Many of the predictions of the model are immediately apparent upon examination of the free energy profile. The existence of two global minima separated by a significant free energy barrier (Fig. 5a) explains the two-state behavior and exponential kinetics. The species at the barrier maximum has two backbone-backbone hydrogen bonds and therefore a lower energy than the coil state, explaining the apparent negative activation energy in the two-state analysis (assuming a simple Arrhenius expression for the rate constants with a temperature-independent prefactor). The global minimum on the folded side of the free energy barrier consists of several molecular conformations, with the species at the lowest free energy having the intact hydrophobic cluster but not the maximum number of backbone-backbone hydrogen bonds and native peptide bonds. This result could explain why the population of the hydrophobic cluster obtained by fitting fluorescence data is higher than the fraction of native dihedral angles estimated by NMR (29).
An interesting prediction of this model of β-hairpin formation is that local and long-range interactions have very different effects on the free energy surface of the hairpin and, therefore, on its equilibrium and kinetic properties. To illustrate this point, we have performed simulations with two variants. In one of these variants, we include a side-chain interaction, which could result from a favorable electrostatic interaction between D47 and K50, which stabilizes the β-turn by 1 kcal/mol. In the other variant, a similar interaction is introduced between the first and last residues in the hairpin by mutating “in machina” glycine 41 to arginine. This computational experiment is similar in spirit to the protein engineering approach to folding kinetics (41–43). When positioned in the β-turn, the interaction is local (between residues i and i + 3). and it significantly affects both the thermodynamics and kinetics of hairpin formation by lowering the free energy of all states, which contain native interactions (Fig. 5a). Both the population of species with the hydrophobic cluster and the fraction of hydrogen bonds increase at all temperatures, and the Tm increases by ~20 K (Fig. 5b). The folding rate is accelerated by about a factor of four, whereas the unfolding rate is slightly decelerated (Fig. 5c). Because the peak of the free energy barrier stays at the same position along the reaction coordinate, the change in rates results simply from the change in the barrier height, as is commonly assumed in interpreting the effects of single residue perturbations in protein folding. When the interaction is introduced between the end residues, it is long range (i,i+15) and its effects on the folding properties are rather insignificant. The Tm changes by only ~2 K, and the change in rates is very small, with the largest change in the unfolding rate. Thus, the simulations suggest that, in hairpins, the interactions closest to the β-turn exert the largest effect on the folding rate; interactions between the ends of the strands may stabilize the hairpin structure but have very little effect on the folding rate.
Another important point raised by our model of β-hairpin formation is that the shape of the free energy barrier and the position of its maximum along the reaction coordinate are determined by a delicate balance between the loss in conformational entropy and stabilization from side-chain interactions. To address this point, we have simulated two variants of the original β-hairpin: a hairpin with the hydrophobic cluster placed one residue closer to the center of the molecule (W44, Y46, F51, V53) and another one with the hydrophobic cluster one residue closer to the ends (W42, Y44, F53, V55). The effects of these changes on the equilibrium and kinetic properties are shown in Figs. 6 b and c, respectively. Moving the hydrophobic cluster one residue in either direction does not modify the interaction energies of the hairpin; however, the
model predicts a dramatic effect on its free energy profile (Fig. 6a). If the cluster is moved closer to the β-turn, both the minimum in the folded ensemble and the top of the free energy barrier are shifted toward less structure (closer to the unfolded ensemble). This is accompanied by an increase in stability, an acceleration of the folding rate, and almost no change in the unfolding rate. If the cluster is moved one residue in the opposite direction (toward the ends), the stability is decreased and the folding rate decreases, and there is only a small change in the unfolding rate. Displacements of the top of the free energy barrier have been reported in folding experiments on small proteins (44). The model indicates that, for a β-hairpin,
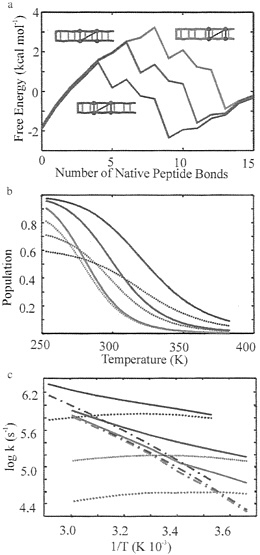
FIG. 6. Prediction of equilibrium and kinetic properties of β-hairpins with repositioned hydrophobic cluster. Red, original hairpin; Blue, hairpin with hydrophobic cluster moved one residue closer to the β-turn; and green, hairpin with hydrophobic cluster moved one residue closer to the ends. (a) Free energy profiles. (b) Population of the hydrophobic cluster (continuous lines) and fraction of hydrogen bonds (dotted lines) for the three hairpins, (c) Arrhenius plot of the kinetics of the three hairpins. Relaxation rates (solid lines), folding rates (dotted lines), and unfolding rates (dashed-dotted lines). The folding and unfolding rates have been calculated as in Fig. 5.
the top of the free energy barrier is simply determined by the position of the stabilizing side chains in the sequence.
Caveats. One criticism of the model that we have presented is that only native interactions are considered. This excludes the possibility, for example, of forming a turn at additional positions in the sequence, which would result in nonnative hydrogen bonds and nonnative hydrophobic interactions. There is no evidence in the NMR data of significant population of other hairpin conformations (29). Nonnative interactions also can affect the kinetics in the same two ways as in proteins (2). They can produce local minima in the energy landscape, which can result in the population of intermediate structures at equilibrium, or they can produce transient trapping of misfolded structures, which are not present at equilibrium. We have not yet found any evidence for equilibrium intermediates in the folding of the β-hairpin. For transient trapping to be observable as a separate kinetic phase, the residence time in the trapped state must be longer than the relaxation time for the overall hairpin-coil transition. Transient trapping does not appear to be occurring in this β-hairpin because the progress curves at all temperatures can be well-fit with a single exponential function (27).
Another criticism of the model is that there are no native backbone or side-chain interactions between two residues unless the peptide bonds of all intervening residues have the native conformation. This postulate excludes the possibility, for example, of initiation by forming the hydrophobic cluster followed by zipping up of the hydrogen bonds. The transition state in this mechanism would be a ~10-residue loop. One is tempted by this mechanism because of the close correspondence of the β-hairpin relaxation time and the time of ~1 μs estimated by Hagen et al. (25, 26) to form a 10-residue loop. A 10-residue loop is predicted by Thirumalai (45) to be the most probable loop size in proteins, longer loops being less probable because of the larger entropy loss and shorter loops because of chain stiffness. One could possibly distinguish between the two mechanisms by measuring the kinetics for a β-hairpin in which the hydrophobic cluster is moved closer to the β-turn. Our model predicts that the rate of formation should speed up because the transition state now occurs earlier along the reaction coordinate (Fig. 6a), whereas the loop model would predict a slower rate of formation. This consideration was in fact one of the motivations for the predictions discussed above.
The most convincing test of the model will of course come from measurements on other β-hairpin peptides. Another approach to both testing and refining the model is to examine the results of simulations. All-atom molecular dynamics simulations of temperature jump kinetic experiments (at experimental temperatures) may be feasible in the near future (10, 11). In the meantime, it should be useful to examine the results of Langevin simulations of simplified representations of the peptide (33). Because large numbers of sufficiently long trajectories are possible with this method, kinetic progress curves actually can be simulated. Examination of these trajectories might reveal dominant mechanisms and structural species that must be included in a kinetic model. The results will, however, depend critically on the choice of potential functions.
Is the model unnecessarily complex? Could we use a much simpler model even a two-state model? The main problem with a two-state model is that it has little predictive value. In a two-state model, one would postulate a transition state structure or, as in the case of proteins, try to determine the transition state by structural perturbation experiments. The examples in Fig. 6 show that small structural perturbations lead to changes in the transition state and would therefore also result in incorrect predictions for the change in rates. Nevertheless, the model could be simplified. If we consider only residue-residue interactions, then in the single sequence approximation, the model reduces to an eight-state model. In
such a model, quartets of dihedral angles change simultaneously in single kinetics steps. This model can explain the experimental data, as well as predict the properties of other β-hairpins. It is, however, not straightforward to extend a model based on interactions to more complex structures because of the difficulty in defining rules that specify the rates of all elementary kinetic steps in terms of just a few parameters.
We thank Attila Szabo and Peter Wolynes for helpful comments on the manuscript.
1. Anfinsen, C.B. (1973) Science 181, 223–230.
2. Bryngelson, J.D., Onuchic, J.N., Socci. N.D. & Wolynes, P.G. (1995) Proteins Struct. Funct. Genet. 21, 167–195.
3. Bryngelson, J.D. & Wolynes, P.G. (1987) Proc. Natl. Acad. Sci. USA 84, 7524–7528.
4. Orland, H., Garel, T. & Thirumalai, D.T. (1996) in Recent Developments in Theoretical Studies of Proteins, ed. Elber, R. (World Scientific, Singapore), pp. 197–268.
5. Dill K.A., Bromberg, S., Yue, K., Feibig, K.M., Yee, D.P., Thomas, P.D. & Chan. H.S. (1995) Protein Sci. 4, 561–602.
6. Karplus, M. & Sail, A. (1995) Curr. Opin. Struct. Biol. 5, 58–73.
7. Shakhnovich, E.I. (1997) Curr. Opin. Struct. Biol. 7, 29–40.
8. Klimov, D.K. & Thirumalai, D. (1996) Proteins Struct. Funct. Genet. 26, 411–441.
9. Guo, Z., Brooks, C.B. & Boczko, E.M. (1997) Proc. Natl. Acad. Sci. USA 94, 10161–10166.
10. Li, A. & Daggett, V. (1996) J. Mol Biol. 257, 412–429.
11. Lazaridis, T. & Karplus, M. (1997) Science 278, 1928–1931.
12. Eaton, W.A., Thompson, P.A., Chan C.-K., Hagen, S.J. & Hofrichter, J. (1996) Structure (London) 4, 1133–1139.
13. Gray, H.B. & Valentine, J.S. (1998) Acc. Chem. Res., in press.
14. Eaton, W.A., Hofrichter, J., Munoz, V. & Thompson, P.A. (1998) Accts, Chem. Res., in press.
15. Zimm, B., Doty, P. & Iso, K. (1959) Proc. Natl. Acad. Sci. USA 45, 1601–1607.
16. Schwarz, G. (1965) J. Mol. Biol. 11, 64–77.
17. Poland, D. & Scheraga, H.A. (1970) in Theory of Helix-Coil Transitions in Biopolymers (Academic, New York).
18. Gruenewald, B., Nicola, C.U., Lustig, A. & Schwarz, G. (1979) Biophys. Chem. 9, 137–147.
19. Chakrabartty, A. & Baldwin, R.L. (1995) Adv. Protein Chem, 46, 141–176.
20. Mun̄oz, V. & Serrano, L. (1995) Curr. Opin. Biotech. 6, 382–386.
21. Williams, S., Causgrove, T.P., Gilmanshin, R., Fang, K.S., Callender, R.H., Woodruff, W.H. & Dyer, R.B. (1996) Biochemistry 35, 691–697.
22. Gilmanshin, R., Williams, S., Callender, R.H., Woodruff, W.H. & Dyer, R.B. (1997) Biochemistry 36, 15006–15012.
23. Thompson, P.A., Eaton, W.A. & Hofrichter, J. (1997) Biochemistry 36, 9200–9210.
24. Jones, C.M., Henry, E.R., Hu, Y., Chan, C-K., Luck, S.D., Bhuyan, A.K., Roder, H., Hofrichter, J. & Eaton, W.A. (1993) Proc. Natl. Acad. Sci. USA 90, 11860–11864.
25. Hagen, S.J., Hofrichter, J., Szabo, A. & Eaton, W.A. (1996) Proc. Natl. Acad. Sci. USA 93, 11615–11617.
26. Hagen S.J., Hofrichter J. & Eaton W.A. (1997) J. Phys. Chem. 100, 12008–12021.
27. Munoz, V., Thompson, P.A., Hofrichter, J. & Eaton, W.A. (1997) Nature (London) 390, 196–199.
28. Gronenborn, A.M., Filpula, D.R., Essig. N.Z., Achari, A., Whitlow, M., Wingfield, P.T. & Clore, G.M. (1991) Science 253, 657–661.
29. Blanco, F.J., Rivas, G. & Serrano, L. (1994) Nat. Struct. Biol. 1, 584–590.
30. Zwanzig, R. (1995) Proc. Natl. Acad. Sci. USA 92, 9801–9804.
31. Ansari, A., Jones, C.M., Henry, E.R., Hofrichter, J. & Eaton. W.A. (1992) Science 256,1796–1798.
32. Ansari, A., Jones, C.M., Henry. E.R., Hofrichter, J. & Eaton, W.A. (1994) Biochemistry 33, 5128–5145.
33. Klimov, D.K. & Thirumalai, D. (1997) Phys. Rev. Lett. 79, 317–320.
34. Schellman, J.A. (1958) J. Phys. Chem. 62, 1485–1494.
35. Qian, H. & Schellman, J.A. (1992) J. Phys. Chem. 96, 3987–3994.
36. Hindmarsh, A.C. & Petzold, L.R. (1995) Comput. Phys. 9, 148–155.
37. Hairer, E. & Wanner. G. (1996) Solving Ordinary Differential Equations II: Stiff and Differential-Algebraic Problems (Springer. Berlin), 2nd Ed.
38. Cohen, S.C. & Hindmarsh, A.C. (1994) CVODE User Guide (Lawrence Livermore Natl. Lab, Livermore, CA).
39. Lawson, C.L. & Hanson. R.J. (1974) Solving Least Squares Problems (Prentice-Hall Englewood Cliffs. NJ).
40. Barrett, R., Berry, M., Chan, T.F., Demmel. J., Donato. J.M., Dongarra, J., Eijkhout, V., Pozo, R., Romine, C. & Van der Vorst, H. (1993) Templates for the Solution of Linear Systems: Building Blocks for Iterative Methods (Soc. Indust. Appl. Math., Philadelphia).
41. Fersht, A.R., Matouschek, A. & Serrano, L. (1992) J. Mol. Biol. 224, 771–782.43.
42. ltzhaki, L.S., Otzen, D.E. & Fersht, A.R. (1995) J. Mol. Biol. 254, 260–288.
43. Onuchic, J., Socci, N.D., Luthey-Schulten, Z. & Wolynes, P.G. (1996) Fold. Des. 1, 441–450.
44. Silow, M. & Oliveberg, M. (1997) Biochemistry 36, 7633–7637.
45. Camacho, C.J. & Thirumalai, D. (1995) Proc. Natl. Acad. Sci. USA 92, 1277–1281.








