Proc. Natl. Acad. Sci. USA
Vol. 95, pp. 5880–5883, May 1998
Colloquium Paper
This paper was presented at the colloquium “Computational Biomolecular Science,” organized by Russell Doolittle, J.Andrew McCammon, and Peter G.Wolynes, held September 11–13, 1997, sponsored by the National Academy of Sciences at the Arnold and Mabel Beckman Center in Irvine, CA.
Coupling the folding of homologous proteins
CHEN KEASAR*†, DROR TOBI*, RON ELBER*‡, AND JEFF SKOLNICK§
*Department of Physical Chemistry. Department of Biological Chemistry, Fritz Haber Research Center for Molecular Dynamics and Wolfson Center for Applied Structural Biology, Hebrew University, Givat Ram Jerusalem 91904, Israel: †Department of Structural Biology, Stanford School of Medicine, Stanford University, Stanford, CA 94305: and §Department of Molecular Biology, Scripps Research Institute, La Jolla, CA 92037
ABSTRACT The empirical observation that homologous proteins fold to similar structures is used to enhance the capabilities of an ab initio algorithm to predict protein conformations. A penalty function that forces homologous proteins to look alike is added to the potential and is employed in the coupled energy optimization of several homologous proteins. Significant improvement in the quality of the computed structures (as compared with the computational folding of a single protein) is demonstrated and discussed.
It is convenient to classify methods of predicting protein conformations into one of two main categories: (a) methods that optimize energy functions and (b) methods that search through databases of protein structures. In the present manuscript we call a, “energy minimization methods”, and b “homology.” The division is not sharp. For example, many of the energy functions that are used in the prediction of three-dimensional conformations of proteins include information extracted from databases on protein structures.
The conformation of the global energy minimum, even if we succeed to find it, may differ from the native fold because of two possible reasons: (1) the empirical energy is inaccurate, and (2) the native fold does not correspond to a global free energy minimum. To address point 1, an adjustment of the energy function may follow, whereas to address point 2 the folding pathways (and not only the most stable state) are required. We propose below a combination of the homology and the energy approaches. The combination improves the prediction of structures of homologous proteins even if their conformations do not correspond to a global minimum of the individual molecules.
In the homology approach, an empirical observation on databases of protein structures is employed: Proteins with comparable sequences adopt a similar structure in the native configuration. This information is used to build models of unknown structures. The required degree of similarity between sequences is uncertain but a bet with significant safety margins is of 40% sequence identity. A model of a protein with an unknown structure can be built by using an experimental structure of a protein with a comparable sequence.
The homology protocol is the most accurate approach we have today to model protein structures on the computer. Its disadvantage is the necessity of having a similar sequence with a known structure.
In this manuscript, we describe a connection between the two approaches that improves the performance of energy optimization techniques while maintaining its generality. In the next section, we describe the algorithm and an example for a “real” protein follows. Finally, we explain why the suggested
coupling optimizes better than straightforward annealing. We suggest two reasons for the improvement. The first source of improvement is smoothing of the potential energy surface, making it more accessible for global optimization. The second reason for improvement in the optimization is due to averaging in sequence space (over the homologous proteins) that enhances weak signals.
The Algorithm. We consider N homologous proteins with sufficient sequence identity that suggests structural similarity. The structure of the family is unknown, making the “energy minimization” approach the right choice to predict the structure (it is the only choice). The N sequences are aligned, using established sequence alignment techniques (1). Here, we assume that the alignment is adequate. The example discussed below did not include deletions or insertion of amino acids into the sequence. However, an extension that includes deletions and insertions is straightforward.
The energy of a homologous set of proteins. An energy function, Etotal, is defined, which includes the sum of all the individual energies of the homologous proteins and a coupling term that penalizes structural diversity.

[1]
Xi is the vector of coordinates for the i-th homologous protein, and εi(Xi) is its unique energy function. Δij(Xi, Xj) is a function that measures and penalizes structural diversity between proteins i and j. The larger is the difference between the two structures; the higher is the value of the penalty function. In Eq. 1, we sum over the diversities of all pairs. Optimization of Etotal) provides a prediction for the structure of the family of the homologous proteins.
Exploring conformations. We used the Lattice Monte Carlo Program (LMCP) of Skolnick and Kolinski (2). The Monte Carlo procedure uses different moves on the lattice to modify a starting conformation of the protein chain. Each of the proteins is modified independently. A displacement δXi is chosen according to the LMCP protocol, so that ⟨δXiδXj⟩i≠j is zero (⟨…⟩ denotes an ensemble average). New protein energies—εi(Xi,+ΔXi) (i=1,…,N)—are computed and supplemented by the i-th measure of structural diversity Δi(Xi+ δXi)= Δij. The displacement in Xi (δXi) is now accepted or rejected according to the usual Monte Carlo criterion with an energy, εi(Xi)+Δi(Xi). The Monte Carlo test is repeated for all the homologous structures {i=1,…,N}.
Δij. The displacement in Xi (δXi) is now accepted or rejected according to the usual Monte Carlo criterion with an energy, εi(Xi)+Δi(Xi). The Monte Carlo test is repeated for all the homologous structures {i=1,…,N}.
©
PNAS is available online at http://www.pnas.org.
‡ | To whom reprint requests should be addressed, e-mailron@fh.huji.ac.il. |
The generation of δXi (but not the decision on its acceptance) depends only on Xi and does not take into account the penalty function on structural diversity. This protocol may lead to a large number of step rejections. However, the above choice is the simplest to use in a parallel computing environment, and it further leaves some room for future publications.
The parallel environment is important because the computations are pursued typically on a cluster of workstations or on a parallel computer with multiple CPUs. Each of the homologous proteins is assigned to one processor. The processor calculates the displacement δXi and the energy εi(Xi)+Δi(Xi) and decides whether to accept or to reject the move. The correlation with other structures is built using the function Δi(Xi) that depends on all the other coordinates. The conformations of the set are therefore sampled from the canonical ensemble with an “energy”, Etotal.
To compute the penalty function Δi(Xi), it is necessary to have the coordinates of all the proteins on each of the processors. The update of the coordinates can be done with every Monte Carlo step. However, to reduce communication overhead, we usually update the coordinates only after a few Monte Carlo steps.
A related algorithm can be easily formulated for molecular dynamics, solving the Newton’s equations of motion:
where M is the mass matrix for protein i. Nevertheless, the lattice approach suggests a number of unique advantages for the protein folding problem, which are discussed elsewhere (3).
We now return to the functional form of the penalty on structural variations. We experiment with two measures:
-
Root mean square difference (RMSD) of the shared Cα coordinates after optimal overlap (4):
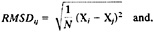
-
L is the fraction of dissimilar contacts in the maps of the two structures. L=(number of dissimilar contacts)/(total number of contacts in the two maps). (Two residues are considered at a contact if their Cα distance is ≤6.5 Å.)
The RMSD is a common and useful measure of global similarity. However, it is doing poorly in detecting similar folds of structural segments. For example, if the secondary structure elements are predicted correctly but their packing is incorrect, the RMSD is typically high. In contrast, L, which is not as widely spread as the RMSD, detects local similarities and shows more uniform decrease in value as the structure quality decreases.
Both functions are useful in comparing the final structure to the native fold; however, the task of forcing the different chains to look alike is best done with the RMSD. The application of L is problematic because maps with no contacts at all have (of course) no dissimilar contacts. As a result, restraining the structures to similar L values pushes the system to unfolded swollen states. We therefore used the RMSD. The specific functional form of Δij(Xi, Xj) is listed below:
Simulation Protocol and Results. We provide a numerical example for a family of pancreatic hormones (5). In Table 1, we list the seven sequences that were used in the runs with coupled optimizations (6).
We performed 100 Monte Carlo simulated annealing runs of the protein 1ppt and 142 coupled runs of structures of seven sequences, which were optimized in parallel. Only one experimental structure (of 1ppt) is available, and we compared with it the results of the computations. In Fig. 1, we show the energies of the 100 Monte Carlo runs of 1ppt as a function of the RMSD from the native structure. Also shown are the energies of the 142 coupled runs.
It is clearly seen that runs, which employed seven coupled proteins, cluster near lower RMSD values and therefore provide better prediction. The lowest energy structure of the coupled and the uncoupled runs (our best guess of the native conformation) are shown in Fig. 2. Again, the coupled runs provide a better answer. The improvement does not require an increase in computational effort. Each of the uncoupled 1ppt runs was seven times longer than the run of the seven sequences.
Another example for a protein family (homeodomain) can be found in ref. 6. Yet, another study employed coupling in a two-dimensional lattice (7) and showed even more profound improvement.
DISCUSSION
Here we discuss the question of ''why.” Why does the proposed algorithm improve structure prediction? We have seen one example, and other examples are available in the literature (6, 7). From a global optimization perspective, it may be surprising that optimizing a system, N times larger (N homologous sequences) is easier than optimizing one sequence at a time. At the limit in which the optimizations are completely independent, they should take approximately N times longer.
Obviously, the coupling plays an important role in increasing the computation efficiency and accuracy. To understand the effect, it is useful to consider a simpler system first in which the “homologous” proteins are all of the same molecule. Hence, only structural diversity remains. Etotal is now Etotal= ![]() [ε(Xi)+Δi]. A single energy function [ε(Xi)] is used for the different conformations of the proteins {i=1,…, N}.
[ε(Xi)+Δi]. A single energy function [ε(Xi)] is used for the different conformations of the proteins {i=1,…, N}.
In Fig. 3, we compare annealing results with coupled and uncoupled energy function for the protein Ifsd. The distribution clearly shows that better energies are obtained when the coupling (of identical proteins) is employed. Hence, a better optimization protocol is obtained without sequence diversity. However, it is important to emphasize that the quality of the structures (as opposed to the energies) is not necessarily better because it depends also on the quality of the energy function.
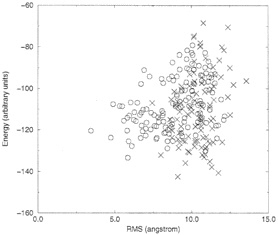
FIG. 1. Comparison between coupled and uncoupled Monte Carlo runs. X, uncoupled runs; black circles, uncoupled runs. Each point is the final configuration of a simulated annealing run. Note that the coupled runs end more frequently at lower energies and lower RMSD values.
The Monte Carlo procedure produces conformations that are sampled from the canonical ensemble. The weight of a coupled state Xi,…, XN at a temperature T is given by![]() Note that Δi depends on the coordinates of the rest of the copies and that, without the coupling, we are getting the classical Boltzmann factor for a set of N noninteracting copies
Note that Δi depends on the coordinates of the rest of the copies and that, without the coupling, we are getting the classical Boltzmann factor for a set of N noninteracting copies ![]()
Consider now, the discrete formula for quantum path integral of a system with a potential energy ε(X) ![]() where m is the mass matrix and ħ is the Planck constant divided by 2π (8). For convenience, we define
where m is the mass matrix and ħ is the Planck constant divided by 2π (8). For convenience, we define
and we also set N+1≡1. The new “coupled” energy Ecoupled resembles
The quantum expression couples only pairs of nearest neighbor structures because the coupling corresponds to a physical entity—the kinetic energy. Nevertheless, if λ is sufficiently large (the protein is closed to be “classical”), the different structures will remain similar at each sampling point, exactly what we wanted to achieve in the folding of homologous proteins. The similarity between Etotal and Ecoupled is therefore self-evident and hints to the origin of the enhanced optimization as discussed below.
Expressions that are related to the above quantum expression were investigated in the global optimization field (9). The key idea in a number of pioneering approaches was to define a new energy function. The new energy function is a local spatial average with different choices of densities: Eaverage(X) =∫E[X]0)ρ(X, X0)dX0. ρ(X, X0) is the density. The result Eaverage(X) is a smoother potential that is easier to minimize (Fig. 4) as was shown by numerous examples (9–13). Examples for smoothing densities are (but not limited to) Gaussians (9–11), square boxes (12), and a discrete sample of points (13). For example, the above quantum expression is an average of ε(X)over a discrete number of sampling points {X1,…, XN}.
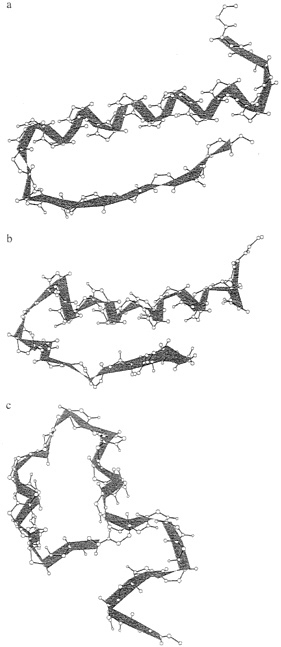
FIG. 2. Comparing the native structure (a) with the lowest energy structures of the coupled (b) and the uncoupled (c) runs.
The discrete averaging has advantages and disadvantages. An advantage is its simplicity. We do not have to perform complex integrals to obtain the average. The smoothing is done by a direct sum over the sampling points. However, because the number of points is small, the averaging is less effective compared with other methods that use analytical densities and integrals. Nevertheless, discrete smoothing is very suggestive for lattice calculations of the type that we present here.
To conclude, one of the reasons that the proposed protocol improves structure prediction is because of spatial potential averaging. This improvement is in the spirit of a number of recent global optimization procedures (9).

FIG. 3. Comparing the optimized energies from multiple simulated annealing runs for coupled and uncoupled simulations. Dark bars, coupled runs; light bars, uncoupled runs.
Another important feature of the present protocol is of averaging in sequence space. We return to the N different sequences. Each of the proteins has a unique energy surface. By virtue of experimental observations, we know that all the homologous protiens share similar structures at their native fold. At approximately the same coordinate Xnative, we expect
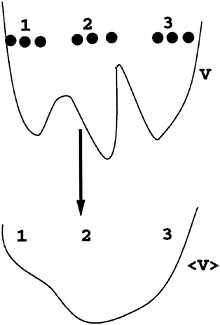
FIG. 4. A schematic drawing of potential smoothing using discrete, local averaging: ⟨V(X)⟩=1/N ![]() V(Xi)·δX,Xi·
V(Xi)·δX,Xi·
all the proteins to be in an energy minimum. Therefore, all of the energies are correlated and the result of the sum ![]() is a quantity, which increases linearly with N.
is a quantity, which increases linearly with N.
On the other hand, for unfolded states the energies of the different homologous structures are not necessarily correlated. Consider for example a correlated mutation at the hydrophobic core of the protein. To maintain the compactness of the hydrophobic core of the native state, valine and tryptophan may replace a pair of phenylalanines. At unfolded conformations, it is not necessary to assume that the contacts and the energies of the above residues are still correlated. It is more likely that the energies are not correlated. We therefore estimate ![]() This estimate is in the spirit of the Random Energy Model as applied to proteins (14).
This estimate is in the spirit of the Random Energy Model as applied to proteins (14).
The new energy surface Etotal is therefore distorted in a favorable way when comparing it to the original εi. The shared minimum (which databases of protein structures support its existence) is deeper compared with other portions of the energy surface. The enhancement of the well depth of the shared minimum may make it the global energy minimum of the new average energy even if originally it was not. This enhancement suggest the new protocol as possibly effective for kinetically stable proteins.
It is the combination of the spatial and sequence averaging, that provides significant improvement in structure prediction of ab initio algorithms as discussed above.
This research was supported by a Binational Science Foundation grant (to R.E. and J.S.) and by National Institutes of Health Grant GM37408 (to J.S.).
1. Sander, C & Schneider, R. (1991) Proteins 9, 56–68.
2. Kolinski, A. & Skolnick, J. (1994) Proteins 18, 338–352.
3. Kolinski, A. & Skolnick, J. (1996) Lattice Models of Protein Folding, Dynamics and Thermodynamics (Chapman & Hall London).
4. Kabsch, W. (1976) Acta Crystallogr. A 32, 922–923.
5. Glover, I. & Blundell, T. (1983) Biopolymers 22, 293–304.
6. Keasar, C., Elber, R. & Skolnick, J. (1997) Fold. Des. 2, 247–259.
7. Keasar, C. & Elber, R. (1995) J. Phys. Chem. 99, 11550–11556.
8. Feynman, R.P. (1982) Statistical Mechanics: A Set of Lectures, (Benjamin Cummins, Reading, MA).
9. Straub, J.E. (1996) Optimization Techniques with Applications to Proteins in Recent Developments in Theoretical Studies of Proteins, ed. Elber, R. (World Scientific, Singapore), pp. 137–197.
10. Piela, L., Kostrowicki, J. & Scheraga, H.A. (1989) J. Phys. Chem. 96, 4024–4035.
11. Shalloway, D. (1992) Global Optimizat. 2, 281(1992).
12. Andricioaei, I. & Straub, J.E. (1996) Comput. Phys. 10, 449–454.
13. Roitberg, A. & Elber, R. (1991) J. Chem. Phys. 95, 9277–9287.
14. Bryngelson, J.D. & Wolynes, P.G. (1989) J. Phys. Chem. 93, 6902–6915.





