Proc. Natl. Acad. Sci. USA
Vol. 95, pp. 5891–5898, May 1998
Colloquium Paper
This paper was presented at the colloquium “Computational Biomolecular Science,” organized by Russell Doolittle, J.Andrew McCammon, and Peter G.Wolynes, held September 11–13, 1997, sponsored by the National Academy of Sciences at the Arnold and Mabel Beckman Center in Irvine, CA.
New methods of structure refinement for macromolecular structure determination by NMR
(coupling constants/chemical shifts/conformational database/diffusion anisotropy/dipolar couplings)
G.MARIUS CLORE* AND ANGELA M.GRONENBORN*
Laboratory of Chemical Physics, Building 5, National Institute of Diabetes and Digestive and Kidney Diseases. National Institutes of Health, Bethesda, MD 20892–0520
ABSTRACT Recent advances in multidimensional NMR methodology have permitted solution structures of proteins in excess of 250 residues to be solved. In this paper, we discuss several methods of structure refinement that promise to increase the accuracy of macromolecular structures determined by NMR. These methods include the use of a conformational database potential and direct refinement against three-bond coupling constants, secondary13C shifts, 1H shifts, T1/T2ratios, and residual dipolar couplings. The latter two measurements provide long range restraints that are not accessible by other solution NMR parameters.
The two major techniques for determining the three-dimensional structures of macromolecules at atomic resolution are x-ray crystallography in the solid state (single crystals) and NMR spectroscopy in solution. Unlike crystallography, NMR measurements are not hampered by the ability or inability of a protein to crystallize. The size of macromolecular structures that can be solved by NMR has been increased dramatically over the last few years (1). The development of a wide range of two-dimensional (2D) NMR experiments in the early 1980s culminated in the determination of the structures of a number of small proteins (2, 3). Under exceptional circumstances, 2D NMR techniques can be applied successfully to determine structures of proteins up to ≈100 residues (4, 5). Beyond ≈100 residues, however, 2D NMR methods fail, principally because of spectral complexity that cannot be resolved in two dimensions. In the late 1980s and early 1990s, a series of major advances took place in which the spectral resolution was increased by extending the dimensionality to three and four dimensions (1). In addition, by combining such multidimensional experiments with heteronuclear NMR, problems associated with large linewidths can be circumvented by making use of heteronuclear couplings that are large relative to the linewidths. The first successful application of these methods to a protein greater than ≈12 kDa was achieved in 1991 with the determination of the solution structure of interleukin 1β, a protein of 18 kDa and 153 residues (6). Concomitant with spectroscopic advances, significant improvements have taken place in the accuracy with which macromolecular structures can be determined. Thus, it is now potentially feasible to determine the structures of proteins in the 15- to 35-kDa range at a resolution comparable to ≈2.5-Å resolution crystal structures (7). The upper limit of applicability is probably 60–70 kDa, and the largest single-chain proteins solved to date are ≈30 kDa, comprising ≈260 residues (8, 9). In this paper, we discuss a number of new refinement strategies aimed at both
facilitating NMR structure determination and increasing the accuracy of the resulting structures. These include direct refinement against three-bond coupling constants (10) and13C and 1H shifts (11–13), as well as the use of conformational database potentials (14, 15). More recently, methods have been developed to obtain structural restraints that characterize long range order a priori (16–18). These methods include making use of the dependence of heteronuclear relaxation on the rotational diffusion anisotropy of nonspherical molecules and of residual dipolar contributions to one-bond heteronuclear couplings arising from small degrees of alignment of molecules in a magnetic field.
General Principles of NMR Structure Determination. Irrespective of the algorithm used, any structure determination by NMR seeks to find the global minimum region of a target function Etot given by: Etot=Ecov+Evdw+ENMR, where “Ecov,” “Evdw,” and “ENMR” are terms representing the covalent geometry (bonds, angles, planarity, and chirality), the nonbonded contacts, and the experimental NMR restraints, respectively (19). Algorithms currently used include simulated annealing in both Cartesian (20, 21) and torsion angle space (22), metric matrix distance geometry (23), and minimization with a variable target function in torsion angle space (24).
The main source of geometric information contained in the experimental NMR restraints is provided by the nuclear Overhauser effect (NOE). The NOE (at short mixing times) is proportional to the inverse sixth power of the distance between the protons, so its intensity falls off very rapidly with increasing distance between proton pairs. Consequently, NOEs usually are observed only for proton pairs separated by ≤5–6 Å. Despite the short range nature of the observed interactions, the short approximate interproton distance restraints derived from NOE measurements can be highly conformationally restrictive, particularly when they involve residues that are far apart in the sequence but close together in space (1, 19).
Systematic bias arising from the different algorithms used to calculate the structures may be introduced via the first two terms, Ecov and Evdw, in Eq. 1. The values of bond lengths, bond angles, planes, and chirality are known to very high accuracy, so it is clear that the deviations from idealized geometry, as represented by the term Ecov, should be kept very small. The second term, Evdw, representing the nonbonded contacts, is associated with considerably more uncertainty than the covalent geometry (25, 26). Given the numerous ways to represent Evdw (for example, a simple van der Waals repulsion term or a complete empirical energy function including a van der
0027–8424/98/955891–8$0.00/0
PNAS is available online at http://www.pnas.org.
|
* |
To whom reprint requests should be addressed. e-mail: clore@vger.niddk.nih.gov and gronenborn@vger.niddk.nih.gov. |
Waals Lennard-Jones 6–12 potential, an electrostatic potential, and a hydrogen bonding potential), it is evident that variability is introduced via Evdw. It is therefore essential to ensure that the calculated structures display good nonbonded contacts.
The uncertainties associated with the covalent geometry and van der Waals terms can introduce errors of ≈0.3 Å in the coordinates (26). The major determinant of accuracy, however, resides in the number and quality of the experimental NMR restraints that enter into the third term, ENMR, in Eq. 1.
Although a high resolution, carefully refined x-ray structure of a given protein may not be identical to the “true” solution structure, it is likely to be reasonably close in many instances, as evidenced, for example, by the excellent agreement (≤ 1 Hz rms deviation) between the experimentally determined values of the 3JHNα coupling constants in solution and their corresponding calculated values from crystal structures (10, 27, 28). Moreover, it is generally the case that three-bond coupling constants, 13C secondary shifts, and 1H shifts calculated from high resolution crystal structures agree better with the experimentally measured values than those calculated from the corresponding NMR structures (refined in the absence of coupling constant and chemical shift restraints) (10–13, 25). It is therefore instructive to examine the dependence of the backbone rms difference between NMR and x-ray structures on the precision of the NMR structures (25). This dependence is shown in Fig. 1 for 14 proteins, for which both NMR and x-ray structures are available and which are representative of some of the different programs used in NMR protein structure
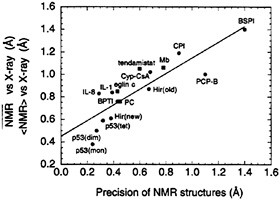
FIG. 1. Correlation between backbone precision of NMR structures and their agreement with x-ray structures. Where the backbone rms difference between the average NMR coordinates (NMR) and the corresponding x-ray structures is available, the values are represented as circles. When only the average backbone rms difference between an ensemble of NMR structures (<NMR>) and the corresponding x-ray structure, is quoted in the literature, squares are used. The straight line represents a linear fit to the data with a slope of 0.70, an intercept of 0.45 Å. and a correlation coefficient of 0.9. The structures are as follows: p53(mon), p53(dim), and p53(tet) are the monomer, dimer, and tetramer, respectively, of the p53 oligomerization domain (51); IL-8, interleukin-8 monomer (52); Hir (new), highly refined structure of hirudin (53); IL-1. interleukin-1β (6, 7); BPTI, bovine pancreatic trypsin inhibitor (54): eglin c (55); PC, French bean plastocyanin (56); tendamistat (57); Hir(old). hirudin (58); Cyp-CsA, cyclophilincyclosporin A complex (59): Mb. carbonmonoxy myoglobin (helices plus heme; ref. 60); CPI, potato carboxypeptidase inhibitor (61); PCP-B, procarboxypeptidase B (62); and BSPI, barley serine proteinase inhibitor 2 (63). The values given exclude conformationally disordered regions as described in the papers cited. Note that the NMR structures of IL-8 and Hir(old) were obtained before the corresponding x-ray structures and that the NMR structure of tendamistat was obtained independently of and at the same time as the x-ray structure. Reproduced from ref. 25.
determination (25). A linear relationship is evident. In addition, in cases in which both low and high precision NMR structures are available for the same protein, the high precision structure is significantly closer to the x-ray structure than the low precision one. The data can be fit to a straight line with a correlation coefficient of 0.9 and a limiting rms difference between NMR and x-ray structures of ≈0.45 Å. Moreover, all of the monomeric NMR structures with a precision of better than 0.5 Å are 0.85 Å or less away from the corresponding crystal structures. Given the fact that the coordinate errors in 1.5- to 2-Å resolution x-ray structures are ≈0.2–0.3 Å (7, 29), these data provide empirical evidence that an accuracy of 0.4–0.8 Å in the backbone coordinates is attainable under appropriate circumstances by using current NMR methodology (25).
The accuracy of NMR structures will be affected by errors in the interproton distance restraints. These errors can arise from two sources: (i) misassignments and (i) errors in distance estimates. Errors due to misassignments may be quite common in low resolution NMR structures. Fortunately, in many cases, these errors are of relatively minor consequence and do not result in the generation of an incorrect fold. Systematic errors in distance estimates may be introduced in attempts to obtain precise distance restraints. For example, interactive relaxation matrix analysis of the NOE intensities (30) and direct refinement against the NOE intensities (31, 32), while accounting for spin diffusion, can result in systematic errors from several sources such as: the presence of internal motions (not only on the picosecond time scale but also on the nanosecond to millisecond time scales); insufficient time for complete relaxation back to equilibrium to occur between successive scans; and differential efficiency of magnetization transfer between protons and their attached heteronucleus in multidimensional heteronuclear NOE experiments (26). For these reasons, it is probably prudent at the present time, at least in cases dealing with proteins, to convert the NOE intensities into loose approximate interproton distance restraints (e.g., 1–8–2.7 Å. 1.8–3.3 Å, 1.8–5.0 Å, and, if appropriate, 1.8–6.0 Å for strong, medium, weak, and very weak NOEs, respectively) with the lower bounds given by the sum of the van der Waals radii of two protons. These distance ranges are sufficiently generous to take into account untoward effects in the conversion of NOE intensities into distances (2, 3, 19, 26). Using this approach, systematic errors in the interproton distance restraints generally will be introduced only at the boundary of two distance ranges.
In the case of experimental structures calculated with an incomplete set of NOE restraints (i.e., comprising <90% of the structurally useful NOEs), there is no doubt that errors, arising both from misassignments as well as from the incorrect classification of NOEs into the various loose approximate distance ranges, will occur, resulting in less accurate structures. This loss in accuracy is due to the fact that, until a significant degree of redundancy is present in the NOE restraints, such errors often can be accommodated readily without unduly comprising the agreement with either the experimental NMR restraints or the restraints for covalent geometry and non-bonded contacts. However, once 90% of the structurally useful NOEs have been assigned and incorporated into the restraints set, corresponding typically to an average of 15 restraints per residue with >60% of the NOEs involving unique proton pairs, two sensitive and complementary techniques can be employed easily to identify and correct such errors.
The first method involves an analysis of the distribution of restraints violations in the ensemble of calculated structures. If a given restraint is systematically violated in more than, for example, 20% of the calculated structures, even by as little as 0.1 Å, it is highly likely that it should either be reclassified into the next looser category (i.e., strong to medium, medium to weak) or that errors in NOE assignments are present (26).
The second approach uses complete cross-validation to assess the completeness of the experimental restraints and the degree to which each distance restraint can be predicted by the remaining ones (33). Typically, this approach involves calculating a series of simulated annealing structures in which the restraints are partitioned randomly into a test set comprising ≈10% of the data and a reference set. Only the reference set is incorporated into the target function, and each calculation is carried out with a different test and reference set pair, thereby permitting one to fully explore the constraining power of the NOE restraints. The average agreement with all of the test sets as well as the atomic rms shift after complete cross-validation then provides an indicator of accuracy.
Finally, a further check on the correctness of the structures is provided by verifying that all short interproton distances (e.g., <3.5 Å) predicted by the structures are in fact observed in the NOE spectra (25). Indeed, this procedure forms the basis of the iterative refinement process; the structures at each successive stage of refinement are used to predict all short interproton distance contacts, which then are searched for in the NOE spectra. In general, the vast majority of interproton distances <3.5 Å, and certainly all of those <2.5 Å, should be observed. Exceptions can occur occasionally if the linewidths of the corresponding resonances are broadened severely because of some sort of intermediate chemical exchange process on the chemical shift scale (caused, for example, by multiple conformations or microheterogeneity) resulting in severe attenuation of the NOE cross peaks.
Additional Experimental NMR Restraints that Define Short Range Order. Although the interproton distance restraints derived from NOEs provide the mainstay of NMR structure determination, direct refinement against other experimental NMR restraints is both feasible and desirable. In this section, we consider experimental restraints that provide short range structural information, specifically three-bond coupling constants (10), secondary 13C chemical shifts (11), and 1H chemical shifts (12, 13).
Three-Bond Coupling Constants. Three-bond coupling constants are related to torsion angles by the Karplus (34) equation: 3J(λ)=Acos2(λ)+Bcos(λ)+C, where λ is the torsion angle corresponding to the three-bond coupling, and A, B, and C are constants obtained by nonlinear optimization to yield the best fit between experimental 3J values and values calculated from a series of very high resolution x-ray structures. The coupling constants can be converted directly into loose torsion angle restraints (19). Alternatively, direct refinement against coupling constants can be achieved by adding the potential EJ=kJ (Jobs–Jcalc)2 (where kJ is a force constant and Jobs and Jcalc are the observed and calculated values of the coupling constants) (10).
From the standpoint of refinement, the most useful coupling constant, in so far that it can be measured accurately and easily by quantitative J correlation spectroscopy and that its Karplus relationship has been parametrized reliably, is the 3JHNα coupling, which is related directly to the ϕ backbone torsion angle (35). The Karplus curve for 3JHNα, however, is symmetric about ϕ=–120°, such that one cannot distinguish ϕ=–120° +α from ϕ=–120°–α from the 3JHNα coupling alone (36). Where appropriate, this degeneracy can be resolved by quantitative J-correlation measurement of the 3Jcoco coupling, which has its steepest ϕ dependence close to ϕ=–120° (36).
It is also worth noting that the relationship between the three-bond amide deuterium isotope shift experienced by 13Cα resonances, 3ΔCα(ND), is related to the backbone ψ angle by a Karplus type relationship of the form 3ΔCα(ND)=30.1+ 22.2 cos (ψ– 90°) ppb (37) and hence can be incorporated into structure refinement in exactly the same manner as three-bond coupling constants.
Secondary 13C Chemical Shifts. There is a clear empirical correlation between the protein backbone conformation, defined in terms of the ϕ and ψ torsion angles, and the 13Cα and 13Cβ secondary chemical shifts (that is, the difference between observed shifts and random coil shifts) (38, 39). In addition, ab initio quantum mechanical calculations have indicated that the ϕ,ψ angles dominate shielding for Cα and Cβ atoms (40). Because the secondary I3Cα and 13Cβ shifts provide information on ψ as well as ϕ and because they are readily measured, it is clearly useful to incorporate them directly into the refinement algorithm.
The strategy that we used makes use of an empirical surface describing the expected Cα and Cβ secondary chemical shifts as a function of the backbone torsion angles ϕ and ψ, derived from the structurally ordered regions of a set of four proteins whose 13C chemical shifts were known and for which high resolution crystal structures are available (38). The expectation surface is given by ![]() exp
exp ![]() ψk)2)/S]}, and similarly for Cβ expected (where S is a Gaussian scale factor given by r2/e0.5 where r is the radius of the Gaussian; in this case r=17.7° and S=450). The average rms difference between the observed chemical shift values and the empirical surface is ≈1.1 ppm. Direct refinement against the 13Gα and I3Cβ shifts is carried out by adding the potential
ψk)2)/S]}, and similarly for Cβ expected (where S is a Gaussian scale factor given by r2/e0.5 where r is the radius of the Gaussian; in this case r=17.7° and S=450). The average rms difference between the observed chemical shift values and the empirical surface is ≈1.1 ppm. Direct refinement against the 13Gα and I3Cβ shifts is carried out by adding the potential ![]() where
where ![]() and kCshift is a force constant (with a value chosen to yield an rms difference between observed and calculated shifts of ≈1 ppm) (11).
and kCshift is a force constant (with a value chosen to yield an rms difference between observed and calculated shifts of ≈1 ppm) (11).
To use simulated annealing to improve the agreement of the observed and expected carbon chemical shifts, the partial derivatives of the energy along ϕ and ψ (i.e., the forces along ϕ and ψ) also must be calculated. These are given by δECshift/ ![]() Because there is no explicit function fitted to the expectation values, the partial derivatives of Cαexpected and Cβexpected with respect to ϕ and ψ are approximated by the local slopes of the expectation value grid about the grid point (ϕ, ψ) at which the energy is evaluated.
Because there is no explicit function fitted to the expectation values, the partial derivatives of Cαexpected and Cβexpected with respect to ϕ and ψ are approximated by the local slopes of the expectation value grid about the grid point (ϕ, ψ) at which the energy is evaluated.
Although the information contained in the secondary 13Cα and 13Cβ chemical shifts is to some extent redundant with that offered by 3JHNα coupling constants, the two experimental measures are complementary (11). Thus, the values of the 3JHNα coupling constants depend only on ϕ, whereas the 13Cα and 13Cβ chemical shifts depend on both ϕ and ψ. Moreover, 3JHNα coupling constants may not be measurable for all residues because of small values of the couplings, line broadening, or chemical shift overlap of the backbone nitrogen atoms. In contrast, 13Cα and 13Cβ shifts are obtained readily for almost all residues.
1H Chemical Shifts. Proton chemical shifts are influenced by short range ring current effects from aromatic groups, magnetic anisotropy of C=O and C-N bonds, and electric field effects arising from charged groups. Recent developments in empirical models for 1H chemical shift calculations have shown that it is now possible to predict 1H chemical shifts for nonexchangeable protons to within 0.23–0.25 ppm for proteins for which high resolution crystal structures are available (41, 42).
The calculated 1H chemical shift σcalc can be decomposed into four terms: the “random coil” (σrandom), “ring current” (σring), “magnetic anisotropy” (σani), and “electric field” (σE) shifts (41). σring depends on the distance and orientation of the aromatic ring to the proton of interest. σani represents the sum of the anisotropies arising from the C=O and C-N bonds of the backbone and the side chain functional groups of Asp, Glu, Asn, and Gin and depends on distance (r–3) and orientation of the proton from these functional groups. Finally, σE depends on the distance (r–2) between the charged heavy atom
and the proton, the angle between the charged heavy atomproton and C-proton vectors, and the charge on the heavy atom.
Direct refinement against 1H chemical shifts is carried out by adding a 1H chemical shift term, Eprot=Σ kprot (σcalc,i – σobs,i)2, where kprot is the force constant and σobs,i and σcalc,i are the observed and calculated 1H chemical shifts, respectively, of proton i (12). For nonstereospecifically assigned methylene and methyl groups, a modification of Eprot is required to make maximal use of the shift information (13). Specifically, this involves making use of a set of potentials that involve the sums and differences of the chemical shifts to automatically handle chemical shifts involving prochiral centers without the need for making a priori stereospecific assignments (13).
Results of Refinement Against Three-Bond Coupling Constants and 13C and 1H Shifts. Provided there are no severe errors in the interproton distance restraints, refinement against 3JHNα coupling constants, 13C shifts, and 1Hshifts reduces the rms difference between calculated and observed values to approximately the level of the expected errors (≈0.5–1 Hz, ≈1 ppm, and ≈0.2–0.3 ppm, respectively) without significantly impairing the agreement with the other restraints in the target function (i.e., experimental interproton distance and torsion angle restraints, covalent geometry, and non-bonded contacts) (10–13). In addition, provided the quality of the initial structures is high, refinement results in only small overall atomic rms shifts with no increase in precision at the expense of accuracy.
We have found 13C shifts particularly useful in regions that are ordered but possess no regular secondary structure. Examples that come to mind are the N-terminal tail of the transcription factor GAGA (43) and the transcriptional coactivator HMG-I/Y (44) bound to the minor groove of DNA. In such cases, the secondary 13C shifts permit one to exclude easily certain backbone conformations.
Whereas coupling constants and 13C shifts are related directly to specific torsion angles, 1H shifts are influenced by close spatial proximity of various functional groups and are particularly useful in the presence of aromatic groups. Indeed, 1H shift refinement was critical in establishing the correct dimer interface in the structure of the C-terminal DNA binding domain of HIV-l integrase (45). Another example is provided by Fig. 2, which illustrates the effect of 1H shift refinement, arising from the presence of a trypophan residue, on the active site of reduced human thioredoxin (12).
Additional NMR Restraints that Define Long Range Order. Until recently, NMR structure determination has relied exclusively on restraints whose information is entirely local and restricted to atoms close in space, specifically NOE-derived short (<5 Å) interproton distance restraints, which may be
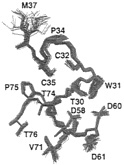
FIG. 2. View of the active site and neighboring regions of reduced human thioredoxin showing a superposition of 40 simulated annealing structure before (blue) and after (red) 1H chemical shift refinement. Reproduced from ref. 12.
supplemented by coupling constants, 13C secondary shifts, and 1H shifts as described above. The success of these methods is mainly due to the fact that short interproton distances between units far apart in a linear array are conformationally highly restrictive. However, there are numerous cases in which restraints that define long range order can supply invaluable structural information (16, 17). In particular, they permit the relative positioning of structural elements that do not have many short interproton distance contacts between them. Examples of such systems include modular and multidomain proteins and linear nucleic acids. Two approaches recently have been introduced that directly provide restraints that characterize long range order a priori. The first relies on the dependence of heteronuclear (15N or 13C) longitudinal (T1) and transverse (T2) relaxation times, specifically T1/T2 ratios, on rotational diffusion anisotropy (16), and the second relies on residual dipolar couplings in oriented macromolecules (17, 18). The two methods provide restraints that are related in a simple geometric manner to the orientation of one-bond internuclear vectors (e.g., N-H and C-H) relative to an external tensor. In the case of the T1/T2 ratios, the tensor is the diffusion tensor (16). In the case of residual dipolar couplings, the tensor may be the magnetic susceptibility tensor for molecules aligned in a magnetic field (17), the molecular alignment tensor for molecules aligned by anisotropic media such as liquid crystals (46), the electric field tensor for molecules aligned by an electric field, or the optical absorption tensor for molecules aligned by polarized light.
Refinement Against T1/T2Ratios. Heteronuclear relaxation has been used for a long time to provide information on internal dynamics. The 15N transverse relaxation time T2 is a function of frequency-dependent and -independent spectral density terms, whereas the 15N longitudinal relaxation time T1 is only a function of the frequency-dependent terms. For axially symmetric rotational diffusion (i.e.,Dzz≠Dxx=Dyy where Dzz, Dxx, and Dyy are the diagonal elements of the diffusion tensor) characterized by diffusion tensor constants parallel (Dǁ=Dzz) and perpendicular (D⊥=[Dxx+Dyy]/2) to the unique axis of the diffusion tensor, the spectral density J(ω), in the limit of very fast, axially symmetric internal motions, is given by ![]() where ω is the angular resonance frequency, and S is the generalized order parameter for rapid internal motion; τ1, τ2, and τ3 are time constants given by (6D⊥)– 1, (D+5D⊥)–1, and (4D+ 2D⊥)–1; and the terms A1, A2, and A3 are given by (1.5cos2θ –0.5)2, 3sin2θcos2θ, and 0.75sin4θ, where θ is the angle between the time-averaged N-H bond vector orientation in the molecular frame and the unique axis of the diffusion tensor (47). In the absence of large amplitude internal motions and conformational exchange line broadening, the 15N T1/T2 ratio for a protein with an axially symmetric diffusion tensor depends only on three variables: the angle θ (arising from the Ak terms) and the diffusion tensor constants D∥ and D⊥. As described below, D∥ and D⊥. are extracted readily from the ensemble of 15N T1and T2 relaxation times.
where ω is the angular resonance frequency, and S is the generalized order parameter for rapid internal motion; τ1, τ2, and τ3 are time constants given by (6D⊥)– 1, (D+5D⊥)–1, and (4D+ 2D⊥)–1; and the terms A1, A2, and A3 are given by (1.5cos2θ –0.5)2, 3sin2θcos2θ, and 0.75sin4θ, where θ is the angle between the time-averaged N-H bond vector orientation in the molecular frame and the unique axis of the diffusion tensor (47). In the absence of large amplitude internal motions and conformational exchange line broadening, the 15N T1/T2 ratio for a protein with an axially symmetric diffusion tensor depends only on three variables: the angle θ (arising from the Ak terms) and the diffusion tensor constants D∥ and D⊥. As described below, D∥ and D⊥. are extracted readily from the ensemble of 15N T1and T2 relaxation times.
Thus, the individual T1/T2 ratios provide a direct measure of the angle θ between the N-H bond vector and the unique axis of the diffusion tensor. This orientation is not known a priori, so we allowed it to float by making use of an external, initially arbitrarily positioned axis, defined by a single C-C bond, positioned 50 Å away from the structure (16). The geometric content of the T1/T2 ratios is incorporated into simulated annealing refinement by adding the potential term Eanis=kanis[(T1/T2)calc–(T1/T2)obs]2, where kanis is a force constant and (T1/T2)obs and (T1/T2)calc are the observed and calculated values of T1/T2, respectively. At each step of the simulated annealing protocol, Eanis is evaluated by calculating the angle between the N-H vectors and the unique axis of the diffusion tensor, defined by the floating C-C bond vector. The desired target value between observed and calculated T1/T2
ratios, based on the experimental uncertainty in the measured T1/T2 values, is achieved by empirically adjusting the value of kanis.
To apply T1/T2 refinement, the values of D∥ and D⊥ must be determined directly from the ensemble of measured T1/T2 ratios without reference to a known structure. For a uniform distribution of N-H bond vectors in space, the probability of finding an N-H vector that makes an angle θ with the unique axis of the diffusion tensor is proportional to sinθ (16). Hence. θ values near 90° are statistically most probable. These are the amides that yield the lowest T1/T2 ratios. The probability of finding an N-H bond vector with θ ≈0° is low, and, consequently, the T1/T2 ratio for θ=0° is not extracted as easily from the range of experimentally observed T1/T2 ratios. Experimentally, (T1/T2)min and an initial estimate of (T1/ T2)max are obtained by taking the average of the lowest and highest T1/T2 ratios, respectively, such that the SDs in their estimates are equal to the measurement error. Initial estimates for D∥ and D⊥ then are obtained by simultaneously best-fitting the complete equations describing (T1/T2)min, (T1/T2)max, and the ratio of these two terms. Because the initial estimate of (T1/T2)max is likely to underestimate the true value of (T1/ T2)max, for the reasons discussed above, the estimated value of (T1/T2)max is increased in a stepwise manner (in increments of 5% up to a 35% increase) yielding new values of D∥ and D⊥. For each set of values, an ensemble of simulated annealing structures is calculated, and the dependence of the rms difference between observed and calculated T1/T2 values. Δ(T1/T2), on the estimated value of (T1/T2)max is examined. The minimum of this function yields the best estimates for D∥ and D⊥. The minimum is relatively shallow, and the structure is not significantly affected by using D∥ and D⊥ values that change (T1/T2)max by up to ±15% but keep (T1/T2)min constant.
The general, fully asymmetric case, in which Dxx≠Dyy, is treated in an analogous manner (16). The 15N T1/T2 ratio then depends not only on the angle θ between the z axis of the diffusion tensor and the N-H vector orientation but also on the angle ϕ that describes the position of the projection of the N-H vector on the x-y plane, relative to the x axis. The rhombicity factor η is defined as 3/2(Dyy–Dxx)/[Dzz–0.5(Dyy+Dxx)]. In practice, for most proteins with large diffusion anisotropy, [2Dzz/(DXX+Dyy) ≥≈1.5], η is found to be smaller than 0.4. Even at the high end of this range (η=0.4), the dependence of the T1/T2 ratio on ϕ is relatively weak (introducing changes in the predicted T1/T2 ratio that are of a magnitude comparable to the uncertainty in the measurements). Although the effect of rhombicity of the diffusion tensor on the T1/T2 ratio is relatively small, including its effect in the structure refinement, procedure does not pose any fundamental problem. In this case, the floating diatomic molecule, used above to describe the orientation of the diffusion tensor in the structure calculations for the axially symmetric case, is replaced by an artificial tetraatomic molecule comprising atoms X, Y, Z, and O, with three mutually perpendicular bonds, X-O, Y-O, and Z-O corresponding to the x, y, and z axes of the diffusion tensor, respectively. Calculation of Eanis is completely analogous to the axially symmetric case but uses the full, five-term expression for the spectral density. A set of structure calculations, carried out for a small number of η values (typically 0, 0.2. and 0.4) then indicates whether inclusion of rhombicity leads to better agreement with the experimental T1/T2 data. As pointed out above, however, the T1/T2 ratio is only a weak function of η, and the exact value of η often is defined poorly by the NMR data.
For the heteronuclear 15N T1/T2 method to be applicable, the molecule must tumble anisotropically (i.e., it must be nonspherical). The minimum ratio of the diffusion anisotropy (D/D⊥) for which heteronuclear T1/T2 refinement will be useful depends entirely on the accuracy and uncertainties in the measured T1/T2 ratios. In practice, the difference between the maximum and minimum observed T1/T2 ratio must exceed the uncertainty in the measured T1/T2 values by an order of magnitude. This typically means that D/D⊥ should be greater than ≈1.5 (16).
Direct refinement against 15N T1/T2 ratios has been applied to the N-terminal domain of enzyme I (EIN), a 30-kDa protein of 259 residues (16). EIN is elongated in shape with a diffusion anisotropy of ≈2. As a result, the observed T1/T2 ratios range from ≈14 when the N-H vector is perpendicular to the diffusion axis to ≈30 when the N-H vector is parallel to the diffusion axis. EIN consists of two domains, and of the 2,818 NOEs used to determine its structure, only 38 involve interdomain contacts (8). Refinement against the T1/T2 ratios resulted in a small change in the relative orientations of the two domains without perturbing the structures of the individual domains.
Refinement Against Residual Dipolar Couplings. The expression for the residual dipolar coupling δ(θ,ϕ) between two directly bonded nuclei can be simplified to the form δ(θ,ϕ)= Da(3cos2θ–1)+3/2 Dr(sin2θ cos2ϕ)], where Da and Dr are the axial and rhombic components of the trace less diagonal tensor D given by 1/3 [D22–(Dxx+Dyy)/2) and 1/3 (Dxx– Dyy), respectively, with Dzz>Dyy≥Dxx; θ is the angle between the interatomic vector and the z axis of the tensor; and ϕ is the angle that describes the position of the projection of the interatomic vector on the x-y plane, relative to the x axis (48). Note that the terms Da and Dr subsume various constants including the gyromagnetic ratios of the two nuclei, the distance between the two nuclei, the generalized order parameter S for internal motion of the internuclear vector, the magnetic field strength, and the medium permeability. [It is worth pointing out that, because Da and Dr scale with S and not S2, the assumption of a uniform S value introduces a negligible error of at most a few percent in the dipolar coupling providing S2≥0.6, particularly when one considers that S2 values in structured regions of a protein typically fall in the 0.85±0.05 range (17)].
The applicability of the residual dipolar coupling method depends on the magnitude of the degree of alignment of the molecule in the magnetic field (17). The magnetic susceptibility of most diamagnetic proteins is dominated by aromatic residues but also contains contributions from the susceptibility anisotropies of the peptide bonds. The magnetic susceptibility anisotropy tensors of these individual contributors are generally not colinear, so the net value of the magnetic susceptibility anisotropy in diamagnetic proteins is usually small. Much larger magnetic susceptibility anisotropies are obtained if many aromatic groups are stacked on each other in such a way that their magnetic susceptibility contributions are additive, as in the case of nucleic acids. Hence, alignment induced by the magnetic field is suited ideally to nucleic acids and proteinnucleic acid complexes (17). In practice, the residual dipolar couplings must exceed the uncertainty in their measured values by an order of magnitude, which typically means that the magnetic susceptibility anisotropy should be ≈–10×10–34 m3 per molecule, which is ≈10 times greater than that for benzene. This translates into values of Da obtained by measuring the difference in one-bond coupling constants at, for example, 360 and 750 MHz of ≈0.5 Hz for N-H vectors and ≈0.9 Hz for C-H vectors. To obtain these values with sufficient accuracy requires that the one-bond couplings be measured by constant-time J-modulated correlation spectroscopy (49). More recently, it has been shown that high degrees of alignment in a magnetic field, corresponding to values of Da of ≈10 Hz for N-H vectors and 18 Hz for C-H vectors, can be achieved readily by the addition of dilute liquid crystalline media, while retaining the sensitivity and resolution of spectra recorded in isotropic media (46). As a result, it becomes feasible to measure several different types of residual dipolar couplings by
simply examining the splittings in 2D or 3D coupled correlation spectra. In particular, the much smaller residual couplings for other types of internuclear vectors, such as C′-N (10 times smaller than N-H) and Cα-C’ and C-C (≈6 times smaller than N-H), are experimentally accessible.
The geometric content of the residual dipolar couplings is incorporated into the simulated annealing protocol by including the term Edipolar=kdipolar(δcalc–δobs)2, where kdipolar is a force constant and δcalc and δobs are the observed and calculated values of the residual dipolar couplings, respectively (17). Just as for Eanis in the case of T1/T2 refinement, Edipolar is evaluated by calculating the θ and ϕ angles between the appropriate bond vectors (e.g., N-H, Cα-H, or Cα-C′) and an external arbitrary axis system, defined by an artificial tetraatomic molecule comprising atoms X, Y, Z, and O, with three mutually perpendicular bonds, X-O, Y-O, and Z-O, representing the x, y, and z axes of the tensor, respectively (17, 18).
To apply residual dipolar coupling refinement, the values of Da and the rhombicity R (defined as Dr/Da) must be determined directly from the experimental data (18). The minimum value of the residual dipolar coupling, δmin, occurs at θ=ϕ= 90°, such that Da is given by -δmin/(1+1.5R). Experimentally, a reliable value of δmin is obtained by taking the average of the smallest residual dipolar couplings such that the SD of the estimated δmin value is equal to the measurement error. The maximum value of the residual dipolar coupling, δmax, which occurs at θ=0°, is given by 2Da. As in the case of the T1/T2 ratios discussed above (16), a reliable estimate of δmax is more difficult to obtain from the experimental data because the probability of finding a bond vector with θ≈0° is low. Consequently, if measurements are available for only a single type of internuclear vector, the value of δmax, and hence the value of Da generally will be underestimated by 15–20%. Nevertheless, the observed value of δmax still can be used to obtain an upper limit for the value of R given by [–2δmin(obs)/ δmax(obs)–1]/1.5 (18).
Because δmin can be determined accurately experimentally (for R<0.6) but Da cannot be obtained independently of R (unless a good estimate of δmax is available), the strategy we use when residual dipolar couplings only have been measured for a single type of internuclear vector involves calculating a series of structure ensembles for different estimates of R. (Note that the rhombicity reaches a maximum value of 2/3 when Dzz= –Dxx and Dyy=0; at this point the z and x axes are interchangeable so that the probability of finding a N-H vector perpendicular to the z axis is the same as finding one parallel to the z axis). The dependence of the rms difference between target and calculated dipolar couplings on the estimated value of R (Rest) shows a minimum when Rest is approximately equal to the target value of R (Rtarget) (18). The same type of dependence is observed for the total energy of the target function, reflecting not only the agreement between target and calculated dipolar couplings but also small changes in the agreement between target and calculated values of the other terms in the target function (18).
Because the distribution of the different vector types relative to the tensor is not identical, it becomes possible, once measurements are available for two or more types of internuclear vectors, to obtain reliable values of Da and R from the observed minimum (δmin), maximum (δmax), and most probable (δP) values of the normalized residual dipolar couplings. The residual dipolar couplings for different internuclear vectors are normalized readily because Da,CD=Da,AB(γCγD/ γAγB)(rAB3/rCD3), where AB and CD are two types of internuclear vector (e.g., N-H and Cα-H); γA, γBγC, and γD the gyromagnetic ratios of atoms A, B, C, and D, respectively; and rAB and rCD the internuclear A-B and C-D distances. A histogram of the normalized residual dipolar couplings displays a powder spectrum with the property that δmin+δmax+ δp=0. The values of Da and R then can be obtained readily by least squares minimization of the following three equations: δmin(obs)=–Da(1+1.5R), δmax(obs)=2Da, and δp(obs)= –Da(1–1.5R). Indeed, model calculations with four different proteins of differing sizes and secondary structure content indicate that, if the N-H, Cα-H. and Cα-C′ residual dipolar couplings are measured for only 50% of the residues, Da and R can be determined in this manner to within better than 5% and ±0.1, respectively, which is quite sufficient because variations in the estimated value of Da and R of ± 10% and ±0.15 have a negligible effect on the calculated structures (18). If only residual dipolar couplings are measured for the NH and Cα-H vectors, Da and R still can be determined to within an accuracy of better than 10% and ±0.15.
An example of the structural impact of residual dipolar coupling refinement is illustrated in Fig. 3 for the case of a complex of the transcription factor GATA-1 with a 16-bp oligonucleotide (17). In this instance, the addition of only 90 dipolar coupling restraints to the ≈1,500 NOE and ≈300 torsion angle restraints resulted in a substantial improvement in the quality of the protein backbone, as judged by an approximately twofold reduction in the number of residues lying outside the most favored region of the Ramachadran ϕ, ψ plot (17). With the exception of a single region, the ensembles of structures calculated with and without dipolar couplings overlap (Fig. 3). There is, however, a substantial displacement (accompanied by a maximal ≈4-Å rms shift in the backbone coordinates of residue 22) in the short loop (residues 21–24) that connects strands β3 and β4. Because this loop has low mobility, as judged from 15N relaxation data, this is a good example illustrating one of the principal shortcomings of NMR structure determination based on NOE measurements, namely an ill-defined region due to lack of long range NOE restraints. The only NOEs observed for residues 22 and 23 are either intraresidue or sequential, and there are no long range NOEs involving residues 21 through 24. Hence, the precision of the backbone coordinates for this loop is lower than that for the α-helix and β-strands. Even though there are loose torsion angle restraints for the ϕ and ψ angles of these residues, accumulation of errors in the experimental restraints (for example, an NOE interproton distance restraint that is slightly too short, even by as little as 0.1 Å) becomes an important
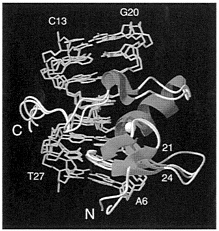
FIG. 3. View showing besifit superpositions of the restrained regularized mean coordinates obtained with and without dipolar coupling restraints. The protein is shown as a ribbon diagram drawn through the Cα positions. The loop between strands β3 and β4 (residues 21–24) is shown in magenta for the structure obtained with dipolar coupling restraints and in grey for the structure obtained without dipolar coupling restraints. Adapted from ref. 17.
factor in determining the orientation of this loop with respect to the rest of the protein.
Refinement with a Conformational Database Potential. In the context of simulated annealing refinement, it is found generally that conventional nonbonded interaction terms (either attractive-repulsive or purely repulsive) have very poor discriminatory power between high and low probability local conformations (14). This can be circumvented by the use of a conformational database potential derived from high resolution, highly refined protein and nucleic acid crystal structures that bias the sampling during simulated annealing refinement to conformations that are energetically possible by limiting the choices of dihedral angles to those that are known to be physically realizable (14, 15).
The database potential, which is partitioned into various one, two, three, and four dimensional distributions (Table 1), is created as follows (14). For each distribution, the fractional probability Pi for a residue to appear within a particular bin (with each dimension digitized in increments of 8–10°) is converted into a potential of mean force EDB(i)=–kDB(lnPi), where kDB is a scale factor. Because the conformational database energy is not a continuous function but rather is known in discrete blocks, the partial derivatives are approximated in a manner analogous to that used for 13C chemical shift potential term (11). To this end, the energy for every rotatable bond (or set of rotatable bonds) being refined against the conformational database potential is defined by looking up the value in the grid bin that encompasses the current dihedral angle(s), and the partial derivatives of the energy with respect to the rotatable bond angles then are approximated by the local slope of the energy function, defined by ∂EDB(ϕi)/∂ϕ≈ –kDB[EDB(ϕi–i)–EDB(ϕi+1)]/2, where EDB (ϕi) is the database energy of bin i along the rotatable bond ϕi and EDB(ϕi–1) and EDB(ϕi÷1) are the database energies of the bins that precede and follow the bin that contains the actual energy value.
Table 1. Summary of database potentials
|
A. Proteins |
|
|
One-dimensional |
|
|
χ4 |
Arg, Lys |
|
Two-dimensional |
|
|
ϕ/ψ |
Gly, Pro, X-Pro, H-bonding*. Val/Ile, rest |
|
χ1/χ2 |
Leu, Ile, Gln/Glu, Arg/Lys/Met, Asn, Asp, Cys(ox), His, Trp, Phe/Tyr |
|
χ2/χ3 |
Met, Gln, Glu, Lys, Arg |
|
Three-dimensional |
|
|
|
Val, Ile, Phe/Tyr/Trp, Leu, X-Pro, Gln/Glu/Arg/Lys/ Met, Cys(red)/His/Asp/Asn, Ser, Thr, Cys(ox), Pro |
|
χ1/χ2/χ3 |
Gln, Glu, Arg, Lys, Met |
|
|
|
|
Four-dimensional |
|
|
B. Nucleic acids |
|
|
Two-dimensional
|
|
|
Three-dimensional
|
|
|
*Residues with a hydrogen bond donor or acceptor in the γ or δ position (Ser, reduced cysteine, Asp, Asn, Ser, and Thr). †The scale factor used for the interresidue |
|
It should be noted that there is one significant difference between the protein and nucleic acids conformational database potentials (15). In the case of the protein conformational database potential, the energy values for the various minima in the multidimensional potential energy surfaces provide a true reflection of the probability of occurrence of particular conformations because protein structures in solution and the crystal state are essentially the same. In the case of nucleic acids, however, and in particular DNA. the frequency of occurrence of different forms in the crystal state does not necessarily reflect their probability of occurrence in solution. For example, in solution under physiological conditions, short DNA oligonucleotides are invariably B-form. In the crystal, however, A, B, or Z-forms can occur depending on the crystallization conditions. As a result, the A and Z forms of DNA are overrepresented in the database, and the energy values for the different minima in the multidimensional potential energy surfaces comprising the nucleic acid conformational database potential do not necessarily reflect their probability of occurrence in solution. This does not, however, affect the positions of the various minima so that, as far as structure refinement is concerned, the nucleic acid conformational database potential still serves its primary function, namely biasing sampling to conformations that are realizable physically.
The effect of incorporating the conformational database potential into refinement is to improve the stereochemistry of the structures in terms of the quality of the Ramachadran plot, the rotamer distributions, and the number of bad contacts (14, 15). If there are no significant errors in the experimental restraints, conformational database refinement will not impact the agreement between the calculated and target experimental, covalent, and van der Waals restraints. The presence of errors in the experimental restraints, however, will be reflected by a large deterioration in the agreement between calculated and target restraints upon conformational database refinement (14). Hence, incorporation of the conformational database provides a good indicator of the quality of both the model and the experimental restraints (14).
Some may regard the introduction of a conformational database energy term as a major step toward empiricism in NMR structure refinement, adding a term with apparently no direct physical counterpart, whose effect will be to make the dihedral angle distributions in NMR refined structures look more like those in crystal structures. However, the combined quality and quantity of high (≤2 Å) resolution protein structures in the crystallographic databases (50) argues strongly against such a viewpoint and makes it very difficult to ignore the available experimental observations relating to dihedral angles in proteins. First, it is invariably the case that high resolution x-ray structures show significantly better agreement with solution observables, such as coupling constants. 13C chemical shifts, and proton chemical shifts, than the corresponding NMR structures, including the very best ones (obtained in the absence of direct coupling constant and chemical shift restraints) (10–13, 27, 28, 41, 42). Hence, in most cases, a high (≥2 Å) resolution crystal structure of a soluble globular protein will provide a better description of the structure in solution than the corresponding NMR structure. Second, the probability distributions for the various dihedral angles observed in the crystallographic database are a direct result of the underlying physical chemistry of the system and as such provide a perfectly reasonable, albeit empirically derived, measure of the relative energetics of different combinations of dihedral angles (14). Third, the discriminating and converging power of the conformational database potential with regard to dihedral angles is significantly better than that of the currently available empirical nonbonded potentials. This point is hardly surprising because the conformational database potential acts
directly on rotatable bonds whereas the nonbonding potentials do not.
A question that is invariably asked about the conformational database potential is whether one will be able to pick up unusual sidechain or backbone conformations. Inspection of high resolution protein x-ray structures indicates that one safely can assume that 90–95% of all residues have a sidechain conformation resembling that of a common rotamer (50). Under these conditions, residues that truly exhibit a skewed rotamer conformation will be spotted by specific discrepancies between the model and the experimental restraints, and in most circumstances such violations will be accounted for by special structural features of the model. Moreover, one should be especially careful in believing a nonrotamer sidechain conformation in NMR structures in the absence of extensive NOE and coupling constant data relating to that particular residue. Exactly the same arguments can be applied to ϕ, ψ angles located in unfavorable regions of the Ramachandran plot, which likewise should be treated with extreme caution unless there is extensive experimental evidence to the contrary (50).
We thank Ad Bax, Dan Garrett, John Kuszewski, and Nico Tjandra for many stimulating discussions.
1. Clore, G.M. & Gronenborn, A.M. (1991) Science 252, 1390– 1399.
2. Wuthrich, K. (1986) NMR of Proteins and Nucleic Acids (Wiley, New York).
3. Clore, G.M. & Gronenborn, A.M. (1987) Protein Eng. 1, 275–288.
4. Dyson, H.J., Gippert, G.P., Case, D.A., Holmgren. A. & Wright, P.E. (1990) Biochemistry 29, 4129–4136.
5. Forman-Kay, J.D., Clore, G.M., Wingfield, P.T. & Gronenborn, A.M. (1991) Biochemistry 30, 2685–2698.
6. Clore, G.M., Wingfield, P.T. & Gronenborn, A.M. (1991) Biochemistry 30, 2315–2323.
7. Clore, G.M. & Gronenborn, A.M. (1991) J. Mol. Biol. 221, 47–53.
8. Garrett, D.S., Seok, Y.J., Liao, D.-I., Peterkofsky, A., Gronenborn, A.M. & Clore, G.M. (1997) Biochemistry 36, 2517–2530.
9. Martin, J.R., Mulder, F.A.A., Karimi-Nejad, Y., van der Zwan, J., Mariani, M., Schipper, D. & Boelens, R. (1997) Structure 5, 521–532.
10. Garrett, D.S., Kuszewski, J., Hancock, T.J., Lodi, P.J., Vuister, G.W., Gronenborn, A.M. & Clore, G.M. (1994) J. Magn. Reson. 104, 99–103.
11. Kuszewski, J., Qin, J., Gronenborn, A.M. & Clore, G.M. (1995) J. Magn. Reson. 106, 92–96.
12. Kuszewski, J., Gronenborn, A.M. & Core, G.M. (1995) J. Magn. Reson. 107, 293–297.
13. Kuszewski, J., Gronenborn, A.M. & Clore, G.M. (1996) J. Magn. Reson. 112, 79–81.
14. Kuszewski, J., Gronenborn, A.M. & Clore, G.M. (1996) Protein Sci. 5, 1067–1080.
15. Kuszewski, J., Gronenborn, A.M. & Clore, G.M. (1997) J. Magn. Reson. 125, 171–177.
16. Tjandra, N., Garrett, D.S., Gronenborn, A M., Bax, A & Clore, G.M. (1997) Nat. Struct. Bioi. 4, 443–449.
17. Tjandra, N., Omichinski, J.G., Gronenborn, A.M., Clore, G.M. & Bax, A. (1997) Nat. Struct. Biol. 4, 732–738.
18. Clore, G.M., Gronenborn, A.M. & Tjandra, N. (1998) J. Magn. Reson., 131, 159–162.
19. Clore, G.M. & Gronenborn, A.M. (1989) CRC Crit. Rev. Biochem. Biol. Biol. 24, 479–564.
20. Clore, G.M., Brünger, A.T., Karplus, M. & Gronenborn, A.M. (1986) J. Mol. Biol. 191, 523–551.
21. Nilges, M., Clore, G.M. & Gronenborn, A.M. (1988) FEBS Lett. 229, 317–324.
22. Stein, E.G., Rice, L.M. & Brünger, A.T. (1997) J. Magn. Reson. 124, 154–164.
23. Havel, T.F. & Wuthrich, K. (1985) J. Mol. Biol l82, 381–394.
24. Braun, W. (1987) Q. Rev. Biophys. 19, 115–157.
25. Gronenborn, A.M. & Clore, G.M. (1995) CRC Crit. Rev. Biochem. Mol. Biol. 30, 351–385.
26. Clore, G.M., Robien, M.A. & Gronenborn, A.M. (1993) J. Mol. Biol. 231, 81–102.
27. Bartik, K., Dobson, C.M. & Redfield, C. (1993) Eur. J. Biochem. 215, 255–266.
28. Wang, A.C. & Bax, A. (1996) J. Am. Chem. Soc. 118, 2483–2494.
29. Luzzati, V. (1952) Acta Crystalhgr. 5, 802–810.
30. Borgias, B.A., Gochin, M., Kerwood, D.J. & James, T.L. (1990) Progr. NMR Spectrosc. 22, 83–100.
31. Yip, P. & Case, D.A. (1991) J. Magn. Reson. 83, 643–648.
32. Nilges, M., Habbazettl, P., Brünger, A.T. & Holak, T.A. (1991) J. Mol. Biol. 219, 499–510.
33. Brünger, A.T., Clore, G.M., Gronenborn, A.M., Saffrich, R. & Nilges, M. (1993) Science 261, 328–331.
34. Karplus, M. (1963) J. Am. Chem. Soc. 85, 2870.
35. Bax, A., Vuister, G.W., Grzesiek, S., Delaglio, F., Wang, A.C., Tschudin, R. & Zhu, G. (1994) Methods Enzymol. 239, 79–106.
36. Hu, J.-S. & Bax, A. (1996) J. Am. Chem. Soc. 118, 8170–8171.
37. Ottiger, M. & Bax, A. (1997) J. Am. Chem. Soc. 119, 8070–8075.
38. Spera, S. & Bax, A. (1991) J. Am. Chem. Soc. 113, 5491–5492.
39. Wishart, D.S. & Sykes, B.D. (1994) J. Biomol NMR 4, 171–180.
40. Oldfield, E. (1995) J. Biomol. NMR 5, 217–225.
41. Osapay, K.A. & Case, D.A. (1991) J. Am. Chem. Soc. 113, 9436–9444.
42. Williamson, M.P. & Asakura, T. (1993) J. Magn. Reson. 101, 63–71.
43. Omichinski, J.G., Pedone, P.V., Felsenfeld, G., Gronenborn, A.M. & Clore, G.M. (1997) Nat. Struct. Biol. 4, 122–132.
44. Huth, J.R., Bewley, C.A., Nissen, M.S., Evans, J.N.S., Reeves, R., Gronenborn, A.M. & Core, G.M. (1997) Nat. Struct. Biol. 4, 657–665.
45. Lodi, P.J., Ernst, J.A., Kuszewski, J., Hickman, A.B., Engelman, A., Craigie, R., Clore, G.M. & Gronenborn, A.M. (1995) Biochemistry 34, 9826–9833.
46. Tjandra, N. & Bax, A (1997) Science 278, 1111–1114.
47. Woessner, D.E, (1962) J. Chem. Phys. 36, 647–654.
48. Bothner-By, A.A. (1995) in Encyclopedia of Nuclear Magnetic Resonance, eds. Grant. D.M. & Harris, R.K. (Wiley, Chichester, U.K.), pp. 2932–2938.
49. Tjandra, N., Grzesiek, S. & Bax, A. (1996) J. Am. Chem. Soc. 118, 6264–6272.
50. Kleywegt, G.J. & Jones, T.A (1997) Methods Enzymol 227, 208–230.
51. Clore, G.M., Ernst, J.A, Clubb, R.T., Omichinski, J.G., Kennedy, W.M.P., Sakaguchi, K., Appella, E. & Gronenborn, A.M. (1995) Nat. Struct. Biol. 2, 321–332.
52. Clore, G.M. & Gronenborn, A.M. (1991) J. Mol Biol. 217, 611–620.
53. Szyperski, T., Güntert, P., Stone, S.R. & Wüthrich, K. (1992) J. Mol. Biol. 228, 1192–1205.
54. Berndt, K.D., Günter, P., Orbons, L.P.M. & Wüthrich, K. (1992) J. Mol Biol. 227, 757–775.
55. Hyberts, S.G., Goldberg, M.S., Havel, T.F. & Wagner, G. (1992) Protein Sci. 1, 736–751.
56. Moore, J.M., Lepre, C., Gippert, G.P., Chazin, W.J., Case, D.A. & Wright, P.E. (1991) J. Mol Biol. 221, 533–555.
57. Billeter, M., Kline, A.D., Braun, W., Huber, R. & Wüthrich, K. (1989) J. Mol Biol. 206, 677–687.
58. Folkers, P.J. M., Clore, G.M., Driscoll, P.C., Dodt, J., Köhler, S. & Gronenborn, A.M. (1989) Biochemistry 28, 2601–2617.
59. Spitzfaden, C., Braun, W., Wider, G., Widmer, H. & Wüthrich, K. (1994) J. Biomol. NMR 4, 463–482.
60. Osapay, K., Theriault, Y., Wright, P.E. & Case, D.A (1994) J. Mol. Biol. 244, 183–197.
61. Clore, G.M., Gronenborn, A.M., Nilges, M. & Ryan, C.A. (1987) Biochemistry 26, 8012–8023.
62. Billeter, M., Vendrell, J., Wider, G., Aviles, F.X., Coll, M., Guasch, A., Huber, R. & Wüthrich, K. (1992) J. Biomolec. NMR 2, 1–10.
63. Clore, G.M., Gronenborn, A.M., James. M.N.G., Kjaer, M., McPhalen, C.A. & Poulsen. F.M. (1987) Protein Eng. 1, 313–318.








