Proc. Natl. Acad. Sci. USA
Vol. 95, pp. 5899–5905, May 1998
Colloquium Paper
This paper was presented at the colloquium “Computational Biomolecular Science,” organized by Russell Doolittle, J.Andrew McCammon, and Peter G.Wolynes, held September 11–13, 1997, sponsored by the National Academy of Sciences at the Arnold and Mabel Beckman Center in Irvine, CA.
Estimation of evolutionary distances under stationary and nonstationary models of nucleotide substitution
(substitution models/rate heterogeneity/stationarity/nonstationarity/estimation bias)
XUN GU* AND WEN-HSIUNG LI†‡
*Institute of Molecular Evolutionary Genetics, 328 Muellcr Laboratory. Pennsylvania State University, University Park, PA 16802: and †Human Genetics Center, SPH, Universitv of Texas, P.O.Box 20334, Houston, TX 77225
ABSTRACT Estimation of evolutionary distances has always been a major issue in the study of molecular evolution because evolutionary distances are required for estimating the rate of evolution in a gene, the divergence dates between genes or organisms, and the relationships among genes or organisms. Other closely related issues are the estimation of the pattern of nucleotide substitution, the estimation of the degree of rate variation among sites in a DNA sequence, and statistical testing of the molecular clock hypothesis. Mathematical treatments of these problems are considerably simplified by the assumption of a stationary process in which the nucleotide compositions of the sequences under study have remained approximately constant over time, and there now exist fairly extensive studies of stationary models of nucleotide substitution, although some problems remain to be solved. Nonstationary models are much more complex, but significant progress has been recently made by the development of the paralinear and LogDet distances. This paper reviews recent studies on the above issues and reports results on correcting the estimation bias of evolutionary distances, the estimation of the pattern of nucleotide substitution, and the estimation of rate variation among the sites in a sequence.
Evolutionary distances (usually designated by d) such as the number of nucleotide substitutions between two DNA sequences (K) are basic quantities in the study of molecular evolution because they are required for computing the rate of evolution in a DNA or protein sequence, for inferring the evolutionary relationships among genes or organisms, and for estimating the divergence dates between taxa or genes (1–9). For these purposes, however, it is essential to obtain reliable estimates of evolutionary distances. Indeed, if the evolutionary distances are not accurately estimated, all distance matrix methods of tree reconstruction may be misleading (5–6, 8). Because accurate estimation of evolutionary distances requires a realistic model of nucleotide substitution, much effort has been made to develop general models of nucleotide substitution (4, 8).
If the process of nucleotide substitution is stationary, i.e., if the nucleotide compositions of the sequences under study have been approximately constant over time, then fairly general models of nucleotide substitution can be developed. For the stationary, time-reversible model (the SR model), Lanave et al. (10), Gu and Li (11), and others (12–14) have developed methods for estimating K. This model includes many other models as special cases (see next page). Moreover, Gu and Li (11) have recently extended the SR model to include rate
variation among sites, i.e., the SRV model, in which SRV stands for stationary, time-reversible, and rate-variable.
When nucleotide frequencies change with time so that stationarity does not hold, phylogenetic reconstruction using distances estimated under a stationary model can be misleading because it tends to group together sequences of similar nucleotide compositions irrespective of their true evolutionary relationships (15–18). Nonstationarity greatly complicates the mathematics. Fortunately, significant progress has been made with the development of the paralinear (19) and LogDet distances (17, 20). However, both methods assume a uniform rate among sites, and so methods for dealing with rate heterogeneity remain to be developed.
An issue related to the estimation of evolutionary distances is the estimation of the pattern of nucleotide substitution. This pattern can be reliably estimated under stationarity (21–23) but is difficult to estimate under nonstationarity. Another problem closely related to distance estimation is how to estimate the degree of rate variation among sites (24–29). Many methods have been proposed for this purpose under a specific distribution (e.g., a gamma distribution). However, how to estimate rate heterogeneity without assuming a specific distribution has been unclear (30). These issues will be considered in this paper.
A further issue is that estimation bias usually occurs when the sequence length is short so that stochastic effects are strong. Although the bias tends to become trivial as the sequence length increases, it is desirable to correct the bias because in practice many sequences studied are actually very short (31–32).
The purpose of this article is to review recent studies on the above issues and to present our results.
Stationary Models
The SR Model. Assume that nucleotide substitution follows a stationary Markov process (10–14). Denote A, G, T, and C as 1, 2, 3, and 4, respectively. Let R be the rate matrix whose ij-th element rij is the rate of change from nucleotide i to nucleotide j (i≠j, i, j=1, 2, 3, 4); the diagonal elements are given by rii=–∑j≠irij. Then the matrix of transition probabilities P for t time units is given by P=eRt, where the ij-th element Pij is the probability of transition from nucleotide i to nucleotide j after t evolutionary time units.
The substitution process is reversible in time if and only if πirij=πjrji, where πi is the equilibrium frequency of nucle
©
PNAS is available online at http://www.pnas.org.
| Abbreviations: SR, stationary time reversible: SRV. SR rate-variable; NR, time-irreversible; TR, time-reversible. |
‡ | To whom reprint requests should be addressed, e-mail: li@hgc.sph.tmc.uth.edu. |
otide i. The preceding relation implies that the off-diagonal elements of R can be expressed as
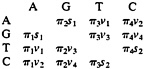
Therefore, the SR model is a nine-parameter model and includes many models as special cases, e.g., the models of Jukes and Cantor (33), Kimura (34), Tajima and Nei (35), Hasegawa et al. (21), and Tamura and Nei (22). The SR model has been studied by many authors (10–14, 23, 36).
Consider two sequences (designated by 1 and 2) that have evolved from O, their common ancestor, t time units ago (Fig. 1). Under stationarity, time-reversibility means that the substitution process from the common ancestor O to sequences 1 and 2 is equivalent to the substitution process from 1 through O to 2 (or from 2 through O to 1), whose transition probability matrix for 2t time units is given by
P=e2tR. [1]
Let λk (k=1, 2, 3, 4) be the k-th eigenvalue of the rate matrix R; one of them is zero, say λ4=0. Let zk be the k-th eigenvalue of P. Eq. 1 implies zk=e2tλk. Gu and Li (11) showed that the evolutionary distance defined by the average number of substitutions per site (i.e.,) ![]() is given by
is given by
[2]
where constants ck are determined by the eigenmatrix of P. Eq. 2 is generally valid since all eigenvalues zk are real under the SR model (11, 37). For example, under the Jukes-Cantor model (33), z1=z2=z3=1–4p/3 and c1=c2=c3=1/4 so that Eq. 2 is reduced to d=–(3/4)ln(1–4p/3), where p is the proportion of nucleotide differences between the two sequences.
The SR distance can be estimated from the data matrix J, whose ij-th element (Jij) is the frequency of sites at which the nucleotides in the two sequences are i and j, respectively. By time-reversibility, we have Jij=πiPij. Therefore, the ij-th element of P (for 2t time units) can be estimated by P̂ij=Jij/πi (i,j=1,…, 4), where πi, and Jij are easily obtained from the sequence data. Let matrix P̂ consist of P̂ij. Its eigenvalues ẑk (k =1,…, 3) can be computed by a standard algorithm, and the constants are given by ![]() (k=1, 2, 3), where uik and vkj are the elements of the corresponding eigenmatrix U and its inverse matrix V, respectively. For
(k=1, 2, 3), where uik and vkj are the elements of the corresponding eigenmatrix U and its inverse matrix V, respectively. For

FIG. 1. Two DNA sequences diverged t time units ago.
details, see Saccone et al. (38), Gu and Li (11), and Li and Gu (39). The sampling variance of d and the variance-covariance matrix for more than two DNA sequences can be found in Gu and Li (11).
Eq. 2 can be used to define many additive distances by choosing appropriate constants ck (Table 1), e.g., the number of nucleotide substitutions per site (K), the number of transitional substitutions per site (A), the number of transversional substitutions per site (B), and the number of substitutions from nucleotides i to j (Dij). These distance measures are useful for phylogenetic analysis and molecular clock testing.
The SRV Model. Rate variation among sites can be incorporated into the SR model by assuming rij=aiju, where aij is a constant and u varies according to a gamma distribution
[3]
with mean ū=α/β; α is the shape parameter and determines the degree of rate variation. Under this model, the (mean) transition probability matrix P for 2t time units is given by
[4]
where I is the identity matrix and the mean rate matrix R̄=ūA where matrix A consists of aij (11). From Eq. 4, one can show that the k-th eigenvalue of P is given by
[5]
where λk is the k-th eigenvalue of R. It follows that the evolutionary distance under the SRV model is given by
[6]
The constants ck are determined in the same manner as above (Table 1). Note that Eq. 4 reduces to Eq. 1 and Eq. 6 to Eq. 2 as α→∞, i.e., the substitution rate is uniform among sites.
Furthermore, Eq. 6 can be generalized to any distribution f(u) for the rate variation among sites. Let G(s)=![]() (u)du be the moment-generating function of f(u). Gu and Li (11) showed that zk=G(2λkt), k=1, 2, 3, 4. Thus, the general additive distance is given by
(u)du be the moment-generating function of f(u). Gu and Li (11) showed that zk=G(2λkt), k=1, 2, 3, 4. Thus, the general additive distance is given by
[7]
where G–1 is the inverse function of the moment-generating function G. For example, consider the invariant+gamma model (26, 40–41): (i) for a given site, the probability of being invariable (i.e., u=0) is θ, whereas the probability of being variable is 1—θ; and (ii) among the sites that are variable, the substitution rate follows a gamma distribution. By applying Eq.
Table 1. The constants ck in the general SR or SRV distance
7, one can show that the evolutionary distance under the invariant + gamma distribution is given by
[8]
For other distributions, see Waddell et al. (30).
Bias-Corrected SR and SRV Distances. Our computer simulation has shown that when the sequence length is short the SR and SRV methods tend to overestimate the evolutionary distance. The bias can be corrected as follows.
Let d̂ be an estimate of the SR or SRV distance. We use the first three terms of the Taylor expansion to obtain an approximate expression of E[d]. For the SR model,
[9]
Therefore, the bias-corrected SR distance is given by
dc=d–δ, [10]
where δ is defined as
[11]
and Var(ẑk) can be obtained by the method of Gu and Li (11).
The bias-corrected distance under the SRV model also can be written as Eq. 10, except that δ is replaced by
[12]
Computer Simulation. Extensive computer simulations on the performance of the SR and SRV methods have been conducted in this study and in Rodriguez et at. (14), Zharkikh (31), and Gu and Li (11). The results can be summarized as follows.
-
When the sequence length (L) is long and the rate of substitution is uniform among sites, the SR method performs well, whereas simpler methods [e.g., Kimura’s two-parameter method (34)] give biased estimates if some assumptions of the method are violated (11, 14, 31). Because the actual substitution pattern of DNA evolution may be complex, the SR method is preferred when the sequences are long, say, longer than 1,000bp.
-
The SR method may give large biases when the sequence length is short (say, L≤200), but the biases can be substantially reduced by the bias-corrected SR distance (Table 2). As L becomes longer than 2,000 bp, the estimation bias virtually decreases to zero. The same comment applies to the SRV method (Table 3).
-
The SR method performs well even when DNA sequence evolution is not time-reversible (see models NR1 and NR2 in Table 2). Therefore, the assumption of time-reversibility, which simplifies the estimation problem considerably, may not have serious effects on distance estimation.
-
When the substitution rate varies among sites, the evolutionary distance can be seriously underestimated by the SR method: note that this bias is systematic and cannot be eliminated by increasing sequence length. As shown in Table 3, the SRV method performs well and the estimation bias vanishes when L is long.
-
The methods developed by Gu and Li (11) for estimating sampling variance under the SR and SRV models appear to be reliable except when L<200 and d>1.0.
-
The mean squared error defined by MSE=bias2+ Var(d) is useful for comparing the relative performance of two methods because for a simple method, the sampling variance
Table 2. The mean of distances (d) over simulation replicates estimated by the bias-corrected SR method and the SR method
|
|
Sequence length (L) |
||
|
Model |
200 |
500 |
2000 |
|
|
(1) d=0.5 |
|
|
|
JC |
0.503 (0.506) |
0.506 (0.516) |
0.501 (0.502) |
|
K2P |
0.507 (0.517) |
0.502 (0.506) |
0.501 (0.502) |
|
TN |
0.508 (0.516) |
0.504 (0.507) |
0.501 (0.502) |
|
TmN |
0.505 (0.516) |
0.505 (0.509) |
0.501 (0.502) |
|
SR |
0.509 (0.517) |
0.503 (0.506) |
0.501 (0.502) |
|
NR1 |
0.509 (0.517) |
0.503 (0.507) |
0.501 (0.502) |
|
NR2 |
0.510 (0.517) |
0.505 (0.509) |
0.501 (0.502) |
|
|
(2)d=1.0 |
|
|
|
JC |
1.036 (1.082) |
1.013 (1.029) |
1.005 (1.008) |
|
K2P |
1.072 (1.093) |
1.008 (1.038) |
1.003 (1.009) |
|
TN |
1.046 (1.089) |
1.015 (1.037) |
1.006 (1.010) |
|
TmN |
1.061 (1.085) |
1.016 (1.050) |
1.005 (1.012) |
|
SR |
1.049 (1.085) |
1.006 (1.038) |
1.005 (1.009) |
|
NR1 |
1.057 (1.090) |
1.009 (1.044) |
1.005 (1.011) |
|
NR2 |
1.071 (1.094) |
1.015 (1.055) |
1.006 (1.012) |
|
The value presented in each case is the mean of d estimated by the bias-corrected SR method and the value in parentheses by the (uncorrected) SR method. Simulation models: JC, the Jukes-Cantor model (33). K2P, Kimura’s two parameter model (34): the transition/ transversion ratio is 4. For TN (Tajima and Nei, Ref. 35), TmN (Tamura and Nei, Ref. 22), SR, and the two time-irreversible models (NR1 and NR2), see Gu and Li (11) for a detailed description. |
|||
-
tends to be smaller but the bias tends to be larger (11). For example, using this criterion, Gu and Li (11) found that SR is superior to JC when L>500 bp and that SRV is always superior to SR when the substitution rate varies among sites.
Estimating the Pattern of Nucleotide Substitution. The pattern of nucleotide substitution can be measured by the off-diagonal elements of the rate matrix R. For simplicity, these elements are usually rescaled, and here, we define the pattern of nucleotide substitution as R*=2tR. Consider two DNA sequences (Fig. 1) under the SR model. Denote the diagonal matrix of the eigenvalues of P=e2tR by diag(z1, Z2,
Table 3. The mean of distance (d) estimated by the SRV method and the bias-corrected SRV method
|
L |
true d |
SR+V model |
NR2+V model |
|
(1) α=0.5 |
|
||
|
200 |
0.3 |
0.317 (0.325) |
0.320 (0.334) |
|
0.5 |
0.520 (0.552) |
0.555 (0.574) |
|
|
1.0 |
1.068 (1.179) |
1.193 (1.303) |
|
|
500 |
0.3 |
0.303 (0.307) |
0.305 (0.310) |
|
0.5 |
0.508 (0.517) |
0.510 (0.520) |
|
|
1.0 |
1.027 (1.061) |
1.037 (1.077) |
|
|
(2) α=1.0 |
|
||
|
200 |
0.3 |
0.312 (0.318) |
0.313 (0.319) |
|
0.5 |
0.513 (0.528) |
0.531 (0.544) |
|
|
1.0 |
1.038 (1.126) |
1.063 (1.149) |
|
|
500 |
0.3 |
0.306 (0.309) |
0.306 (0.309) |
|
0.5 |
0.508 (0.514) |
0.502 (0.507) |
|
|
1.0 |
1.013 (1.037) |
1.022 (1.053) |
|
|
(3) α=2.0 |
|
||
|
200 |
0.3 |
0.307(0.311) |
0.308 (0.312) |
|
0.5 |
0.514 (0.526) |
0.514 (0.524) |
|
|
1.0 |
1.046 (1.132) |
1.060 (1.146) |
|
|
500 |
0.3 |
0.300 (0.302) |
0.300 (0.301) |
|
0.5 |
0.503 (0.508) |
0.502 (0.507) |
|
|
1.0 |
1.012 (1.034) |
1.015 (1.043) |
|
|
The value presented in each case is the mean of d estimated by the bias-corrected SRV method, and the value in parentheses by the (uncorrected) SRV method. See the note of Table 2 for details. |
|||
z3, z4). By matrix theory, we have P=U diag(z1, z2, z3, z4)U–1, where U is the eigenmatrix of P. Then, the substitution pattern R*=2tR=In P can be expressed as
R*=U diag(ln z1, In z2, In z3, In z4)U–1, [13]
Therefore, using the same procedure, we can estimate the evolutionary distance and the pattern of nucleotide substitution simultaneously. In the same manner, under the SRV model one can show that the pattern of nucleotide substitution can be estimated by
[14]
where ![]() (see also ref. 42).
(see also ref. 42).
It is known that estimation of the pattern of nucleotide substitution can be significantly improved by using n>2 sequences, but the estimation procedure becomes complex because it needs to consider the phylogenetic tree of the sequences, which may be unknown. The following simple method does not require knowledge of the tree topology. For a given pair of sequences i and; j, which diverged tij time units ago, the transition probability matrix under the SR model is P(ij)=e2tijR. By multiplying P(ij) over all pairs of sequences, we have
[15]
where τ=∑i<jtij. Similarly, under the SRV model, one can show that
[16]
Therefore, when the transition probability matrix for each pair of sequences has been estimated, which is denoted by P̂ij, we first compute P̂(2τ)=IIi<jP̂ij. Then, under the SR or SRV model, the substitution pattern R*=2τR for n sequences can be estimated by an approach similar to that for the case of two sequences. The sampling variances for the estimated substitution pattern can be obtained by the analytical method developed by Gu and Li (11) or by a simple resampling technique (e.g., bootstrapping).
When many sequences are considered for estimating the substitution pattern, the time scale τ in Eq. 16 can be very large, resulting in some elements in R* larger than one. Because we are more concerned with the relative rates among the types of nucleotide substitutions, it is better to provide a normalized substitution pattern. A simple normalization procedure is to compute ![]() where M=n(n–1)/2 and the weight wij=1/dij
where M=n(n–1)/2 and the weight wij=1/dij
A General Measure of Rate Variation Among Sites
Gu et al. (26) suggested a normalized measure (ρ) for evaluating the relative strength of the rate variation among sites:
[17]
where ![]() Var(u) and ū are the variance and mean of the evolutionary rate (u) for any distribution f(u). As ρ varies from 0 to 1, the rate heterogeneity increases from a uniform rate over sites (ρ=0 or Cv=0) to the maximum heterogeneity (ρ=1 or Cv=∞). Therefore, ρ can directly reflect rate heterogeneity, and unlike the shape parameter α of the gamma distribution, it does not depend on a specific distribution.
Var(u) and ū are the variance and mean of the evolutionary rate (u) for any distribution f(u). As ρ varies from 0 to 1, the rate heterogeneity increases from a uniform rate over sites (ρ=0 or Cv=0) to the maximum heterogeneity (ρ=1 or Cv=∞). Therefore, ρ can directly reflect rate heterogeneity, and unlike the shape parameter α of the gamma distribution, it does not depend on a specific distribution.
In the following we describe a simple method for estimating ρ without assuming a specific model for the rate variation among sites. We assume (i) at each site nucleotide substitution follows a Poisson process, and (ii) the evolutionary rate u varies among sites according to the distribution f(u). Let X be the number of substitutions at a nucleotide site with rate u. Then, the first two conditional moments of X are given by E[X|u]=uT and E[X2|u]=uT+(uT)2, respectively, where T is the total evolutionary time. It follows that the first two (unconditional) moments of X over all sites are E[X]= E[E(X|u)]=TE[u], and E[X2]=E[E[X2|u]]=TE[u]+ T2E[u2], respectively, where E[u] and E[u2] are the first two moments of f(u), respectively. Let m=E[X] and V=E[X2] –m2, and let ū=E[u] and Var(u)=E[u2]–(ū)2. One can show that m=ūT and V=ūT+Var(u)T2, and so ![]() Therefore, the parameter ρ is given by
Therefore, the parameter ρ is given by
[18]
To estimate ρ from sequence data, we need to know the number of substitutions at each site. Conventionally, this number is inferred by the parsimony method (43) when the phylogenetic tree is known. However, the parsimony method tends to underestimate the true number of substitutions (29, 44). Gu and Zhang (29) solved this problem by using a combination of ancestral sequence inference and maximum likelihood estimation. Let X̂i be the number of substitutions at the ith site estimated by Gu and Zhansfs method (29). Then, ![]() (L is the sequence length) so that ρ̂ can be easily obtained from Eq. 18 without knowing the distribution f(u).
(L is the sequence length) so that ρ̂ can be easily obtained from Eq. 18 without knowing the distribution f(u).
The biological meaning of ρ can be easily understood by using the following simple model. Let v be the mutation rate at a site. For invariant sites, the substitution rate is 0, and for the other sites, the rate is hv, where 0<h≤1. The average substitution rate of the gene is therefore u=(1–θ)hv, where θ is the frequency of invariable sites. It is easy to show that Cv![]() and ρ=θ. Thus, the substitution rate can be expressed as
and ρ=θ. Thus, the substitution rate can be expressed as
u=(1–ρ)hv. [19]
This formula predicts a negative correlation between substitution rate and the rate variation among sites, which has been observed by J.Zhang and X.Gu (unpublished results).
Nonstationary Models
LogDet and Paralinear Distances. The paralinear (19) and LogDet (17, 20) distances have been proposed to deal with nonstationarity. They are based on the most general model of nucleotide substitution. Historically, these methods can be traced back to Barry and Hartingan (13) and Cavender and Felseinstein (45).
Consider the evolution of two sequences (Fig. 1). Denote the diagonal matrix of nucleotide frequencies at node k (k=0, 1, 2) by ![]() where the subscript; j refers to nucleotide j. Let J be the data matrix as defined previously. Then, the paralinear distance (between sequences 1 and 2) is defined as
where the subscript; j refers to nucleotide j. Let J be the data matrix as defined previously. Then, the paralinear distance (between sequences 1 and 2) is defined as
[20]
where det( ) means the determinant of a matrix, and for a diagonal matrice, we have ![]() A related measure is the LogDet distance (17, 20), which is defined as
A related measure is the LogDet distance (17, 20), which is defined as
[21]
In Eq. 21, the constant –In 4 is added because it does not change any property of the original LogDet distance but makes the biological interpretation easier (32). The paralinear and LogDet distances have the following properties:
-
Both distances are based on the most general model of nucleotide substitution, i.e., the 12-parameter model (17, 19–20, 31). Moreover, they are valid even if the rate matrix R varies among lineages. Therefore, in the case where the assumption of a uniform substitution rate among sites holds, the paralinear and LogDet distances are very useful for phylogenetic reconstruction when nucleotide frequencies are nonstationary (19–20, 32).
-
For the neighbor-joining method and related methods, the two distance measures give the same tree topology (32). However, there are some differences between the two distances. First, the paralinear distance between two sequences is the sum of “paralinear” lengths of the branches involved. Thus, the branch lengths under a given tree can be well estimated from the paralinear distance matrix by the least-squares method. In contrast, this property does not hold for the LogDet distance. Second, the LogDet distance is particularly useful for testing the molecular clock hypothesis under non-stationarity, whereas the paralinear distance is not suitable for this purpose (see Eqs. 27 and 28).
-
The biological interpretation of the two distances can be described as follows. Let
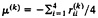 be the arithmetic mean rate in lineage k(k=1, 2), and μ =(μ(1)+μ(2))/2. Gu and Li (32) showed that the expected paralinear distance (Eq. 20) is given by
be the arithmetic mean rate in lineage k(k=1, 2), and μ =(μ(1)+μ(2))/2. Gu and Li (32) showed that the expected paralinear distance (Eq. 20) is given by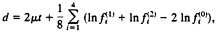
[22]
and the expected LogDet distance (Eq. 21) is given by
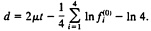
[23]
Note that, when the nucleotide frequency is stationary, Eq. 22 reduces to d=2μt. which is the expected number of substitutions between the two sequences and is equivalent to the SR distance with ck=1/4 (Eq. 2). Eq. 23 reduces to d=2μt if
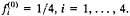
-
The approximate sampling variance of the paralinear distance is given by
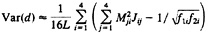
[24]
and that of the LogDet distance is given by
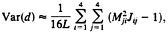
[25]
where L is the sequence length and Mij is the ij-th element of M=J–1 (13, 20, 32). For more than two sequences, the method for computing the variance-covariance matrix of the two distances has been developed by Gu and Li (32).
Bias-Corrected Paralinear and LogDet Distances. Because the data matrix J and the nucleotide frequencies can be directly estimated from the sequence data, the estimation of paralinear and LogDet distances is simple (19–20). However, our simulation study has revealed that the true (paralinear or LogDet) distance can be overestimated when the sequences are short (32), a situation similar to the SR/SRV distance. Gu and Li (32) obtained the following bias-corrected paralinear or LogDet distance.
d̂c=d̂–2 Var(d̂), [26]
where d̂ and Var(d̂) are the estimates of the “standard” paralinear or LogDet distance and the sampling variance, respectively (see Eqs. 20, 21, 24, 25).
The performance of the bias-corrected distances has been examined by extensive computer simulation (32). We considered two DNA sequences (Fig. 1) that evolve under a very general model: in one lineage the nucleotide substitution follows a time-reversible model (TR) and in another lineage it follows a time-irreversible model (NR). The rate matrices of TR and NR are designed to be very different, and the equilibrium GC% is 70% in TR but only 17% in NR (see ref. 32 for the detail). Moreover, The initial GC% at node O (Fig. 1) is set to be 15%, 50%, and 70%, in three cases. Our simulation results indicate that, when the sequence length is short, the bias-corrected paralinear or LogDet distance performs considerably better than the uncorrected method (Table 4).
Testing the Molecular Clock Hypothesis Under Nonstationarity. The relative rate test (2) can be described as follows. Consider three species as shown in Fig. 2, where species 3 is an outgroup. To test whether the evolutionary rate in lineage O1 is the same as that in lineage O2 (i.e.. the molecular clock hypothesis), one tests whether or not the difference D=d13–d23 is significantly different from zero. Wu and Li (2), Gu and Li (46), Muse and Weir (47), Tajima (48), and others have developed tests for the case of stationarity. When the nucleotide frequencies are nonstationary, D≠0 can arise from differences in nucleotide frequencies between the two sequences. Gu and Li (32) showed that this problem can be avoided by using the LogDet distance; that is,
D=d13–d23=(μ(1)–μ(2))t, [27]
where t is the divergent time between species 1 and 2 (Fig. 2). To test whether D is significantly different from zero, one can estimate the sampling variance of D, V(D)=V(d13)+V(d23) –2 Cov(d13, d23) by the method of Gu and Li (32). When the sequence is long, the statistic ![]() follows approximately the standard normal distribution (2). Actually, this new relative rate test can be easily generalized to the two-cluster
follows approximately the standard normal distribution (2). Actually, this new relative rate test can be easily generalized to the two-cluster
Table 4. Statistical performances of the bias-corrected paralinear distance
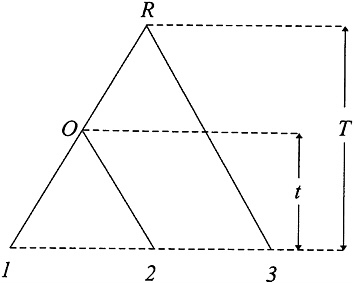
FIG. 2. The phylogeny used for molecular clock testing.
test of Li and Bousquet (49) and Takezaki et al. (50), who considered the case of stationarity (Gu and Li, unpublished data).
On the other hand, if dij is measured by the paralinear distance, one can show that D'=d13–d23 is given by
[28]
Obviously, D' is affected by differences in nucleotide frequencies and thus not suitable for testing the molecular clock hypothesis.
Discussion
In the above, we discussed the estimation of evolutionary distances and related issues under three models of nucleotide substitution: the SR model (10–14, 36), the SRV model (11), and the nonstationary model (13, 17, 19–20, 32, 45). The conclusions can be summarized as follows. (i) Under stationarity, the evolutionary distances and the pattern of nucleotide substitution can be estimated under the SR or SRV model, (ii) When the nucleotide frequencies are nonstationary, the paralinear or LogDet distances should be used. However, although both distances lead to the same tree topology, the branch lengths of a tree can be appropriately estimated only from the paralinear distances, whereas the molecular clock hypothesis should be tested by the LogDet distance. (iii) The proposed bias-corrected methods for the SR/SRV and paralinear/ LogDet distances are useful when the sequences are shorter than 500 bp. (iv) A general measure for the rate variation among sites is proposed, which does not depend on any specific distribution of rates.
In principle, the SR/SRV and paralinear/LogDet distances can be easily extended to more complex models in which the dimension of the rate matrix R is >4 (51–55). Two interesting cases are the amino acid-based model (a general 20×20 model) and the codon-based model (a general 61×61 model). However, our preliminary simulation showed that, even for the amino-acid based model, these distances are subject to large sampling variances unless the sequence is very long, say, larger than 2,000 amino acids; the sampling variance would be much larger for the codon-based model. Indeed, because there are too many unknown parameters, the distances cannot be estimated accurately. Thus, one should be cautious when applying these methods to analyze amino acid sequence data.
We suggested to use ρ (related to the coefficient of variation Cv) as a general measure of rate heterogeneity. However, Waddell et al. (30) questioned its usefulness because they found, for a given sequence data set, the estimated Cv value differs under different assumptions of rate distribution. This dilemma has now been removed because we have developed a method for estimating ρ (or Cv) that does not require any specific model of rate distribution. Apparently, the discrepancy found by Waddell et al. (30) is caused by sampling errors or the unsuitability of the model.
When the nucleotide frequencies are not stationary, the parlinear and LogDet methods provide concise and elegant distance measures for phylogenetic inference and molecular clock testing. However, how to incorporate the effect of heterogeneity into these two distances is a problem that remains to be solved.
This study was supported by National Institutes of Health Grants GM 30998 (to W.H.L.) and GM 20293 (to Masatoshi Nei, Pennsylvania State University).
1. Li, W.H., Wu, C.I. & Luo, C.C. (1985) in Molecular Evolutionary Genetics, ed. MacIntyre, R.J. (Plenum, New York), pp. 1–94.
2. Wu, C.I. & Li, W.H. (1985) Proc. Nati Acad. Sci. USA 82, 1741–1745.
3. Saitou, N. & Nei, M. (1987) Mol. Biol. Evol. 4, 406–425.
4. Nei, M. (1987) Molecular Evolutionary Genetics (Columbia Univ. Press, New York).
5. Nei, M. (1996) Annu. Rev. Genet. 30, 371–403.
6. Felsenstein, J. (1988) Annu. Rev. Genet. 22, 521–565.
7. Doolittle, R.E., Feng, D.F., Tsang, S., Cho, G. & Little, E. (1996) Science 271, 470–477.
8. Li, W.H. (1997) Molecular Evolution (Sinauer, Sunderland, MA).
9. Gu, X. (1997) Mol Biol. Evol. 14, 861–866.
10. Lanave, C., Preparata. G., Saccone, C. & Serio, G. (1984) J. Mol. Evol. 20, 86–93.
11. Gu, X. & Li, W.H. (1996) Proc. Natl. Acad. Sci. USA 93, 4671–4676.
12. Tavare, S. (1986) Lect. Math. Life Sci. 17, 57–86.
13. Barry, D. & Hartigan, J.A. (1987) Biometrics 43, 261–276.
14. Rodriguez, F., Oliver, J.F., Marin, A. & Medina, J.R. (1990) J. Theor. Biol. 142, 485–501.
15. Hasegawa, M. & Hashimoto, T. (1993) Nature 361, 23.
16. Sogin, M.L., Hinkle, G. & Leipe, D.D. (1993) Nature 362, 795.
17. Steel, M.A. (1994) Appl. Math. Lett. 7, 19–24.
18. Galtier, N. & Gouy, M. (1996) Proc. Natl. Acad. Sci. USA 92, 11317–11321.
19. Lake, J.A. (1994) Proc. Natl. Acad. Sci, USA 91, 1455–1459.
20. Lockhart, P.J., Steel, M.A. Hendy, M.D. & Penny, D. (1994) Mol. Biol. Evol. 11, 605–612.
21. Hasegawa, M., Kishino, H. & Yano, T. (1985) J. Mol. Evol. 22, 160–174.
22. Tamura, K. & Nei, M. (1993) Mol. Biol. Evol. 10, 512–526.
23. Yang, Z. (1994) J. Mol. Evol. 39, 105–111.
24. Uzzel, T. & Corbin, K.W. (1971) Science 172, 1089–1096.
25. Yang, Z. (1993) Mol Biol. Evol. 10, 1396–1401.
26. Gu, X., Fu, X.Y. & Li, W.H. (1995) Mol. Biol. Evol. 12, 546–557.
27. Sullivan, J.K., Holsinger, K.E. & Simon, C. (1995) Mol. Biol. Evol. 12, 988–1001.
28. Kelly, C. & Rice, J. (1996) Math. Biosci. 133, 85–109.
29. Gu, X. & Zhang, J. (1997) Mol. Biol. Evol. 14, 1106–1113.
30. Waddell, P.J., Penny, D. & Moore, T. (1997) Mol. Phylogenet. Evol. 8, 33–50.
31. Zharkikh, A. (1994) J. Mol. Evol. 39, 315–329.
32. Gu, X. & Li, W.H. (1996) Mol. Biol. Evol. 13, 1375–1383.
33. Jukes, T.H. & Cantor, C.R. (1969) in Mammalian Protein Metabolism, ed. Munro, H.N. (Academic. New York), pp. 21–123.
34. Kimura, M. (1980) J. Mol. Evol. 16, 111–120.
35. Tajima, F. & Nei, M. (1984) Mol. Biol. Evol. 1, 269–285.
36. Steel, M., Szekely, L. & Hendy, M. (1994) J. Comp. Biol. 1, 153–163.
37. Keilson, J. (1979) Markov Chain Models: Rarity and Exponentially (Springer, New York).
38. Saccone, C., Lanave C., Pesole, G. & Preparata, G. (1990) Methods Enzymol. 183, 570–583.
39. Li, W.H. & Gu, X. (1996) Methods Enzymol. 266, 449–459.
40. Miyamoto, M.M. & Fitch, W.M. (1996) Syst. Biol. 45, 568–575.
41. Tourasse, N. & Gouy, M. (1997) Mol. Biol. Evol. 14, 287–298.
42. Yang, Z. & Kumar, S. (1996) Mol. Biol. Evol. 13, 650–659.
43. Fitch, W.M. (1971) Syst. Zool. 20, 406–416.
44. Wakeley, J. (1993) J. Mol. Evol. 37, 613–623.
45. Cavender, J.A. & Felsenstein, J. (1987) J. Classification 4, 57–71.
46. Gu, X. & Li, W.H. (1992) Mol. Phvlogenet. Evol. 234, 185–192.
47. Muse, S.V. & Weir, B.S. (1992) Genetics 132, 269–276.
48. Tajima, F. (1993) Genetics 135, 599–607.
49. Li, P. & Bousquet, J. (1992) Mol. Biol. Evol. 9, 1185–1189.
50. Takezaki, N., Rzhetsky, A. & Nei, M. (1995) Mol. Biol. Evol. 12, 823–833.
51. Dayhoff, M.O. (1978) Atlas of Protein Sequence and Structure (Natl. Biomed. Res. Found., Silver Spring, MD), Vol. 5.
52. Schoniger, M. & von Haeseler, A. (1994) Mol. Phylogenet. Evol. 3, 240–247.
53. Golding, N. & Yang, Z. (1994) Mol. Biol. Evol. 11, 725–736.
54. Muse, S.V. & Gaut, B.S. (1994) Mol. Biol. Evol. 11, 715–724.
55. Rzhetsky, A. (1995) Genetics 141, 771–783.








