Proc. Natl. Acad. Sci. USA
Vol. 95. pp. 5913–5920, May 1998
Colloquium Paper
This paper was presented at the colloquium “Computational Biomolecular Science,” organized by Russell Dootittle, J.Andrew McCammon, and Peter G.Wolynes, held September 11–13, 1997, sponsored by the National Academy of Sciences at the Arnold and Mabel Beckman Center in Irvine, CA.
A unified statistical framework for sequence comparison and structure comparison
(sequence analysis/structure analysis/fold family/database statistics/protein evolution)
MICHAEL LEVITT*† AND MARK GERSTEIN‡
*Department of Structural Biology, Stanford University, Stanford. CA 94305: and ‡Molecular Biophysics and Biochemistry Department, P.O. Box 208114. Yale University. New Haven, CT 06520–8114
ABSTRACT We present an approach for assessing the significance of sequence and structure comparisons by using nearly identical statistical formalisms for both sequence and structure. Doing so involves an all-vs.-all comparison of protein domains [taken here from the Structural Classification of Proteins (scop) database] and then fitting a simple distribution function to the observed scores. By using this distribution, we can attach a statistical significance to each comparison score in the form of a P value, the probability that a better score would occur by chance. As expected, we find that the scores for sequence matching follow an extreme-value distribution. The agreement, moreover, between the P values that we derive from this distribution and those reported by standard programs (e.g., BLAST and FASTA validates our approach. Structure comparison scores also follow an extreme-value distribution when the statistics are expressed in terms of a structural alignment score (essentially the sum of reciprocated distances between aligned atoms minus gap penalties). We find that the traditional metric of structural similarity, the rms deviation in atom positions after fitting aligned atoms, follows a different distribution of scores and does not perform as well as the structural alignment score. Comparison of the sequence and structure statistics for pairs of proteins known to be related distantly shows that structural comparison is able to detect approximately twice as many distant relationships as sequence comparison at the same error rate. The comparison also indicates that there are very few pairs with significant similarity in terms of sequence but not structure whereas many pairs have significant similarity in terms of structure but not sequence.
Comparison is a most fundamental operation in biology. Measuring the similarities between “things” enables us to group them in families, cluster them in trees, and infer common ancestors and an evolutionary progression. Biological comparisons can take place at many levels, from that of whole organisms to that of individual molecules. We are concerned here with the comparison on the latter level, specifically, with comparisons of individual protein sequences and structures. (For an example of systematic comparison applied to whole organisms, see refs. 1 and 2.)
Our overall aim is to describe these two types of comparisons in a self-consistent, unified framework. For sequence or structure comparison, each act of comparing one “entity” to another (that is, either comparing two sequences or two structures) involves two steps. First, the two objects are aligned optimally through the introduction of gaps in such a way as to maximize their residue-by-residue similarity. This operation generates some form of total similarity score for the number of residues matched—traditionally, a percent identity for sequences or an rms for structures, although we will use other measures. Second, one has to assess the significance of this score in the context of what is known about the proteins currently in the database.
In earlier papers, Gerstein and Levitt (3, 30) extended the work of Subbiah et al. (4) and Laurents et al. (5) and described an approach for structural alignment in an analogous fashion to the traditional approach for sequence alignment (6–9). Like sequence alignment, this method involves applying dynamic programming to a matrix of similarities between individual residues to optimize their overall correspondence through the introduction of gaps.
In this paper, we tackle the second of the two steps in protein comparison: assessing significance. We developed a simple empirical approach for calculating the significance of an alignment score based on doing an all-vs.-all comparison of the database and then curve fitting to the distribution of scores of true negatives. This allows us to express the significance of a given alignment score in terms of a P value, which is the chance that an alignment of two randomly selected proteins would obtain this score. We applied our approach consistently to both sequences and structures. For sequences, we could compare our fit-based P values with the differently derived statistical score from commonly used programs such as BLAST and FASTA (10–13). The agreement we found validated our approach. For structure alignment, we followed a parallel route to derive an expression for the P value of a given alignment in terms of the structural alignment score.
Our work followed on much that recently has been done assessing the significance of sequence and structure comparison. One of the major developments in the past few years has been the implementation of probabilistic scoring schemes (13–16). These give the significance of a match in terms of a P value rather than an absolute, “raw” score (such as percent identity). This places scores from very different programs in a common framework and provides an obvious way to set a significance cutoff (that is, at P=<0.0001 or 0.01%). P values were first used in the BLAST family of programs, where they are derived from an analytic model for the chance of an arbitrary ungapped alignment (10, 17). P values subsequently have been implemented in other programs, such as FASTA and gapped BLAST by using a somewhat different formalism (13, 18, 19).
©
PNAS is available online at http://www.pnas.org.
† | To whom reprint requests should be addressed, e-mail: michael.levitt©stanford.edu. |
There are currently many methods for structural alignment (20–31). Some of these are associated with probabilistic scoring schemes. In particular, one method (VAST) computes a P value for an alignment based on measuring how many secondary structure elements are aligned as compared with the chance of aligning this many elements randomly (28). Another method (27, 32) expresses the significance of an alignment in terms of the number of standard deviations it scores above the mean alignment score in an all-vs.-all comparison (i.e., a Z-score).
Data Sci Used for Testing. One of the most important aspects of our analysis is that we carefully tested it against the known structural relationships. This testing allowed us to decide unambiguously whether a given comparison resulted in a true or false-positive and to decide objectively between different statistical schemes. In particular, structures were taken from the Protein Data Bank (33–34) and definitions of domains, structural classes, and structural similarities were taken from the Structural Classification of Proteins (scop) database (version 1.32: refs. 35–37). The creators of scop have clustered the domains in the Protein Data Bank on the basis of sequence identity (38, 39). At a sequence identity level of 40%, this clustering resulted in 941 unique sequences corresponding to the known structural domains. These 941 sequences were what we used as test data for both the sequence and structure comparisons. They contained 390 different superfamilies and 281 different folds. Because they had a considerably closer and more certain relationship than fold pairs, we concentrated here on superfamily pairs. These 2.107 nontrivial, pairwise relationships between the domains formed our set of true-positives.
Sequence Comparison Statistics. Sequence matching was done with standard approaches: In particular, we used the SSEARCH implementation of the Smith-Waterman algorithm (7) [from the FASTA package, version 3, (12, 40); the URL is ftp://ftp.virginia.edu/pub/fasta], with a gap-opening penalty of –12. a gap-extension penalty of –2, and the BLOSUM50 substitution matrix [which has a maximal match score of 13 (for C to C) and an average match score of –0.36].
A probability-density function for sequence-comparison scores. Each pairwise sequence comparison was best quantified by three numbers, Sseq, n, and m, where Sseq is the raw sequence alignment score and n and m are the lengths of the two sequences compared. Comparing all possible pairs of sequences allowed us to calculate an observed probability density, ρ°seq, for the chance of finding a pair of sequences with particular values for Sseq and ln(nm). Fig. 1A shows the density for pairs between all sequences. This includes the scores for
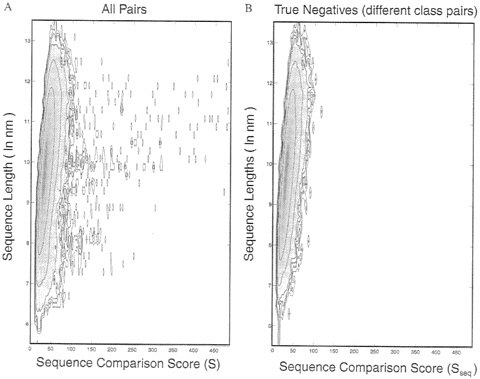
FIG. 1. A probability-density distribution for sequence comparison scores, ![]() contoured against Sseq, the sequence alignment score (along the horizontal axis) and ln(nm), where n and m are the lengths of the pair sequences (along the vertical axis). This density is related closely to the raw data (via normalization) obtained by counting the number of pairs with particular S and ln(nm) values. Because of the wide range of density values, contours of log
contoured against Sseq, the sequence alignment score (along the horizontal axis) and ln(nm), where n and m are the lengths of the pair sequences (along the vertical axis). This density is related closely to the raw data (via normalization) obtained by counting the number of pairs with particular S and ln(nm) values. Because of the wide range of density values, contours of log ![]() are drawn with an interval of 1 (a full order of magnitude). When contouring the logarithm of a density function, special attention must be paid to the zero values. Here, a zero value is set to 0.001, which effectively lifts the entire surface by 3 log units. The data then are smoothed by averaging with a Gaussian function [exp(~s/(ΔSseq/3)2)] over a window 14 units wide along the Sseq axis. This smoothing together with the treatment of zeros serves to emphasize the smallest observed counts (values of 1) by surrounding them with three contour levels. (A) Data from all 884,540 pairs between any one of the 941 sequences and any other sequence (pairs A-B and B-A are both included). The significant sequence matches are seen as the isolated spots at high values of the score Sseq, (B) Data from 352.168 pairs, including only those pairs of sequences in different scop classes. We also exclude pairs between an all-α or all-β domain and an α+β domain, as well as sequences that are not in one of the five main scop classes: α, β, α/β, α+β. and α+β (multidomain). This exclusion is done to ensure that no significant matches will be found, which indeed is seen in the figure by the absence of any outlying spots at high score values. Thus, the density in B is free of any significant matches and shows the underlying density distribution expected for comparison of unrelated sequences.
are drawn with an interval of 1 (a full order of magnitude). When contouring the logarithm of a density function, special attention must be paid to the zero values. Here, a zero value is set to 0.001, which effectively lifts the entire surface by 3 log units. The data then are smoothed by averaging with a Gaussian function [exp(~s/(ΔSseq/3)2)] over a window 14 units wide along the Sseq axis. This smoothing together with the treatment of zeros serves to emphasize the smallest observed counts (values of 1) by surrounding them with three contour levels. (A) Data from all 884,540 pairs between any one of the 941 sequences and any other sequence (pairs A-B and B-A are both included). The significant sequence matches are seen as the isolated spots at high values of the score Sseq, (B) Data from 352.168 pairs, including only those pairs of sequences in different scop classes. We also exclude pairs between an all-α or all-β domain and an α+β domain, as well as sequences that are not in one of the five main scop classes: α, β, α/β, α+β. and α+β (multidomain). This exclusion is done to ensure that no significant matches will be found, which indeed is seen in the figure by the absence of any outlying spots at high score values. Thus, the density in B is free of any significant matches and shows the underlying density distribution expected for comparison of unrelated sequences.
≈300 sequence pairs that are related closely, which clearly show up as “spots” on the right side of the plot. These high-scoring “true-positives” are removed in Fig. 1B, which shows the density for just the pairs in different structural classes (42), i.e., the pairs that definitely are unrelated. This is the density distribution that we aim to fit.
Fig. 2A shows the density distribution as a function of Sseq for sections at constant ln(nm). The clear linear relationship between log![]() and Sseq at high values of Sseq is indicative of an extreme-value distribution
and Sseq at high values of Sseq is indicative of an extreme-value distribution
The variable “Z” was defined in terms of Sseq and ln(nm) by using the “Z-score-like” expression Z=(Sseq–μseq)/σseq, where μseq=a ln(nm)+b and σseq= a are the most likely sequence score and width parameter for the distribution. The two adjustable parameters a and b were obtained by fitting the calculated density ![]() (Z) to the observed density
(Z) to the observed density ![]() (Z) for all values of Sseq and In(nm). Substituting for μseq and σseq for Z above gave Z=(Sseq–a ln(nm)–b)/a=Sseq/a–ln(nm) –b/a.
(Z) for all values of Sseq and In(nm). Substituting for μseq and σseq for Z above gave Z=(Sseq–a ln(nm)–b)/a=Sseq/a–ln(nm) –b/a.
To derive specific values for the a and b parameters, we fit the above formulas to the observed density distribution obtained by comparing pairs in different scop classes, getting a= 5.84 and b=–26.3. The fit was done by least-squares optimization by using the simplex minimizer in MATLAB (Math Works, Natick, MA). It has a residual of 0.084, which was calculated by using the standard relation r=∑ wi(Oi–Cj)2/∑ Wi(Oi)2, where i indexes “bins” with particular Sseq and ln(nm) values, ![]() is the observed density in a bin, Ci= log
is the observed density in a bin, Ci= log![]() is the calculated density in a bin, wi=1/Ni is a weighting factor, Ni is the number of sequence pairs in a bin, and the summation is over all bins, I, with ln(nm) between 5.9 and 13.5.
is the calculated density in a bin, wi=1/Ni is a weighting factor, Ni is the number of sequence pairs in a bin, and the summation is over all bins, I, with ln(nm) between 5.9 and 13.5.
A cumulative sequence distribution function, giving the P value. To estimate the statistical significance of a particular comparison in terms of particular Sseq, n, and m values, we needed the cumulative distribution function Pseq(z>Z), which is defined as the probability that matching any two random sequences will give a z value greater than or equal to Z. This is just the integral of ![]() =exp(–z–exp(–z))=exp(–z) exp(–exp(–z)), from z=Z to z=∞, so that Pseq(z>Z)=1–exp(–exp(–Z)). Writing Z in terms of Sseq, n, and m gives
=exp(–z–exp(–z))=exp(–z) exp(–exp(–z)), from z=Z to z=∞, so that Pseq(z>Z)=1–exp(–exp(–Z)). Writing Z in terms of Sseq, n, and m gives
Pseq(s>Sseq)=1–exp(–exp(–Sseq/a+ln(nm)+b/a)),
where the parameters a and b are given above.
Relation to BLAST P value. For sequence comparison without gaps, Karlin and Altschul (10, 11) derived the following cumulative distribution function: PK&A(S>Sseq)=1– exp(–exp(– λ(Sseq–ln(Kmn)/λ)))=1–exp(–exp(–λ(Sseq +ln(Kmn)/λ))), where λ and K are calculated analytically based on the sequence composition and amino acid scoring
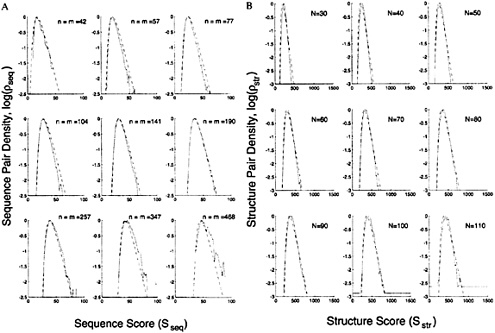
FIG. 2. Cross-sections of the sequence and structure density distribution show they are both extreme-value distributions and that the calculated distribution fits the observed distribution well. (A) Plots of the logarithm of the observed, log ![]() and calculated, log
and calculated, log![]() sequence pair densities against the sequence match score Sseq; log
sequence pair densities against the sequence match score Sseq; log![]() is taken from the data for pairs in different classes (Fig. 1B). Each panel shows the variation of the density with Sseq for a particular value of ln(nm), the product of the lengths of the sequences compared; this value is indicated by assuming n=m and showing the value of n. The observed density is clearly an extreme-value distribution with a linear fall-off of log
is taken from the data for pairs in different classes (Fig. 1B). Each panel shows the variation of the density with Sseq for a particular value of ln(nm), the product of the lengths of the sequences compared; this value is indicated by assuming n=m and showing the value of n. The observed density is clearly an extreme-value distribution with a linear fall-off of log ![]() with Sseq. The calculated distribution obtained with a two-parameter fit (dashed line, see text) is a good fit for all values of n [(or ln(nm)]. (B) Plots of the logarithm of the observed, log
with Sseq. The calculated distribution obtained with a two-parameter fit (dashed line, see text) is a good fit for all values of n [(or ln(nm)]. (B) Plots of the logarithm of the observed, log![]() and calculated, log
and calculated, log![]() structure pair densities against the structure match score
structure pair densities against the structure match score ![]() taken from the data for pairs in different classes (Fig. 4B). Each panel shows the variation of the density with Sstr for a particular value of the number of aligned residues, N. The calculated distribution obtained with a five-parameter fit (dashed line, see text) is a good fit for all values of N.
taken from the data for pairs in different classes (Fig. 4B). Each panel shows the variation of the density with Sstr for a particular value of the number of aligned residues, N. The calculated distribution obtained with a five-parameter fit (dashed line, see text) is a good fit for all values of N.
matrix. Comparison of their analytical form with our P value expression shows that λ=1/a and K=exp(b/a). Substituting the specific values for a and b that we calculated from the fit. we found that λ=0.171 and K=0.011. For the particular database sequences and amino acid scoring matrix used here, the values for λ calculated by Karlin and Altschul’s formula ranged from 0.217 to 0.259, all somewhat larger than our value for λ.
Relation to
The value used by FASTA in judging the significance of a sequence similarity is known as the expectation value or E value (here Efa). The P value, defined above, gives the statistical significance of a single comparison whereas the E value is an estimate of the expected number of false-positives (dissimilar matches with a significant score) for a search of the entire database. With Ndb entries in the database, the E value Eseq is calculated from our Pseq(s>Sseq) as Eseq=Ndb Pseq. The E values we obtained were very similar to those found by FASTA over a very wide range of values (Fig. 3). When one considers that our closed-form Eseq depends on only two parameters for all pairs whereas Efa is optimized separately for each query sequence (941×2=1,882 parameters in all), this agreement is astonishing.

FIG. 3. The statistical significance derived here is shown to be similar to that derived in a completely different way by the sequence comparison program SSEARCH from the FASTA package (13). We plotted the expected number of errors per search of the database obtained by Pearson’s method, log(Efa), against the same value calculated here, log(Eseq) (which is a function of the sequence match score Sseq and the length of the two sequences). To be more specific, Efa is the E value output by the FASTASSEARCH program whereas Eseq is calculated as 940Pseq(s>Sseq) for score Sseq. The accuracy of our simple two-parameter fit is confirmed by the fact that most pairs of log(Efa) and log(Eseq) values are perfectly correlated, lying along the line log(Efa)=log(Eseq) over the entire range.
Measuring coverage vs. error rate to compare different formalisms for significance-statistics. We have presented two forms of E value statistics for sequence comparison: our method, Eseq, which is based on fitting a two-parameter model to the observed distribution of alignment scores; and the FASTA method Efa, which is based on fitting different distributions for each query. Now we naturally are led to ask whether there is an objective way to decide which formalism performs the best on some representative test data.
The seminal work of Brenner et al. (39) and Brenner (43) provides a framework for such an assessment by using the known true-positives in the scop database and a coverage-vs.-error plot. To compare any two significance-statistics formalisms, we proceeded as follows for each:
(i) For each of the pairs in the all-vs.-all comparison (941× 940 pairs), we determined an E value and noted whether the pair was a true-positive or true-negative (for true-positives, both sequences must belong to protein domains with the same fold in the scop classification). (ii) We sorted the pairs by increasing E value. (iii) We counted down the list from best to worst until the number of false-positives was 1% of the total number of database entries (here, this was 9 false-positives, which is ≈1% of 941). (iv) We got the threshold E value at this point, which ideally should be close to 0.01, so as to correspond to the 1% error rate per query. (5) Finally, we got the number of entries that were more significant than the threshold E value; this number defined the coverage, which should be as large as possible.
Here, we compared the coverage and error rate of our sequence score statistics with those of FASTA (Eseq vs. Efa). At the threshold E value, our sequence statistics had log Eseq= –1.98 and a coverage of 328, and the FASTA statistics had a log Efa of –1.68 and a coverage of 379. The FASTA statistics had better coverage, but our statistics had an almost perfect threshold value, which should be –2 for 1% error rate.
Structure Comparison Statistics. The procedure we used for pairwise structural alignment is described in detail in Gerstein and Levitt (3, 30) and is summarized only briefly here. Our core method was based on iterative application of dynamic programming. As such, it was a simple application of the Needleman-Wunsch sequence alignment (6). It originally was derived from the ALIGN program of Cohen (21, 31), with many subsequent refinements. One starts with two structures in an arbitrary orientation. Then one computes all pairwise distances between every atom in the first structure and every atom in the second, which results in an interprotein distance matrix in which each entry, dij, corresponds to the distance between residue i in the first structure and residue j in the second (interresidue distances usually are expressed between α-carbons). This distance matrix, dij, can be converted into a similarity matrix, Sij, through the relationship Sij=M/(1+ (dij/do)2), where M=20 and do=5Å.
One applies dynamic programming to the similarity matrix to get equivalences (using a gap opening penalty of M/2=10 and no gap extension penalty) and uses them to least-squares fit the first structure onto the second one (44). Then one repeats the procedure, finding all pairwise distances and doing dynamic programming to get new equivalences, until the process converges. After an alignment is determined, it can be “refined” by eliminating the worst-fitting pairs of aligned residues and then refitting to get a new rms in a similar fashion to the core-finding procedure in Gerstein and Altman (45, 46). This refinement is necessary because the dynamic programming used tries to match as many residues as possible. (It is a global, as opposed to local, method.)
The structural comparison score and the rms. At the end of the procedure, we were left with a number of scores characterizing our final alignment. The score optimized by dynamic program
ming was the sum of the similarity matrix scores Sij minus the total penalty for opening gaps. We refer to this as “Sstr.” To be more explicit, it was computed from the following formula:
Sstr=M(∑ 1/(1+ (dij/d0)2)–Ngap/2),
where Ngap is the total number of gaps (not including gaps at the end of a chain) and the summation is carried out over all pairs, ij, of equivalenced residues. The more traditional score is the rms deviation in α-carbon position after doing a least-squares fit on the aligned atoms (the “rms”). rms-based statistics were used in our earlier work (for example, refs. 3–5) and have been used in almost all other work in structural alignment.
A probability-density function for structural alignment scores. To derive significance-statistics for the structural alignment score Sstr, we proceeded exactly as we did for sequence comparison. Structural alignment of all pairs in the database gave us an observed probability distribution for comparison scores ![]() which was a function of the number of residues matched N and the comparison score Sstr (Fig. 4A. This distribution contained the many pairs of structures that were similar, and these pairs stood out with high Sstr scores. Fig. 4B shows data for pairs that were in different scop structural classes and, therefore, should not have had any structural similarity. Fig. 4B is much “cleaner” than Fig. 4A and shows the underlying distribution expected for the comparison of structures that are not similar.
which was a function of the number of residues matched N and the comparison score Sstr (Fig. 4A. This distribution contained the many pairs of structures that were similar, and these pairs stood out with high Sstr scores. Fig. 4B shows data for pairs that were in different scop structural classes and, therefore, should not have had any structural similarity. Fig. 4B is much “cleaner” than Fig. 4A and shows the underlying distribution expected for the comparison of structures that are not similar.
Fig. 2B shows the density distribution as a function of Sstr for sections at constant N. There is a close parallel between the structural alignment score Sstr and the sequence alignment score, Sseq, in Fig. 2A, and both can be modeled by an extreme-value distribution. Thus, we fit the calculated structure density by ![]() (Z)=exp(–Z–exp(–Z)), where the variable Z is defined in terms of Sstr and N by using Z=(Sstr –μstr)/σstr. The most likely structure score μstr and the width parameter σstr have a more complicated dependence on sequence length N than was the case for sequences with μstr(N) =c ln(N)2+d ln(N)+e (if N<120), μstr(N)=a ln(N)+ b(if N≥120) and σslr(N)=f ln(N)+g(if N<120) and σstr(N)=f ln(120)+g(if N≥120).
(Z)=exp(–Z–exp(–Z)), where the variable Z is defined in terms of Sstr and N by using Z=(Sstr –μstr)/σstr. The most likely structure score μstr and the width parameter σstr have a more complicated dependence on sequence length N than was the case for sequences with μstr(N) =c ln(N)2+d ln(N)+e (if N<120), μstr(N)=a ln(N)+ b(if N≥120) and σslr(N)=f ln(N)+g(if N<120) and σstr(N)=f ln(120)+g(if N≥120).
Continuity of function values and slopes allows a and b to be written in terms of c, d, and e. To be more specific, at N=120, a ln(N)+b=c ln(N)2+d ln(N)+e and a=2c ln(N)+d. Thus, the expressions for μstr(N) and σstr(N) involve five independent parameters: c, d, e, f, and g. We determined these five parameters via least-squares optimization by using the SIMPLEX minimizer in MATLAB, which yielded c=18.4, d= –4.50, e=2.64, f=21.4, g=–37.5 (a=419.3 and b= 171.8 were derived as described above). The residual was 0.288. It was given by the same formula as was used for the residual in the sequence statistics fit with ![]() and wi=1, and the summation was over bins with any value of Sstr and N between 30 and 170 residues. The resulting fit of the observed and calculated distribution (Fig. 2B) was good for all values of N and Sstr.
and wi=1, and the summation was over bins with any value of Sstr and N between 30 and 170 residues. The resulting fit of the observed and calculated distribution (Fig. 2B) was good for all values of N and Sstr.
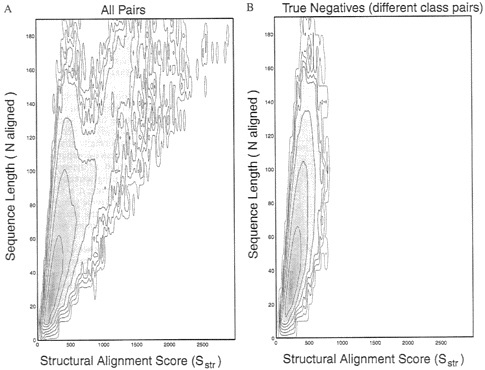
FIG. 4. The logarithm of the density distribution for structure comparison scores, ![]() is contoured against Sstr, the structural alignment score (along the horizontal axis), and N, the number of aligned residues (along the vertical axis). By following the protocol used for Fig. 1, the raw data obtained by counting the number of pairs with the particular Sstr and N values are “lifted” and smoothed over a window 90 units wide along the Sstr axis, and the log value is contoured in intervals of 1 log unit. Given the different scales used for Sseq and Sstr, the extent of smoothing is very similar for both. (A) Data from all 884, 540 pairs between any one of the 941 sequences and any other sequence. (B) Data from 352,168 pairs, including only those pairs of sequences in different scop classes (described in Fig. 1). Comparison of A and B shows that the true-positive structural matches are seen in the contours at the higher values of the alignment score Sstr and also at higher values of the number of matches N, The density in B is free of these significant matches and shows the underlying density distribution expected for comparison of unrelated structures.
is contoured against Sstr, the structural alignment score (along the horizontal axis), and N, the number of aligned residues (along the vertical axis). By following the protocol used for Fig. 1, the raw data obtained by counting the number of pairs with the particular Sstr and N values are “lifted” and smoothed over a window 90 units wide along the Sstr axis, and the log value is contoured in intervals of 1 log unit. Given the different scales used for Sseq and Sstr, the extent of smoothing is very similar for both. (A) Data from all 884, 540 pairs between any one of the 941 sequences and any other sequence. (B) Data from 352,168 pairs, including only those pairs of sequences in different scop classes (described in Fig. 1). Comparison of A and B shows that the true-positive structural matches are seen in the contours at the higher values of the alignment score Sstr and also at higher values of the number of matches N, The density in B is free of these significant matches and shows the underlying density distribution expected for comparison of unrelated structures.
A cumulative structure distribution function, giving the P value. To estimate the statistical significance of a particular structure comparison in terms of its Sstr and N values, we proceeded as we did for sequence comparison. We integrated the score distribution to determine a cumulative distribution function Pstr, defined as the probability that matching two random structures will give a z value greater than or equal to Z. The structure score distribution has the same extreme-value form as the sequence score distribution, so the derivation of Pstr follows that of Pseq, with Pstr(z>Z)=1–exp[–exp(–Z)], where Z is expressed in terms of Sstr and N by using
Z=(Sstr–(c ln(N)2+d ln(N)+e))/(f ln(N)+g), N<120
Z=(Sstr–(a ln(N)+b))/(f ln(120)+g), N≥120
and the seven parameters a, b, c, d, e, f, and g are given above.
Structural comparison statistics based on rms. The traditional characterization of a structural alignment is in terms of the number of residues matched, N, and the rms deviation from fitting these matched residues, R. It is convenient to focus on ln(R), which ensures that there is good separation of values for small R. where the significant pairs occur. We calculated a probability distribution ![]() [ln(R),N] for the observed rms values of true-negative pairs in the same fashion as we did earlier for the observed distribution of structural alignment scores
[ln(R),N] for the observed rms values of true-negative pairs in the same fashion as we did earlier for the observed distribution of structural alignment scores ![]() (Sstr,N).
(Sstr,N).
The fact that log ![]() varies very slowly with ln(R) near the maximum (Fig. 5) led us to fit the calculated density by using
varies very slowly with ln(R) near the maximum (Fig. 5) led us to fit the calculated density by using ![]() (Z)=exp(–Z4), where Z is defined in terms of ln(R) and N as Z=(ln(R)-μrms(N))/σrms (N), with μrms(N)=c ln(N)2 +d ln(N)+e(if N<60), μrms(N)=a ln(N)+b (if N≥60)
(Z)=exp(–Z4), where Z is defined in terms of ln(R) and N as Z=(ln(R)-μrms(N))/σrms (N), with μrms(N)=c ln(N)2 +d ln(N)+e(if N<60), μrms(N)=a ln(N)+b (if N≥60)
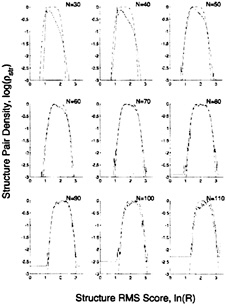
FIG. 5. The fit to the structure pair density by using the rms score. The observed, log![]() and calculated, log
and calculated, log![]() structure pair density distributions are plotted against the rms score ln(R) for different numbers of aligned residues. N. The observed structure pair density, which is derived from pairs in different classes, is clearly not an extreme-value distribution because it is symmetrical about the maximum value and falls off faster than a linear function with increasing Z. In fact, it is best fit by exp(–Z4). The calculated distribution obtained with a five-parameter fit (dashed line) is a good fit when the number of aligned residues exceeds 50.
structure pair density distributions are plotted against the rms score ln(R) for different numbers of aligned residues. N. The observed structure pair density, which is derived from pairs in different classes, is clearly not an extreme-value distribution because it is symmetrical about the maximum value and falls off faster than a linear function with increasing Z. In fact, it is best fit by exp(–Z4). The calculated distribution obtained with a five-parameter fit (dashed line) is a good fit when the number of aligned residues exceeds 50.
and σrms(N)=f ln(N)+g(if N<60), σrms(N)=f ln(60)+ g (if N≥60). The values of the five independent parameters c, d, e, f, and g were determined by least-squares optimization by using the SIMPLEX minimizer in MATLAB. which yielded c= 0.155, d=–0.619, e=1.73, f=0.0922, and g=0.212, (a= 0.872 and b=0.650 were determined as before to ensure continuity.)
To estimate the statistical significance of a particular comparison in terms of its R and N values, we derived a cumulative distribution function Prms(z>Z), defined as the probability that any z will be less than or equal to a given Z. This was just the integral of ρcrms(z) from z=–∞ to z=Z. Because the function exp(–z4) cannot be integrated analytically, we integrated it numerically for z from –5 to Z and tabulated its value for 10,000 different Z values from –5 to 5.
Comparing structure comparison statistics: Alignment score Sstrvs. rms. Once we had derived structure comparison statistics based on structural alignment score Sstr and rms, we could compare them. The same coverage-vs.-error scheme used above to compare the two formulae for sequence alignment significance could be used again here. When assessed in terms of coverage (number of true-positives found) at a given error rate on our test data, the E value statistics based on Sstr gave a much better performance (i.e., had a larger coverage) than those based on rms. To be more specific, we compared the two approaches (Estr vs. Erms) in exactly the same way that we previously had compared our sequence E value to that produced by FASTA (Eseq vs. Efa). We found that, at the 1% error threshold, the rms-based statistics have log(Erms)=–32.8 and a coverage of 202 whereas the structural-alignment score statistics have log(Estr)=–1.58 and a coverage of 627. Clearly, the statistics based on Sstr perform much better because the threshold is much more reliable (i.e., closer to the value of –2 for an error rate of 1%) and the true-positive coverage is >3-fold higher. The difference between Estr and Erms is striking and confirms that the structure score is much better than the rms score.
There are other reasons why the structural alignment score Sstr is a more reliable indicator than rms: (i) Sstr depends most strongly on the best-fitting atoms whereas rms depends most on the worst-fitting atoms; (ii) Sstr penalizes gaps, whereas rms does not; and (iii) Sstr is formally analogous to the score one gets from a standard sequence comparison, Sseq, because both quantities are derived from a “dynamic-programming” similarity matrix. As dynamic programming finds a maximum score over many possible alignments, it is reasonable that both Sstr and Sseq should follow an extreme value distribution. However, this is not a trivial result, as the scores are not independent, random variables whose maximum must follow such a distribution.
Relationship Between Sequence Comparison and Structure Comparison. Having derived sequence and structure significance scores by using all-vs.-all comparisons on the same database of 941 sequences and structures, we were in a position to compare directly structure and sequence significance scores. Fig. 6 shows such a comparison for the 2,107 pairs of proteins in our data set that are considered to be related evolutionarily according to scop (i.e., they are the true-positives in the same superfamily). The lines at log(Eseq)=–2 and at log(Estr)=–2 divide the 2,107 true-positive pairs among four quadrants, depending on whether their sequence or structure matches are significant, as follows:
Top right (1,204 pairs; nonsignificant sequence match, non-significant structure match). Over half (1,204 of 2,107) of the pairs of domains thought to be evolutionarily related by scop fall into this category of having no significant match, indicating that the combination of manual measures used in scop is more sensitive than either automatic sequence or structure comparison.
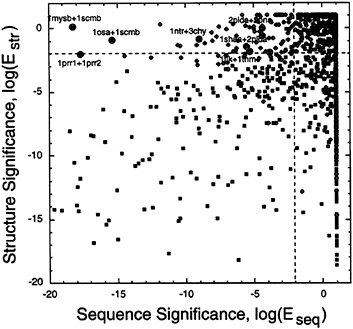
FIG. 6. Comparison of structure significance with sequence significance. Plots of the structure significance. log(Estr), against the sequence significance, log(Eseq). for the 2,107 pairs of proteins judged to be homologous in the scop database (in the same superfamily). Pairs are distinguished by the extent of their structural match, with solid squares used for pairs with N≥70 and unfilled diamonds used for N<70. The horizontal and vertical dashed lines, which divide the figure into four quadrants, are at log(Estr)=–2 and at log(Eseq)=–2, respectively. Both of these thresholds correspond to an E value of 10– 2 and P value of 10–2/941=10–5 so that we judge matches with lower values to be significant at the 1% level.
Lower left (244 pairs; significant sequence match, significant structure match). These pairs are evenly distributed in the lower left quadrant, indicating that the sequence and structure significance scores are on the same scale.
Lower right (576 pairs: nonsignificant sequence match, significant structure match). There are many more pairs with good structure matches but without sequence matches than the converse (sequence match but no structure match). This fact objectively shows how structure is conserved more than sequence in evolution. These 576 pairs are very good test cases for threading algorithms that match a sequence to a structure, and we currently are testing them in this way.
Top left (83 pairs: significant sequence match, nonsignificant structure match). Almost all of the pairs (70 of 83) in this category involve matches with a small number of residues (N< 70). For such short matches, the structures may be deformed and may not match well. There are seven labeled pairs that are exceptions because the match is extensive (N>70), but the pairs structurally are less similar than would be expected from the strong sequence match. These seven exceptions involve 11 coordinate sets. Three of these sets were solved by x-ray crystallography to only medium resolution (>2.9 Å, lmys, 1scm. and 1tlk), five were solved by NMR (1prr. 1ntr, 2pld, 2pna, and 1tnm), and three are high resolution x-ray structures (better than 1.7 Å for losa, 3chy, and 1sha). None of the seven exceptional pairs involved two high resolution structures, and it seems likely that some of the seven exceptions would have had a more significant structural match if both structures in the pair were determined to a high resolution. Furthermore, as determined from consultation of a Database of Macromolecular Movements (ref. 47: see database at http://bioinfo.mbb.yale.edu/MolMovDB), some of the seven exceptions involved proteins that had been solved in different conformational states. In particular, losa, 1mys. and 1scm involved proteins with the highly flexible calmodulin fold. These are clearly examples for which one would expect sequence similarity but structural differences.
DISCUSSION AND CONCLUSION
Summary. We have presented an approach for assessing in a unified statistical framework the significance of a given comparison of proteins, whether involving sequences or structures. For either sequence or structure we fit an extreme-value distribution to the observed distribution obtained from the all-vs.-all comparison of the database (i.e., between pairs of scop domains in different structural classes). For sequence comparison, this extreme-value distribution is as expected: We empirically observed for gapped alignments what Karlin and Altschul (11) derived for ungapped ones. We also gave a simple formula for the E value that is likely to be useful for pairwise comparisons without involving searches of the entire database.
For structure comparison, we found that the score distribution follows an extreme-value distribution when expressed in terms of the structural alignment score Sstr. By using this measure, expressions for statistical significance can be formulated in an almost identical way for structure as they are for sequence. It is important to realize that, although the Sstr is produced naturally by our specific alignment method, it can be calculated from any arbitrary structural alignment. Thus, by using our formulas, a significance can be computed from the results of any structural alignment program. Using the more traditional rms deviation as a score does not lead to as reliable a measure of structural significance.
In connection with this, it is interesting that recent work (39, 43) indicates that the significance statistics based on optimized “sum” scores from dynamic programming (i.e., Smith-Waterman scores, which are essentially sums of BLOSUM matrix
values minus gap penalties) perform much better than those based on the traditional measure of sequence similarity, percentage identity, which parallels the poor performance of our structural alignment statistics based on the traditional rms. It is disconcerting that such well established and intuitive measures such as percentage identity or rms perform so much worse than the statistical measures based on the sequence or structure alignment scores.
Furthermore, it is surprising that over half of the relationships between distant homologues in scop were not statistically significant (at a rate of 1% error per query) using either pure sequence comparison or pure structure comparison. Almost all of the pairs found by sequence comparison were found by structure comparison, but there were many pairs found by structure comparison that were not found by sequence comparison. Overall, structural comparison was able to detect about twice as many of the scop distant homology superfamily pairs as sequence comparison (at the same rate of error).
Future Directions. The approach we have used to derive statistical significance easily could be generalized to other contexts. In particular, it can be adapted to provide significance statistics for threading. We have not presented a detailed examination of the significance values for specific pairs of sequences or structures. Such an examination could prove to be a useful endeavor in the future, particularly if it focused on pairs of proteins with the same fold but insignificant E values and those with different folds but significant E values. These two classes of pairs characterize the twilight zone for structure, which has yet to be described fully.
We thank S.E.Brenner for carefully reading the manuscript and S.E.Brenner and T.Hubbard for providing the pdb40d-1.32 database. M.G. acknowledges the National Science Foundation for support (Grant DB1–9723182), and M.L. acknowledges the Department of Energy (Grant DE-FG03–95ER62135).
1. Rohlf, F. & Slice, D. (1990) Syst. Zool. 39, 40–59.
2. Bookstein, F.L. (1991) Morphometric Tools for Landmark Data (Cambridge Univ. Press, Cambridge, U.K.).
3. Gerstein, M. & Levitt, M. (1998) Protein Sci. 7, 445–456.
4. Subbiah, S., Laurents, D.V. & Levitt, M. (1993) Curr. Biol 3. 141–148.
5. Laurents, D.V., S. Subbiah & Levitt, M. (1994) Protein Sci. 3, 1938–1944.
6. Needleman, S.B. & Wunsch, C.D. (1971) J. Mol. Biol 48, 443–453.
7. Smith, T.F. & Waterman, M.S. (1981) J. Mol. Biol. 147, 195–197.
8. Doolittle, R.F. (1987) Of Urft and Orfs (Univ. Sci. Books, Mill Valley, CA).
9. Gribskov, M. & Devereux, J. (1992) Sequence Analysis Primer (Oxford Univ. Press, New York).
10. Karlin, S. & Altschul, S.F. (1990) Proc. Natl. Acad. Sci. USA 87, 2264–2268.
11. Karlin, S. & Altschul, S.F. (1993) Proc. Natl. Acad. Sci USA 90, 5873–5877.
12. Lipman, D.J. & Pearson, W.R. (1985) Science 227, 1435–1441.
13. Pearson, W.R. (1996) Methods Enzymol. 266, 227–259.
14. Karlin, S., Bucher, P., Brendel, V. & Altschul, S.F. (1991) Annu. Rev. Biophys. Biophys. Chem. 20, 175–203.
15. Altschul, S.F., Boguski, M.S., Gish. W. & Wootton, J.C. (1994) Nat. Gen. 6, 119–129.
16. Bryant, S.H. & Altschul, S.F. (1995) Curr. Opin. Struct. Biol. 5, 236–244.
17. Altschul, S.F. & Gish, W. (1996) Methods Enzymol. 266, 460– 480.
18. Pearson, W.R. (1997) Comput. Appl. Biosci. 13, 325–332.
19. Altschul, S.F., Madden, T.L., Schaffer, A.A., Zhang, J., Zhang, Z., Miller, W. & Lipman, D.J. (1997) Nucleic Acids Res. 25, 3389–3402.
20. Remington, S.J. & Matthews, B.W. (1980) J. Mol. Biol. 140, 77–99.
21. Satow, Y., Cohen, G.H., Padlan, E.A. & Davies, D.R. (1987) J. Mol. Biol. 190, 593–604.
22. Taylor, W.R. & Orengo, C.A. (1989) J. Mol. Biol. 208, 1–22.
23. Artymiuk, P.J., Mitchell, E.M., Rice, D.W. & Willett, P. (1989) J. Inform. Sci. 15, 287–298.
24. Sali, A. & Blundell, T.L. (1990) J. Mol. Biol. 212, 403–428.
25. Vriend, G. & Sander, C (1991) Proteins 11, 52–58.
26. Russell, R.B. & Barton. G.B. (1992) Proteins 14, 309–323.
27. Holm, L. & Sander, C. (1993) J. Mol. Biol. 233, 123–128.
28. Gibrat, J.F., Madej, T. & Bryant, S.H. (1996) Curr. Opin. Struct. Biol. 6, 377–385.
29. Falicov, A. & Cohen, F.E. (1996) J. Mol. Biol. 258, 871–892.
30. Gerstein, M. & Levitt. M. (1996) in Proc. Fourth Int. Conf. on Intell. Sys. Mol. Biol. (American Association for Artificial Intelligence Press. Menlo Park, CA), pp. 59–67.
31. Cohen, G.H. (1998) J. Appl. Crystallography (in press).
32. Holm, L. & Sander, C. (1996) Science 273, 595–602.
33. Bernstein, F. C., Koetzle, T.F., Williams, G.J., Meyer, E.E., Jr., Brice, M.D., Rodgers, J.R., Kennard, O., Shimanouchi, T. & Tasumi. M. (1977) J. Mol. Biol. 112, 535–542.
34. Abola, S.J., Prilusky J & Manning, N.O. (1997) Methods Enzymol. 277, 556–571.
35. Murzin, A., Brenner, S.E., Hubbard, T. & Chothia, C. (1995) J. Mol. Biol. 247, 536–540.
36. Brenner, S., Chothia, C., Hubbard, T.J.P. & Murzin, A.G. (1996) Methods Enzymol. 266, 635–642.
37. Hubbard, T.J. P., Murzin, A.G., Brenner, S.E. & Chothia, C. (1997) Nucleic Acids Res. 25, 236–239.
38. Brenner, S., Hubbard, T., Murzin, A. & Chothia, C. (1995) Nature (London) 378, 140.
39. Brenner, S., Chothia, C., Hubbard, T. (1998) Proc. Natl. Acad. Sci. USA (in press).
40. Pearson, W.R. & Lipman, D.J. (1988) Proc. Natl. Acad. Sci. USA 85, 2444–2448.
41. Henikoff, S. & Henikoff, J.G. (1993) Proc. Natl. Acad. Sci. USA 19, 6565–6572.
42. Levitt, M. & Chothia, C (1976) Nature (London) 261, 552–558.
43. Brenner, S.E. (1996) Ph.D. thesis (Cambridge Univ., Cambridge, U.K.).
44. Kabsch, W. (1976) Acta Cryst. A 32, 922–923.
45. Gerstein, M. & Altman, R. (1995) Computer Applications in the Biosciences 11, 633–644.
46. Gerstein, M. & Altman, R. (1995) J. Mol. Biol. 251, 161–175.
47. Gerstein, M., Lesk, A.M. & Chothia, C. (1994) Biochemistry 33, 6739–6749.








