Proc. Natl. Acad. Sci. USA
Vol. 95, pp. 5921–5928, May 1998
Colloquium Paper
This paper was presented at the colloquium “Computational Biomolecular Science,” organized by Russel Doolittle, J.Andrew McCammon, and Peter G.Wolynes, held September 11–13, 1997, sponsored by the National Academy of Sciences at the Arnold and Mabel Beckman Center in Irvine, CA.
Folding funnels and frustration in off-lattice minimalist protein landscapes
HUGH NYMEYER,* ANGEL E.GARCÌA,†AND JOSÉ NELSON ONUCHIC*‡
*Department of Physics. University of California at San Diego, La Jolla, California 92093–0319; and †Theoretical Biology and Biophysics Group. T10 MS K710. Los Alamos National Laboratory, Los Alamos, New Mexico 87545
ABSTRACT A full quantitative understanding of the protein folding problem is now becoming possible with the help of the energy landscape theory and the protein folding funnel concept. Good folding sequences have a landscape that resembles a rough funnel where the energy bias towards the native state is larger than its ruggedness. Such a landscape leads not only to fast folding and stable native conformations but, more importantly, to sequences that are robust to variations in the protein environment and to sequence mutations. In this paper, an off-lattice model of sequences that fold into a β-barrel native structure is used to describe a framework that can quantitatively distinguish good and bad folders. The two sequences analyzed have the same native structure, but one of them is minimally frustrated whereas the other one exhibits a high degree of frustration.
The ability of proteins to spontaneously fold into unique three-dimensional structures has been amazing scientists for the last few decades. Since the beginning of molecular biology, it has been recognized that proteins are responsible for controlling most functions in living organisms, and that their functionality strongly depends on their shape. How are these biological molecules able to fold? This question has been a puzzle that has not yet been completely answered, but a lot has been learned in recent years.
Energy landscape theory and the funnel concept provide the theoretical framework towards a quantitative understanding of the folding question (1, 2). This alternative view for the folding mechanism replaced the earlier idea that there must exist a single pathway for the folding event with clearly defined chemical intermediates (3, 4). After early seminal contributions by Gō (5), Bryngelson and Worynes realized in the late 1980s (6, 7) that a Kill understanding of folding process would have to involve a global overview of the protein energy landscape. Inspired by this view, Leopold and collaborators (8) introduced the concept of a funnel landscape to describe good folding sequences, a landscape that resembles a partially rough funnel riddled with traps where the protein can transiently reside. In such a funnel there is not a unique folding pathway but a multiplicity of folding routes, all converging towards the native state. Late in the folding process, the protein may be trapped in single pathways but, at this stage, most of the protein has already found its correct folding configuration and the search becomes limited. Several other groups have also participated in the development of this new view that has flourished in the 1990s. Even though the following list is clearly incomplete, in addition to the previous references, the reviews in refs. 9–20 provide a detailed description of the landscape perspective.
The description that follows provides a qualitative understanding of a funnel landscape. Unlike protein-like heteropolymers, random heteropolymers with a tendency to collapse do not have a well defined three-dimensional conformation, but a collection of completely different low energy structures. How can we differentiate between these two kind of sequences? Imagine that we want to discover a sequence that favors a particular structure, called the native structure. A major task at this point is to choose a good reaction coordinate (or order parameter) that measures the similarity between this native structure and any other conformation that may be adopted by this heteropolymer. For lattice minimalist models, a successful coordinate has been Q, the fraction of native tertiary contacts (9, 21–25). For real proteins many other choices are possible and, in most cases, several of them may be necessary, such as fraction of native secondary structures and fraction of native helix caps (1, 26). For our pictorial description we consider only a single Q, varying between 0 and 1 (native structure). As shown in Fig. 1, an ideally designed folding sequence has the energy of its conformations proportional to Q plus some roughness introduced by the nonnative contacts. This correlation between energy and structure not only introduces a bias that favors the native configuration but it also proportionally biases all nonnative conformations, depending on their degree of similarity to the folded state. This correlation is responsible for the funnel shape of the landscape. It is important to notice that even conformations that are completely different but have similar Q (native parts are different) have similar energies. A random sequence would display no such correlation between energy and structure, leading to the rough landscape shown in Fig. 1.
For a protein-like heteropolymer to have the energy proportional to the global order parameter Q, its stabilizing contacts should be equally distributed throughout the entire structure. All native interactions should favor folding, and they should be equally important—i.e., the system exhibits no “frustrated” interactions. This is the ideal situation and, although real proteins may not be so perfect, they clearly need to minimize frustration, an idea proposed by Bryngelson and Wolynes (6). Because proteins are finite systems, if they have a single ground state, there is always a temperature below which this lowest-energy state is stable. This temperature is called the folding temperature, Tf. On the other hand, because the landscape is rugged, there is also a temperature below which the kinetics is controlled by long-lived low-energy traps
©
PNAS is available online at http://www.pnas.org.
| Abbreviations: MD, molecular dynamics; MFPT, mean first passage time; MODC, molecule optimal dynamic coordinates. |
‡ | To whom reprint requests should be addressed, e-mail: jonuchic©ucsd.edu. |
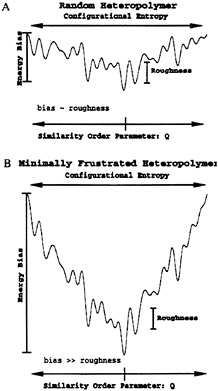
FIG. 1. (a) Energy landscape for a random heteropolymer. Notice that the presence of low energy states that are completely dissimilar is a direct consequence of the small energy bias toward the native state relative to the roughness of the landscape, (b) Funnel-like energy landscape for a minimally frustrated heteropolymer. A clearly favored native structure can be observed in the bottom of this funnel. Because of this dominant bias, all the other low energy states are similar to the native one.
and not by the bias toward the native conformation. This temperature is called the glass temperature, Tg. Minimally frustrated sequences require sufficient bias to have the folding temperature larger than the glass temperature. Therefore this competition between energetic bias toward native conformation and roughness is fundamental in determining the folding mechanism, and it leads to a diversity of folding scenarios that are discussed elsewhere (2). All these ideas are further explored later in this paper.
Sequences with a good folding funnel not only are fast folders at temperatures around the folding temperature but, most importantly, they are robust folders. Robustness is an essential property in biology. Minor variations in the folding environment such as small changes in pH, temperature, denaturant concentration, or, even more interesting, variations because of mutations may affect the native configuration in favor of other low-energy structures. If these other low-energy structures are similar to the folded one, the consequences are minor. The “new” native conformation is very similar to the “old” one. The observed linear dependence between logarithms of the folding/unfolding rates and the folding free energy is a direct indication that this is the case for proteins (27–31). Frustrated sequences, on the other hand, not only are slow folders but also may have the structure of their native state drastically changed under minor variations of the conditions described above.
This diversity of scenarios suggested by the landscape theory and the funnel concept can be observed by simulations of protein folding in computer models. Such simulations can be carried out at many different levels. Ideally they should be at the atomistic level but, because of computational limitations, this approach has limited itself to insights into local aspects of folding (32, 33) and characterizing ensembles of states for unfolded proteins (34–37). Thus minimalist models have been of major importance in our understanding of protein folding. Lattice models have been the center of these studies. They include the simple ones exploited in the early 1980s (5, 38, 39), and more recently in studies by several other groups (8, 12, 15, 16, 20, 40–46). These models have really improved our present understanding of protein folding. Off-lattice models have also been studied (47–54), but little has been done in this landscape context, making this point the focus of this paper.
In addition to simulations, new experiments have been devised to probe early folding events and to explore the landscape of small fast-folding proteins (NMR dynamic spectroscopy, protein engineering, laser-initiated folding, and ultrafast mixing; see, for example, refs. 13, 14, 28, and 55–67, 85). Fast-folding proteins fold on millisecond timescales and have a single domain—i.e., they have a single, well defined, funnel (68). The combination of landscape theory, simulations, and this new family of experiments is providing the basis for a quantitative understanding of the protein folding mechanism.
In this paper we show results for an off-lattice minimalist model where we explore the behavior of two folding sequences with the same native structure, but with one containing a higher degree of frustration. A quantitative landscape framework for quantifying differences between good and bad folding sequences emerges from this comparison. Because most of the existent landscape analysis has been performed for lattice simulations, we present in the next section a summary of some selected results in the lattice to help with our discussion of the off-lattice simulations.
A Summary of Lattice Minimalist Models
Minimalist models of protein folding must contain all the features necessary to understand the folding mechanism. In its simplest version a heteropolymer must contain at least two kinds of monomers whose interactions obey some simplified interaction rule—i.e., heteropolymers may be thought as a necklace of beads of two or more kinds. The question to be answered is what sequences of beads are able to fold into a unique three-dimensional structure. In an effort to mimic the hydrophobic effect, Dill and collaborators (12) proposed the first set of interactions, called the HP model, where the interactions between H (hydrophobic) groups are attractive and all the other ones are zero. Another popular model, which is used for our simulations of 27-mers in a cubic lattice, is the one where the interactions between nearest neighbor beads of the same color are more favorable (strong attractive interaction) than the ones between beads of different colors (weak interaction). Sequences built with two kinds of beads are called two-letter code, three kinds of beads are three-letter codes, and so on.
The low-energy states of heteropolymers composed of random sequences of two or more kinds of beads are collapsed states that try to maximize the number of contacts between beads of the same color. The polymeric nature of the chain, however, prohibits all favorable interactions from being satisfied simultaneously, and some contacts occur between beads of different color. These are clearly frustrated interactions, because the polymer would rather have the maximum number of favorable interactions. Thus different low-energy states may have different structures with a different set of frustrated contacts.
The 27-mer in a cubic lattice is a nice system to simulate because, even though it is not possible to enumerate all its conformations, we can enumerate all its maximally collapsed configurations that are ≈103,000 3×3×3 cubes. The details of these studies can be found elsewhere (see for example, refs. 21, 40, and 69). Investigation of several two-letter or three-letter sequences has taught us that most of the sequences are bad folders, and the good folding ones maximize the number of favorable (strong) native contacts and minimize the number of strong nonnative contacts in unfolded conformations. This strategy maximizes the energy bias toward the native state and at the same time reduces the ruggedness of the landscape, which is mostly determined by the nonnative contacts. As expected, by increasing the number of different kinds of beads, it becomes easier to obtain minimally frustrated sequences.
How can we quantify good folders? The simplest measure, proposed by Bryngelson and Wolynes, is to determine the folding temperature (Tt) and the glass temperature (Tg) of a sequence. The folding temperature can be easily determined, and it has been chosen as the temperature where the native state is occupied 50% of the time. For good folding sequences, the protein-like heteropolymer really behaves as a two-state system—i.e., depending on the temperature, the protein is mostly folded or unfolded, and it is rarely found in some intermediate conformation. In this case, folding is a cooperative sharp first-order-like transition and, therefore, any quantity that is able to distinguish between these two states can be used as a probe of the folding transition. This is not the case for bad folders, where this transition is broad and noncooperative. The discussion in the later section on signatures of folders for our off-lattice models makes this distinction clear.
How is the glass temperature identified? The situation is more problematic, but it can be clearly defined. On the basis of the fact that long-lived traps are the source of the glass transition, Socci and Onuchic provided an operational definition for the glass transition (69). If trapping were not a problem, lowering the temperature should speed up folding because it favors collapse. As the temperature gets lowered, however, there is a point where a substantial slowdown of folding happens. This temperature has been called the kinetic glass transition and is similar to the “thermodynamic” glass transition proposed by Bryngelson and Wolynes (2, 70).
A more sophisticated analysis has been developed recently. It has been shown that for a good folding sequence around Tf, the kinetics of its folding event can be described as a stochastic motion of a few reaction coordinates (or order parameters) on an effective potential defined by the free energy as function of these order parameters (7, 22, 25, 71). In the simplest possible representation, this motion can be assumed to be diffusive, with a configurational diffusion coefficient that incorporates, in an average sense, transient occupation of short-lived traps.§ In this regime the folding event is exponential and the folding time can be estimated by using diffusive reaction rate theory (22, 72). As the temperature gets closer to the glass temperature, this description completely breaks downs. The protein is now being caught in long-lived traps, and the folding kinetics is controlled by the escape time from these traps. Because there is a full ensemble of these times, the kinetics of the folding event becomes nonexponential. This behavior is illustrated in Fig. 2 for a minimally frustrated three-letter code 27-mer.
Clearly, a lot has been learned about the folding mechanism by investigating these lattice models. The question is how can we use these ideas to understand folding of real proteins
|
§ |
Refs. 1 and 71 provide a detailed description for this formalism, including the dependence of the glass transition on the order parameters. |
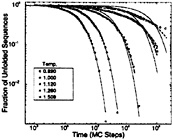
FIG. 2. Log-log plots [as proposed by Frauenfelder and collaborators (84)] of the distribution of folding times for a minimally frustrated three-letter code 27-mer. Time is shown in units of the number of Monte Carlo (MC) steps. The solid lines represent single-exponential fits through the data. Calculations were performed by Socci and collaborators (71). Around Tf=1.509, single exponentials, consistent with the diffusive picture, are a good representation of the data. As the temperatures approach the glass temperature (Tg≈1), escape from long-lived traps starts to control the dynamics, leading to an stretched-exponential (power-law) behavior as expected for glass dynamics. The dashed line at T=1.12 is a double-exponential fit and the dashed ones at T=1.00 and 0.89 are stretched-exponential fits.
beyond a qualitative way. Because lattice models include only tertiary contacts, a quantitative correspondence between these models and real proteins needs to consider additional order parameters, particularly secondary structure formation. An attempt towards this goal has been taken by Onuchic and collaborators (21). Using an analytical theory of helix-coil transition in collapsed heteropolymers to renormalize the secondary structure, they have proposed a law of corresponding states to relate small fast-folding proteins (around 50–60 amino acids) with lattice simulations of a minimally frustrated three-letter code 27-mer.
This correspondence between lattice models and real proteins, however, still is very limited. To explore all possible folding scenarios, there is a need to include these additional reaction coordinates (order parameters) explicitly. The offlattice minimalist models are suited for this task. Simple off-lattice models of proteins can have protein-like shapes with well defined secondary structural elements, as in real proteins. In addition, the continuum character of the configurational variables forces the unique folded state to be one basin of attraction with an entropy proportional to the volume of the basin and not a single conformation.
In this paper we show how the quantitative analysis that has been performed for lattice models to distinguish between good and bad folders can be generalized for off-lattice models. It should become clear how this framework can be used to analyze any other models, including the ones with a full atomistic description. The system analyzed here has the native conformation of a small four-strand β-barrel protein, and it is investigated for two different sequences, a minimally frustrated one and a frustrated one. The comparison between the results obtained for both of them makes apparent how the landscape theory and the funnel concept can be used to quantitatively explore the folding of protein-like heteropolymers and even of real proteins.
The β-Barrel Model
Two sequences, one minimally frustrated and one frustrated, are analyzed. Both of them are Cα protein models, 46 monomers long, which fold into β-barrel-shaped structures but have different potentials. The first sequence, introduced by Honeycutt and Thirumalai (73), is (B)9(N)3(PB)4(N)3(B)9(N)3(PB)5P with monomers that are labeled hydrophobic (B), hydrophilic (P). or neutral (N). This model, which we refer to as the BPN model, has
been studied on several other occasions (10, 49, 50), and similar α-helical models have also been studied (74).
The energetics of the BPN model is described by a potential:
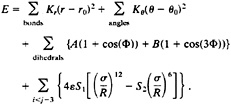
The van der Waals interaction is used to mimic the hydrophobic/hydrophilic character of the different monomer types. To achieve this, the S1 and S2 coefficients are chosen to create attractive interactions between all BB monomer pairs, repulsive ones between all PP and PB pairs, and only excluded volume interactions between the pairs PN, BN, and NN, BB interactions have S1=1 and S2=1, PP and PB interactions have S1=2/3 and S2=–1, and all interactions involving N monomers have S1=1 and S2=0.¶
As becomes clear further on, this model exhibits a high degree of frustration, probably due to the long range and nonspecific character of the interactions. To contrast with the BPN model, we developed a minimally frustrated one. In this model only the interactions between monomers that form native contacts—i.e., contacts found in the native β-barrel— are attractive. By doing that we remove the roughness created by nonnative contacts, recovering nearly ideal folding behavior (see discussion in the introduction). We refer to this model as the Gō-like model because it is similar to the one introduced by Gō and collaborators (76).||
To construct the Gō-like model, we take a quenched structure from the BPN model and identify all contacts of the type i,j >i+3 within a distance of 1.167σ. This produces 47 pairs of monomers distributed mainly between the B-monomers (see Fig. 3); several of the monomers in the turns and in one end have no contacts. All attractive van der Waals interactions between monomers are turned off except for these 47 pairs. All other pairs have only the repulsive 1/r12 term, responsible for excluded volume. The native pairs have an attractive interaction with a well depth of ε and an energy minimum at 1.2σ. This choice of interactions results in only minor differences between the ground state structure and the original quenched model. All bond and angle interactions are the same as in the BPN model. (There are many possible ways to construct a Gō-like model, because the choice of the number of native contacts is somewhat arbitrary. The one adopted by us is reasonable for the purpose of building a minimally frustrated sequence with this native conformation, but it is not unique.)
Already in the development of these potentials, the differing level of robustness of the two models is apparent. Although both models are weakly sensitive to changes in the angle interactions, the BPN model is very sensitive to changes in the
|
¶ |
For both models, we work in reduced units—i.e., all units are defined in terms of the monomer mass M, the bond length σ, and the energy ε. Time is thus measured in units of |
|
|| |
This model is also similar to the associative memory hamiltonian used by Wolynes and collaborators (48) in the limit of a single memory. |
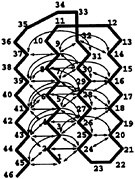
FIG. 3. An illustration of the ground state of the Gō-like model. Each arrow represents an attractive interaction that exists between two monomers. There are 47 of these interactions. The only nonbonded interaction between two monomers without a connecting arrow is a repulsive 1/r12 term responsible for excluded volume.
strength of the dihedral energy interaction, unlike the Gō-like model. Weakening of the intrinsic trans preferences in the BPN model by 25% makes the original native structure unstable at all temperatures. On the other hand, the dihedral preferences in the Gō-like model can be strengthened or weakened while maintaining the same ground state structure. Even total elimination of the backbone rotamer preferences (A=0.0ε and B=0.2ε), adopted by us in this paper, reduces the stability by only 36%, leaving a wide temperature window between Tf and Tg.
Signatures of Good and Bad Folders
Thermodynamics. The first clear indication of the different degrees of frustration between these models comes from analyzing their thermodynamic properties. Similar to what is observed in lattice simulations (1, 71), minimally frustrated systems are characterized by equivalent folding pathways, and such systems have cooperative folding transitions.
Figs. 4 and 5 show the specific heat and the degree of folding
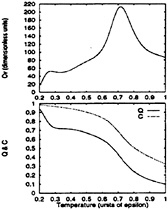
FIG. 4. The specific heat, Cv, of the BPN model (Upper) is contrasted with the collapse and folding denaturation curves (Lower). Compared to the minimally frustrated Gō-like model (see Fig. 5), it shows a reduced level of cooperativity. Notice that collapse occurs prior to folding and that, even at the lowest temperature, the number of native contacts is far from maximal. Reliable sampling could not be performed below 0.4ε because at these temperatures the kinetics is controlled by escape from long-lived traps. In particular, the lowest bump in the specific heat is partially an artifact of the low T sampling.
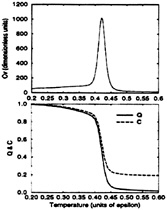
FIG. 5. The specific heat. Cv, of the Gō-like model versus temperature (Upper) is contrasted with the mean values of Q and C versus temperature (Lower). Notice the simultaneity of the collapse and folding events as well as the high degree of cooperativity of the folding transition.
(Q) and collapse (C) order parameters as a function of temperature for both models. The difference in folding cooperativity between them is noticeable. The BPN model has a broad transition region centered at Tc≈0.72ε that is mainly a collapse transition, although the collapsed structures are rather restricted in their conformations. Nearly all the collapsed structures have a four-stranded topology like the ground state. This similarity is reflected in the increase in the folding order parameter simultaneously with the collapsed one. Fig. 6 provides strong evidence that most of the entropy is lost upon collapse. Even though states ≈70% similar to the native one are formed below Tc, the native state itself is not populated until well below this temperature. The temperature at which this occurs is not known exactly because it is below
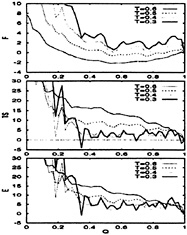
FIG. 6. The thermodynamic functions plotted as a function of the folding order parameter, Q, for the BPN model. F is the free energy, TS is the temperature times the entropy, and E is the energy. The temperatures are measured in units of ε(0.6ε is just below the collapse temperature). All curves are in units of kBT for and are shifted relative to the native state. The lack of an energy bias toward the native state is apparent. The entropy plots also illustrate the onset of glassy behavior at temperatures below 0.5ε (model runs out of entropy at Q≈0.3). At these low temperatures, the dynamics becomes controlled by the escape time from long-lived traps.
T=0.4ε, temperatures where our sampling is not reliable. Notice from Fig. 6 that for temperatures below 0.5ε, this model “runs out” of entropy at Q≈0.3, indicating that its kinetics is now controlled by escape from long-lived low-energy traps (glassy regime). The structural properties of these low-energy structures is discussed in the subsection on the ground state.
In contrast to the BPN model, the Gō-like model shows a single sharp peak for the specific heat centered at 0.42ε. This “latent heat” coincides with increases in Q and C, thus collapse and folding occur simultaneously at this temperature.
Even though several order parameters can monitor collapse and folding [for example, rms deviation from the native conformation, principal component analysis coordinates (77, 78), radius of gyration, secondary structure measures, and contact measures], in all our analysis C and Q are used to probe collapse and folding, respectively. Both of them have been normalized to 1 (relative to the maximum number of contacts in the quenched native configuration). (Of course this means that there are a few states with C>1.) For the purpose of calculating Q or C, we define contacts to exist between any two monomers with indices i and j>i+3 that are within 1.8σ of each other, even though when we determined the “native” contacts for the native structure a shorter cutoff is used. This flexibility allows the native contacts to fluctuate slightly. For the BPN model, we used a cutoff of 1.2ε to define native contacts, which are exactly the attractive ones in the Gō-like model. The details of our results are relatively insensitive to the choice of cutoff for classifying contacts as native.
The thermodynamic functions for both models are plotted versus Q in Figs. 6 and 7. The curves have been shifted to have the energy, entropy, and free energy equal to zero at the native state. The Gō-like model shows a very good funnel: the energy and entropy increase smoothly with Q. This behavior, as expected from landscape theory (1, 6–8), has also been observed in lattice simulations (22, 71). The individual energy and entropy terms are very large, around 10 to 100 kBT, but they almost cancel each other, yielding a much smaller residual free energy [recall that our potentials already renormalize the effect of the solvent (2)] and, as in lattice models, a small free energy barrier of ≈3kBTf exists at the folding temperature. Also, since the low-energy states are all very similar to the
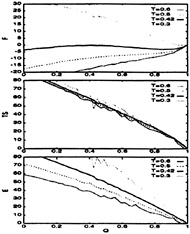
FIG. 7. The thermodynamic functions plotted as a function of the folding order parameter, Q, for the Gō-like model. The temperatures are measured in units of ε. All curves are in units of kBT for and are shifted relative to the native state. Notice that, even for temperatures far below the folding temperature, this model does not “run out” of entropy, indicating the presence of a very good funnel as expected for minimally frustrated systems.
native configuration (Q≈1), this system is very robust and therefore, as discussed in the introduction, insensitive to reasonable changes in the environment (changes in temperature or changes that affect the potential) and mutations.
The behavior of the BPN model (Fig. 6) differs sharply from that of the Gō-like model. The free energy plots indicate a noncooperative second-order-like collapse transition near Tc (0.72ε) with little preference among collapsed structures. The native structure is selected from a large ensemble of dissimilar low-energy structures. Most of the energy gain is used upon collapse, leaving almost nothing to bias the search among collapsed states toward the native configuration. As discussed above, the entropy decreases sharply for states with Q>0.3 for temperatures just below the collapse temperature (around 0.5ε). This entropy crisis heralds the onset of a glassy dynamics that is controlled by escape from long-lived low-energy traps. This glassy behavior is supported by three other effects that become prominent near and below this temperature: a rapid increase in the folding time as the temperature is reduced, the existence of nonexponential relaxation, and the occurrence of specific folding trajectories that are unrelated to the underlying free energy surface as plotted versus a few order parameters. Also, because low energy states may be so dissimilar, this model shows no robustness. Minor changes in the environment and mutations may cause dramatic changes in the structure of the native state (see further discussion in the next two subsections).
Sampling for the determination of the thermodynamic behavior is done using the AMBER (79) program. Molecular dynamics (MD) simulations are performed at constant temperature (80) with a coupling time of 0.1τ and a time step of 0.005τ. Samples taken at several temperatures are combined by using multiple histograms (81). Simulations are done at various temperatures ranging from 0.02ε to 1.2ε. Each temperature simulation is preceded by a 2-million-step equilibration that starts from the final conformation of the previous higher temperature simulation. At each temperature 4,000 configurations are collected.
Kinetics. To fully explore the dynamics of the folding event, a series of folding simulations is performed for both models at different temperatures. MD simulations are done using a leap-frog Langevin integrator (adapted from ref. 82). We do measurements of kinetic quantities with a γ of 0.2τ–1, which is a factor of 10 larger than the measured value for amino acids in water (83). We do not believe the use of a lower friction constant will qualitatively change our results, although folding timescales are probably decreased by a factor of 10. Simulations of the Gō-like model for different values of the friction constant show a folding rate that varies linearly for γ greater than 2.0τ–1, and this variation appears to be temperature independent. No appreciable difference in folding behavior is noticed for the different values of γ. The same dependence is also observed for the BPN model (72).
On the order of 100 simulations are performed at each temperature. Each simulation is preceded by 200,000 simulation steps at 1.6ε to unfold and randomize the system. The final coordinates and velocities of this simulation are used as the starting point for the folding simulations. Q is calculated for every tenth structure, and the simulation is halted when a native structure with Q=1 is reached. The length of the folding run is used to calculate the mean first passage time (MFPT) for each temperature. The MFPT times increase rapidly at low and high values of temperature. In the BPN model, the minimum MFPT is about 900τ and occurs at 0.6ε. In the Gō-like model, the minimum MFPT is about 100τ and occurs at 0.2ε.
The increase in the folding rate at low and high temperatures is a prediction of the energy landscape theory (2, 7). As discussed in the preceding section and ref. 22, the increase in the MFPT at high temperatures is caused by the growth of the
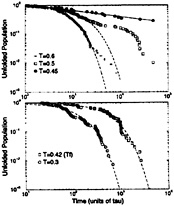
FIG. 8. Log-log plots of the unfolded population as a function of time for the BPN model (Upper) and the Gō-like model (Lower). The dashed lines are exponential fits to the data, and the single solid line is a power-law fit for the BPN model. From Upper, we can notice that the BPN model starts to become nonexponential at temperatures just below collapse (around T=0.6ε). Deviations from single-exponential behavior are caused by a few deep traps with different escape times. Around this temperature, the kinetics is roughly bi-exponential. As the temperature gets lower, the number of these low-energy traps increases substantially, leading to the power-law decay. The onset of nonexponential kinetics in the Gō-like model does not occur until temperatures much lower than the folding temperature (around T = 0.1ε). All simulations are truncated at 50,000 τ.
folding barrier, whereas the increase at low temperatures (before the glass transition) is due to changes in the prefactor of the folding rate, which depends on a configurational diffusion coefficient that averages the effect of short-lived traps.
Similar to lattice models (see the preceding section and ref. 69), a simple way to estimate the glass transition is to use the operational definition of a kinetic glass transition temperature Tg, the temperature at which the MFPT for folding has fallen to 1% of its maximal value. The approximate value of Tg for the BPN model is 0.4ε, and for the Gō-like model it is 0.05ε.** This gives for the two models a Tf/Tg ratio of about 0.9 and 8. respectively. These ratios place the BPN and Gō-like models squarely in the groups of strongly and minimally frustrated systems.
A hallmark of glassy dynamics is nonexponential relaxation. As in Fig. 2, Fig. 8 shows log-log plots of the unfolded population as a function of time for both sequences. In these plots, an exponentially decaying population falls sharply, whereas glassy dynamics exhibits a power-law (or stretched exponential) decay (71, 84). The BPN model starts to deviate from exponential folding around 0.6ε, where the decay is bi-exponential. This is evidence that the system is starting to be trapped in nonnative conformations. At 0.45ε there is a continuum of folding times, controlled by the escape times from a large ensemble of long-lived low-energy traps. This is reflected in a power-law decay with folding times ranging from 500τ to at least 50,000τ, the time limit for individual folding simulations. The second relaxation time, at temperatures where the kinetics is roughly bi-exponential, is most likely caused by a trap in which the first completely hydrophobic strand is bent backwards to contact itself. Although there are several unfavorable dihedrals in this conformation, the large number of BB contacts makes it an exceptionally low-energy trap. On the other hand, the Gō-like model decay can be fit by
|
** |
The ruggedness for the Gō-like model is very small because the energy is roughly proportional to Q. This is apparent from Fig. 7, where the entropy as a function of Q is almost temperature independent. |
a single exponential for temperatures much lower than the folding temperature, all the way down to ≈0.1ε. Therefore, no long-lived traps exists for the relevant temperatures around Tf. The lack of folding events in either system within the first 10–20τ is due to the intrinsic collapse time; systems that fold in this time are collapsing directly into the native structure.
Single folding runs of the BPN model (T≈0.5ε) show long-lived traps that are not visible from plots of the potential of mean force. These trapped trajectories individually show little relation to this effective potential. This behavior becomes prominent near and below Tg because the folding kinetics is then controlled by escape from low-energy long-lived traps.
The Nature of the Ground State. The inherent frustration of the BPN model compared to the Gō-like one can be visualized by measuring the occupation of the different collapsed states. Using MD trajectories of both models, we perform a cluster analysis of the collapsed states in terms of collective motions that best (in a least-square sense) represent the system fluctuations. These coordinates are called molecule optimal dynamic coordinates (MODC) (77, 78). The MODCs are obtained by diagonalizing the covariance matrix of selected dynamic variables (in our case, the Cartesian coordinates for the sequence beads). The largest eigenvalue MODC best describes the atomic fluctuations and, in this case, is sufficient to differentiate the various long-lived low-energy traps.
In Fig. 9 Upper, a low temperature trajectory of the BPN model is plotted, using the two primary MODCs for this trajectory. Fig. 9 Lower shows the free energy as a function of the primary MODC. Superimposed in Lower is the free energy of the Go-like model, when the same MODCs are used, showing that only the native cluster is occupied. The Gō-like model trajectory, not shown here, occupies only the native cluster instead of the ensemble of different structures occupied by the BPN one.
Notice that each cluster does not necessarily correspond to a single structure. The rms deviation between structures in different clusters is about 1σ and within a single cluster is less than 1/2σ, whereas crystallographic structures of proteins have backbone rms deviations of about 1/3 the typical Cα–Cα distance—i.e., 1/3σ. Also, structures in different clusters have different packing arrangements of the hydrophobic monomers. Therefore, each cluster corresponds to one or a few different packing arrangements. Most differ by a combined longitudinal translation and 180° rotation of one or more of the
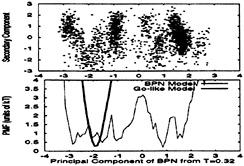
FIG. 9. Cluster analysis of a low temperature trajectory (T≈ 0.32ε) for both models. Upper plots a trajectory for the BPN model as function of the first two MODCs, and it shows that multiple clusters are often occupied. A trajectory for the Gō-like model, not shown here, mostly occupies the native cluster. Supporting these observations, Lower shows the potential of mean force (PMF) for both models as a function of the first MODC. Each minimum corresponds to a different cluster. While the PMF for the BPN model has several low-energy minima, the Gō-like PMF has a single, well-defined, minimum at the native cluster.
strands, and inteconversion among them involves “reptation-like” moves (53).
Concluding Remarks
A framework based on the energy landscape theory and the funnel concept, which is able to quantitatively estimate the degree of frustration of folding sequences, has been presented. Thermodynamic and kinetic measures are used to distinguish between good folders (minimally frustrated) and bad folders (frustrated). Good folding sequences have a weakly rugged funnel-like landscape with low energy states that have structurally similar configurations. The folding kinetics is exponential for temperatures around Tf, and the system is very robust to reasonable changes in the environment and mutations. The situation reverses for frustrated sequences. The landscape is rugged and the low-energy states are dissimilar. Around Tf, the kinetics is controlled by escape from different low-energy traps and therefore is nonexponential. The robustness observed for good folding sequences becomes nonexistent.
Also, a comparison between two sequences that fold into the same native conformation, one frustrated and one minimally frustrated, has been presented as an application of this framework. Notice, however, that the landscape theory predicts a diversity of folding scenarios that cannot be discussed by a single example. Even though different order parameters may be necessary to describe different systems and their respective folding scenarios, this framework will apply for all of them. By departing from the minimalist lattice models and moving to off-lattice ones, we can now develop a much richer collection of folding models and understand the folding conditions for each of them. In addition, this framework is not limited to minimalist models. It can be applied for folding of proteins at full atomistic representation. At this level the kinetic data will be very limited, but the thermodynamic analysis alone is already very informative. By comparing these results with the ones obtained for the minimalist models, we should be able to identify the possible folding scenarios and quantitatively understand the folding mechanism for real proteins at an atomic resolution.
We thank Nick Socci, Gerhard Hummer, Jorge Chahine, Peter Wolynes, Joan Shea, and Charlie Brooks for helpful discussions. This work was supported by the National Science Foundation (Grant MCB-9603839). It was also partially supported by Los Alamos/ University of California directed research and development (UCDRD) funds and by molecular biophysics training grant (NIH T32 GN08326) for H.N.
1. Onuchic, J.N., Luthey-Schulten, Z. & Wolynes, P.G. (1997) Annu. Rev. Phys. Chem. 48, 545–600.
2. Bryngelson, J.D., Onuchic, J.N., Socci, N.D. & Wolynes, P.G. (1995) Proteins Struct. Funct. Genet. 21, 167–195.
3. Englander, S.W. & Mayne, L. (1992) Annu. Rev. Biophys. Biomol. Struct. 21, 243–265.
4. Kim, P.S. & Baldwin, R.L. (1990) Annu. Rev. Biochem. 59, 631–660.
5. Gō, N. (1983) J. Stat. Phys. 30, 413–423.
6. Bryngelson, J.D. & Wolynes, P.G. (1987) Proc. Natl. Acad. Sci, USA 84, 7524–7528.
7. Bryngelson, J.D. & Wolynes, P.G. (1989) J. Phys. Chem. 93, 6902–6915.
8. Leopold, P.E., Montal, M. & Onuchic, J.N. (1992) Proc. Natl. Acad. Sci. USA 89, 8721–8725.
9. Dill, K.A. & Chan, H.S. (1997) Natl. Struct. Biol. 4, 10–19.
10. Guo, Z.Y. & Thirumalai, D. (1995) Biopolymers 36, 83–102.
11. Garel, T., Orland, H. & Thirumalai, D. (1996) in Recent Developments in Theoretical Studies of Proteins, ed. Elber.R. (World Scientific, Singapore), pp. 197–268.
12. Dill, K.A., Bromberg, S., Yue, K., Fiebig, K.M., Yee, D.P., Thomas, P.D. & Chan, H.S. (1995) Protein Sci. 4, 561–602.
13. Fersht, A.R. (1997) Curr. Opin. Struct. Biol. 7, 3–9.
14. Eaton, W.A., Munoz, V., Thompson, P., Chan, C.K. & Hofrichter, J. (1997) Curr. Opin. Struct. Biol. 7, 10–14.
15. Mirny, L.A., Abkevich, V. & Shakhnovich, E.I. (1996) Folding Design 1, 103–116.
16. Sail, A., Shakhnovich, E. & Karplus, M. (1994) J. Mol. Biol. 235, 1614–1636.
17. Schcraga, H.A. (1992) Protein Sci. 1, 691–693.
18. Honig, B. & Cohen, F.E. (1996) Folding Design 1, R17–R20.
19. Zwanzig, R. (1995) Proc. Natl. Acad. Sci. USA 92, 9801–9804.
20. Pande, V.S., Grosberg, A.Y. & Tanaka, T. (1994) Proc. Natl. Acad. Sci. USA 91, 12972–12975.
21. Onuchic, J.N., Wolynes, P.G., Luthey-Schulten, Z. & Socci, N.D. (1995) Proc. Natl. Acad. Sci. USA 92, 3626–3630.
22. Socci, N.D., Onuchic, J.N. & Wolynes, P.G. (1996) J. Chem. Phys. 104, 5860–5868.
23. Socci, N.D., Nymeyer, H. & Wolynes, P.G. (1997) Physica D 107, 366–382.
24. Guo, Z., Brooks, C. & Bockzo, E. (1997) Proc. Natl. Acad. Sci. USA 94, 10161–10166.
25. Plotkin, S.S. & Wolynes, P.G. (1998) Phys. Rev. Lett., in press.
26. Saven, J.G. & Wolynes, P.G. (1996) J. Mol. Biol. 257, 199–216.
27. Wolynes, P.G., Schulten, Z.L. & Onuchic, J. (1996) Chem. Biol. 3, 415–432.
28. Riddle, D.S., Santiago, J.V., Bray, S.T., Doshi, N., Grantcharova, V., Yi, Q. & Baker, D. (1997) Nat. Struct. Biol. 4, 805–809.
29. Scalley, M.L. & Baker, D. (1997) Proc. Natl. Acad. Sci. USA 494, 10636–10640.
30. Mines, G.A., Pascher, T., Lee, S.C., Winkler, J.R. & Gray, H. (1996) Chem. Biol. 3, 491–497.
31. Itzhaki, L.S., Otzen, D.E. & Fersht, A.R. (1995) J. Mol. Biol. 254, 260–288.
32. Hirst, J.D. & Brooks, C.L. (1995) Biochemistry 34, 7614–7621.
33. Simmerling, C. & Elber, R. (1994) J. Am. Chem. Soc. 116, 2534–2547.
34. Boczko, E.M. & Brooks, C.L. (1995) Science 269, 393–396.
35. Daggett, V. & Levitt, M. (1993) J. Mol. Biol. 232, 600–619.
36. Hünenberger, P.H., Mark, A.E. & van Gunsteren, W.F. (1995) Proteins 21, 196–213.
37. Hansmann, U.H.E. & Okamoto, Y. (1993) J. Comput. Chem. 14, 1333–1338.
38. Miyazawa, S. & Jernigan, R.L. (1985) Macromolecules 218, 534–552.
39. Covell, D.G. & Jernigan, R.L. (1990) Biochemistry 29, 3287– 3294
40. Socci, N.D. & Onuchic, J.N. (1995) J. Chem. Phys. 103, 4732– 4744.
41. Hao, M.-H. & Scheraga, H.A. (1994) J. Phys. Chem. 98, 4940– 4948.
42. Camacho, C.J. & Thirumalai, D. (1993) Phys. Rev. Lett. 71, 2505–2508.
43. Govindarajan, S. & Goldstein, R.A. (1996) Proc. Natl. Acad. Sci. USA 93, 3341–3345.
44. Reva, B.A., Finkelstein, A.V., Rykunov, D.S. & Olson, A.J. (1996) Proteins 26, 1–8.
45. de Araújo, A.F.P. & Pochapsky, T.C. (1996) Folding Design 1, 299–314.
46. Shrivastava, I., Vishveshwara, S., Cieplak, M., Maritan, A. & Banavar, J.R. (1995) Proc. Natl. Acad. Sci. USA 92, 9206–9209.
47. Levitt, M. & Warshel, A. (1975) Nature (London) 253, 694–698.
48. Friedrichs, M.S., Goldstein, R.A. & Wolynes, P.G. (1991) J. Mol. Biol. 222, 1013–1034.
49. Guo, Z., Thirumalai, D. & Honeycutt, J.D. (1992) J. Chem. Phys. 97, 525–535.
50. Guo, Z. & Brooks. C.L., III. (1997) Biopolymers 42, 745–757.
51. Sasai, M. (1995) Proc. Natl. Acad. Sci. USA 92, 8438–8442.
52. Irbäck, A. & Potthast, F. (1995) J. Chem. Phys. 103, 10298–10305.
53. Berry, R.S., Elmaci, N., Rose, J.P. & Vekhter, B. (1997) Proc. Natl. Acad. Sci. USA 94, 9520–9524.
54. Nelson, E.D., Eyck, L.T. & Onuchic, J.N. (1997) Phys. Rev. Lett. 79, 3534–3537.
55. Burton, R.E., Huang, G.S., Daugherty, M.A., Calderone, T.L. & Oas, T.G. (1997) Nat. Struct. Biol. 4, 305–310.
56. Elove, G.A., Bhuyan, A.K. & Roder, H. (1994) Biochemistry 33, 6925–6935.
57. Jennings, P. & Wright, P. (1993) Science 262, 892–896.
58. Plaxco, K.W. & Dobson, C.M. (1996) Curr. Opin. Struct. Biol. 6, 630–636.
59. López-Hernández, E. & Serrano, L. (1996) Folding Design 1, 43–55.
60. Sosnick, T.R., Mayne, L. & Englander, S.W. (1996) Proteins 24, 413–426.
61. Ballew, R.M., Sabelko, J. & Gruebele, M. (1996) Nat. Struct. Biol. 3, 923–926.
62. Phillips, C M., Mizutani, Y. & Hochstrasser, R.M. (1995) Proc. Natl. Acad. Sci. USA 92, 7292–7296.
63. Williams, S., Causgrove, T.P., Gilmanshin, R., Fang, K.S., Callender, R.H., Woodruff, W.R & Dyer, R.B. (1996) Biochemistry 35, 691–697.
64. Mathews, C.R. (1993) Annu. Rev. Biochem. 62, 653–683.
65. Cordes, M.H.J., Davidson, A.R. & Sauer, R.T. (1996) Curr. Opin. Struct. Biol. 6, 3–10.
66. Raschke, T.M. & Marqusee, S. (1997) Nat. Struct. Biol. 4, 298–304.
67. Lin, L., Pinker, R.J., Forde, K., Rose, G.D. & Kallenbach, N.R. (1994) Nat. Struct. Biol. 1, 447–452.
68. Wolynes, P.G., Onuchic, J.N. & Thirumalai, D. (1995) Science 267, 1619–1620.
69. Socci, N.D. & Onuchic, J.N. (1994) J. Chem. Phys. 101, 1519– 1528.
70. Wang, J., Onuchic, J. & Wolynes, P.G. (1996) Phys. Rev. Lett. 76, 4861–4864.
71. Socci, N.D., Onuchic, J.N. & Wolynes, P.G. (1998) Proteins Struct. Funct. Genet., in press.
72. Klimov, D.K. & Thirumalai, D. (1997) Phys. Rev. Lett. 79, 317–320.
73. Honeycutt, J.D. & Thirumalai, D. (1992) Biopolymers 32, 695– 709.
74. Guo, Z. & Thirumalai, D. (1996) J. Mol. Biol. 263, 323–343.
75. Ryckaert, J.P., Ciccotti, G. & Berendsen, H.J.C (1977) J. Comput. Physiol. 23, 327–341.
76. Ueda, Y., Taketomi, H. & Gō, N. (1978) Biopolymers 17, 1531–1548.
77. García, A.E. (1992) Phys. Rev. Lett. 68, 2696–2699.
78. García, A.E., Hummer. G., Blumfield, R. & Krumhansl, J.A. (1997) Physica D 107, 225–239.
79. Pearlman, D.A., Case, D.A., Caldwell, J.W., Ross, W.S., Cheatham, T.E., III, Ferguson, D.M., Seibel, G.L., Singh, U.C., Weiner, P. & Kollman, P. (1995) AMBER, version 4.1 (Univ. of California, San Francisco).
80. Berendsen, H.J. C., Postma, J.P.M., van Gunsteren, W.F., DiNola, A. & Haak, J.R. (1984) J. Chem. Phys. 81, 3684–3690.
81. Ferrenberg, A.M. & Swendsen, R.H. (1989) Phys. Rev. Lett. 63, 1195–1198.
82. van Gunsteren, W.F. & Berendsen, H.J.C. (1982) Mol. Phys. 45, 637–647.
83. Lide, D.R., ed. (1994) Handbook of Chemistry and Physics (CRC, Boca Raton, FL), 75th Ed., pp. 6–253.
84. Frauenfelder, H., Parak, F. & Young, R.D. (1988) Annu. Rev. Biophys. Biophys. Chem. 17, 451–479.
85. Grantcharova, V. & Baker, D. (1997) Biochemistry 36, 15685– 15692.








